
 , 周杰2, 王健1
, 周杰2, 王健1 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 中山大学 生物医学工程学院, 广东 广州 510275
收稿日期:2021-08-19
基金项目:国家自然科学基金资助项目(51775097)。
作者简介:孙尧(1993-), 女, 辽宁鞍山人, 东北大学博士研究生;
孙志礼(1957-), 男, 山东巨野人, 东北大学教授, 博士生导师。
摘要:多状态多阶段任务系统常见于关键性系统, 其可靠性要求较高而其可靠度计算又相对困难.为实现该类系统可靠度的精准预测, 研究了部件劣化符合马尔科夫过程的多状态多阶段任务系统的可靠度理论计算方法.首先, 基于工作效率与需求的关系对该类系统可靠度进行了界定.其次, 依据条件概率理论, 建立了多阶段任务系统任务成功完成的概率公式.基于此, 根据部件劣化的马尔科夫性及部件状态的跨阶段依赖性, 推导了多状态多阶段任务系统的可靠度理论计算方法, 并提出一种快速穷举部件状态组合的方法用于提高该计算方法的计算效率.最后, 通过与蒙特卡罗模拟方法对比, 验证了推导的可靠度理论计算方法的准确性与计算的有效性.
关键词:马尔科夫过程多状态多阶段任务系统条件概率系统可靠度蒙特卡罗模拟
Theoretical Calculation Method of Reliability for Multi-state Phased-Mission Systems
SUN Yao1, SUN Zhi-li1

 , ZHOU Jie2, WANG Jian1
, ZHOU Jie2, WANG Jian1 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. School of Biomedical Engineering, Sun Yat-sen University, Guangzhou 510275, China
Corresponding author: SUN Zhi-li, E-mail: zhlsun@mail.neu.edu.cn.
Abstract: Multi-state phased-mission systems(MS-PMSs)are often used in critical systems and require high reliability. However, their reliability calculation is relatively difficult. In order to make an accurate prediction of reliability for such systems, the theoretical calculation method of reliability for MS-PMSs with component degradation conforming to Markov process is studied. First, the reliability for such systems is defined based on the relationship between working efficiency and demand. Then, according to the conditional probabilistic theory, the probability of mission success is formulated. On the basis, according to the Markov property of component degradation and the dependence on component states among phases, the theoretical calculation method of reliability for MS-PMSs is derived, and a fast exhaustion method of component state combination is proposed to improve the computational efficiency of the calculation method. Finally, by comparing with the Monte-Carlo simulation method, the accuracy and computational effectiveness of the derived theoretical calculation method are verified.
Key words: Markov processmulti-state phased-mission system(MS-PMS)conditional probabilitysystem reliabilityMonte-Carlo simulation
随着科技发展及人们需求的提高, 系统逐渐复杂化, 表现为系统的多状态特性及任务的多阶段性, 此类系统称为多状态多阶段任务系统(multi-state phased-mission system, MS-PMS)[1-2].MS-PMS广泛存在于航空航天、通信、电力等领域, 且经常被配置到关键应用中, 一旦发生故障, 会造成很大的经济损失甚至人员伤亡.因此, 对该类系统的任务可靠度有很高的要求[3].然而, 系统的多状态特性与跨阶段依赖性导致其可靠性计算及评估极其困难.目前, 这方面的研究已成为该领域的热点.
现阶段关于多阶段任务系统(phased-mission system, PMS)的可靠性研究大多针对二态PMS.Xing等[4]针对具有共因故障的PMS提出了一种基于二元决策图的可靠性分析方法.Mo等[5]针对多模式失效的PMS提出一种基于多元决策图的可靠性分析方法.Levitin等[6]提出一种精确评估由二态不可修部件组成的PMS可靠度的方法.
关于PMS可靠性研究的方法大致分为模拟方法与解析方法.与解析方法相比, 模拟方法可用于更一般的系统, 但计算效率明显较低[2].解析方法主要分为两大类: 第1类为组合模型方法[5, 7-9].该类方法可有效处理大规模系统, 但只能用于部件相互独立的情形.第2类为状态空间方法[10-13].该类方法在建立系统动态行为方面具有优势, 但一般只能处理中小规模系统.
随着系统复杂化, 针对多状态系统(multi-state system, MSS)可靠性的研究逐渐广泛[14-16].然而, 关于MS-PMS可靠性的研究还不多见.Shrestha等[17]应用多状态多元决策图评估了MS-PMS的可靠度.Yang等[18]应用加速模拟评估方法对MS-PMS进行了可靠度的估计.Cheng等[19]评估了公共总线性能共享的MS-PMS的可靠性.Yi等[20]通过对通用生成函数方法的扩展, 提出一种多阶段任务的线性滑动窗口系统的可靠性评估方法.可见, 现阶段对MS-PMS可靠度计算主要为基于决策图的分析与蒙特卡罗方法的模拟估计, 以及特殊情形下的MS-PMS可靠性评估.缺少相应的可靠度理论计算方法.
为了进一步研究MS-PMS可靠度的精准计算, 本文推导了部件劣化符合马尔科夫过程的MS-PMS可靠度的理论计算方法, 并提出一种快速穷举部件状态组合的方法用于提高该计算方法的计算效率.通过蒙特卡罗模拟方法验证了该理论计算方法的准确性与计算有效性.该计算方法为复杂MS-PMS的可靠度精准预测提供了理论基础.
1 MS-PMS描述及其可靠的界定1.1 系统描述图 1为本文所研究的MS-PMS的连接结构.
图 1(Fig. 1)
 | 图 1 系统串并联结构Fig.1 System series-parallel structure |
系统含有M个并联子系统, 其中子系统m(m∈{1, …, M})含有xm个部件.所有子系统串联而成整个系统.系统一共含有
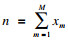
部件状态组合可向量化表示为Y=(Y1, …, Yn).同时, 根据系统结构, 系统工作效率G可表示为
 | (1) |
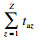
图 2(Fig. 2)
 | 图 2 系统工作效率变化Fig.2 Variation of system working efficiency |
任务可靠意味着任务执行期间任一时刻的系统工作效率都不低于该任务的需求.将任务z可靠记为事件Az.同时, 将任务z结束时刻系统工作效率不低于任务z的需求记为事件A′z.很明显, Az发生, A′z一定发生, 即A′z?Az.再者, 部件在运行过程中逐渐劣化且不进行任何维修活动, 即gi(i∈{1, …, n})在部件运行过程中随机下降.同时, 式(1)为单调不增函数.因此, 系统工作效率在运行中也随机下降.由此可知, A′z发生, Az一定发生, 即Az?A′z.由A′z?Az与Az?A′z可推出Az=A′z.因此, 任务z可靠可以等效表示为G(ta1+…+taz)≥Wz.
MS-PMS可靠即为每个任务均可靠, 即执行到任意时刻都有系统工作效率不低于当前所处任务的需求.将MS-PMS可靠记为事件A, 则
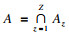
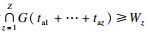
2 MS-PMS可靠度理论计算方法2.1 MS-PMS可靠度理论计算方法的推导事件A发生的概率即MS-PMS的可靠度为
 | (2) |
 | (3) |
假设部件的劣化过程符合齐次马尔科夫过程.记部件i(i∈{1, …, n})的状态转移率矩阵如下:
 | (4) |
将部件i的初始状态记为YiD(YiD∈{0, 1, …, Ki}), 其运行时长为t′时的状态概率向量
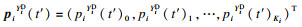
 | (5) |
 | (6) |
 | (7) |
 | (8) |
部件的劣化具有马尔科夫性, 而且部件间的相关性及其他外界因素等不考虑.因此, 基于式(6), 系统由Y(hh)(hh∈{1, …, H})运行taz(z=1, …, Z)时长后转为Y(h)(h∈{1, …, H})的概率如下:
 | (9) |
对于任务1, 初始的部件状态组合为YA1, 则任务1结束时刻部件状态组合为Y(h)(h∈{1, …, H})的概率为
 | (10) |
 | (11) |
 | (12) |
即便确定任务1可靠, 也不能确定在任务2开始时刻的部件状态组合, 而只能确定每种组合的概率.应基于任务1可靠这个先验信息对YA2=Y(h)(h∈{1, …, H})的概率重新分配如下:
 | (13) |
 | (14) |
 | (15) |
同理, 仍要先确定在任务1与2均可靠的条件下, 任务3开始时刻的每种部件状态组合的概率.基于任务1与2可靠这个先验信息对YA3=Y(h)(h∈{1, …, H})的概率重新分配如下:
 | (16) |
 | (17) |
 | (18) |
第1步, 直接按式(10)求得任务1结束时刻的部件状态组合的概率, 进而按式(12)求得任务1可靠度P(A1).
第2步, 对于任务z(z∈{2, …, Z}), 在任务1~z-1均可靠的条件下, 任务z结束时刻部件状态组合为Y(h)(h∈{1, …, H})的概率为
 | (19) |
 | (20) |
 | (21) |
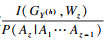
第3步, 将所得的条件概率相乘获得MS-PMS的可靠度.
因为每一个条件概率的求解都是在前一个条件概率基础上的, 必须按P(A1), P(A2|A1), …, P(AZ|A1… AZ-1)顺序依次求解.
2.2 MS-PMS可靠度理论计算的实现推导的MS-PMS可靠度理论计算方法的伪代码如图 3所示.
图 3(Fig. 3)
 | 图 3 MS-PMS可靠度理论计算方法伪代码Fig.3 Pseudocode of the theoretical calculation method of reliability for MS-PMSs |
图中, R[v]表示向量R的第v个元素; R[v, d]表示矩阵R的v行d列元素; le(R)表示向量R的维数; GR(v)表示矩阵R的第v行对应的部件等效状态组合对应的系统工作效率值.矩阵YH表示样本空间YH.YH有n列, 每行按部件顺序排列一种组合, 而行数即为样本空间数目H.
获得样本空间YH的常规方法是多层循环逐个获得部件状态组合(方法二), 该方法运行相对较慢.本文基于每个部件状态重复规律提出一种快速方法(方法一), 可提高MS-PMS可靠度的计算效率.
3 MS-PMS可靠度理论计算方法验证以图 4所示系统为例, 通过与蒙特卡罗模拟方法对比, 验证推导的MS-PMS可靠度理论计算方法的准确性与计算的有效性.
图 4(Fig. 4)
 | 图 4 用于理论计算方法验证的系统Fig.4 System using for the validation of the theoretical calculation method |
部件相关参数如表 1所示.
表 1(Table 1)
| 表 1 用于计算方法验证的系统部件参数 Table 1 Component parameters of the system using for validation of the theoretical calculation method |
假设系统要完成Z=3个任务.任务运行时长依次为分别为4, 3, 4, 任务需求依次为80, 60, 45.MS-PMS可靠度理论计算方法与蒙特卡罗方法的对比结果如图 5和6所示, 其中N为蒙特卡罗方法的模拟次数.
图 5(Fig. 5)
 | 图 5 理论计算方法与蒙特卡罗方法的结果Fig.5 Results of the theoretical calculation method and the Monte-Carlo simulation (a)—N=100;(b)—N=1 000;(c)—N=5 000;(d)—N=10 000. |
图 6(Fig. 6)
 | 图 6 理论计算方法与蒙特卡罗方法的运算时长Fig.6 The computational time of the theoretical calculation method and the Monte-Carlo simulation |
分别分析N为100, 1 000, 5 000及10 000的情形, 且每种情形进行10次模拟.如图 5所示, 随着N逐渐增大, 模拟结果逐渐稳定于理论计算结果.这说明推导的MS-PMS可靠度理论计算方法是准确的.
同时, 由图 5和6可看出, N为100时, 虽然模拟运算时长小于理论计算的运算时长, 但模拟结果波动性很大; N达到5 000时模拟结果与理论计算结果还没达到可接受的吻合, 这时模拟运算时长已大于理论计算的运算时长; N=10 000时, 模拟结果与理论计算结果几乎一致且模拟结果也相对稳定, 但是模拟时长显著大于计算时长.这表明推导的MS-PMS可靠度理论计算方法显著快于蒙特卡罗模拟方法.
此外, 图 6还显示, 相比于方法二, 应用方法一穷举部件状态组合可使理论计算的运算时长缩短约0.04 s, 即方法一可提高该可靠度理论计算方法的计算速度.特别是对于维修策略优化问题, 一般采用智能优化算法(遗传算法、差分进化算法等), 该可靠度要进行多次计算.例如, 种群规模与进化代数均为50, 则要进行50×50=2 500次可靠度计算, 应用方法一比方法二节省约2 500×0.04 s=100 s.因此, 对于维修决策, 快速穷举部件状态组合方法的作用更显著.
基于以上分析, 推导的MS-PMS可靠度理论计算方法不仅是准确的, 而且在计算上也是有效的, 同时提出的快速穷举部件状态组合方法可进一步提高该理论计算方法的运算效率.
4 结论1) 对于蒙特卡罗模拟估计MS-PMS可靠度的方法, 随着模拟次数的增加, 得到的MS-PMS可靠度的模拟值逐渐趋于稳定, 且稳定于用推导的理论计算方法得到的MS-PMS计算结果, 这说明推导的MS-PMS可靠度理论计算方法是准确的.
2) 对于蒙特卡罗方法, 当模拟次数足够使MS-PMS可靠度的模拟值稳定于其理论计算结果时, 其运算时长明显大于理论计算方法的运算时长.这说明推导的MS-PMS可靠度理论计算方法比蒙特卡罗模拟方法运算更快, 在计算上是有效的.
3) 对于推导的MS-PMS可靠度理论计算方法, 分别应用提出的快速方法与常规循环方法来穷举部件状态组合.对比结果表明, 利用提出的快速方法穷举部件状态组合比利用常规循环方法还可进一步加快该方法的运算速度, 使该理论方法在计算上更有效.
参考文献
| [1] | Shrestha A, Xing L, Dai Y. Reliability analysis of multi-state phased-mission systems[C]// Reliability & Maintainability Symposium. Piscataway: IEEE, 2009: 151-156. |
| [2] | Li X Y, Huang H Z, Li Y F, et al. Reliability assessment of multi-state phased mission system with non-repairable multi-state components[J]. Applied Mathematical Modelling, 2018, 61: 181-199. DOI:10.1016/j.apm.2018.04.008 |
| [3] | 鄢民强. 考虑维修性的多阶段任务系统可靠性分析方法研究[D]. 成都: 电子科技大学, 2011. (Yan Min-qiang. Research on reliability analysis method of multi-state phased-mission system considering maintainability[D]. Chengdu: University of Electronic Science and Technology of China, 2011. ) |
| [4] | Xing L D, Levitin G. BDD-based reliability evaluation of phased-mission systems with internal/external common-cause failures[J]. Reliability Engineering & System Safety, 2013, 112: 145-153. |
| [5] | Mo Y C, Xing L D, Dugan J B. MDD-based method for efficient analysis on phased-mission systems with multimode failures[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 44(6): 757-769. |
| [6] | Levitin G. Recursive algorithm for reliability evaluation of non-repairable phased mission systems with binary elements[J]. IEEE Transactions on Reliability, 2012, 61(2): 533-542. DOI:10.1109/TR.2012.2192060 |
| [7] | Tang Z, Dugan J B. BDD-based reliability analysis of phased-mission systems with multimode failures[J]. IEEE Transactions on Reliability, 2006, 55(2): 350-360. DOI:10.1109/TR.2006.874941 |
| [8] | Zang X Y, Wang D Z, Sun H R, et al. A BDD-based algorithm for analysis of multistate systems with multistate components[J]. IEEE Transactions on Computers, 2003, 52(12): 1608-1618. DOI:10.1109/TC.2003.1252856 |
| [9] | Xing L D, Dai Y S. A new decision-diagram-based method for efficient analysis on multistate systems[J]. IEEE Transactions on Dependable & Secure Computing, 2009, 6(3): 161-174. |
| [10] | Wang C N, Xing L D, Levitin G. Competing failure analysis in phased-mission systems with functional dependence in one of phase[J]. Reliability Engineering & System Safety, 2012, 108: 90-99. |
| [11] | Wu X Y, Hillston J. Mission reliability of semi-Markov systems under generalized operational time requirements[J]. Reliability Engineering & System Safety, 2015, 140: 122-129. |
| [12] | Mura I, Bondavalli A. Markov regenerative stochastic Petri nets to model and evaluate phased mission systems dependability[J]. IEEE Transactions on Computers, 2001, 50(12): 1337-1351. DOI:10.1109/TC.2001.970572 |
| [13] | Wang Z K, Zeng S K, Guo J B, et al. A Bayesian network for reliability assessment of man-machine phased-mission system considering the phase dependencies of human cognitive error[J]. Reliability Engineering & System Safety, 2021, 207: 107385. |
| [14] | Ding Y, Lin Y, Peng R, et al. Approximate reliability evaluation of large-scale multi-state series-parallel systems[J]. IEEE Transactions on Reliability, 2019, 68(2): 539-553. DOI:10.1109/TR.2019.2898459 |
| [15] | Bao M, Ding Y, Singh C, et al. A multi-state model for reliability assessment of integrated gas and power systems utilizing universal generating function techniques[J]. IEEE Transactions on Smart Grid, 2019, 10(6): 6271-6283. DOI:10.1109/TSG.2019.2900796 |
| [16] | 刘宇, 李翔宇, 张小虎. 考虑载荷动态分配机制的多状态系统可靠性建模及优化[J]. 机械工程学报, 2016, 52(6): 197-205. (Liu Yu, Li Xiang-yu, Zhang Xiao-hu. Multi-state system reliability modelling and optimization with considering dynamic load distribution mechanism[J]. Journal of Mechanical Engineering, 2016, 52(6): 197-205.) |
| [17] | Shrestha A, Xing L, Dai Y. Reliability analysis of multistate phased-mission systems with unordered and ordered states[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2011, 41(4): 625-636. DOI:10.1109/TSMCA.2010.2089513 |
| [18] | Yang H J, Lv J W, Xu Y F. An accelerated simulation assessment approach for mission success probability of multi-state phased mission systems[C]//Proceedings of the 32nd Chinese Control and Decision Conference(CCDC). Shenyang: Northeastern University Press, 2020: 3907-3912. |
| [19] | Cheng C, Yang J, Li L. Reliability assessment of multi-state phased mission systems with common bus performance sharing considering transmission loss and performance storage[J]. Reliability Engineering & System Safety, 2020, 199: 106917. |
| [20] | Yi K X, Kou G, Gao K Y, et al. Optimal allocation of multi-state elements in a sliding window system with phased missions[J]. Journal of Risk and Reliability, 2021, 235(1): 50-62. |
| [21] | Li Y F, Peng R. Availability modeling and optimization of dynamic multi-state series-parallel systems with random reconfiguration[J]. Reliability Engineering & System Safety, 2014, 127: 47-57. |
