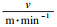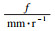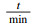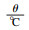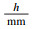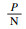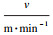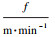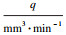黄贤振, 孙良仕, 丁鹏飞, 朱会彬
东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期：2021-07-12
基金项目：国家自然科学基金资助项目(51975110)；“兴辽英才”计划项目(XLYC1907171)；中央高校基本科研业务费专项资金资助项目(N2003005, N21003005)。
作者简介：黄贤振(1982-), 男, 山东定陶人, 东北大学教授, 博士生导师。

摘要：为了保证刀具寿命的同时尽可能地提高加工效率, 对切削参数进行优化至关重要.因此, 建立了车削过程中的刀具磨损模型, 可用于预测多种切削条件下任意时刻的刀具磨损量, 从而推导出刀具寿命模型.考虑不确定性参数对车削加工的影响, 建立了基于可靠性的车削优化模型, 并采用序列优化与可靠性评估方法对优化模型进行求解以获得最优切削参数.最后, 通过实例验证了该方法在高温镍基合金GH4169车削参数优化中的优势和可行性.
关键词：车削加工GH4169刀具磨损序列优化可靠性评估可靠性优化
Optimization of Turning Parameters of GH4169 Based on Reliability
HUANG Xian-zhen, SUN Liang-shi, DING Peng-fei, ZHU Hui-bin
School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: HUANG Xian-zhen, E-mail: xzhhuang@mail.neu.edu.cn.

Abstract: It is critical to optimize the cutting parameters in order to increase the machining efficiency as much as possible while ensuring tool life. Therefore, a model of tool wear in the turning process is established to predict tool wear at any time under various cutting conditions. Thereby, a model of tool life is derived. Considering the influence of uncertain parameters on turning processing, a reliability-based optimization model of turning is established, and the optimization model is solved by the sequential optimization and reliability assessment(SORA)method to obtain the optimal cutting parameters. Finally, an example verifies the advantage and feasibility of this method in the parameter optimization of turning nickel-based superalloy GH4169.
Key words: turning processGH4169tool wearsequential optimizationreliability assessment(SORA)reliability-based optimization
镍基高温合金GH4169是一种在高温条件下具有优良的力学性能、稳定性能和抗疲劳性能的多组元复杂合金, 在航空航天领域应用十分广泛^[1].但是, 材料的难加工性导致了镍基高温合金GH4169的加工效率不高, 刀具也由于磨损严重很容易失效.因此, 在镍基高温合金GH4169的车削过程中, 通过优化切削参数来保证刀具使用寿命、提高加工效率至关重要.
为了延长刀具的使用寿命, 有关刀具磨损的研究一直被人们所关注.Thakur等^[2]和Bhatt等^[3]分别进行了高速车削Inconel 718的实验, 通过观察实验现象, 他们都得到了相同的结论: 硬质合金刀具的主要磨损机理是磨料磨损和粘结磨损.Costes等^[4]在CBN刀具车削Inconel 718的实验中, 发现刀具失效主要是由粘结、扩散和磨料磨损导致的.关于磨损模型的建立, Usui等^[5]以粘结磨损为基础, 建立了刀具磨损的解析模型.Takeyama等^[6]基于刀具与工件间的元素扩散, 建立了一种以扩散磨损理论为基础的数学模型.Luo等^[7]将粘结磨损和扩散磨损结合起来, 提出了一种新的刀具磨损解析模型.
切削参数优化对高效率、高质量加工具有十分重要的意义.因此, 在过去的几十年里, 研究****们为此做出了巨大的努力.Davoodi等^[8]以切削速度和进给速率为切削变量建立了响应面模型, 并使用满意度函数法对刀具寿命和材料去除率进行了多响应优化, 以达到最大的生产效率.Mia等^[9]提出了一种基于田口信噪比的车削优化方法, 并对最小润滑量条件下的车削过程进行了粗糙度、刀具磨损以及材料去除率的参数优化.Selvakumar等^[10]使用基于Box-Behnken设计的响应面法, 根据刀具磨损各变量之间的相互关系和相互作用, 对微车削参数进行了优化.Gupta等^[11]使用粒子群优化技术对钛合金车削加工参数进行了优化, 并观察到优化结果与满意度函数法所获得的结果非常接近.Tian等^[12]提出了一种考虑刀具磨损的切削参数优化方法, 并在算例中得到了验证.
以上研究为刀具磨损分析和车削参数优化奠定了基础, 但是, 对于具有理论基础且考虑切削参数的时变刀具磨损解析模型的研究还很少.除此之外, 在上述车削参数优化的研究中都把加工参数认为是确定的, 而实际上, 由于加工过程中的不确定因素, 加工条件往往不可能被准确地预测, 因此, 加工参数具有不确定性.本文提出了一种考虑不确定性因素的车削参数优化方法.首先, 基于磨损机理, 建立了一种考虑切削参数的时变刀具磨损模型, 从而推导出车削过程中的刀具寿命模型.其次, 建立了基于可靠性的优化模型, 并采用序列优化与可靠性评估(SORA)方法对优化模型进行求解.最后, 通过数值算例说明了该方法在高温镍基合金GH4169车削参数优化中的应用.
1 刀具磨损分析和寿命研究刀具寿命是指在一定的加工条件下, 刀具从开始切削加工到磨损量达到磨钝标准时所经历的时间, 由磨损量进行判定.后刀面磨损是刀具失效的主要形式, 目前也普遍以后刀面平均磨损宽度作为刀具的磨损量, 即后刀面磨损量VB.当VB达到磨钝标准时, 则认为刀具失效, 而刀具恰好失效的时间即为刀具寿命.因此, 在刀具寿命的研究过程中, 刀具磨损的分析极为重要.
刀具磨损是切削加工过程中各种因素协同影响而产生的结果, 主要有粘结磨损、磨粒磨损和扩散磨损等形式.对于涂层硬质合金刀具切削GH4169的加工来讲, 粘结磨损是刀具后刀面产生磨损量的主要机理^[13].从18世纪起, 刀具粘结磨损的研究就被广泛关注^[14], 而在过去****们提出的粘结磨损模型中, Archard所建立的粘结磨损模型更是受到了普遍的认可.该模型如式(1)所示.

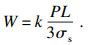(1)

其中: W为粘结磨损量; L为切削长度; P为法向载荷; σ_s为材料的屈服强度; k为磨损系数.
又因L=vt, 其中, v为切削速度, t为切削时间.故单位长度的磨损率为

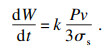(2)

单位时间间隔Δt内, 粘结磨损的变化率dW可根据图 1得到

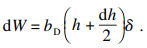(3)

图 1(Fig. 1)

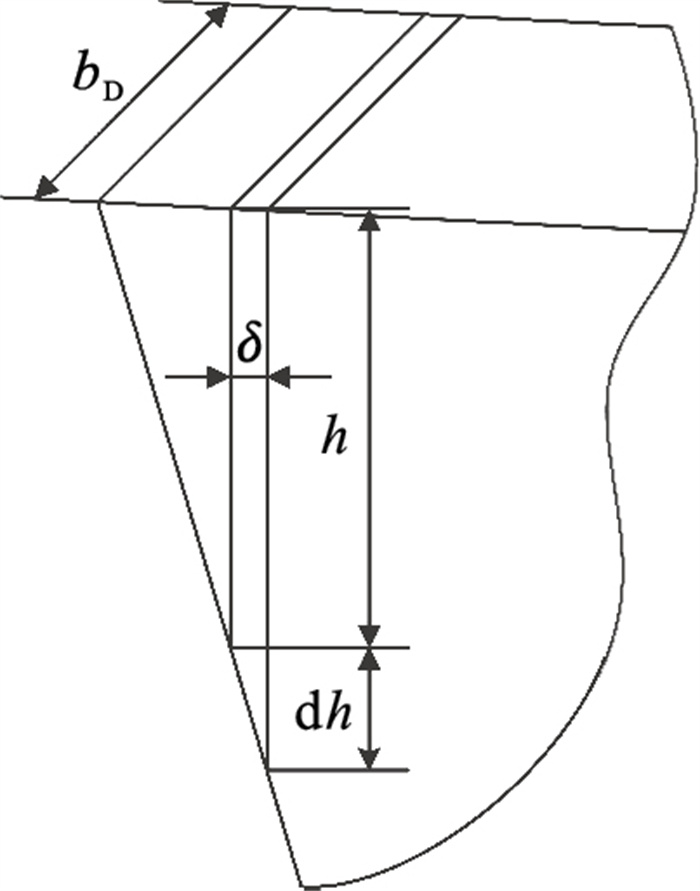图 1 刀具磨损示意图Fig.1 Schematic diagram of tool wear

其中: b_D为切削宽度; h为磨损宽度; δ为磨损厚度.
而切削宽度b_D为

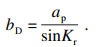(4)

其中: a_p为切削深度; K_r为刀具主偏角.
又根据图 2可知

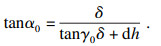(5)

图 2(Fig. 2)

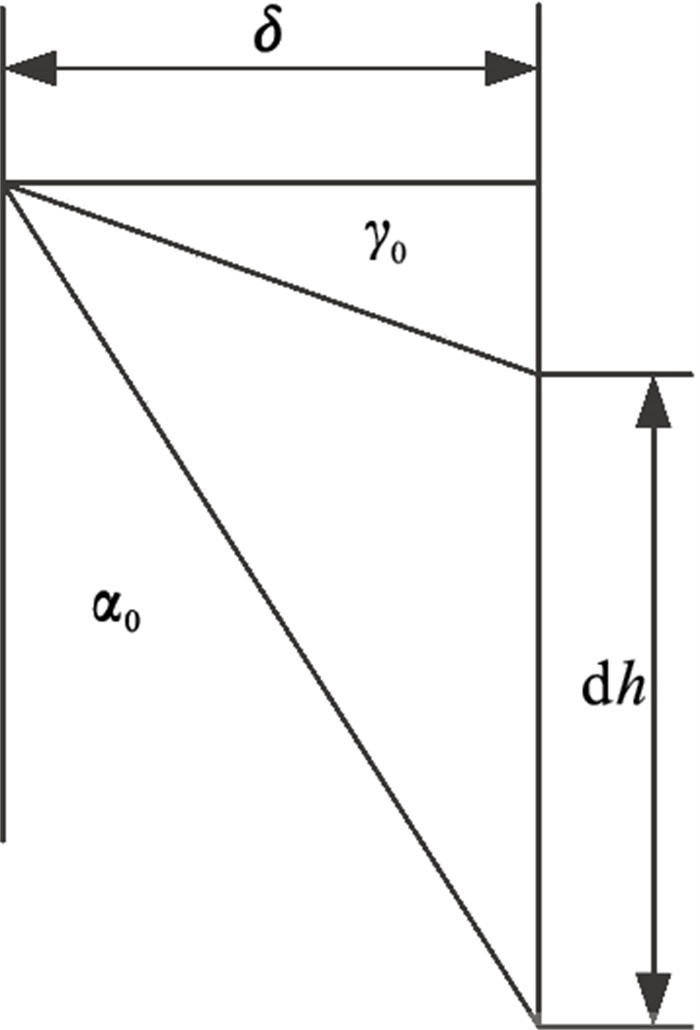图 2 局部放大示意图Fig.2 Schematic diagram of partial enlargement

由于dh非常小, 所以由式(3)~式(5)近似得到刀具磨损率为

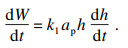(6)

其中, .
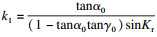
由式(2)、式(6)联立, 左右两端进行积分可得

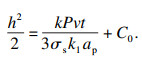(7)

由于在刚开始切削时, 刀具还未发生磨损, 即t=0时, h=0.由此可以计算得到C₀=0.因此, 式(7)可得

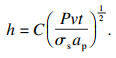(8)

其中, .
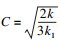
Acchar等^[15]通过大量的切削试验, 得到材料屈服强度与温度之间的关系.在此基础上, 常艳丽^[16]对曲线进行了拟合, 得到了GH4169屈服强度σ_s与温度θ的关系为

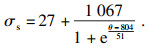(9)

在切削加工过程中, 后刀面法向力P主要与切削深度a_p、切削速度v和进给量f有关, 可表示为

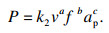(10)

切削温度θ主要与切削速度v和进给量f有关, 表示为

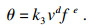(11)

其中, k₂, k₃, a, b, c, d, e为系数.
将式(9)~式(11)代入式(8)中, 最终得到刀具的磨损模型为

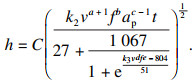(12)

当刀具磨损宽度达到极限磨损宽度0.3 mm时, 刀具失效, 此时即为刀具寿命.因此, 根据涂层硬质合金刀具的磨损宽度与时间以及切削参数的关系, 可推导出刀具的寿命模型为

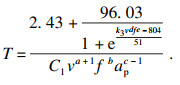(13)

其中, C₁=C²k₂.
2 车削参数优化在传统的车削参数优化中, 人们往往没有考虑机床的车削参数和结构参数的不确定性, 而是把它们看作一个确定值.确定性优化后所求得的最优解通常会落在约束的边界上, 如果设计变量一旦因为不确定性发生变化, 所求的最优解就会在约束边界周围波动, 很有可能会进入失效域, 最后造成可靠性太差而无法满足期望要求^[17].因此, 为了保证优化结果的可靠性, 在传统的车削参数优化的基础上, 引进了一种基于可靠性的参数优化.
2.1 可靠性优化可靠性优化是在可靠性的基础上, 结合传统的确定性优化算法产生的.与传统的确定性优化不同, 在优化过程中, 参数具有随机不确定性的情况, 以及约束中含有可靠性约束, 以保证约束的可行性.所以, 基于可靠性的车削参数优化模型可表示为

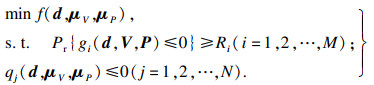(14)

其中: f(·)表示目标函数; g_i(·)是第i个失效模型的极限状态函数; q_j(·)为第j个不等式约束; M和N分别为可靠性和不等式约束的个数；d为确定性设计矢量；V为随机设计矢量；P为随机参数矢量.μ_V和μ_P分别为V和P的平均值；P_r表示可靠度计算；R_i是第i个约束的目标可靠度.
关于可靠度的计算, 本文采用改进的一次二阶矩法(AFOSM), 由以下三个步骤组成.
1) 将随机变量标准正态化.将原本处于X空间中的随机变量X=(X₁, X₂)转化到U空间中, 变为服从标准正态分布的变量U=(U₁, U₂).转换公式为

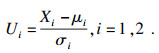(15)

其中: X_i表示随机参数; μ_i和σ_i分别为X_i的平均值和标准差.
随机变量标准正态化后, 原始空间的均值点被映射到标准正态空间的原点上.这样, X空间上的失效面g_X(x)=0就映射为U空间上相对应的失效面g_U(u)=0.
2) 搜索最大可能失效点u_MPP.最大可能失效点u_MPP位于失效面g_U(u)=0上, 从几何的角度上来看, u_MPP是失效面上到坐标原点距离最短的一点, 那么, 搜索u_MPP实质上可以看作一个求解最优化的问题.在标准正态空间中, 从坐标原点到失效面g_U(u)=0的最短距离定义为可靠度指标β.因此, 求解如下最优化问题, 就可以得到可靠度指标β和u_MPP.

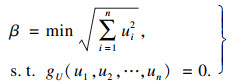(16)

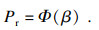3) 计算可靠度P_r.可靠度P_r可以用式(17)进行计算:

(17)

其中, Φ(·)表示标准正态分布的累积分布函数.
2.2 序列优化与可靠性评估方法从式(14)中可以看出, 描述可靠性优化问题的模型是一个嵌套循环结构, 其外部循环用于确定性优化, 而内部嵌套循环用于分析约束的可靠性.这种传统的可靠性优化方法, 每一次外部优化的进行都需要一系列完整的可靠性分析, 所以计算量大, 效率非常低.针对此问题, Du等^[18]提出了序列优化与可靠性评估(SORA)方法, 这也是目前最常用的可靠性优化方法之一.
SORA的主要思想是将可靠性评估和确定性优化完全分离, 每个循环内部都是先进行确定性的优化分析, 再进行可靠性评估, 可靠性分析的次数与循环次数相同, 相比于嵌套循环结构, 极大地提高了优化求解的效率.在可靠性评估时, 为了保证算法的稳定性和效率, 每次迭代都采用基于逆MPP的搜索算法.
1) 逆MPP搜索算法的可靠性评估.为了保证序列优化与可靠性评定方法求解的稳定和高效, 采用了一个有效且稳定的基于逆MPP的搜索算法.将可靠性优化约束进行等价变换, 则优化模型改写为

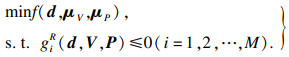(18)

其中, g^R表示g(d, V, P)的R-百分比, 来源于式(19):

(19)

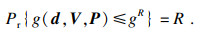g^R的几何意义如图 3所示, 其值可通过逆MPP方法计算得到^[19].
图 3(Fig. 3)

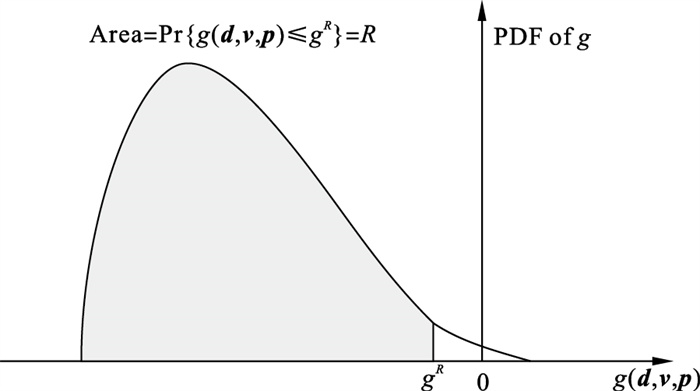图 3 gR的几何意义Fig.3 Geometric meaning of gR

若给定期望可靠度R, 则可靠度指标β可计算得

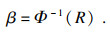(20)

其中, Φ^-1(·)是标准正态分布的逆函数.
逆MPP问题实际上也是一个最优化问题, 其优化模型为

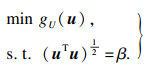(21)

其中, u=[u_V, u_P], u_V和u_P分别是v和p的标准形式.
通过式(21)题的求解, 可以找到MPP点.然后, 将所求的最优解u_MPP代入目标函数中, R-百分比也可以计算得到, 如式(22)所示:

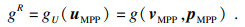(22)

g^R决定了MPP点是否满足可靠性要求.如果不满足, 则执行下一步.
2) SORA法的实施步骤.在每次的循环中, 首先要解决的就是确定性优化问题, 每一次循环的确定性优化模型都是通过上一次循环得到的MPP点的信息建立的.但是, 在第一次的循环中没有MPP点的信息, 所以, 第一次的确定性优化把随机变量V和随机参数P的均值μ_V和μ_P作为初始点.下面是在概率优化的第一步循环中, 确定性优化的模型:

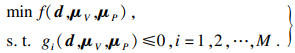(23)

在求解上述的优化问题后, 可以得到最优解, 即新的设计点.然后, 在最优解处采用逆MPP搜索算法进行可靠性评估.初步优化不能达到可靠性要求, 因此, 进行下一步循环.为了保证概率约束的可行性, MPP点必须在确定性可行域内, 因此, 当进入到第二步循环时, 等效确定性优化模型的约束应该被修正, 使得MPP点至少落在确定性约束的边界上, 以保证概率约束的可行性.采用s作为要移动的向量, 移动的距离为确定性优化得到的设计点和MPP点之间的距离, 则确定性优化的约束被重新表示为

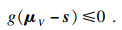(24)

在第二步循环中, 修正的约束使得可行域变窄, 它的优化模型变为

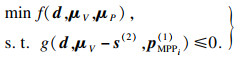(25)

其中, .
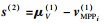
以此类推, 推导出通用优化模型.在τ+1步循环中, 优化模型为

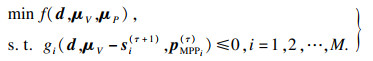(26)

其中, .
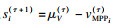
重复进行循环过程, 直到目标收敛和所有的可靠性要求都得到满足时, 可靠性优化完成.SORA方法的流程图如图 4所示.
图 4(Fig. 4)

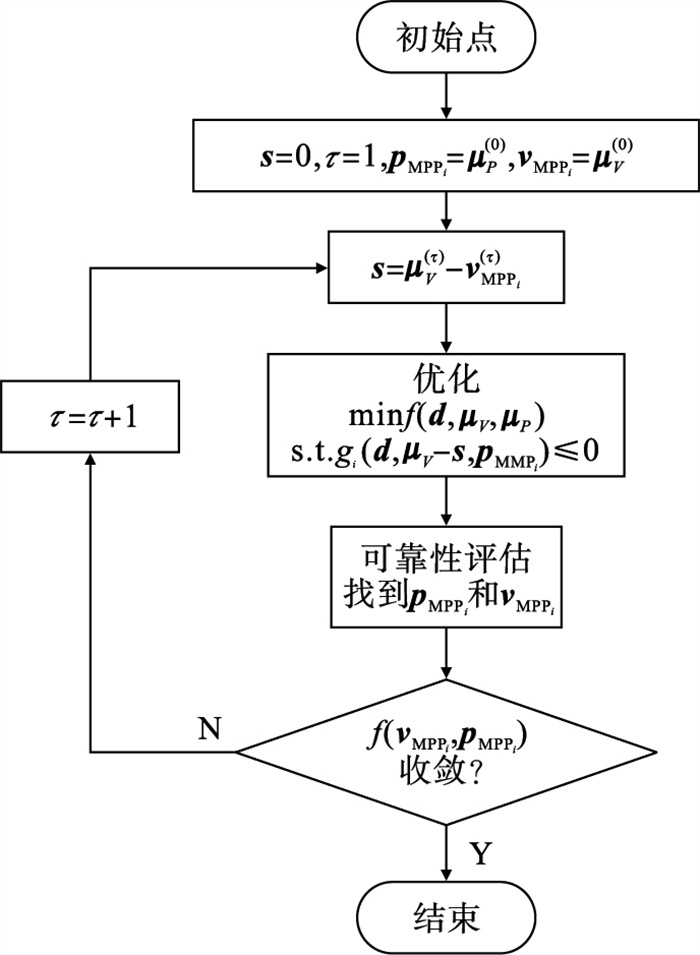图 4 SORA方法流程图Fig.4 Flow chart of SORA method

3 计算实例3.1 刀具寿命模型拟合本文的实验数据来自哈尔滨工业大学郝兆朋所做的PVD-TiAlN涂层刀具车削镍基高温合金GH4169试验^[20], 加工工件为?100 mm×500 mm的棒料, 该试验的车削余量采用一次全部切除, 固定切削深度为1 mm进行车削加工, 试验数据见表 1.基于该试验数据, 采用最小二乘法和线性回归法, 将式(10)和式(11)进行数据拟合, 求解模型中的各个系数得
表 1(Table 1)

表 1 试验数据Table 1 Test data 20 0.08 0.5 510 0.05 258 20 0.10 2 520 0.11 271 20 0.12 4 534 0.15 292 20 0.16 6 550 0.18 305 30 0.08 4 590 0.08 252 30 0.10 6 615 0.14 274 30 0.12 0.5 595 0.04 281 30 0.16 2 617 0.09 294 40 0.08 6 670 0.18 243 40 0.10 4 676 0.15 267 40 0.12 2 680 0.15 281 40 0.16 0.5 692 0.05 293 50 0.08 2 715 0.16 245 50 0.10 0.5 720 0.1 266 50 0.12 6 740 0.28 283 50 0.16 4 753 0.42 307

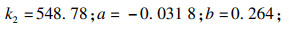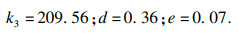表 1 试验数据 Table 1 Test data

因此, 可以拟合出后刀面法向力P和切削温度θ的模型:

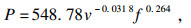(27)

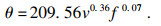(28)

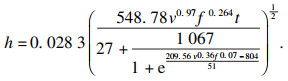将数据代入模型中, 计算C的平均值为0.028 3.从而, 刀具的磨损模型也可以得到, 如式(29)所示.

(29)

为了验证上述模型的正确性, 在给定进给量f=0.1 mm/r的条件下, 使用该模型对刀具磨损量进行预测, 并与实验值和经典乘法模型预测值进行对比分析, 结果显示该模型能够更好地预测车削过程中的刀具后刀面磨损量, 如图 5所示.
图 5(Fig. 5)

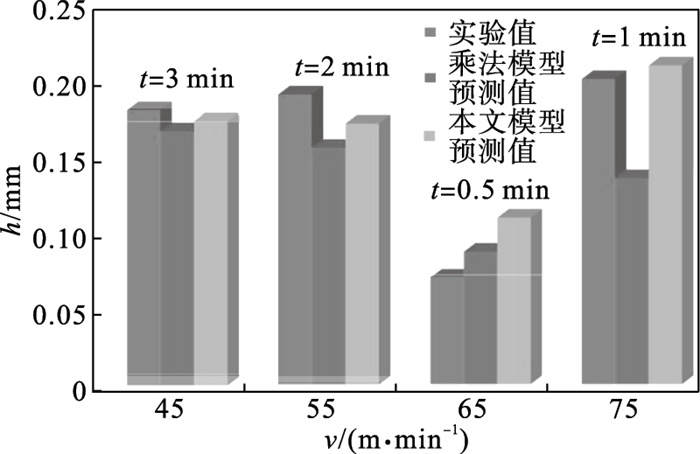图 5 预测值与试验值对比Fig.5 Comparison of predicted values and experimental values

因此, 可推导出刀具的寿命模型为

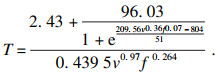(30)

3.2 车削参数优化本文将车削加工参数视为随机变量.在有足够的试验数据的情况下, 通过对试验数据的信度检验和统计分析, 可以得到切削速度v和进给量f的平均值, 分别为25 m/min和0.1 mm/r.
建立优化模型时, 首先要选择出适宜的设计变量.在本文的涂层硬质合金刀具车削GH4169过程中, 切削效率主要与切削速度v和进给量f有关.因此, 本文选择切削速度v和进给量f作为设计变量.然后, 建立车削优化模型中的目标函数和约束函数.在车削加工过程中, 切削参数的选取直接影响加工效率.在满足使用要求的前提下, 切削参数值越大, 加工效率越高, 但是在加大切削用量以提高加工效率的同时, 也会导致刀具磨损过快和刀具寿命降低, 两者显然造成了矛盾.结合企业的实际情况, 权衡两个要求, 将刀具寿命作为约束条件, 在保证刀具寿命的前提下, 实现加工效率的提高.最终, 本文以工件的最大加工效率为目标函数, 以刀具寿命、切削温度、后刀面法向力和主轴转速的可靠性为约束函数.
1) 目标函数.加工效率可以用材料去除率表示, 其表达式为

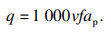(31)

式中, q为材料的去除率, mm³/min.由于在本文的切削加工中, 车削余量会被一次全部切除.因此, 材料去除率修改为

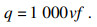(32)

2) 约束条件.在车削的参数优化中, 有诸多复杂多变的因素相互作用影响优化目标, 使得优化过程受到了限制, 这种限制被称作约束条件.本文优化模型的约束条件主要从几个方面考虑:
优化变量约束.
① 切削速度约束:

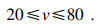(33)

单位为m/min.
② 进给量约束:

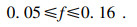(34)

单位为mm/r.
可靠性约束.
本文分别将刀具寿命、切削温度、后刀面法向力及主轴转速的可靠性作为约束条件, 其模型为

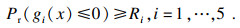(35)

其中, 期望可靠度R_i=0.99.
① 刀具寿命约束:

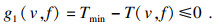(36)

其中: T_min为允许的刀具寿命下限, 其数值为5 min.T(v, f)为刀具寿命, 其模型见式(30).
② 切削温度约束:

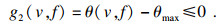(37)

其中: θ_max为允许的切削温度上限, 其数值为700 ℃; θ(v, f)为瞬时切削温度, 其模型见式(28).
③ 后刀面法向力约束:

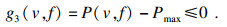(38)

其中: P_max为允许的法向力上限, 其数值为300 N; P(v, f)是瞬时法向力, 其模型见式(27).
④ 主轴转速约束:

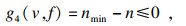(39)

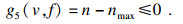(40)

其中: n_min为允许主轴转速下限, n_max为允许主轴转速上限, 其数值分别为50 r/min和160 r/min; n为主轴转速, 与切削速度v有关, 其公式:

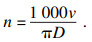(41)

3) 优化结果分析.使用2.2节所介绍的SORA方法进行车削参数的可靠性优化.除此之外, 为了展现可靠性优化的效果, 还使用了传统的车削参数优化方法进行对比, 其结果如表 2所示.
表 2(Table 2)

表 2 优化结果对比Table 2 Comparison of optimization results 车削参数 R1 R2 R3 R4 R5 初始值 25 0.1 — — — — — 2 500 传统的车削参数优化 40.777 9 0.158 7 0.940 9 0.508 0 0.494 1 0.998 8 0.877 5 6 471.5 基于可靠性的车削参数优化 28.630 8 0.111 4 1 0.994 7 0.962 4 0.988 3 0.999 9 3 189.8

表 2 优化结果对比 Table 2 Comparison of optimization results

从表 2中可以明显看出, 车削参数优化后, 材料去除率得到了极大的提高, 从2 500 mm³/min成倍地提高到了6 471.5 mm³/min.但是, 刀具寿命的可靠性约束条件不能满足要求, 其中, 切削温度约束和后刀面法向力约束的可靠性甚至低到了0.508 0和0.494 1.而在基于可靠性的参数优化后, 虽然材料去除率只提高到了3 189.8 mm³/min, 但所有约束的可靠性都满足了要求, 尤其是切削温度约束和后刀面法向力约束的可靠性有大幅度的提高.
4 结论1) 本文建立了车削过程中的刀具磨损模型, 并与传统的磨损模型进行比较, 该模型具有更好的预测效果, 从而, 基于此模型建立了刀具寿命模型.
2) 将SORA方法应用于GH4169车削过程中切削参数的可靠性优化.以加工效率为目标函数, 以刀具寿命、切削温度、后刀面法向力以及主轴转速的可靠性为约束函数进行优化, 优化后的切削速度v和进给量f分别为28.630 8 m/min和0.111 4 mm/r.
3) 通过实例计算, 该方法的应用能够在保证刀具寿命的前提下, 找到实现最大加工效率的切削参数, 并且结果可靠度极高, 为加快企业生产提供了参考.
参考文献

[1]	Akhtar W, Sun J F, Chen W Y. Effect of machining parameters on surface integrity in high speed milling of super alloy GH4169/Inconel 718[J]. Materials and Manufacturing Processes, 2016, 31(5): 620-627. DOI:10.1080/10426914.2014.994769
[2]	Thakur D G, Ramamoorthy B, Vijayaraghavan L. Study on the machinability characteristics of superalloy Inconel 718 during high speed turning[J]. Materials and Design, 2009, 30(5): 1718-1725. DOI:10.1016/j.matdes.2008.07.011
[3]	Bhatt A, Attia H, Vargas R, et al. Wear mechanisms of WC coated and uncoated tools in finish turning of Inconel 718[J]. Tribology International, 2010, 43(5/6): 1113-1121.
[4]	Costes J P, Guillet Y, Poulachon G, et al. Tool life and wear mechanisms of CBN tools in machining of Inconel 718[J]. International Journal of Machine Tools & Manufacture, 2007, 47(7/8): 1081-1087.
[5]	Usui E, Shirakashi T. Analytical prediction of cutting tool wear[J]. Wear, 1984, 100(1/2/3): 129-151.
[6]	Takeyama H, Murata R. Basic investigation of tool wear[J]. Journal of Engineering for Industry, 1963, 85(1): 33-37. DOI:10.1115/1.3667575
[7]	Luo X, Cheng K, Holt R, et al. Modeling flank wear of carbide tool insert in metal cutting[J]. Wear, 2005, 259(7/8/9/10/11/12): 1235-1240.
[8]	Davoodi B, Eskandari B. Tool wear mechanisms and multi-response optimization of tool life and volume of material removed in turning of N-155 iron-nickel-base superalloy using RSM[J]. Measurement, 2015, 68: 286-294. DOI:10.1016/j.measurement.2015.03.006
[9]	Mia M, Dey P R, Hossainc M S, et al. Taguchi S/N based optimization of machining parameters for surface roughness, tool wear and material removal rate in hard turning under MQL cutting condition[J]. Measurement, 2018, 122: 380-391.
[10]	Selvakumar S, Sreebalaji V S, Ravikumar K. Machinability analysis and optimization in micro turning on tool wear for titanium alloy[J]. Materials and Manufacturing Processes, 2021, 36(7): 792-802. DOI:10.1080/10426914.2020.1866198
[11]	Gupta M K, Sood P K, Sharma V S. Machining parameters optimization of titanium alloy using response surface methodology and particle swarm optimization under minimum-quantity lubrication environment[J]. Materials and Manufacturing Processes, 2016, 31(13): 1671-1682. DOI:10.1080/10426914.2015.1117632
[12]	Tian C, Zhou G H, Zhang J J, et al. Optimization of cutting parameters considering tool wear conditions in low-carbon manufacturing environment[J]. Journal of Cleaner Production, 2019, 226: 706-719. DOI:10.1016/j.jclepro.2019.04.113
[13]	Akhtar W, Sun J F, Sun P F, et al. Tool wear mechanisms in the machining of nickel based super-alloys: a review[J]. Frontiers of Mechanical Engineering, 2014, 9: 106-119. DOI:10.1007/s11465-014-0301-2
[14]	高彩桥, 刘家浚. 材料的粘着磨损与疲劳磨损[M]. 北京: 机械工业出版社, 1999: 13-20, 24-34. (Gao Cai-qiao, Liu Jia-jun. Adhesive wear and fatigue wear of materials[M]. Beijing: China Machine Press, 1999: 13-20, 24-34.)
[15]	Acchar W, Gomes U U, Kaysser W A, et al. Strength degradation of a tungsten carbide-cobalt composite at elevated temperatures[J]. Materials Characterization, 1999, 43(1): 27-32. DOI:10.1016/S1044-5803(98)00056-4
[16]	常艳丽. 镍基高温合金GH4169的切削力与刀具磨损试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. (Chang Yan-li. Experimental research on cutting force and tool wear of GH4169[D]. Harbin: Harbin Institute of Technology, 2011. )
[17]	王新刚, 徐馷悉, 李尚杰. 不确定结构的区间可靠性优化设计[J]. 东北大学学报(自然科学版), 2020, 41(4): 521-527. (Wang Xin-gang, Xu Pei-xi, Li Shang-jie. Optimal design of interval reliability for uncertain structures[J]. Journal of Northeastern University(Natural Science), 2020, 41(4): 521-527.)
[18]	Du X, Chen W. Sequential optimization and reliability assessment method for efficient probabilistic design[J]. Journal of Mechanical Design, 2004, 126(2): 225-233. DOI:10.1115/1.1649968
[19]	李海燕, 井元伟. 基于SORA的多学科协同优化可靠性优化方法[J]. 东北大学学报(自然科学版), 2018, 39(1): 1-5. (Li Hai-yan, Jing Yuan-wei. SORA-based reliability optimization method for multidisciplinary collaborative optimization[J]. Journal of Northeastern University(Natural Science), 2018, 39(1): 1-5.)
[20]	郝兆鹏. 切削GH4169的相关机理及高效切削技术的基础研究[D]. 哈尔滨: 哈尔滨工业大学, 2013. (Hao Zhao-peng. Research on related mechanism and high efficiency cutting technology in machining nickel-based superalloy GH4169[D]. Harbin: Harbin Institute of Technology, 2013. )