
 , 陈帅军1,2
, 陈帅军1,2 1. 北京科技大学 金属矿山高效开采与安全教育部重点实验室, 北京 100083;
2. 北京科技大学 土木与资源工程学院, 北京 100083
收稿日期:2021-05-18
基金项目:国家自然科学基金资助项目(52004017, 52174106);中国博士后科学基金资助项目(2020M670138);中央高校基本科研业务费专项资金资助项目(FRF-TP-19-026A1, FRF-IDRY-20-021)。
作者简介:孙浩(1992-),男,安徽阜阳人,北京科技大学讲师,博士;
金爱兵(1974-),男,江苏兴化人,北京科技大学教授,博士生导师。
摘要:针对当前多口放矿研究中存在的放矿口间距阈值和应力分布等问题, 基于刚性块体模型开展不同放矿口间距和放矿方式条件下的放矿数值试验, 对多放矿口间的矿岩颗粒均匀流与应力演化规律进行量化研究.研究结果表明: 多口放矿条件下能够产生矿岩颗粒均匀流的放矿口间距阈值介于1.0~1.25倍的松动体最大宽度.矿岩颗粒流动体系内存在明显的应力拱效应, 放矿过程中松动体上方的垂直应力会逐渐向两侧非松动区域转移.在所研究的取值范围内, 采场底部最大垂直应力已接近初始垂直应力的1.8倍.放矿过程中采场内非松动区域的配位数约为8~9, 且空间高度越低其配位数越大; 在松动区域内越接近放矿口的位置, 其矿岩颗粒越松散且运移与接触变化的无序程度越高.
关键词:多放矿口矿岩颗粒均匀流应力演化刚性块体模型
Uniform Flow and Stress Evolution Laws of Caved Ore and Rock Partides Between Multiple Drawpoints
SUN Hao1,2, SU Nan1,2, JIN Ai-bing1,2

 , CHEN Shuai-jun1,2
, CHEN Shuai-jun1,2 1. Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing 100083, China;
2. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China
Corresponding author: JIN Ai-bing, E-mail: jinaibing@ustb.edu.cn.
Abstract: Aiming at the problems such as the threshold of drawpoint spacing and stress distribution in the research of multiple draw interaction, numerical tests based on the rigid block model were carried out under the conditions of different drawpoint spacings and draw modes, and uniform flow and stress evolution laws of caved ore and rock between multiple drawpoints were quantitatively studied. The results showed that the threshold of drawpoint spacing that produces uniform flow of caved ore and rock lies between 1.0 and 1.25 times of the maximum width of the isolated movement zone under the condition of multiple drawpoints. There is an obvious stress arching effect in the particle flow system, and the vertical stress above movement zones gradually transfers to the immobile zones on both sides during the draw process. The maximum vertical stress at the bottom of stope is nearly 1.8 times of the initial vertical stress within the range of values studied. The coordination number within the immobile zones is about 8~9 during the draw process, and the lower the space height, the larger the coordination number is. Within the movement zones, the closer to the drawpoints, the looser the caved ore and rock are, and the more disordered the migration and contact variations among particles are.
Key words: multiple drawpointscaved ore and rock particlesuniform flowstress evolutionrigid block model
当前国内外地下金属矿山面临的挑战主要包括: 更深的开采环境、更高的地应力、更大的生产需求以及更多的开采成本等[1-2].针对崩落法矿山, 随着开采深度的不断增加, 崩落矿岩层高度及其对采场底部结构的荷载随之不断增大, 故合理的采场结构参数和放矿控制措施, 尤其是放矿口间距和放矿方式对崩落矿岩流动特性、采场底部结构稳定性以及矿石贫损指标的影响将愈发关键.基于此, 探究不同放矿口间距和放矿方式条件下多放矿口间的矿岩颗粒相互作用规律十分必要.
目前评估崩落法矿山采场结构参数和放矿控制措施优劣的主要标准[3-4]多为: 崩落矿岩接触面(ore-waste interface)是否均匀下降, 换言之崩落矿岩层是否形成均匀流(uniform flow), 即相邻放矿口上方的两个松动体(isolated movement zone, IMZ)是否相交(interaction).而已有文献中针对形成崩落矿岩接触面均匀下降或均匀流现象的放矿口间距(drawpoint spacing)阈值问题, 存在如下两种不同观点: ①Laubscher[3]基于Marano[5]以砂子为介质的三维放矿物理试验结果以及自身经验提出: 当多放矿口同时出矿时, 相邻放矿口间距Ds可设计为单口放矿所得松动体最大宽度wIMZ的1.5倍, 即Ds≤1.5wIMZ时两相邻松动体即可出现相交现象.Hancock[6]利用离散元软件ESyS-Particle, 开展了基于球形颗粒的多口放矿数值模拟研究, 亦发现: 当相邻放矿口间距小于或等于松动体最大宽度的1.5倍时, 即可形成崩落矿岩的均匀流.②Trueman等[7]开展基于粗破碎千枚岩散体的大型三维放矿物理试验研究, 发现: 多口放矿条件下, 当相邻放矿口间距为单口放矿所得松动体最大宽度wIMZ的1.2倍, 即Ds=1.2wIMZ时两相邻松动体仍未出现相交现象.考虑到放矿物理模型的材质为钢材[8], 表面较为光滑, 而实际放矿边界具有更高的摩擦系数, 故矿岩散体间的应力拱效应(stress arching effect)更为显著.基于此, Trueman等[7]认为: 在相邻放矿口间距大于松动体最大宽度即Ds>1.0wIMZ的条件下, 两相邻松动体可能不会相交.
放矿过程中采场内不同空间位置所处应力环境, 尤其是采场底部结构所受应力及其演化规律是分析矿岩颗粒间应力拱效应和运移规律的途径之一, 也是优化放矿口间距和放矿方式的关键指标.Lorig[8], Pierce[9]基于Janssen公式[10]和极限平衡方法探究了采场底部结构所受垂直应力和崩落矿岩堆积密度、摩擦系数及放矿区域的水力半径等因素之间的定量关系.Castro等[11]以智利大型地下铜矿EI Teniente矿为工程背景, 通过相似比为1∶ 200的放矿物理试验研究不同放矿方式下诱发垂直应力的演化规律.
综上所述, 目前在多口放矿研究中对于实现矿岩颗粒均匀流的放矿口间距阈值问题仍有争议, 对不同放矿口间距和放矿方式下采场内不同空间位置所处应力环境及其演化规律的研究尚浅.因此, 本文基于刚性块体模型(rigid block model)开展多口放矿数值试验研究, 对多放矿口间的矿岩颗粒均匀流与应力演化规律进行量化研究.研究结果是对现行放矿理论的有益补充, 可为崩落法矿山采场结构与支护参数设计、放矿控制与管理等提供有益参考.
1 不同放矿口间距下的矿岩颗粒相互作用规律研究相邻放矿口间距为影响矿岩颗粒是否产生均匀流的主要因素.为确定能够产生矿岩颗粒均匀流(两相邻松动体相交)的放矿口间距阈值, 首先需要确定松动体的最大宽度.底部放矿物理试验中的松动体形态变化往往难以直接观测, 而通过放矿数值试验可以实现松动体形态的可视化.本文以地下矿山开采过程中在自然崩落或爆破作用下形成的矿岩颗粒体系为研究对象, 首先基于松动体的最大宽度开展不同放矿口间距下的多口放矿数值试验, 研究放矿口间距阈值以及不同区域内矿岩颗粒间的应力演化规律.
1.1 放矿数值试验设计1) 放矿数值试验方案.作者前期已基于自主研制的大型三维放矿物理试验平台(图 1a)开展相似比为1∶ 25的单口底部放矿物理试验研究, 并首次基于刚性块体模型[12](图 1b)构建放矿数值模型.通过放矿物理试验与模拟结果的对比分析, 证明了刚性块体模型在崩落矿岩流动特性研究中的可靠性与优越性, 并确定了松动体的最大宽度[13], 为本次多口条件下的放矿数值试验研究奠定了模型基础.
图 1(Fig. 1)
 | 图 1 三维放矿物理试验平台与刚性块体模型Fig.1 The 3D physical draw platform and rigid block models (a)—放矿物理试验平台;(b)—放矿数值试验中所用的刚性块体模型. |
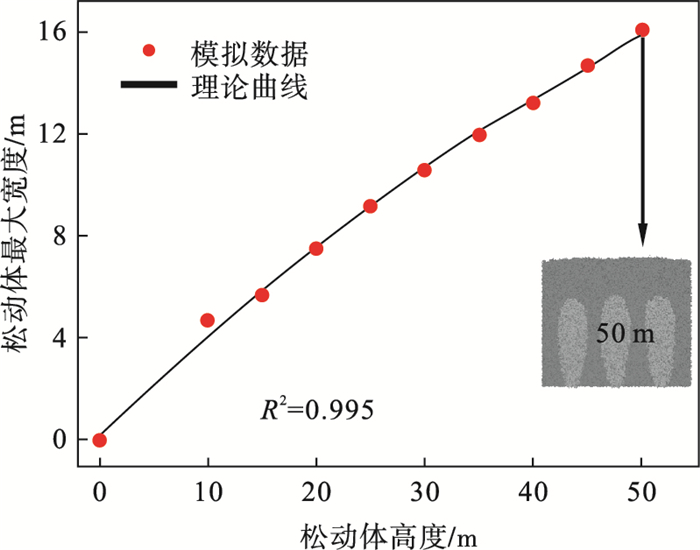
图 2为前期基于刚性块体模型的单口放矿数值试验所得松动体高度与最大宽度关系曲线[13].如图 2所示, 松动体高度为50 m时, 其最大宽度约16 m.基于此, 本次模拟共设计如表 1所示的12, 16, 20和24 m共四种不同放矿口间距下的放矿数值试验, 探究在松动高度为50 m范围内矿岩颗粒产生均匀流的放矿口间距阈值与应力演化规律.
图 2(Fig. 2)
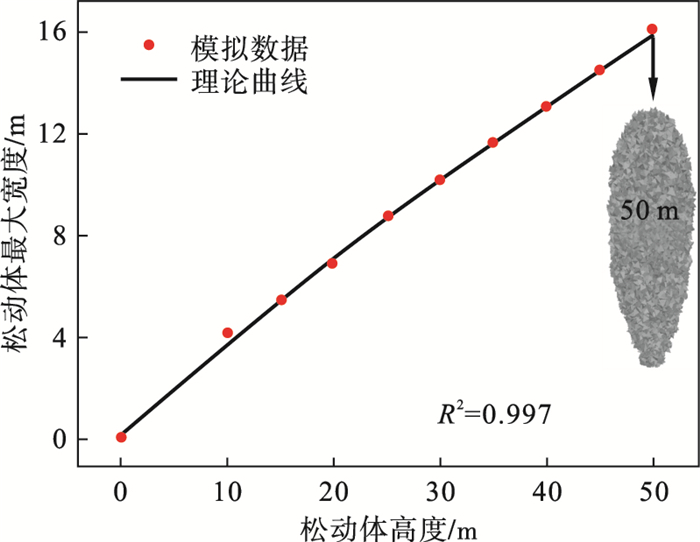 | 图 2 单口条件下松动体高度与最大宽度关系的放矿数值模拟数据和理论曲线对比[13]Fig.2 Comparison between the data of numerical draw test and theoretic curve for the relationship between the height and maximal width of IMZ[13] |
表 1(Table 1)
| 表 1 不同放矿口间距下的数值模拟方案 Table 1 Schemes of numerical simulation with different drawpoint spacings |
2) 放矿数值模型构建.综合考虑上述不同放矿口间距下的数值试验方案以及数值计算效率, 构建如图 3所示的长×宽×高=80 m×40 m×70 m的多口放矿数值模型.图 3a中模型底部深色区域即为三个放矿口, 相邻放矿口间距可根据不同的模拟方案进行调节.为了更加清晰地显示矿岩颗粒均匀流等运移状态, 故以10 m为单位将模型内不同高度的矿岩颗粒设置成如图 3b所示的两种不同颜色.此外, 在放矿开始前于模型内布设如图 3b所示的直径为6 m的15个测量球域, 监测不同空间区域内配位数以及块体所受水平应力与垂直应力的演化过程.其中, 第1~3号、7~9号和13~15号测量域分别布设于放矿口1~3的正上方10, 25和40 m处; 而第4~6号和10~12号测量域分别于相邻放矿口间的中线位置对称布设, 同一高度相邻测量域的布设间距与相邻放矿口布设间距的一半即0.5Ds保持一致.
图 3(Fig. 3)
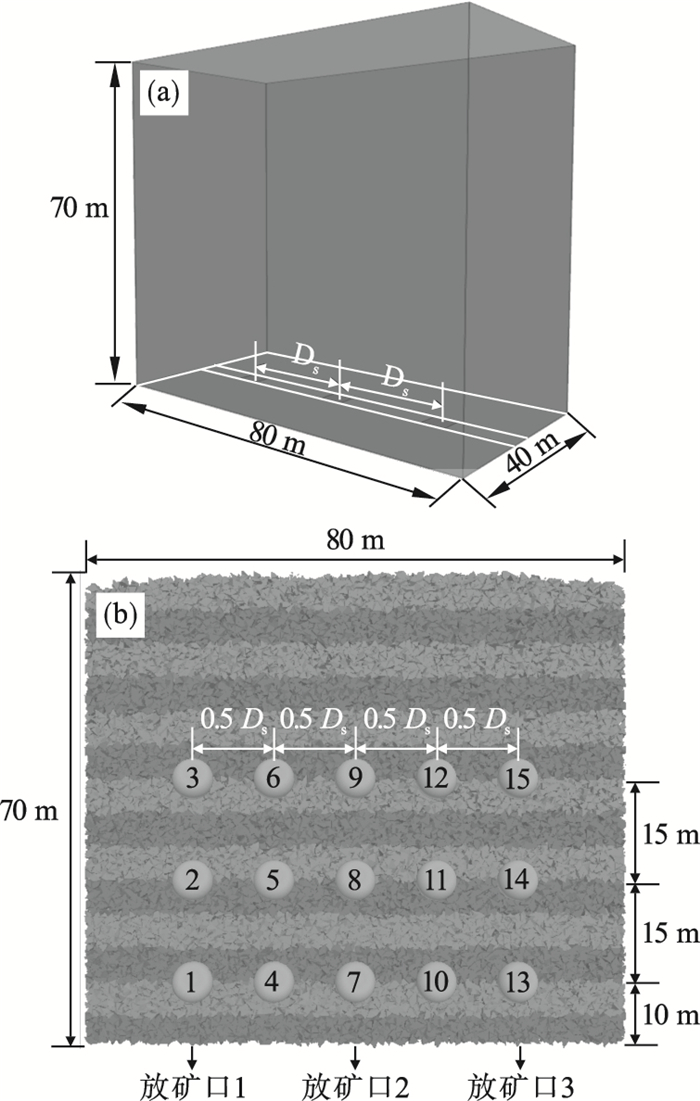 | 图 3 多口放矿数值模型Fig.3 The numerical model of multiple drawpoints (a)—多口放矿数值模型墙体;(b)—多口放矿数值模型纵剖面图和测量球域布设. |
3) 放矿数值试验过程.整个放矿数值试验过程如下: ①基于刚性块体模型(图 1b)和“雨落法”[14]生成如图 3b所示的放矿数值模型, 并赋予墙体与刚性块体相应的细观力学参数(表 2).需要说明的是, 有关块体形状、级配及细观参数的确定等介绍可见文献[13], 为避免重复, 故此处不再赘述.待整个模型达重力平衡状态后, 监测并统计模型内不同空间位置的初始水平应力σh, 0与垂直应力σv, 0; ②打开放矿口1~3使之同时出矿, 监测、记录整个放矿过程中包括松动体形态演化过程在内的矿岩颗粒运移情况、不同空间区域内配位数(coordination number, CN)以及块体所受水平应力σh与垂直应力σv的变化过程; ③当矿岩颗粒松动高度达50 m时停止出矿, 并在模拟过程中保持20 m的覆岩高度不变.
表 2(Table 2)
| 表 2 墙体与刚性块体细观参数 Table 2 Meso-parameters of walls and rigid blocks | ||||||||||||||||||||||||||||||||||||||||||
1.2 放矿数值试验结果分析四组放矿数值试验结束后, 从矿岩颗粒运移演化和粒间的应力演化等方面对比分析不同放矿口间距下的矿岩颗粒相互作用规律, 确定产生矿岩颗粒均匀流的放矿口间距阈值.
1) 运移演化规律分析.图 4为四种放矿口间距下松动高度达50 m即停止出矿时刻的矿岩颗粒运移纵剖面图.如图 4a和图 4b所示, 当放矿口间距Ds为12 m(0.75wIMZ)和16 m(1.0wIMZ)时, 在35 m和45 m等不同高度的矿岩颗粒层已出现不同范围近似水平下降的现象, 即相邻松动体已相交; 而如图 4c和图 4d所示, 当放矿口间距Ds为20 m(1.25wIMZ)和24 m(1.5wIMZ)时, 同一高度的矿岩颗粒层均呈“波浪状”, 不同高度的矿岩颗粒层均未出现均匀下降的现象, 即可认为相邻松动体间未产生相互影响.由上述分析可知: 能够产生矿岩颗粒均匀流的放矿口间距阈值介于1.0~1.25倍的松动体最大宽度.
图 4(Fig. 4)
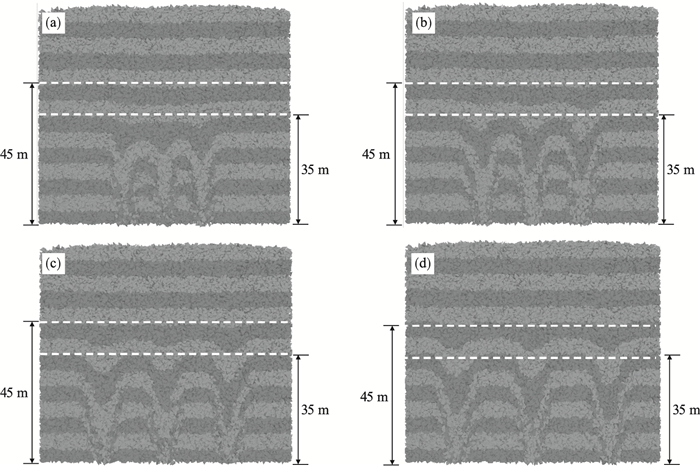 | 图 4 不同放矿口间距下的矿岩颗粒运移纵剖面图Fig.4 Longitudinal profiles of movement of caved ore and rock with different drawpoint spacings (a)—试验1(Ds=12 m); (b)—试验2(Ds=16 m); (c)—试验3(Ds=20 m); (d)—试验4(Ds=24 m). |
以试验4为例, 由于三个松动体的形态变化基本一致, 故统计并计算不同高度时三个松动体的最大宽度及其均值, 得到如图 5所示的放矿口间距Ds为24 m时的松动体形态纵剖面图,以及松动体高度与平均最大宽度的拟合曲线.由图 5可知: 50 m高度时,三个松动体形态均呈倒置水滴形, 松动体高度与其最大宽度之间满足倒置水滴理论[15]所述幂函数关系(式(1)), 拟合优度R2大于0.995:
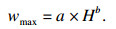 | (1) |
 | 图 5 试验4所得松动体高度与平均最大宽度关系的放矿数值模拟数据和理论曲线对比Fig.5 Comparison between the data of numerical draw test and theoretic curve for the relationship between the height and average maximal width of IMZs obtained in test 4 |
式中: wmax为松动体的最大宽度; H为松动体的高度;a和b为拟合系数.此外, 图 5从定量角度证明: 当放矿口间距较大时(如Ds>1.5wmax), 相邻松动体之间彼此独立, 其形态演化规律与单口放矿条件下的松动体形态演化规律相同, 依然符合倒置水滴理论.
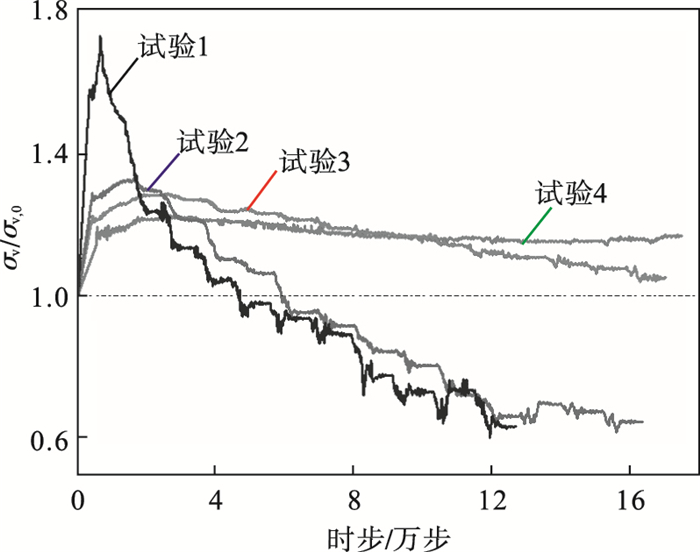
2) 应力演化规律分析.统计四组放矿数值试验中不同测量球域(图 3b)内的矿岩颗粒间配位数以及所受水平与垂直应力的演化过程.其中, 图 6为不同放矿口间距条件下第4号测量域内垂直应力的变化过程.由图 6可知: ①在四组放矿试验的初始阶段, 第4号测量域所在区域为两相邻放矿口间的非松动区域, 该区域内垂直应力σv较放矿前的初始垂直应力σv, 0均呈快速增加的趋势.随后, 当放矿口间距较小时(如试验1和试验2), 矿岩颗粒的松动范围逐渐波及第4号测量域, 即颗粒逐渐出现松动现象, 故该区域内的垂直应力逐渐减小至初始垂直应力的0.6倍左右; 而当放矿口间距较大时(如试验4), 第4号测量域所在区域始终为两相邻放矿口间的非松动区域, 故该区域内的垂直应力基本稳定在初始垂直应力的1.2倍左右.②放矿口间距越小, 两相邻放矿口间的非松动区域所受垂直应力越大, 且最大垂直应力出现的时刻越早.其中, 当放矿口间距Ds为12 m(试验1), 第4号测量域内的最大垂直应力已接近初始垂直应力的1.8倍(图 6中的试验1曲线).由此分析可知: 若设计的相邻放矿口间距过小, 可能会威胁两放矿口间采场底部结构的稳定性.
图 6(Fig. 6)
 | 图 6 不同放矿口间距条件下第4号测量域内垂直应力的变化过程Fig.6 Variations of vertical stress within measurement region No. 4 under different drawpoint spacings |
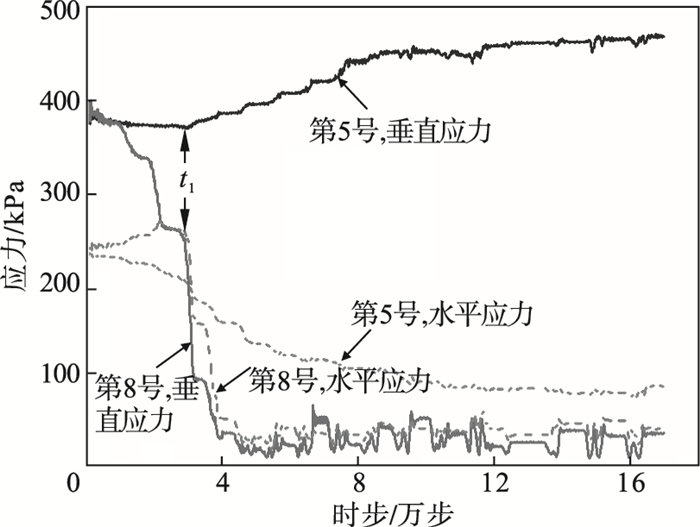
为了进一步分析松动区域与非松动区域内应力演化间的联系及差异性, 故以放矿口间距较大的试验4为例, 图 7为试验4所得第5号和第8号测量域内水平与垂直应力的变化过程.由图 3b和图 7可知: ①第8号测量域处于放矿口2正上方且不受两侧放矿口影响, 故该测量域内水平与垂直应力变化规律与单口放矿条件下的应力变化规律一致, 即随着松动体范围自下而上不断接近和到达第8号测量域所在高度时, 该处水平应力呈先增大后减小的趋势, 垂直应力则逐渐减小; 而当松动体范围超过第8号测量域所在高度时, 该处矿岩颗粒变得较为松散, 水平与垂直应力均在较低数值范围内呈波动变化的趋势;②第5号测量域处于两放矿口间的非松动区域, 该处水平应力不断减小; 垂直应力在放矿开始阶段无显著变化, 而在t1时刻即松动体范围到达第8号测量域所在高度时, 垂直应力开始逐渐增大, 表明在放矿过程中松动体上方的垂直应力会逐渐向两侧的非松动区域转移.
图 7(Fig. 7)
 | 图 7 试验4所得第5号和第8号测量域内水平与力的变化过程Fig.7 Variations of horizontal and vertical stresses within measurement regions No.5 and No.8 obtained in test 4 |
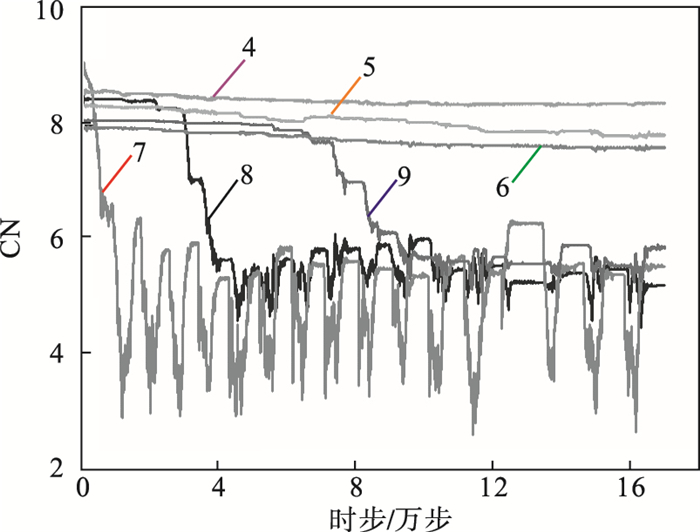
图 8为试验4所得第4~9号测量域内配位数的变化过程.由图 8分析可知: ①在整个放矿过程中, 处于非松动区域的第4~6号测量域内CN的数值基本为8~9, 均无显著变化,且空间高度越低即上覆岩层高度越大, 其配位数越大.②随着松动范围依次到达第7~9号测量域, 其CN亦依次减小; 此外, 与非松动区域内配位数变化不同的是, 在松动体范围内, 空间高度越低其CN越小但波动范围越大, 表明越接近放矿口的位置, 其矿岩颗粒越松散且运移与接触变化的无序程度越高.
图 8(Fig. 8)
 | 图 8 试验4所得第4~9号测量域内配位数的变化过程Fig.8 Variations of coordination number within measurement regions No. 4~No.9 obtained in test 4 |
2 不同放矿方式下的矿岩颗粒相互作用规律研究由于实际崩落法矿山存在矿-岩接触面不水平、个别放矿口堵塞等情况, 各放矿口并非始终保持同时出矿的方式.因此, 在对不同放矿口间距下矿岩颗粒运移和应力演化规律研究的基础上, 设计数值试验进一步探究不同放矿方式下的矿岩颗粒相互作用规律.
2.1 放矿数值试验设计为避免相邻放矿口间过多的矿石残留与损失, 实际崩落法矿山采场中设计的放矿口间距应能保证矿岩颗粒出现均匀流(两相邻松动体相交)[16].因此, 基于上节研究结果, 本次不同放矿方式下的数值试验中均保持放矿口间距为16 m(1.0wIMZ)不变, 具体设计方案如表 3所示.其中, 表 3中放矿口间距为16 m且放矿口1, 2, 3同时出矿的试验组作为本次放矿数值试验的对照组, 而放矿数值模型及其细观参数均与上节不同放矿口间距下的数值试验设计保持一致, 分别如图 3和表 2所示.
表 3(Table 3)
| 表 3 不同放矿方式下的数值试验方案 Table 3 Schemes of numerical simulation using different draw modes |
2.2 放矿数值试验结果分析三组放矿数值试验结束后, 依然从矿岩颗粒运移和应力演化两方面对比分析不同放矿方式下的矿岩颗粒相互作用规律.
1) 运移演化规律分析.图 9为不同放矿方式下停止出矿时刻的矿岩颗粒运移纵剖面图.与图 4b所示同时出矿方式下的矿岩颗粒运移结果相比, 相同之处在于图 9所示不同顺次出矿或间断出矿方式下的矿岩颗粒层在35 m和45 m等不同高度均已产生不同程度的相互作用, 即相邻松动体已相交; 不同之处在于同一高度的矿岩颗粒层并非均呈近似水平下降, 而是由于放矿方式的不同出现了不同程度的倾斜或非均匀下降的现象.由上述分析可知: 针对实际放矿过程中由于个别放矿口堵塞、矿岩自然或强制崩落效果不佳以及放矿管理不善等原因造成的矿-岩接触面不水平等情形, 可以通过改变各放矿口的出矿顺序调控矿岩颗粒的运移轨迹, 进而优化矿-岩接触面, 提高矿石回收率或减少废石提前混入.
图 9(Fig. 9)
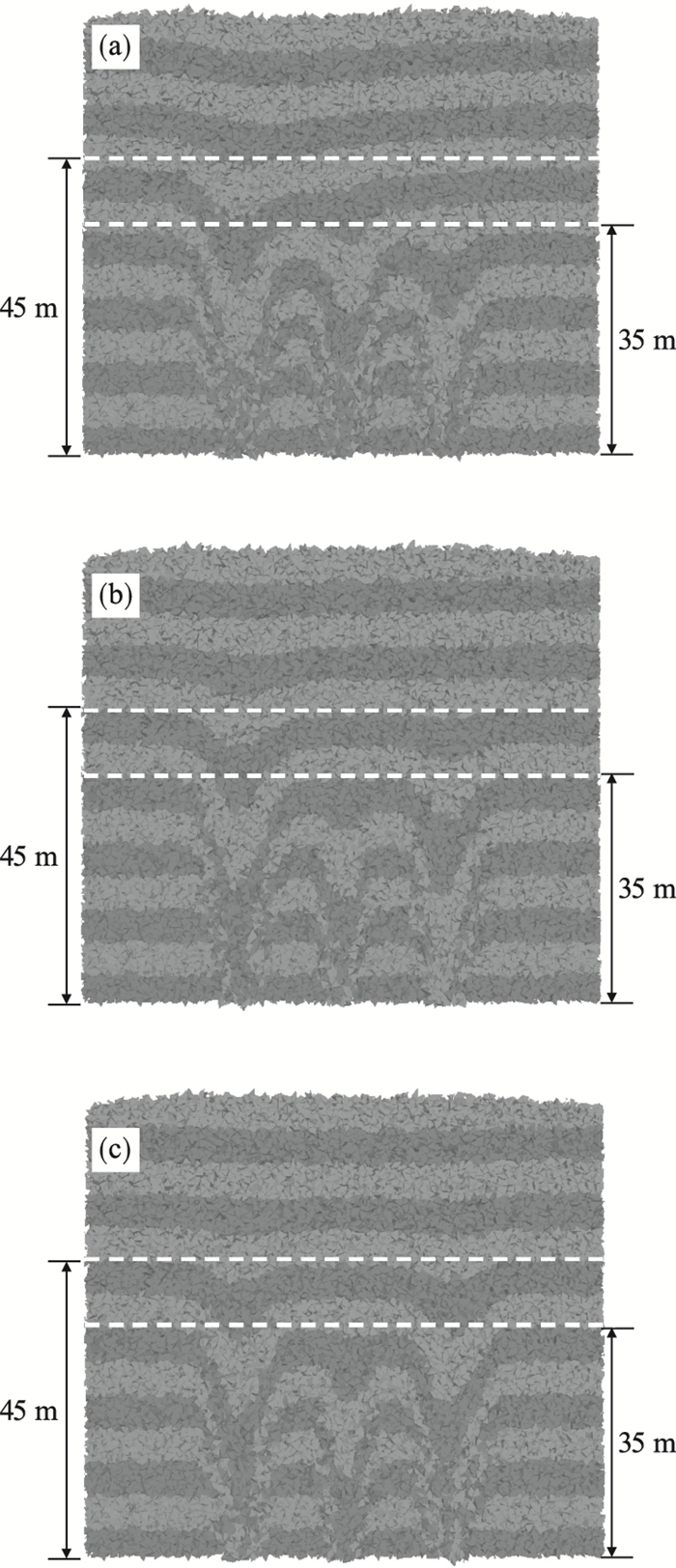 | 图 9 不同放矿方式下的矿岩颗粒运移纵剖面图Fig.9 Longitudinal profiles of movement of caved ore and rock with different draw modes (a)—试验1;(b)—试验2;(c)—试验3. |
2) 应力演化规律分析.统计包括对照试验在内的四组放矿数值试验中不同测量球域(图 3b)内水平应力与垂直应力的演化过程.其中, 图 10为不同放矿方式条件下第4号测量域内垂直应力的变化过程.由图 10中圆圈内曲线变化趋势所示: ①相同的是, 在四组放矿试验的初始阶段, 第4号测量域内垂直应力σv较放矿前的初始垂直应力σv, 0均出现明显激增的现象; ②不同的是, 在放矿初始阶段试验1~3中仅放矿口1出矿, 放矿口2未出矿, 因此仅有放矿口1上方的垂直应力向第4号测量域所在非松动区域转移, 三组试验中该区域内的最大垂直应力为初始垂直应力的1.3倍左右; 而对照试验中放矿口1和2同时出矿, 故两侧放矿口上方的垂直应力均向第4号测量域所在非松动区域转移, 因而与试验1~3相比, 对照试验中该区域内的最大垂直应力稍大一些.由此分析可知: 在放矿口间距不变的条件下, 不同放矿方式对采场底部所受最大垂直应力无显著影响.
图 10(Fig. 10)
 | 图 10 不同放矿方式下第4号测量域内垂直应力的变化过程Fig.10 Variations of vertical stress within measurement region No. 4 under different draw modes |
图 11为不同放矿方式下第3号和第8号测量域内水平应力的变化过程.如图 11a中圈1和圈2两圆圈内曲线变化趋势所示, 当松动范围逐渐接近和到达第3号测量域所在区域时, 试验1~3中第3号测量域内水平应力均出现不同程度激增的现象, 而对照试验中第3号测量域内水平应力无明显增加.这是由于放矿方式不同而产生的差异, 具体而言: 对于试验1~3, 由于放矿口1先于放矿口2和3出矿, 当松动范围逐渐接近和到达第3号测量域所在区域时, 其四周均为非松动区域, 即第3号测量域四周矿岩颗粒仍处于密实接触的状态, 应力拱效应[17]显著, 因此该区域存在明显的垂直应力转移、水平应力激增的现象.而对照试验采用的是同时出矿方式, 当松动范围逐渐接近和到达第3号测量域所在区域时, 其四周已形成均匀流, 即第3号测量域四周矿岩颗粒已处于松散接触的状态, 无显著应力拱效应, 因此该区域水平应力无明显增加.与之类似, 如图 11b中圆圈1, 2, 3, 4内曲线变化趋势所示, 不同放矿方式会影响第8号测量域四周应力分布状态, 因此四组试验中第8号测量域内水平应力会在不同放矿阶段出现不同程度的激增现象.由此分析可知: 不同放矿方式会显著影响采场内不同时刻和不同空间位置的应力分布状态, 进而影响整个矿岩颗粒体系的松动范围和流动特性.
图 11(Fig. 11)
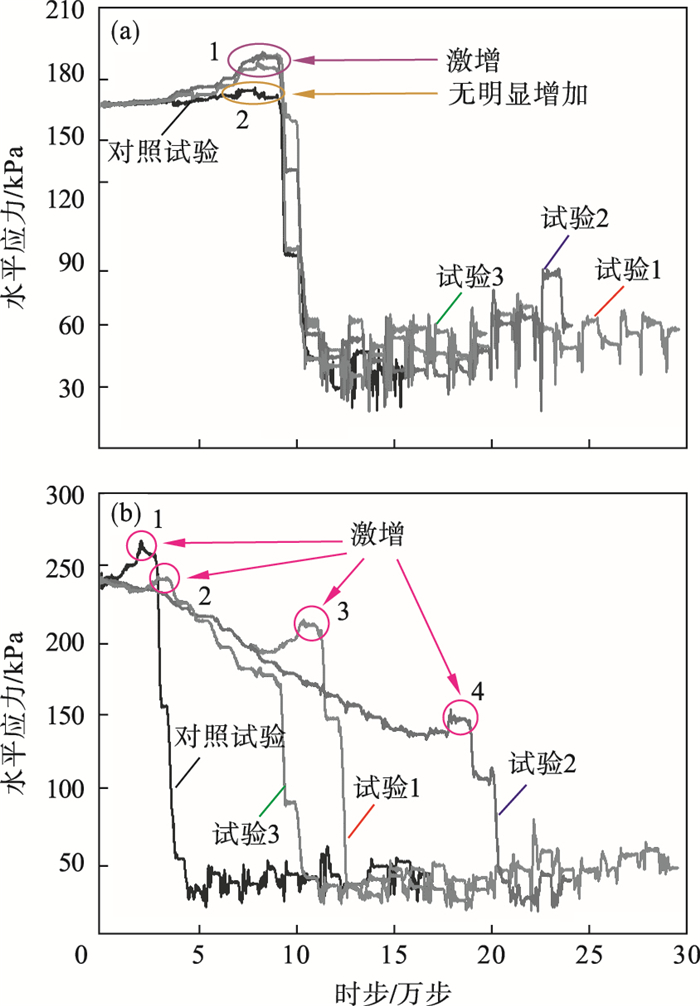 | 图 11 不同放矿方式下第3号和第8号测量域内水平应力的变化过程Fig.11 Variations of horizontal stress within measurement regions No.3 and No.8 under different draw modes (a)—第3号测量域;(b)—第8号测量域. |
3 讨论众所周知, 矿岩颗粒流动体系内存在不同形式、不同强度的拱结构/应力拱[11, 13], 而多放矿口间的矿岩颗粒相互作用规律和拱结构及应力转移之间亦存在显著的关联机制.因此, 从拱结构和应力转移(图 12)的角度对本文研究所得放矿口间距阈值和应力演化规律等问题作如下讨论.
图 12(Fig. 12)
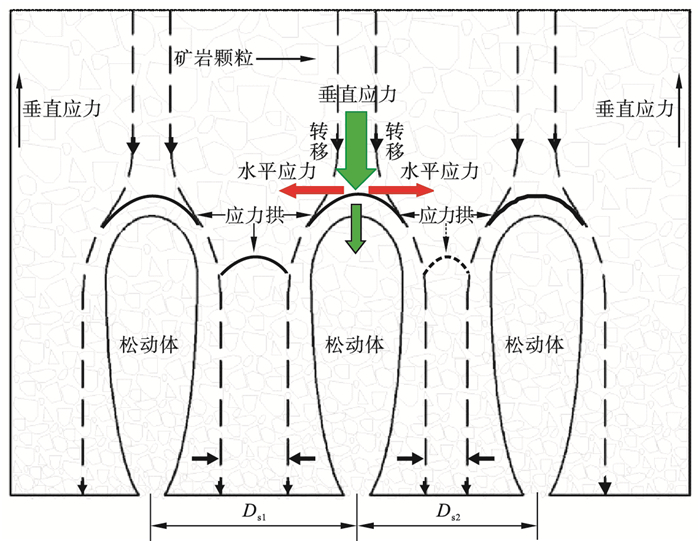 | 图 12 不同放矿口间距下的矿岩颗粒流动体系内应力拱和应力转移示意图Fig.12 Schematic of stress arch and stress transfer within the particle flow system of caved ore and rock with different drawpoint spacings |
1) 本文研究所得能够产生矿岩颗粒均匀流(两相邻松动体相交)的放矿口间距Ds的阈值介于1.0~1.25倍的松动体最大宽度wIMZ, 而非Laubscher[3]基于以砂子为介质的室内试验得出的1.5wIMZ.这是由于地下矿山开采过程中由爆破作用或自然崩落形成的矿岩散体是一种典型而复杂的颗粒物质体系, 其与玉米、小麦、大豆等农作物以及砂子等颗粒物质相比, 具有粒径分布范围广、形状复杂多变以及强度、内摩擦角大等特点, 故矿岩颗粒间存在显著的应力拱效应.因此, 在放矿口间距为松动体最大宽度的1.5倍条件下, 当两相邻松动体上方垂直应力向中间的非松动区域转移时, 非松动区域内垂直应力明显增大(如图 6中试验4对应的曲线).若以砂子为介质, 则诱发垂直应力将导致两放矿口间的非松动区域出现松动进而形成均匀流; 而以矿岩颗粒为介质, 则非松动区域内形成拱结构的矿岩颗粒间能够承受一定垂直应力而仍处于稳定状态.
2) 对于放矿口间距为松动体最大宽度的1.0倍时已能够产生矿岩颗粒均匀流这一现象, 则是与应力拱的形成条件相关.如图 12所示, 当放矿口间距较大时(如Ds1), 两放矿口间的矿岩颗粒可形成较为稳定的拱结构; 当放矿口间距逐渐减小时, 应力拱的拱长、跨度及其稳定性随之逐渐减小; 而当间距减小至某一值以下时(如Ds2), 由上覆矿岩自重产生的垂直应力以及由两相邻松动体上方转移而来的垂直应力的叠加作用会超过应力拱的承载极限, 组成该应力拱的矿岩散体间的关键接触出现断裂, 应力拱崩塌, 即矿岩颗粒间将难以形成稳定的拱结构(如图 11a中对照试验对应的曲线, 其水平应力无明显增加), 两放矿口间的矿岩颗粒随之产生松动.因此, 不同放矿口间距和放矿方式条件下的矿岩颗粒相互作用规律本质上可认为是矿岩颗粒流动体系内粒间力学行为的作用结果.
4 结论1) 放矿口间距和放矿方式两因素显著影响采场内矿岩颗粒运移和应力演化.多口放矿条件下能够产生矿岩颗粒均匀流的放矿口间距阈值介于1.0~1.25倍的松动体最大宽度, 对于实际崩落法矿山的采场结构参数优化具有一定借鉴意义.
2) 矿岩颗粒流动体系内存在明显的应力拱效应, 放矿过程中松动体上方的垂直应力会逐渐向两侧的非松动区域转移.在所研究的取值范围内, 采场底部最大垂直应力已接近初始垂直应力的1.8倍.因此, 若实际采场设计的相邻放矿口间距过小, 可能会威胁两放矿口间采场底部结构的稳定性.
3) 同时出矿方式下, 同一高度的矿岩颗粒层可形成近似水平下降的均匀流; 而顺次出矿或间断出矿方式下, 同一高度的矿岩颗粒层会出现不同程度的倾斜或非均匀下降的现象.因此实际生产中, 应综合考虑矿岩崩落效果和生产进度安排等因素, 通过改变各放矿口的出矿顺序调控矿岩颗粒运移轨迹, 进而优化矿-岩接触面, 提高矿石回收率或减少废石的提前混入.
4) 放矿过程中采场内非松动区域的配位数约为8~9, 且空间高度越低其配位数越大; 在松动区域内, 空间高度越低其配位数越小但波动范围越大, 即松动体内越接近放矿口的位置, 其矿岩颗粒越松散且运移与接触变化的无序程度越高.
参考文献
| [1] | 蔡美峰, 薛鼎龙, 任奋华. 金属矿深部开采现状与发展战略[J]. 工程科学学报, 2019, 41(4): 417-426. (Cai Mei-feng, Xue Ding-long, Ren Fen-hua. Current situation and development strategy of deep mining in metal mines[J]. Chinese Journal of Engineering, 2019, 41(4): 417-426.) |
| [2] | Fairhurst C. Some challenges of deep mining[J]. Engineering, 2017, 3(4): 527-537. DOI:10.1016/J.ENG.2017.04.017 |
| [3] | Laubscher D H. Block cave manual, design topic: drawpoint spacing and draw control[D]. Brisbane: University of Queensland, 2000. |
| [4] | Pierce M E. A model for gravity flow of fragmented rock in block caving mines[D]. Brisbane: University of Queensland, 2009. |
| [5] | Marano G. The interaction between adjacent draw points in free flowing materials and it application to mining[J]. Chamber Mines Journal, 1980, 22: 25-32. |
| [6] | Hancock W. Gravity flow of rock in caving mines: numerical modelling of isolated, interactive and non-ideal draw[D]. Brisbane: University of Queensland, 2013. |
| [7] | Trueman R, Castro R, Halim A. Study of multiple draw-zone interaction in block caving mines by means of a large 3D physical model[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(7): 1044-1051. DOI:10.1016/j.ijrmms.2007.11.002 |
| [8] | Lorig L. Relation between caved column height and vertical stress at the cave base[R]. Houston: JKMRC and Itasca Consulting Group Inc, 2000. |
| [9] | Pierce M E. Forecasting vulnerability of deep extraction level excavations to draw-induced cave loads[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2019, 11(3): 527-534. DOI:10.1016/j.jrmge.2018.07.006 |
| [10] | Janssen H A. Experiments regarding grain pressure in soils[J]. Zeitschrift Des Vereines Deutscher Ingenieure, 1895, 39(35): 1045-1049. |
| [11] | Castro R, Gómez R, Pineda M, et al. Experimental quantification of vertical stresses during gravity flow in block caving[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 127: 104237. DOI:10.1016/j.ijrmms.2020.104237 |
| [12] | Itasca Consulting Group Inc. PFC 6.0 documentation[EB/OL]. (2019-01-01)[2021-05-16]. http://docs.itascacg.com/pfc600/pfc/docproject/index.html. |
| [13] | 孙浩, 陈帅军, 高艳华, 等. 基于刚性块体模型的近-远场崩落矿岩流动特性[J]. 工程科学学报, 2021, 43(2): 205-214. (Sun Hao, Chen Shuai-jun, Gao Yan-hua, et al. Rock flow characteristics of near-far field caving based on rigid block model[J]. Chinese Journal of Engineering, 2021, 43(2): 205-214.) |
| [14] | Sun H, Jin A B, Davide E, et al. A numerical based approach to calculate ore dilution rates using rolling resistance model and upside-down drop shape theory[J]. Rock Mechanics and Rock Engineering, 2020, 53(10): 4639-4652. DOI:10.1007/s00603-020-02180-6 |
| [15] | Jin A B, Sun H, Wu S C, et al. Confirmation of the upside-down drop shape theory in gravity flow and development of a new empirical equation to calculate the shape[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 92: 91-98. DOI:10.1016/j.ijrmms.2016.12.005 |
| [16] | Castro R. Study of the mechanisms of gravity flow for block caving[D]. Brisbane: University of Queensland, 2006. |
| [17] | Roberto A, Maza D, Pugnaloni L A. Identification of arches in two-dimensional granular packings[J]. Physical Review E: Statal Nonlinear and Soft Matter Physics, 2006, 74(2): 021303. DOI:10.1103/PhysRevE.74.021303 |
