
 , 任子洋, 黄友鹤, 于霞
, 任子洋, 黄友鹤, 于霞 东北大学 信息科学与工程学院, 辽宁 沈阳 110819
收稿日期:2021-06-03
基金项目:国家自然科学基金资助项目(61973067, 61903071)。
作者简介:李鸿儒(1968-),男,内蒙古赤峰人,东北大学教授,博士生导师。
摘要:现有心律不齐研究多数围绕心电信号中不同频率特性成分的分离展开, 而不同子序列的信息量对于最终目标决策的贡献则缺少研究与分析.为增强高贡献度子序列对于分类器的影响, 提出了一种变权重奇异谱分析与深度学习结合的识别方法.通过奇异谱分析获得多个子序列, 结合各个子序列的奇异值计算随机森林下的基尼系数, 并将其作为权重.变权重的序列样本用于训练神经网络模型, 更高效地挖掘了有用信息, 进一步提高了识别精度, 最终的心律不齐识别准确率为98.35%, Macro-F1为97.95%.相对于传统的定值权重, 本文提出的变权重识别方法在各个性能指标上均有明显提升.
关键词:心电图奇异谱分析深度学习心律不齐识别随机森林
Recognition Method of Arrhythmia Based on Variable Weight Singular Spectrum Analysis
LI Hong-ru

 , REN Zi-yang, HUANG You-he, YU Xia
, REN Zi-yang, HUANG You-he, YU Xia School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: LI Hong-ru, E-mail: lihongru@ise.neu.edu.cn.
Abstract: Many existing arrhythmia researches focus on the separation of different frequency characteristic components in the ECG signal. However, the contribution of different subsequences to the final target decision-making is lack of research and analysis. In order to enhance the impact of high-contribution subsequences on the classifier, a recognition method combining variable weight singular spectrum analysis and deep learning is proposed. Multiple subsequences are obtained through singular spectrum analysis.The Gini coefficient under the random forest is calculated by the singular value of each sequence and used as the weight. The sequence samples with variable weights are used to train the neural network model, which can mine useful information more efficiently and further improve the recognition accuracy. The accuracy rate of final arrhythmia recognition is 98.35%, and Macro-F1 is 97.95%. Compared with the traditional fixed weight, the proposed recognition method of variable weight has a significant improvement in various performance indicators.
Key words: lectrocardiogram(ECG)singular spectrum analysis(SSA)deep learningarrhythmia recognitionrandom forest
年龄的增长以及饮食作息的不正常导致心脏逐渐衰弱, 并伴随着慢性疾病的发作, 这会对人体造成巨大损伤.临床医护人员对于心电图(electrocardiogram, ECG)的分析往往需要结合自身的经验, 这使得诊治具有主观性且需要一定的时间成本.心脏病早期的体现通常为心律不齐, 因此对于心律失常的智能分析识别在心脏病预测的研究中具有重要意义.
早期对于ECG的分析一般包括预处理、特征提取和分类三个环节[1].最早的研究[2-3]从形态学出发, 有效提取了ECG的主要组分, 也有****采用频域算法, 包括小波变换[4-7]和经验模态分解[8-9]等算法, 以较小的失真获得具有不同频率特性的子序列.但小波变换在提高时间精度的同时会损失频率精度, 经验模态分解存在模态混叠的现象, 二者的分解序列均存在部分畸变.Yucelbas等[10]对比了奇异值分解、变分模态分解和小波变换在ECG分类中的性能, 奇异值分解的识别性能明显高于其余二者, 因此在考虑保留形态完整性的前提下如何提高频率信息的分离效率是后续识别的关键.Barrios等[11]最早提出一种基于奇异谱分析(singular spectrum analysis, SSA)的心电信号与肌电信号分离算法, 在时域和频域上, 与传统的信号分离算法进行对比, 均具有更好的性能; 还有围绕着SSA与心电去噪的研究[12-13], 也验证了该算法相较于传统算法的高效性.现有的研究对ECG进行拆分后没有考虑到子序列所包含信息量对于最终决策的贡献, 直接将定值权重或者去除高频的分量子序列作为输入样本.文献[14-15]结合多个分类器并配置不同权重进行投票分类, 明显提高了小样本类别的识别精度.变权重可以增强包含信息量高的子序列对于识别系统的影响, 因此根据子序列的信息量进行加权处理可能会更好地表达有效信息.
深度学习应用于心电领域的研究主要围绕着卷积神经网络(convolutional neural networks, CNN)[16-20]、循环神经网络(recurrent neural network, RNN)[21]以及长短期记忆网络(long short-term memory, LSTM)[22-23]开展.相较于独立的CNN与LSTM, 基于1D-CNN和LSTM结合[24-26]的模型在最新的研究中被证明具有更强的分类性能.Huang等[27]提取频谱图并利用2D-CNN网络层进行分类; Yildirim[28]提出了一种基于小波分解序列的双向LSTM网络模型, 利用小波变换提取的序列分量进行训练, 结合心电信号不同频率特性组分的学习大幅度提高了识别精度.因此, 使用更好的分解方法挖掘有效信息并与深度学习结合是提升识别效果的一个方向.
综上所述, 为了权衡心电信息中不同模态的信息量, 本文提出了一种变权重SSA与CNN,LSTM连接的组合网络, 采用由决策目标主导的可变权重代替传统的固定不变权重, 对奇异谱分解后包含不同信息量的模态进行变权重处理, 然后将变权重后的分量模态重组为新的序列输入至CNN-LSTM网络中进行分类.同时对比了多种权重计算算法, 选择识别精度最高的随机森林分类器各个特征的基尼系数作为权重, 利用变权重的序列训练深度学习模型, 更高效地挖掘潜在的信息, 从而提升心律不齐的识别精度.
1 数据库介绍1.1 数据集划分美国麻省理工学院开发的心律失常数据库MIT-BIH记录了48名病人30 min 2个导联的心电信号和类别标签.部分研究按照正常(N)、左束支阻滞(LBBB)、右束支阻滞(RBBB)、房性早搏(APC)和室性早搏(PVC)五类进行分类.研究者的分析主要围绕着患者内(intra-patient)[29-30]和患者间(inter-patient)[31-32]两种分类方式展开.Chazal等[33]将这些病人的记录分为2个数据集DS1和DS2, 前者用于训练模型并评估分类器性能, 后者用于测试分类结果的有效性.这两个样本集合所包含的病人序号如表 1所示.
表 1(Table 1)
| 表 1 MIT-BIH库中划分的数据集DS1, DS2 Table 1 Datasets DS1 and DS2 divided in the MIT-BIH library |
Kiranyaz等[34]提出patient-specific的分类方式, 从测试集数据中提取5 min的数据(占整体测试集的15%~18%)加入训练集, 可以一定程度克服患者间的特异性.因此本文选择从DS2中取出每个病人前15%的数据加入训练集, 表 2为本文数据集的构成.
表 2(Table 2)
| 表 2 数据集划分数量表 Table 2 Dataset division number |
1.2 预处理对于较长时序的心电信号需要进行逐拍的划分, 每个心拍应该包括P, Q, R, S和T波段, 一般以R波峰为中心, 本文采用Pan-Tompkins算法[35]检测出R波峰, 并取前127个节点和后128个节点, 作为单个心拍的样本序列.将提取到的多个序列进行z-score标准化, 这种处理有助于多种ECG序列的形态统一, 在后续奇异值计算时, 也会减少主成分幅值过大导致的权重失衡.
2 算法结构本文提出一种变权重子序列与深度学习分类器结合的心律不齐识别算法, 结合SSA与随机森林下的基尼系数提取变权重子序列, 将其作为1D-CNN与LSTM组合网络的输入, 进行心律不齐的识别, 图 1为本文的算法流程框架.
图 1(Fig. 1)
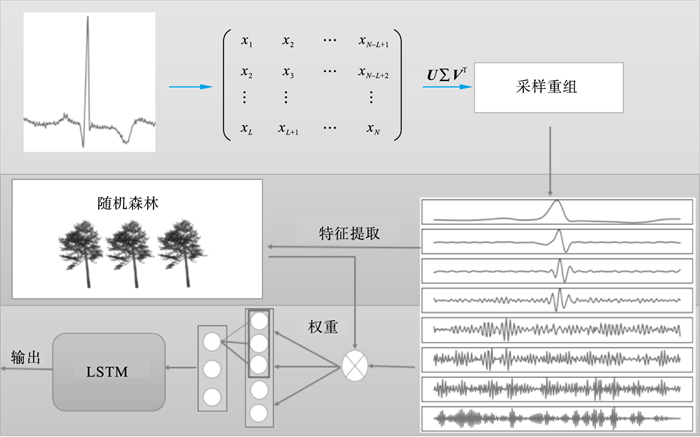 | 图 1 算法流程框架Fig.1 Algorithm flow frame |
2.1 奇异谱分析SSA是一种基于相空间重构的信号分解法, 通过奇异值分解得到原始信号的不同成分序列, 奇异值较大的序列为ECG的主要平稳信号, 奇异值较小的序列则代表ECG的高频组分.信号分解主要包括嵌入、分解、分组和对角平均化四个过程, 首先对于时间序列[x1, x2, …, xN], N=256为序列长度, 利用合适长度为8的序列窗口建立轨迹矩阵X, 通过奇异值分解(singular value decomposition, SVD)实现轨迹矩阵的拆分变换, 计算协方差矩阵XXT的特征值λ1>λ2>…>λL≥0和对应的特征向量[U1, U2, …, UL]:
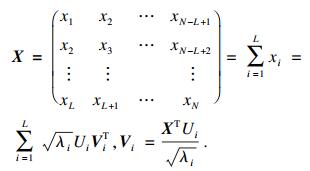 | (1) |
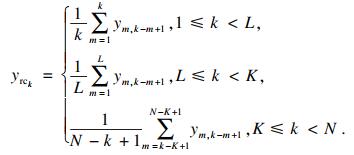 | (2) |
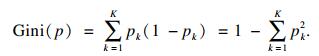 | (3) |
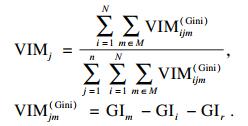 | (4) |
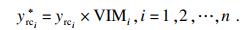 | (5) |
本文采用多层CNN与LSTM连接的组合网络, 将CNN的输出作为LSTM的输入, 在减少计算复杂度的基础上进行时序数据的分析, 图 2为神经网络整体结构.
图 2(Fig. 2)
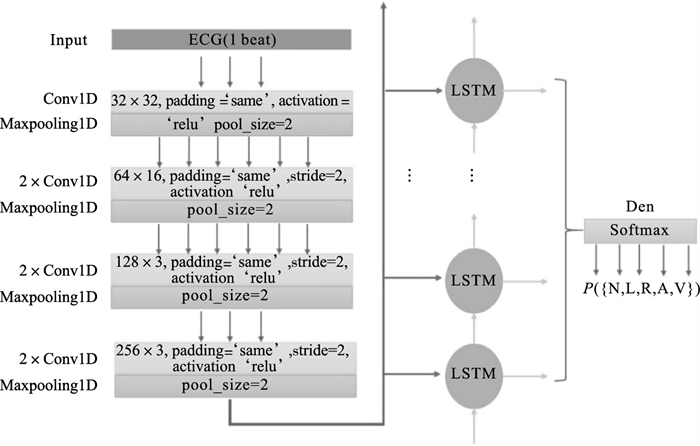 | 图 2 神经网络结构图Fig.2 Neural network structure diagram |
对于网络结构中的参数更新, 则需要一个非凸优化的损失函数, 本文采用交叉熵损失函数并以Adam的方式进行参数优化更新.
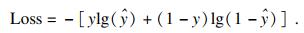 | (6) |
3 实验结果及分析3.1 评价指标关于网络训练结果性能的比较, 本文采用灵敏度(sensitivity, Sen)、特异性(specificity, Spe)、准确率(accuracy, Acc)以及综合性能描述指标F1-score,Macro-F1进行评判.各项指标的计算如式(7)所示, 其中Macro-F1为各类别的F1-score均值.
 | (7) |
图 3(Fig. 3)
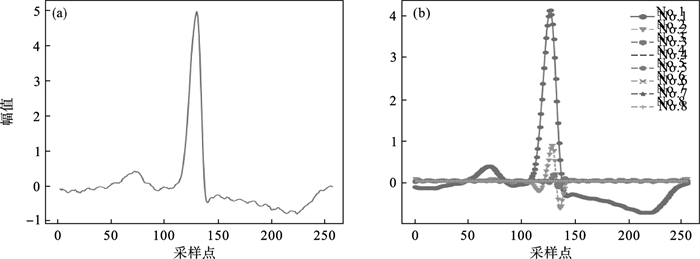 | 图 3 子序列可视化Fig.3 Visualization of sub-sequence (a)—初始信号;(b)—多个子序列. |
将奇异值分解得到的多个子序列特征值作为每个样本的特征, 训练各个分类器, 按照式(3)计算得到各个子序列所对应的权重, 表 3为各个分类器得到的权重.
表 3(Table 3)
| 表 3 特征权重 Table 3 Feature weight |
3.3 模态分量的训练结果将提取到的序列输入到图 2中的网络模型中, 进行神经网络的训练, 迭代训练200次后, 模型准确率及损失函数不再产生较大变化, 最终对于DS2的分类准确率最高可达到98.35%, 模型训练过程的准确率上升曲线及最终得到的DS2分类混淆矩阵如图 4所示.
图 4(Fig. 4)
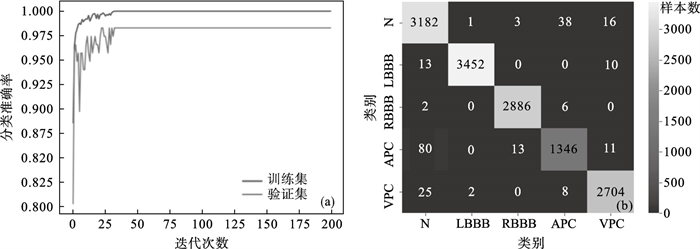 | 图 4 模型训练过程及分类混淆矩阵Fig.4 Model training process and classification confusion matrix (a)—训练集和验证集的准确率上升曲线;(b)—测试集混淆矩阵. |
模型对于训练样本的学习逐渐收敛, 最终训练集的分类准确率接近100%.从表 4中可以看出, 测试集识别结果的灵敏度和准确率较高, N类的特异性接近99%, 模型对于LBBB和RBBB两类具有较好的综合能力.
表 4(Table 4)
| 表 4 识别性能指标 Table 4 Recognition performance indicators | ||||||||||||||||||||||||||||||
本文采用五折交叉验证对非变权重子序列、非变权重去噪子序列(仅保留奇异值总占比平均达到95.81%的前三个子序列)、变权重去噪子序列及变权重子序列作为输入的识别方法性能进行了对比, 同时采用多种计算权重的算法以说明随机森林计算权重的有效性, 对比实验结果如表 5所示.
表 5(Table 5)
| 表 5 变权重SSA的识别性能对比 Table 5 Recognition performance comparison of variable weight singular spectrum analysis? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
从表 5中可看出, 变权重子序列的识别性能相较于非变权重子序列在各项指标均有明显提升, 这证明变权重的方式高效地保留了与决策相关的信息.为了说明变权重算法的优越性, 本文也进行了去噪后子序列的变权重对比实验, 如表 5中的第4, 5行所示, 在预处理去噪后, 变权重的学习方式依然能够明显增强识别性能, 因此本文的算法对于ECG分解子序列的选择具有一定适应性.
为了说明随机森林权重的高效性, 本文采取了其他权重计算(分类)方法, 包括主成分分析、线性判别分析与AdaBoost算法, 对比结果如表 6所示.
表 6(Table 6)
| 表 6 不同权重算法的识别性能对比 Table 6 Recognition performance comparison of different weighting algorithms ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
本文结合变权重的小波分解序列及变分模态分解的模态分量作为输入样本进行对比说明, 其中小波分解选择db6小波基获得8个子序列, 变分模态分解设置保真度系数及中心频率更新参数为0、中心频率初始化参数为1及惩罚因子为2 000, 获得8个模态分量, 二者的分类准确率均低于基于SSA分解子序列输入的模型算法.本文的算法在各类的指标上均取得了更好的效果, 说明SSA对于决策目标的表征能力较强.表 7为上述三种分解算法五折交叉验证下平均识别性能的对比.
表 7(Table 7)
| 表 7 小波分解与变分模态分解的识别性能 Table 7 Recognition performance of wavelet decomposition and variational modal decomposition ? | ||||||||||||||||||||||||||||||||||||||||||||||||||
3.4 讨论随机森林内部的参数设置会改变最终的识别准确率, 包括其弱分类器数量的影响, 表 8为不同个体分类器数量下的准确率.
表 8(Table 8)
| 表 8 不同数量个体分类器的识别准确率 Table 8 Recognition accuracy of different numbers of individual classifier |
从表 8中看出, 随机森林的结构差异产生的权重变化会影响到最终的识别效果, 复杂的结构会带来模型的过拟合, 因此权重的最优决策有助于提高识别准确率.
表 9为现有的心律不齐识别研究成果对比.文献[31, 36-38]未采用深度学习进行分类, 利用传统的特征和分类器, 识别精度相对较低.文献[37]的研究得到较高的识别准确率, 但由于患者内的识别任务无法解决样本间差异的问题, 存在较大的泛化误差, 而文献[24]的研究未进行数据平衡, 大类的样本数量远超小样本数量.本文利用变权重的子序列, 对于数据平衡后的样本, 提高了患者间分类的准确率.由于缺少临床的数据, 因此无法对线下病例进行实际验证.
表 9(Table 9)
| 表 9 心律失常识别的研究 Table 9 Research on arrhythmia recognition |
4 结语本文以均衡不同频率特性子序列间的信息量为目的, 提出了一种基于变权重奇异谱分析和深度学习结合的心律不齐识别算法.选择奇异谱分析算法对心电信号不同频率特性组分进行分离, 结合奇异值训练随机森林模型并得到各个特征的基尼系数作为权重, 低频序列的权重值占比较大, 而高频组分则权重较小.将变权重子序列用于训练神经网络模型, 最终测试集分类准确率为98.35%.通过仿真对比, 奇异谱分析相较于小波分解、变分模态分解, 分解得到的多个模态子序列作为输入样本的识别精度最高, 子序列所包含的信息更加有效.而变权重的学习方式可以增强高信息量子序列对于识别系统的影响, 相较于以往研究的权重统一, 在各个指标上均有明显提升.为进一步验证算法的有效性, 在现有研究去噪处理后加入变权重环节, 仍然能够得到识别性能提升的结果.因此本文的算法有效增加了高信息量子序列的权重, 使潜在的有效信息得到更好的表达, 进一步提高了识别精度.对于权重的计算算法, 仍未寻找到严格意义上的最优决策, 因此寻求一个计算最佳权重的自适应算法对于后续变权重的心律不齐识别研究有重要意义.
参考文献
| [1] | Berkaya S K, Uysal A K, Gunal E S, et al. A survey on ECG analysis[J]. Biomedical Signal Processing and Control, 2018, 43: 216-235. DOI:10.1016/j.bspc.2018.03.003 |
| [2] | Sharma M, Tan R S, Acharya U R. A novel automated diagnostic system for classification of myocardial infarction ECG signals using an optimal biorthogonal filter bank[J]. Computers in Biology and Medicine, 2018, 102: 341-356. DOI:10.1016/j.compbiomed.2018.07.005 |
| [3] | 郑秀玉, 卢瑞祥. 基于FIR滤波和数学形态学的心电信号预处理算法[J]. 中国医疗设备, 2015, 30(9): 20-23. (Zheng Xiu-yu, Lu Rui-xiang. ECG signals pre-processing based on FIR filtering and mathematical morphology[J]. China Medical Device, 2015, 30(9): 20-23. DOI:10.3969/j.issn.1674-1633.2015.09.005) |
| [4] | Singh O, Sunkaria R K. ECG signal denoising via empirical wavelet transform[J]. Australasian Physical & Engineering Sciences in Medicine, 2016, 40(1): 1-11. |
| [5] | 方明占. 基于小波变换的心电信号去噪算法研究[D]. 桂林: 桂林电子科技大学, 2012. (Fang Ming-zhan. Research on denoising algorithm of ECG signal based on wavelet transform[D]. Guilin: University of Electronic Technology, 2012. ) |
| [6] | Awal M A, Mostafa S S, Ahmad M, et al. An adaptive level dependent wavelet thresholding for ECG denoising[J]. Biocybernetics & Biomedical Engineering, 2014, 34(4): 238-249. |
| [7] | Chaudhary M S, Kapoor R, Sharma A K. Comparison between different wavelet transforms and thresholding techniques for ECG denoising[C]//International Conference on Advances in Engineering & Technology Research. Unnao, India: IEEE, 2014: 1-6. |
| [8] | Satija U, Ramkumar B, Manikandan M S. Automated ECG noise detection and classification system for unsupervised healthcare monitoring[J]. IEEE Journal of Biomedical and Health Informatics, 2018, 22(99): 722-732. |
| [9] | Rakshit M, Das S. An efficient ECG denoising methodology using empirical mode decomposition and adaptive switching mean filter[J]. Biomedical Signal Processing & Control, 2018, 40: 140-148. |
| [10] | Yucelbas S, Yucelbas C, Tezel G, et al. Automatic sleep staging based on SVD, VMD, HHT and morphological features of single-lead ECG signal[J]. Expert Systems with Applications, 2018, 102: 193-206. DOI:10.1016/j.eswa.2018.02.034 |
| [11] | Barrios M J, Romero F, Javier F, et al. A simple SSA-based denoising technique to remove ECG interference in EMG signals[J]. Biomedical Signal Processing and Control, 2016, 30: 117-126. DOI:10.1016/j.bspc.2016.06.001 |
| [12] | Mortezaee M, Mortezaie Z, Abolghasemi V. An improved SSA-based technique for EMG removal from ECG[J]. Innovation and Research in Biomedical Engineering, 2019, 40(1): 62-68. |
| [13] | Mukhopadhyay S K, Krishnan S. A singular spectrum analysis-based model-free electrocardiogram denoising technique[J]. Computer Methods and Programs in Biomedicine, 2020, 188: 105304-105318. DOI:10.1016/j.cmpb.2019.105304 |
| [14] | Deepthi S, Ravikumar A, Nair R V. Evaluation of classification techniques for arrhythmia screening of astronauts[J]. Procedia Technology, 2016, 24: 1232-1239. DOI:10.1016/j.protcy.2016.05.099 |
| [15] | Kandala R, Huli R D, Pawiak P, et al. Towards real-time heartbeat classification: evaluation of nonlinear morphological features and voting method[J]. Sensors, 2019, 19(23): 5079. DOI:10.3390/s19235079 |
| [16] | Ylldlrlm ?, P?awiak P, Tan R S, et al. Arrhythmia detection using deep convolutional neural network with long duration ECG signals[J]. Computers in Biology and Medicine, 2018, 102: 411-420. DOI:10.1016/j.compbiomed.2018.09.009 |
| [17] | Oh S L, Ng E Y K, Tan R S, et al. Automated beat-wise arrhythmia diagnosis using modified U-net on extended electrocardiographic recordings with heterogeneous arrhythmia types[J]. Computers in Biology and Medicine, 2018, 105: 92-101. |
| [18] | Xiong Z, Nash M P, Cheng E, et al. ECG signal classification for the detection of cardiac arrhythmias using a convolutional recurrent neural network[J]. Physiological Measurement, 2018, 39(9): 094006-094015. DOI:10.1088/1361-6579/aad9ed |
| [19] | Sellami A, Hwang H. A robust deep convolutional neural network with batch-weighted loss for heartbeat classification[J]. Expert Systems with Applications, 2019, 122: 75-84. DOI:10.1016/j.eswa.2018.12.037 |
| [20] | Yang W, Si Y, Wang D, et al. Automatic recognition of arrhythmia based on principal component analysis network and linear support vector machine[J]. Computers in Biology and Medicine, 2018, 101: 22-32. DOI:10.1016/j.compbiomed.2018.08.003 |
| [21] | Zhang C, Wang G, Zhao J, et al. Patient-specific ECG classification based on recurrent neural networks and clustering technique[C]//Iasted International Conference on Biomedical Engineering. Innsbruck, Austria: IEEE, 2017: 63-67. |
| [22] | Faust O, Hagiwara Y, Hong T J, et al. Deep learning for healthcare applications based on physiological signals: a review[J]. Computer Methods & Programs in Biomedicine, 2018, 161: 1-13. |
| [23] | Yildirim ?, Baloglu U B, Tan R S, et al. A new approach for arrhythmia classification using deep coded features and LSTM networks[J]. Computer Methods and Programs in Biomedicine, 2019, 176: 121-133. DOI:10.1016/j.cmpb.2019.05.004 |
| [24] | Oh S L, Ng E Y K, Tan R S, et al. Automated diagnosis of arrhythmia using combination of CNN and LSTM techniques with variable length heart beats[J]. Computers in Biology & Medicine, 2018, 102: 278-287. |
| [25] | Tan J H, Hagiwara Y, Pang W, et al. Application of stacked convolutional and long short-term memory network for accurate identification of CAD ECG signals[J]. Computers in Biology & Medicine, 2018, 94: 19-26. |
| [26] | Andersen R S, Peimankar A, Puthusserypady S. A deep learning approach for real-time detection of atrial fibrillation[J]. Expert Systems with Application, 2019, 115: 465-473. DOI:10.1016/j.eswa.2018.08.011 |
| [27] | Huang J, Chen B, Yao B, et al. ECG arrhythmia classification using STFT-based spectrogram and convolutional neural network[J]. IEEE Access, 2019, 7(99): 92871-92880. |
| [28] | Yildirim ?. A novel wavelet sequences based on deep bidirectional LSTM network model for ECG signal classification[J]. Computers in Biology & Medicine, 2018, 96: 189-202. |
| [29] | 束伟伟. 基于深度学习的心电信号分类方法研究[D]. 南昌: 江西财经大学, 2020. (Shu Wei-wei. Research on ECG signal classification method based on deep learning[D]. Nanchang: Jiangxi University of Finance and Economics, 2020. ) |
| [30] | Mousavi S, Afghah F. Inter-and intra-patient ECG heartbeat classification for arrhythmia detection: asequence to sequence deep learning approach[C]//ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing(ICASSP). Brighton: IEEE, 2019: 1308-1312. |
| [31] | Shi H, Wang H, Zhang F, et al. Inter-patient heartbeat classification based on region feature extraction and ensemble classifier[J]. Biomedical Signal Processing and Control, 2019, 51: 97-105. DOI:10.1016/j.bspc.2019.02.012 |
| [32] | 宋新景. 基于残差连接网络与度量学习的短期心电信号分类方法研究[D]. 济南: 山东大学, 2020. (Song Xin-jing. Research on short-term ECG signal classification method based on residual connection network and metric learning[D]. Jinan: Shandong University, 2020. ) |
| [33] | Chazal P D, Dwyer M O, Reilly R B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features[J]. IEEE Transactions on Biomedical Engineering, 2004, 51(7): 1196-1206. DOI:10.1109/TBME.2004.827359 |
| [34] | Kiranyaz S, Ince T, Gabbouj M. Real-time patient-specific ECG classification by 1-D convolutional neural networks[J]. IEEE Transaction on Biomedical Engineering, 2016, 63(3): 664-675. DOI:10.1109/TBME.2015.2468589 |
| [35] | Pan J, Tompkins W J. A real-time QRS detection algorithm[J]. IEEE Transactions on Biomedical Engineering, 2007, 54(3): 230-236. |
| [36] | Sadiq A T, Shukr N H. Classification of cardiac arrhythmia using ID3 classifier based on wavelet transform[J]. Iraqi Journal of Science, 2013, 54: 1167-1175. |
| [37] | Sabut S, Sahoo S, Kanungo B, et al. Multiresolution wavelet transform based feature extraction and ECG classification to detect cardiac abnormalities[J]. Measurement, 2017, 108(108): 55-66. |
| [38] | Yao Q, Wang R, Fan X, et al. Multi-class arrhythmia detection from 12-lead varied-length ECG using attention-based time-incremental convolutional neural network[J]. Information Fusion, 2020, 53: 174-182. DOI:10.1016/j.inffus.2019.06.024 |
