基于动态双重前缀的模糊相似性连接算法

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-11-20

于长永, 王雯函, 温秀静, 赵宇海
东北大学计算机科学与工程学院, 辽宁沈阳 110169
收稿日期：2021-09-07
基金项目：国家自然科学基金资助项目(61772124)。
作者简介：于长永(1981-)，男，辽宁海城人，东北大学副教授。

摘要：针对相似性连接问题, 提出了动态双重前缀的模糊相似性连接算法.与之前的算法不同的是, 本文采用双重前缀, 即在查找候选以及构建索引时使用不同的前缀来提高过滤效率，并在此基础上进行了优化.首先通过取各个前缀生成的候选集合的交集来缩小候选集合; 其次提出最大区分任选前缀, 利用此前缀进行预验证来减少最终进入到验证过程的候选对, 以此来减少连接时间.并且在三个真实数据集上进行实验, 将本文算法与Silkmoth算法以及MF-Join算法进行比较, 结果表明所提算法可以生成更小的候选集集合并且需要更少的连接时间.
关键词：相似性连接任选前缀候选前缀过滤验证过程
Fuzzy Similarity Join Algorithm Based on Dynamic Double Prefixes
YU Chang-yong, WANG Wen-han, WEN Xiu-jing, ZHAO Yu-hai
School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: WANG Wen-han, E-mail: wwhneu@126.com.

Abstract: Focusing on the similarity join problem, a fuzzy similarity join algorithm was proposed based on dynamic double. The difference from the previous algorithms is that double prefixes are introduced, which improves the filtering efficiency when searching for candidates and building indexes due to the differences of prefixes. On this basis, optimization is realized. First, the candidate set is narrowed by taking the intersection of the candidate sets generated by each prefix. Afterwards, the maximum distinguishing arbitrary-selected prefix is proposed, and this prefix is used for pre-verification to reduce the final candidate pairs that enter the verification process, thereby reducing the join time. Experiments are conducted on three real datasets, and the proposed algorithm is compared with the Silkmoth and MF-Join. The results show that the proposed algorithm can generate a smaller set of candidate set and requires less join time.
Key words: similarity joinarbitrary-selected prefixcandidateprefix filterverification process
相似性查找和相似性连接是数据库中处理和分析数据的重要且基础的操作.相似性查找旨在查询与给定query满足相似性条件的数据库中的所有记录.相似性连接旨在从两个集合中找到所有相似的对.它们有许多实际应用, 如数据清理与集成、近似重复检测和信息提取等.例如当两个购物网站要合并时, 两个网站对同一商品的描述不完全一致, 此时就需要找出两个网站中的同一商品并最终合并.因为该数据集很大, 高效处理数据是一种重要需求, 所以相似性连接在该情况下是一种必不可少的操作.
对于传统的Jaccard算法, 根据过滤算法原理, 大致可分为以下三种类型: ①基于前缀过滤的算法; ②基于鸽笼和划分思想的过滤算法; ③基于树型数据结构的过滤算法.前缀过滤算法是基于两个数据的前缀至少共享一个元素来实现的^[1-3].文献[1]首次提出了前缀过滤的思想, 并利用倒排索引实现了快速的相似性连接算法；文献[2]通过将各记录中的元素按照频率由小到大的顺序排序优化了前缀过滤；文献[3]进一步缩小了前缀的长度，利用共享元素的位置信息对候选进行位置过滤，而且该文还对位置过滤的思想进行推广, 提出了后缀过滤.基于鸽笼和划分的过滤算法^[4-6]主要思想是先根据鸽笼原理将每条记录划分为特定个数的不相交的段, 再将这些段作为签名构建索引, 最后计算出至少有一个共有段的记录对的集合作为候选集.文献[4]首次利用鸽笼原理提出了PartEnum；文献[5]首次提出了基于全局元素划分的鸽笼过滤算法；文献[6]则在鸽笼原理的基础上进行了优化, 提出了一个新的过滤框架来覆盖基于鸽笼原理的过滤框架, 并且大多数基于鸽笼原理进行分区的算法都有可能通过采用这个新原理来提高过滤功能.基于树型数据结构的过滤算法^[7-8]与上述算法不同, 它们不生成签名来构建倒排索引, 而是将记录组织到树中, 在树中进行过滤.
由于传统的相似性连接问题在寻找相似对时有一些情况并不适用.例如{sweet, hot}和{hit, sweot}, 虽然它们很相似, 但是不论是基于token的相似性函数或者基于字符的相似性函数, 它们的相似度都很低, 并且基于token的相似性函数的相似度甚至为0, 所以文献[9]首次提出了模糊相似性连接问题, 利用该算法提出的token敏感签名在前缀过滤的基础上进行过滤可减少候选的数量；并且该算法在记录级使用基于token的相似性函数, 而在元素级仅仅支持基于字符的相似性函数.文献[10]则在记录级以及元素级都支持基于token的相似性函数.其在前缀过滤生成签名的部分进行了改进, 利用该算法生成的签名以及其提出的检测过滤器和最近邻过滤器进行过滤可大量减少候选的数量, 但它在过滤的过程中并没有考虑到token的长度、元素的长度以及token在元素中的位置对过滤性能的影响, 所以其过滤效率并不是很高.由于文献[11]是基于鸽笼原理划分记录中的元素来生成签名, 共享同一签名的元素对应的记录视为候选对, 但由于该算法并没有考虑到记录中匹配的元素的个数对整体相似性的影响, 在记录之间一旦有匹配的元素就将其视为候选对, 造成候选集中假阳性较高, 并且由于该算法通过将全局元素划分来对应各个元素的划分, 所以部分元素的划分中可能生成空集, 但没有考虑到出现空集时的处理办法.为了解决这些问题, 本文提出了一个基于动态双重前缀的相似性连接算法.与之前的基于前缀过滤算法不同的是, 之前的算法采用固定前缀, 而本文采用了双重前缀方法, 即在查找候选以及构建索引时使用不同的前缀来提高过滤效力.在此基础上又对双重前缀过滤方法进行了优化, 在保证不漏解的情况下取各种前缀生成的候选集合的交集来缩小候选集合.还设计了一种预验证方法来减少验证阶段所花费的不必要的时间.
1 问题定义首先介绍用来解决模糊相似性连接问题的一些必要的符号.在数据集中

, 每个

称为一条记录, 在

中第i个记录表示为R_i.在两条记录R与S之间的记录级相似性用SIM(R, S)来表示.每条记录由元素组成, 记录R_i中的第j个元素用r_{i, j}来表示.在两个元素r_i与s_j之间的元素级相似性用sim(r_i, s_j)来表示.其中SIM(R, S)∈[0, 1], 1代表完全一致, 0代表完全不相似, 即没有公共元素, 同理sim(r_i, s_j)∈[0, 1].在元素内部, 每个元素r_{i, j}由token组成.在数据集中所有token的并集用U来表示.记录R_i的长度与元素r_{i, j}的长度分别用|R_i|和|r_{i, j}|来表示.
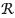
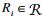
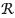
与之前的研究^[9-11]一样, 本文也采用fuzzy overlap来实现模糊相似性连接.给定两条记录R与S和元素级相似性阈值δ, 构建一个二部图G=((X, Y), E), X与Y中的顶点分别是记录R与S中的元素.对于任意的两个元素r_i和s_j, 如果sim(r_i, s_j)≥δ, 在二部图r_i和s_j之间会存在一条边, 该边的权重为r_i和s_j的相似值.下面是fuzzy overlap的定义.
定义1(fuzzy overlap) ??给定两条记录R与S, 以及元素级相似性阈值δ, G是两条记录相应的二部图, R与S之间的fuzzy overlap值为二部图G中的最大加权二部匹配值, 表示为

.
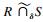
下面利用fuzzy overlap来定义带有元素级相似性阈值δ限制的记录级相似性函数.

定义2(模糊相似性连接) ??给定两个记录集合

, φ和元素级相似性阈值δ, 以及记录级相似性阈值τ, 模糊字符串相似性连接的目的是找出所有的

, S∈φ, 满足SIM_δ(R, S)≥τ.
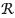
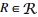
在本文中, 主要使用Jaccard相似性函数, 并且本文研究的问题是自连接问题, 即

.
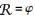
2 基于任选前缀的相似性连接算法2.1 任选前缀定理1(任选前缀过滤原理) ??设A和B表示任意的两个集合, 若|A∩B|≥t, 当i+j≤t－1时，则|A_subⁱ∩B_sub^j|≥1成立.
当

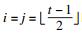
时, 称A_subⁱ和B_sub^j为对应阈值t的集合A与集合B的任选前缀, 分别记作AS－prefix_t(A)和AS－prefix_t(B).
对于模糊Jaccard相似性, 若SIM_δ(R, S)≥τ, 则

, 则R与S的二部图的最大匹配至少包含

条边, 即R与S至少共享

对相似的(Jaccard相似性大于δ)元素.将

称为记录级fuzzy overlap阈值.
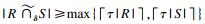
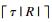
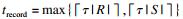
对于Jaccard相似性, 若元素r_i和s_j, 满足sim(r_i, s_j)≥δ, 则

, 即r_i和s_j至少共享

个token.将

称为元素级overlap阈值.
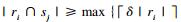
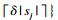
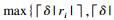
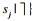
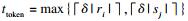
下面利用记录级fuzzy overlap阈值t_record和元素级overlap阈值t_token定义模糊Jaccard相似性连接问题中记录的双重任选前缀.
定义3(双重任选前缀) ??给定记录R, 模糊Jaccard相似性阈值τ和δ, 设P¹(R)={AS－prefix_{t_token}(r_i)|i=1, 2, …, |R|}表示记录R的每个元素的任选前缀构成的集合.记录R的双重任选前缀定义为AS－prefix_{t_record}(P¹(R)), 记作P²(R)={r′₁, r′₂, …, r′_N}, 其中N=|R|－|(t_record－1)/2|.
根据定理1和上面的共享元素与共享token的数量, 很容易得到以下的结论:
定理2 ??给定记录R和S, SIM_δ(R, S)≥τ, 则对于任意的双重任选前缀P²(R)和P²(S), 一定存在r′_i∈P²(R)和s′_j∈P²(S), 满足:
1) r′_i∩s′_j≠

;
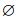
2) r_i和s_j满足长度过滤;
3) r_i和s_j对于共享token满足位置过滤.
基于定理2, 提出了基于双重任选前缀的模糊Jaccard相似性连接算法, 如表 1所示.
表 1(Table 1)

表 1 算法1Table 1 Algorithm 1

算法1 Double-prefix framework

Input:

, the set of records; δ, the element-level similarity threshold; τ, The record-level similarity threshold
Output:

, The set of result
1 ???Initialize sets

;
2 ???for each record

do
3??????????????P_query²(R)=OptimalPrefixQuery(R); //选择查询前缀
4??????????????for each r′_j∈P_query²(R)
5??????????????????????for each e_k∈r′_j
6????????????????????????????????????????Generate candidates by C_cur=GenCandi(e_j, L); C=C∪C_cur;
7??????????????????????P_index²(R)=ImprLowFrePrefixIndex(R);
8????????????????????????Update index L by inserting P_index²(R) into L;
9 ???for each (R, S)∈C
10?????????????if(Verify_pre(R, S)==1)????????????????//预验证
11????????????????????if(Verify_final(R, S)==1)
12?????????????????????????

;
13 ???return

表 1 算法1 Table 1 Algorithm 1

2.2 查询最优任选前缀根据定义1和定理2, 对于任意的e_{i, j, k}∈r′_i，j∈P_query²(R_i), 算法将利用R₁, R₂, …, R_i－1的索引生成候选集合C(e_{i, j, k})=GenCandi(e_k, L).假设记录R_i中元素r_{i, j}中的token e_{i, j, k}的候选集合用C_{i, j, k}表示, 那么元素r_{i, j}可形成的候选为

其中

.在确定P_query¹(R_i)时, 为了保证元素的候选集合最小, 应选择N₁个token, 使得这些token形成的候选并集中候选的数量最小.选取P_query¹(R_i)的目标是在每个元素r_{i, j}中找到一组k₁, k₂, …, k_N₁, 使得C_{i, j}¹(k₁, k₂, …, k_N₁)最小.即为

然后在P_query¹(R_i)中选择P_query²(R_i), 由于在确定P_query¹(R_i)时元素中的前缀token已经确定, 记录R_i可形成的候选集合为

其中

.在确定P_query²(R_i)时, 为了保证记录的候选集合最小, 应选择N₂个元素, 使得这些元素已经选好的任选前缀形成的候选并集中候选的数量最小.即P_query²(R_i)中的双重任选前缀应使C_i²(j₁, j₂, …, j_N₂)最小,

根据定理2, 若SIM_δ(R_i, R_j)≥τ(j=1, 2, …, i－1), 则一定存在r′_{i_k}∈P_query²(R_i), r′_{j_l}∈P_index²(R_j)使得

, 且R_i, R_j满足长度过滤, r_{i_k}, r_{j_l}满足长度过滤, r_{i_k}, r_{j_l}对于每个共享token满足位置过滤.采用上述方法获取的P_query²(R_i)中的双重任选前缀满足定理2.
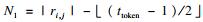
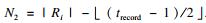
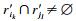
基于上述分析, 提出OptimalPrefixQuery(R_i)算法, 如表 2所示.
表 2(Table 2)

表 2 算法2Table 2 Algorithm 2

算法2 OptimalPrefixQuery(R_i)

Input: L, index; R, a record; δ, the element-level similarity threshold; τ, the record-level similarity threshold
Output: P_query²(R_i), the query prefix of R_i
1?????? Initialize the set of query prefix as

;
2?????? for each r_{i, j}∈R_i do
3?????????????? for each e_{i, j, k}∈r_{i, j} do
4?????????????????? C_{i, j, k}←GenCandi(e_{i, j, k}, L);
5?????????????

;
6?????? C_{i, j}¹(k₁, k₂, …, k_N₁)={∪_m=1^N₁C_{i, j, k_m}|

…, |r_{i, j}|};
7?????? P_query¹(R_i)=arg minC_{i, j}¹(k₁, k₂, …, k_N₁);
8??????

9??????

10????? P_query²(R_i)=arg minC_i²(j₁, j₂, …, j_N₂);
11????? return P_query²(R_i)

表 2 算法2 Table 2 Algorithm 2

2.3 索引最优任选前缀在传统前缀方法中, 所有的记录按照同一个顺序将元素进行排序, 然后选取前面固定个元素作为该记录的前缀.其中的顺序一般选择元素的频数升序的顺序.被选择的前缀中的元素是该记录中频数较低的元素.这样做有利于减少频数高的元素引起的大量候选.本文采用这种方法来选择索引前缀, 称之为低频前缀.同时, 选择索引前缀时在低频前缀的基础上作了一些改进.
由于R_i的索引前缀仅用于与其后面处理的记录的过滤, 即是否与R_i+1, R_i+2, …, R_n形成候选.因此, 构造查询前缀时, 考虑的不应该是各个token在所有记录中的频数.对于待处理记录R_i, 选择所有未处理记录R_i, R_i+1, R_i+2, …, R_n中各个token的低频前缀作为索引前缀.
基于上述分析提出ImprLowFrePrefixIndex(R_i)算法, 如表 3所示.
表 3(Table 3)

表 3 算法3Table 3 Algorithm 3

算法3 ImprLowFrePrefixIndex(R_i)

Input: L, index; R, a record; δ, the element-level similarity threshold; τ, the record-level similarity threshold
Output: P_index²(R_i), the index prefix of R_i
1 ??Initialize the set P_index²(R_i) of index prefix and the set P_index¹(R_i) of element index prefix as

;
2 ??for each r_{i, j}∈R_i
3???????????????for each e_{i, j, k}∈r_{i, j} do
4????????????????????????Count total frequency fre_{e_{i, j, k}} in R_i, R_i+1, R_i+2, …, R_n;
5???????????????Sort the token by fre_{e_{i, j, k}} in ascending order;
6???????????????

7?????????????????Select N₁ tokens in order and add them into P_{ri, j}¹;
8???????????????

9??

10??

11?? Sort P_{ri, j}¹ by Fre_{i, j} in ascending order;
12?? P_index²(R_i)=∪_j=1^N₂P_{ri, j}¹;
13?? return P_index²(R_i)

表 3 算法3 Table 3 Algorithm 3

2.4 索引本节主要介绍该算法在过滤过程中使用到的索引结构.由于在过滤过程中需要将P_index²(R_i)中的r′_{i_k}的前缀token构建倒排索引.不同的索引结构对过滤算法的性能有很大的影响, 基于树的结构提出了长度-位置索引树, 如图 1所示, 它包含三个部分: ①记录长度层.所有长度为m的记录都存储在m节点中, m指向的所有节点的记录长度都为m.②元素长度层.节点n指向的所有节点对应的元素长度都为n.③倒排索引层.在倒排索引层中, 每个倒排索引都是一个键值对, 键是token, 值是该token对应的位置pos_{r_i}(v)以及记录id和元素id的对.倒排索引L_{m, n}是由长度为m的记录且元素的长度为n构建的.
图 1(Fig. 1)

图 1 树的索引结构Fig.1 Index structure of trees

下面介绍在token生成候选集合时如何利用该索引结构进行过滤, 如表 4所示.
表 4(Table 4)

表 4 算法4Table 4 Algorithm 4

算法4 GenCandi(e_j, L)

Input: e，a token; δ，the element-level similarity threshold; τ，the record-level similarity threshold; L，index
Output: C，the set of candidates
1 ??Initialize the candidates set C as

;
2 ??for m∈[τ|R|, R]
3?????? for

4???????????? Find pre-candidates by traversing L_{m, n};
5????????????

6???????????????? E←1+min(|r_i|－pos_{r_i}(e), n－pos_C(e))+min(pos_{r_i}(e)－1, pos_C(e)－1);
7???????????? if Over>E break;
8???????????? else
9???????????????? add it into C;
10 ??return C

表 4 算法4 Table 4 Algorithm 4

3 优化3.1 生成候选的优化给定两个集合A, B, 若在A的某一个任意任选前缀与B的任意任选前缀中有公共token, 即在A的候选集合中有B；而在另一任选前缀中与B并没有公共token, 即此时A的候选集合中并没有B, 那么此时可以断定集合A与B并不相似.
基于此现象, 为了减小验证过程所花费的时间, 可以在集合中多次选取不同任选前缀, 利用不同任选前缀生成的候选的交集来缩小候选集合.然后将此发现应用到二重前缀过滤算法中.
定理3?? 设R₁为任意一条记录, C″为采用R₁的任选前缀生成的候选集合, C为采用最优任选前缀生成的候选集合, 那么R₁的最终候选集合为C′←C∩C″.
基于上述分析, 提出了优化生成候选算法, 该算法分为三阶段来完成.首先初始化候选集合C′为空集并确定任意选择的前缀生成的候选集合C″.在每个元素中任意选择N₁个token将其加入到S¹(R_i)中, 随后在S¹(R_i)中任意选择N₂个子元素添加到S²(R_i)中, 确定S²(R_i)中的每个子元素中的每个token生成的候选, 并将候选对添加到C″中.然后确定采用最优任选前缀生成的候选集合C.利用OptimalPrefixQuery()来生成记录的查询前缀, 利用生成的查询前缀以及GenCandi()来确定查询前缀生成的候选集合C.最后取C″与C的交集.
3.2 预验证最大区分任选前缀引理1(任选前缀过滤原理) ??设A和B表示任意的两个集合, 若对于任意的i+j≤t－1, |A_subⁱ∩B_sub^j|≥1都成立, 那么|A∩B|≥t成立.
根据定理1和定理3可知, 条件“|A∩B|≥t”等价于条件“对于任意的i+j≤t－1, |A_subⁱ∩B_sub^j|≥1”.对于两个记录R和S, 下面的条件等价:

(1)

存在一个匹配, 使得

(2)

根据计算的sim(r_i, s_j)来构建相应的二部图, 其中r_i∈R, s_j∈S.如果sim(r_i, s_j)>δ, 那么在二部图中r_i与s_j就相应的有一条边.若两元素FAJC_δ(R, S)>τ, 则

.令

, 由上面的条件可知, 下面的结论成立, 并且这些结论是等价的:
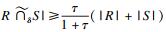
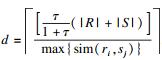
存在一个匹配, 边的个数为

(3)

对于任意的i+j≤d－1,

(4)

由式(3)和式(4)可以推出, 在二部图中去掉任意少于等于d-1个顶点, 图中至少还有一条边存在.
定义4(最大区分任选前缀) ??设degree(x_i)表示二部图中顶点x_i的度数, 设X_d－1={x₁, x₂, …, x_d－1}?(R∪S)表示记录R和S形成的二部图顶点集合的一个子集, 满足X_d－1=

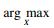
{e|v_s(e)?X, v_e(e)?X, |X|=d－1, X?(R∪S)}.将R－X_d－1和S－X_d－1称为记录R和S的d最大区分前缀.
定理4(最大区分前缀确认) ??记录R和S的m最大区分前缀的二部图中至少存在一条边等价于记录R和S的二部图中存在一个匹配, 其包含边的个数e≥d.
由于在预验证阶段, 所有候选对的记录的长度都已知, 所以d很容易求得.根据定理4可知, 如果在R₁与R₂的d最大区分前缀的二部图中仍有两个顶点之间互相连接, 那么该候选对经过预验证进入最终候选集合进行最后验证.否则, R₁与R₂不能通过过滤器被过滤掉.
基于上述分析, 本文提出了预验证阶段最大区分任选前缀算法.首先根据求得的R₁与R₂中元素之间的相似值来构建相应的二部图.随后根据两个记录的长度计算最大匹配中元素个数阈值d, 并且根据阈值d来确定二部图中需去除d-1个顶点.然后在二部图中去除度数最大的顶点以及与该顶点相连接的边, 每去除一个顶点以及相连接的边后都需更新各顶点的度数.此时若二部图G中仍有两个顶点之间有边相连, 那么该预候选对经过预验证进入验证阶段.否则, 该候选对被过滤掉.
4 结果与讨论所有实验均在具有Intel Xeon(R)CPU处理器, 16 GB RAM, 运行Ubuntu 14.04.1的服务器上进行. 所有算法均使用C ++实现, 并使用GCC 4.8.4进行编译.
4.1 数据集在三个广泛使用的数据集上来评估ASOP算法.DBLP: 计算机科学出版物的数据集, 其中包含题目、作者、出版商等属性.将每个属性看成一个元素, 元素中的每个单词看作一个token, 从中随机选择了100万个.QUERY LOG: 搜索引擎中的查询日志.将每行中的单词看成一个元素, 从中随机选择了80万个.WEBTABLE: 大型WEB数据库, 其中包含来自WEB的数百万个html表.本文从中随机选择了50万个.具体细节如表 5所示.
表 5(Table 5)

表 5 数据集Table 5 Datasets

数据集	数据量/万个	平均记录长度	平均元素长度
DBLP	100	4.23	5.24
QUERY LOG	80	3.94	5.78
WEBTABLE	50	3.56	5.96

表 5 数据集 Table 5 Datasets

4.2 本文算法的表现用AS代表在第2节提出的基于任选前缀的相似性连接算法; ASO代表在第2节AS的基础上加上生成候选的优化算法; ASOP代表在ASO的基础上对候选进行预验证的过程.整个过程所需要的连接时间如图 2所示.从图 2中可以看到随着相似性阈值τ的增长, 三种算法的连接时间都呈下降趋势, 且ASOP算法的连接时间明显比ASO以及AS低很多.
图 2(Fig. 2)

图 2 不同数据集上所提算法的连接时间Fig.2 Join time of the proposed algorithm in different datasets (a)—DBLP；(b)—QUERY LOG；(c)—WEBTABLE.

4.3 与最先进的算法作比较将本文的方法与最先进的两种算法Silkmoth以及MF-Join作比较.在该实验中, 固定元素级相似性阈值δ=0.8, 如图 3所示.从图中可以看出: 1)不论在哪个数据集中, 本文提出的ASOP算法的整体性能要远好于Silkmoth以及MF-Join; 2)在三种数据集中, MF-Join的连接时间都要比Silkmoth少; 3)在三个数据集中, ASOP的连接时间要远低于MF-Join.
图 3(Fig. 3)

图 3 改变τ的值与当前最先进的方法作比较Fig.3 Varying τ to compare with the state-of-the-art methods (a)—DBLP；(b)—QUERY LOG；(c)—WEBTABLE.

接下来通过改变元素级相似性阈值δ来对三种算法的连接时间进行讨论.在该实验中, 固定相似性阈值τ=0.85, 实验结果如图 4所示.从图中可以看出, 不论在哪个数据集中, 随着阈值δ的改变, 本文算法的整体表现仍要好于Silkmoth和MF-Join.
图 4(Fig. 4)

图 4 改变δ的值与当前最先进的方法作比较Fig.4 Varying δ to compare with the state-of-the-art methods (a)—DBLP；(b)—QUERY LOG；(c)—WEBTABLE.

5 结语本文针对相似性连接问题, 提出了ASOP算法, 并在三个数据集上来评估该算法.从实验结果中可以看出, 不论是连接过程所需要的时间、或是生成的候选对的数量, 本文提出的ASOP算法的效率都优于Silkmoth以及MF-Join算法.但是由于在构建索引部分加入了token的长度以及位置信息, 这就会导致索引所占的空间复杂度很大, 今后可以在缩小索引空间上进一步优化.
参考文献

[1]	Chaudhuri S, Ganti V, Kaushik R. A primitive operator for similarity joins in data cleaning[C]//International Conference on Data Engineering. Tianjin: IEEE, 2006: 5-17.
[2]	Bayardo R J, Ma Y, Srikant R. Scaling up all pairs similarity search[C]//International World Wide Web Conference Committee. Alberta: ACM, 2007: 131-140.
[3]	Xiao C, Wang W, Lin X M. Efficient similarity joins for near duplicate detection[C]//International World Wide Web Conference. Beijing: ACM, 2008: 131-140.
[4]	Arasu A, Ganti V, Kaushik R. Efficient exact set-similarity joins[C]//International Conference on Very Large Data Bases. Seoul: ACM, 2006: 918-929.
[5]	Deng D, Li G L, Wen H, et al. An efficient partition based method for exact set similarity joins[J]. Proceedings of the VLDB Endowment, 2015, 9(4): 360-371. DOI:10.14778/2856318.2856330
[6]	Qin J B, Xiao C. Pigeonring: a principle for faster thresholded similarity search[J]. Proceedings of the VLDB Endowment, 2018, 12(1): 28-42.
[7]	Zhang Y, Li X X, Wang J, et al. An efficient framework for exact set similarity search using tree structure indexes[C]//International Conference on Data Engineering. Toronto: IEEE, 2017: 759-770.
[8]	Zhang Y, Wu J C, Wang J. A transformation-based framework for KNN set similarity search[C]//Transactions on Knowledge and Data Engineering. Beijing: IEEE, 2020: 409-423.
[9]	Wang J N, Li G L, Fe J H. Fast-join: an efficient method for fuzzy token matching based string similarity join[C]//International Conference on Data Engineering. Bali: IEEE, 2011: 458-469.
[10]	Deng D, Albert K, Samuel M, et al. Silkmoth: an efficient method for finding related sets with maximum matching constraints[J]. Proceedings of the VLDB Endowment, 2017, 10(10): 1082-1093.
[11]	Wang J, Lin C B, Carlo Z. MF-join: efficient fuzzy string similarity join with multi-level filtering[C]//International Conference on Data Engineering. Guilin: IEEE, 2019: 386-397.

基于动态双重前缀的模糊相似性连接算法

本站小编 Free考研考试/2022-11-20

相关话题/

领限时大额优惠券,享本站正版考研考试资料!