

东北大学 软件学院, 辽宁 沈阳 110169
收稿日期:2021-04-02
基金项目:国家自然科学基金青年基金资助项目(61902057); 辽宁省自然科学基金资助项目(2020-MS-083)。
作者简介:丁来旭(1993-),男,内蒙古兴安盟人,东北大学硕士研究生。
摘要:网络表示学习可以有效解决推荐面临的数据稀疏问题.本文对网络表示学习中LINE算法和DeepWalk算法进行改进, 提出混合推荐算法并应用于电影推荐场景.该算法通过学习用户喜好特征、厌恶特征和相似用户特征, 生成三个低维特征向量.将三个低维特征向量线性组合拼接成用户表示向量, 以余弦相似度作为相似性指标, 将相似用户关联的电影推荐给目标用户, 实现电影推荐.实验结果表明, 所提出的推荐算法相较于次优算法, 在MovieLens数据集上的准确率和F1指标分别提升12 % 和7 %, 在MovieTweetings数据集上的准确率和F1指标分别提升16 % 和18 %.本文提出的基于多维特征表示学习的推荐算法在电影推荐类场景中, 具有显著的优越性.
关键词:网络表示学习推荐算法多维特征学习(MFL)LINEDeepWalk
Recommendation Algorithm Based on Multi-dimensional Feature Representation Learning in Complex Networks
DING Lai-xu, LIU Hong-juan


School of Software, Northeastern University, Shenyang 110169, China
Corresponding author: LIU Hong-juan, E-mail: liuhj@swc.neu.edu.cn.
Abstract: Network representation learning can effectively solve the problem of data sparsity in recommendation. In this paper, LINE and DeepWalk in network representation learning were improved, and a hybrid recommendation algorithm was proposed to be applied to movie recommendation scene. The new algorithm generates three low dimensional feature vectors by learning user preference feature, user aversion feature and similar user feature. Three low dimensional feature vectors are linearly combined to form a user representation vector, and cosine similarity is used as the similarity index to recommend the movies associated with similar users to target users. Experimental results show that, compared with the suboptimal algorithm, the accuracy and F1 index of the proposed algorithm are improved by 12 % and 7 % respectively on MovieLens dataset, and 16 % and 18 % respectively on MovieTweetings dataset. The recommendation algorithm based on multi-dimensional feature representation learning proposed in this paper has significant advantages in movie recommendation scenes.
Key words: network representation learningrecommendation algorithmmulti-dimensional feature learning(MFL)LINEDeepWalk
现今, 大数据所蕴含的信息给人们生活带来了无限的便利, 但与此同时, 信息价值良莠不齐, 人们被大量低价值信息包围, 如何快速地获取有价值的信息, 成为亟需解决的难题.因此,推荐系统应运而生, 其核心目的就是通过信息技术手段, 快速匹配用户需求和有效信息.随着研究的深入, 推荐系统精度逐渐提高, 但传统的推荐算法只有在用户评分充足的情况下, 推荐效果较好.而事实上评分矩阵往往是稀疏的, 以电影评分为例, 大多数用户仅仅看过几十部电影就参与评分, 同时也存在着大量影片评分较少的现象.数据稀疏会严重影响推荐精度, 甚至导致算法失灵.
近年来, 网络表示学习逐渐成为研究热点[1-2].网络表示学习, 又名图嵌入、网络嵌入, 通过对网络结构的学习, 生成网络节点的向量表示, 将节点向量表示作为后续任务的输入, 完成多样化应用任务, 例如链路预测、可视化和推荐任务等.
Zhao等[3]首次将网络表示学习应用于推荐系统, 将矩阵视为网络, 通过网络表示学习生成节点的低维向量表示, 根据向量的相似性分别进行项目推荐和标签推荐.Barkan等[4]提出了ITEM2VEC算法, 将自然语言处理中的负采样(negtive sampling)和跳词(skip-gram)技术应用于ITEM2VEC算法中, 学习物品在低维空间的向量表示, 进行相似物品推荐.网络中的节点本身具有独特的属性信息, 将这些信息融入到学习过程, 会提高表示学习的准确度. Li等[5]将时间属性融入到表示学习的过程中, 提升了推荐效果.网络可以表示多样的信息关系,通过对网络结构的拆分,使得嵌入过程具有更强的解释性,基于这一思想,Xu等[6]提出PGCN(path conditioned graph convolutional network)算法.
无论是对网络进行拆分, 还是对网络进行整体嵌入, 基于网络表示学习的推荐算法对权重的处理往往体现在连边被采样的概率上, 并不能反映出用户对物品的偏好.本文以电影推荐场景为例, 提出基于多维特征表示学习(multi-dimensional feature representation learning, MFL)的混合推荐算法.该算法对电影评分网络进行拆分, 基于改进LINE算法对用户喜爱电影和厌恶电影进行层次推进式学习.基于改进的DeepWalk算法, 获取相似用户序列, 捕获相似用户特征.将喜好特征、厌恶特征和相似用户特征线性组合后, 连接为用户最终的特征向量, 以余弦相似度作为相似性度量指标, 完成电影推荐任务.公共数据集上的实验结果表明, 本文提出的MFL推荐算法在准确率和F1指标上, 相比于其他算法表现良好, 具备一定的优越性.
1 相关研究1.1 推荐算法发展传统的推荐算法只能捕获到用户和物品直接相邻的一阶关系, 对于物品共现等二阶以上的关系, 难以展现.同时,相关算法也存在着大规模稀疏矩阵导致的算法失灵问题.随着深度学习技术的发展, 将用户数据和物品数据输入到算法模型, 通过大量训练, 可以捕获到用户和物品之间的高阶关系, 扩展已有信息, 从而实现更加精准的推荐.
2016年, Cheng等[7]提出了Wide & Deep模型, 该模型是由浅层神经网络Wide部分和深层神经网络Deep部分组成, 前者使模型具有记忆能力, 后者使模型具有泛化能力.通过训练优化模型参数, 将产生的结果拼接, 送到输出层, 完成推荐.Wide & Deep模型同时考虑到低阶和高阶特征, 但对低阶特征需要手工干预.Guo等[8]提出的DeepFM模型保留高低阶特征的同时, 可以避免人工干预, 成为推荐领域炙手可热的算法之一.
1.2 网络表示学习近年来, 深度神经网络成功地应用于自然语言处理领域.Mikolov等[9]提出word2vec算法, 其核心思想是将单词和短语映射到低维向量空间, 以捕获单词之间的语义关系, 算法引入负采样的跳词技术极大地提高了任务处理能力, 因其高效准确已扩展到自然语言处理以外的其他领域.
网络表示学习是指从网络数据中学习得到网络中每个节点的向量表示, 节点表示就可以作为节点的特征应用于后续的网络应用任务中[10].
DeepWalk[1]算法首次将词嵌入算法应用到网络表示学习领域.算法将复杂网络结构视为自然语言处理中的“语料库”, 通过随机游走的方式, 获取节点序列, 将节点在序列中出现的概率等同于单词在句子中出现的概率, 通过词嵌入模型, 获取节点的网络表示.Node2vec[11]是DeepWalk的改进算法, 在游走的过程中考虑深度优先和广度优先, 分别反映出节点邻居的宏观特性和微观特性, 从而获取网络结构信息, 进行网络表示学习.BiasedWalk[12]是基于Node2vec的改进算法, 与源点距离较近的点具有更高相似性, 通过控制距离进行深度和广度游走, 既能保留高阶邻近信息, 又能够捕获节点间的同质关系和等价关系.在网络游走过程中, 有些节点相距较远, 但是结构相似, 常规游走难以捕获这类关系.Struc2vec[13]通过构建带权层次图, 在带权层次图中随机游走采样顶点序列, 可以有效地捕获相距较远但结构相似的节点.
相较于通过游走学习网络结构,嵌入学习的算法是通过定义损失函数方式进行网络学习, 其中具有代表性的网络表示学习算法是LINE算法[2].LINE算法同时考虑到网络的一阶相似和二阶相似, 将相邻的两个节点视为一阶相似, 共同邻居的节点视为二阶相似.通过自定义的损失函数方式, 对所有一阶和二阶相似度的节点对进行概率建模, 该算法能有效地保存网络的局部信息和全局信息.SDNE(structural deep network embedding)[14]是LINE算法的扩展工作, 二阶相似度通过无监督学习来捕获全局结构, 一阶相似度通过监督学习来保留局部结构, 该模型对两个部分联合优化, 保留网络信息.
2018年, 阿里巴巴团队在DeepWalk的基础上, 将节点本身特征加入到嵌入模型, 提出EGES(enhanced graph embedding with side information)算法[15], 将嵌入算法应用于十亿级的数据, 是嵌入领域为数不多的应用于工业生产的算法.
2 MFL推荐算法MFL推荐算法可以分为以下四个步骤:
1) 将用户对电影的评分矩阵视为复杂网络, 其中用户和电影视为网络节点, 评分视为网络连线权重.以连线权重作为区分, 将网络分为高权重子网和低权重子网.
2) 基于改进的LINE算法, 学习高权重子网的网络结构, 生成用户向量和电影向量.将高权重子网生成的电影向量作为低权重网络学习的输入, 学习低权重子网结构, 生成低权重子网的用户向量.
3) 从全网节点中, 随机抽出对电影有相同评分的用户节点, 形成用户节点序列, 将用户节点序列输入到CBOW(continuous bag-of-word)[16]算法中, 学习相似用户的特征.
4) 将每个用户节点生成的三个维度特征向量线性组合后拼接成最终的用户向量.以向量的余弦距离作为节点间相似指标, 生成目标用户的相似用户集, 将相似用户关联的电影推荐给目标用户, 完成推荐任务.
2.1 推荐问题的形式化描述评分矩阵作为推荐算法的输入, 常常是由<u, i, t>作为记录组成的, 其中u代表用户编号, i代表电影编号, t代表用户对电影的评分.用户和电影构成网络中的节点, 其中U={u1, u2, …, um}为用户集, I={i1, i2, …, in}为电影集, E={eij |i=1, 2, …, n; j=1, 2, …, m}为连边集, 当存在一条连边eij=t, 代表用户ui对电影ij的评分为t.该网络可以表示为G=(V, E, W), 其中, V=U∩I, E?U×I, W为连边上的权重矩阵.网络表示学习算法对网络结构信息进行学习, 生成网络节点的低维向量表示.向量的相似性作为用户相似性的指标, 选取最相似的Top-k个用户, 将相似用户集关联的电影构成电影推荐集, 推荐给目标用户.
2.2 喜好特征和厌恶特征的学习2.2.1 喜好特征的网络表示学习提取网络连边权重大于最大权重一半的边, 生成用户喜爱网络(高权重子网), 例如, 对于最高评分为5的评分网络, 凡是评分大于等于3分的连边均被提取.
电影节点向量表示u′j∈ Rd, 用户节点向量表示ui∈ Rd.
对于每一个边<i, j>, 利用softmax函数, 用户节点vi生成电影节点vj的条件概率为
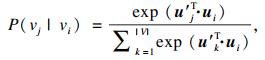 | (1) |
用户节点vi生成电影节点vj的经验分布为
 | (2) |
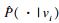
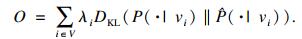 | (3) |
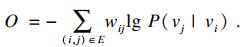 | (4) |
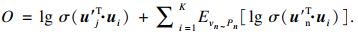 | (5) |

经过迭代优化, 生成两类向量, Φ1和Φ′分别代表用户的喜好特征向量和电影向量.
2.2.2 厌恶特征的网络表示学习提取网络连边权重小于最大权重一半的边, 形成用户厌恶网络, 对用户厌恶的网络进行学习, 学习的目标函数为
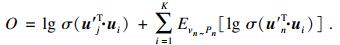 | (6) |
厌恶网络学习和喜爱网络学习的区别主要体现在两点: 首先, 在用户喜爱网络的表示学习中, 不对用户节点和电影节点初始化设定; 在厌恶网络学习中, 电影节点需要初始化设定, 其设定值为喜爱网络输出的电影向量, 用户节点不作初始化设定.其次, 在训练的过程中, 喜好网络对全部节点进行学习, 包括电影节点和用户节点; 相对地, 在厌恶网络表示学习的过程中, 电影向量被锁定, 仅对用户向量进行学习.
2.2.3 算法1描述算法1描述见表 1.
表 1(Table 1)
| 表 1 算法1 Table 1 Algorithm 1 |
2.3 相似用户的网络表示学习具有相似特征的用户会对同一部电影具有相似的评价.受DeepWalk[1]算法的启发, 对同一电影相同评分的用户随机抽取, 将随机抽出的节点序列视为自然语言处理中的语句进行处理, 评估一个序列中特定用户出现的概率作为本部分算法的基础.对于某个电影节点vj, 在对其有相同评分的用户中, 随机抽取用户, 构成一个抽样序列Wvj, 其包含用户节点Wvj1, Wvj2, Wvj3, …, Wvjmax, max为最大序列长度.本文中, 随机抽取用户序列的最大序列长度设置为max=100.实际采样过程会出现可供采样的用户节点数量过少的情况.为避免由此导致的重复训练, 在采样过程中, 设置采样序列长度最小值min, 当一部电影同一评分的用户小于min时, 跳过本次采样, 本文中min=10.多组相似用户序列构成提取网络信息的“语料库”.
将抽取的序列输入到自然语言处理算法CBOW模型[16]中.对于某一部电影vj, 抽取得到的序列为Wvj=(v1, v2, v3, …, vk), 本文希望通过训练语料库, 最大化概率P(vi|v1, …, vi-1, vi+1, …, vk).其中每一个节点都可以通过低维向量进行表示, 随后最大化概率P可转换为如下公式:
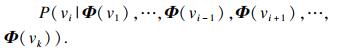 | (7) |
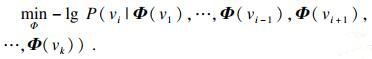 | (8) |
表 2(Table 2)
| 表 2 算法2 Table 2 Algorithm 2 |
2.4 电影推荐对于一个用户节点, 将会生成三组向量Φ1, Φ2, Φ3, 分别代表用户喜好特征、厌恶特征和相似用户特征.用户节点vi最终的低维向量可以表示为Φ1, Φ2, Φ3线性组合, 即
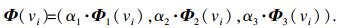 | (9) |
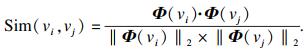 | (10) |
3 实验3.1 数据集实验数据来源于2个开放的数据集MovieLens[17]和MovieTweetings[18].MovieLens数据集来源于Group平台, 包括用户6 040个, 电影3 952部, 评分数量100 000次.在对用户和电影节点学习的过程中, 1个用户没有喜爱的电影, 346部电影无人喜欢, 无法完成喜爱特征提取, 去除与之相关的数据记录, 最终数据处理后的结果如表 3所示.MovieTweetings更新于2020年9月24日, 包含69 324个用户和36 383部电影, 共有评分888 452个.为体现不同算法在稀疏数据上的表现差异, 推荐任务的推荐目标为评分表中有40个以上评分记录的用户, 满足条件的用户数据如表 3所示.实验数据集随机分为两部分, 取80 % 的数据作为训练集, 其余数据作为测试集.
表 3(Table 3)
| 表 3 数据集摘要统计 Table 3 Dataset summary statistics |
3.2 对比算法及评价指标实验中, 对比算法包括DeepWalk[1]、LINE[2]、BiasedWalk[12]、Struc2vec[13]和GraphWave[19], 算法的嵌入维度为200, 其余参数均为默认值.
DeepWalk算法是一种经典的提取网络特征算法, 通过随机游走获取游走序列, 将游走序列输入到嵌入算法中, 从而获得网络节点的低维向量表示, 游走长度默认为10, 窗口大小默认为5.LINE算法通过对相邻节点对和有公共邻居节点对的概率建模, 保存网络的局部信息和全局信息, 最终获取节点的低维向量表示, 负采样数默认为5.Struc2vec算法在带权层次图中随机游走, 可以有效地捕获相距较远但结构相似的节点, 游走长度为10, 窗口大小为5.BiasedWalk算法通过控制距离进行深度和广度游走, 既能保留高阶邻近信息, 又能够捕获节点间的同质关系和等价关系, 游走长度默认为80, 窗口大小10.GraphWave算法是一种全新的网络嵌入方法, 利用波动扩散方式学习节点网络邻域, 将小波视为图上的概率分布, 采样步长默认为20.
对于MFL推荐算法, α1=0.5, α2=0.3, α3=0.2, d=200, max=100, min=10, windows_size=40.
每个算法选出最相似的三个用户, 将三个用户关联的电影组成电影推荐集, 推荐给目标用户.测评指标包括准确率、召回率和F1指标.
准确率:
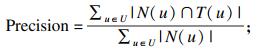 | (11) |
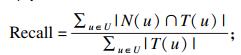 | (12) |
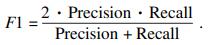 | (13) |
为了有效衡量不同方法的推荐效果, 减少测试集中单人观影记录较少导致的数据异常, 仅对测试集中观影记录10次以上的用户进行推荐.
3.3 实验结果根据3.2节参数的设定, 实验结果如表 4所示.
表 4(Table 4)
| 表 4 电影推荐的实验结果 Table 4 Experimental results of movie recommendation |
对比几个算法, 可以发现, 在MovieLens数据集上, MFL算法准确率和F1指标要好于其他算法.在召回率方面, 除DeepWalk算法外, 其他几个算法表现接近.DeepWalk算法在不加限制的随机游走的过程中, 会频繁经过观影记录较多的用户, 在推荐过程中, 目标用户总会被观影记录较多的用户匹配, 以牺牲准确率为代价提高了召回率, DeepWalk算法虽然推荐的电影数量较多, 但用户满意的较少, 推荐过程中并没有精确反映出用户特征.基于这一点,MFL算法能更加精准地匹配出用户需求, 能更有效地完成推荐任务.在MovieTweetings数据集中, 数据记录要比MovieLens更为稀疏, 且需要推荐的备选电影是MovieLens的10倍, 这就导致所有推荐算法在各项指标上均呈现出不同程度的下降.召回率方面, 几个算法的差距明显缩小, 可以表明, 在更大规模的稀疏数据上, 提高推荐数量并不能有效改善推荐质量.MFL算法在两个数据集中的准确率和F1指标均是表现最好的方法, 由此可见MFL算法的优越性.
MFL算法相比于次优算法LINE, 在MovieLens数据集上的准确率和F1指标分别提升12 % 和7 %, 在MovieTweetings数据集上的准确率和F1指标分别提升16 % 和18 %, 说明该算法能有效缓解稀疏性带来的负面影响, 面对稀疏矩阵, 具备一定的优越性.
MFL推荐算法充分考虑用户的多维特征, 分别对用户的喜好特征和厌恶特征进行学习, 同时还对相似用户特征进行学习.喜好能反映用户特征, 厌恶同样也能反映用户特征.因此, 通过多维学习, MFL算法能更好地刻画出用户特征, 同时该算法面对稀疏矩阵同样有良好的表现, 相比于其他嵌入推荐算法, MFL算法能实现更加精准的推荐.
4 敏感度分析MFL推荐算法对结果具有影响的参数包括向量的线性组合系数α、嵌入维度d.在相似用户学习过程中, 采样相似用户最大序列长度max和最小序列长度min, 以及窗口大小window_size.实验随机抽取MovieLens数据集中10 % 的用户, 对抽取的用户进行电影推荐, 并对实验结果进行分析.
4.1 向量的线性组合系数α对于系数α, 实验以0.1为步长, 对比了三个特征向量在不同权重下的F1指标表现.通过实验数据, 给出适用于电影推荐的系数α取值范围, 以系数范围代表值作为正文部分的实验系数.实验结果如图 1、图 2所示.
图 1(Fig. 1)
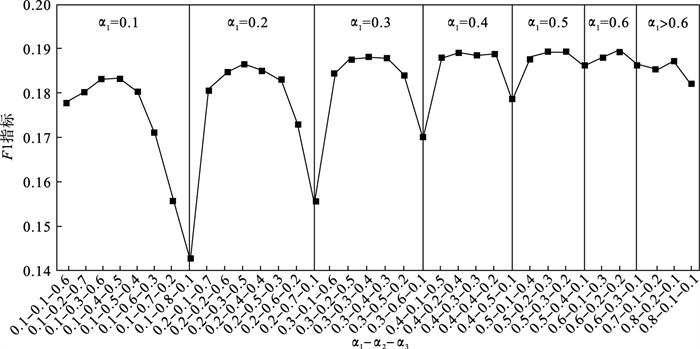 | 图 1 参数α的影响(以α1分区)Fig.1 The influence of parameter α(partition by α1) |
图 2(Fig. 2)
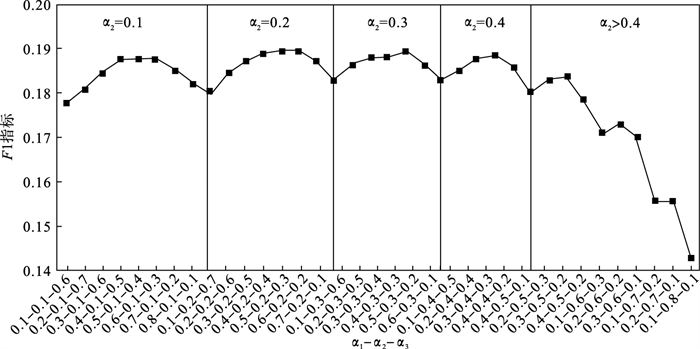 | 图 2 参数α的影响(以α2分区)Fig.2 The influence of parameter α(partition by α2) |
由图 1可知, 当α1取固定值时, α2和α3具有一定的互补性.在每个α1的区间段内, 当α2和α3取值较为接近时, 推荐效果较好, 说明在α1区间段内, α2和α3均对推荐作出了贡献.与此同时, 随着α1的取值逐渐提高, 区段推荐效果的平均值也在提高, 当α1取0.5和0.6时, 曲线趋势逐渐稳定且推荐效果较好, 说明当尽可能充分地学习用户喜爱电影时, 推荐可以抑制最坏的情况, 避免推荐失效.具体到实际电影推荐任务场景中, α1最佳取值范围为0.5~0.6.将图 1的横坐标稍作变换, 将α2作为区段的区分, 如图 2所示.可以看出, α2最佳取值为0.1~0.4, 推荐效果稳定, 且推荐质量较高.若α2取值大于0.4, 推荐效果恶化, 说明当α2的权重过大时, 网络表示学习过于强调用户对厌恶电影的学习, 忽略了喜爱电影和邻居节点的学习, 使得推荐效果恶化, 符合应用场景的实际情况.同时, 由图 2可以看出, 区段高点较大概率出现在区段的2/3处, 即α1取值在α3的2倍附近, 推荐达到阶段高点.结合图 1和图 2可知, 以0.1为步长的权重分配下, (α1, α2, α3)综合表现最佳的两组代表权重分别为(0.6, 0.2, 0.2)和(0.5, 0.3, 0.2).由两组权重的对比实验发现, 两组权重在F1指标上, 推荐效果接近.准确率方面, 第二组权重组合的准确率略微高于第一组权重组合, 综合考虑, 本文正文实验采用的权重数据组合为(0.5, 0.3, 0.2).
4.2 嵌入维度d的确定对于嵌入维度d, 主要对比了50, 100, 200, 300, 400, 500这6个维度下的F1指标, 这6个维度下F1指标如图 3所示.
图 3(Fig. 3)
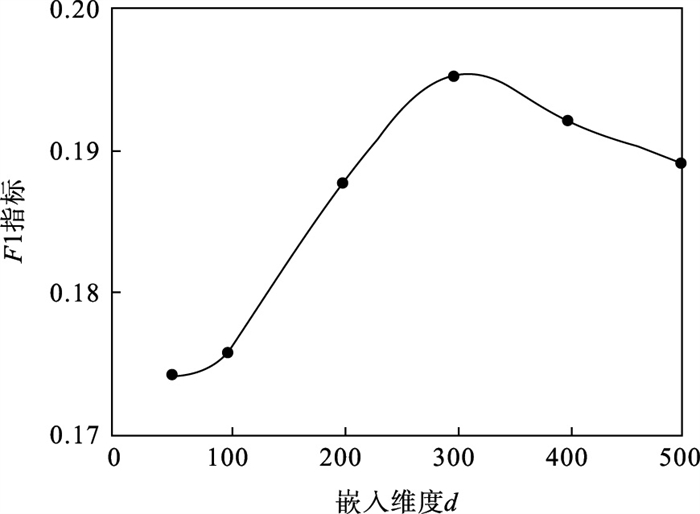 | 图 3 参数d的影响Fig.3 The influence of parameter d |
由图 3可知, 随着嵌入维度的增加, 衡量推荐效果的F1指标呈现出先上升后逐渐平稳并略下降的趋势.起初随着维度的增加, 网络表示学习的过程能更好地学习网络结构信息, 当嵌入维度增加到了一定的阈值时, 维度增加并不能提升网络表示的效果.对于高维度的网络表示学习, 随着嵌入维度的提升, 其时间和空间的开销也将增大, 权衡性能, 本文选择嵌入维度d为200.
4.3 最大采样长度max的选择对于最大采样长度max, 本文主要对比15, 25, 50, 75, 100, 150, 200, 300这8个参数对F1指标的影响, 如图 4所示.
图 4(Fig. 4)
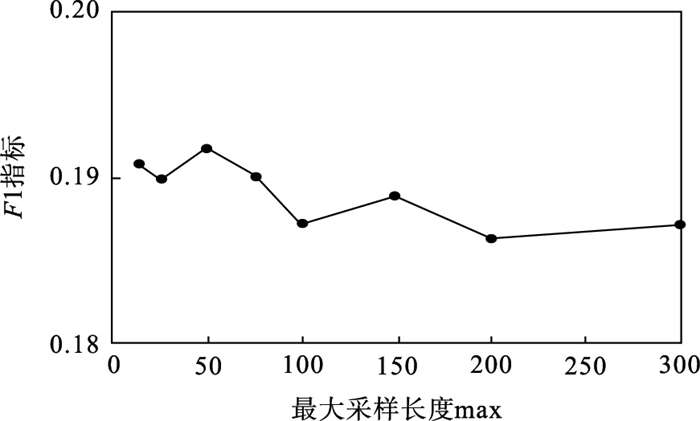 | 图 4 参数max的影响Fig.4 The influence of parameter max |
从图 4的实验结果可得, 随着max的增加, 推荐效果平稳略微下降, 但下降幅度有限.可以看出, 最大采样长度max对整体的评价指标影响不大.其中表现最好的参数max=50和表现较差的参数max=200, F1指标的相差幅度仅为2 %, 远低于参数α和嵌入维度d对推荐效果的影响.本文max默认选取为100.
4.4 最小采样长度min在最小采样长度min的实验中, min分别取0, 5, 10, 20, 30, 其余参数均为默认, 结果如图 5所示.
图 5(Fig. 5)
 | 图 5 参数min的影响Fig.5 The influence of parameter min |
4.5 窗口大小window_sizewindow_size设置为10, 20, 30, 40, 50, 其余参数均为默认, 实验结果如图 6所示.
图 6(Fig. 6)
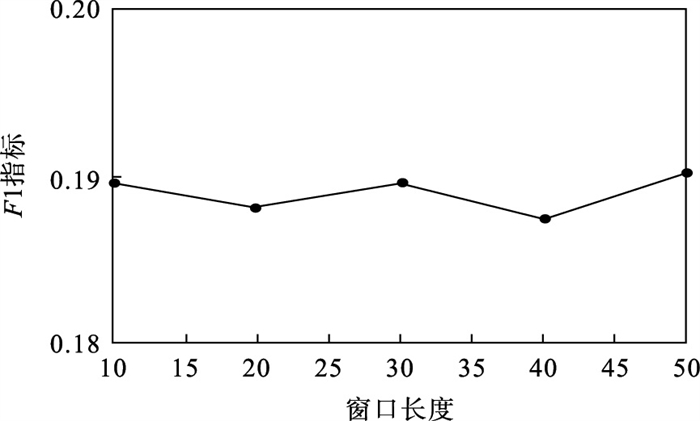 | 图 6 参数window_size的影响Fig.6 The influence of window_size |
从图 5和图 6的实验结果可知, 最小采样长度min和窗口大小window_size对推荐效果影响并不大.
通过以上参数敏感度分析可知, 在MovieLens数据集中, 对电影推荐效果影响较大的参数是线性组合系数α和嵌入维度d.其余参数最大采样长度max和最小采样长度min, 以及window_size同样会对推荐产生影响, 但影响有限, 远不及线性组合系数和嵌入维度对结果的影响.
5 结语本文以电影推荐场景为例, 提出了一种基于网络表示学习的MFL推荐算法.该算法对网络表示学习算法LINE和DeepWalk进行改进, 分别学习用户喜爱特征、厌恶特征以及相似用户特征, 将三个低维特征向量线性组合拼接成最终的用户向量, 以余弦相似度作为相似性指标, 将相似用户关联的电影推荐给目标用户, 完成电影推荐任务.
MFL推荐算法在2个公共数据集上分别进行验证, 最终实验结果表明, 在MovieLens数据集上, 准确率和F1指标分别提升12 % 和7 %; 在MovieTweetings数据集上, 准确率和F1指标分别提升16 % 和18 %.表明本文提出的算法在电影推荐类的场景中, 具有较好的推荐效果.
实际应用中, 用户特征并不会一成不变, 会随着时间的推移而发生一定的变化.因此在未来的工作中, 考虑将时间因素引入到推荐算法中, 从而实现更加精准地推荐.
参考文献
| [1] | Perozzi B, Al-Rfou R, Skiena S. DeepWalk: online learning of social representations [C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2014: 701-710. |
| [2] | Tang J, Qu M, Wang M, et al. LINE: large-scale information network embedding[C]// Proceedings of the WWW 2015—Proceedings of the 24th International Conference on World Wide Web. Florence: International World Wide Web Conferences Steering Committee, 2015: 1067-1077. |
| [3] | Zhao W X, Huang J, Wen J R. Learning distributed representations for recommender systems with a network embedding approach[C]//Asia Information Retrieval Symposium. Cham: Springer, 2016: 224-236. |
| [4] | Barkan O, Koenigstein N. ITEM2VEC: neural item embedding for collaborative filtering[C]// Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, MLSP. Salerno: Institute of Electrical and Electronics Engineers, 2016: 1-6. |
| [5] | Li Y, Chen W, Yan H. Learning graph-based embedding for time-aware product recommendation [C]// Proceedings of the International Conference on Information and Knowledge Management. Singapore: Association for Computing Machinery, 2017: 2163-2166. |
| [6] | Xu Y, Zhu Y, Shen Y, et al. Learning shared vertex representation in heterogeneous graphs with convolutional networks for recommendation[C]// Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI). Macao: International Joint Conferences on Artificial Intelligence, 2019: 4620-4626. |
| [7] | Cheng H T, Koc L, Harmsen J, et al. Wide & deep learning for recommender systems[C]// Proceedings of the ACM International Conference Proceeding Series. Boston: Association for Computing Machinery, 2016: 7-10. |
| [8] | Guo H, Tang R, Ye Y, et al. DeepFM: a factorization-machine based neural network for CTR prediction[C]// Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI). Melbourne: International Joint Conferences on Artificial Intelligence, 2017: 1725-1731. |
| [9] | Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]// Proceedings of the Advances in Neural Information Processing Systems. Lake Tahoe: Neural Information Processing Systems Foundation, 2013: 3111-3119. |
| [10] | 涂存超, 杨成, 刘知远, 等. 网络表示学习综述[J]. 中国科学(信息科学), 2017, 47(8): 980-996. (Tu Cun-chao, Yang Cheng, Liu Zhi-yuan, et al. Network representation learning: an overview[J]. Scientia Sinica (Informationis), 2017, 47(8): 980-996.) |
| [11] | Grover A, Leskovec J. Node2vec: scalable feature learning for networks[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: Association for Computing Machinery, 2016: 855-864. |
| [12] | Nguyen D, Malliaros F D. BiasedWalk: biased sampling for representation learning on graphs[C]//2018 IEEE International Conference on Big Data(Big Data). Seattle: Institute of Electrical and Electronics Engineers, 2018: 4045-4053. |
| [13] | Ribeiro L F R, Saverese P H P, Figueiredo D R. Struc2vec: learning node representations from structural identity[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Halifax: Association for Computing Machinery, 2017: 385-394. |
| [14] | Wang D, Cui P, Zhu W. Structural deep network embedding[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: Association for Computing Machinery, 2016: 1225-1234. |
| [15] | Wang J, Huang P, Zhao H, et al. Billion-scale commodity embedding for E-commerce recommendation in Alibaba[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. London: Association for Computing Machinery, 2018: 839-848. |
| [16] | Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[C]//Proceeding of the 1st International Conference on Learning Representations. Scottsdale: International Conference on Learning Representation, 2013: 1-12. |
| [17] | Harper F M, Konstan J A. The movielens datasets: history and context[J]. ACM Transactions on Interactive Intelligent Systems, 2015, 5(4): 1-19. |
| [18] | Dooms S, Bellogin A, Pessemier T D, et al. A framework for dataset benchmarking and its application to a new movie rating dataset[J]. ACM Transactions on Intelligent Systems & Technology, 2016, 7(3): 1-28. |
| [19] | Donnat C, Zitnik M, Hallac D, et al. Learning structural node embeddings via diffusion wavelets[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. London: Association for Computing Machinery, 2018: 1320-1329. |
