
 , 李坦, 张亮
, 李坦, 张亮 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期:2021-05-20
基金项目:国家重点研发计划项目(2021YFF0306405)。
作者简介:金博丕(1987-), 男, 吉林白城人, 东北大学博士研究生;
王 宏(1960-), 女, 辽宁沈阳人, 东北大学教授, 博士生导师。
摘要:针对步进电机在细分控制下使用传统续流模式导致的响应时间和电流纹波问题, 提出一种智能调节续流模式策略.首先, 详细分析了缓慢续流、快速续流和固定混合续流模式.其次, 设计了一种可自动计算最佳续流模式的智能调节方法, 该方法基于固定关断时间, 可在一个PWM周期内对固定续流时间中快速续流的百分比进行优化, 旨在提高电机细分控制运动性能.然后, 基于已搭建的实物平台, 对比分析了传统续流模式和智能调节续流模式的电流纹波.最后, 该方法成功应用于ALNES S7卫星SADA.结果表明所提出的方法在响应时间和电流纹波之间达到了一种平衡, 使得细分控制更加平稳.
关键词:步进电机智能调节续流模式细分控制电流纹波
Microstepping Control of Stepper Motors Using the Smart Regulation in Decay Mode
JIN Bo-pi, WANG Hong

 , LI Tan, ZHANG Liang
, LI Tan, ZHANG Liang School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Hong, E-mail: hongwang@mail.neu.edu.cn.
Abstract: Aiming at the problems of response time and current ripple caused by the traditional decay modes of stepper motors under the microstepping control, a strategy for the smart regulation of decay mode were proposed. First, the traditional slow decay mode, fast decay mode and fix mixed decay mode were analyzed in detail. Second, a smart regulation scheme of decay mode was designed, which can automatically calculate the optimal decay mode. This scheme can dynamically adjust the fast decay percentage of the total fixed off time within a PWM (pulse width modulation) cycle to improve the performance of the microstepping control. Finally, a test platform was built to compare and analyze the current ripple of the traditional decay modes and the smart regulation in decay mode. This method was successfully applied to SADA of ALNES S7 satellite. The experimental results show that the proposed method achieves a balance between response time and current ripple, which makes the microstepping control more stable.
Key words: stepper motorsmart regulationdecay modemicrostepping controlcurrent ripple
步进电机是一种非线性增量式的机电执行单元, 它可以提供一种开环的速度和位置控制[1].由于其长寿命、高可靠、外围简单、自保持等特点, 近年来步进电机在尖端技术领域中的应用得到快速增长, 例如卫星太阳帆板驱动机构[2]、通讯天线转台、外科手术机器人等[3].但是由于常用的步进电机一般为每圈200步, 即每步1.8°, 如此大的整步步幅, 会导致低速时转动轴的振荡, 细分控制被广泛应用以解决此类问题[4].
细分控制可以提高分辨率, 使电机旋转得更加平滑[5].基于理论上的分析, 8细分就可以得到最优的位置控制, 但是细分越高, 力矩越平稳[6].文献[1]设计了一种基于大脑情感学习模式的控制, 可以去除意外的干扰, 提高了瞬态响应的稳定性; 文献[4]采用了一种基于奇异摄动理论的简化力矩调制细分算法, 在不需要电流反馈的条件下实现良好的系统跟踪性能; 文献[7]提出了基于细分控制的负载角预估器, 只需检测一相电流和电压即可在开环条件下控制电机防止失步; 文献[8]介绍了一种自适应PI算法, 对细分电流进行优化, 可以有效降低功耗同时不发生失步;文献[9]则给出了一种基于振动最优化来减少步进电机开环位置误差的方法.
大部分的文献都集中在讨论控制的算法, 少有研究在细分的底层控制中引入不同续流模式以优化步进电机驱动的电流控制.本文提出了一种智能调节续流模式的步进电机细分控制, 提高电流控制的鲁棒性, 使电机相电流正弦度更高, 低速时振动更小, 高速时响应更快, 运动更为平稳.
1 步进电机的续流策略1.1 快速续流对于两相步进电机, 驱动的方式常为8只MOS管组成的2对H桥.快速续流模式是指在全部MOS管关断时, 电流从MOS管寄生二极管导通流经电机绕组, 并迅速减小直至达零或下一个PWM周期.图 1为一相绕组H桥的电流示意, 在续流过程中, 电流为负向.
图 1(Fig. 1)
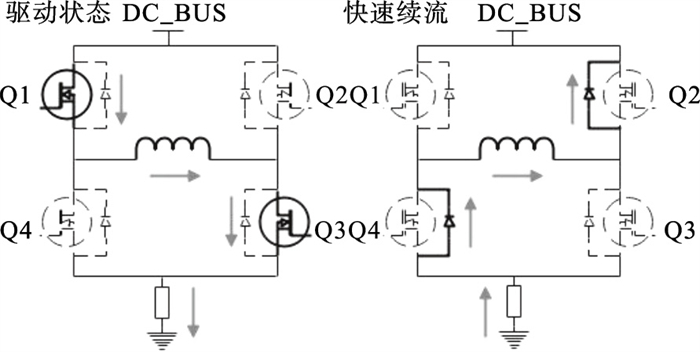 | 图 1 H桥中驱动和快速续流电流流经途径Fig.1 Current flow paths of drive and fast decay in H-bridge |
为了加快续流的速度, 同时保护寄生二极管, 还可利用MOS管导通电阻小的特点, 在快速续流期间反向开通另一对MOS管Q2和Q4, 但是在电流下降到零时必须立刻关断.
该模式下对电流的变化响应迅速, 但是电流的下降速率很可能比绕组通电时形成的电流上升速率更快, 易造成较大的电流纹波, 增加电机运行的噪声和振动, 影响控制精度[10].在一般的控制方法中若不增加额外的操作, H桥将默认处于快速续流模式, 实际应用中效果很差, 从电机的振荡特性来看, 不建议此模式作为基本的续流方法.
1.2 缓慢续流缓慢续流则是关断高压侧的MOS管, 同时开通2只低压侧MOS管, 电流从2只MOS管流过电机绕组, 电流的下降速率取决于电机的电气时间常数, 相对于快速续流时间较长.缓慢续流模式相当于将电机绕组短路, 具有阻尼效果, 电流产生的电磁力矩抵消了电机的惯性力矩, 起到快速制动的效果.图 2为一相绕组H桥的电流示意, 此时无法使用低压侧串联电阻接地的方式检测到电流的大小.
图 2(Fig. 2)
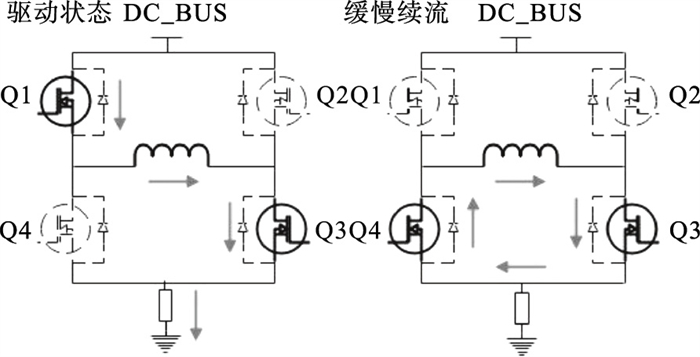 | 图 2 H桥中驱动和缓慢续流电流流经途径Fig.2 Current flow paths of drive and slow decay in H-bridge |
该模式下, 虽然电流纹波很小, 但是响应时间较长, 加上反向电动势的影响, 在电流下降段尤其容易发生实际电流跟踪不上期望的电流正弦波, 影响电机控制的效果.
1.3 混合续流由前文分析可知, 快速续流对于电流的跟踪效果较好, 缓慢续流对于减少电流纹波效果较好, 混合续流便是将二者结合.在电流波形的上升部分, 采用缓慢续流, 尽可能地释放反向电动势, 减少其随着转速增加带来的影响; 而在电流波形下降部分, 采用快速续流, 使电流可以有效跟踪给定值.此外, 最常用的混合续流方法是固定缓慢续流和快速续流在一个周期内的百分比[11], 一般是以快速续流开始, 使电流快速减小, 跟随目标值, 缓慢续流结束, 降低电流的纹波, 整个关断时长为常量.改变百分比对电机细分驱动有不同的影响.常用的百分比为快速续流在整个关断周期内占比25 % 或33 %.采用混合续流模式, 电流下降的速度高于缓慢续流, 而低于快速续流, 电流纹波也介于二者之间.
1.4 振荡与续流步进电机的绕组通电励磁后, 每运动一步, 转子在电磁力矩的作用下向平衡点转动, 在到达平衡点后由于惯量, 转子并不会立即停止, 而是会超越平衡点发生过冲.随后转子向平衡点返回, 表现为围绕平衡点在一个稳定区间内振荡至零.若存在负载, 电机相对于空载时稳定区间变窄, 这时发生振荡极易超出稳定区间.若离开了这个稳定区间, 此时转子不能在电磁力矩的作用下返回平衡点, 则产生了失步的现象.电磁力矩可表示为
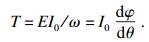 | (1) |
步进电机的电磁力矩和齿槽力矩中的非正弦分量也会导致运动过程中产生谐波, 对电机实际运行会产生影响.在考虑三次谐波的影响下, 各相的交链磁通可表示为
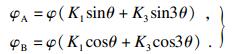 | (2) |
细分控制是将每个整步的各相电流以阶梯状n步逐渐变化, 使电流曲线呈正弦波形状[12-13], A相比B相超前90°.图 3为任意一相的电流波形的概念图. 步进电机由于其自身特性, 即使在细分控制下, 仍然表现为单步运动[14], 只是在细分下每次运行微步, 1微步等于1整步除以细分数.细分控制可以改善步进电机的阻尼特性, 步距角的减小, 使得运动更加平滑.细分控制的相电流为
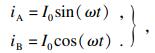 | (3) |
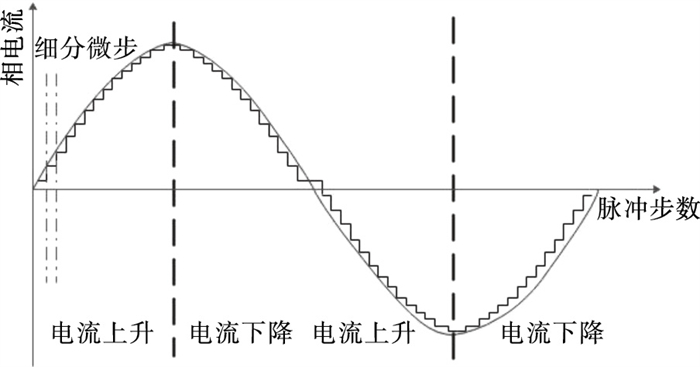 | 图 3 电机一相绕组的细分控制电流波形Fig.3 Current profile under microstepping control of one coil of a stepper motor |
由于运动过程中, 转子与定子的磁场同步, 则转子角度还可表示为
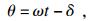 | (4) |
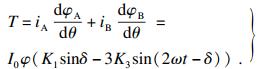 | (5) |
续流模式可以有效减少反向电动势, 加快转子振荡的衰减速度, 有益于下一步换相的控制.但是续流引起的纹波也会影响电流波形的正弦形状, 导致使用了更高微步数的细分控制而振荡却未有明显削弱.尤其在高速运行的工作状态, 输入脉冲频率太快, 对细分控制需要更高的响应速度去保证电流跟踪性能.综上, 细分控制需要与续流模式有效结合起来, 以进一步解决步进电机振荡问题, 实现更优异的驱动效果.
2 智能调节续流模式理想的续流模式设置取决于电源电压、电机特性、工作电流、电机转速、反向电动势等, 这些参数会变化, 这对调节续流模式产生困难.一般的方法需要观察电机电流曲线来调试, 既耗时又费力.即使是设置好的参数, 随着一些情况的变化, 也可能变得不再最优化.以下是传统的混合续流模式存在的一些限制:
① 为了获得更快的阶跃响应, 通常会选择快速续流, 然而在达到保持电流时又会造成过冲和纹波;
② 针对不同的电机有不同的参数, 每次都需要重新调试配置参数;
③ 对于使用电池供电的电机, 随着电源电压的下降, 初始的设置可能不再理想;
④ 由于温度变化或衰老导致电机电阻发生变化, 也需要调整续流参数的设置.
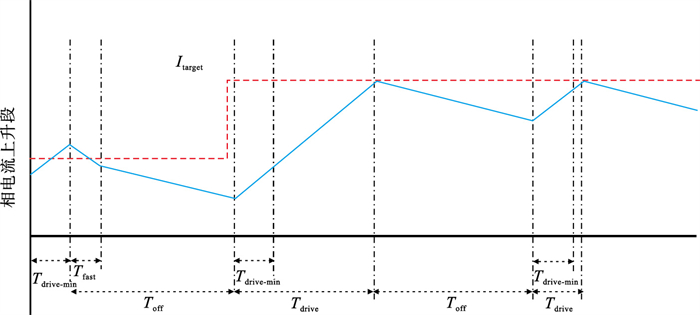
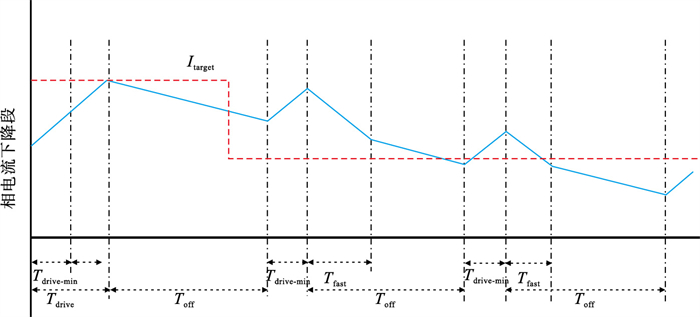
为解决上述问题, 本文提出一种智能调节续流模式, 可以自动计算最优的续流模式, 自适应电机各项参数, 在获得更快的阶跃响应同时可以保持更小的电流纹波, 电流上升段和下降段的控制曲线示意分别如图 4和图 5所示.
图 4(Fig. 4)
 | 图 4 智能调节续流模式上升段Fig.4 Increasing current of the smart regulation in decay mod |
图 5(Fig. 5)
 | 图 5 智能调节续流模式下降段Fig.5 Decreasing current of the smart regulation in decay mode |
智能调节续流模式每个PWM周期由导通阶段、快速续流和缓慢续流三个阶段组成.采用固定关断时长Toff, 在电流调节的每个周期中动态优化快速-缓慢续流的百分比, 从而避免了繁琐的手动调试的步骤.首先给定一个PWM的最小开通时间Tdrive-min, 在这期间不对电流进行检测, 以屏蔽MOS管开通瞬间采样电阻上的尖峰噪声, 在达到Tdrive-min时开始对电流采样.若电流低于Itarget, 则PWM保持开通, 直至电流升至Itarget, 然后进行时长为Toff的缓慢续流.若电流高于Itarget, 则进入快速续流模式, 运行时长Tfast, 时间长度由超调量决定, 如果超调量较高, 则延长快速续流的时间长度; 如果超调量较低, 则缩短, 即通过改变快速续流在固定关断时间中的百分比来提高响应速度, 并最大程度地减小电流纹波.
以步进电机任意一相绕组进行分析, 由图 4可见, 在PWM开通Tdrive-min后, 相电流超过了给定的目标电流, 随后进入时长为Tfast的快速续流模式, 最后进入缓慢续流执行完Toff.在下一个PWM周期, 目标电流发生改变, 在开通Tdrive-min后, 相电流并未达到给定值, 故PWM保持开通升至Itarget, 进入Toff的缓慢续流模式, 即百分比为0的快速续流状态.图 5中示意的相电流下降段与上升段同理, PWM持续开通至相电流达到给定值后, 进入缓慢续流模式.在下一个PWM周期, 目标电流下降, 相电流在开通Tdrive-min后, 远大于给定值, 则增加Tfast的百分比.在第3个PWM周期中, 相电流仍然高于Itarget, 但是超调下降, 故Tfast的百分比也相应减小.整个控制流程以此类推, 控制的框图如图 6所示.
图 6(Fig. 6)
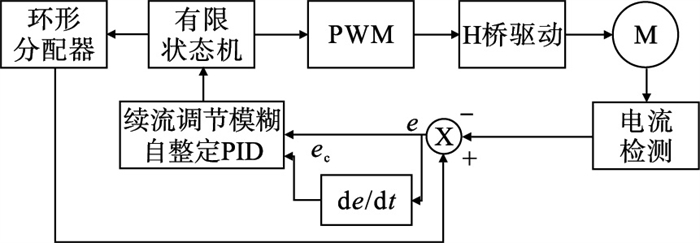 | 图 6 智能调节续流控制框图Fig.6 Block diagram of the smart regulation in decay mode |
环形分配器实现电机的细分控制, 输出电流的参考值, 与电流反馈值做差, 而不是简单比较大小输出开关量.通过模糊自整定PID(proportion integral differential)调节器, 得到快速续流的比例, 以快速准确地跟踪目标电流的变化.缓慢续流阶段中无法得到电流测量值, 通过定时器终止.Tdrive-min和Toff的取值对电流控制的影响是比较明显的, 为了平衡电流纹波、响应速度与功耗, 在实际应用中, 上述二值取为2 μs和16 μs.
步进电机具有两个独立的绕组, 因此需要2个PID调节器, 分别对其进行控制.在快速续流过程中, 电机一相绕组的电压平衡方程可表示为
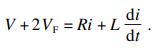 | (6) |
则电机的传递函数为
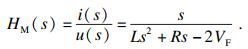 | (7) |
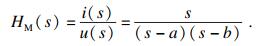 | (8) |
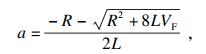 | (9) |
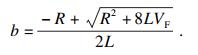 | (10) |
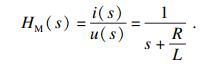 | (11) |
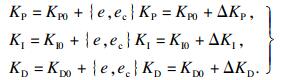 | (12) |
| 表 1 模糊PID规则表 Table 1 Fuzzy PID rules | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
将e和ec的论域定义在[-1, 1], KP, KI, KD的论域定义为[0, 20].控制器结构见图 7.
图 7(Fig. 7)
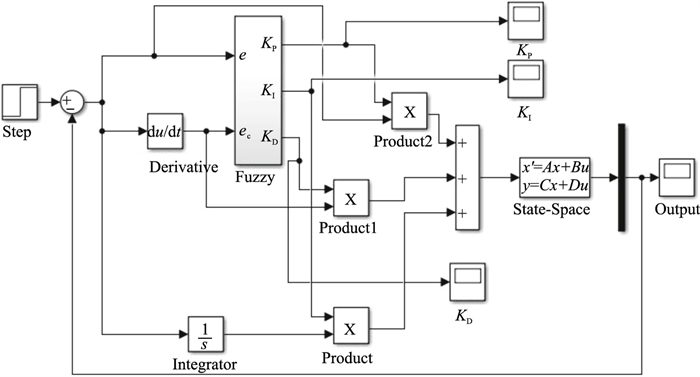 | 图 7 模糊PID控制器Fig.7 Fuzzy PID controller |
取R=3.8 Ω, L=2.3 mH, 采样周期1 μs, 进行仿真得到模糊PID阶跃响应曲线如图 8所示.
图 8(Fig. 8)
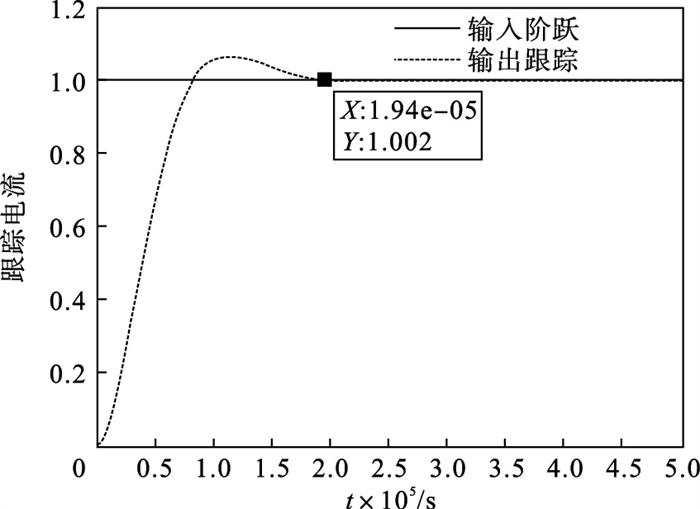 | 图 8 模糊PID响应曲线Fig.8 Response curve of fuzzy PID |
3 实验及结果分析通过实物平台对智能调节续流模式和传统续流模式的性能进行验证.选用FAULHABER的步进电机DM66200H,使用Tektronix电流钳TCP0030A对电机相电流波形进行测量.在实验中采用256细分, 母线电压28 V, 给定相电流有效值0.1 A, 设置15 r/min和240 r/min的速度测试了两组波形, 续流模式分别采用: 上升段缓慢模式/下降段缓慢模式、上升段缓慢模式/下降段快速模式、上升段混合模式/下降段混合模式以及智能调节续流模式共4种模式, 电流波形对比如图 9~图 16所示.图中横坐标为时间,纵坐标为幅值.
图 9(Fig. 9)
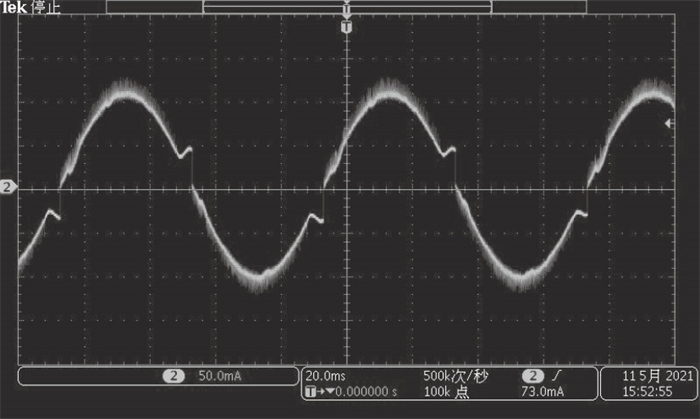 | 图 9 上升段缓慢/下降段缓慢续流@15 r/minFig.9 Phase current using slow decay mode for increasing and decreasing@15 r/min |
图 10(Fig. 10)
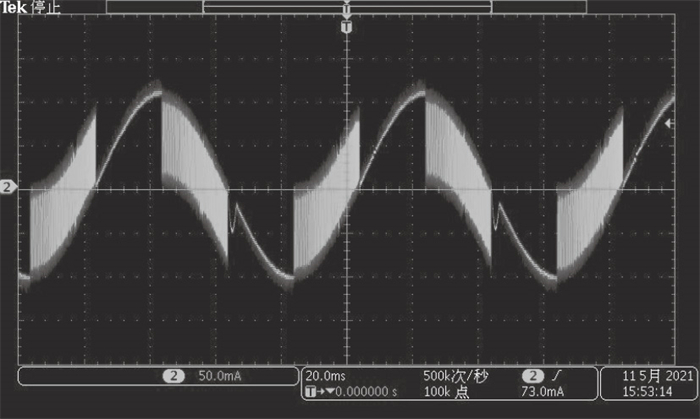 | 图 10 上升段缓慢/下降段快速续流@15 r/minFig.10 Phase current using slow decay mode for increasing and fast decay mode for decreasing@15 r/min |
图 11(Fig. 11)
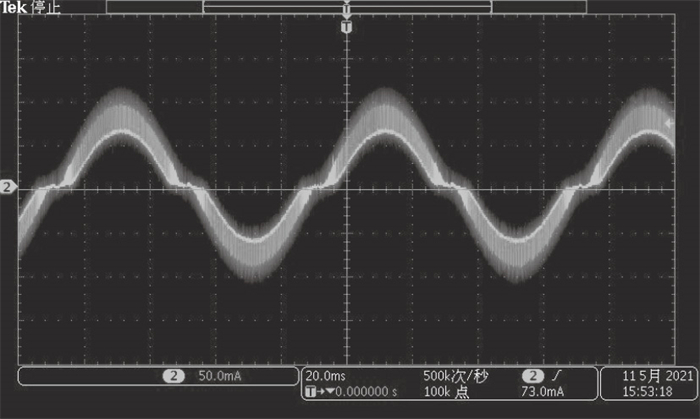 | 图 11 上升段混合/下降段混合续流@15 r/minFig.11 Phase current using mix decay mode for increasing and decreasing@15 r/min |
图 12(Fig. 12)
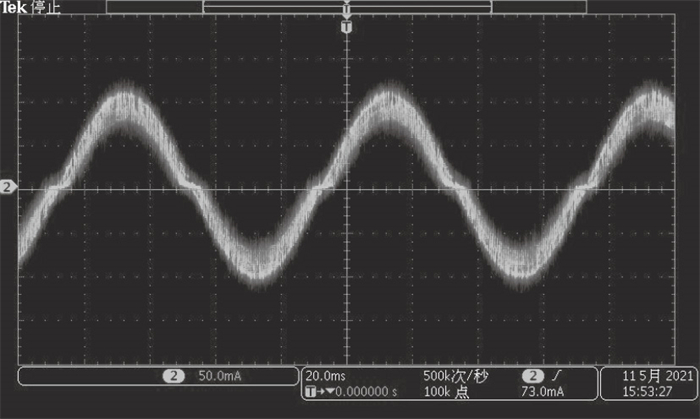 | 图 12 智能调节续流模式@15 r/minFig.12 Decay mode using smart regulation@15 r/min |
图 13(Fig. 13)
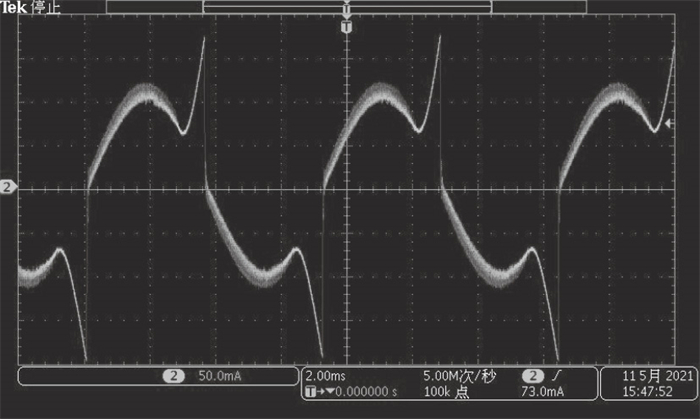 | 图 13 上升段缓慢/下降段缓慢续流@240 r/minFig.13 Phase current using slow decay mode for increasing and decreasing@240 r/min |
图 14(Fig. 14)
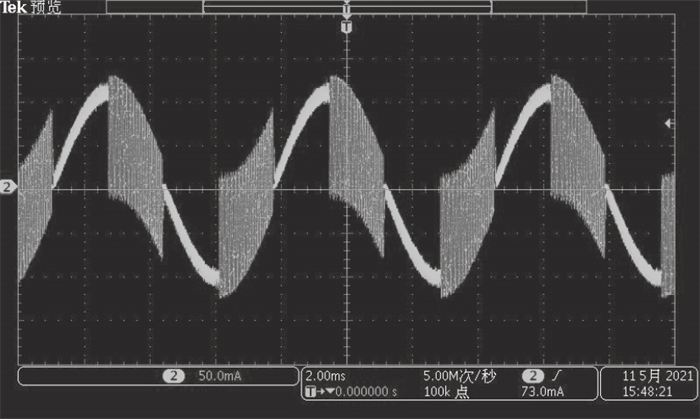 | 图 14 上升段缓慢/下降段快速续流@240 r/minFig.14 Phase current using slow decay mode for increasing and fast decay mode for decreasing@240 r/min |
图 15(Fig. 15)
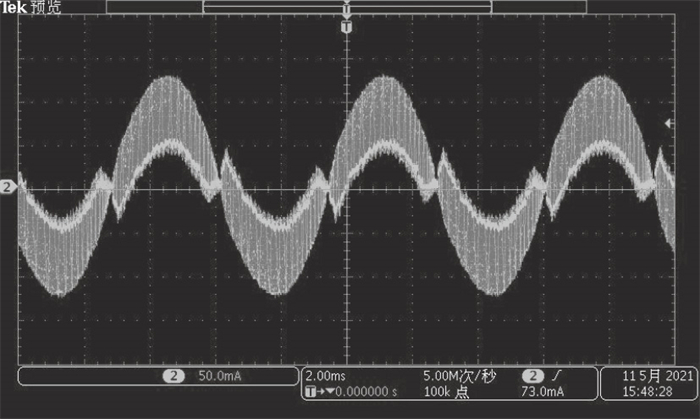 | 图 15 上升段混合/下降段混合续流@240 r/minFig.15 Phase current using mix decay mode for increasing and decreasing@240 r/min |
图 16(Fig. 16)
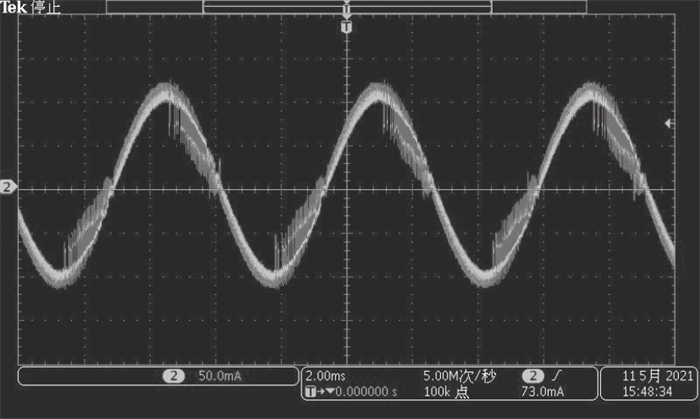 | 图 16 智能调节续流模式@240 r/minFig.16 Decay mode using smart regulation @240 r/min |
由图 9可知, 在15 r/min的低速运行下, 缓慢续流的纹波最小, 但是在下降段由于响应时间过长, 电流下降较慢, 无法跟踪正弦电流给定曲线, 导致了一段电流控制异常.而图 10中, 仅在下降段采用快速续流, 电流下降速率超过导通时的速率, 造成了极大的电流纹波; 图 11中采用了固定快速续流比例为33 % 的混合续流模式, 纹波相对快速续流模式减少, 由于没有针对电机进行固定比例的手动调试, 在过零点出现明显变形; 图 12采用了智能调节续流模式, 在电流纹波和响应速度之间寻求了一种平衡, 且最大程度地保持了电流的正弦曲线形状.
细分控制在高速运行的效果弱于低速运行时, 输入的脉冲频率增加, 对于N细分控制更是N倍的增长, 加大了对电流跟踪能力的要求与挑战.图 13中步进电机处于240 r/min的高转速状态, 可见缓慢续流模式在下降段的波形非常不理想, 续流速度过慢甚至导致电流在跟踪正弦波下降波形时大幅增加; 而图 14和图 15也可见正弦形状严重畸变, 快速续流在下降段造成极大的纹波, 固定混合续流依然采用了快速续流占比33 % 的方式, 没有进行手动调节比例导致纹波和正弦度都很差; 图 16中采用了智能调节续流模式, 使得细分控制在高速下运行电流曲线依然较为平滑,并且由于纹波的减少, 可以使电流控制的效率也变得更高, 电机发热量得到有效抑制.
在步进电机高转速运行时, 由于应用的细分很高, 目标电流的更新频率相应也很快, 智能调节续流模式下, 电流的控制实际上处于变频的状态.在电流上升段, 电流未达到目标值时, 该相绕组持续开通, 直至达到目标值后进入缓慢续流, 这时电流下降斜率较小, 有助于下一次跟踪; 若电流在开通后超过目标值, 则对应进入快速续流, 降低下一个周期开通后的幅值.在电流下降段, 电流其实很容易就超过目标值, 这个阶段会多次进入快速续流模式.由图 12和图 16对比可见, 高速时上升段波形相对低速时比较平滑, 而下降段则纹波较大.
图 17为成功应用该控制方法的导航通信一体化增强系统——微厘空间S7卫星SADA产品, 包含1台四轴步进电机控制器(SADE)和2台双轴运动机构(SADM).对其进行精度测试验证, 测量工具为Leica AT960-MR型激光跟踪仪, 采样频率1 000 Hz, 动态测量达到的关键控制指标为: 绝对定位精度<±0.1°, 速度平稳性在0.05~0.2(°)/s速度区间内≤±0.01(°)/s,在0.2~0.6(°)/s速度区间内≤±10 %.
图 17(Fig. 17)
 | 图 17 微厘空间S7卫星SADA产品Fig.17 ALNES S7 SADA |
4 结论1) 本文分析了步进电机缓慢续流、快速续流和固定混合续流的方法和问题, 本文所述方法能够有效解决响应速度和电流纹波的问题.
2) 提出了智能调节续流模式的步进电机细分控制方法, 该方法使用固定关断时间, 动态调整混合续流百分比, 变频控制电机, 可实现高平稳运动.
3) 通过实验对比分析了智能调节续流模式在高/低速下和其他常用的传统续流模式的电流波形.结果表明, 本文提出的方法适配高/低转速, 迭代优化续流模式的配置模式能够有效降低电流纹波、提高响应速率、保持电流的正弦曲线形状, 显著地提高了步进电机细分控制的性能.在航天任务产品上得到了实际的应用, 测试结果满足各项指标要求, 具有良好的实际应用价值.
参考文献
| [1] | Sabir R, Murat Y, Metin D. Ripple reduction at speed and torque of step motors used on a two-axis robot arm[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26: 759-767. DOI:10.1016/j.rcim.2010.05.003 |
| [2] | Li R, Guo F, Yu C X, et al. Development and validation of a mechatronic solar array drive assembly for min/micro-satellites[J]. Acta Astronautica, 2017, 134: 54-64. DOI:10.1016/j.actaastro.2017.01.047 |
| [3] | Ghanooni P, Yazdani A M, Mahmoudi A, et al. Robust precise trajectory tracking of hybrid stepper motor using adaptive critic-based neuro-fuzzy controller[J]. Computers and Electrical Engineering, 2020, 81: 1-18. |
| [4] | Kim W, Shin D, Lee Y, et al. Simplified torque modulated microstepping for position control of permanent magnet stepper motors[J]. Mechatronics, 2016, 35: 162-172. DOI:10.1016/j.mechatronics.2016.02.002 |
| [5] | Stijn D, Bram V, Jasper D V, et al. Sensorless load angle control for two-phase hybrid stepper motors[J]. Mechatronics, 2017, 43: 6-17. DOI:10.1016/j.mechatronics.2017.02.003 |
| [6] | Robert K, Tomasz S, Andrzej P, et al. An influence of the stepping motor control and friction models on precise positioning of the complex mechanical system[J]. Mechanical Systems and Signal Processing, 2016, 70/71: 397-413. DOI:10.1016/j.ymssp.2015.09.030 |
| [7] | Jasper D V, Stijn D, Kurt S. Load angle estimation for dynamic stepping motor motion applications[J]. Mechatronics, 2018, 53: 229-240. DOI:10.1016/j.mechatronics.2018.06.017 |
| [8] | Jasper D V, Michiel H, Florian V, et al. Current reduction in stepping motor applications using an adaptive PI controller based on linearized dynamics[J]. IFAC PapersOnLine, 2018, 51(4): 107-112. DOI:10.1016/j.ifacol.2018.06.046 |
| [9] | Pillans J. Reducing posotion errors by vibration optimization of stepper motor drive waveforms[J]. IEEE Transactions on Industrial Electronics, 2020, 68(6): 5176-5183. |
| [10] | 冒建亮, 叶桦, 李奇. 基于FPGA的步进电机电流优化控制策略[J]. 信息与控制, 2015, 44(5): 585-591. (Mao Jian-liang, Ye Hua, Li Qi. Optimized current control strategy for stepper motor based on FPGA[J]. Information and Control, 2015, 44(5): 585-591.) |
| [11] | Wang R, Wu J, Huang W J. Design of high dynamic performance driver for stepper motor[J]. Control Engineering of China, 2015, 22(2): 222-226. |
| [12] | Ming Y S, Chieh L F, Tsung C M. Micro-stepping control of a two-phase linear stepping motor with three-phase VSI inverter for high-speed applications[J]. IEEE Transactions on Industry Applications, 2004, 40(5): 1257-1264. DOI:10.1109/TIA.2004.834040 |
| [13] | Gaan D R, Kumar M, Sudhakar S. Frequency modulation based microstepping of stepper motor for real time position tracking applications[C]//2016: IEEE International Conference on Power Electronics, Drives and Energy System. Trivandrum, India. IEEE, 2016: 1-6. |
| [14] | 杜永龙, 黄惠东, 康兴国, 等. 改善步进电机低频特性的续流回路方法[J]. 探测与控制学报, 2009, 31(5): 60-63. (Du Yong-long, Huang Hui-dong, Kang Xing-guo, et al. Continuous current circuit applied to improving low frequency characteristic of stepper motor[J]. Journal of Detection & Control, 2009, 31(5): 60-63. DOI:10.3969/j.issn.1008-1194.2009.05.014) |
