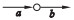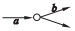于长永, 金建宇, 刘鹏, 赵宇海
东北大学 计算机科学与工程学院，辽宁 沈阳 110169
收稿日期：2021-05-07
基金项目：国家自然科学基金资助项目(61772124)。
作者简介：于长永(1981-)，男，辽宁海城人，东北大学副教授。

摘要：针对基因序列比对问题提出了一种DBG(de Bruijn图)模型，称为MiniDBG.它可以存储最小边集的位置列表，并通过位置列表有效地定位图上的任何节点、边和路径，从而实现对基因的序列比对.介绍了MiniDBG模型及基于该模型的路径定位算法，并对算法进行了证明.同时将MiniDBG与基于BWT和基于位置列表的路径定位方法进行了比较，实验结果表明，在频繁比对的情况下，MiniDBG的性能优于其他两种方法.
关键词：基因序列比对De Bruijn图最小边集位置列表路径定位算法
A De Bruijn Graph Localization Algorithm Based on Minimal Set of Edges
YU Chang-yong, JIN Jian-yu, LIU Peng, ZHAO Yu-hai
School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: YU Chang-yong, E-mail: cyyneu@126.com.

Abstract: A DBG(de Bruijn graph)model called MiniDBG for gene sequence alignment is proposed. It can store the position list of the minimum edge set, and effectively locate any node, edge and path on the graph through the position list, so as to achieve sequence alignment of genes. The MiniDBG model and the path location algorithm based on the model are introduced, and the algorithm is proved. Meanwhile, the MiniDBG is compared with the path location method based on BWT and location list. Experimental results show that the performance of MiniDBG is better than those of the other two methods in the case of frequent alignment.
Key words: gene sequence alignmentde Bruijn graphminimal set of edgesposition listpath location algorithm
DBG(de Bruijn图)是生物信息学中最有用的数据结构之一，例如，DBG最初用于组装数十亿个短基因组序列^[1-2]，DBG也被用于其他领域，如基因组序列比对^[3-6]，在人群中发现基因多样性^[7-8]，预测细菌的毒性^[9]，以及检测共线性块^[4].
近年来，由于DBG具有能够处理基因组重复区域^[10-11]的特性，而基因组的高度重复问题也是目前大多数现有方法的瓶颈，因此DBG常用于处理基因组序列.对于基于FM-index的方法，高重复的子字符串可能会导致后缀的定位过程耗时较长；对于基于gram的方法，由于存在过滤失败的情况，高度重复的子字符串可能会造成候选集较大.为了避免重复子字符串的影响，提出了很多种子选择方法，以OSS^[10]为例，将频率最小的种子定义为最优种子，提出一种求解种子选择问题的动态规划算法.此外，在文献[11]中，用DBG处理参考序列重复引起的问题，但忽略了其他信息，如分支节点和由分支节点组成的路径.DeBGA是一个功能强大的映射器，但它可能会丢失由DBG模型中的分支节点和路径表示的映射位置.
DBG的一个重要特性是，参考序列的每个子字符串都是图上的路径，但并非所有DBG上的路径都是参考序列子字符串.如果一个路径是参考序列的子字符串，则称它为真路径，否则为假路径.DBG模型不仅可以对参考序列进行索引，还可以在参考序列上定位图的每条边和路径.近年来有关DBG的研究主要集中在图的索引和快速构建方面.例如，文献[12-13]提出了有效构造DBG的方法，文献[14]提出了一种时间和空间友好的压缩染色DBG的索引方法，文献[15]提出了一个DBG的紧凑表示，它允许无限数量的节点和边的增加和删除.然而，关于在参考序列上定位DBG的节点、边和路径的方法却很少.文献[16]提出了一种新的图数据组装结构，称为连接的de Bruijn图(LdBG)，但该模型不能用于定位参考序列上的路径，显然也无法存储所有边的位置列表.
本文提出了一种DBG模型，称为MiniDBG，可以用于在read-mapping中索引参考序列.该模型存储了最小边集的位置列表.有了位置列表，MiniDBG可以有效地定位任何边、节点和路径.实验结果表明，MiniDBG能有效地在参考序列上定位边和路径，且存储成本较低.
1 基础知识X为字母表Σ={A, C, G, T}上的基因组参考序列，A, C, G, T是生物学DNA中的四种碱基.X长度用|X|来表示.X[i]表示X上的第i个字符.索引从1开始，用X[i, j]表示X上从i到j的子字符串，X的前缀和后缀由X[*, i]和X[i, *]来表示.给定一个参考序列X和子字符串k-mer，k-mer是基因组参考序列X中长度为k的字符串，用DBG(X, k)来表示X的de Bruijn图：
V={v_i|v_i是k-mer并且v_i是X上的字符串}；
E={e_ij|v_i[k-1, *]=v_j[*, k-1], |p_ij|≠0}；
P={p_ij|p_ij=list(e_ij)}.
其中V, E, P分别为图的顶点集合、边集合和位置列表集合.集合V由序列X上出现的一系列长度为k的字符串组成.e_ij是一条从v_i到v_j并且满足v_i[k-1, *]=v_j[*, k-1]的边，并且|p_ij|≠0.p_ij是e_ij的位置列表(将e_ij看作X上长度为k+1的子字符串)，能够按照从前到后的顺序保存e_ij在X上出现的位置.|p_ij|表示p_ij的长度.
给定参考序列X和整数k，找到边的位置列表的集合，用P_min表示，并需要满足以下条件：
① DBG′(X, k)=(V, E, P_min)可以通过P_min的位置列表的并集定位每一条边；
② 对于任意的P′?P_min, DBG″(X, k)=(V, E, P′)不能满足条件1.
DBG′(X, k)=(V, E, P_min)为参考序列X上字符串长度为k的MiniDBG.
2 路径定位算法2.1 MiniDBG模型MiniDBG是传统DBG的一种压缩存储形态，通过对分支、非分支节点进行区分，找到图中的超级边，以及超级边所对应的最小边，最终生成最小边的位置列表.对最小边及最小边位置列表进行存储，从而实现传统DBG的压缩存储.
定义1 (非分支节点、单路径)：
如果DBG(X, k)上的一个顶点v_i满足：入度与出度相等且为1，则v_i被称为非分枝节点，否则为分支节点.对于一个DBG(X, k)上的一条路径h=v_i1v_i2… v_ik，如果其每个节点都是非分支节点，则称之为单路径.如果v_i的入度不为1，则称v_i为入分支节点；如果v_i的出度不为1，则称v_i为出分支节点.对于一条边e_ij，如果v_i是出分支节点，则e_ij为一条出边.
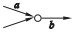
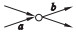
假设边a和b是相邻的，a为节点的入边, b为节点的出边，相邻边位置的关系分为4种：
① a是非分支入边，b是非分支出边；
② a是非分支入边，b是分支出边；
③ a是分支入边，b是非分支出边；
④ a是分支入边，b是分支出边.
用a=b, a>b, a < b和a?b去表示这4种关系, 如表 1所示.
表 1(Table 1)

表 1 四种邻接边的关系Table 1 Relationship of four types of adjacent edges 举例 关系 表示 list(b)-1=list(a) a=b list(b)-1?list(a) a>b list(a)+1?list(b) a < b list(a)+1, list(b) a?b

表 1 四种邻接边的关系 Table 1 Relationship of four types of adjacent edges

定义2 (超级边)：
为了在DBG模型中存储尽可能少的位置列表，首先需要消除等价位置列表的影响，在此引入超级边.对于一条边e_i0j0∈E，如果满足v_ix和v_jy为分支节点，其中x=0, …, p-1；y=0, …, q-1, v_ip和v_jq为分支节点，那么包含该边的路径e_ipjq^s=e_ipip-1…e_i1i0e_i0j0e_j0j1…e_jq-1jq是一条超级边.
在移位操作下，超级边内各边的位置列表相同，因此将超级边的位置列表定义为其第一条边的位置列表：
在某些情况下，边的超级边仍然是它本身.因为超级边上的边的位置列表彼此是等价的，超级边的位置列表可以表示超级边上所有的边.为了消除超级边中等价位置列表的影响，DBG可以看作是一个新的图，称为super-DBG，它由分支节点和超级边组成.
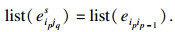算法1给出了超级边的生成过程.T表示用于保存结果的节点列表，第2~6行为向右扩展边缘的过程，直至到达分支节点.同样，第7~11行向左扩展边缘，直至到达分支节点.T在扩容过程中按顺序依次保存节点.
算法1 ??生成给定边的超级边Gen_super_edge(e_i0j0)：
输入: 图DBG(X, k)=(V, E), 一条边e_i0j0;
输出: e_ipjq^s=e_ipip-1… e_i1i0e_i0j0e_j0j1 … e_jq-1jq, 其中e_ipjq^s=Gen_super_edge(e_i0j0);
1:T=?;k=0;l=0;
2: while 1
3: ????insert v_jk into T at the tail termination;
4: ????if v_jk is branching
5: ??????break;
6: ????v_jk+1=v_jk.successor(); k+ +;
7:while 1
8: ????insert v_il into T at the head termination;
9: ????if v_il is branching
10: ??????break;
11:v_il+1=v_ik.precursor(); l+ +;
12: Return T.
定义3 (最小超级边)：
一条超级边e_ij^s，如果节点v_i的出度和v_j的入度都大于1，那么e_ij^s是一条最小超级边.
一条超级边e_ij^s，如果节点v_i的出度大于1，那么e_ij^s是一条出分支超级边；如果节点v_j的入度大于1，那么e_ij^s是一条入分支超级边.
令E₀^s, E_in^s和E_out^s分别为DBG(X, k)的最小超级边、入分支超级边和出分支超级边，则有E₀^s=E_in^s∩E_out^s, E₀^s?E_in^s, E₀^s?E_out^s.
对于一个最小超级边e_ij^s，相邻的超级边e_jk^s或e_li^s都不满足条件：
对于任意超级边e_ij^s，根据最小超级边位置列表的并集，可以计算出e_ij^s的位置列表.
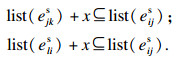算法2描述了基于MiniDBG模型计算一条边的位置列表的过程.第3~4行对应于输入边的超级边是最小超级边的情况(Δ为偏移量)，超级边中第一条边的位置列表保存在MiniDBG模型中.第5~18行对应输入边的超级边不是最小超级边的情况；这里分两种情况：①超级边从入分支节点开始；②超级边在出分支节点结束.其中E_l-表示从顶点l出发的边的集合，E_-k表示在顶点k结束的边的集合.
显然，超级边可以从入分支节点开始，同时又在出分支节点结束.在这种情况下，位置列表可以通过情况①或②计算.
算法2 ??计算每条边的位置列表Gen_list(e_ij)：
输入: 图DBG(X, k)=(V, E, P_min), 一条边e_ij;
输出: list(e_ij)，其中list(e_ij)=Gen_list(e_ij);
1:list(e_ij)=?;
2:e_kl^s=Gen_super_edge(e_ij);
3: if e_kl^s∈E_min
4: ????return list(e_kl^s)+Δ;
5:else if v_l is out-branching
6: ????for e_lu in E_l-
7:??????e_ly^s=Gen_super_edge(e_lu);
8:??????if v_y is in-branching
9: ????????list(e_ij) =list(e_ij) ∪ (list(e_ly^s)+Δ);
10: ?????else
11: ?list(e_ij)=list(e_ij)∪(Gen_list(e_lu)+Δ);
12:else if v_k is in-branching
13: ????for e_uk in E_-k
14:??????e_yk^s=Gen_super_edge(e_uk);
15: ????if v_y is out-branching
16:??????list(e_ij)=list(e_ij)∪(list(e_yk^s)+Δ);
17: ????else
18: ?list(e_ij)=list(e_ij)∪(Gen_list(e_uk)+Δ);
19: Return list(e_ij).
2.2 MiniDBG路径定位算法定理1 ?? DBG中的闭环路径示例如图 1所示，对于一个闭环路径，在循环路径中至少存在一个入分支节点和一个出分支节点.
图 1(Fig. 1)

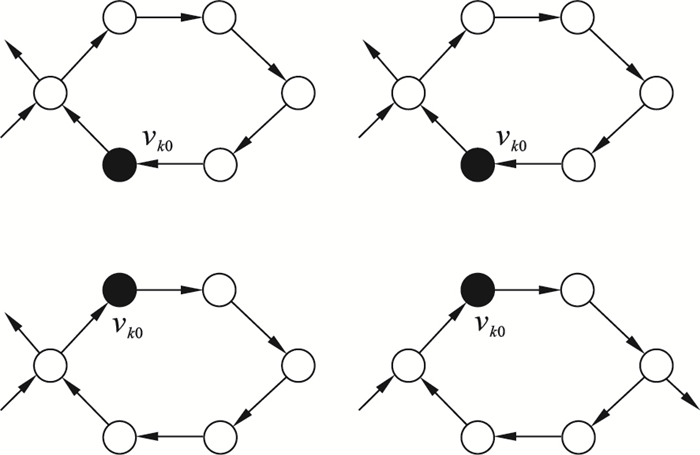图 1 DBG中的闭环路径Fig.1 Closed loop path in the DBG

定理2 ?? 将整条路径h=e_i0i1e_i1i2… e_in-1i_n进行分割，得到路径片段h_seg=e_ikik+1e_ik+1ik+2… e_ik+l-1ik+l，则有以下结论：
① ?q, k≤q≤k+l-1满足list(h_seg)=list(e_iqiq+1)-(q-k).
② e_iqiq+1是最小超级边.
③ h_seg中除e_iqiq+1之外没有任何边是最小超级边.
定理3 ??图DBG(X, k)上的路径h=e_i0i1e_i1i2… e_in-1in一定满足以下结论：
① h可以用一个超级边序列等价地表示h′=e_j0j1^se_j1j2^s… e_jm-1jm^s;
② 路径上的边有相同的位置列表list(h)=list(h′);
③
根据定理3可以推得基于MiniDBG模型的路径位置列表计算方法，如算法3所示.第1行，L=Ω表示结果位置列表，并初始化为一般集合.R_pre表示初始的边与当前的超级边之间的关系.类似地，R_cur表示当前超级边和下一条边之间的关系.l表示当前超级边的长度.Get_relationship(*, *) 表示根据连接两条边的节点的类型获取两条相邻边之间的关系.第4~5行，算法跳过“=”关系，如果某一步骤后的交集为空，则算法返回的路径为假路径.
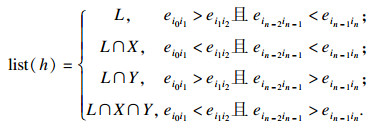算法3 ??计算给定路径的位置列表：
输入: DBG(X, k)=(V, E, P_min), 一路径e_i0i1e_i1i2… e_in-1in;
输出: list(e_i0i1e_i1i2… e_in-1in);
1:L=Ω; R_pre=′′; R_cur=′?′; l=1;
2: for(k=0;k < n-1;k+ +)
3:R_pre=R_cur; k=k+l-1;l=1;
4: ????while(R_cur=Get_relationship(e_ik+lik+l+1, e_ik+l+1ik+l+2)=′=′)
5: ????l+ +;
6: ????if R_pre=′?′or R_pre=′>′
7: ????????if R_cur=′?′or R_cur=′ < ′
8: ????????????L=L∩(list(e_ikik+1)-k);
9: ????????????if L=?
10:????????????????return L;
11: k=k+l-1;
12: ??if R_cur=′>′or R_cur=′?′
13: L=L∩(list(e_in-1in)-n+1);
14: Return L.
为了定位一个点v_i，MiniDBG方法必须定位从v_i开始或在v_i结束的边.然后结合所有边的位置生成节点v_i的位置列表.定位节点比定位边花费更多的时间.然而，k为n+1的图上的节点列表相当于k取n的图上的边列表.因此，MiniDBG可以通过设置较小的k来减少定位所花费的时间.
对于边的定位，如果是一条最小边，MiniDBG将返回边的位置列表；对于非最小边，MiniDBG会生成一组最小边，并结合最小边位置列表得到原始边的位置列表.这个过程递归地调用定位边的方法，直到所有边都最小为止.对于路径，MiniDBG首先检查所有的节点和边是否在图上：如果不是，则返回空列表；否则，MiniDBG将使用定理3中的公式计算路径的位置列表.在此过程中，一旦获取的位置列表的交集为空，算法返回并且路径的位置列表为空.所有这些操作都是为了避免在定位假路径上浪费时间.
3 实验结果所有实验在一台搭载了4个Intel(R)Xeon(R)E5-2640 2.40 GHz CPU的服务器上完成，每个CPU有10个核心，服务器内存空间为160 GB，并搭载了4台NVDIA Tesla K40显卡.操作系统为Ubuntu 16.04.SHDex算法在eclipse中实现，并使用C和C++ 编程.
本文使用了以下数据集：从NCBI RefSeq数据库下载了所有的62E大肠杆菌菌株数据^[17](http://www.ncbi.nlm.nih.gov/refseq/)，选取其中之一称为D1数据集；62E中全部数据集称为D2；文献[12]中引用的人类基因组数据在本文中被用作数据样本D3.
k-mer长度为k的顶点对应的图和k-mer长度为k-1的边对应的图是一样的；因此，MiniDBG可以设置较小的k-mer长度.对于FM-index，当后缀数组间隔为空时，路径为假路径，定位过程结束.
测试MiniDBG在增加查询长度的同时定位字符串的性能.当字符串长度L增加时，查找子字符串的时间开销C_me增加.结果如图 2所示.MiniDBG的内存开销非常小.随着字符串长度L的增加，MiniDBG耗费了可接受的时间来定位这些字符串.在图 2c中，随着查询子字符串长度L的增加，时间成本增加得非常缓慢.
图 2(Fig. 2)

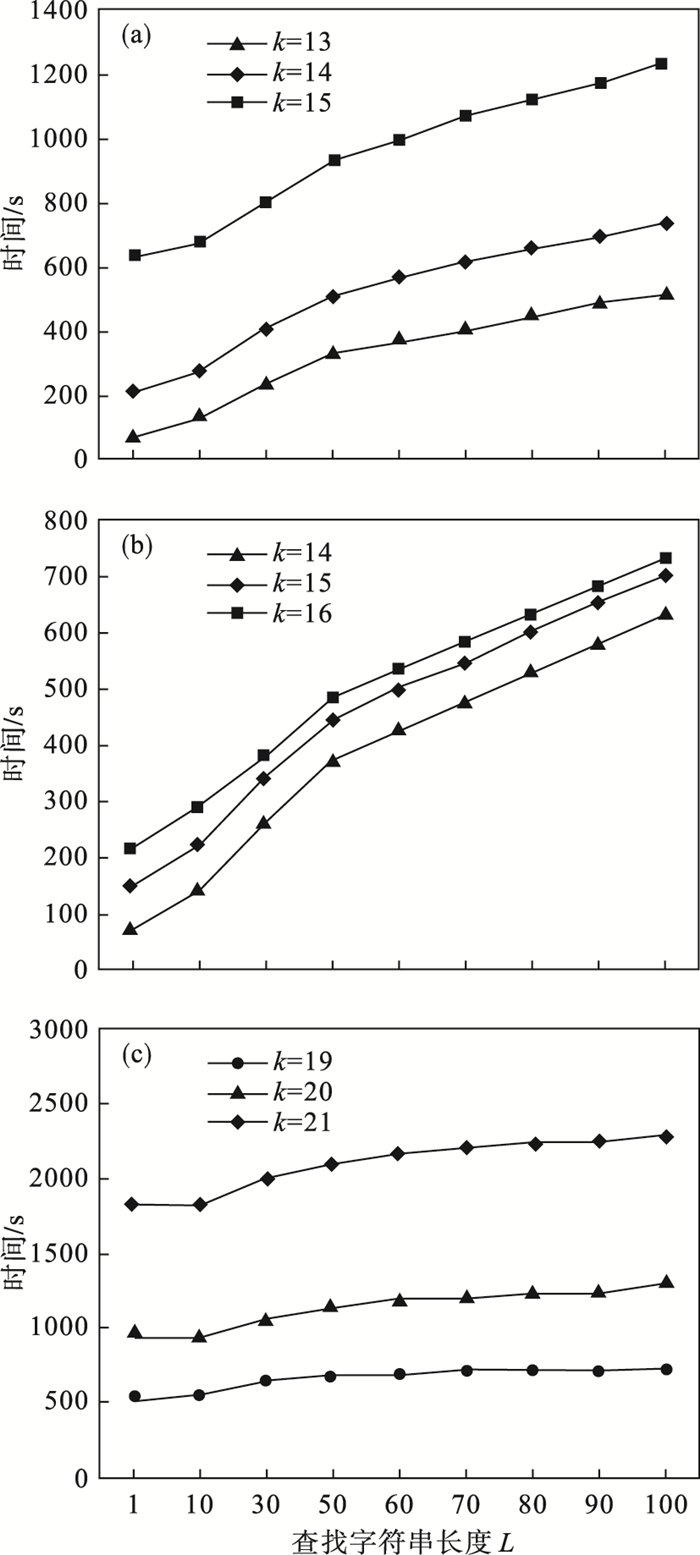图 2 子字符串长度增加时查找子字符串的时间成本Fig.2 Time costs for locating substrings while the length of the strings increases (a)—D1数据集；(b)—D2数据集；(c)—D3数据集.

图 3~图 5为在数据集D1，D2和D3上定位子字符串的时间开销，图例中F和M分别代表FM-index和MiniDBG.查找子字符串是由参考序列上的滑动窗口生成的.查询总数为5 521 840，图中显示了定位查找子字符串的总时间开销.对于FM-index，查找的子字符中长度分别从9/10/15到17/20/23.对于MiniDBG，查找的子字符串长度从k+1到k+9，参数k分别为9/10/19到14/15/21.
图 3(Fig. 3)

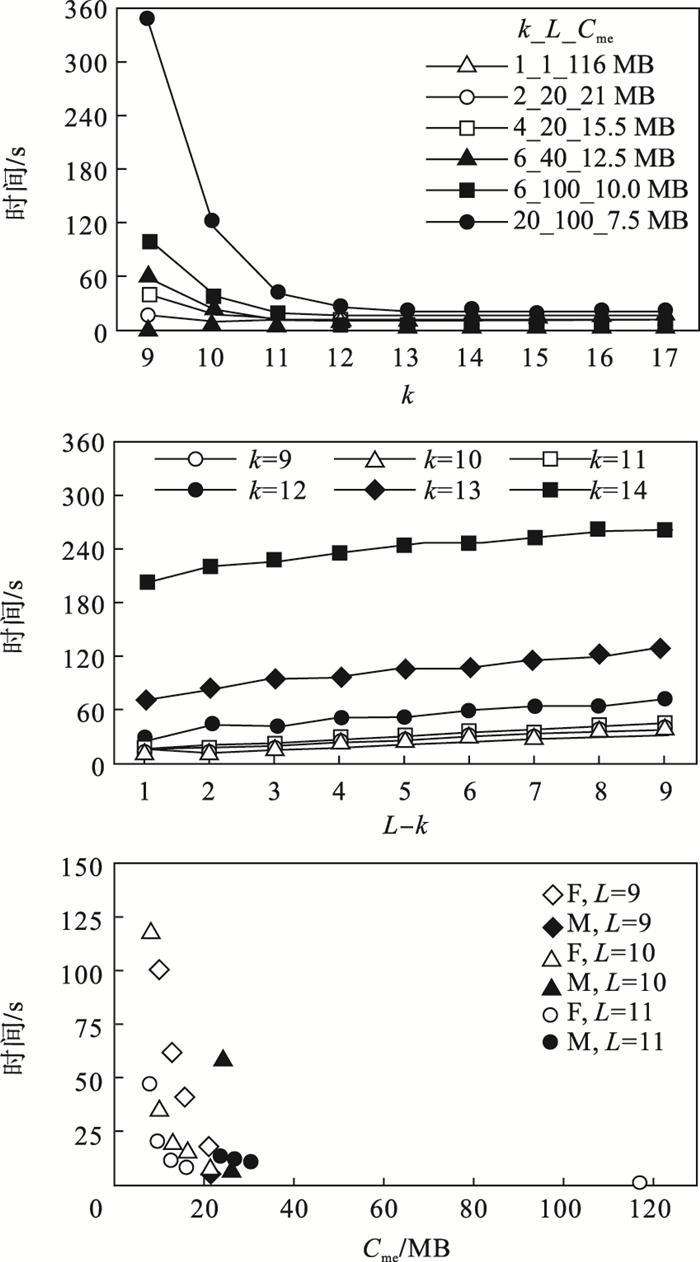图 3 在数据集D1上定位子字符串的时间开销Fig.3 Time costs for locating substrings on D1

图 4(Fig. 4)

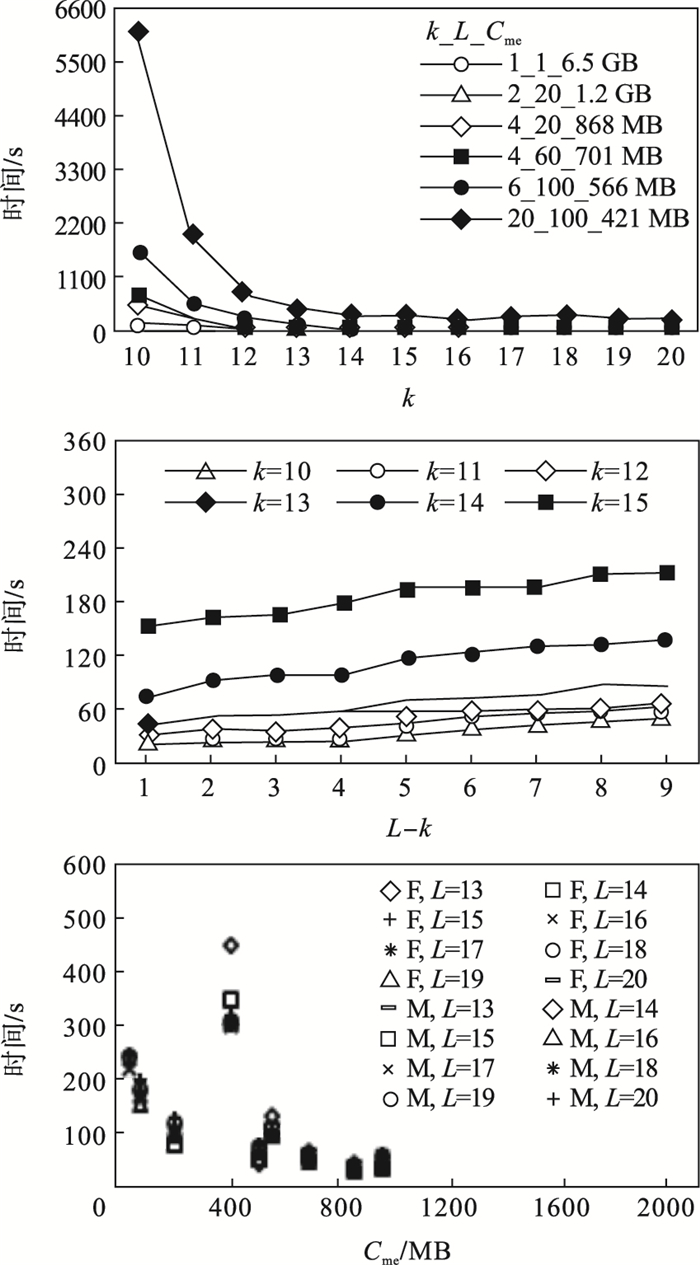图 4 在数据集D2上定位子字符串的时间开销Fig.4 Time costs for locating substrings on D2

图 5(Fig. 5)

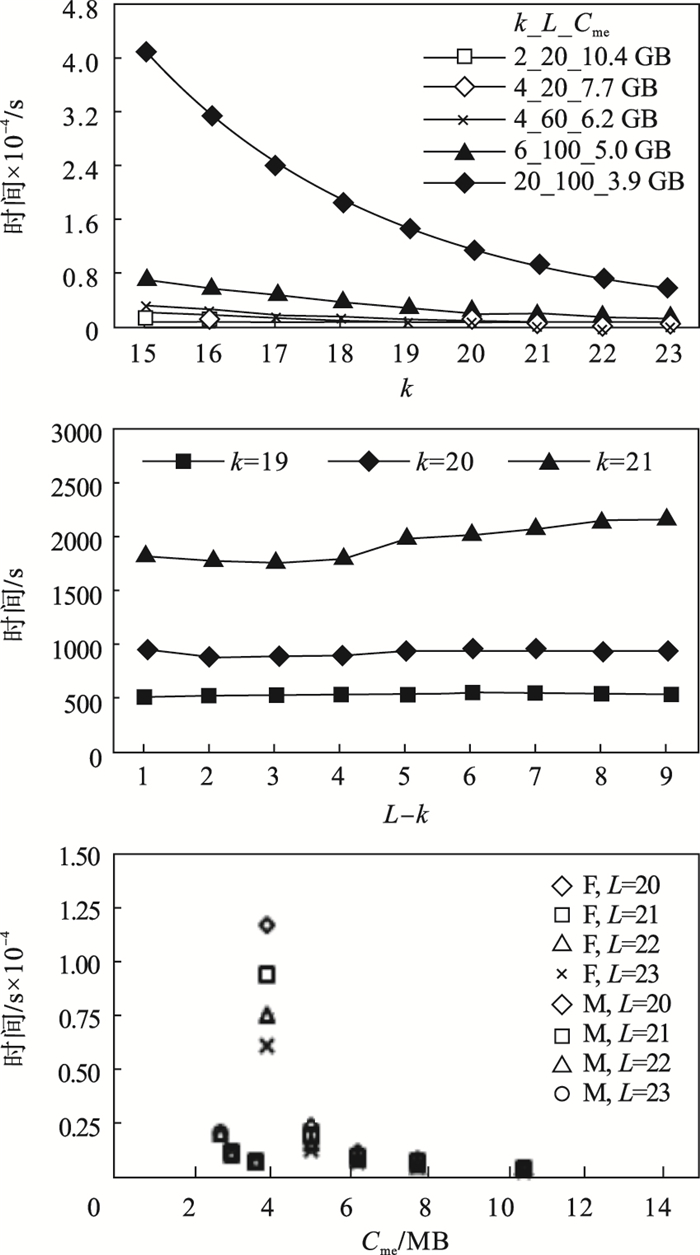图 5 在数据集D3上定位子字符串的时间开销Fig.5 Time costs for locating substrings on D3

从实验结果中得到如下结论：
1) 对于非频繁查询(特别是在参考序列上只出现一次的查询)，FM-index比MiniDBG效率更高，如图 3所示.对于在参考序列上出现超过10次的频繁查询，MiniDBG的效率更高，如图 4所示，这是因为FM-index和MiniDBG的工作方式不同.FM-index首先计算查找字符串的后缀数组间隔，然后针对间隔内的每个索引计算后缀数组的值；因此，间隔越大，花费的时间就越多.对于MiniDBG，它可以一次性获得所有位置，而不像FM-index需要依次计算每个后缀数组.
2) MiniDBG在字符串定位时比FM-index更灵活.在原子串上增加一个字符的定位问题中，FM-index需要重新计算后缀数组的所有值.例如，给定“CGT”的位置，只添加一个基数的“ACGT”或“CGTA”的位置必须重新计算得出；而对于MiniDBG，只需要添加一条边，可以通过将新边的列表与原始列表合并来计算.
3) MiniDBG查找字符串的时间开销比FM-index更低，即使它比FM-index占用更少的内存.如图 4所示，在数据集D2上，FM-index在需要566 MB内存的情况下，耗费104，94和94 s来分别定位长度为14，15和16的字符串；而MiniDBG能够分别使用519，221和221 MB内存进行同样的查询操作，分别只需要41，76和93 s.如图 5所示，在数据集D3上，FM-index使用5 GB的内存，在2 150，1 715，1 396和1 132 s内定位长度为20，21，22，23的字符串；而MiniDBG分别使用3.6，3，3和3 GB的内存进行相同的查询操作，仅需515，955，900和902 s.
4 结语本文提出了MiniDBG模型，用于存储最小边位置列表，以便在参考序列上定位图的边和路径，并给出了基于MiniDBG模型的路径定位算法.讨论了k-mer长度增加时位置列表所占内存的大小.通过实验验证了模型和算法的有效性.
参考文献

[1]	Miller J R, Koren S, Sutton G. Assembly algorithms for next-generation sequencing data[J]. Genomics, 2010, 95(6): 315-327. DOI:10.1016/j.ygeno.2010.03.001
[2]	Schatz M C, Delcher A L, Salzberg S L. Assembly of large genomes using second-generation sequencing[J]. Genome Research, 2010, 20(9): 1165-1173. DOI:10.1101/gr.101360.109
[3]	Minkin I, Pham H, Starostina E, et al. C-Sibelia: an easy-to-use and highly accurate tool for bacterial genome comparison[J/OL]. F1000 Research, 2013[2021-04-10]. https://f1000research.com/articles/2-258/v1. DOI: 10.12688/f1000research.2-258.v1.
[4]	Minkin I, Patel A, Kolmogorov M, et al. A scalable and comprehensive synteny block generation tool for closely related microbial genomes[M]// Algorithms in Bioinformatics. Berlin: Springer Berlin Heidelberg, 2013: 215-229.
[5]	Pham S K, Pevzner P A. DRIMM-Synteny: decomposing genomes into evolutionary conserved segments[J]. Bioinformatics, 2010, 26(20): 2509-2516. DOI:10.1093/bioinformatics/btq465
[6]	Raphael B, Zhi D G, Tang H X, et al. A novel method for multiple alignment of sequences with repeated and shuffled elements[J]. Genome Research, 2004, 14(11): 2336-2346. DOI:10.1101/gr.2657504
[7]	Dilthey A, Cox C, Iqbal Z, et al. Improved genome inference in the MHC using a population reference graph[J]. Nature Genetics, 2015, 47: 682-688. DOI:10.1038/ng.3257
[8]	Iqbal Z, Caccamo M, Turner I, et al. De novo assembly and genotyping of variants using colored de Bruijn graphs[J]. Nature Genetics, 2012, 44: 226-232. DOI:10.1038/ng.1028
[9]	Bradley P, Gordon N C, Walker T M, et al. Rapid antibiotic-resistance predictions from genome sequence data for Staphylococcus aureus and Mycobacterium tuberculosis[J]. Nature Communications, 2015, 6: 10063. DOI:10.1038/ncomms10063
[10]	Xin H, Nahar S, Zhu R, et al. Optimal seed solver: optimizing seed selection in read mapping[J]. Bioinformatics, 2016, 32(11): 1632-1642. DOI:10.1093/bioinformatics/btv670
[11]	Liu B, Guo H Z, Brudno M, et al. deBGA: read alignment with de Bruijn graph-based seed and extension[J]. Bioinformatics, 2016, 32(21): 3224-3232. DOI:10.1093/bioinformatics/btw371
[12]	Minkin I, Pham S, Medvedev P. TwoPaCo: an efficient algorithm to build the compacted de Bruijn graph from many complete genomes[J]. Bioinformatics, 2017, 33(24): 4024-4032.
[13]	Guo H Z, Fu Y L, Gao Y, et al. deGSM: memory scalable construction of large scale de Bruijn graph[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2019[2021-04-09]. https:/ieeexplore.ieee.org/document/8703070. DOI: 10.1109/TCBB.2019.2913932.
[14]	Fatemeh A, Hirak S, Avi S, et al. A space and time-efficient index for the compacted colored de Bruijn graph[J]. Bioinformatics, 2018, 34(13): i169-i177. DOI:10.1093/bioinformatics/bty292
[15]	Alipanahi B, Kuhnle A, Puglisi S J, et al. Succinct dynamic de Bruijn graphs[J]. Bioinformatics, 2021, 37(14): 1946-1952. DOI:10.1093/bioinformatics/btaa546
[16]	Isaac T, Garimella K V, Zamin I, et al. Integrating long-range connectivity information into de Bruijn graphs[J]. Bioinformatics, 2018, 34(15): 2556-2565. DOI:10.1093/bioinformatics/bty157
[17]	Pruitt K D, Brown G R, Hiatt S M, et al. RefSeq: an update on mammalian reference sequences[J]. Nucleic Acids Research, 2014, 42(D1): D756-D763. DOI:10.1093/nar/gkt1114