

1. 中国科学院 成都计算机应用研究所,四川 成都 610041;
2. 中国科学院大学,北京 100049;
3. 西南民族大学 计算机科学与技术学院,四川 成都 610225
收稿日期:2021-04-13
基金项目:中央高校基本科研业务费专项资金资助项目(2020NYB18)。
作者简介:金瑾(1988-), 女, 四川成都人,中国科学院成都计算机应用研究所博士研究生;
王鹏(1975-), 男, 四川成都人,西南民族大学教授,博士生导师。
摘要:多尺度量子谐振子优化算法(MQHOA)是近年提出的一种基于量子物理的自然计算方法.本文针对该算法未能充分利用迭代中历史信息的问题,提出一种历史数据驱动的多尺度量子谐振子优化算法(HI-MQHOA).在两步迭代过程中,HI-MQHOA引入历史数据作为驱动,形成下一代个体分布的参数及动态调整算法尺度.形成的下一代个体分布参数可以有效指导算法的开发和探索,动态尺度调整可以避免早熟停滞.通过多个经典测试函数验证,该算法在解的质量、准确率和伸缩性方面优于MQHOA和改进的MQHOA,以及其他自然计算算法.
关键词:优化算法量子谐振子多尺度数据驱动历史信息
Historical Data-Driven Multi-scale Quantum Harmonic Oscillator Optimization Algorithm
JIN Jin1,2, WANG Peng3


1. Chengdu Institution of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China;;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Computer Science and Technology, Southwest Minzu University, Chengdu 610225, China
Corresponding author: WANG Peng, E-mail: qhoalab@163.com.
Abstract: The multi-scale quantum harmonic oscillator optimization algorithm(MQHOA)is a natural calculation algorithm based on quantum physics proposed in recent years. Aiming at the problem that the algorithm fails to make full use of the historical information in the iteration, this paper proposes a historical information-driven multi-scale quantum harmonic oscillator optimization algorithm(HI-MQHOA). In the two-step iterative process, HI-MQHOA introduces historical data as a driver to form the parameters of the next generation individual distribution and dynamically adjust the scale of the algorithm. The next generation individual distribution parameters can effectively guide the development and exploration of the algorithm, and dynamic scaling can avoid premature stagnation. Verified by several classical test functions, the algorithm is superior to MQHOA, improved MQHOA and other natural computing algorithms in solution quality, accuracy and scalability.
Key words: optimization algorithmquantum harmonic oscillatormulti-scaledata drivenhistorical information
工业设计、控制、自动化等应用场景普遍存在优化问题.近年来,自然计算方法解决了大量的优化问题.这些算法包括蚁群算法[1]、粒子群算法[2]、差分进化算法[3]、人工蜂群算法[4]、烟花算法[5]、头脑风暴算法[6]、象群优化算法[7]、教与学优化算法[8]、狮群算法[9],以及协方差自适应进化策略(CMA-ES)[10].
多尺度量子谐振子优化算法(MQHOA)是基于量子物理理论提出的自然计算方法[11],该算法把优化问题通过势阱等效转化为对薛定谔方程的求解问题.算法主要包含两个迭代过程:第一是量子谐振子过程,粒子依据波函数的模方,生成满足一定参数分布的采样点,再根据这些粒子适应度值判断下一次采样的种群;第二是多尺度过程,尺度按照2n递减,在每个量子谐振子过程中,利用目标函数的简单统计均值信息,对高能级暂稳态进行一定扰动.
在多尺度过程中,大部分目标函数的信息未能被成功利用,虽然量子隧穿效应能够一定程度上避免算法陷入局部最优解,但单纯的尺度衰减容易导致算法早熟停滞.针对这一问题,众多****不断提出改进的MQHOA.最新关于MQHOA的研究主要针对算法中的统计均值及迁移策略[12].文献[13]讨论多谐振子改进的MQHOA,文献[14]利用群体稳定性及更严格的个体约束来提高算法的收敛速度及鲁棒性.这些研究表明,目标函数应该保留关于可行和不可行的关键信息,使用目标函数的信息有助于提高算法的性能,对更好地计算和评估下一代个体具有重要作用.基于上述思想,本文提出了历史数据驱动的多尺度量子谐振子优化算法(HI-MQHOA).
在MQHOA的两步迭代过程中,HI-MQHOA通过分析较优历史数据提高MQHOA的性能;利用目标函数的历史信息解决MQHOA的收敛问题,运用目标函数产生的信息引导算法寻找最优解.实验表明,在给定测试集上,HI-MQHOA优于其他MQHOA的改进版本和一些主流优化算法.基于HI-MQHOA优秀的全局搜索性能和快速收敛特性,该算法也适用于大规模优化问题.
1 标准MQHOA1.1 MQHOA物理模型量子力学中波函数可以体现粒子在空间某位置出现的概率.由文献[15]可知,薛定谔方程可以描述量子系统,定态薛定谔方程的表达式如下:
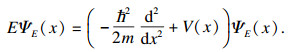 | (1) |
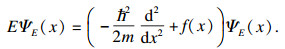 | (2) |
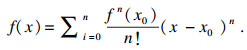 | (3) |
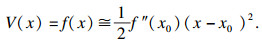 | (4) |
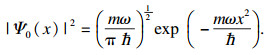 | (5) |
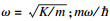
1.2 MQHOA基本流程MQHOA包括两个过程[11],即在同一尺度上的量子谐振子过程(QHO过程)和多尺度过程.
QHO过程又包括能级稳定和能级过渡过程.能级稳定过程实现了量子系统进入一个相对稳定的亚稳态:根据具体策略生成候选解,计算出能级稳定准则所需的取值;如果不满足条件,则继续进行该能级稳定过程,即生成新的解,并重复计算和判断.能级过渡过程通过一定的扰动策略,使解空间中当前最优解发生变化并移动到较好的解位置,从而实现能级过渡目标.
多尺度过程的主要作用是,引导算法从高能态的大范围搜索到低能态的小范围搜索过程.多尺度调整过程采用了衰减策略,使算法在较小的尺度上重复从高能量级到基态的过程;然后,再重复量子谐振子过程,在新的尺度层面上对解空间进行更全面的搜索.多尺度过程提高采样精度.
2 MQHOA存在的问题及改进在标准的MQHOA中,粒子的QHO过程仅使用了统计均值信息,而忽略了其他有用信息.本文利用历史数据驱动的方法,提出HI-MQHOA.该算法在两个方面优于MQHOA及其改进算法.以下是详细说明.
2.1 基于多元统计分析改进的QHO过程在MQHOA基础版中,算法的波函数被定义为多个一维正态分布的叠加,即
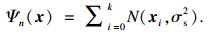 | (6) |
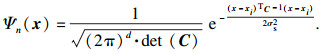 | (7) |
 | (8) |
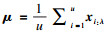
对此,本文提出新的均值向量生成模型.该模型由当代信息产生下一代个体分布参数.首先,按照适应度值对个体进行排序:x1 < x2 < … < xλ,设置一个系数α控制历史信息的利用比例,计算出的均值向量为
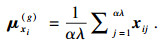 | (9) |
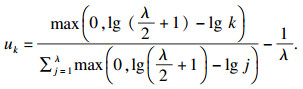 | (10) |
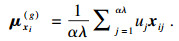 | (11) |
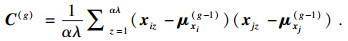 | (12) |
表 1(Table 1)
| 表 1 历史数据驱动的采样模型(算法1) Table 1 Historical data driven sampling model |
2.2 动态调整的多尺度过程MQHOA采用固定衰减的多尺度过程,而固定衰减有两个不足:一是衰减的系数一直为0.5,这个衰减系数并不会根据具体问题发生变化;二是过早的衰减会导致算法早熟停滞.因此,HI-MQHOA采用动态机制调整的多尺度过程.由上面改进QHO过程的分析可知,当代个体根据适应度值排序,根据均值向量或差值向量生成下一代个体,由于协方差自带尺度信息[17],因此可以由协方差矩阵的信息产生动态尺度衰减.动态尺度设置如下:
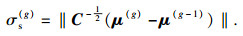 | (13) |
3 HI-MQHOA本节探讨的伪代码是基于第2节关于多元统计分析改进的QHO过程,以及动态调整的多尺度过程的阐述.HI-MQHOA伪代码(算法2)见表 2.
表 2(Table 2)
| 表 2 HI-MQHOA伪代码(算法2) Table 2 Pseudo code of HI-MQHOA |
算法中采样模型的设置基于以下考虑:
1) 种群的收敛方向.选择最优的部分作为下一代个体生成的参数,可以使下一代个体分布在近似梯度方向上.
2) 算法搜索的范围.如果最优个体不包含在采样范围内,则下一次搜索应扩大种群的搜索范围;如果采样范围内包含了最优个体,此时应减小探索的区域,使算法能够智能感知最优解的范围.
4 实验与分析在HI-MQHOA中,需要设置的参数是种群数k、生成指导信息的参数α及种群个体数λ.对于HI-MQHOA,α的值通常在(0, 1)之间,较小的α使算法更快收敛,而较大的α使算法更有效地利用目标函数的值.结合这些信息,通过验证,当α=0.3时,算法的性能达到最佳.
本文通过选定的测试函数集验证HI-MQHOA的有效性[18].该测试函数集包含常见的单模和多模函数,测试函数如表 3所示.其中,f1~f5为单模函数,f6~f14为多模函数,这些函数的最优解均为0.
表 3(Table 3)
| 表 3 测试函数 Table 3 Benchmark functions |
在接下来的实验中,算法的终止条件为最大迭代次数10 000×d, 其中d代表问题的维度.为了排除随机性的影响,每个实验会重复51次.
4.1 参数选择及历史数据驱动的有效性验证为了验证本文算法的有效性,将HI-MQHOA分别与MQHOA和IS-MQHOA进行比较.为确保公平,每个算法的种群数量设置与文献[12]一致,即λ=40.为了测试算法的鲁棒性,本文引入成功率(SR)作为测度,SR表示在精度为10-6时找到最优解的比率.
对于k的选择,相关实验结果表明,k=1时效果最好.因此,在接下来的实验中,均设置k=1.表 4记录了HI-MQHOA和IS-MQHOA的Wilcoxon无符号秩检验结果,显著性水平为95 %.实验结果表明,在14个测试函数上,HI-MQHOA均明显优于IS-MQHOA.
表 4(Table 4)
| 表 4 Wilcoxon秩检验实验结果 Table 4 Wilcoxon rank sum results | ||||||||||||||||||||||||||||||||||||||||
参数{α, λ}的值也是通过实验来选取.如表 5所示,当参数为{0.3, 40}时,HI-MQHOA在函数f1, f2, f5, f7, f8, f11, f12和f13上解的平均值及方差均优于其他算法.参数为{0.3, 40}时,HI-MQHOA排名第1的次数为8,{0.2,40}时为4,{0.1,40}为3;而参数为{0.3,80}时HI-MQHOA优于其他算法的次数为0.因此,对于HI-MQHOA来说,并不是种群越大越好.随着种群规模的增加,算法的计算复杂度会增加,但寻优性能并未随之变得更好.所以,单纯增加种群规模,提升算法性能的效果是有限的,有时可能导致性能下降.根据实验结果分析可知,HI-MQHOA所涉及的参数{k, α, λ}的值为{1, 0.3, 40}.
表 5(Table 5)
| 表 5 不同参数下的性能比较 Table 5 Performance comparison with different parameters | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.2 仿真数据对比分析为了全面分析HI-MQHOA的性能,本文选取以下对比算法:
1) QPSO(quantum PSO): QPSO是一种功能强大的量子行为粒子群优化算法,能非常有效地解决小规模优化问题[19].
2) 标准粒子群优化算法(standard PSO, SPSO): PSO的标准版本,常被用作测试其他优化算法的基准[20].参数为:c1=c2=0.5+ln x, w=1/(2 ln 2).
3) DE: 一种优秀的自然计算算法[21].参数设置为:F=0.5, CR=0.9.
4) ABC:在ABC中,食物源个数SN设置为100,limit是与食物源相关的另一个参数.当收集到的食物源数量超过limit的值时,它们就会被丢弃[4].
5) CMA-ES: 在CMA-ES中,新的候选解根据多元正态分布的参数进行采样[10].
6) BBFWA: 一种具有竞争力的群体智能算法,已经得到广泛应用[22].
在维度等于60的条件下,对这些算法进行测试,实验结果如表 6所示.为了直观分析表 6数据,图 1展示了几个算法平均值优于其他算法的次数.从图中可以看出,HI-MQHOA的优化结果优于除f1, f2, f4, f5和f13以外的其他算法,取得最好的平均排名;其次是DE和CMA-ES,表明HI-MQHOA具有解决复杂函数问题的能力.由于ABC和BBFWA没有一次超越其他算法,因此没有在图 1中显示.
表 6(Table 6)
| 表 6 60维函数下HI-MQHOA与其他算法的性能对比 Table 6 Comparison of HI-MQHOA with other heuristic algorithms, where dimension is 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 1(Fig. 1)
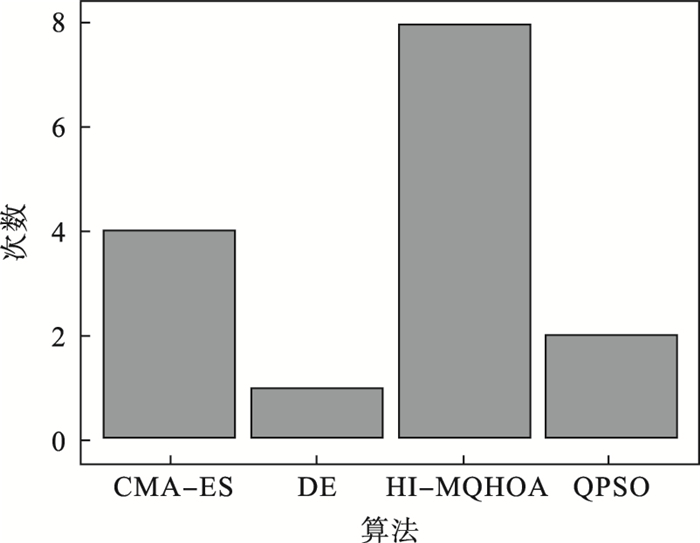 | 图 1 不同算法在测试中平均值优于其他算法的次数Fig.1 Times that the algorithm outperforms others on mean value during testing |
为了验证算法间性能差异是否明显,HI-MQHOA与其他算法之间还进行了Wilcoxon符号秩检验.图 2展示了HI-MQHOA显著优于其他算法的次数.在该实验中,将测试函数分为5个单模和9个多模进行对比.从图中可以看出,在单模函数方面,HI-MQHOA优于ABC和BBFWA算法5次,而优于QPSO算法4次,优于CMA-ES算法2次;在多模函数上,HI-MQHOA优于ABC,BBFWA和QPSO算法7次,优于DE算法5次,优于CMA-ES算法3次.HI-MQHOA在单模函数上性能不及CMA-ES和DE算法;在多模函数方面,HI-MQHOA的结果明显优于ABC,BBFWA和QPSO算法.
图 2(Fig. 2)
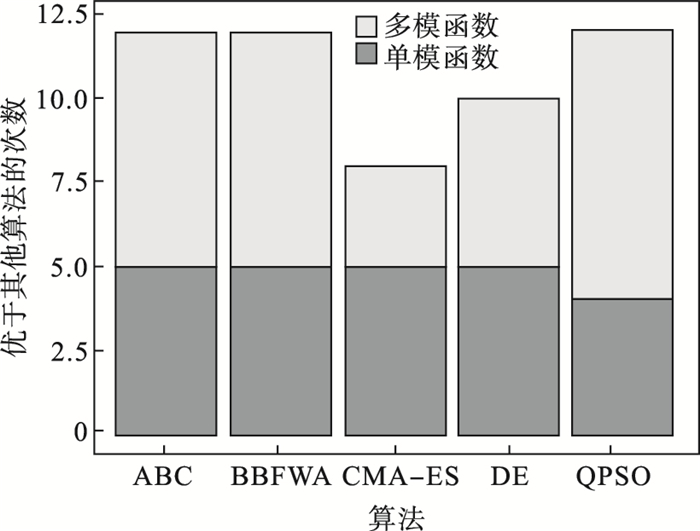 | 图 2 不同算法的性能对比Fig.2 Performance comparison of different algorithms |
由表 6、图 1及图 2的分析看出,对于多模函数,HI-MQHOA能够较为精确地找到最优解,因为HI-MQHOA能够较好地平衡探索和开发.而对于单模问题,HI-MQHOA优势不够明显,原因在于算法提出的动态尺度在面对复杂多模问题时具备优势,而对于单模问题不具备优势,因为单模问题要求算法能够快速定位解的位置,从而更好地开发以获得高精度的解.QPSO和CMA- ES在单模函数f1, f2上表现优于HI-MQHOA,但是它在多模问题上面临早熟的问题.这也再次证明了对于优化问题不存在一成不变的最优解决方法[23].
4.3 HI-MQHOA解决高维优化问题在工程应用场景中,许多优化问题涉及大量的变量.因此,在设计算法时应考虑到可伸缩性.上述维度为60的实验证实,HI-MQHOA,CMA-ES和DE这三种算法整体性能最好.本节讨论HI-MQHOA在高维(d=200)优化问题中的应用.
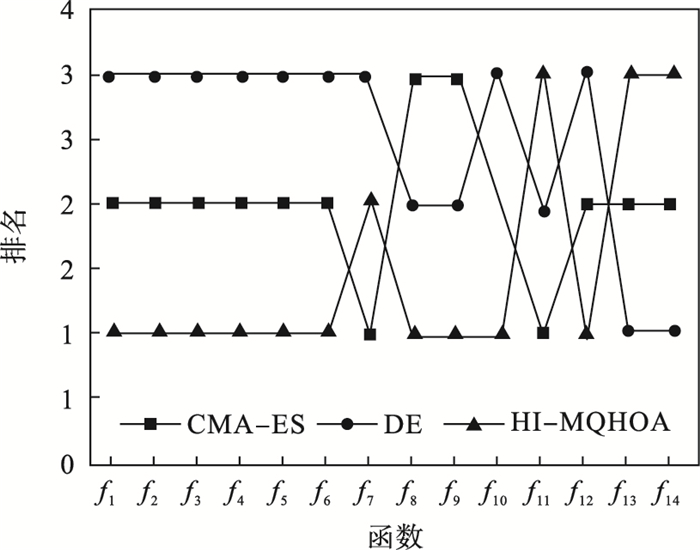
实验的均值排名结果如表 7和图 3所示.表 7所示,除f13和f14外,HI-MQHOA的标准差性能优于CMA-ES和DE,表明HI-MQHOA具有很好的稳定性;从寻优准确率上看,只要HI-MQHOA能够找到最优解,准确率均为100 %,表现出良好的寻优性能.图 3中横坐标为14个测试函数,纵坐标为排名情况.除f7, f13和f14外,HI-MQHOA优化结果的平均值优于CMA-ES和DE,体现了HI-MQHOA的优势.以上分析证实了HI-MQHOA具有解决高维优化问题的潜力.
表 7(Table 7)
| 表 7 高维函数测试结果 Table 7 Test result of high dimensional benchmark function | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 3(Fig. 3)
 | 图 3 高维函数均值排名的可视化Fig.3 Visualization of the mean ranking of high dimensional functions |
5 结语本文提出HI-MQHOA,解决了MQHOA历史信息利用率低的问题.首先,通过选择最优部分解的质心来获取指导信息,充分利用了算法中的历史数据;其次,通过两代最优部分解的质心之间距离,自适应调整算法的尺度.这两部分的改进,使算法能够在搜索空间中更加合理地进行探索和开发.同时,不仅与MQHOA及IS-MQHOA的对比实验,验证了历史数据驱动机制的有效性,而且与其他主流算法的对比实验,也验证了算法在最优化领域的潜力.另外,HI-MQHOA可以有效解决高维全局优化问题,说明算法具有良好的延展性.总之,利用历史数据驱动机制来改进自然计算的原理简单有效,对其他算法的设计具有一定的指导意义.
参考文献
| [1] | Dorigo M, Birattari M, Stutzle T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39. DOI:10.1109/MCI.2006.329691 |
| [2] | 瞿博阳, 梁静, Suganthan P N. 双局部粒子群算法解决环境经济调度问题[J]. 计算机工程与应用, 2014, 50(11): 1-6. (Qu Bo-yang, Liang Jing, Suganthan P N. Two local best based multi-objective particle swarm optimization algorithm to solve environmental/ economic dispatch problem[J]. Computer Engineering and Application, 2014, 50(11): 1-6. DOI:10.3778/j.issn.1002-8331.1304-0404) |
| [3] | 王柳静, 张贵军, 周晓根. 基于状态估计反馈的策略自适应差分进化算法[J]. 自动化学报, 2020, 46(4): 752-766. (Wang Liu-jing, Zhang Gui-jun, Zhou Xiao-gen. Strategy self-adaptive differential evolution algorithm based on state estimation feedback[J]. Acta Automatica Sinica, 2020, 46(4): 752-766.) |
| [4] | Karaboga D, Basturk B A. Powerful and efficient algorithm for numerical function optimization: artificial bee colony(ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x |
| [5] | 谭营, 郑少秋. 烟花算法研究进展[J]. 智能系统学报, 2014, 9(5): 515-528. (Tan Ying, Zheng Shao-qiu. Recent advances in fireworks algorithm[J]. CAAI Transactions on Intelligent Systems, 2014, 9(5): 515-528.) |
| [6] | Shi Y H. Brain storm optimization algorithm[C]//International Conference on Swarm Intelligence. Chongqing, 2011: 303-309. |
| [7] | Wang G G, Deb S, Coelho L. Elephant herding optimization[C]//2015 3rd International Symposium on Computational and Business Intelligence(ISCBI). Bali, Indonesia, 2015: 1-5. |
| [8] | 刘三阳, 靳安钊. 求解约束优化问题的协同进化教与学优化算法[J]. 自动化学报, 2018, 44(9): 1690-1697. (Liu San-yang, Jin An-zhao. A co-evolutionary teaching learning-based optimization algorithm for constrained optimization problems[J]. Acta Automatica Sinica, 2018, 44(9): 1690-1697.) |
| [9] | 张聪明, 刘立群, 马立群. 一种新的群智能算法: 狮群算法[J]. 计算机科学, 2018, 45(6): 114-116. (Zhang Cong-ming, Liu Li-qun, Ma Li-qun. New swarm intelligent algorithms: lions algorithm[J]. Computer Science, 2018, 45(6): 114-116.) |
| [10] | Hansen N, Müller S D, Koumoutsakos P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation(CMA-ES)[J]. Evolutionary Computation, 2003, 11(1): 1-18. DOI:10.1162/106365603321828970 |
| [11] | Wang P, Ye X G, Li B, et al. Multi-scale quantum harmonic oscillator algorithm for global numerical optimization[J]. Applied Soft Computing, 2018, 69(1): 655-670. |
| [12] | Ye X G, Wang P. Impact of migration strategies and individual stabilization on multi-scale quantum harmonic oscillator algorithm for global numerical optimization problems[J]. Applied Soft Computing, 2019, 85: 105800. DOI:10.1016/j.asoc.2019.105800 |
| [13] | Xin G, Wang P. Exploring superposition state in multi-scale quantum harmonic oscillator algorithm[J]. Applied Soft Computing, 2021, 107: 107398. DOI:10.1016/j.asoc.2021.107398 |
| [14] | Wang P, Li B, Jin J, et al. Multi-scale quantum harmonic oscillator algorithm with individual stabilization strategy[C]// International Conference on Swarm Intelligence. Shanghai, 2018: 624-633. |
| [15] | Griffiths D J, Schroeter D F. Introduction to quantum mechanics[M]. 3rd ed. Cambridge: Cambridge University Press, 2018. |
| [16] | Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies[J]. Evolutionary Computation, 2001, 9(2): 159-195. DOI:10.1162/106365601750190398 |
| [17] | Hauschild M, Pelikan M. An introduction and survey of estimation of distribution algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(3): 111-128. DOI:10.1016/j.swevo.2011.08.003 |
| [18] | Jamil M, Yang X S. A literature survey of benchmark functions for global optimization problems[J]. International Journal of Mathematical Modeling and Numerical Optimization, 2013, 4(2): 150-194. DOI:10.1504/IJMMNO.2013.055204 |
| [19] | Sun J, Xu W B, Feng B. A global search strategy of quantum-behaved particle swarm optimization[C]//IEEE Conference on Cybernetics and Intelligent Systems. Singapore, 2004: 8503878. |
| [20] | Zambrano-Bigiarini M, Clerc M, Rojas R. Standard particle swarm optimization 2011 at CEC-2013: a baseline for future PSO improvements[C]// IEEE Congress on Evolutionary Computation. Cancún, Mexico, 2013: 6557848. |
| [21] | Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [22] | Li J Z, Tan Y. The bare bones fireworks algorithm: a minimalist global optimizer[J]. Applied Soft Computing, 2018, 62(1): 454-462. |
| [23] | Wolpert D H, Macready W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82. DOI:10.1109/4235.585893 |
