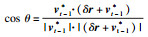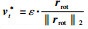1. 东北大学 计算机科学与工程学院,辽宁 沈阳 110169;
2. 沈阳航空航天大学 计算机学院,辽宁 沈阳 110136
收稿日期:2021-06-04
基金项目:国家自然科学基金青年基金资助项目(61902260); 国家自然科学基金资助项目(61972266)。
作者简介:范纯龙(1973-), 男, 辽宁营口人, 东北大学博士研究生;
夏秀峰(1964-),男,山东胶南人,沈阳航空航天大学教授;
乔建忠(1964-),男,辽宁沈阳人,东北大学教授,博士生导师。
摘要:在面向样本集的通用对抗攻击中,导致多数样本输出错误的通用扰动设计是研究关键.本文以典型卷积神经网络为研究对象,对现有通用扰动生成算法进行总结,提出采用批量随机梯度上升训练策略和球面投影搜索策略相结合的通用扰动生成算法.算法的每次迭代计算,首先从样本集中抽取小批量样本,采用随机梯度上升策略计算出使损失函数值下降的通用对抗扰动,然后将通用扰动投影到半径为ε的高维球面上,从而缩小通用扰动的搜索空间.算法还引入了正则化技术以改善通用扰动的生成质量.实验结果证明该算法与基线算法对比,攻击成功率显著提升,通用扰动的求解效率提高约30倍.
关键词:卷积神经网络通用扰动球面投影梯度上升对抗攻击
A General Adversarial Attack Method Based on Random Gradient Ascent and Spherical Projection
FAN Chun-long1,2, LI Yan-da2, XIA Xiu-feng2, QIAO Jian-zhong1


1. School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China;;
2. School of Computer, Shenyang Aerospace University, Shenyang 110136, China
Corresponding author: QIAO Jian-zhong, E-mail: qiaojianzhong@mail.neu.edu.cn.
Abstract: In general adversarial attacks oriented to sample sets, the general perturbation design that causes most sample to output errors is the key to the research. This paper takes the typical convolutional neural networks as the research object, summarizes the existing general perturbation generation algorithms, and proposes a general perturbation generation algorithm that combines batch random gradient ascent and spherical projection search. In each iteration of the algorithm, a small batch of samples are extracted from the sample set, and the general perturbation is calculated by using the random gradient rising strategy which reduces the value of the loss function. The general perturbation is then projected to the high-dimensional spherical surface with a radius of ε, so as to reduce the search space of general disturbances. The algorithm also introduces a regularization technique to improve the generation quality of general disturbances. Experimental results show that compared with the baseline algorithm, the attack success rate is significantly increased, and the solution efficiency of general perturbation is improved by about 30 times.
Key words: convolutional neural networkgeneral perturbationspherical surface projectiongradient ascentadversarial attack
深度神经网络在图像分类研究中的应用表现出良好的分类效果[1],现在已发展成为一种重要的学习模型并广泛应用.但研究中发现[2],如果在用于图像分类的卷积神经网络输入上做一些微小的特定改变,就会导致图像分类结果错误,这一现象迅速推动了神经网络安全性、鲁棒性研究的兴起.这种对神经网络输入的微小改变称为对抗扰动,改变后的神经网络输入称为对抗样本,利用对抗样本使神经网络产生错误输出的过程称为对抗攻击.
如果一个对抗扰动能够使样本集内大量样本的输出结果发生错误,则该对抗扰动称为通用扰动.本文对现有通用扰动生成方法进行了总结,并以图像分类神经网络为具体研究对象,在给定神经网络模型和训练数据集的条件下,提出一种通用对抗扰动的贪心迭代算法,采用随机梯度上升扰动求解策略和扰动的固定模长球面投影约束策略.经实验验证,该算法取得了更为高效、快速的攻击效果.
1 相关工作神经网络对抗攻击使神经网络在实际应用中面临重大安全威胁,可能对自动驾驶等系统[3]造成难以估计的后果;因此,对其开展深入研究是神经网络应用[4-5]中必须面对的关键问题,也是当前安全领域研究的热点,对提高神经网络的安全性[4]有重要意义.
从提出神经网络对抗攻击开始,研究者们就对抗攻击问题进行了大量研究,依据模型已知程度可以分为黑盒攻击、白盒攻击,黑盒攻击[5-6]只能通过查询输入样本的神经网络输出分类结果发起对抗攻击,白盒攻击[7-8]则利用模型的结构、参数等信息开展对抗攻击,常见方法有基于梯度信息的算法、基于神经网络几何解释的算法[7-8]等.依据攻击样本数量不同,可以分为单样本攻击和通用样本攻击,单样本攻击[9]针对每个样本都需要生成不同的对抗扰动;通用样本攻击[10-11]是利用样本集产生一个通用扰动,能够改变样本集中多数样本的网络输出结果.
近年,大量通用样本攻击方法被提出.通用对抗扰动(universal adversarial perturbation, UAP)生成算法分析每个样本的决策边界,通过迭代的方法逐步寻找与输入图像无关的通用扰动.GD-UAP[12]对图像的特征空间进行破坏,以产生数据无关的通用扰动.UPSET(universal perturbations for steering to exact targets)[13]算法利用残差网络生成与特定图像样本无关的通用扰动.CD-UAP(class discriminative UAP)[14]提出利用不同损失函数来处理目标类和非目标类图像,以生成通用扰动.文献[15]通过分析网络参数的特征映射,并求解雅可比矩阵的奇异向量来生成通用扰动,该算法有较低的样本数据依赖性.Hayes等[16]采用生成对抗网络技术产生数据无关的通用扰动.NAG[17]设计了一个易于训练的框架,对扰动的分布进行建模,进而可以得到表现良好的通用扰动.本文针对用于图像分类的典型卷积神经网络,开展白盒通用样本攻击研究.
2 通用扰动生成方法针对白盒通用对抗攻击问题,本文提出采用批量随机梯度上升的通用扰动迭代计算技术,并将通用扰动模长限定为常量,从而将通用扰动理解为高维球面上的点,将通用扰动求解理解为点在高维球面上移动的角度和方向计算问题,然后结合实验结果,对算法又进行了正则化改进.
2.1 问题描述通用扰动是一个向量,可以叠加到样本上形成攻击样本,并使尽可能多的样本网络输出结果与攻击样本网络输出结果不一致.通用扰动的质量可描述如下:
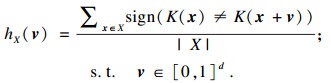 | (1) |
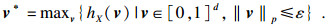 | (2) |
2.2 算法改进思想为获得更好的通用扰动算法,本文总结和分析了UAP等对抗扰动生成算法,归纳为三点:①通用扰动v*是通过迭代逐步生成,每次迭代处理一个样本x;②第t次迭代时,生成仅攻击样本x的最优对抗扰动rxt;③设vt= vt-1*+ rxt,则根据‖ vt‖p与ε的关系,依据式(3)计算第t次通用扰动vt*.
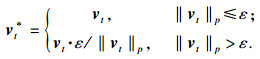 | (3) |
首先,通用扰动迭代求解过程中,每次处理一个样本,先求解其最优扰动,再计算通用扰动,这是一种串行迭代模式,限制了通用扰动求解效率的提升.寻找具有较好并行性的通用扰动生成算法,支持对样本集数据的高效处理,是提升算法效率的关键.
其次,每次迭代时,样本的最优扰动rxt的方向与通用扰动vt-1*的方向夹角可能很大,这意味着rxt对求解通用扰动的影响可能是负面的,而与多数样本扰动方向相近的次优扰动可能是更好的选择,样本最优扰动求解不是必须的.论文中用于求解样本最优扰动的DeepFool等算法,为了能够得出尽可能小的对抗扰动,通常也采用迭代求解策略,并且需要多次计算反向传播梯度,计算开销大.
最后,通用扰动的p-范数模长通常会随着迭代次数增大到给定阈值.随着该模长的增大,‖ rxt‖p与‖ vt-1*‖p间的比值越来越小,导致‖ vt-1*+ rxt‖ p在小范围内起伏不定,呈现陷入局部最优解搜索的情况,通用扰动攻击效果就难以再得到显著提高.
结合上述分析,本文提出一种基于随机梯度上升和球面投影的通用扰动生成算法,思想如下:
1) 神经网络是采用随机梯度下降方法来调优权重参数,那么当权重参数固定时,也可以把通用扰动作为参数来进行批量训练使其优化.随机梯度下降是使样本对应的标签概率上升,而通用扰动则是使样本对应的标签概率下降,所以需要采用随机梯度上升的训练策略,使通用扰动求解过程在原理上支持样本集的分轮分批训练,本质上提高了其计算的并行性.
2) 使用随机梯度上升训练通用扰动,需要设计训练的目标损失函数,文中采用交叉熵损失函数,并在目标损失函数中增加正则化项,限制个别维度的取值过大,形成明显的图像噪点.
3) 通用扰动迭代过程中,p-范数模长会逐渐增大,并导致求解陷入局部极值,因此,本文选择2-范数模长,并直接将通用扰动模长设为固定值ε,使通用扰动的迭代求解转化为在高维空间超球面上点的搜索问题,即寻找通用扰动在球面上的移动方向和距离.
基于上述思想,通用扰动求解算法的搜索空间减小至高维超球面,并且通过随机梯度上升的批量样本训练策略大幅减少反向传播查询次数.经过实验验证,算法在NiN,ResNet,VGG等典型分类器上能够快速生成高质量的通用扰动.
2.3 改进的通用扰动求解算法2.3.1 基于随机梯度上升的样本攻击图像样本集X中的某个样本x的神经网络分类预测标签为Kx,其定义见式(4),其中C为图像类别数,pk(x)为样本x在第k个图像类别上的输出概率.
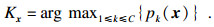 | (4) |
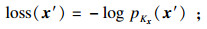 | (5) |
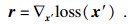 | (6) |
2.3.2 基于球面投影的通用扰动求解算法为进一步提高通用扰动迭代求解时的模长变化影响,文中选择2-范数模长作为通用扰动求解时的约束条件,并且整个迭代过程中,保持通用扰动的2-范数模长固定为阈值常量ε,使得每次迭代产生的通用扰动模长不再变化,从而将通用扰动的解空间限制在了半径为ε的超球面上,大幅缩小了通用扰动的求解范围,有助于提高搜索效率.
为描述一次迭代攻击过程,设待攻击样本集为X,当前开展的是第t次迭代,经过第t-1次迭代后生成的通用扰动是vt-1*, BatchSize是每次随机梯度上升计算时批量样本的数量,v*为待求解的通用扰动,则迭代过程如下:
1) 通用扰动的迭代训练过程中,每一轮迭代时,首先随机生成样本集X的一个划分集合Si,且Si中的某个元素sij满足|sij|=BatchSize,包含BatchSize个样本.每一次迭代训练时,从Si中选择不同的sij,称为第i轮第j批次迭代样本集.
2) 设第t次迭代计算时对应的样本集为sij,则s*={ x+ vt-1*| x∈sij}为本次计算随机梯度上升时使用的样本集,然后依据随机梯度上升计算出s*上的通用扰动r.
3) r确定了vt-1*在球面上的移动方向,扰动向量r+ vt-1*和vt-1*确定的超平面和半径为ε的超球面的交线,就是vt-1*的移动方向,即向量需要从vt-1*方向转到r+ vt-1*方向.设vt-1*转过角度的上限为θ,而vt-1*和r+ vt-1*间的夹角可能与θ相差很大,不利于迭代收敛过程,为此需要设置一个放大系数δ,使vt-1*和rrot=δ r+ vt-1*间的夹角正好等于θ.
4) rrot向量和半径为ε的超球面的交点,就是vt-1*转动到的目标位置.依据向量间夹角余弦公式(7),可以计算出r的放大系数δ, δ的具体求解方法可采用数值计算方法.
5) 当求解出r的放大系数δ后,就可以求解出rrot,然后利用式(8)计算出第t次迭代的通用扰动vt*,即vt-1*在特定平面内转动到rrot方向,然后将rrot的模长缩短到ε,保证vt*落在半径为ε的超球面上,从而形成一次有效迭代.
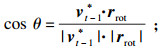 | (7) |
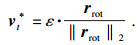 | (8) |
表 1(Table 1)
| 表 1 超球面通用攻击算法 Table 1 Hyperspherical general adversarial attacks algorithm | ||||||||||||||||||||||||||||
另外,通用扰动每次在球面上转过的角度是一个预先设置好的参数,对求解过程会产生重要影响.如果每次转动的角度θ过小,则通用扰动容易落入局部极小值;如果角度θ过大,则易在迭代后期出现震荡现象,解质量不稳定.因此,在通用扰动求解过程中,添加了一个转角收敛系数η,利用该系数与迭代轮数i构成一个动态转角调控参数ηi,以此让通用扰动的转角在计算初期较大,计算后期逐渐变小.实验发现该策略对算法收敛速度几乎无影响,但可以使后期迭代收敛更为稳定,解质量更好.
2.3.3 算法生成通用扰动质量的优化上述算法将通用扰动的求解空间从一个高维空间的超球体限定到超球面,减小了搜索空间,但仍然是一个复杂的高维空间.在这个球面空间上,存在多个通用扰动的局部近似解,均能对样本集生成有效的通用扰动.从实验结果看,不同的v0*初始化值,求解出的通用扰动差异较大,但其攻击成功率都较为接近,从通用扰动的具体分布情况看,这些不同的解表现出两个方面的特点:一是不同的通用扰动往往具有共同的热点区域,即使它们的迭代起始点不同,即随机初始化结果不同,但是最终生成的通用扰动具有肉眼可观察的相似模式,且模式呈现较强的区域聚集性;二是算法生成的通用扰动可能在个别像素点上的值改变较大,从而在通用扰动中存在比较鲜明的肉眼可观察的像素点改变.
上述现象的产生可能受到多种因素的影响.首先,相似的攻击模式更多地体现为一种波动纹理,并且不同的通用扰动间差异虽然大,但是波动纹理在肉眼观察下却很相似,这与随机梯度上升训练的方法相关,体现为一种统计上的相似性.另外,可观察的噪声点则是因为通用扰动训练过程中的损失函数与输出概率之外的其他约束无关,无法感知单点值的较大改变,并约束这个改变的影响.求解一个样本集X上的通用扰动,本文算法内使用了2-范数模长的限制来控制通用扰动的质量,以满足扰动不易被视觉感知的要求;但2-范数模长限制并没有约束个别像素点上发生较大的颜色变化,也没有对扰动的区域进行限定.
为减少部分像素因像素值改变过大带来的单点噪声问题,本文在损失函数中引入正则化项,其作用是在通用扰动的训练过程中引入像素值改变的最大阈值限制,从而迫使训练过程中,算法在搜索通用扰动的近似解时,避免出现少数像素点因扰动过大而造成易于观察的单点噪声.
具体地,本文引入正则化参数ξ,损失函数修改为式(9):
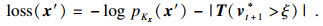 | (9) |
实验结果表明,正则化方法在部分条件下会让通用扰动的攻击成功率稍有降低,但可以有效抑制噪声点的出现,防止部分像素点的无穷范数过大,对通用扰动的质量控制起到了积极的作用.
3 实验在给定实验数据集和基准算法的条件下,对基于随机梯度上升和球面投影的通用扰动生成算法进行了验证.实验结果表明,该算法能够快速生成良好的通用扰动,性能较已有典型通用扰动生成算法显著提升,求解的通用扰动不但取得了更好的攻击效果,通用扰动生成效率也大幅提高.
3.1 实验条件设置本文选用CIFAR-10图像分类数据集和SVHN门牌号码数据集作为实验用数据集,并基于这两个数据集的训练集,分别训练了NiN[18],VGG[19]和ResNet[20]三种不同规模的经典神经网络分类器.从各数据集中依次抽取250, 500, 750, 1 000张样本作为通用扰动的训练集;另外各测试数据集中额外抽取1 000张样本,作为求得通用扰动的验证集.
本文选用UAP算法作为与本文提出的HGAA算法及其正则化算法HGAA-Z进行性能对比的基线方法,Seyed-Mohsen在UAP算法中首次提出了白盒通用扰动生成的思想,是该场景下的典型算法.实验中,不同算法通用扰动的2-范数模长均限制为2,含有正则化参数的损失函数中,正则化参数设置为0.9.
文中所有实验均在一台工作站上完成,工作站搭载有NVIDIA GeForce RTX2080Ti GPU显卡一块,采用Python编程开发环境和Pytorch框架.
3.2 算法攻击效率为了验证本文算法求解通用扰动的效率,选取3个指标与基线算法对比,分别为反向传播查询次数、相邻2轮通用扰动求解结果间的夹角余弦值cos θ,以及每轮通用扰动在训练集上的攻击成功率,即扰动比hX(v*).
首先,在给定训练集上统计UAP的反向传播查询次数.以NiN模型和CIFAR-10数据集为例,分别对250, 500, 750, 1 000四个样本集进行通用扰动训练,UAP调用反向传播的平均次数分别为74 312, 197 628, 319 712, 421 364,单个样本的平均调用次数均超过300次,HGAA算法反向传播的次数与迭代的轮数和批样本数有关,在50轮、每轮50批样本的情况下,4个训练样本集中,单个样本的平均调用次数均为1.效率差距在时间上也能够直接反映出来,训练250, 500, 750, 1 000张样本集时,UAP算法耗时分别为311, 628, 835, 1 186 s,而HGAA算法耗时仅12, 19, 26, 32 s.
其次,选用ResNet模型、CIFAR-10数据集,设置通用扰动的2-范数模长的值为2,训练样本数为1 000,迭代轮数为40,对UAP, HGAA, HGAA-Z三种算法在训练集上进行相邻轮夹角余弦和攻击成功率对比,如图 1、图 2所示.从相邻轮通用扰动夹角的变动情况看,HGAA算法在经过迭代后,每次更新的夹角在2°左右,而UAP算法的夹角在8°左右,并且存在较大波动,反映出HGAA算法求解通用扰动的稳定性更好;从攻击成功率看,HGAA算法的攻击成功率远高于UAP算法,并且攻击成功率的波动幅度很小,收敛速度更快.实验结果证明,基于随机梯度上升的球面投影算法求解通用扰动的效果更好,效率更高.
图 1(Fig. 1)
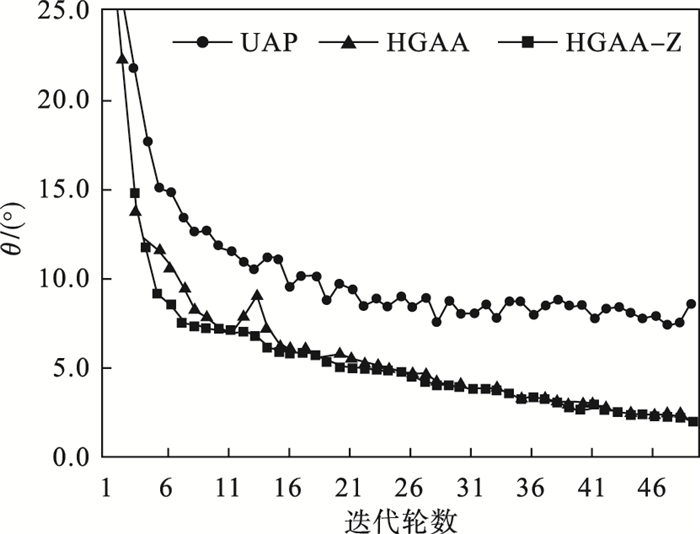 | 图 1 通用扰动间的夹角Fig.1 Angle between general adversarial attacks |
图 2(Fig. 2)
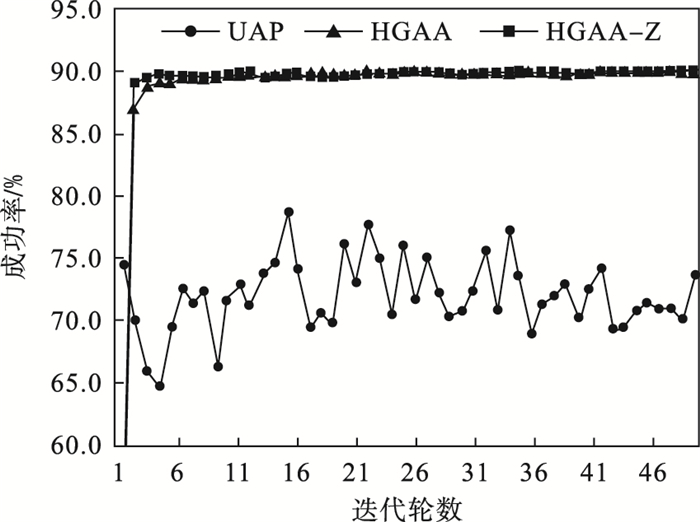 | 图 2 通用扰动的攻击成功率Fig.2 Attack success of general adversarial attacks |
3.3 算法攻击效果为了验证HGAA算法生成通用对抗扰动的效果,分别定义通用扰动在训练集上的攻击成功率ηT=hT(v*)和在测试集上的攻击成功率ηV=hV(v*).这两个指标反映了通用扰动分别对训练集和测试集的攻击效果.由于UAP的通用扰动约束为‖ v‖p≤ε,因此在进行对比实验的时候,限定UAP求解的通用扰动2-范数模长最大值为2.另外,实验中还计算了HGAA和HGAA-Z算法的无穷范数指标.
相关实验结果见表 2,从表中数据结果可以看出,同等2-范数模长约束条件下,UAP求解出的通用扰动模长全部达到了2-范数模长的阈值2,说明对于通用扰动而言,2-范数模长的大小更多是出于保持图像质量的要求,通用扰动的解大概率地处于2-范数模长等于阈值的高维球面上.另外,与UAP算法相比较,本文算法在不同的数据集和模型上均表现出更好的性能,攻击成功率较UAP提高10 % ~20 %,训练集和测试集攻击成功率的波动也有所减小.再有,采用或者不采用正则化策略,本文两种算法的攻击成功率相差不大,未发现引入正则化损失函数,导致算法攻击成功率降低的情况,甚至在样本数量较多的实验中,采用正则化策略,其攻击成功率表现似乎更好;并且正则化方法使通用扰动的无穷范数明显降低,说明正则化技术对提高通用扰动质量是有效的.
表 2(Table 2)
| 表 2 不同算法的效果对比 Table 2 Comparison of different algorithms | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.4 关键参数对算法性能的影响1) 2-范数模长阈值的影响.为研究2-范数模长阈值变化对HGAA算法攻击效果的影响,选择VGG11模型、CIFAR10数据集、500样本的训练集,测试了通用扰动的攻击成功率与2-范数模长阈值变化的关系.从表 3可以看出,模型在训练集和测试集上的攻击成功率均随着2-范数模长的增加而增加,但增幅逐步放缓;从无穷范数的变化可以看出,通用扰动的无穷范数也随着2-范数模长的增加而增大,并基本保持同步的增长态势.表 3的数据说明,适当选择2-范数模长阈值,能够获得较好的攻击成功率和攻击质量.
表 3(Table 3)
| 表 3 2-范数模长阈值影响 Table 3 Effect of 2-norm modulus length threshold |
2) 正则化参数ξ的影响.前面的实验结果已经验证了正则化损失函数的设置能够降低通用扰动的无穷范数.为了更好地认识正则化参数的影响,在前面的实验条件下,对正则化参数ξ的取值与通用扰动性能的关系进行了实验,并与不引入正则化损失函数的算法结果进行对比,比较的指标包括训练集攻击成功率、测试集攻击成功率和无穷范数.通过表 4可以发现,正则化参数ξ的大小直接影响通用扰动的生成质量.整体上看,当ξ增大时,攻击成功率也随着增大,直到其值大于0.1后,成功率略有下降.正则化对通用扰动的攻击成功率的影响与取值密切相关,并且对通用扰动中单像素模长的抑制非常明显.实验看,当ξ值为0.090左右时,正则化带来了良好的效果,攻击成功率较高,且单像素模长符合阈值约束.另外,文中对正则化参数ξ的分析相对简单,正则化设置策略还需要进一步研究,需要根据具体模型慎重选择,以实现正则化阈值参数的自适应选择能力.
表 4(Table 4)
| 表 4 正则化系数影响 Table 4 Influence of regularization coefficients | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 结论1) 本文针对有训练集的神经网络白盒攻击场景条件,采用随机批量梯度上升的通用扰动训练策略,即利用批量样本计算平均损失函数,进而生成通用对抗扰动,这样就将单样本迭代转化为批量样本迭代,从而显著提高通用扰动生成效率.
2) 将通用扰动的搜索空间从高维超立方空间限定到通用扰动模长为常量的高维球面上,从而缩小通用扰动的搜索空间,并进一步提出了基于球面投影的通用扰动HGAA生成方法,通过迭代扰动的结果计算历史累计扰动在高维球面上的一定距离和方向,实现通用扰动在球面上的搜索,方法不但提高了通用扰动的攻击效果,而且提升了通用扰动的质量.
3) 文中对通用扰动的损失函数进行优化,为防止单像素色相变化剧烈导致的可观测噪声问题,在损失函数中引入了正则化项,直接对无穷范数的增长进行约束,使通用扰动的人眼可察觉程度进一步降低.
4) 通过实验验证了本文算法的有效性,并对模长阈值、正则化系数两个通用对抗样本生成控制参数进行了实验分析,给出了两个参数取值的实验参考依据.
总之,在给定的实验数据集和神经网络分类模型上,本文算法生成的通用扰动在训练样本集和测试样本集上的攻击成功率均大幅超过基线算法,算法的时间复杂度降低近2个数量级,效果和效率改善明显.但文中实验样本数据集的规模依然较小,基线算法及比对场景有待增加,以便针对算法的适应性和关键控制参数的影响进行全面分析,为优化改进算法提供依据,以生成更有效的通用扰动.
参考文献
| [1] | Deng J, Dong W, Socher R, et al. ImageNet: a large-scale hierarchical image database[C]//Proceedings of 2009 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2009: 248-255. |
| [2] | Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks[C/OL]//Proceedings of 2nd International Conference on Learning Representations. 2014[2021-05-20]. https://www.researchgate.net/publication/259440613_Intriguing_properties_of_neural_networks. |
| [3] | Chen C, Seff A, Kornhauser A, et al. DeepDriving: learning affordance for direct perception in autonomous driving[C]//Proceedings of 2nd International Conference on Computer Vision. Piscataway: IEEE, 2015: 2722-2730. |
| [4] | Jia R, Lian P. Adversarial examples for evaluating reading comprehension systems[C]//Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2017: 2021-2031. |
| [5] | Samanta S, Mehta S. Towards crafting text adversarial samples[EB/OL]. [2021-05-25]. http://arxiv.org/abs/1707.02812. |
| [6] | Goodfellow I J, Shlens J, Szegedy C. Explaining and harnessing adversarial examples[C]// Proceedings of 3rd International Conference on Learning Representations. 2015[2021-05-20]. https://arxiv.org/pdf/1412.6572.pdf. |
| [7] | Sarkar S, Bansal A, Mahbub U, et al. UPSET and ANGRI: breaking high performance image classifiers[EB/OL]. [2021-05-25]. https://arxiv.org/pdf/1707.01159.pdf. |
| [8] | Chen P Y, Zhang H, Sharma Y, et al. ZOO: zeroth order optimization based black-box attacks to deep neural networks without training substitute models[C]//Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security. New York: ACM, 2017: 15-26. |
| [9] | Dong Y P, Liao F Z, Pang T Y, et al. Discovering adversarial examples with momentum[EB/OL]. [2021-05-25]. https://arxiv.org/pdf/1710.06081v1.pdf. |
| [10] | Papernot N, McDaniel P, Jha S. The limitations of deep learning in adversarial settings[C]//Proceedings of IEEE European Symposium on Security and Privacy. Saarbrucken, 2016: 372-387. |
| [11] | Moosavi-Dezfooli S M, Fawzi A, Fawzi O, et al. Universal adversarial perturbations[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2017: 86-94. |
| [12] | Moosavi-Dezfooli S M, Fawzi A, Frossard P. DeepFool: a simple and accurate method to fool deep neural networks[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2016: 2574-2582. |
| [13] | Carlini N, Wagner D. Towards evaluating the robustness of neural networks[C]//Proceedings of 2017 IEEE Symposium on Security and Privacy. Piscataway: IEEE, 2017: 39-57. |
| [14] | Zhang C N, Benz P, Imtiaz T, et al. CD-UAP: class discriminative universal adversarial perturbation[C]//Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence. Menlo Park: AAAI, 2020: 6754-6761. |
| [15] | Oseledets I, Khrulkov V. Art of singular vectors and universal adversarial perturbations[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 8562-8570. |
| [16] | Hayes J, Danezis G. Learning universal adversarial perturbations with generative models[C] //Proceedings of IEEE Security and Privacy Workshops. Piscataway: IEEE, 2018: 43-49. |
| [17] | Mopuri K R, Ojha U, Garg U, et al. NAG: network for adversary generation[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 742-751. |
| [18] | Lin M, Chen Q, Yan S C, et al. Network in network[C]//Proceedings of 2nd International Conference on Learning Representations. [2021-05-15]. https://arxiv.org/pdf/1312.4400.pdf. |
| [19] | Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[C]//Proceedings of 3rd International Conference on Learning Representations. [2021-05-18]. https://arxiv.org/pdf/1409.1556.pdf. |
| [20] | He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2016: 770-778. |
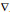 s*loss(s*)
s*loss(s*)