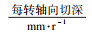, 金天, 周秩同, 付麒麟
, 金天, 周秩同, 付麒麟 东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004
收稿日期:2021-04-29
基金项目:河北省自然科学基金资助项目(2020501014);国家自然科学基金资助项目(51705070)。
作者简介:王海艳(1973-), 女, 河北秦皇岛人, 东北大学副教授。
摘要:通过分析碳纤维增强复合材料螺旋铣制孔过程的分层机理,提出一种基于经典板壳理论的用于解析复合材料螺旋铣孔出口分层的临界轴向力模型.模型分析表明,螺旋铣孔过程剩余的未切削材料厚度是影响材料出口分层的重要因素;随着未切削材料厚度的减小,材料发生出口分层的概率增加.开展了复合材料螺旋铣孔实验研究,结果显示,模型轴向力临界值最大偏差为13.48 %.全因子实验结果显示,轴向力随着主轴转速的增加而降低,随每齿进给量的增加而增加,随每转轴向切深的增加而增加;刀具磨损与轴向力大小呈线性关系,当每齿进给量为0.02 mm/齿、主轴转速为6 000 r/min、每转轴向切深为0.1 mm/r时材料所受轴向力最小.
关键词:螺旋铣碳纤维增强复合材料(CFRP)分层临界轴向力
Critical Axial Force Model in Helical Milling of Carbon Fiber Reinforced Composites
WANG Hai-yan

 , JIN Tian, ZHOU Zhi-tong, FU Qi-lin
, JIN Tian, ZHOU Zhi-tong, FU Qi-lin School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: WANG Hai-yan, E-mail: hywang16@126.com.
Abstract: Through a delamination mechanism analysis in the helical milling of carbon fiber reinforced polymers(CFRP), a critical axial force model is put forward based on the classic theory of plates and shells, which is used to resolve the exit delamination state.The model analysis shows that the thickness of the uncut material is an important factor affecting the material's exit delamination in the helical milling process, and with the decrease of the thickness, the probability of exit delamination increases. Experimental study on the helical milling of CFRP is carried out, and the results show that the maximum deviation of the critical axial force of the model is about 13.48 %. The full-factor experimental results show that the axial force decreases with the rise of the spindle speed, increases with the rise of the feed per tooth, and increases with the rise of the axial cutting depth per revolution. The tool wear has a linear relationship with the axial force. Under the conditions of 0.02 mm/t feed per tooth, 6 000 r/min spindle speed and 0.1 mm/r axial cutting depth per revolution, the axial force is the minimum.
Key words: helical millingcarbon fiber reinforced polymer (CFRP)delaminationcritical axial force
碳纤维增强复合材料(carbon fiber reinforced polymers,CFRP)具有比强度高、轻质、耐腐蚀、可设计性强等诸多优越特性,在航空等领域获得越来越广泛的应用[1-3],对于CFRP孔连接部件的要求越来越高.CFRP本身非均质、各向异性的物理特性导致在二次加工的过程中,常发生纤维拉出、基体撕裂、分层等缺陷,严重影响产品精度和寿命[4].
螺旋铣孔是一种新型的制孔加工工艺,相对于传统钻孔,具有轴向切削力小、切削温度低、适用于多种孔径等优点[5-6].Iyer等[7]对比了多种制孔方法,并进行硬质工具钢螺旋铣孔实验,证明了在加工质量和刀具寿命方面螺旋铣孔技术具有的优越性.Wang等[8]建立了螺旋铣孔过程切削力的解析模型,通过单因素螺旋铣孔实验验证了模型的正确性,并从力的层面分析了螺旋铣孔的刀具磨损与孔质量问题.螺旋铣孔极大地改善了CFRP制孔加工质量,然而制孔过程中临界力变化带来的孔壁纤维分层和撕裂等问题仍未得到解决.
分层缺陷是CFRP螺旋铣孔加工过程中最频发的问题之一,铣刀刀刃在沿螺旋轨迹向下切削过程中会产生较大的临界轴向力,当临界轴向力持续作用于CFRP层间结合界面时,初始裂纹会沿着材料层间结合方向向外延伸,进而导致材料失效[9].这种缺陷会导致成孔的强度和刚度受损,严重影响制孔成品率及成孔的承载能力和疲劳寿命.国内外****对复合材料分层现象的研究发现,复合材料分层与临界轴向力有关,局部高度集中的应力会导致材料发生层间破坏[10];同时,复合材料弯曲刚度在切削过程中会随着材料厚度变小而降低,刀具沿轴向铣孔至出口时,材料刚度与铣刀轴向力间的失衡会导致较严重的孔出口缺陷.
Cheng和Dharan[11]使用临界推力模型分析预测材料分层现象,并进行了大量的应力分析和对分层裂纹的实验分析,提高了模型的准确度.Liu等[12]基于经典板壳理论、线弹性断裂力学等理论,针对特定的布拉德钻,提出了一种用于预测孔壁和孔出口分层的临界轴向力解析模型.Jamel等[13]考虑椭圆分层裂纹中非对称叠加顺序的多向层合板弯曲与拉伸耦合问题,对复合材料楔形边与刀具主切削刃的相互作用区域进行了分析建模.Ijaz等[14]修正了Allix和Ladevèze提出的经典静态损伤模型,据此提出一种疲劳载荷下复合材料层合板分层裂纹扩展的疲劳损伤模型,并通过仿真和实验验证了模型的准确性.
国内外关于复合材料分层的临界力模型大多停留于钻孔,螺旋铣孔分层轴向力模型的研究较少,因此,本文考虑断续铣削条件下孔出口的分层情况,提出一种CFRP螺旋铣孔临界轴向力模型,预测特定分层条件下临界轴向力的变化.
1 螺旋铣孔运动学螺旋铣孔工艺的运动学过程是一种区别于传统钻孔的复合运动,如图 1所示:加工时刀具沿孔中心线作轴向进给运动,并以给定的偏心量以孔中心线为中心作公转圆周运动,同时还伴随着铣刀的自转运动,这种螺旋式的复合运动使得加工时可以通过调节偏心量和刀具直径来控制加工孔径的大小.
图 1(Fig. 1)
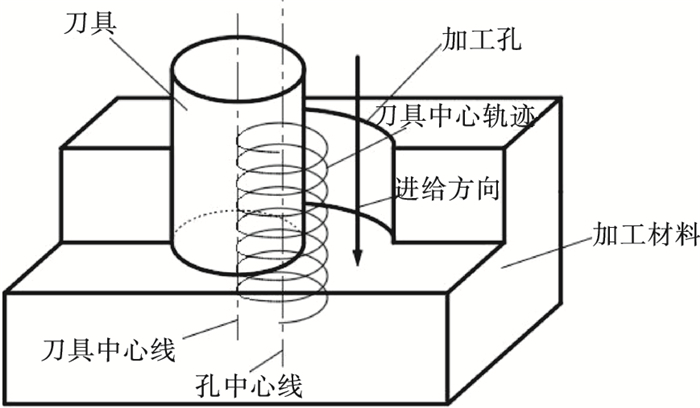 | 图 1 螺旋铣孔运动示意图Fig.1 Schematic of the helical milling hole movement |
螺旋铣孔过程的参数主要为主轴转速nz(r/min)和刀具中心螺旋进给速度vf(mm/min),其中,螺旋进给速度vf可分解为刀具中心切向速度vfht(mm/min)和刀具轴向进给速度vfha(mm/min),即
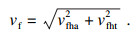 | (1) |
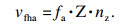 | (2) |
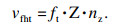 | (3) |
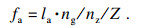 | (4) |
每齿切向进给量为
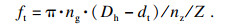 | (5) |
2 分析模型2.1 建模方法铣刀加工运动可分为圆周周向铣削和轴向进给铣削,刀具轴向进给所产生的轴向力是造成孔出口分层的主要因素,如图 2所示,随着铣孔持续深入,铣刀逐渐接近孔出口区域,当切削刃轴向力超过复合材料层间结合强度,孔壁就会产生分层裂纹,并随着孔加工过程不断向侧向延伸,进而导致孔壁分层.
图 2(Fig. 2)
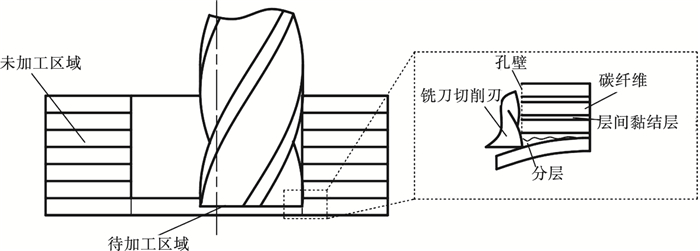 | 图 2 孔出口分层机理Fig.2 Delamination mechanism of the hole exit area |
CFRP铣孔过程中,可将待加工材料建模为各向异性的正交圆形板,由于复合材料螺旋铣孔过程产生的分层现象主要来自于螺旋铣刀加工方向垂直向下的临界轴向力,如图 3所示,根据经典板壳理论[15],圆形板内处于平衡状态的单元可表示为
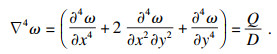 | (6) |
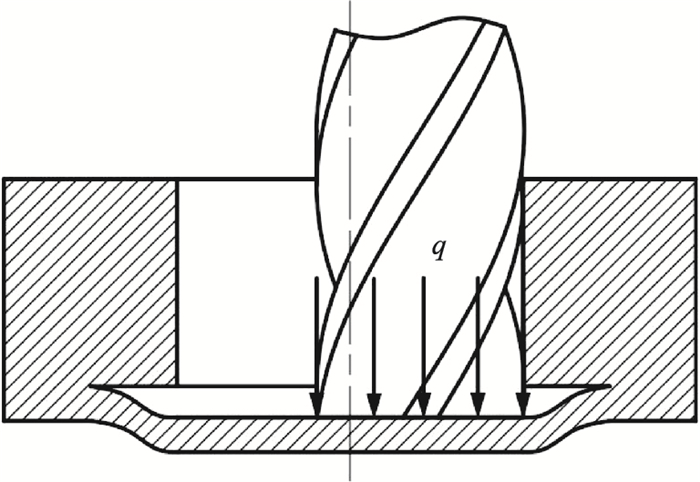 | 图 3 孔出口分层载荷Fig.3 Force at the hole exit area |
考虑螺旋铣孔加工方式,将其转化为极坐标形式:
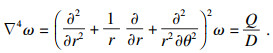 | (7) |
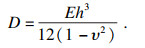 | (8) |
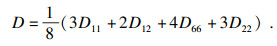 | (9) |
根据上述平衡方程可求解出各个瞬时状态下,由变化的应力及边界条件所得到的板弯曲挠度及斜率,采用线弹性断裂力学中的虚功理论,利用临界轴向力做功、应变能和裂纹扩展做功的能量交换关系来判定分层的发生标准[11],其中能量守恒定律可写为
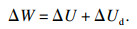 | (10) |
2.2 出口分层2.2.1 模型公式将式(7)作进一步转化,可以得到
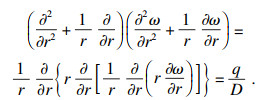 | (11) |
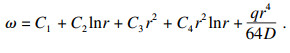 | (12) |
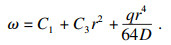 | (13) |
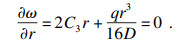 | (14) |
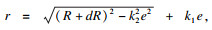
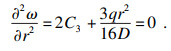 | (15) |
式中:θ为极坐标下的偏置角度;R为加工孔半径;e为刀具与加工孔的偏心量.将特定条件下具体参数代入式(14)和式(15)可求得具体的积分常数.将上述边界条件代入式(12),可求得对应的挠度值.
2.2.2 能量原理根据经典板壳理论,板单元体的总应变能等于弯曲应变能和扭转应变能之和,单元体的应变能可写为
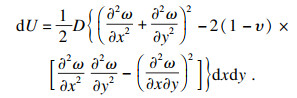 | (16) |
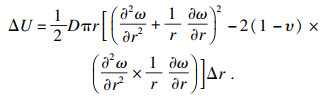 | (17) |
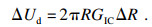 | (18) |
刀具做功为
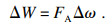 | (19) |
将式(17)、式(18)及式(19)代入式(10),可以得到螺旋铣孔过程出口分层临界轴向力为
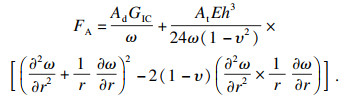 | (20) |
3 CFRP螺旋铣孔实验实验设备为五轴数控机床DMC75V,测力仪器采用Kistler 9257B三维测力仪,同时搭配数据采集分析软件DynoWare对数据进行滤波分析,采用支持Kistler的电荷放大器5261和NI数据采集卡6221E采集切削力数据,实际实验平台如图 4所示.实验材料为T700碳纤维增强树脂复合材料板,厚度为10 mm,板材长度和宽度为245 mm×120 mm,铺层厚度约为0.125 mm.为了减小螺旋铣孔过程中轴向力对刀具和加工质量的影响,刀具选用四刃专用螺旋铣孔刀具,材料是微粒钨钢(55HRC),TiA1N涂层,刀具直径6 mm,前角5°,螺旋角35°. 待加工孔的预加工孔径为10 mm,偏心量为2 mm.实验采用全因子方法,设置3个水平,具体参数见表 1.以主轴转速为5 333 r/min、每齿进给量0.04 mm/齿、每转轴向切深0.1 mm/r的切削参数螺旋铣孔80个.
图 4(Fig. 4)
 | 图 4 碳纤维复合材料螺旋铣孔实验设备Fig.4 Experiment setup for the helical milling of CFRP |
表 1(Table 1)
| 表 1 铣削参数表 Table 1 Milling parameters |
4 结果分析4.1 模型分析图 5为采用专用铣刀对CFRP进行螺旋铣孔过程中测得的轴向切削力,可以看出铣刀在A点处接触CFRP板,力开始上升,在B点到达顶峰,原因可能是由于刀具在切削硬度较高的材料时会有部分磨损,未完全切入材料时会造成冲击导致切削开始阶段的轴向切削力较高,这也是螺旋铣孔入口分层的主要原因之一;B点后轴向力回落并逐渐趋于平稳,在这一过程中属于入口阶段工件的层间断裂较少,孔壁质量较好.C点处轴向力下降,铣孔结束.
图 5(Fig. 5)
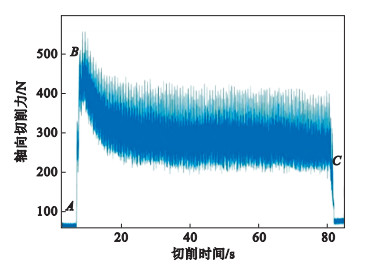 | 图 5 螺旋铣孔过程的轴向力变化Fig.5 Variation of axial force during the helical milling process |
图 6为轴向力与未切削厚度的关系.
图 6(Fig. 6)
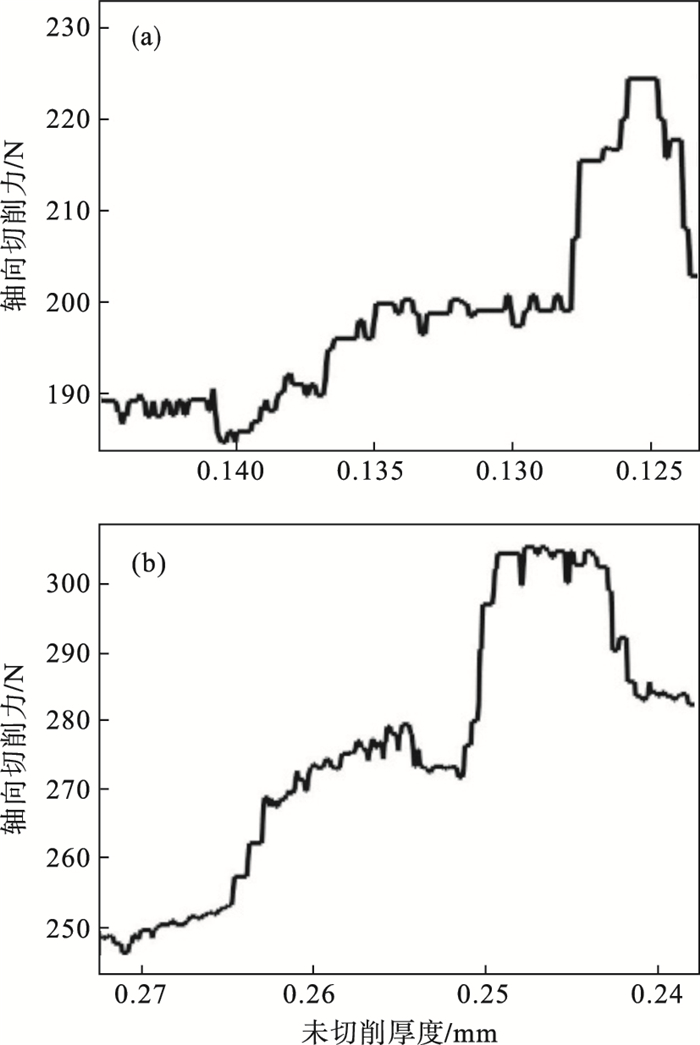 | 图 6 轴向力与未切削厚度的关系Fig.6 Relationship between the axial force and uncut thickness |
从图 6中可以看出,刀具向下进给过程中,轴向力呈波动上升趋势,并在到达顶峰后突然下降,这是由于刀具施加的轴向力到达了临界值,复合材料层间发生了分层裂纹并开始向侧向扩展,峰值即为CFRP分层的临界轴向力.需要注意的是,图 6b中分层开裂并未发生在0.25 mm处,而是发生在剩余厚度接近0.24 mm的铺层的下部,这是由于刀具轴向力作用下的CFRP未切削厚度会发生厚度误差[13].
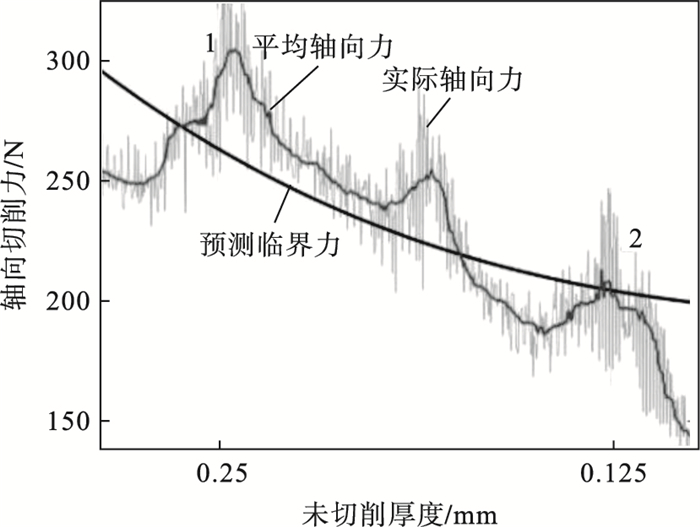
图 7为螺旋铣孔过程不同未切削厚度条件下模型预测的临界轴向力、实际轴向力和平均轴向力的对比图.随着未切削厚度的减小,当材料未切削厚度小于一定值时,可将剩余材料区域视为复合材料各向异性薄板.剩余薄板的抗弯刚度随厚度减小而逐渐变低,材料出口铺层的层间结合强度变小,在1点处(未切削厚度约为0.25 mm),实际轴向力大于层间临界轴向力,开始发生出口分层.随着螺旋铣孔过程的不断进行,孔的层间临界轴向力越来越低,实际轴向力也开始变低.在2点处(未切削厚度为0.125 mm),最后一层CFRP铺层被刀具底刃撕裂,开始产生分层,这是由于区域抗弯刚度会影响纤维铺层间的结合强度,当抗弯刚度小于一定值时,切削刃产生的轴向力会在割破纤维之前使CFRP铺层产生极大的弯曲挠度,挠度产生的撕裂会破坏材料层间的黏结,进而扩展为严重的孔出口分层.
图 7(Fig. 7)
 | 图 7 不同未切削厚度各轴向力变化Fig.7 Variation of the axial forces with different uncut thicknesses |
通过比较未切削厚度分别为0.125 mm和0.25 mm条件下的实际临界轴向力和预测临界轴向力.可以发现,随着铺层数下降,临界轴向力下降29 %,实际临界值与预测临界值较吻合,最大偏差为13.48 %;出现这种现象的主要原因是机床在实验过程中发生了振动,且轴向力会使铺层厚度发生偏差.
图 8为不同切削参数下CFRP螺旋铣孔出口缺陷图像,可以看出左图孔出口分层、撕裂和毛刺较严重,材料纤维层间断裂时,切削刃未完全切断出口纤维束;右图中材料出口缺陷减少,这是由于通过控制切削参数使轴向力低于层间结合力的临界值,孔出口形成时纤维断裂方式由挤压改为切割,出口质量提高.
图 8(Fig. 8)
 | 图 8 加工孔的出口质量Fig.8 Hole-making quality in the hole exit zone |
4.2 实验结果讨论4.2.1 切削参数螺旋铣孔过程中轴向力的大小是影响孔出口分层的重要因素之一,通过全因子实验探究各切削参数对轴向力变化的影响,从而选择最优参数以减小铣孔过程中产生的轴向力,使得轴向力尽可能小于复合材料层间结合强度临界值,这对于减少螺旋铣孔加工缺陷具有重要意义.
在轴向切深为0.2 mm/r条件下主轴转速和每齿进给量对轴向力的影响如图 9所示.可以发现,随着每齿进给量的增加,材料所受的轴向力增大;主轴转速增加,则轴向力逐渐减小;在所选的切削参数范围内,当主轴转速为6 000 r/min、进给量为0.02 mm/齿时材料所受的轴向力最小.
图 9(Fig. 9)
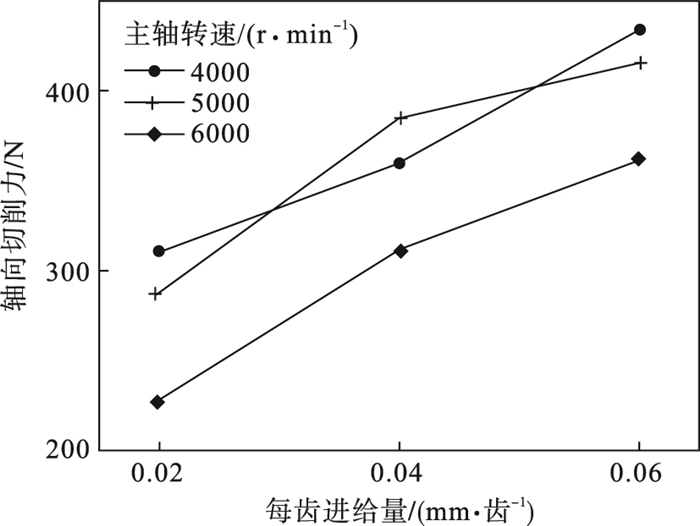 | 图 9 主轴转速和进给量对轴向力的影响Fig.9 Influence of the spindle speed and feed rate on axial force |
在主轴转速为4 000 r/min条件下轴向切深和进给量对轴向力的影响如图 10所示.可以发现,随着进给量的增加,材料所受的轴向力接近线性增加;同时,轴向力随着每转轴向切深的增加而增大,当轴向切深为0.1 mm/r、进给量为0.02 mm/齿时材料所受的轴向力最小.
图 10(Fig. 10)
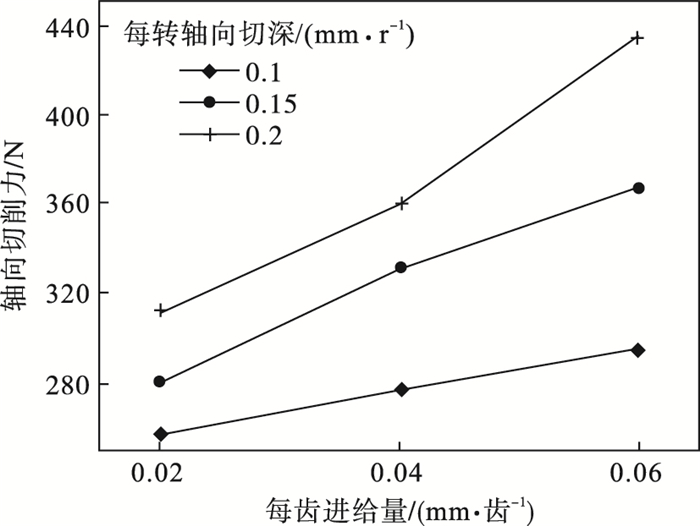 | 图 10 轴向切深和进给量对轴向力的影响Fig.10 Influence of the axial cutting depth and feed rate on the axial force |
综合上述切削参数对轴向力的影响,为了得到尽量小的轴向力,需要选择较高的主轴转速、较低的进给量和轴向切深.
4.2.2 刀具磨损刀具磨损也是影响螺旋铣孔轴向力变化的重要因素之一,图 11为使用同一刀具以同一组切削参数(主轴转速5 333 r/min、每齿进给量0.04 mm/齿、每转轴向切深0.1 mm/r)连续加工80个孔时的平均轴向切削力.可以看出,随着刀具加工孔数量的增多,轴向切削力在逐渐变大,这可能是由于铣孔过程中刀具与工件挤压摩擦会产生切削热,且考虑到螺旋铣孔特殊的运动方式,铣刀会受到来自侧向的切削力冲击,在高温高压环境下刀具易产生疲劳损伤,同时由于CFRP材料的高硬度导致了刀具出现典型的磨粒磨损,刀具磨损的加剧直接导致了轴向切削力的增大.因此,减少刀具磨损也是控制轴向力以减轻复合材料出口分层的方式之一.
图 11(Fig. 11)
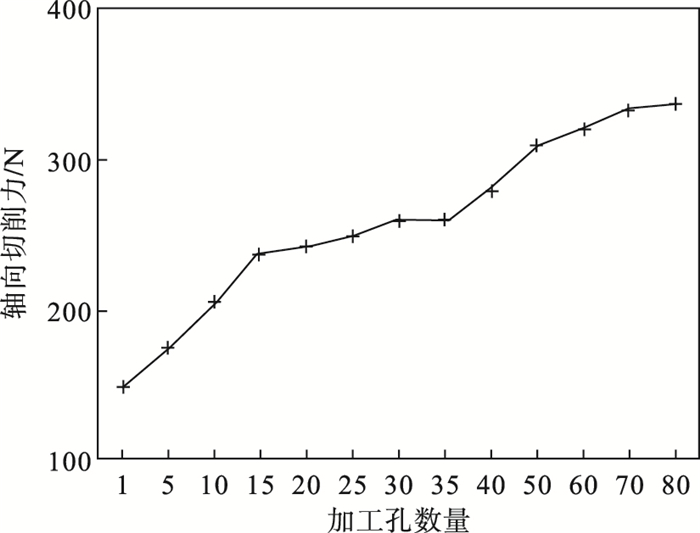 | 图 11 刀具磨损对轴向力影响Fig.11 Influence of tool wear on the axial force |
5 结论1) 基于板壳理论、虚功原理及线弹性断裂力学,对CFRP螺旋铣孔过程的临界轴向力、弯曲挠度变化进行了分析,提出了一种关于CFRP螺旋铣孔过程分层临界轴向力模型.
2) 模型考虑了螺旋铣孔运动学加工特性,讨论了孔出口分层的机制,并根据材料的实际条件设置了螺旋铣孔的铣削力实验.
3) 对比实验数据与分析模型,发现模型与实验数据吻合较好,预测轴向力临界值最大偏差为13.48 %,当未切削厚度为0.25 mm时,未切削厚度临界值会产生一定的误差.随着铺层数下降,临界轴向力下降29 %.
4) 对不同切削参数下螺旋铣孔轴向切削力变化进行分析,得出每齿进给量为0.02 mm/齿、主轴转速为6 000 r/min、每转轴向切深0.1 mm/r条件下时材料所受轴向力最小.
参考文献
| [1] | 齐振超, 刘书暖, 程晖. 基于三维多相有限元的CFRP细观切削机理研究[J]. 机械工程学报, 2016, 52(15): 170-176. (Qi Zhen-chao, Liu Shu-nuan, Cheng Hui. Research on the mesoscopic cutting mechanism of CFRP based on three-dimensional multiphase finite element models[J]. Journal of Mechanical Engineering, 2016, 52(15): 170-176.) |
| [2] | 董辉跃, 陈光林, 周兰, 等. CFRP复合材料/钛合金叠层螺旋铣孔工艺[J]. 复合材料学报, 2017, 34(3): 540-549. (Dong Hui-yue, Chen Guang-lin, Zhou Lan, et al. Processing research on orbital drilling of CFRP/Ti-6Al-4V stacks[J]. Acta Materiae Compositae Sinica, 2017, 34(3): 540-549.) |
| [3] | Rey P A, LeDref L, Senatore J, et al. Modeling of cutting forces in orbital drilling of titanium alloy Ti-6Al-4V[J]. International Journal of Machine Tools and Manufacturing, 2016, 106: 75-88. DOI:10.1016/j.ijmachtools.2016.04.006 |
| [4] | 罗益锋. 先进材料在高端装备的应用进展[J]. 高科技纤维与应用, 2014, 39(5): 1-8. (Luo Yi-feng. Application developments of advanced materials in high level equipment[J]. Hi-Tech Fiber & Application, 2014, 39(5): 1-8.) |
| [5] | 杨国林, 董志刚, 康仁科, 等. 螺旋铣孔技术研究进展[J]. 航空学报, 2020, 41(7): 18-32. (Yang Guo-lin, Dong Zhi-gang, Kang Ren-ke, et al. Research progress of helical milling technology[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(7): 18-32.) |
| [6] | Pereira R B D, Brandāo L C, de Paiva A P, et al. A review of helical milling process[J]. International Journal of Machine Tools and Manufacture, 2017, 120: 27-48. DOI:10.1016/j.ijmachtools.2017.05.002 |
| [7] | Iyer R, Koshy P, Ng E. Helical milling: an enabling technology for hard machining precision holes in AISI D2 tool steel[J]. International Journal of Machine Tools and Manufacture, 2006, 47(2): 205-210. |
| [8] | Wang H Y, Qin X D, Li H, et al. Analysis of cutting forces in helical milling of carbon fiber-reinforced plastics[J]. Journal of Engineering Manufacture, 2013, 227(1): 62-74. DOI:10.1177/0954405412464328 |
| [9] | Rahme P, Landon Y, Lachaud F, et al. Delamination-free drilling of thick composite materials[J]. Composites Part A, 2015, 72: 148-159. DOI:10.1016/j.compositesa.2015.02.008 |
| [10] | Karimi N Z, Minak G, Kianfar P, et al. Analysis of damage mechanisms in drilling of composite materials by acoustic emission[J]. Composite Structures, 2015, 131(1): 107-114. |
| [11] | Cheng H O, Dharan H. Delamination during drilling in composite laminates[J]. Journal of Manufacturing Science and Engineering, 1990, 112(3): 236-239. |
| [12] | Liu S N, Yang T, Liu C, et al. An analytical delamination model of drilling aramid fiber-reinforced plastics by brad drill[J]. The International Journal of Advanced Manufacturing Technology, 2020, 108(14): 3279-3290. |
| [13] | Jamel S, Redouane Z, Salah M, et al. Critical thrust force predictions during drilling: analytical modeling and X-ray tomography quantification[J]. Composite Structures, 2016, 153: 886-894. |
| [14] | Ijaz H, Saleem W, Zain-ul-Abdein M, et al. Fatigue delamination crack growth in GFRP composite laminates: mathematical modeling and FE simulation[J/OL]. International Journal of Aerospace Engineering, 2018[2021-03-05]. https://www.hindawi.com/journals/ijae/2018/2081785/. DOI: 10.1155/2018/2081785. |
| [15] | Timoshenko S, Woinowsky-Krieger S. Theory of plates and shells[M]. New York: Mcgraw-Hill Book Company, 1959. |