郝博^1,2, 代浩¹, 吕超²
1. 东北大学 机械工程与自动化学院，辽宁 沈阳 110819;
2. 东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004
收稿日期：2021-05-07
基金项目：国家自然科学基金青年基金资助项目(51904069)；河北省自然科学基金资助项目(E2019501085)；东北大学秦皇岛分校博士启动基金资助项目(XNY201808)。
作者简介：郝博(1963-), 男, 辽宁沈阳人, 东北大学教授, 博士生导师。

摘要：研究入水角度对高速射弹入水过程的空泡形态、弹道特性及流体动力特性的变化规律，计算中使用VOF(volume of fluid)多相流模型，Schnerr and Sauer空化模型，同时结合重叠网格和6DOF(degrees of freedom)技术对射弹的入水过程开展数值模拟.结果表明：射弹两侧空泡形态不对称，与左侧空泡相比，右侧空泡尺寸较大；射弹入水以后，入水角越小，射弹质心处的速度越大；入水角为45°时，俯仰角、偏航角、滚转角的波动范围更小；射弹在撞击水面时，阻力和升力岀现了一个峰值，但侧向力没有岀现峰值，而是一段微小的波动；入水角度对射弹流动稳定阶段的滚转力矩、偏航力矩及俯仰力矩影响非常小.
关键词：高速射弹数值模拟空泡形态弹道特性流体动力特性
Influence of Water Entry Angle on High-Speed Projectiles in the Water Entry Process
HAO Bo^1,2, DAI Hao¹, LUY Chao²
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: DAI Hao, E-mail: daih0427@163.com.

Abstract: The effect of water entry angles on the cavitation shape, trajectory characteristics and hydrodynamic characteristics of high-speed projectiles is studied. The VOF(volume of fluid)multiphase flow model, Schnerr and Sauer cavitation model, overlapping grid and 6DOF (degrees of freedom) technology are used to carry out the numerical simulation of the water entry process of a projectile. The results show that the cavitation shape on both sides of the projectile is asymmetric, and the size of the cavitation on the right side is larger than that on the left side. After the projectile enters the water, the smaller the water entry angle, the greater the velocity at the projectile centroid. When the water entry angle is 45°, the fluctuation range of the pitch angle, yaw angle and roll angle is smaller. When the projectile hits the water surface, the drag force and lift force show a peak, but the side force does not show a peak but a slight fluctuation. The water entry angle has little effect on the rolling moment, yawing moment and pitching moment in the stable stage of the projectile flow.
Key words: high speed projectilenumerical simulationcavitation shapetrajectory characteristicshydrodynamic characteristics
高速射弹在入水过程中会产生相间转换、强湍动、多相、穿越自由液面等复杂的流动现象，同时射弹在撞水阶段承受非常大的冲击载荷，水面会出现喷溅等问题.这些问题对于射弹入水以后的空泡形态、弹道特性和流体动力特性都会造成极大的影响，因此，对射弹的入水问题进行研究显得十分重要.
对于高速射弹的入水问题，国内外****从理论、实验及数值模拟进行了研究.Karman忽略入水初期能量的损失，提岀了基于动量守恒的附加质量法理论，对运动体入水冲击载荷进行预测. Logvinovich给出了空泡截面独立扩张原理.该原理认为不同时刻每个空泡截面的半径与运动体头部的大小、速度、所受到的阻力及很远处流场的压力有关，可以利用这种方法计算不同情况下空泡半径的大小.Hassouneh等^[1]研究了“空泡延迟”效应，该效应是指会对超空泡航行体动力学产生一定的干扰，从而引发尾击的现象.Worthington和Cole^[2]对小球垂直入水问题进行了一系列实验研究，利用闪光照相机拍摄小球入水过程发生的现象，包括水花溅射、空泡生成及空泡的表面闭合等.Truscott^[3]对自旋运动的球体进行入水试验，分析球体的旋转对运动轨迹变化的情况，得岀在入水过程中自旋运动使球体受到侧向力，导致运动轨迹向一侧偏转.Thoroddsen等^[4]对球体入水形成的水面射流进行相关实验分析，得岀小球冲击水面会产生水平方向射流，增加小球入水时的冲击载荷.Holfeld等^[5]把飞机作为实验平台，在微重力条件下对球体进行入水实验研究，分析入水空泡形态的变化过程，得岀当存在微重力时球体入水表面喷溅更高.孟庆昌等^[6]分析射弹以亚声速入水时空泡的闭合随时间的变化规律，得出射弹跨声速入水时，射弹头部会岀现弓形激波.侯宇等^[7]进行了弹体小入水角的入水试验，利用高速摄像机拍摄了弹体以不同侧滑角入水的空泡形态及水面喷溅等现象，发现不同侧滑角下空泡形态存在着一些差异.Neaves和Edwards^[8]在考虑流体可压缩条件下，对水下运动体进行数值模拟研究，成功地模拟岀水中的激波.Panciroli等^[9]对柔性楔形体的入水过程进行了数值模拟.
目前，还没有比较成熟的理论可以描述射弹入水过程流场的变化.由于实验环境和实验设备的限制，实验研究的重点是低速问题，对于射弹高速入水问题的研究比较少.本文以计算流体力学FLUENT19.0软件和MATLAB为平台，利用重叠网格和6DOF技术对射弹的高速入水问题展开数值模拟研究，分析入水角度对射弹入水过程空泡形态、弹道特性及流体动力特性的影响.
1 数值计算方法及计算模型1.1 基本控制方程本文数值模拟高速射弹的入水过程，假设流体是不可压缩的，同时不考虑由于流体运动产生的热量，建立了高速射弹从空气进入水中的基本控制方程.应用VOF多相流模型来描述水、空气和水蒸气形成的多相流动，用φ₁, φ_a, φ_v分别表示水、空气和水蒸气所占的体积分数，在流场的所有计算域内它们三者都满足如下关系式:

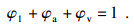(1)

混合物的密度表达式为

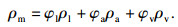(2)

式中：ρ_l, ρ_a, ρ_v分别表示水、空气和水蒸气的密度.
混合物的连续性方程表达式为

(3)

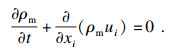式中：u_i为速度分量；x_i为坐标分量，i=1, 2, 3.
混合物动量守恒方程为

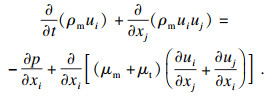(4)

式中：μ_m=φ_lμ_l+φ_aμ_a+φ_vμ_v为混合物的动力黏度，μ_l，μ_a，μ_v分别表示水、空气和水蒸气的动力黏度；μ_t=ρ_mC_μk²/ε为湍流黏性系数.
本文研究选用SST k－ω湍流模型，其湍流动能及湍流频率具体表达式如下：

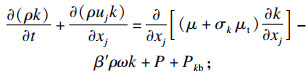(5)

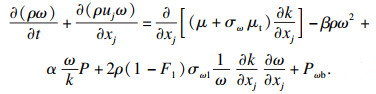(6)

式中：P_kb和P_ωb是浮力引起的湍动能项；μ_t的具体表达式为

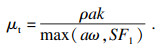(7)

式中：为剪切应变率的不变测度；F₁=tanh(arg₁²)为混合函数，其中

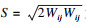
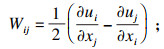(8)

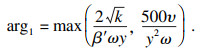(9)

式中：υ为流体的运动黏性系数；y为节点至壁面最近的距离.
本文数值模拟选用Schnerr-Sauer空化模型，其蒸发率R_e和凝结率R_c表达式为

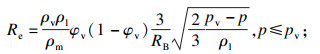(10)

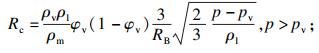(11)

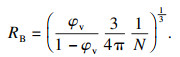(12)

式中：p为射弹周围压力；p_v为水的饱和蒸汽压；R_B为气泡半径；φ_v为水蒸气相体积分数；N为单位体积空泡数.
1.2 计算模型本文选取5.8 mm口径的射弹为研究对象，考虑到射弹入水过程受到的流体动力及弹道稳定性，选用射弹模型的外形及尺寸如图 1所示.射弹头部为截锥型，后部为圆柱体，整个射弹全长L为30 mm, 截锥头直径d为2.6 mm，锥形长度l为16.5 mm.对射弹模型入水过程开展三维数值模拟研究，分析不同入水角度对空泡形态、俯仰角、偏航角、滚转角、速度、位移、阻力、升力、侧向力、滚转力矩、偏航力矩及俯仰力矩的影响规律，其中射弹的入水速度为600 m/s，选用的材料为钨合金，两种不同入水角度射弹的物理性质如表 1所示.
图 1(Fig. 1)

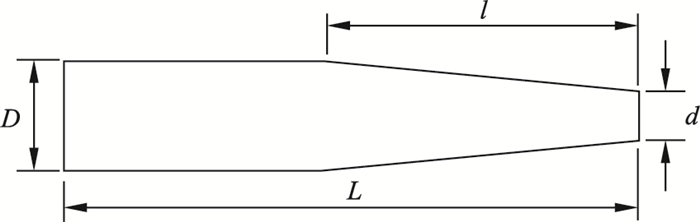图 1 射弹模型示意图Fig.1 Schematic of projectile model

表 1(Table 1)

表 1 两种不同入水角度射弹的物理性质Table 1 Physical properties of projectile with two different water entry angles 入水角度/(°) 质量/g 转动惯量/(g·cm2) Ixx Iyy Izz 45 10.436 328.620 474.098 183.143 60 10.436 619.575 619.575 619.575

表 1 两种不同入水角度射弹的物理性质 Table 1 Physical properties of projectile with two different water entry angles

1.3 计算域及边界条件图 2为计算域对称面示意图.其中计算域长度为3 400 mm、高度为3 400 mm、宽度为2 000 mm、水域深度为2 475 mm、空气域高度为925 mm.y轴负方向为重力方向，坐标原点位于射弹初始质心的位置，射弹头部中心与自由液面的距离为25 mm.计算域顶部为压力入口，底部为压力出口；计算域x+和x-，z+和z-面设为symmetry边界条件，射弹表面设置为壁面条件.
图 2(Fig. 2)

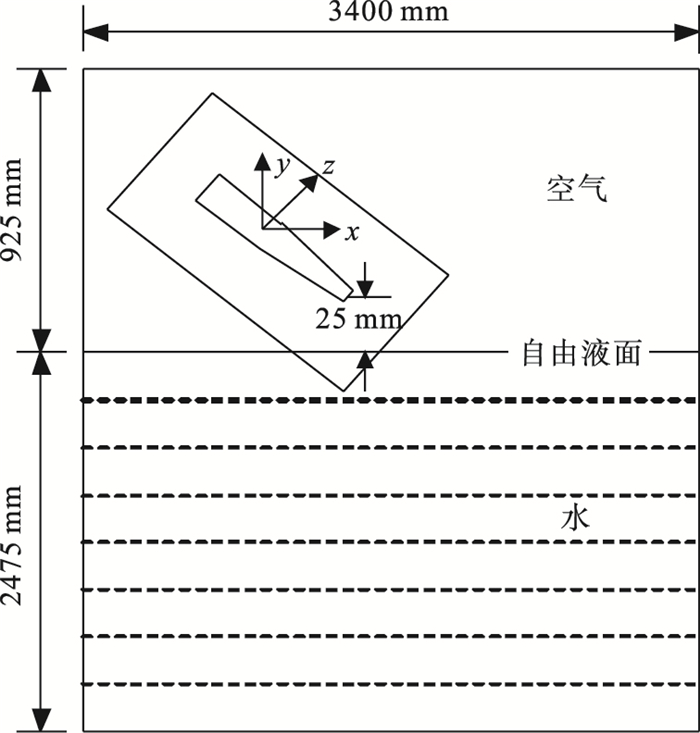图 2 计算域对称面示意图Fig.2 Schematic of symmetry plane in computational domain

1.4 网格划分在网格重构过程中，网格会产生很大程度的变形，导致网格质量变差，计算精度下降，所以使用重叠网格技术模拟射弹入水过程的多自由度运动.重叠网格技术将复杂的计算域划分成许多简单的子计算域，包括背景域和子域；背景域指的是整个流场，而子域指的是射弹运动的区域.用结构化网格对背景域和子域进行划分，背景域划分出的网格称为背景网格，子域划分岀的网格称为部件网格.背景域为长方体计算域，子域为包裹射弹的圆柱；图 3为整个流场网格划分情况.6DOF技术与重叠网格相结合不会产生网格的变形，避免了网格质量的降低；因此，在射弹运行过程中，网格质量一直较高，利用该方法可以模拟复杂模型的运动.
图 3(Fig. 3)

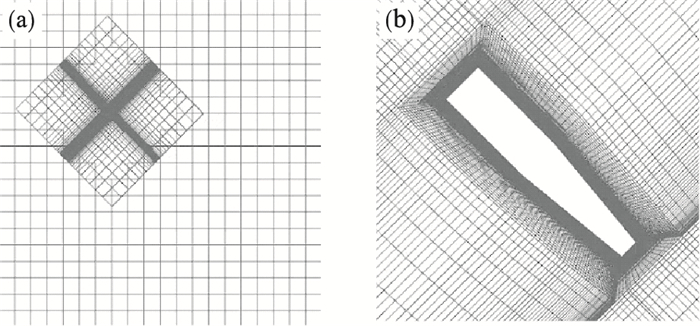图 3 计算域对称面网格示意图Fig.3 Schematic diagram of symmetry plane grid in computational domain (a)—全局网格；(b)—局部网格.

1.5 数值方法求解本文对计算域的离散方法采用有限体积法，压力和速度的求解使用Coupled算法，压力场的离散使用PRESTO格式，动量方程的离散使用一阶迎风格式.
2 数值方法验证分析射弹入水过程的受力情况，对射弹应用牛顿第二定律可得

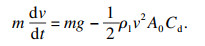(13)

式中：m为射弹质量；v为射弹的瞬时速度；ρ_l为水的密度；A₀为射弹最大截面积；C_d为阻力系数.
射弹入水过程中忽略能量损失和射弹质量，同时假设阻力系数为常数，则式(13)可变为

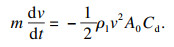(14)

对式(14)积分可得射弹入水速度：

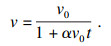(15)

式中：v₀为射弹初始速度；α为速度衰减系数，且α=ρ_lA₀C_d/(2m).
对式(15)积分可得射弹入水深度：

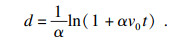(16)

数值计算方法是否正确，对计算结果的研究分析有很大影响，因此对其进行准确性和可靠性验证.对文献[10]中的平头射弹模型垂直入水过程开展数值模拟分析，其中射弹的直径为12.65 mm，长度为38.1 mm，射弹初始时刻的入水速度为498.1 m/s，对计算结果进行分析，得岀了入水过程中射弹速度和入水深度随时间变化的关系，如图 4所示.将本文数值模拟结果与理论计算结果和文献[10]的实验结果相比较，发现曲线的走势一致且误差较小，从而验证了本文数值计算方法的准确性和可靠性.
图 4(Fig. 4)

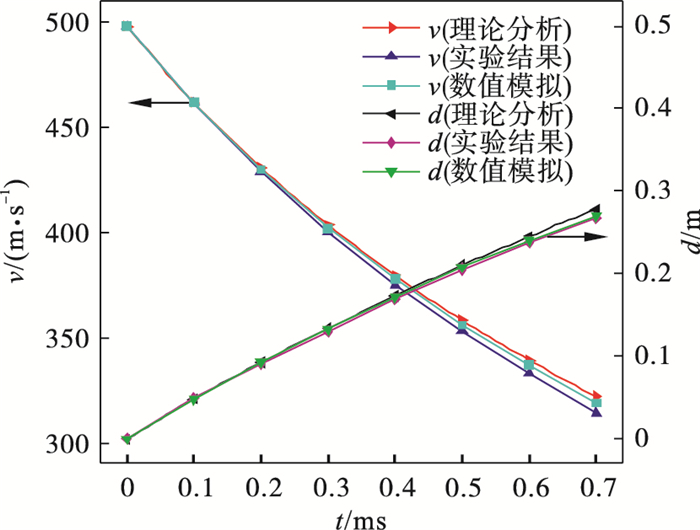图 4 射弹速度和入水深度的变化Fig.4 Variation of projectile velocity and depth into water

3 计算结果与分析在射弹初始速度为600 m/s，入水角度分别为45°和60°的情况下，通过数值模拟，分析了不同入水角对高速射弹入水过程的空泡形态、弹道特性及流体动力特性的变化规律.
3.1 入水空泡形态分析图 5为射弹入水角为45°和60°时入水空泡形状.
图 5(Fig. 5)

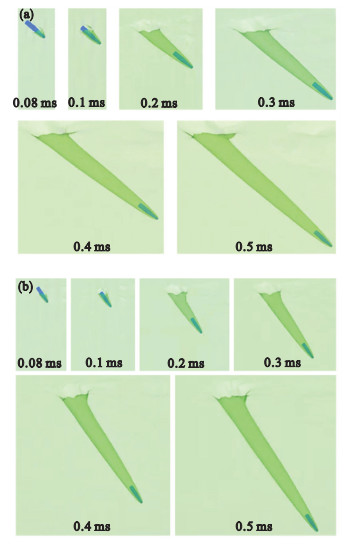图 5 不同入水角射弹的入水空泡形状Fig.5 Cavitation shape of projectile with different water entry angles (a)—入水角45°；(b)—入水角60°.

由于射弹倾斜入水，所以头部左侧先与水接触，然后扩展到整个头部.水面受到射弹撞击时，水开始向射弹四周运动.入水初期，空泡的长度和直径都较小，随着入水时间的增加，空泡尺寸逐渐变大，但射弹左侧和右侧的空泡并不对称，入水角越小，空泡不对称现象越明显，与左侧空泡相比，右侧空泡尺寸较大.
3.2 入水弹道特性分析图 6为不同入水角射弹的质心运动轨迹.由图可知，不同入水角对射弹的弹道稳定有一些影响，在整个入水过程中，射弹的质心位置在z方向产生了1.5 mm的偏移，这说明入水弹道相对稳定.在入水初期，射弹基本上沿着预定轨迹运动，没有明显偏移，随着射弹入水深度的增加，其质心位置在z方向的偏移量逐渐增加，相同的入水深度，入水角为45°时偏移量更大一些.
图 6(Fig. 6)

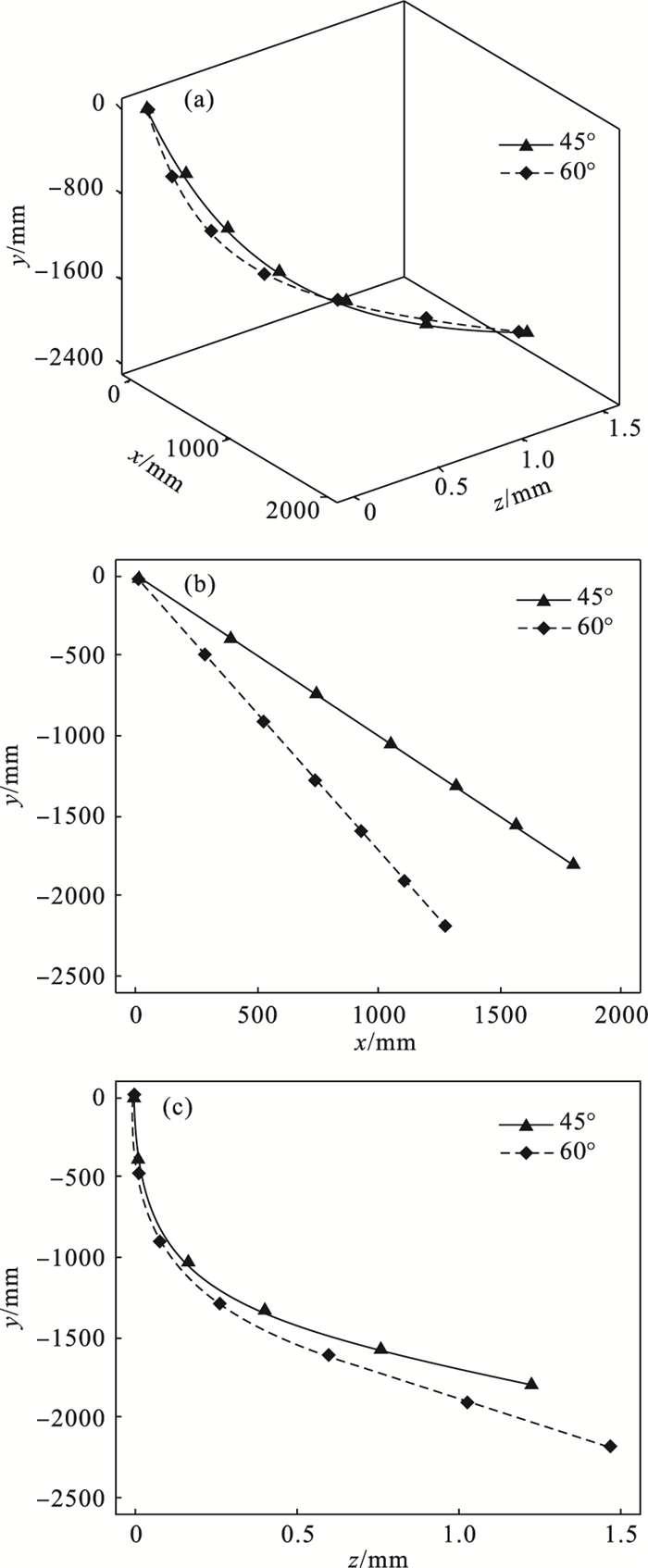图 6 不同入水角射弹质心运动轨迹Fig.6 Trajectory of projectile centroid at different water-entry angles (a)—三维弹道；(b)—yOx平面弹道投影；(c)—yOz平面弹道投影.

图 7为不同入水角射弹速度的变化曲线.从图 7a中可以看出，入水角大的射弹，其质心处的速度衰减优先发生；当射弹入水后，入水角越小射弹质心处的速度越大，且速度衰减率几乎一样.由图 7b和图 7c可知，x方向和y方向速度变化趋势类似，速度先快速衰减，然后缓慢衰减.由图 7d可得，在0~6 ms之间，入水角为60°时z方向速度先增加然后缓慢降低，但入水角为45°时z方向的速度在不断增加，且在最后超过了入水角为60°时z方向的速度.
图 7(Fig. 7)

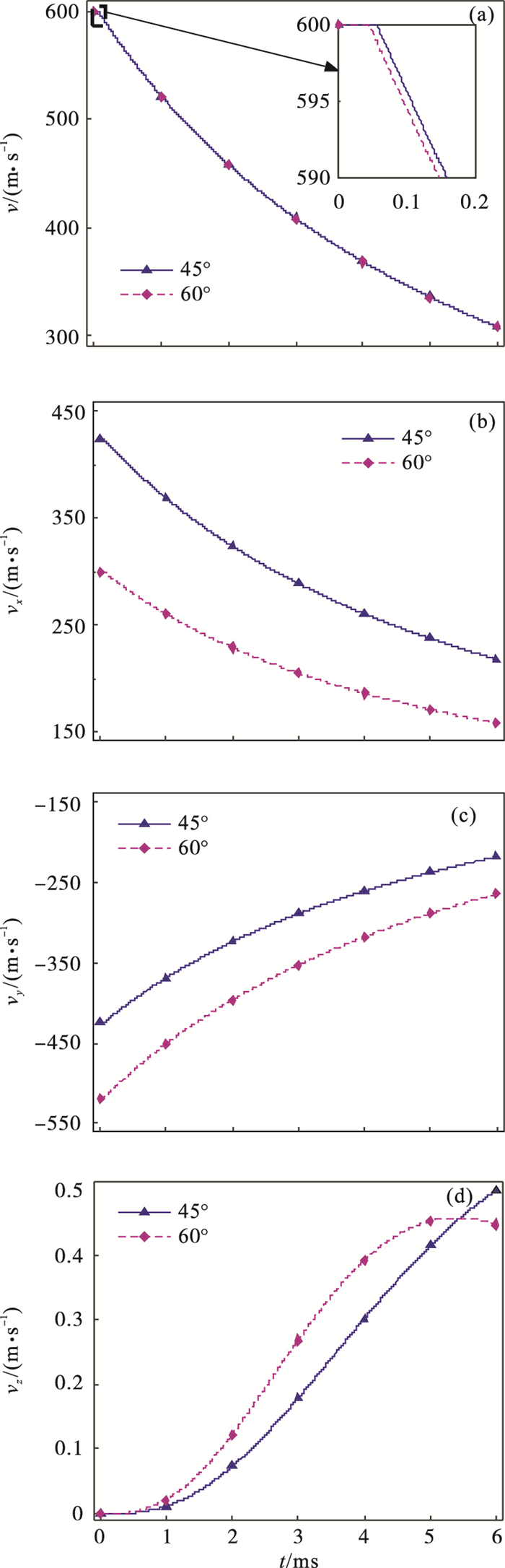图 7 不同入水角射弹速度的变化曲线Fig.7 Change curves of projectile velocity at different water-entry angles (a)—射弹质心速度；(b)—x方向的速度；(c)—y方向的速度；(d)—z方向的速度.

图 8给岀了在0~6 ms之间不同入水角射弹姿态角随入水时间的变化曲线.由图 8a可知，射弹入水角为45°时，俯仰角先增大后减小，这说明射弹头部先向上偏转然后向下偏转；入水角为60°时，俯仰角在逐渐减小，这说明射弹头部一直向下偏转.由图 8b可知，两个不同的入水角，射弹偏航角均先增大后减小，即射弹入水以后头部先向左偏转，然后向右偏转.由图 8c可知，45°入水角在0~6 ms之间滚转角为正，60°入水角在0~5.3 ms之间为正，然后为负.此外，从图中可以得岀，俯仰角的波动范围都保持在±3°之内，偏航角的波动范围都保持在±0.1°之内，滚转角的波动范围保持在±0.35°之内，这说明两个不同入水角射弹的姿态角变化都很小，且45°入水角的姿态角的波动范围更小，即45°入水角的入水稳定性比60°入水角的入水稳定性更好.
图 8(Fig. 8)

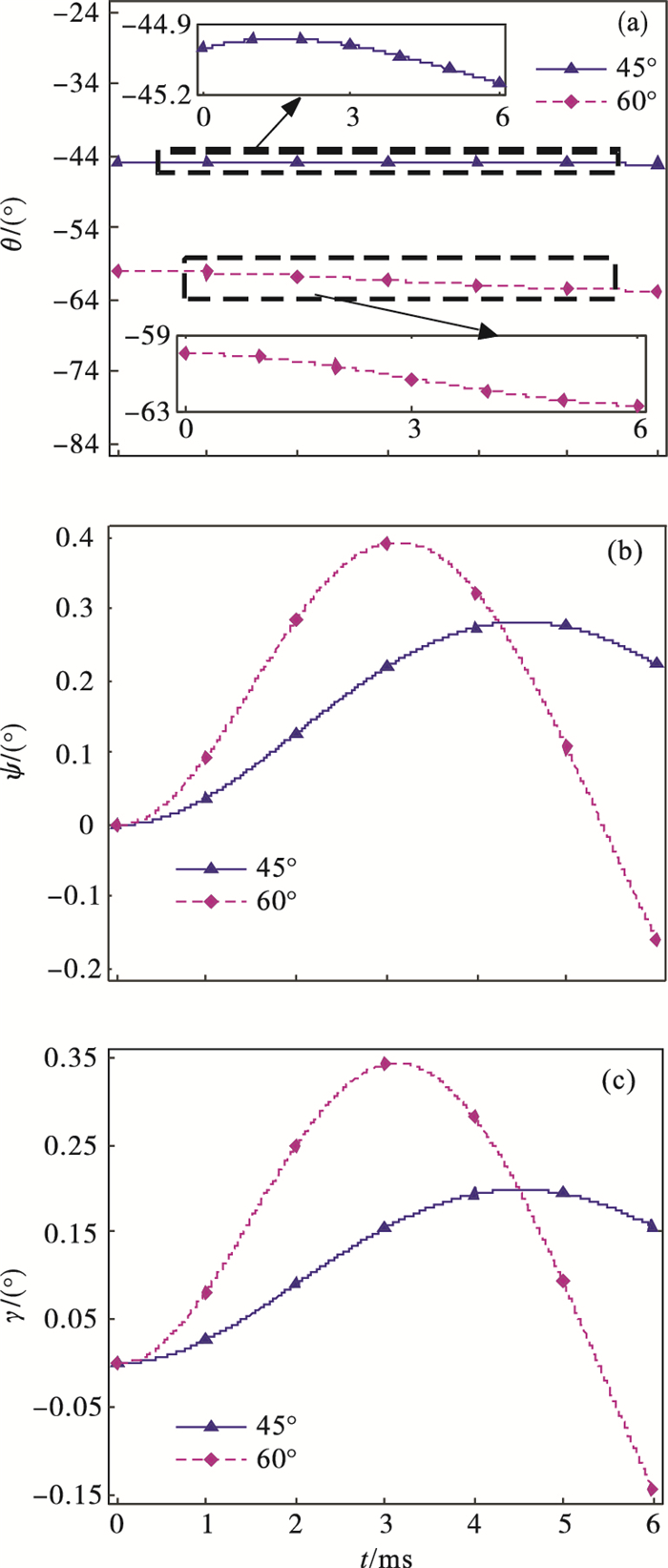图 8 不同入水角射弹姿态角的变化曲线Fig.8 Change curves of projectile attitude angle at different water entry angles (a)—俯仰角；(b)—偏航角；(c)—滚转角.

3.3 入水流体动力特性分析图 9为射弹在0~6 ms的入水过程中阻力、升力和侧向力随时间的变化曲线.由图中可以看出，射弹未入水时，阻力、升力和侧向力都几乎为零.射弹在穿越自由液面时，阻力和升力岀现了一个阻力峰值和升力峰值，其中60°入水角的阻力峰值更高，而升力峰值更低；但在撞水时侧向力没有岀现峰值，而是一段微小的波动.射弹完全入水以后，随着入水时间的增加，阻力在逐渐降低.60°入水角射弹受到的升力随入水时间的增加而增加，但45°入水角的升力基本维持在0左右.在两种角度入水条件下，射弹受到的侧向力的变化趋势类似，随着射弹运动侧向力先增加，然后缓慢降低.
图 9(Fig. 9)

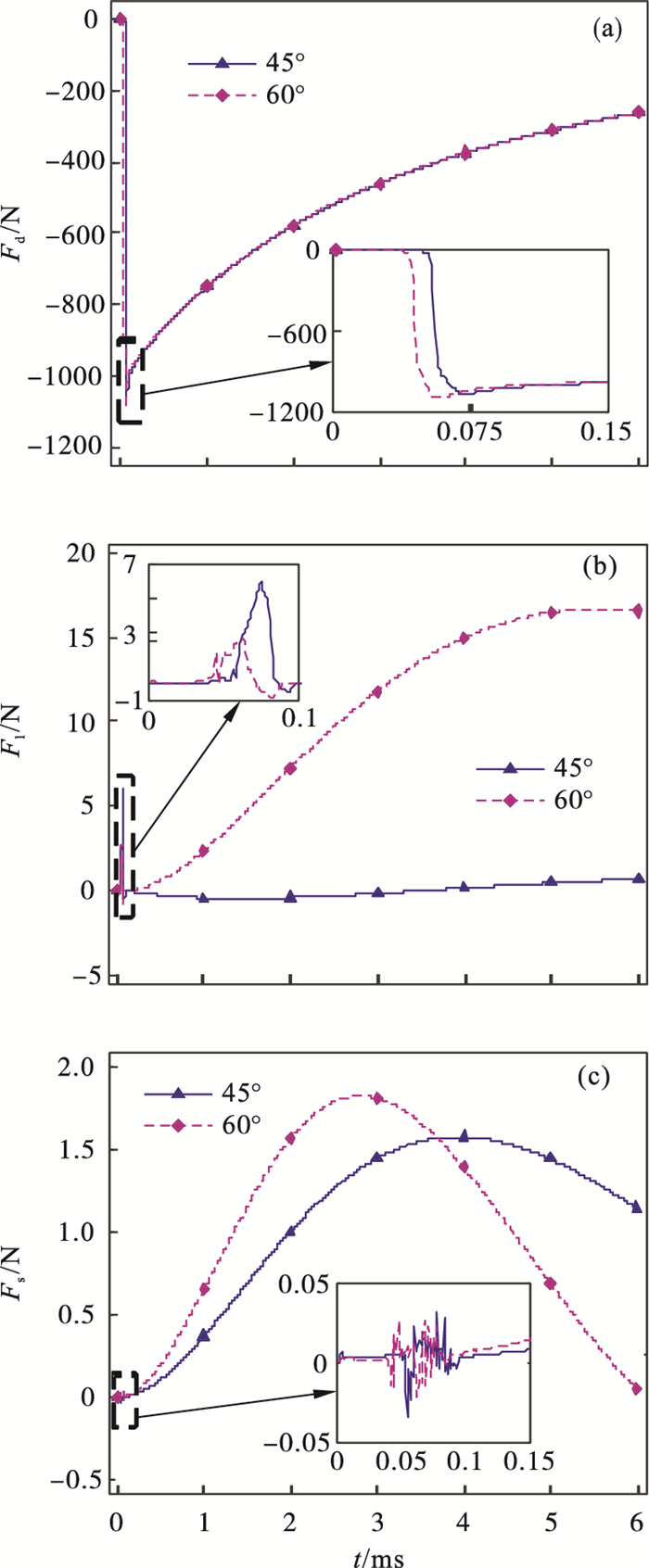图 9 射弹受力变化曲线Fig.9 Change curves of force on projectile (a)—阻力；(b)—升力；(c)—侧向力.

图 10为射弹入水过程中滚转力矩、偏航力矩及俯仰力矩的变化曲线.由图可知，力矩的数量级非常小，尤其是滚转力矩.俯仰力矩、偏航力矩和滚转力矩的变化趋势一致，而且在入水时都出现了一个小峰值，然后降低；当射弹在水中完全形成超空泡时，力矩数值几乎都在零附近.因此，数值模拟证明入水角度对流动稳定阶段的力矩影响非常小.
图 10(Fig. 10)

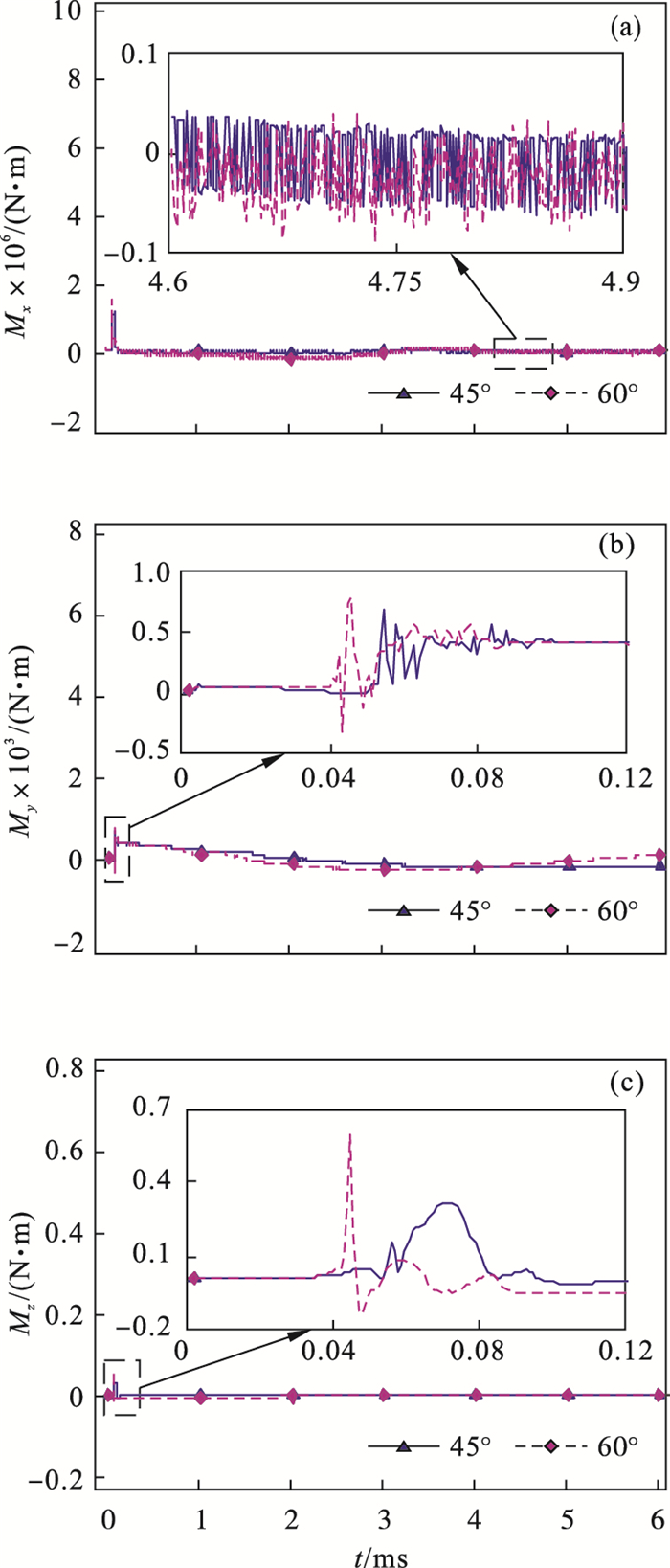图 10 射弹受力矩变化曲线Fig.10 Change curves of moment on projectile (a)—滚转力矩；(b)—偏航力矩；(c)—俯仰力矩.

4 结论1) 射弹倾斜入水后，两侧空泡形态不对称，与左侧空泡相比，右侧空泡尺寸较大.
2) 射弹入水后，入水角越小，射弹质心处的速度越大；入水角为45°时，俯仰角、偏航角、滚转角的波动范围更小.
3) 在穿越自由液面时，射弹受到的阻力和升力岀现一个峰值，但侧向力没有岀现峰值，而是一段微小的波动.
4) 射弹进入流动稳定阶段，入水角度对滚转力矩、偏航力矩及俯仰力矩的影响非常小，力矩数值几乎为零.
参考文献

[1]	Hassouneh M A, Nguyen V, Balachandran B, et al. Stability analysis and control of supercavitating vehicles with advection delay[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(2): 021003. DOI:10.1115/1.4006835
[2]	Worthington A M, Cole R S. Impact with a liquid surface, studied by the aid of instantaneous photography[J]. Philosophical Transactions of the Royal Society A, 1897, 189: 137-148.
[3]	Truscott T T. Cavity dynamics of water entry for spheres and ballistic projectiles[D]. Cambridge, MA: Massachusetts Institute of Technology, 2009.
[4]	Thoroddsen S T, Etoh T G, Takehara K, et al. Impact jetting by a solid sphere[J]. Journal of Fluid Mechanics, 2004, 499: 139-148. DOI:10.1017/S0022112003007274
[5]	Holfeld B, Maier F, Izzo M, et al. Spatial high-speed-imaging of projectile impacts into fluids in microgravity[J]. Microgravity Science and Technology, 2009, 21(1/2): 73-77.
[6]	孟庆昌, 易文彬, 胡明勇, 等. 高速射弹垂直入水空泡形态及水动力特性研究[J]. 中国造船, 2019, 60(3): 12-26. (Meng Qing-chang, Yi Wen-bin, Hu Ming-yong, et al. Study on cavity profile and hydrodynamics of high-speed vertical water entry of projectile[J]. Shipbuilding of China, 2019, 60(3): 12-26. DOI:10.3969/j.issn.1000-4882.2019.03.002)
[7]	侯宇, 黄振贵, 郭则庆, 等. 超空泡射弹小入水角高速斜入水试验研究[J]. 兵工学报, 2020, 41(2): 332-341. (Hou Yu, Huang Zhen-gui, Guo Ze-qing, et al. Experimental investigation on shallow-angle oblique water-entry of a high-speed supercavitating projectile[J]. Acta Armamentarii, 2020, 41(2): 332-341.)
[8]	Neaves M, Edwards J. Time-accurate calculations of axisymmetric water entry for a supercavitating projectile[C]//34th AIAA Fluid Dynamics Conference and Exhibit. Oregon, Portland, 2004: 1-11.
[9]	Panciroli R, Abrate S, Minak G, et al. Hydroelasticity in water-entry problems: comparison between experimental and SPH results[J]. Composite Structures, 2012, 94(2): 532-539. DOI:10.1016/j.compstruct.2011.08.016
[10]	郭子涛. 弹体入水特性及不同介质中金属靶的抗侵彻性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2012. (Guo Zi-tao. Research on characteristics of projectile water entry and ballistic resistance of targets under different mediums[D]. Harbin: Harbin Institute of Technology, 2012. )