赵勐^1,2, 肖明^1,2, 陈俊涛^1,2, 左双英³
1. 武汉大学 水资源与水电工程科学国家重点实验室, 湖北 武汉 430072;
2. 武汉大学 水工岩石力学教育部重点实验室, 湖北 武汉 430072;
3. 贵州大学 资源与环境工程学院, 贵州 贵阳 550025
收稿日期：2021-05-09
基金项目：国家自然科学基金资助项目(52079097); 国家重点研发计划项目(2015CB057904)。
作者简介：赵勐(1994-), 男, 江苏淮安人, 武汉大学博士研究生;
肖明(1957-), 男, 湖南株洲人, 武汉大学教授, 博士生导师。

摘要：层间剪切、挤压破碎带是影响互层状岩体地下洞室围岩稳定的重要因素.针对互层状岩体层间剪切、挤压破坏问题, 引入界面单元模型模拟其接触特性.在此基础之上, 对该接触面模型算法进行改进, 针对接触面边界上节点可能存在的接触状态: 黏结、滑移、张开和嵌入, 建立了相应的接触状态判别准则和修正迭代算法, 可以有效模拟互层状岩体层间非线性滑移破坏问题.将本文模型应用于巴基斯坦阿扎德帕坦水电站地下厂房围岩稳定性分析中, 对比横观各向同性模型计算结果, 表明考虑接触后在层间过渡处应力和位移呈现非连续性变化, 且量值增大; 层间出现了错动位移, 在主厂房边墙侧中下部较为明显.
关键词：互层状岩体地下洞室界面单元剪切滑移数值模拟
Stability Analysis of Surrounding Rock of Underground Caverns Considering Contact State of Interbedded Layered Rock Mass
ZHAO Meng^1,2, XIAO Ming^1,2, CHEN Jun-tao^1,2, ZUO Shuang-ying³
1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;
2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education, Wuhan University, Wuhan 430072, China;
3. College of Resources and Environment Engineering, Guizhou University, Guiyang 550025, China
Corresponding author: XIAO Ming, E-mail: mxiao@whu.edu.cn.

Abstract: The interlayer shearing and crushing fracture zone are the key factors affecting the stability of surrounding rock of underground caverns in interbedded layered rock mass. For the problem of the interlayer shearing and crushing failure of interbedded layered rock mass, the interface element model was introduced to simulate the interlayer contact characteristics. Based on this, the contact model algorithm was improved. In view of the possible contact states for nodes on the boundary of the contact surface such as bonding contact, slipping contact, opening and embedding contact, the corresponding contact state criterion and modified iterative algorithm were established, which can effectively simulate the nonlinear slip damage between layers of interbedded layered rock mass. Then, the proposed model was applied to the stability calculation of the surrounding rock of underground powerhouse of Azad Patan Hydropower Station in Pakistan. Compared with the calculation results of the transverse isotropic model, the stress and displacement at the interlayer transition zone vary discontinuously and increase after considering the contact; dislocation displacement occurs between layers, which is more obvious in the middle and lower parts of the side wall of the main underground caverns.
Key words: interbedded layered rock massunderground caverninterface elementshear slipnumerical simulation
层状岩体在复杂地质构造作用下, 由于具有多种优势节理面, 其力学行为和破坏模式与一般岩体相异, 表现出明显的各向异性^[1], 如琅琊山抽水蓄能电站、乌东德和白鹤滩水电站等.层状岩体的结构依其所赋存地质环境的多样性而具有不同形式, 王思敬等^[2]将其划分为3种主要类型: 互层状结构、薄层状结构和夹层状结构.在层状岩体中进行地下工程建设, 尤其对于软硬互层状岩体, 由于其既具有层状岩体变形和强度性质的各向异性特征, 又受到岩体软硬互层的影响, 当岩层倾角较大时, 结构面发育明显, 在构造应力作用下, 层间剪切、挤压破碎带较为常见.因此, 针对互层状岩体, 考虑不同岩性介质相互接触作用对岩土体发生剪切滑移破坏的影响, 能更好地描述岩体破坏模式, 具有重要的现实意义.
目前国内外****关于层状岩体模拟主要有两类方法, 一种是将层状岩体分离成层间岩块和层面, 分别采用不同模型来模拟这两种介质, 黄书岭等^[3]分别对母岩和节理面建立不同的屈服准则, 提出层状岩体多节理本构模型, 描述其变形和强度各向异性; 徐国文等^[4]采用基于PFC-FLAC的连续-离散耦合算法, 对岩石和层理面用不同本构模型模拟, 并运用于层状软岩隧道围岩的稳定性分析中; 另一种是将节理面等效考虑进岩体中, 把层状岩体看成是横观各向同性体, 利用层状弹性体系力学理论分析其变形和强度性质的各向异性特征.该方向的研究主要归结为以下两类:
1) 基于张量函数形式的强度准则.Pietruszczak等^[5]引入微结构张量a_ij, 将各向同性准则映射到各向异性中; 钟世英等^[6]将微结构张量参数引入到Jaeger针对岩体沿节理面滑移破坏提出的M-C准则中, 并将其运用到白鹤滩水电站的柱状节理分析中; 李良权等^[7]提出一种改进的各向异性Hoek-Brown强度准则, 并进行参数敏感性分析; 但上述方法引入参数过多且确定麻烦.
2) 引入各向异性函数的强度准则.该法主要将层面对岩体破坏的影响因素及材料力学参数的各向异性考虑进各向同性的屈服准则中, 推导岩体强度与相关参数之间的函数关系.Jaeger^[8]认为抗剪强度是破坏面与主应力夹角的函数, 并给出相关的表达式; Zhang等^[9]在文献[8]的基础上提出具体的层状岩体黏聚力和内摩擦角的表达式; 韩昌瑞等^[10]建立相应强度参数方程, 引入到M-C屈服准则中, 并运用到深埋长隧道锚固支护中.
本文针对互层状岩体采用“隐含层面”的建模技术, 在计算中通过输入层面方位角实现应力、位移和荷载在层状法向坐标系和整体坐标系之间转换^[11].对于软、硬互层交界面处, 由于层间剪切错动带发育, 需考虑其应力及位移在层面两侧的不连续性^[12], 但常规连续有限元模型难以解决这个问题, 本文引入FLAC^3D专门模拟岩土体接触面力学行为的界面单元^[13], 分析计算中可能出现的多种接触状态并提出判别修正方法.针对接触面边界节点对发生的嵌入问题, 基于Desai薄层单元的嵌入控制方法^[14], 改进界面单元边界节点对发生嵌入时的迭代算法.以巴基斯坦阿扎德帕坦水电站互层状岩体为例, 应用本文的研究方法, 分析在构造应力作用下, 不同岩性介质相互接触作用对互层状岩体层间剪切挤压带和地下洞室的影响, 以期对复杂互层状岩体中地下洞室围岩稳定分析进行有益探索.
1 层状岩体弹性本构关系在地质构造作用下, 层状各向异性岩体由于优势层理面的存在, 具有明显的变形各向异性.一般将其等效处理成横观各向同性介质, 在平行于层面方向是各向同性的, 在垂直于层面方向具有与层面不同的弹性主方向.依据层状弹性体系力学理论^[15], 层状法向坐标系下层状各向异性介质的弹性矩阵如式(1)所示:

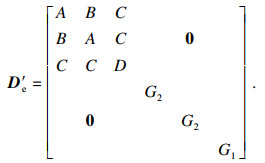(1)

式中: A=E₁(1-nμ₂²)/m; B=E₁(μ₁+nμ₂²)/m; C=E₁μ₂(1+μ₁)/m; D=E₂(1-μ₁²)/m; G₁=E₁/2(1+μ₁); G₂=E₁E₂/[E₁(1+2μ₁)+E₂]; n=E₁/E₂, m=(1+μ₁)(1-μ₁-2nμ₂²), E₁, μ₁, G₁分别表示层面切向的弹性模量、泊松比和剪切模量, E₂, μ₂, G₂分别表示层面法向的弹性模量、泊松比和剪切模量.
由于局部的层状法向坐标系通常与计算的整体坐标系不一致, 需要通过三维坐标系下的坐标转换矩阵R和应力转换矩阵S将层状法向坐标系Ox′y′z′下的刚度矩阵Κ′和弹性矩阵D′转换到整体坐标系Oxyz下的刚度矩阵Κ和弹性矩阵D ^[11]:

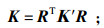(2)

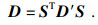(3)

2 互层状岩体接触系统数值模型对于互层状岩体, 在水平向构造应力和竖直向自重应力联合作用下, 层间剪切、挤压破碎带发育, 此种破坏特性在陡倾角岩层下更为常见, 互层状岩体介质在外荷载作用下将难以保持整体连续变形.本文基于FLAC^3D界面单元接触理论^[13], 推导出4种不同接触状态的判别准则及修正方法, 对接触边界节点相互“嵌入”时的迭代方法进行改进, 从而解决互层状岩体层间非整体连续变形问题.
2.1 接触面本构模型本文的计算模型通过在互层状岩体层间接触部位设置FLAC^3D中提供的界面单元的方法来模拟其接触特性.界面单元是无厚度接触面单元, 附属于三维实体单元的网格面, 由一系列三节点的三角形平面单元构成.因此, 不像等效连续模型一样层间网格共用同一节点, 接触面模型可以模拟互层状岩体层间滑移和分离行为^[13].
未施加外荷载时, 接触面处于黏结状态, 其本构模型如图 1所示, 接触面的法向和切向接触力分别由下式确定:

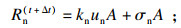(4)

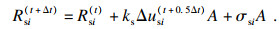(5)

图 1(Fig. 1)

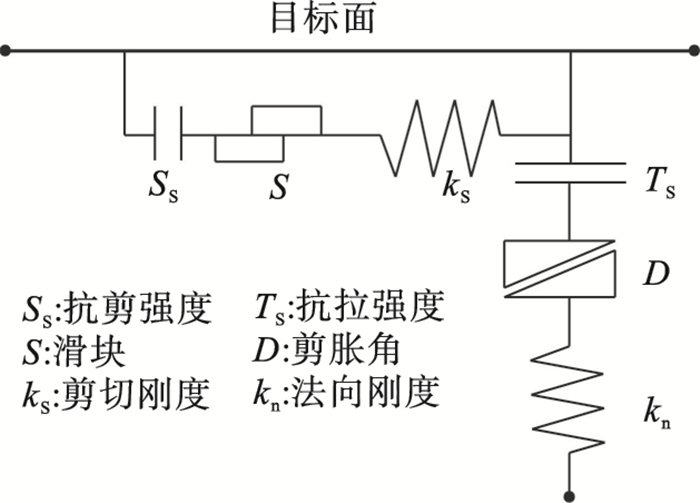图 1 接触面单元的本构关系示意图Fig.1 Diagram of constitutive relation for interface

式中: R_n^(t+Δt)和R_s^(t+Δt)分别为t+Δt时刻的法向和切向接触力; u_n为接触面节点侵入到目标面的法向绝对位移; Δu_si为相对剪切位移增量; σ_n和σ_si分别为接触面应力初始化产生的附加法向和切向应力; k_n和k_s分别为界面单元的法向和切向刚度; A为接触节点所代表的面积.
2.2 接触边界条件外荷载施加前, 互层状岩体接触面上接触节点处于“点对点”的接触方式, 接触点对间存在黏结力.如图 2所示, 对于发生接触的两种介质M₁, M₂, 相应的接触边界上的点对i和i′需要满足接触边界条件, 包括位移接触条件和接触力边界条件.
图 2(Fig. 2)

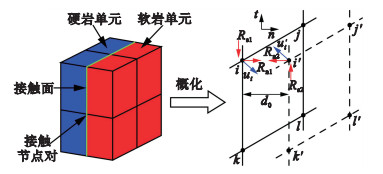图 2 接触示意图Fig.2 Diagram of contacts

对于接触面两侧的物质, 在法向上假定其不会相互嵌入，即满足法向接触条件; 在切向上当接触面接触时, 若无相对滑动产生, 则点对还应满足切向位移协调条件, 如式(6)所示:

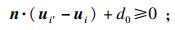(6)

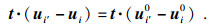(7)

式中: n为接触节点对的法线方向矢量; d₀为接触节点对i和i′的初始法向间隙; t代表与法线方向矢量n对应的切线方向矢量.
发生接触时, 接触面两侧节点对的法向接触力R_n1, R_n2和切向接触力R_s1, R_s2需满足以下条件:

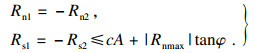(8)

式中，c, φ为接触面的黏聚力和内摩擦角.
2.3 接触面屈服准则2.3.1 拉伸破坏对垂直于接触面的拉伸破坏情况, 先计算沿接触面法向局部坐标下的应力分量:

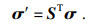(9)

根据单轴拉伸强度准则, 由局部坐标下的应力分量校核接触面发生拉伸破坏时的应力状态, 当

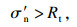(10)

说明接触面的局部法向应力超过极限抗拉强度R_t, 接触面节点脱离目标面, 产生缝隙且切应力和正应力变为0.
2.3.2 剪切滑移破坏对平行于接触面的破坏情况, 根据Coulomb抗剪强度准则校核沿接触面是否发生滑移:

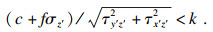(11)

式中: f为接触面的摩擦系数; k为接触面滑动安全系数.此时沿接触面方向将发生剪切滑移破坏.
2.4 接触状态判别准则及修正方法根据接触面边界上节点对的位移相互关系和受力状态, 结合Coulomb抗剪强度准则和法向抗拉强度准则, 分析节点对可能存在的4种接触状态: 黏结、滑移、张开和嵌入状态.接触面上的节点荷载和该节点所处的接触状态有关, 在弹塑性非线性分析时, 节点对发生滑移时超出抗剪强度的切向接触力和发生张开时超出抗拉强度的法向接触力需进行转移^[11].由于黏结接触无需对接触力进行修正，故对滑移、张开和嵌入这3种接触状态的判别准则及修正方法详述如下.
2.4.1 滑移接触状态对于接触面边界节点对发生滑移时, 需对下式进行判断:

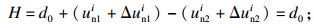(12)

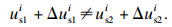(13)

式中: u_n1ⁱ, u_n2ⁱ和u_s1ⁱ, u_s2ⁱ分别表示第i时步开始时节点对1, 2的法向位移和切向位移; Δu_n1ⁱ, Δu_n2ⁱ和Δu_s1ⁱ, Δu_s2ⁱ表示第i时步中节点对1, 2的法向和切向位移增量, 受拉为正.
若节点对同时满足式(12)和式(13)条件, 则判定节点对发生滑移.此时节点对的受力情况如下式所示:

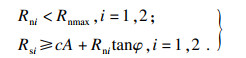(14)

此时, 沿接触面方向节点对将发生剪切滑移, 应将超出抗剪强度的切向力

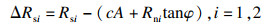(15)

进行转移, 将其转换成等效节点荷载, 并将所有接触面单元的上述节点荷载累加，作为下一时步的增量荷载, 同时该组节点对的法向接触力和切向接触力修正如下:

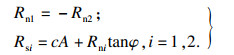(16)

2.4.2 张开接触状态对于接触面边界节点对发生张开时, 需对式(12)中变量H值进行判断.
若H>d₀, 则判定节点对发生张开, 此时节点对间不传力, 法向刚度及切向刚度参数均设置为0, 即此时步中该节点对的法向和切向接触力均修正为

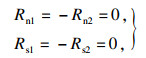(17)

直至该节点对重新闭合.需注意的是，对于发生开裂破坏的单元, 在上述处理过后, 直接标记分离状态, 不再进行额外处理.
2.4.3 嵌入接触状态及调整对上述两种接触状态进行判断及节点力修正时, 还需进行节点对位移判别, 以检查接触面两侧节点是否发生嵌入.对发生嵌入的节点对, 基于Desai薄层单元的嵌入控制方法^[14], 对其位移和节点力进行修正, 使相互侵入的节点退回到黏结或滑移接触状态, 具体步骤如下:
1) 遍历每一接触面两侧节点对, 计算式(12)中变量H值;
2) 若H≥0, 则节点对未发生嵌入, 继续遍历下一组节点对;
3) 若H < 0, 则节点对发生嵌入, 应对节点对的位移进行修正.计算α值如下:

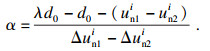(18)

式中，λ为控制嵌入判别精度的百分数, 通常取1 % ^[14], 当节点对嵌入值小于λd₀时, 忽略不计.
4) 计算(α-1)Δu_n1ⁱ和(α-1)Δu_n2ⁱ, 并转换至整体坐标系, 据此得到接触面两侧节点对的位移修正值, 可求出点对的节点修正荷载ΔQ:

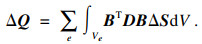(19)

式中: B为单元应变矩阵; ΔS为整体坐标系下接触节点对的位移修正值向量; V_e为单元体积; 为对绕节点i的所有单元求和.
将求得的节点修正荷载ΔQ按等值反向的原则施加在接触面两侧的节点对上, 更新节点接触力, 重新计算节点变形, 得到新的点对法向位移, 依此循环迭代直至满足平衡条件.
2.5 接触判别计算流程在进行互层状岩体层间接触计算时, 先假定初始时步内接触节点对无相对滑动, 均处于黏结接触状态.基于接触边界条件, 求解当前时步下节点对法向、切向的接触力及位移, 判别节点的接触状态并修正.在本文所提出的接触判别迭代计算中, 需注意的是, 对于节点处于张开状态, 在进行接触力修正时, 认为节点先退回至黏结接触, 再达至其余接触状态^[16].具体接触判别计算流程见图 3所示.
图 3(Fig. 3)

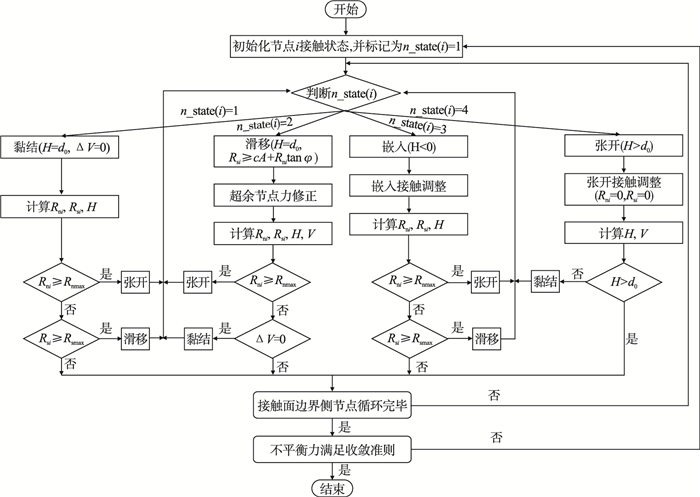图 3 接触判别计算流程Fig.3 Flow chart of contact discriminant computation

3 工程实例及分析3.1 工程概况阿扎德帕坦水电站位于巴基斯坦的Jhelum河上, 为该河段水电开发中的一级.引水发电系统位于河流左岸, 电站采用地下厂房“一洞室”方案, 仅保留主机洞室, 主变电站及开关站均布置在户外, 主厂房内安装4台机组, 机组间距为40.0 m, 主机洞室开挖尺寸长×宽×高为175.6 m×24.9 m×60.15 m.
阿扎德帕坦水电站工程区地质条件复杂, 厂房区基岩岩性为砂岩与非砂岩类，呈互层状分布, 且具有层状各向异性特征.地层主要为单斜构造, 岩层总体走向NE10°, 倾向NE, 倾角65°~75°(地表较缓, 厂房部位较陡)；受构造应力影响, 层间剪切、挤压破碎带较为常见.
3.2 计算模型和计算条件综合分析该水电站的地形、地质特征, 考虑到互层状岩体发育明显, 本文在计算时主要选取穿越2号、4号机组段的Ⅳ类岩层与周围的Ⅲ类岩层共同组成互层状岩体为研究对象, 计算模型均采用八节点六面体单元进行离散, 共剖分了266 104个单元和278 775个节点, 其中开挖单元26 784个, 如图 4、图 5所示.三维计算坐标x轴顺水流向与厂房纵轴线方向垂直, y轴与厂房纵轴线方向重合, z轴与大地坐标重合, 3个方向的计算范围分别为170, 160, 236.80 m.根据设计院提供的资料, 锚固支护型式及参数见表 1, 共分7期进行开挖计算分析, 开挖分期模型见图 5.
图 4(Fig. 4)

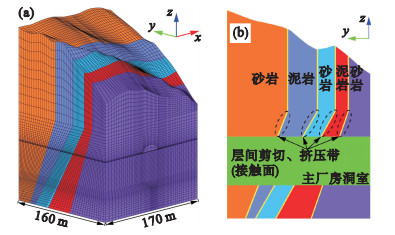图 4 互层状岩体三维有限元模型Fig.4 3D FE model of interbedded layered rock mass (a)—三维有限元模型；(b)—模型剖面示意图.

图 5(Fig. 5)

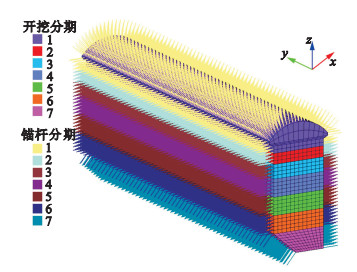图 5 开挖支护模型Fig.5 Excavation and support model

表 1(Table 1)

表 1 洞室支护型式及参数Table 1 Support pattern and parameters of the cavern 部位 支护型式及参数 452.0 m高程以上边墙和顶拱 系统锚杆: ?28@1.5 m×1.5 m, L=7.0 m, 梅花型; 预应力锚杆: ?32@4.5 m, L=10.0 m, T=100 kN; 预应力锚索: L=15.0 m@4.0 m, P=1 500 kN; 钢纤维喷混凝土δ=25. 452.0 m高程以下边墙 系统锚杆: ?28@1.5 m×1.5 m, L=7.0 m, 梅花型; 预应力锚杆: ?32@4.5 m, L=10.0 m, T=100 kN; 钢纤维喷混凝土δ=25.

表 1 洞室支护型式及参数 Table 1 Support pattern and parameters of the cavern

三维初始应力场根据设计院提供的实测地应力反演分析得到, 侧压力系数取k_x=1.3, k_y=1.4, k_z=1.1.互层状岩体砂岩与泥岩材料物理力学参数取值见表 2.开挖过程中通过释放开挖单元应力并将其施加到开挖临空面周围单元来模拟开挖释放荷载, 该地下厂房在开挖过程中采用喷锚支护等支护措施^[17].锚杆和锚索的模拟采用FLAC^3D中的Cable单元^[13], 能有效模拟锚杆对围岩的加固效果.
表 2(Table 2)

表 2 材料物理力学参数Table 2 Physical-mechanical parameters of materials 状态 岩体类别 干密度 ρd/(g·cm-3) 变形模量 E0/GPa 泊松比μ 岩体抗剪断强度 抗拉强度 Rm/MPa 抗压强度 Rb/MPa f′ c′/MPa 平行于层面 Ⅲ 2.58 7 0.23 0.675 0.525 1.75 40 Ⅳ 2.52 3 0.29 0.475 0.375 0.225 20 垂直于层面 Ⅲ 2.58 6 0.285 1.0 1.35 1.15 40 Ⅳ 2.52 2 0.335 0.65 0.55 0.175 20 接触面 — — — — 0.38 0.35 — —

表 2 材料物理力学参数 Table 2 Physical-mechanical parameters of materials

计算工况分两种: ①采用横观各向同性模型分析互层状岩体对开挖地下洞室的影响; ②采用本文改进的界面单元模拟互层状岩体层间相互接触作用对开挖地下洞室的影响.
3.3 计算结果分析为了论证采用本文改进的界面单元模拟互层状岩体层间剪切、挤压破坏的合理性, 本文分别采用横观各向同性模型和含界面单元模型进行数值模拟, 选取主厂房洞室对比分析锚固支护分期开挖下洞周围岩的变形和应力分布规律.
3.3.1 围岩变形分布规律对于工况①, 采用不考虑接触的横观各向同性模型进行分析计算(见图 6a), 厂房开挖完毕, 洞周围岩变形在3.00~9.00 cm, 最大变形量出现在泥、砂岩层间过渡处10 m范围内, 边墙位移从上至下先增大后减小.由于将层面等较大的节理等效考虑进岩体单元中, 围岩层间相对位移为0, 互层状岩体在岩层面两侧位移变化连续, 没有出现位移值的不连续跳跃情况.
图 6(Fig. 6)

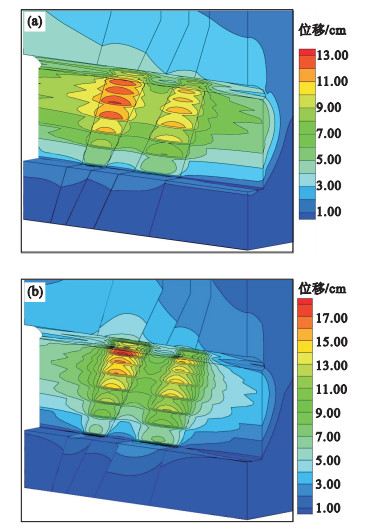图 6 主厂房洞周位移分布Fig.6 The displacement distribution for the main cavern (a)—工况①；(b)—工况②.

对于工况②, 采用本文考虑多种接触状态的含界面单元模型(见图 6b), 厂房开挖完毕, 洞周围岩变形在5.00~13.00 cm, 相对于工况①增大约2.00~4.00 cm.从图 6b可以看出, 互层状岩体在层间出现了错动位移, 取主厂房顶拱、边墙和底部不同监测点进行分析, 主厂房洞室各监测点处错动位移随开挖分期的变化如图 7所示. 随开挖进行, 顶拱的位移逐步发生回弹, 错动位移值略有减小, 最终稳定在0.48 mm附近, 主厂房洞室其余各部位的错动位移值逐渐增大.尤其对于上下游边墙侧, 在开挖至第3~4期时, 高边墙逐渐形成, 错动位移值增加较为明显, 开挖完毕时, 该位移值约为4.91~5.25 mm, 局部最大值出现在边墙侧中下部(见图 7), 该处高边墙效应明显, 是围岩稳定分析中重点支护部位.对比两种工况, 结果表明对于互层状岩体, 当考虑层间接触作用后, 围岩变形要比等效连续模型的略大, 且导致厂房边墙侧产生的相对变形要比顶拱和底部大, 层间接触面处于滑移状态.
图 7(Fig. 7)

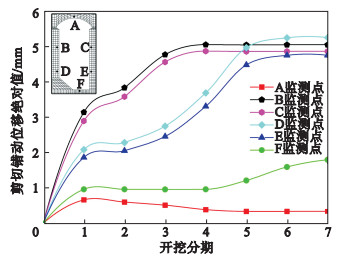图 7 主厂房洞室围岩各监测点相对位移变化过程Fig.7 Relative displacement change process of monitoring points in surrounding rock of the main cavern

3.3.2 围岩应力分布规律采用不考虑接触的横观各向同性模型进行模拟时，主厂房洞室开挖完毕，围岩边墙侧第一主应力不断减小，在边墙一定范围内形成了应力松弛区，量终第一主应力稳定分布在-4.65~-0.96 MPa，第三主应力分布在-1.23~0.20 MPa.由图 8a可知，互层状岩体在层间剪切带附近主应力值有所降低，降幅在1.0 MPa左右，该附近应力云图沿接触面向下突出，但是仍然保持连续变化，未产生突变.
图 8(Fig. 8)

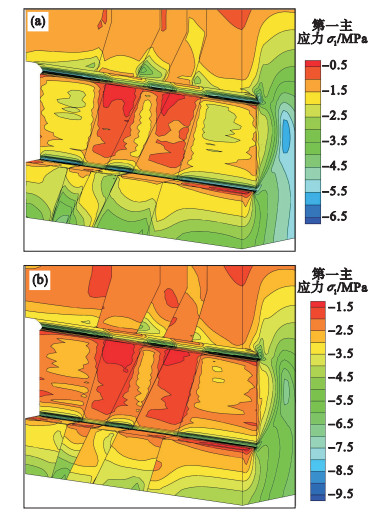图 8 主厂房洞周围岩第一主应力分布Fig.8 The 1st principal stress distribution in the surrounding rock of the main cavern (a)—工况①；(b)—工况②.

工况②采用本文考虑多种接触状态的含界面单元模型进行计算分析, 开挖完毕后, 主厂房洞室边墙侧第一主应力分布在-6.68~-1.05 MPa, 第三主应力分布在-2.03~0.41 MPa, 相较于工况①的计算结果, 应力增加约为10.53 % ~43.66 %, 上下游边墙侧局部拉应力超过岩体抗拉强度, 导致部分围岩开裂破坏, 且主要出现在层间剪切带附近(见图 9b).表明对于互层状岩体, 泥、砂岩软硬间错分布, 软岩穿过部分厂房边墙处应力较大, 受力情况复杂, 层状岩体层间相对滑移对厂房开挖时应力扰动影响较大.
图 9(Fig. 9)

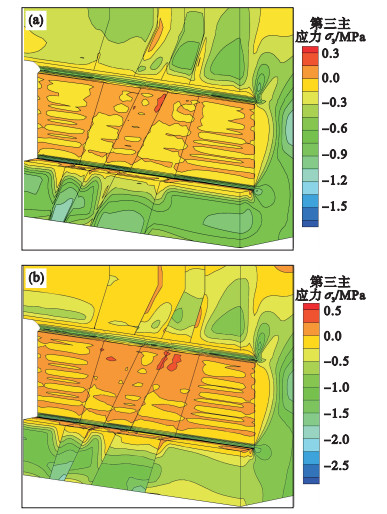图 9 主厂房洞周围岩第三主应力分布Fig.9 The 3rd principal stress distribution in the surrounding rock of the main cavern (a)—工况①；(b)—工况②.

工况②采用改进的界面单元接触算法, 在层间接触带两侧应力的变化不连续, 软岩与两侧硬岩的应力值相差较为明显, 呈现交错分布现象^[18]. 从图 8b和图 9b可看出, 在互层状岩体层间过渡处, 第一主应力值出现明显跌落, 应力降幅在1.4 MPa左右, 第三主应力降幅在0.6 MPa左右.
从图 8和图 9可以看出, 采用改进的接触面单元模拟互层状岩体层间的接触状态, 洞周围岩位移和应力呈现非连续变化, 能够比较好地模拟互层状岩体层间剪切、挤压破坏情况, 与工程实际更为吻合.
4 结论1) 基于FLAC^3D界面单元接触理论, 改进界面接触面模型算法, 针对界面单元接触边界发生黏结、滑移、张开和嵌入等接触状态建立了相应的判别准则和修正迭代算法, 充分考虑互层状岩体层间相互作用特点, 能有效模拟构造应力作用下在互层状岩体中开挖地下洞室时发生的非线性剪切滑移破坏现象.
2) 将本文所建模型应用于地下洞室的开挖计算中, 与传统有限元的横观各向同性模型对比, 结果表明, 当考虑多种接触状态时, 岩体层间过渡处应力和位移呈现非连续变化规律, 且量值也进一步增大.在构造应力和开挖荷载作用下, 互层状岩体层间易发生相互错动, 且在上下游边墙侧中下部较为明显.本文模型可运用于实际工程计算，为互层状岩体层间非连续性接触问题的模拟提供了一种有效的实现途径.
参考文献

[1]	耿大新, 杨林德. 层状岩体的力学特性及数值模拟分析[J]. 地下空间, 2003, 23(4): 38-41. (Geng Da-xin, Yang Lin-de. Mechanical properties and numerical simulation of sandwich rock[J]. Underground Space, 2003, 23(4): 38-41.)
[2]	王思敬, 黄鼎成. 中国工程地质世纪成就[M]. 北京: 地质出版社, 2004. (Wang Si-jing, Huang Ding-cheng. Collection of the century achievements in China's engineering geology[M]. Beijing: Geological Publishing House, 2004.)
[3]	黄书岭, 丁秀丽, 邬爱清, 等. 层状岩体多节理本构模型与试验验证[J]. 岩石力学与工程学报, 2012, 31(8): 1627-1635. (Huang Shu-ling, Ding Xiu-li, Wu Ai-qing, et al. Study of multi-joint constitutive model of layered rockmass and experimental verification[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(8): 1627-1635. DOI:10.3969/j.issn.1000-6915.2012.08.016)
[4]	徐国文, 何川, 汪耀, 等. 层状软岩隧道围岩破坏的连续-离散耦合分析[J]. 西南交通大学学报, 2018, 53(5): 966-973. (Xu Guo-wen, He Chuan, Wang Yao, et al. Failure analysis on surrounding rock of soft-layered rock tunnel using coupled continuum-discrete model[J]. Journal of Southwest Jiaotong University, 2018, 53(5): 966-973. DOI:10.3969/j.issn.0258-2724.2018.05.013)
[5]	Pietruszczak S, Mroz Z. Formulation of anisotropic failure criteria incorporating a microstructure tensor[J]. Computers and Geotechnics, 2000, 26(2): 105-112. DOI:10.1016/S0266-352X(99)00034-8
[6]	钟世英, 徐卫亚. 基于微结构张量理论的柱状节理岩体各向异性强度分析[J]. 岩土力学, 2011, 32(10): 3081-3084. (Zhong Shi-ying, Xu Wei-ya. Anisotropic failure criterion incorporating microstructure tensor for rock mass with columnar joints[J]. Rock and Soil Mechanics, 2011, 32(10): 3081-3084. DOI:10.3969/j.issn.1000-7598.2011.10.032)
[7]	李良权, 张春生, 王伟. 一种改进的各向异性Hoek-Brown强度准则[J]. 岩石力学与工程学报, 2018, 37(sup 1): 3239-3246. (Li Liang-quan, Zhang Chun-sheng, Wang Wei. A modified Hoek-Brown failure criterion for anisotropic rock mass[[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(sup 1): 3239-3246.)
[8]	Jaeger J C. Shear failure of anisotropic rocks[J]. Geological Magazine, 1960, 97(1): 65-72. DOI:10.1017/S0016756800061100
[9]	Zhang Y J, Zhang W Q. 3D FEM analysis for layered rock considering anisotropy of shear strength[J]. Journal of Central South University of Technology, 2010, 17(6): 1357-1363. DOI:10.1007/s11771-010-0642-x
[10]	韩昌瑞, 白世伟, 王玉朋, 等. 层状岩体深埋长隧道锚杆支护优化设计[J]. 岩土力学, 2016, 37(sup 1): 409-414. (Han Chang-rui, Bai Shi-wei, Wang Yu-peng, et al. Optimum design of rock bolts supporting long-deep tunnel in layered surrounding rock mass[J]. Rock and Soil Mechanics, 2016, 37(sup 1): 409-414.)
[11]	左双英, 史文兵, 梁风, 等. 层状各向异性岩体破坏模式判据数值实现及工程应用[J]. 岩土工程学报, 2015, 37(sup 1): 191-196. (Zuo Shuang-ying, Shi Wen-bing, Liang Feng, et al. Numerical simulation and engineering application for failure modes and criterion of layered anisotropic rock mass[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(sup 1): 191-196.)
[12]	赵健, 肖明, 陈俊涛, 等. 基于单元重构与节点分离的大型地下洞室软弱结构面模拟方法[J]. 湖南大学学报(自然科学版), 2017, 44(3): 134-142. (Zhao Jian, Xiao Ming, Chen Jun-tao, et al. Simulation methodology of weak structural planes in large underground chamber based on element reconstruction and node separation[J]. Journal of Hunan University(Natural Sciences), 2017, 44(3): 134-142.)
[13]	Itasca Consulting Group Inc. Fast Lagrangian analysis of continua in 3 dimension(Version 5.0)user's guide[R]. Minneapolis, Minnesota: Itasca Consulting Group, Inc, 2012.
[14]	Desai C S, Zaman M M, Lightner J G, et al. Thin-layer element for interfaces and joints[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1984, 8(1): 19-43. DOI:10.1002/nag.1610080103
[15]	Pande G N, Beer G, Williiam J R. Numerical methods in rock machaincs[M]. Chichester: John Wiley and Sons Inc, 1990.
[16]	Ahn Y J, Barber J R. Response of frictional receding contact problems to cyclic loading[J]. International Journal of Mechanical Sciences, 2008, 50(10/11): 1519-1525.
[17]	左双英, 肖明, 来颖. 基于FLAC3D的某水电站大型地下洞室群开挖及锚固效应数值分析[J]. 武汉大学学报(工学版), 2009, 42(4): 432-436. (Zuo Shuang-ying, Xiao Ming, Lai Ying. Numerical analysis of excavation and anchorage effect on complex underground caverns of a hydropower station with FLAC3D[J]. Engineering Journal of Wuhan University, 2009, 42(4): 432-436.)
[18]	杨帆, 陈卫忠, 郑朋强, 等. 急倾斜软硬互层巷道变形破坏机制及支护技术研究[J]. 岩土力学, 2014, 35(8): 2367-2374. (Yang Fan, Chen Wei-zhong, Zheng Peng-qiang, et al. Research on mechanism of deformation and failure for steeply inclined roadways in soft-hard alternant strata and its support technology[J]. Rock and Soil Mechanics, 2014, 35(8): 2367-2374.)