宋盛渊¹, 吴峰¹, 白皓², 王海宇³
1. 吉林大学 建设工程学院，吉林 长春 130026;
2. 四川高速公路建设开发集团有限公司，四川 成都 610041;
3. 四川绵九高速公路有限责任公司，四川 江油 621799
收稿日期：2021-03-25
基金项目：国家自然科学基金资助项目(42177139, U1702241)；地质灾害防治与地质环境保护国家重点实验室开放基金资助项目(SKLGP2018K017)。
作者简介：宋盛渊(1987-)，男，山西汾阳人，吉林大学副教授，博士生导师。

摘要：以乌东德库岸滑坡为例，充分考虑其发育的地质环境，选取滑坡发育特征、岸坡结构与岩性特征、地质构造与地形地貌特征、灾害诱发因素共4类因子作为滑坡易发性的影响因素.构建单因素分级标准，将库岸滑坡灾害易发性划分为四个等级，即重度易发、中度易发、轻度易发与不易发.应用区间数与集对分析理论，建立基于联系期望概念的库岸滑坡灾害易发性评价新模型，可系统分析滑坡易发性评价指标的区间形式及演化态势.实例分析结果表明，该方法评判结果可靠，且能简化区间数之间关系的分析过程.
关键词：地质灾害库岸滑坡易发性区间数集对分析
Evaluation of Reservoir Bank Landslide Susceptibility Degree Based on Interval Number and Set Pair Analysis Theory
SONG Sheng-yuan¹, WU Feng¹, BAI Hao², WANG Hai-yu³
1. College of Construction Engineering, Jilin University, Changchun 130026, China;
2. Sichuan Expressway Construction & Development Group Co., Ltd., Chengdu 610041, China;
3. Sichuan Mianjiu Expressway Co. Ltd., Jiangyou 621799, China
Corresponding author: SONG Sheng-yuan, E-mail: songshengyuan@126.com.

Abstract: The paper takes the Wudongde reservoir bank landslide as an example and fully considers the developed geological environment. The four impact factors including development feature of landslide, bank slope structure and lithology characteristics, geological structure and topography characteristics, disaster inducing factors are selected as landslide susceptibility factors. A single-factor grading standard is established to divide the susceptibility of reservoir bank landslide disasters into four levels: severe, moderate, mild and good. Based on the interval number and set pair analysis theory, a new model of connectional expectation for landslide susceptibility evaluation is introduced. This model can be used to analyze variation trend of landslide impact factors. The case study shows that the new method is reliable and can simplify the analysis process of the relationship between interval numbers.
Key words: geological disasterreservoir bank landslidesusceptibilityinterval numberset pair analysis
近年来，随着我国西部大开发的快速进行，重大水电工程在西部地区上游河段相继开工建设.上述河段大部分位于青藏高原及其边缘，受板块之间相互挤压的作用，岸坡岩体结构破碎、重力型地质灾害频发，尤其滑坡灾害的发生会给人类带来不可估量的危害.科学合理地评价复杂地质环境下库岸滑坡灾害的易发性，对促进大型工程建设和地质灾害防治工作的开展具有极其关键的指导作用^[1].
迄今为止，用于滑坡灾害易发性评价的主要方法是在工程地质定性分析的基础上，结合数学和统计学方法而发展起来的一种综合评价方法^[2].Lee和Min ^[3]基于GIS平台，利用逻辑回归模型对韩国Yongin地区的滑坡灾害进行了易发性评价.Yesilnacar和Topal ^[4]对土耳其Hendek地区的滑坡进行了易发性分区，并对比分析了神经网络模型与逻辑回归模型的评价结果.李倩^[5]采用可拓学模型对贵州省规划铁路网滑坡进行了危险性评估.王佳佳等^[6]采用信息量模型，以GIS为技术手段，对三峡库区范围内部分滑坡开展了易发性评价.范强等^[7]采用证据权法对贵州桐梓河流域的滑坡进行了易发性评价，并采用成功率曲线对评价结果进行了验证.Hadmoko等^[8]分别采用半定量和统计方法对印度尼西亚Kayangan流域的滑坡进行了易发性评价，评价结果表明统计方法比半定量法具有更高的准确率.总而言之，上述研究均是将数学方法有效地运用于滑坡灾害易发性评价中，但鲜有考虑影响滑坡易发性因素的模糊性、非线性和不确定性.上述特性使得影响因素的具体数值不易确定，即影响滑坡易发性的因素具有区间数的特点.最近发展起来的区间数和集对分析理论可为解决滑坡易发性这一不确定问题提供新的研究方法.
本文首先应用区间数表征滑坡易发性评价因子，进而采用集对分析理论研究各因子内在的确定和不确定性，尝试从新的视角下解决复杂地质环境下滑坡灾害易发性评价问题，极大程度地减轻由于人为主观性对评价过程造成的影响，力争使评价结果能够客观有效地呈现出自然界事物的本质，最终为防灾减灾提供科学依据.
1 评价方法与理论1.1 区间数理论在自然界中，不确定性事物的属性通常是在一定范围内改变的；如果用一个确定的数值来表示的话，并不能合理地反映事物属性的变化.因此，本文尝试采用二元区间数来表示研究对象的某个属性.具体定义如下^[9]：
令R为实数集，对任意的x^-∈ R和x⁺∈ R，且x^-≤x⁺，则称[X]=[x^-, x⁺]为二元区间数.其中，x^-和x⁺分别是区间数[X]的下、上极限.如果x^->0，那么[X]为正二元区间数；如果x⁺ < 0，那么[X]为负二元区间数；如果x^- < 0且x⁺>0，那么[X]为异二元区间数；如果x^-=x⁺，那么区间数[X]退化为普通实数X.二元区间数的期望E([X])定义如下：

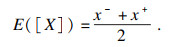(1)

目前，区间数的研究正处于起步阶段，对于区间数之间的联系与对比问题尚未得到很好的解决.本文试图将集对分析理论与区间数相结合，用以分析区间数之间的动态变化关系.
1.2 集对分析理论从唯物辩证角度分析，自然界事物都具有“确定性”和“不确定性”的两面特性，且两面性质之间可以相互影响、相互转化.近年来发展起来的集对分析理论是由我国****赵克勤提出的，重点用于事物确定性与不确定性之间相互作用的分析^[10].如果两个集合具有一定的联系，那么它们可构成一个集对，由集合X和Y构成的集对可以表示为.上述两个集合的同异反关系可以用联系度μ_{(X, Y)}表示，具体公式如下：

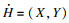
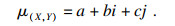(2)

式中：i∈[-1, 1]，表示差异度系数；j=-1，表示对立度系数；a，b，c分别为样本评价指标与滑坡灾害易发性等级之间的同一度、差异度和对立度，且a+b+c=1.
对不确定事物评价时，可用区间数[X_mn] = [x_mn^-, x_mn⁺]表示样本m的第n个评价指标，并根据式(1)计算其期望为E([X_mn]).同理，也可用区间数[Y_{n, k}]=[y_{n, k}^-, y_{n, k}⁺]表示第n个指标第k个等级的分级标准，其期望为E([Y_{n, k}]).实测数据[X_mn]与等级区间[Y_{n, k}]的同异反评判准则为：若x_mn^->y_{n, k}^-且x_mn⁺ < y_{n, k}⁺时，则样本[X_mn]与等级[Y_{n, k}]为同一性关系；若x_mn^->y_{n, k}⁺或x_mn⁺ < y_{n, k}^-时，则样本[X_mn]与等级[Y_{n, k}]为对立性关系；除此之外，样本[Y_{n, k}]与等级[Y_{n, k}]为差异性关系，具体关系如图 1所示.
图 1(Fig. 1)

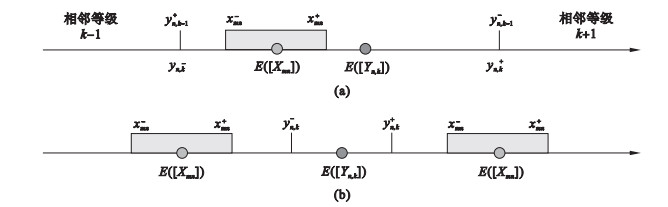图 1 联系期望的关系示意图Fig.1 Schematic diagram of relationship between connectional expectation (a)—联系期望同一关系；(b)—联系期望对立关系.

样本的评价指标分为两类：效益型指标是指数值随等级增加而增大的指标，而成本型指标则反之.以集对分析理论为基础，分别建立了对应于效益型指标的联系期望的计算公式(3)和成本型指标的联系期望的计算公式(4)^[11].

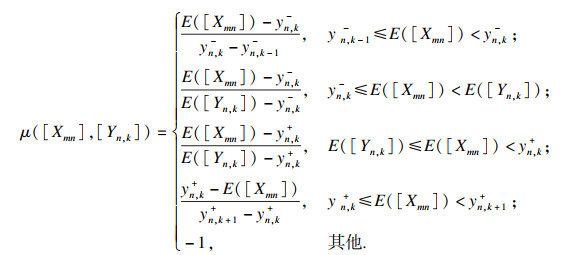(3)

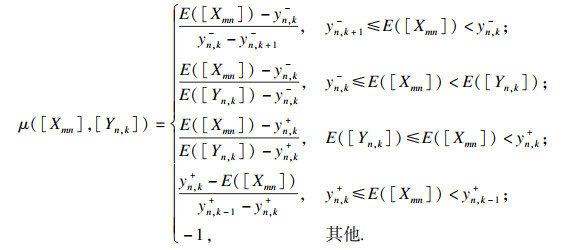(4)

μ([X_mn], [Y_{n, k}])为第m个样本的第n个指标关于评价等级k的联系期望.对于第n个指标取权重系数W_n，则样本m关于等级k的集成联系期望为

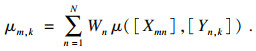(5)

如果

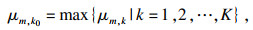(6)

则此样本的评价等级为k₀.
2 研究区概况与影响因素乌东德水电站坐落于我国长江上游的金沙江河段上，大坝高265 m，正常蓄水位975 m，库尾至攀枝花地区，控制流域面积40.61×10⁴ km².库区内构造侵蚀作用严重，沟壑切割深度达600~2 000 m，属中山地貌，地势变化如图 2所示.库区内地层具有双层结构的特征，包含有盖层和基底.库区地处青藏高原的东缘，新生代活动强烈，主要受川滇南北构造带影响.
图 2(Fig. 2)

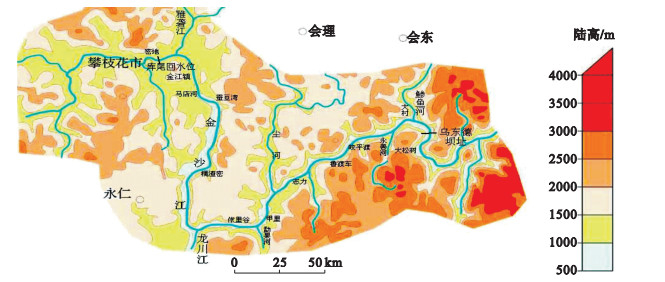图 2 乌东德库区地势概略图Fig.2 The landform map of Wudongde reservoir area

现场调查发现，乌东德水电站库区内发育有大量的滑坡和潜在滑坡.因此，结合工程实际需求，需要对库岸分段进行滑坡灾害易发性评价.本文以地形地貌、地层岩性、地质构造等为依据，将库区岸坡划分为5个大段19个亚段，左右岸共计38个库岸段，每个库岸段将作为一个评价样本，对每个库岸段滑坡易发性进行研究.
在对各库岸段滑坡灾害易发性评价时，为使评价结果准确、合理，应全面、科学地选取其影响因子.本文参照国内外****经常采用的因子^{[1, 3, 6]}，通过对库岸段内滑坡和潜在滑坡的全面考虑，从滑坡发育特征、岸坡结构与岩性特征、地质构造与地形地貌特征、灾害诱发因素四个方面为基本点，选取了较为普遍的14个评价指标.
1) 滑坡发育特征B1：库岸滑坡的发育特征对库岸的稳定性起着决定性作用，滑坡灾害发育越频繁，库岸稳定性越差.库岸滑坡发育特征主要包括：滑坡段与岸段长度比(n₁)、滑坡个数(n₂)、滑坡体体积(n₃).
2) 岸坡结构与岩性特征B2：坡体结构是指坡体内原有的控制性结构面与临空面的组合关系，主要由坡面倾向、岩层倾向、岩体结构等几个方面组成.地层岩性是组成岸坡的物质基础，是控制岸坡稳定性的主要因素，岩性、岩层厚薄和风化程度直接影响岸坡物质的力学性质.因此，岸坡结构与岩性特征主要包括：坡体结构(n₄)、风化程度(n₅)、岩体结构(n₆)、岩性组合(n₇)、岩层厚度(n₈).
3) 地质构造与地形地貌特征B3：地质构造严重影响岸坡的稳定性，断层既可降低坡体完整性，又是关键的渗流路径，对岸坡的稳定性极其不利.另外，地形地貌对滑坡规模、滑坡成因都将产生影响.因此，地质构造与地形地貌特征主要包括：与断层的距离(n₉)、坡度(n₁₀)、起伏度(n₁₁)、植被覆盖率(n₁₂).
4) 灾害诱发因素B4：地震、降雨和冰雪融化等是地质灾害常见的诱发因素，而本研究区内无降雪，故灾害诱发因素主要考虑：库区最大地震烈度(n₁₃)、日最大降雨量(n₁₄).
本文是在大量野外地质调查的基础上完成的.其中，滑坡个数(n₂)、滑坡体体积(n₃)、坡体结构(n₄)、风化程度(n₅)、岩体结构(n₆)、岩性组合(n₇)、岩层厚度(n₈)、植被覆盖率(n₁₂)是通过现场调查获取的；滑坡段与岸段长度比(n₁)、与断层的距离(n₉)、坡度(n₁₀)、起伏度(n₁₁)是通过航片解译结合现场调查获取的；库区最大地震烈度(n₁₃)、日最大降雨量(n₁₄)是通过资料搜集获取的.
3 滑坡易发性评价模型3.1 确定评价等级标准库岸滑坡灾害易发性划分等级，虽未形成统一标准，但通常将其划分为4个等级：不易发(Ⅰ)、轻度易发(Ⅱ)、中度易发(Ⅲ)、重度易发(Ⅳ).本文根据现场实际调查情况，并参照国内外评价标准^{[1, 12-13]}，综合确定了各指标的分级标准，具体量化值见表 1.
表 1(Table 1)

表 1 库岸滑坡灾害易发性分级标准Table 1 Classification standard of landslide susceptibility degree on the reservoir area 目标层A 准则层B 方案层N 易发性等级 不易发(Ⅰ) 轻度易发(Ⅱ) 中度易发(Ⅲ) 重度易发(Ⅳ) 库岸滑坡灾害易发性评价 滑坡发育特征B1 滑坡段与岸段长度比n1/ % 0~5 5~20 20~40 40~100 滑坡个数n2 0~1 1~2 2~4 4~40 滑坡体体积n3×10-5/m3 0~5 5~20 20~400 400~4 000 岸坡结构与岩性特征B2 坡体结构n4 逆向坡(0~1) 横向坡(1~2) 斜向坡(2~3) 顺向坡(3~4) 风化程度n5 微风化(0~1) 弱风化(1~2) 强风化(2~3) 全风化(3~4) 岩体结构n6 整体状(0~1) 块状(1~2) 层状(2~3) 碎裂、散体状(3~4) 岩性组合n7 硬岩(0~1) 硬岩夹软岩(1~2) 软岩夹硬岩(2~3) 软岩、松散体(3~4) 岩层厚度n8 巨厚层(0~1) 厚层(1~2) 中厚层(2~3) 薄层(3~4) 地质构造与地形地貌特征B3 与断层的距离n9/m 500~10 000 100~500 10~100 0~10 坡度n10 /(°) 0~20 20~30 30~40 40~90 起伏度n11/m 0~20 20~40 40~60 60~150 植被覆盖率n12/% 75~100 50~75 25~50 0~25 灾害诱发因素B4 库区最大地震烈度n13 0~3 3~5 5~7 7~12 日最大降雨量n14/mm 0~50 50~100 100~150 150~1 000 注：第4~7列括号中的数值表示将定性指标进行定量化的区间数，这个区间数并没有实际的含义，仅表示一个事物的属性.

表 1 库岸滑坡灾害易发性分级标准 Table 1 Classification standard of landslide susceptibility degree on the reservoir area

3.2 确定权重系数美国****Saaty提出的层次分析法是一种将决策问题看作是一个受多因素影响的多目标决策方法.该方法根据各因素的隶属关系形成递阶层次结构(目标层、准则层、方案层)，且在每层中构造比较判断矩阵J^[14-15].通过计算判断矩阵的特征值，得到每一层的各因素对上一层因素的优先权重，最终采用递阶合并的方法得到方案层各因素对目标层的权重.
同一层中各因素的重要性，可用比较判断矩阵来表示，该矩阵通常由数字1~9及其倒数构成.在构建判断矩阵时，各因素的重要性是通过邀请多位相关领域的专家采用打分方式综合考虑确定的.建立一级指标的判断矩阵J_B如下：
根据矩阵理论，求得判断矩阵的最大特征值λ_max=4.078 7，将其对应的特征向量归一化，得到一级指标的权向量W_B=[0.413 4, 0.328 8, 0.176 7, 0.081 1].为了确定合理的权重，应检验判断矩阵的一致性.一致性比率C_RB=0.029 2 < 0.1，满足检验结果.
同理，分别对二级指标建立判断矩阵J_N^B1, J_N^B2, J_N^B3, J_N^B4，计算权向量并检验一致性，结果如下：
计算方案层对目标层的组合权向量W_N=[0.204 0, 0.128 5, 0.081 0, 0.111 2, 0.084 3, 0.058 9, 0.047 3, 0.027 2, 0.078 7, 0.050 3, 0.029 0, 0.018 6, 0.054 1, 0.027 0]，因此，对整个递阶层次结构的一致性检验：
满足检验结果.
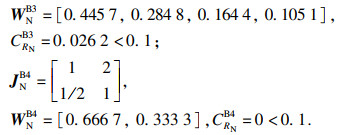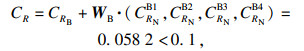3.3 确定评价样本等级第一，确定评价样本和评价标准中各指标的区间数期望，通过式(1)计算.第二，建立评价样本指标与评价标准间的集对，基于联系期望的同异反准则计算各指标的联系期望.在计算联系期望时，与断层的距离(n₉)和植被覆盖率(n₁₂)作为成本型指标，通过式(4)计算；其余指标通过式(3)计算.第三，综合权重值W_N，确定各评价样本关于评价等级k的集成联系期望，通过式(5)计算.第四，确定各评价样本的易发性等级，通过式(6)计算.结果见表 2.根据本文评价结果绘制的库岩滑坡易发性分段图如图 3所示.
表 2(Table 2)

表 2 库岸滑坡灾害易发性评价结果Table 2 Evaluation result of landslide susceptibility degree on the reservoir area 左岸 μm, 1 μm, 2 μm, 3 μm, 4 本文结果 现场调查结果 右岸 μm, 1 μm, 2 μm, 3 μm, 4 本文结果 现场调查结果 ZⅤ2 -0.270 3 -0.362 0 -0.663 7 -0.787 7 Ⅰ Ⅰ YⅤ2 -0.168 3 -0.289 0 -0.714 9 -0.885 4 Ⅰ Ⅰ ZⅤ1 -0.260 8 -0.136 6 -0.469 7 -0.746 2 Ⅱ Ⅱ YⅤ1 -0.317 9 -0.471 1 -0.529 9 -0.757 2 Ⅰ Ⅰ ZⅣ3 -0.703 9 -0.183 9 -0.377 8 -0.166 8 Ⅳ Ⅳ YⅣ3 -0.520 3 -0.817 3 -0.476 2 -0.345 0 Ⅳ Ⅳ ZⅣ2 -0.351 3 -0.332 6 -0.560 7 -0.812 6 Ⅱ Ⅰ YⅣ2 -0.344 0 -0.323 0 -0.556 2 -0.815 1 Ⅱ Ⅰ ZⅣ1 -0.405 9 -0.249 9 -0.113 7 -0.690 1 Ⅲ Ⅲ YⅣ1 -0.524 5 -0.180 3 -0.218 2 -0.603 1 Ⅱ Ⅱ ZⅢ3 -0.293 1 -0.328 8 -0.602 0 -0.836 9 Ⅰ Ⅰ YⅢ3 -0.493 0 0.161 3 -0.364 7 -0.879 4 Ⅱ Ⅱ ZⅢ2 -0.162 5 -0.047 6 -0.461 6 -0.816 2 Ⅱ Ⅱ YⅢ2 -0.390 4 -0.133 7 -0.182 3 -0.746 3 Ⅱ Ⅱ ZⅢ1 -0.230 0 -0.276 3 -0.608 6 -0.893 1 Ⅰ Ⅰ YⅢ1 -0.282 4 0.267 6 -0.593 7 -0.910 3 Ⅱ Ⅱ ZⅡ 6 -0.172 3 -0.206 3 -0.726 6 -0.910 1 Ⅰ Ⅰ YⅡ 6 -0.173 3 -0.557 9 -0.582 2 -0.788 3 Ⅰ Ⅰ ZⅡ 5 -0.127 7 -0.727 8 -0.557 8 -0.694 1 Ⅰ Ⅰ YⅡ 5 -0.260 7 -0.180 2 -0.686 4 -0.167 7 Ⅳ Ⅳ ZⅡ 4 -0.310 4 -0.544 9 -0.357 8 -0.391 7 Ⅰ Ⅰ YⅡ 4 -0.422 6 -0.691 1 -0.657 6 -0.494 7 Ⅰ Ⅰ ZⅡ 3 -0.844 6 -0.280 7 0.107 9 -0.517 1 Ⅲ Ⅲ YⅡ 3 -0.748 7 -0.130 8 -0.078 2 -0.602 6 Ⅲ Ⅱ ZⅡ 2 -0.566 4 -0.867 5 -0.585 0 -0.169 5 Ⅳ Ⅳ YⅡ 2 -0.562 1 -0.487 3 -0.232 3 -0.224 3 Ⅳ Ⅳ ZⅡ 1 -0.553 4 -0.399 9 -0.068 2 -0.526 0 Ⅲ Ⅲ YⅡ 1 -0.824 1 -0.420 7 -0.136 4 -0.134 6 Ⅳ Ⅳ ZⅠ 5 -0.630 6 -0.552 4 0.079 4 -0.387 4 Ⅲ Ⅲ YⅠ 5 -0.933 7 -0.802 4 -0.103 5 0.164 6 Ⅳ Ⅳ ZⅠ 4 -0.822 1 -0.670 5 -0.184 1 -0.004 5 Ⅳ Ⅳ YⅠ 4 -0.798 4 -0.207 9 0.061 6 -0.640 4 Ⅲ Ⅲ ZⅠ 3 -0.920 8 -0.543 5 -0.080 8 -0.126 5 Ⅲ Ⅲ YⅠ 3 -0.846 4 -0.120 0 -0.081 4 -0.517 0 Ⅲ Ⅱ ZⅠ 2 -0.458 4 -0.067 4 -0.213 4 -0.724 5 Ⅱ Ⅱ YⅠ 2 -0.894 5 -0.505 1 0.102 4 0.237 1 Ⅳ Ⅳ ZⅠ 1 -0.178 1 -0.668 7 -0.572 9 -0.704 9 Ⅰ Ⅰ YⅠ 1 -0.503 1 -0.278 1 -0.170 2 -0.617 2 Ⅲ Ⅲ 注：各库岸段编号中，Z表示位于金沙江左岸，Y表示位于金沙江右岸.

表 2 库岸滑坡灾害易发性评价结果 Table 2 Evaluation result of landslide susceptibility degree on the reservoir area

图 3(Fig. 3)

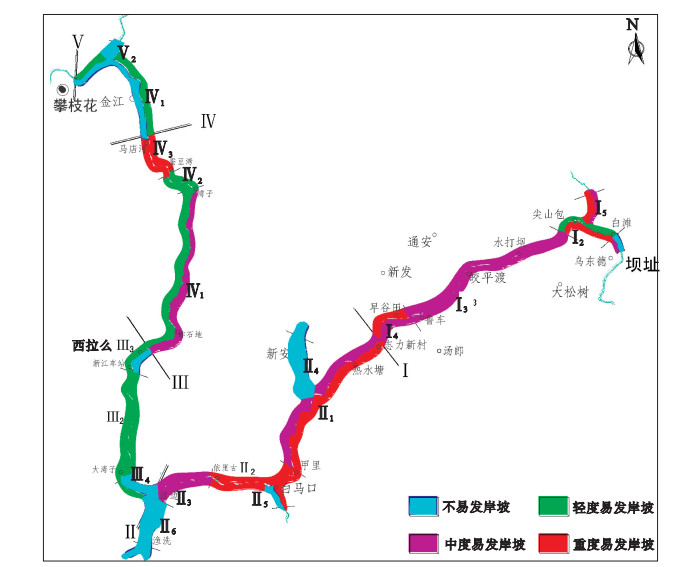图 3 库岸滑坡灾害易发性分段图Fig.3 Segmental diagram of landslide susceptibility degree on the reservoir area

现场调查时，会对每个库岸滑坡灾害易发性进行定性评价，此结果为现场定性调查结果；而本文中根据现场调查与搜集的影响因素，采用区间数与集对分析理论对库岸滑坡灾害易发性进行了定量评价.从表 2能够得出：本文评价结果与现场定性调查结果吻合度高，准确率可达89.5 %.在评价结果不吻合的4个库岸段中，本文评价等级均比现场定性调查等级高.究其原因，在现场调查时将无滑坡发育的库岸段划分为不易发岸坡.但是，在没有滑坡发育的库岸段中，由于岩体结构较破碎或到断层距离较近等因素而造成一些不稳定斜坡的存在，使得岸坡易发性较高，故本文结果偏于保守是符合实际的.
4 结语库岸滑坡灾害易发性评价是一个受滑坡发育特征、岸坡结构与岩性特征、地质构造与地形地貌特征、灾害诱发因素影响的不确定性问题，采用二元区间数来探究每个影响因子的动态变化规律，能够更好地揭示自然界事物发展的客观本质.
基于集对分析理论中联系度的概念，分析了评价样本与评价标准间的同异反关系，最终构建了库岸滑坡灾害易发性评价的新模型.通过对乌东德库岸滑坡的易发性分析可知，本文提出的区间数-集对分析方法，不仅评价结果准确可靠，而且可使不确定性问题的对比分析更简化.
参考文献

[1]	黄发明, 陈佳武, 唐志鹏, 等. 不同空间分辨率和训练测试集比例下的滑坡易发性预测不确定性[J]. 岩石力学与工程学报, 2021, 40(6): 1155-1169. (Huang Fa-ming, Chen Jia-wu, Tang Zhi-peng, et al. Uncertainties of landslide susceptibility prediction under different spatial resolutions and different proportions of training and testing datasets[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(6): 1155-1169.)
[2]	李雪平, 唐辉明. 基于GIS的分组数据Logistic模型在斜坡稳定性评价中的应用[J]. 吉林大学学报(地球科学版), 2005, 35(3): 361-365. (Li Xue-ping, Tang Hui-ming. Application of GIS based grouped data logistic model in evaluation of slope stability[J]. Journal of Jilin University (Earth Science Edition), 2005, 35(3): 361-365.)
[3]	Lee S, Min K. Statistical analysis of landslide susceptibility at Yongin, Korea[J]. Environmental Geology, 2001, 40(9): 1095-1113. DOI:10.1007/s002540100310
[4]	Yesilnacar E, Topal T. Landslide susceptibility mapping: a comparison of logistic regression and neural networks methods in a medium scale study, Hendek region(Turkey)[J]. Engineering Geology, 2005, 79(3/4): 251-266.
[5]	李倩. 贵州省规划铁路网滑坡危险性评估[J]. 中南大学学报(自然科学版), 2011, 42(10): 3170-3175. (Li Qian. Landslide risk assessment for planning railway network in Guizhou Province[J]. Journal of Central South University(Science and Technology), 2011, 42(10): 3170-3175.)
[6]	王佳佳, 殷坤龙, 肖莉丽. 基于GIS和信息量的滑坡灾害易发性评价——以三峡库区万州区为例[J]. 岩石力学与工程学报, 2014, 33(4): 797-808. (Wang Jia-jia, Yin Kun-long, Xiao Li-li. Landslide susceptibility assessment based on GIS and weighted information value: a case study of Wanzhou District, Three Gorges Reservoir[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(4): 797-808.)
[7]	范强, 巨能攀, 向喜琼, 等. 证据权法在滑坡易发性分区中的应用——以贵州桐梓河流域为例[J]. 灾害学, 2015, 30(1): 124-129. (Fan Qiang, Ju Neng-pan, Xiang Xi-qiong, et al. Application of weights of evidence method in landslide susceptibility zoning—a case study on Tongzi river basin in Guizhou[J]. Journal of Catastrophology, 2015, 30(1): 124-129.)
[8]	Hadmoko D S, Lavigne F, Samodra G. Application of a semiquantitative and GIS-based statistical model to landslide susceptibility zonation in Kayangan Catchment, Java, Indonesia[J]. Natural Hazards, 2017, 87: 437-468. DOI:10.1007/s11069-017-2772-z
[9]	胡启洲, 张卫华. 区间数理论的研究及其应用[M]. 北京: 科学出版社, 2010. (Hu Qi-zhou, Zhang Wei-hua. Research and application of interval number theory[M]. Beijing: Science Press, 2010.)
[10]	赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000. (Zhao Ke-qin. Set pair analysis and its preliminary application[M]. Hangzhou: Zhejiang Science and Technology Press, 2000.)
[11]	汪明武, 赵奎元, 张立彪. 基于联系期望的膨胀土和改良土胀缩性评价模型[J]. 岩土工程学报, 2014, 36(8): 1553-1557. (Wang Ming-wu, Zhao Kui-yuan, Zhang Li-biao. A novel evaluation model based on connectional expectation for swelling-shrinkage grade of untreated and treated expansive clay[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1553-1557.)
[12]	Varnes D J. Landslide hazard zonation: a review of principles and practice[M]. Paris: Unesco Press, 1984.
[13]	唐睿旋. 堆积层滑坡单体稳定性评估及区域易发性评价研究[D]. 武汉: 中国地质大学, 2017. (Tang Rui-xuan. Research on stability evaluation of individual colluvial landslides and regional landslide susceptibility analysis[D]. Wuhan: China University of Geosciences, 2017. )
[14]	张紫杉, 王述红, 王斐笠. 基于空间块体表征的岩质边坡稳定性综合评价[J]. 东北大学学报(自然科学版), 2018, 39(6): 896-901. (Zhang Zi-shan, Wang Shu-hong, Wang Fei-li. Comprehensive assessment of rock slope stability based on spatial block identification[J]. Journal of Northeastern University(Natural Science), 2018, 39(6): 896-901.)
[15]	余云燕, 陈仁朋, 陈云敏, 等. 一种基于模糊数学的桩基质量综合评定方法[J]. 中国公路学报, 2002, 15(2): 68-71. (Yu Yun-yan, Chen Ren-peng, Chen Yun-min, et al. Research on fuzzy comprehensive evaluation method of pile foundation[J]. China Journal of Highway and Transport, 2002, 15(2): 68-71.)