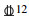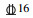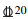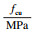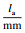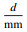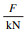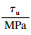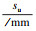张玉, 刘伯权, 吴涛, 陈旭
长安大学 建筑工程学院，陕西 西安 710061
收稿日期：2021-03-22
基金项目：国家自然科学基金资助项目(51878054);陕西省重点研发计划项目(2020GY-248)。
作者简介：张玉(1988-)，女，山东泰安人，长安大学博士研究生;
刘伯权(1956-)，男，甘肃定西人，长安大学教授，博士生导师;
吴涛(1976-)，男，安徽霍山人，长安大学教授，博士生导师。

摘要：研究变形钢筋与轻骨料混凝土间的黏结-滑移性能，完成了9组中心拉拔试验，分析了轻骨料混凝土强度、锚固长度、粗骨料类型及钢筋的直径对黏结应力的影响.结合试验结果，采用厚壁模型，给出了轻骨料混凝土黏结强度的解析解，并建立了钢筋与轻骨料混凝土间的黏结应力-滑移曲线本构模型.结果表明：轻骨料混凝土的黏结-滑移性能主要受砂浆强度影响，使得该类混凝土与变形钢筋间的黏结应力优于普通混凝土；黏结强度随着轻骨料混凝土的强度提高而增加，随着黏结长度的降低而增加；本文提出的本构模型能够较为准确地预测试验曲线.
关键词：轻骨料混凝土拉拔试验黏结强度黏结-滑移本构模型厚壁圆筒模型
Bond-Slip Behavior Between Reinforcement Bars and High-Strength Lightweight Aggregate Concrete
ZHANG Yu, LIU Bo-quan, WU Tao, CHEN Xu
School of Civil Engineering, Chang'an University, Xi'an 710061, China
Corresponding author: ZHANG Yu, E-mail: zhangyu88521@163.com.

Abstract: Nine groups of pull-out tests on the bond-slip behavior between reinforcement bars and lightweight aggregate concrete were completed.The effect of lightweight aggregate concrete strength, anchorage length, coarse aggregate type and bar diameter on bond strength was analyzed. Combined with the test results, the analytical solution of bond strength of lightweight aggregate concrete was given by using thick wall model, and a constitutive model between reinforcement and lightweight aggregate concrete was established.Test results indicate that the bond-slip behavior of the lightweight aggregate concrete is mainly affected by the mortar strength, making the bond stress between the concrete and reinforcement bars better than that between normal weight concrete and reinforcement bars. The bond strength increases with the increase of strength of lightweight aggregate concrete and with the decrease of anchorage length. The proposed bond stress-slip constitutive model shows good precision to predict test curves.
Key words: lightweight aggregate concretepull-out testbond strengthbond-slip constitutive modelthick-wall cylinder model
轻骨料混凝土具有轻质高强、环保节能等优势，已被广泛应用于建筑工程中；但轻质多孔的轻骨料在降低混凝土密度的同时，改变了材料内部结构，导致轻骨料混凝土与普通混凝土力学性能存在差异.部分研究指出，轻骨料强度低、脆性较大，不利于与钢筋间的机械咬合作用，轻骨料混凝土试件的黏结强度劣于普通混凝土^[1-3]；但在相同或相近强度下，轻骨料混凝土配合比中的水胶比更低，有利于砂浆基质强度提升，对化学胶结力和机械咬合力起到正面作用^[4].Martin^[5]在研究中发现，轻骨料混凝土和普通混凝土的黏结强度差异不显著.Chen等^[6]和李渝军等^[7]通过拉拔试验发现高强轻骨料混凝土试件的黏结强度优于同等条件下的普通混凝土.此外，低强度的轻骨料(而非界面过渡区)被视为材料内部的最弱相^[8]，导致裂缝会直接穿过骨料形成，而这种更为直接的开裂行为使得轻骨料混凝土具有更好的均质性.已有研究指出，与黏结长度相等的普通混凝土相比，轻骨料混凝土内部的黏结应力分布更均匀^[9].
国内外****就黏结-滑移理论模型展开了大量研究，多采用分段函数描述黏结应力-滑移曲线的各个阶段^[10-14].各模型曲线形状较为相似，但对黏结强度、特征滑移量等特征值的计算存在差异.现行欧洲规范^[10-11]定义了一个极限黏结滑移量常数；国内规范^[12]认为极限黏结强度只与混凝土抗拉强度有关，滑移量只与钢筋特征存在线性关系.对于轻骨料混凝土来说，普通混凝土的各特征值只能作为参考，需进一步研究提出适用于轻骨料混凝土的黏结-滑移计算模型.
基于此，采用页岩陶粒配制了4种强度等级的轻骨料混凝土，强度按照从小到大的顺序依次记为A，B，C，D.通过中心拉拔试验研究了不同因素对轻骨料混凝土与变形钢筋的黏结-滑移性能的影响.基于厚壁圆筒模型推导了黏结强度计算公式，建立了适用于轻骨料混凝土的黏结-滑移本构模型.
1 试验概况1.1 原材料采用碎石型页岩陶粒、渭河中砂和P.O 42.5水泥制备轻骨料混凝土，基本力学指标见表 1.配合比中掺入粉煤灰、硅灰及聚羧酸高效减水剂.拉拔试件中心埋设变形钢筋，其基本力学指标见表 2.
表 1(Table 1)

表 1 骨料性能Table 1 Aggregate properties 粗骨料 细骨料(中砂) 堆积密度/(kg·m-3) 860 细度模数 2.56 表观密度/(kg·m-3) 1 512 堆积密度/(kg·m-3) 1 510 孔隙率/% 43.12 表观密度/(kg·m-3) 2 620 吸水率(1 h)/% 2.20 含泥量/% 43.12 吸水率(24 h)/% 2.60 含水率/% 2.20 筒压强度/MPa 6.90 最大粒径/mm 2.60 粒径/mm 5~16

表 1 骨料性能 Table 1 Aggregate properties

表 2(Table 2)

表 2 钢筋力学指标Table 2 Mechanical indexes of reinforcement bars 指标 实测直径/mm 12.17 16.61 20.81 屈服强度/MPa 471 431 463 极限强度/MPa 628 577 569 弹性模量/GPa 195 195 194

表 2 钢筋力学指标 Table 2 Mechanical indexes of reinforcement bars

1.2 配合比设计轻骨料混凝土配合比中水泥用量较大，为保证混凝土流动性，加入一定量的高效减水剂^[15].同时设计普通混凝土配合比用于对照，各配合比见表 3.
表 3(Table 3)

表 3 配合比参数Table 3 Mix proportion parameters 配料 LC30 LC40 LC50 LC60 C50 水泥 320 360 400 440 360 粉煤灰 80 90 100 66 90 硅灰 — — — 44 — 骨料/(kg·m-3) 603 606 616 607 1 010 减水剂/(kg·m-3) 0.8 2.6 4.3 5.5 2.6 砂率/% 40 40 40 40 40 水胶比 0.5 0.4 0.3 0.26 0.4

表 3 配合比参数 Table 3 Mix proportion parameters

1.3 试件设计结合国内规范^[15-16]和试验研究需求，拉拔试件长、宽、高均为200 mm的正方体，内部无横向约束.为防止试件发生劈裂破坏，将相对保护层厚度设置为c/d≥4.5，见图 1.图中，d和l_a分别代表钢筋的直径和锚固长度，c表示混凝土的保护层厚度，钢筋两端伸出试件作为自由端和加载端.采用PVC管预留无黏结段.各组试件预留标准立方体试块用于材性测试.依据研究目的将本试验拉拔试件设计为9组，试件参数见表 4，其中(以A16-80为例)，A表示轻骨料混凝土强度等级，16表示钢筋直径d为16 mm，80表示锚固长度l_a为80 mm；此外，E表示普通混凝土.
图 1(Fig. 1)

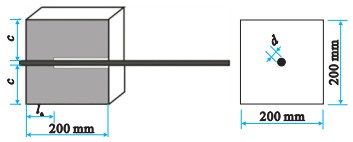图 1 试件尺寸Fig.1 The size of specimen

表 4(Table 4)

表 4 试件参数Table 4 Specimen parameters 试件类型 混凝土强度等级 la/mm d/mm 数量 A16-80 LC30 80 16 3 B16-80 LC40 80 16 3 C16-80 LC50 80 16 3 D16-80 LC60 80 16 3 D16-120 LC60 120 16 3 D16-50 LC60 50 16 3 D12-50 LC60 50 12 3 D20-50 LC60 50 20 3 E16-80 C50 80 16 3

表 4 试件参数 Table 4 Specimen parameters

1.4 加载量测方案加载装置如图 2所示，采用1 000 kN万能试验机进行加载，分别测量加载端和自由端位移用于计算相对滑移.根据峰值荷载和式(1)，可计算出各组试件的黏结应力值：

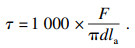(1)

图 2(Fig. 2)

图 2 试验装置Fig.2 Test setup

式中：τ为黏结应力；F为荷载峰值.
2 试验结果及分析2.1 破坏过程与破坏特征根据加载过程中的观测，将轻骨料混凝土黏结滑移破坏分为三类：拔出破坏、屈服后拔出、拉断破坏，分别对应试件破坏时的钢筋状态，其中钢筋拉断破坏表示试件未达到黏结强度即发生破坏.表 5给出各拉拔试件破坏模式.
表 5(Table 5)

表 5 试验值和试件破坏模式Table 5 Test data and failure mode of specimens 试件类型 破坏模式 A16-80-1 A16-80-2 A16-80-3 39.4 79 76 80 16 16 16 65.56 64.16 69.35 16.52 16.80 17.25 2.06 2.18 2.33 P P P B16-80-1 B16-80-2 B16-80-3 48.7 80 80 77 16 16 16 91.80 89.99 83.88 22.84 22.39 21.69 1.86 2.09 1.35 Y Y Y C16-80-1 C16-80-2 C16-80-3 62.7 75 80 80 16 16 16 87.06 95.73 93.35 23.11 23.82 23.23 1.22 1.23 1.08 Y Y Y D16-80-1 D16-80-2 D16-80-3 83.2 75 78 75 16 16 16 108.00 115.78 112.29 28.66 29.55 29.80 1.90 — 2.12 Y Y Y D16-120-1 D16-120-2 D16-120-3 83.2 120 120 120 16 16 16 125.72 124.43 123.35 — — — — — — R R R D16-50-1 D16-50-2 D16-50-3 83.2 45 50 50 16 16 16 72.91 78.97 76.65 32.23 31.42 30.50 1.19 0.48 2.01 P P P D12-50-1 D12-50-2 D12-50-3 83.2 50 49 48 12 12 12 47.65 47.92 45.99 25.28 25.94 25.42 1.80 1.58 0.77 Y Y Y D20-50-1 D20-50-2 D20-50-3 83.2 50 50 50 20 20 20 94.60 82.86 99.91 30.11 26.38 31.80 2.17 0.85 0.48 P P P E16-80-1 E16-80-2 E16-80-3 57.2 80 80 74 16 16 16 86.96 91.57 79.11 21.63 22.77 21.27 1.43 1.15 1.67 Y Y P ??注：P，Y，R分别表示钢筋拔出、屈服后拔出、拉断；fcu为混凝土立方体抗压强度；τu为极限黏结应力；su为极限黏结应力τu对应的滑移量.

表 5 试验值和试件破坏模式 Table 5 Test data and failure mode of specimens

2.2 黏结-滑移曲线锚固段平均滑移量s_L采用式(2)计算：

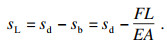(2)

式中：s_L为滑移值；s_d为位移计的测定量；s_b为钢筋的拉伸值；F为荷载峰值；L为黏结的起点到夹具的起点总长；E为钢筋的弹性模量；A为钢筋的截面积.由式(1)和式(2)计算得到的黏结应力τ与钢筋滑移量s，可绘制出各组试件τ-s曲线图，见图 3.
图 3(Fig. 3)

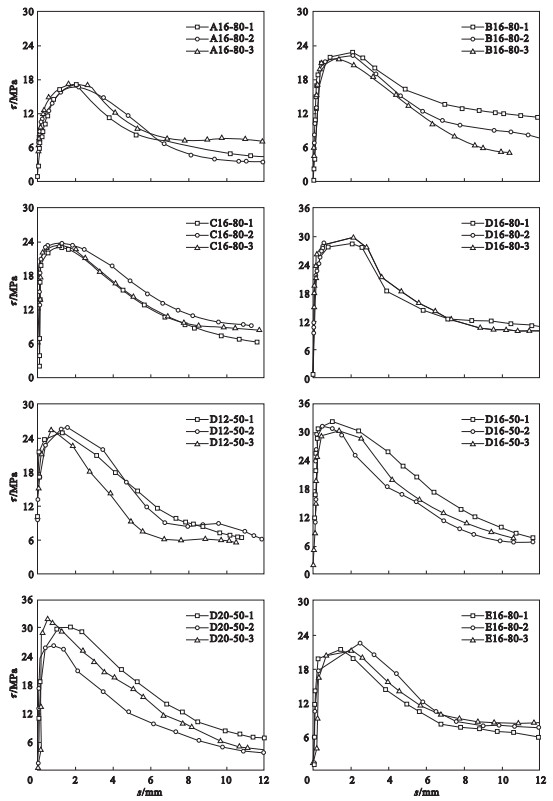图 3 黏结应力-滑移曲线Fig.3 Bond stress-slip curves

以D20-50-1~ D20-50-3试件为例，试验曲线可分为微滑移段、上升段、下降段和残余段：
1) 微滑移段：由τ-s曲线可见，加载之初，未出现滑移现象，此时化学胶结作用起主导作用.
2) 上升段：黏结区域的化学胶结作用随着荷载的不断提高而慢慢消失，肋前混凝土受到挤压，其周围混凝土产生内裂缝，加载端和自由端均出现滑移，此时黏结力以摩阻力和机械咬合力为主；τ-s曲线呈现弯曲上升，直到峰值τ_u.
3) 下降段：达到荷载峰值后包裹在肋周围的混凝土在滑移量增大的同时慢慢被挤碎，咬合作用慢慢丧失，曲线处于下降状态.
4) 残余段：此时肋周围混凝土对钢筋约束作用基本消失，以摩擦力为主的黏结力基本不再变化.
3 黏结性能影响因素分析3.1 轻骨料混凝土强度轻骨料混凝土强度对极限黏结强度的影响如图 4a所示.从图中可知，在其他影响因素相同的前提下，在一定范围内，混凝土强度的提高显著增加了轻骨料混凝土试件的极限黏结强度，B16-80，C16-80与D16-80分别比A16-80提高了32.3 %，38.7 %，74.0 %，这是因为钢筋与混凝土间的化学胶结力和机械咬合作用会随着轻骨料混凝土强度的增大而增大.
图 4(Fig. 4)

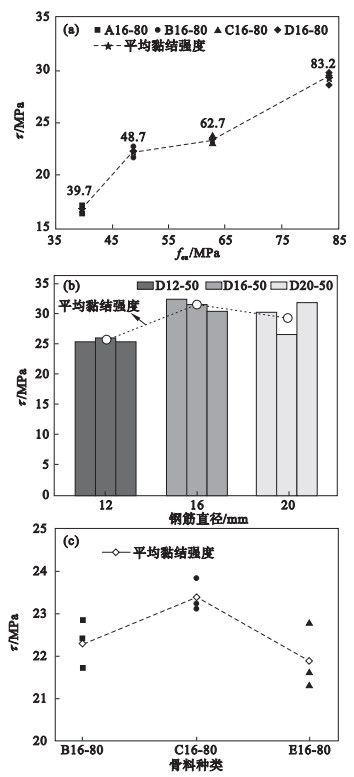图 4 影响因素对黏结强度的影响Fig.4 Effect of influencing factors on bond strength

3.2 钢筋直径钢筋直径对黏结强度的影响如图 4b所示.已有研究表明^{[7, 17]}，钢筋直径会对黏结滑移性能产生影响，极限黏结强度会随着钢筋直径的减小而提高.由图 4b可见，随着钢筋直径的减小，轻骨料混凝土与钢筋间的极限黏结强度呈现先增大后降低趋势，这说明虽然钢筋肋高和肋间距均随着钢筋直径的增大而增大，但对其周围混凝土的挤压已经不再是单一的影响因素，需要同时结合保护层厚度考虑其对极限黏结强度的影响.
3.3 锚固长度由于锚固长度为120 mm的试件均未获得黏结应力峰值，因此以D16-50和D16-80试件为例进行对比.由表 6可看出：锚固长度对其黏结滑移性能影响显著，中等锚固长度的平均黏结应力比短黏结试件降低了约7 %，黏结应力与锚固长度之间存在线性下降关系.这是由于黏结区域越长，钢筋与混凝土界面黏结力非线性越强，导致其平均黏结强度越低.
表 6(Table 6)

表 6 极限黏结应力理论值Table 6 Theoretical values of ultimate bond stress 编号 θ/(°) μ τu, p/MPa τu, t/MPa Δ=τu, p/τu, t A16-80 20 0.25 18.43 16.85 1.09 B16-80 20 0.25 20.92 22.30 0.94 C16-80 20 0.25 24.34 23.38 1.04 D16-80 20 0.25 28.51 29.34 0.97 D16-50 20 0.25 28.51 31.4 0.91 D12-50 15 0.20 28.03 25.54 1.09 D20-50 25 0.30 29.79 29.43 1.01 ??注：τu, p表示极限黏结应力理论值；τu, t表示极限黏结应力试验值.

表 6 极限黏结应力理论值 Table 6 Theoretical values of ultimate bond stress

3.4 骨料种类从图 4c试件C16-80和E16-80对比结果可知：在混凝土强度相同的前提下，轻骨料混凝土试件的平均黏结强度比普通混凝土试件提高了约7 %.这是因为相近强度下轻骨料混凝土试件水胶比更低，砂浆基质强度更高，水泥砂浆在凝结硬化过程中产生的干缩变形会相对减小，内裂缝不易出现，且水泥石与碎石型陶粒间有着牢固的黏结^[18].
4 黏结-滑移本构模型4.1 轻骨料混凝土与钢筋的黏结应力τ_u4.1.1 混凝土开裂模型Hillerborg等^[19]提出了一种虚拟裂缝模型来描述混凝土的拉应力与裂缝宽度之间的软化曲线，其曲线和坐标轴所包围的区域面积为断裂能G_F.
软化本构曲线可表示为

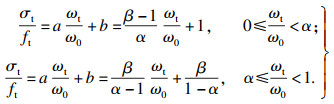(3)

式中：ω_t为裂缝宽度，mm；σ_t为混凝土裂缝间的内聚力，MPa；f_t为混凝土劈裂抗拉强度，MPa；ω₀为黏结力等于零时对应的裂缝宽度，mm.结合式(3)和图 5，根据文献[20]可确定α，β，a，b取值分别为0.222，0.667，-1.5，1.
图 5(Fig. 5)

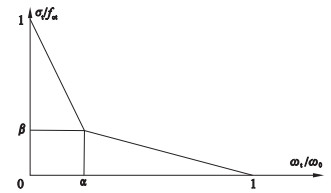图 5 双线性软化本构曲线Fig.5 Bilinear softening constitutive curve

本试验根据欧洲规范^[10]中G_F的定义来获得轻骨料混凝土的断裂能.本试验中轻骨料混凝土试件的G_F在70~135 N/mm之间，考虑到欧洲规范^[10]给出的结果普遍较低，因此，为简化后续讨论，所有轻骨料混凝土试件的G_F取值为95 N/mm.根据式(4)可得裂缝宽度ω₀的近似值为0.1 mm.

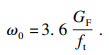(4)

4.1.2 物理模型Thanyawat等^[21-22]和Gao等^[23]通过引入厚壁圆筒模型推导出混凝土与钢筋间黏结应力-滑移关系的分析方法，见图 6.为得到适用于轻骨料混凝土极限黏结应力τ_u的计算方法，本文对τ_u的推导过程进行了简要分析.
图 6(Fig. 6)

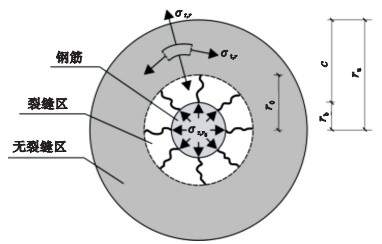图 6 厚壁圆筒模型Fig.6 Thick wall cylinder model

图 6中σ_{r, rs}是由混凝土与钢筋之间相互作用力和摩擦力共同作用产生的.根据弹性力学理论^[24]可得到径向应力σ_{r, r}的表达式为

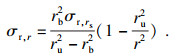(5)

式中：r_b，r_u分别为筒体的内半径和外半径.
基于力平衡原理，钢筋表面无裂缝区引起的径向应力σ_{r, rs}^LE可表示为

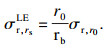(6)

式中：r₀为开裂区的半径；σ_{r, r0}为开裂与未开裂混凝土界面处的径向应力，可表示为^[22]

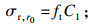(7)

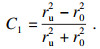(8)

同时，沿径向轴线的裂缝间的混凝土径向应力σ_{r, rs}^NL可表示为^[22]

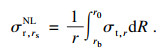(9)

式中σ_{t, r}为裂缝传递的环向拉应力.
将裂缝间的混凝土弹性变形2πrε_{t, r}(ε_{t, r}为半径r处环向拉应变)与裂缝宽度nω_{t, r}(n为混凝土中裂缝的数量)相加，可得到半径r处混凝土的总环向伸长量Δ_{t, r}.假定混凝土在不同半径处的环向变形相等，则环向拉应力可表示为^[23]

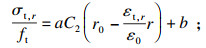(10)

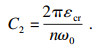(11)

式中：ε_cr为开裂和未开裂混凝土界面处的径向应变.
根据式(9)~式(11)可得到沿径向轴线的裂缝间的混凝土径向应力σ_{r, rs}^NL的具体表达式：

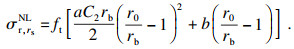(12)

根据式(5)和式(12)可得到与极限黏结应力对应的径向应力σ_u的表达式^[23]：

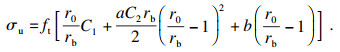(13)

根据式(12)和式(13)可得^[23]：

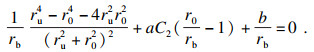(14)

将a和b代入式(14)，其中C₂由式(11)计算可得，为了获得近似解，取ε_cr=f_t/E₀，其中E₀采用Carreira等^[25]提出的计算公式.假定保护层厚度c为钢筋半径的3倍，通过计算可得到r₀/r_u的计算式：

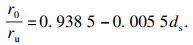(15)

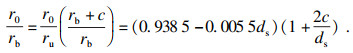(16)

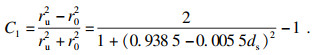(17)

式中d_s为钢筋直径.
考虑到摩擦力与黏结强度有关，因此可得到极限黏结应力τ_u的表达式：

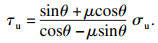(18)

式中：θ为混凝土破坏面与钢筋纵轴之间的角度；μ为钢筋与其周围混凝土之间的摩擦系数，根据文献[13]通常取0.25~0.35.结合式(13)、式(16)、式(17)和(18)即可计算得到轻骨料混凝土黏结应力，对本文各试件的计算结果见表 6.
4.2 残余黏结应力τ_r建立残余黏结应力τ_r与极限黏结应力τ_u之间的关系，即τ_r=kτ_u.当k=0时模型简化为无摩擦的两段式模型，当k=1时表示黏结强度仅由界面摩擦力承担；因此，取0 < k < 1.根据试验结果k取平均值为0.26，见表 7.
表 7(Table 7)

表 7 残余黏结应力Table 7 Residual bond stress 编号 τu/MPa τr/MPa k k A16-80 18.43 3.71 0.20 0.26 B16-80 20.92 5.80 0.28 C16-80 24.34 7.82 0.32 D16-80 28.51 10.06 0.35 D16-50 28.51 6.96 0.24 D12-50 28.03 6.10 0.22 D20-50 29.79 6.72 0.23

表 7 残余黏结应力 Table 7 Residual bond stress

4.3 黏结-滑移曲线指数上升段：随着荷载增大，内部微裂缝发展，黏结应力逐渐降低，当黏结应力达到极限黏结应力τ_u时，对应的滑移量为s_u.指数上升段与Mo模型^[20]吻合较好，且0 < γ < 1，通过拟合公式(20)得出γ值，见图 7.由表 5可知锚固长度、钢筋直径以及混凝土强度对s_u的影响不显著.因此在本试验中，s_u可取为1.1 mm.

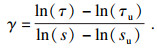(19)

图 7(Fig. 7)

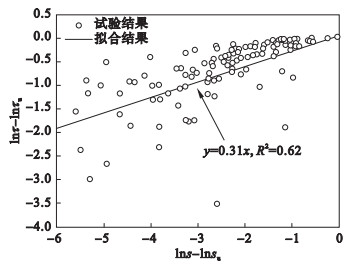图 7 指数α回归Fig.7 Exponential α regression

经分析，本文建议的本构关系式为

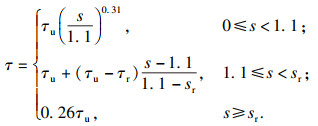(20)

式中s_r表示残余黏结应力对应的滑移量.
5 模型验证图 8对模型曲线和试验曲线进行了比较, 同时将试验数据代入国内外****提出的本构模型^[12-14]进行对比.可以看出本文建立的黏结-滑移本构模型曲线与试验曲线较为吻合，相比所选取的国内外模型具有更高的准确性.
图 8(Fig. 8)

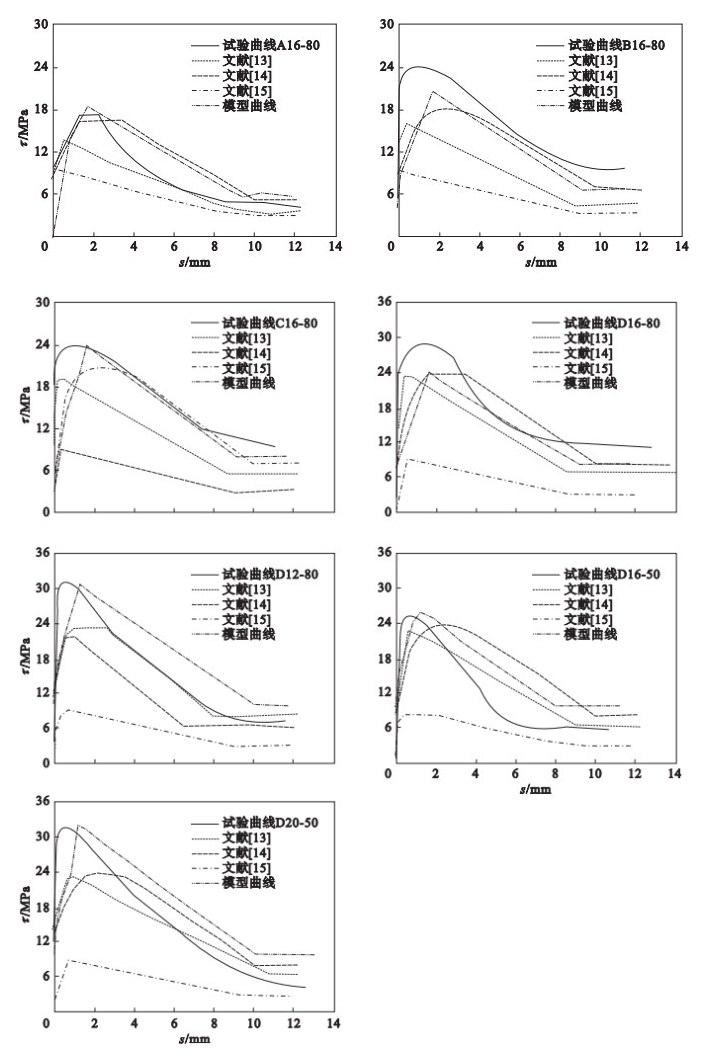图 8 本文模型，其他模型与试验曲线对比Fig.8 Comparison of proposed model, other models and test curves

6 结论1) 轻骨料混凝土的黏结-滑移性能随着混凝土强度的增加近似呈线性增长.
2) 轻骨料混凝土的黏结强度随钢筋直径的增长呈现先增大后减小的趋势，相同混凝土强度与锚固长度条件下钢筋直径16 mm的黏结应力最多可提高23 %.相同强度条件下，轻骨料混凝土试件的黏结强度高于普通混凝土试件.
3) 本文所建立的黏结强度模型与试验结果吻合较好，所提出的本构模型能够较好地预测轻骨料混凝土的黏结-滑移曲线.
参考文献

[1]	Baldwin J W. Bond of reinforcement in lightweight aggregate concrete[D]. Columbia: University of Missouri, 1965.
[2]	Hossain K M A. Bond characteristics of plain and deformed bars in lightweight pumice concrete[J]. Construction and Building Materials, 2008, 22(7): 1491-99. DOI:10.1016/j.conbuildmat.2007.03.025
[3]	ACI Committeeand IOS. Building code requirements for structural concrete and commentary: ACI 318-19[S]. Farmington Hills, Michigan: American Concrete Institute, 2019.
[4]	陈旭. 纤维增韧高强轻骨料混凝土力学性能及黏结锚固性能研究[D]. 西安: 长安大学, 2017. (Chen Xu. Experimental study on mechanical properties and bond behavior of fiber-reinforced high strength lightweight aggregate concrete[D]. Xi'an: Chang'an University, 2017. )
[5]	Martin H. Bond performance of ribbed bars-influence of concrete composition and consistency[C]// Proceedings of the International Conference on Bond in Concrete. Paisley, 1982: 289-299.
[6]	Chen H J, Huang C H, Kao Z Y. Experimental investigation on steel-concrete bond in lightweight and normal weight concrete[J]. Structural Engineering and Mechanics, 2004, 17(2): 141-152. DOI:10.12989/sem.2004.17.2.141
[7]	李渝军, 叶列平, 程志军, 等. 高强陶粒混凝土与变形钢筋黏结锚固强度的试验研究[J]. 建筑科学, 2006, 22(4): 51-55. (Li Yu-jun, Ye Lie-ping, Cheng Zhi-jun, et al. Bond strength between high-strength lightweight aggregate concrete and deformed bar[J]. Building Science, 2006, 22(4): 51-55. DOI:10.3969/j.issn.1002-8528.2006.04.013)
[8]	Lo T Y, Cui H Z. Effect of porous lightweight aggregate on strength of concrete[J]. Materials Letters, 2004, 58(6): 916-919. DOI:10.1016/j.matlet.2003.07.036
[9]	陆春阳, 王卫玉, 李丕宁. 陶粒混凝土与变形钢筋黏结锚固性能的试验研究[J]. 广西大学学报(自然科学版), 2007, 32(1): 6-9. (Lu Chun-yang, Wang Wei-yu, Li Pi-ning. Experiment research on bond behavior between deformed bar and lightweight concrete[J]. Journal of Guangxi University(Natural Science Edition), 2007, 32(1): 6-9. DOI:10.3969/j.issn.1001-7445.2007.01.002)
[10]	CEB-FIP. Structural concrete—textbook on behavior, design and performance, updated knowledge of the CEB-FIP model code 1990[S]. Stuttgart: Sprint-Druck, 1999.
[11]	International Federation for Structural Concrete. MC2010 bulletin 55: model code for concrete structures 2010[S]. Lausanne: International Federation for Structural Concrete, 2010.
[12]	中国建筑科学研究院. 混凝土结构设计规范: GB50010—2010[S]. 修订版. 北京: 中国建筑工业出版社, 2015. (China Academy of Building Research. Code for design of concrete structures: GB50010—2010[S]. Rev. ed. Beijing: China Architecture & Building Press, 2015. )
[13]	徐有邻. 钢筋混凝土黏结滑移本构关系的简化模型[J]. 工程力学, 1997, sup(sup): 34-38. (Xu You-lin. Simplified model of bond-slip constitutive relationship of reinforced concrete[J]. Engineering Mechanics, 1997, sup: 34-38.)
[14]	Harajli M H. Bond stress-slip model for steel bars in unconfined or steel FRC or FRP confined concrete[J]. Engineering Structures, 2009, 135(5): 509-518. DOI:10.1061/(ASCE)0733-9445(2009)135:5(509)
[15]	中国建筑科学研究院. 混凝土结构试验方法标准: GB50152—1992[S]. 北京: 中国建筑工业出版社, 1992. (China Academy of Building Research. Standard for test method of concrete structure: GB50152—1992[S]. Beijing: China Architecture & Building Press, 1992. )
[16]	中国建筑科学研究院. 混凝土结构试验方法标准: GB50152—2012[S]. 北京: 中国建筑工业出版社, 2012. (China Academy of Building Research. Standard for test method of concrete structure: GB50152—2012[S]. Beijing: China Architecture & Building Press, 2012. )
[17]	徐有邻, 邵卓民, 沈文都. 钢筋与混凝土的黏结锚固强度[J]. 建筑科学, 1988, 4(4): 8-14. (Xu You-lin, Shao Zhuo-min, Shen Wen-du. Bond strength between reinforcing bars and concrete[J]. Building Science, 1988, 4(4): 8-14.)
[18]	王卫玉. 陶粒混凝土与钢筋黏结锚固性能的试验研究[D]. 南宁: 广西大学, 2005. (Wang Wei-yu. Tests and research on bond behavior between deformed bar and lightweight concrete[D]. Nanning: Guangxi University, 2005. )
[19]	Hillerborg A, Modeer M, Petersson P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and Concrete Research, 1976, 6(6): 773-781. DOI:10.1016/0008-8846(76)90007-7
[20]	Petersson P E. Crack growth and development of fracture zones in plain concrete and similar materials[D]. Lund, Sweden: Lund Institute of Technology, 1981.
[21]	Thanyawat P, Panedpojaman P. Modeling of bonding between steel rebar and concrete at elevated temperatures[J]. Construction and Building Materials, 2012, 27(1): 130-140. DOI:10.1016/j.conbuildmat.2011.08.014
[22]	Thanyawat P, Panedpojaman P. Modeling of mechanical bond-slip for steel-reinforced concrete under thermal loads[J]. Engineering Structures, 2013, 48: 497-507. DOI:10.1016/j.engstruct.2012.10.015
[23]	Gao X L, Li N K, Ren X D. Analytic solution for the bond stress-slip relationship between rebar and concrete[J]. Construction and Building Materials, 2019, 197: 385-397. DOI:10.1016/j.conbuildmat.2018.11.206
[24]	Timoshenko S P, Goodier J N. Theory of elasticity[M]. 3rd ed. New York: McGraw-Hill, 1970.
[25]	Carreira D J, Chu K H. Stress-strain relationship for plain concrete in compression[J]. Journal of the American Concrete Institute, 1985, 82(6): 797-804.