
 , 姜楠2
, 姜楠2 1. 东北大学 工商管理学院, 辽宁 沈阳 110169;
2. 光大证券股份有限公司,广东 深圳 518030
收稿日期:2021-05-28
基金项目:国家自然科学基金资助项目(71872035);辽宁省社会科学规划项目(L10BJY018)。
作者简介:郭莉(1977-), 女, 辽宁铁岭人, 东北大学副教授。
摘要:新技术应该及早采纳还是延迟采纳,涉及到企业构建持续竞争力.基于Farzin的最优技术采纳模型,从新技术的预期收益和出现时机两个方面重新界定新技术的不确定性,构建了制造企业采纳新技术的动态规划模型,并进行了数值算例分析.研究表明:对于较快出现或较快增长的新技术,企业的时间策略是等待和慎重评估,以免陷入技术陷阱(越引进越落后);而对于变动成本(设备升级成本、人力配备及其他管理成本等)较大的技术,企业的时间策略是及早采纳.
关键词:技术不确定性时间策略创新技术创新采纳
Time Strategies of Innovative Technology Adoption Considering Technical Uncertainty
GUO Li1

 , JIANG Nan2
, JIANG Nan2 1. School of Business Administration, Northeastern University, Shenyang 110169, China;
2. Everbright Securities Co., Ltd., Shenzhen 518030, China
Corresponding author: GUO Li, E-mail: lguo@mail.neu.edu.cn.
Abstract: Whether an innovative technology should be adopted early or with delay involves the construction of sustainable competitiveness. Based on Farzin's optimal technology adoption model, the uncertainty of innovative technologies is redefined from two aspects of expected income and occurrence time of innovative technologies, a dynamic programming model for manufacturing enterprises is constructed to adopt innovative technologies, and a numerical example analysis is given. The research shows that for the technologies that appear or grow rapidly, the time strategy of enterprises is to wait and carefully evaluate, so as to avoid falling into the technology trap(the more introduced, the more backward); for technologies with large variable costs(equipment upgrading cost, manpower allocation and other management costs), enterprises' time strategy is to adopt them as soon as possible.
Key words: technical uncertaintytime strategyinnovative technologyinnovation adoption
新技术面临较大技术风险和高昂的先期开发、运转和维护成本,这些技术的不确定性影响企业的技术采纳决策.目前,国内外****主要从技术预期价值收益和技术出现时机两个角度界定了技术的不确定性.一方面,采纳者对新技术价值存在不确定性的预期.Dixit和Pindyck [1]以市场对产品需求的不确定性为切入点,判断企业何时采纳创新技术能获得最大利润.Zeng等[2]考虑了技术不确定性背景下的末端治理技术的采纳决策问题,揭示了政策因素对技术价值的影响.李娅楠等[3]考虑了绿色技术的产量和成本对企业绿色生产决策的影响,建立了两阶段决策模型,发现技术学习因素会促进企业绿色技术的采纳.丁志刚等[4]关注到碳税变化所引起的低碳技术期望收益的不确定性,并由此影响供应链提早或推迟采纳低碳技术.可见,过往的研究多数将技术不确定性归结为企业对新技术的经济价值的不确定性预期.
另一方面,关于技术出现时机的不确定性,国内外****展开了一些研究.Farzin等[5]提出,创新技术不断随机出现的过程基本服从齐次泊松分布的假设,其自身逐代改良的过程可被描述为均匀分布,并结合动态规划思想建立了企业最优技术采纳决策模型;在此基础上,Huisman[6]对模型进行了扩展,假设每当出现更新一代技术时,上一代技术的采纳成本会大幅降低,而潜在的技术采纳企业能够提前预测这种成本突降幅度,由此做出投资决策;代宏坤和徐玖平[7]用泊松过程来描述技术出现的不确定性,构建了企业最优技术采纳决策模型;但在考虑创新技术为企业带来的价值时,仅仅关注了技术在提高产出效率方面的作用,忽略了降低可变成本的积极作用.Guo和Zhu[8]、Reinhardt等[9],以及Ghorban[10]都考虑了技术出现时机的不确定性,但缺乏对技术的经济价值的考虑.
综上所述,在决策优化模型中,技术的不确定性体现在经济价值的不确定性和技术出现时机的不确定性两个方面.以往文献往往侧重对其中某一方面的研究,将二者结合的研究成果较少;专注节能减排等新技术不确定性的研究更少.本文运用动态规划理论,考虑新技术经济价值(定义为提高产出效率和降低生产成本两个方面)的不确定性和新技术出现时机的不确定性,构建改进的决策模型,以确定是否采纳创新技术,并通过数值算例分析了在投入成本、产出效率和技术进步速度不确定的条件下企业采纳创新技术的时间策略.
1 构建是否采纳创新技术的决策模型1.1 问题描述企业是否采纳创新技术的过程是一个动态决策过程,单纯的利润流模型不能成为企业采纳新技术的决策方程,还需要考虑企业在整个动态决策过程中总的期望利润.技术不确定性带来两个风险:一是提早采纳新技术后出现更先进的技术;二是延迟采纳新技术后出现比现有技术落后的技术.这些不确定性使企业需要考虑何时采纳技术才能使总的期望利润最大,这个时间点及其对应的采纳条件即最优时间策略.
动态决策过程中总的期望利润A,不仅包括不采纳新技术而继续以原有旧技术生产所能得到的生产销售利润B,也包括因不采纳新技术而带来的等待成本C,即企业采纳技术的决策方程是A=B+C.
1) 期望利润A:在技术产出效率、生产费率均不稳定的随机改进阶段,企业在t时刻采纳新技术的预期利润.以(θ, ω)代表新技术,其中θ和ω分别表示新技术的产出效率和生产费率.
2) 预期利润B:在技术产出效率、生产费率均不稳定的随机改进阶段,企业在t时刻不采纳新技术(θ, ω),而以原有旧技术(θ0, ω0)生产时的预期利润.其中,θ0和ω0分别表示原有技术的产出效率和生产费率.
3) 预期利润C:在技术产出效率、生产费率均不稳定的随机改进阶段,企业不采纳当前新技术(θ, ω),而是等待未来新技术产出效率、生产费率进一步改进到(θ+dθ, ω-dω)时的等待利润.
根据技术效率是否提高, 等待过程分为两种情况:
4) 预期利润D:经过等待,新技术水平未能改进时的预期利润,此时技术参数仍为(θ, ω).
5) 预期利润E:经过等待,新技术水平获得改进时的预期利润,此时技术参数为(θ+dθ, ω-dω).
由此可知, 等待过程的期望利润为C=D+E.
再进一步思考, 虽然技术水平得到提高, 但企业仍需视改进程度能否令其满意来决定是否投资采纳新技术,这又可分为两种情况:
6) 预期利润F:技术改进程度不理想,企业暂不投资新技术时的预期利润.
7) 预期利润G:技术改进程度理想,企业即刻投资新技术时的预期利润.
由此可知,经过等待,技术获得改进的期望利润为E=F+G.
综上所述, 企业投资采纳创新技术的最优决策方程表达式为A=B+D+F+G.
企业采纳新技术的预期利润概念模型如图 1所示.
图 1(Fig. 1)
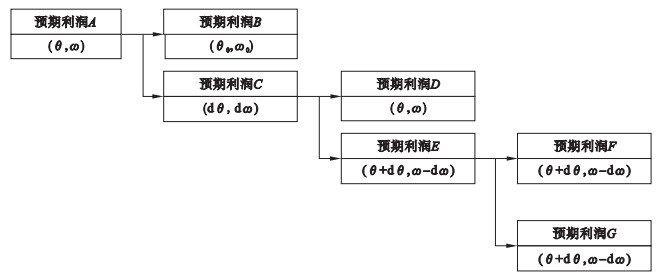 | 图 1 企业采纳新技术的预期利润概念模型Fig.1 Concept framework of anticipated profits of companies adopting innovative technologies |
1.2 基本假设对公司生产、成本、销售收入、投资、资本利率等情况进行分析,沿袭Farzin等[5]的思路,模型基本假设如下:
假设1??企业生产单一产品,产品的市场价格为p,且企业采纳新技术后仍保持原有市场竞争性, 则产品价格p不变.
假设2??银行贷款利率为r.
假设3??企业投资采纳一项新技术的成本包括固定部分和可变部分,其中固定成本为I,可变成本与企业新旧技术水平差距成正比.
假设4??企业只采纳一次创新技术, 之后一直以此技术进行生产作业.
假设5??技术产出效率、生产费率均不稳定,且相互独立并随机改进,技术演化过程中的不确定因素包括创新技术出现的速度、技术产出效率的改进程度和技术生产费率的改进程度.新技术出现的事件独立,根据文献[5-7]对技术出现不确定性进行泊松分布的假设,设定在(t, t+Δt)内,带来产出效率提升的新技术出现的速度服从λ1·Δt的泊松分布,产出效率提升程度u1服从(0, u1)上的均匀分布;而在同一时间段(t, t+Δt)内,带来生产费率缩减的新技术出现的速度服从λ2·Δt的泊松分布,生产费率缩减程度u2服从(0, u2)上的均匀分布.
1.3 基于技术不确定性的新技术采纳模型一项新技术带来的改进效果可能体现在技术产出效率的提升或者技术生产费率的缩减,也可能二者同时发生.基于此,新技术的不确定性体现在新技术的出现速度、技术产出效率和技术生产费率的改进效果.
记企业目前使用的技术产出效率为θ0,投入单位物料对应的生产费用为ω0,则记企业期初的技术水平参数为(θ0, ω0);t时刻出现的新技术产出效率为θ,生产费率为ω,记为新技术(θ, ω),企业需要决定是否在t时刻采纳新技术.之后随技术进一步演化,在(t, t+Δt)时间段内出现的新技术,将技术产出效率提升至(θ, θ+u1) 范围,同时技术生产费率缩减至(ω, ω-u2)范围.企业要做的最优决策是在(θ, θ+u1)和(ω, ω-u2)中分别确定技术的产出效率决策阈值θ*和生产费率决策阈值ω*,从而确定一个最优技术水平阈值(θ*, ω*).
根据概念模型(图 1)提供的思路:企业采纳创新技术的决策方程是A=B+C.假设当前最新可得的技术水平为(θ, ω),而企业采用原技术(θ0, ω0)作业,继续等更高水平技术出现,设F(θ, ω)为企业于该状态下的期望利润现值——状态A.
设企业生产利润为f(θ, ω),则企业采用原技术生产时的利润为f(θ0, ω0).企业不采纳当前最新技术(θ, ω),而以原技术水平(θ0, ω0)生产,则该企业在(t, t+Δt)时间段里的生产利润为f(θ0, ω0)·Δt——状态B.
企业使用原有技术(θ0, ω0)生产的过程亦是等待过程,有等待成本.企业预计等待一段时间后采纳更高水平技术,那时技术水平改进至(θ+dθ, ω-dω),该等待过程的期望利润为E[F(θ+dθ, ω-dω)].
银行贷款利率为r,则折现因子为
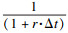
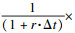
综上可得企业采纳创新技术的决策方程为
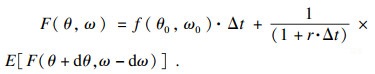 | (1) |
企业以参数为(θ, ω)的技术水平生产某特定产品时,投入ν单位生产资料后,企业将获得收入p·θ·νa,损耗的生产费用为ω·ν.则企业采纳参数为(θ, ω)的技术后,生产利润为f(θ, ω)=p·θ·νa- ω·ν.因企业追求利润最大化,则有f(θ, ω)=max(p·θ·νa-ω·ν),且ν*=(a·p·θ/ω)1/(1-a)时最大.将ν*表达式代入f(θ, ω)=p·θ·νa-ω·ν,得到
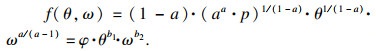 | (2) |
因此,可知企业使用原技术参数(θ0, ω0)生产将在Δt期间获得利润的表达式为
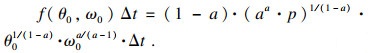 | (3) |
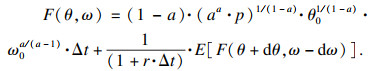 | (4) |
1) 使用某技术生产作业,对应的产出效率、生产费率均没有得到进一步改进,即等待过程中没有出现更优技术,最优可得技术水平参数仍为(θ, ω)——状态D.由假设5可知发生这种情况的可能性为(1-λ1·Δt)(1-λ2·Δt),所以期望利润为(1-λ1·Δt)·(1-λ2·Δt)·F(θ, ω).
2) 最优可得技术水平有所改进——状态E.由假设5可知发生该情况可能性为1-(1-λ1·Δt)(1-λ2·Δt).记改进后技术水平参数为(θ+dθ, ω-dω).根据技术产出效率增幅dθ和生产费率减幅dω分以下四种情形讨论:
① 技术改进程度使得产出效率和生产费率均不理想的情形,即
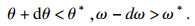 |
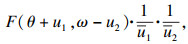 |
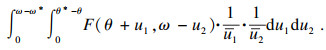 |
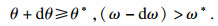 |
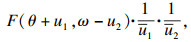 |
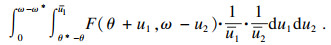 |
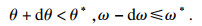 |
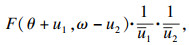 |
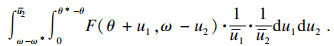 |
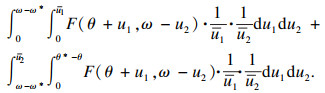 |
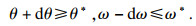 |
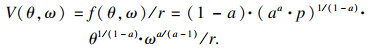 |
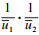
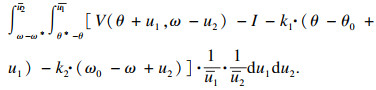 |
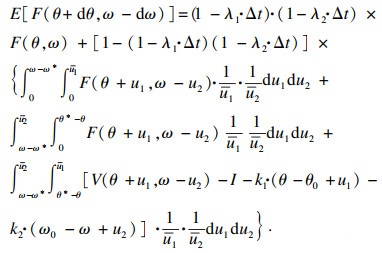 | (5) |
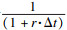
企业投资采纳创新技术的最优决策方程基本型为A=B+C,代入各状态对应的期望利润数学表达,整理可得
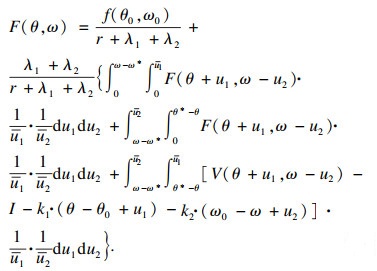 | (6) |
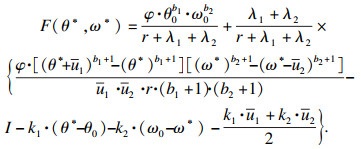 | (7) |
1.5.2 方程边界条件当θ=θ*且ω=ω*时,表示当前最优可得技术的两项参数分别为θ*和ω*;而企业原技术的两项参数分别为θ0和ω0.此时对企业来说,选择(θ*, ω*)并一直生产下去的期望利润现值为V(θ*, ω*)-I-k1·(θ*-θ0)-k2·(ω0-ω*);而继续使用原技术生产,等待更优技术出现的期望利润现值为F(θ*, ω*).对是否采纳新技术进行决策时二者的阈值没有区别,故可得方程:
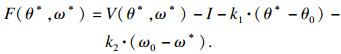 | (8) |
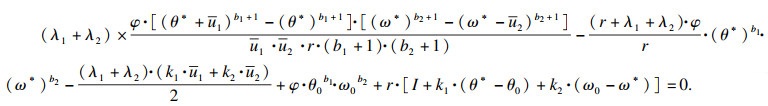 | (9) |
2 企业最优创新采纳模型的数值分析2.1 参数设定已知钢铁企业是否采纳干法脱硫技术的决策阈值为(θ*, ω*),通过MATLAB软件对式(9)进行仿真分析,得出最优决策阈值与其他变量的关系图,用来解释各变量对决策阈值θ*的影响.首先设定外生参数及变量的取值范围.
1) 外生参数设定:
① 脱硫后节约罚款(折合成产成品)市场价格p=500;
② 企业采纳新技术投资成本的固定部分按照与产成品市场价格成一定比例来确定:I=300 000元,表示企业为采纳新技术付出的一次性购买成本;
③ 设产出弹性a=0.5为固定参数,则企业的生产函数为
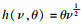
2) 各变量的取值范围与设定值见表 1.
表 1(Table 1)
| 表 1 参数设定 Table 1 Parameter and variable setting |
2.2 数值分析2.2.1 最优产出效率与最优生产费率的关系将产出效率阈值θ*作为自变量,其他变量全部按照表 1设为固定值,可得生产费率阈值ω*与θ*的关系曲线(见图 2),从而观察最优决策阈值(θ*, ω*)解集曲线的大体走势.
图 2(Fig. 2)
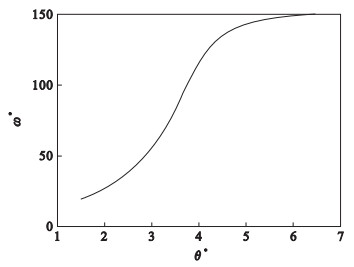 | 图 2 θ*与ω*的关系Fig.2 Relationship between θ* and ω* |
由图 2可知,当企业采纳新技术提高产出效率决策阈值θ*时,生产费率的决策阈值ω*也必然升高,因而采纳新技术生产费率降幅(dω=ω0-ω*)相对较小时,企业也会停止等待而选择投资并采纳新技术,反之亦然.
由此可见,新技术的产出效率提升空间大于生产费率的缩减空间.这是因为生产费率的缩减空间只能在原费率水平之下,且不可能变为负值;新技术能使产品制造过程中的单位生产费率降低至原来的一半较为少见,并且原技术生产费率越低意味着新技术能带来的成本压缩空间越小.相反,新技术产出效率的提升空间没有绝对上限,条件成熟时产出效率有可能提升至多倍.因此,从长期来看,新技术产出效率的提升更为关键.
2.2.2 变量与最优解的关系由于决策阈值为“双阈值”,为便于求解和作图,将其中一个阈值设为已知,任意取ω*=118(此时产出效率提升3倍,生产费率缩减1/5).分别将θ0,ω0,λ1,λ2,u1,u2,k1,k2作为自变量,得到各变量与决策阈值θ*的关系,如图 3所示.
图 3(Fig. 3)
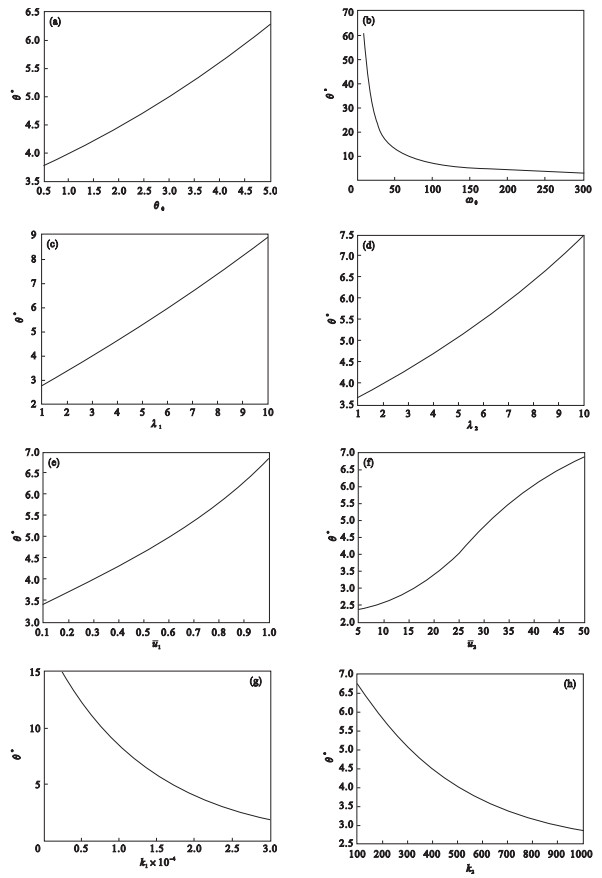 | 图 3 各变量与决策阈值θ*的关系Fig.3 Relationship between variables and θ* |
由图 3a可知,原技术的产出效率越高,对应的决策阈值越大;图 3b则表明企业原技术的生产费率越低,对应的决策阈值越大.总体来看,当其他条件不变时,企业原有技术水平越高,则采纳新技术的决策阈值越大,企业采纳新技术越滞后.
由图 3c和图 3d可知,决策阈值随λ1与λ2增大而增大,所以当其他条件不变时,只要新技术出现的速度加快,企业未来采纳新技术的决策阈值就会变大.总之,技术革新的速度越快,对行业产生影响的可能性就越大,企业对新技术的采纳越理性和审慎,因而企业采纳新技术越滞后.
由图 3e和图 3f可知,决策阈值随u1与u2的增大而增大.这说明当其他条件不变时,新技术带来的改变越大,决策阈值越大.因此,技术进步越快,后发优势越明显,企业采纳新技术越滞后.
由图 3g和图 3h可知,制造企业的技术采纳决策阈值随k1与k2的增大而减小.这说明当其他条件(包括新旧技术水平差距)不变时,企业变动采纳成本越高,企业未来创新技术采纳决策阈值就越小.
3 结论1) 企业采纳新技术的决策阈值为“双阈值”,产出效率的提高与生产费率的降低具有替代性,而且从长期看,产出效率的提升更为关键;这与以往单纯关注技术的成本优势的研究结论不同.制造业应该更多地关注新技术的产出效率,因为产出效率的提升空间远大于生产费率的缩减空间.
2) 对于那些以较快速度达到最高产出效率或最低生产费率的新技术,企业可能为了较大幅度地提高生产效率或降低生产成本而较早地采纳新技术,由此使得企业有可能被锁定在一个相对低效率的新技术上,而没能采纳以后出现的效率更高的新技术.因此,对于较快出现或较快增长的新技术(如干法烟气脱硫工艺),企业的策略是等待和慎重评估,以免陷入“越引进越落后”的技术陷阱;而对于那些变动成本(设备升级成本、人力配备及其他管理成本等)较大的新技术,企业的策略是及早采纳.
3) 企业在采纳新技术时面临的变动成本越高,就越容易做出采纳新技术的决策.对于大型制造业、化工和钢铁等行业而言,原材料、电力和燃料等变动成本消耗巨大,一旦在新材料或新能源方面有任何技术突破,都会对企业经营产生深远影响,企业对能使变动成本降低的新技术需求最为强烈.
本研究存在的不足之处:一方面,由于本文采用模型优化求解,研究结论受模型设定变量的影响较大,因此未来研究可以考虑市场规模、跨代产品的竞争与互补关系等外部因素对决策模型的影响;另一方面,本文从单次技术的采纳决策出发,实际上,制造企业可能面临更多的是一系列连续技术的采纳决策问题,如何将连续技术的动态变化影响纳入投资决策模型,有待于今后进一步探讨.
参考文献
| [1] | Dixit A K, Pindyck R S. Investment under uncertainty[M]. Princeton: Princeton University Press, 1994. |
| [2] | Zeng B X, Zhu L, Yao X. Policy choice for end-of-pipe abatement technology adoption under technological uncertainty[J]. Economic Modeling, 2020, 87: 121-130. DOI:10.1016/j.econmod.2019.07.012 |
| [3] | 李娅楠, 林军, 钱艳俊. 环境规制下企业绿色生产决策及技术学习因素影响研究[J]. 管理学报, 2019, 16(5): 721-727. (Li Ya-nan, Lin Jun, Qian Yan-jun. Study on the effect of green production decision and technological learning factors under the environmental regulations[J]. Chinese Journal of Management, 2019, 16(5): 721-727. DOI:10.3969/j.issn.1672-884x.2019.05.011) |
| [4] | 丁志刚, 陈涵, 徐琪. 碳交易与碳税双重风险下供应链低碳技术采纳时机决策研究[J]. 软科学, 2020, 34(7): 101-107. (Ding Zhi-gang, Chen Han, Xu Qi. Carbon reduction technology adoption timing considering carbon transaction and carbon tax risks[J]. Soft Science, 2020, 34(7): 101-107.) |
| [5] | Farzin Y H, Huisman K J M, Kort P M. Optimal timing of technology adoption[J]. Journal of Economic Dynamics and Control, 1998, 22(5): 779-799. DOI:10.1016/S0165-1889(97)00097-3 |
| [6] | Huisman K J M. Technology investment: a game theoretic real options approach[J]. Technovation, 2003, 23(11): 901-925. |
| [7] | 代宏坤, 徐玖平. 企业技术采纳时间的优化模型与模拟[J]. 系统工程理论与实践, 2005, 25(9): 8-14. (Dai Hong-kun, Xu Jiu-ping. Optimal model of enterprise technology adoption and its simulation[J]. Systems Engineering—Theory & Practice, 2005, 25(9): 8-14.) |
| [8] | Guo J X, Zhu L. Optimal timing of technology adoption under the changeable abatement coefficient through R & D[J]. Computers & Industrial Engineering, 2016, 96: 216-226. |
| [9] | Reinhardt R, Hietschold N, Gurtner S. Overcoming consumer resistance to innovations—an analysis of adoption triggers[J]. R & D Management, 2019, 49(2): 139-154. |
| [10] | Ghorban H S. Strategic technology adoption in networked markets[C]//Proceedings of the Future Technologies Conference(FTC). [S. l. ], 2018: 1158-1175. |
