乔梁¹, 李琳琳¹, 任俊超²
1. 北京科技大学 自动化学院, 北京 100083;
2. 东北大学 理学院, 辽宁 沈阳 110819
收稿日期：2021-03-19
基金项目：国家自然科学基金资助项目(62003033)；广东省基础与应用基础研究联合基金资助项目(2019A1515111141)；中央高校基本科研业务费专项资金资助项目(FRF-TP-19-033A1)。
作者简介：乔梁(1985-), 男, 内蒙古呼和浩特人, 北京科技大学讲师, 博士。

摘要：针对奇异系统提出一种静态输出反馈控制设计新方法.首先, 利用矩阵迹不等式研究奇异系统容许性问题, 并提出奇异系统容许(正则、无脉冲、稳定)的代数判据.其次, 在系统容许性分析理论结果基础上, 设计静态输出反馈控制器保证闭环奇异系统容许性, 同时给出矩阵迹不等式的求解方法完成输出反馈控制器设计.与已有的基于线性矩阵不等式求解静态输出反馈控制器方法不同, 本文所提方法不需要对输出矩阵进行特殊设定.最后, 通过仿真例子表明所提理论方法的可行性和有效性, 并且此方法也适用于正常系统输出反馈控制设计.
关键词：奇异系统代数判据容许性静态输出反馈矩阵迹
New Output Feedback Design Method for Singular Systems Based on Algebraic Criteria
QIAO Liang¹, LI Lin-lin¹, REN Jun-chao²
1. School of Automation and Electrical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. School of Sciences, Northeastern University, Shenyang 110819, China
Corresponding author: LI Lin-lin, E-mail: linlin.li@ustb.edu.cn.

Abstract: A new design method of the static output feedback control for singular systems is proposed. Firstly, by using the matrix trace inequality, the admissibility issue of singular systems is introduced and the algebraic criteria of admissibility for this kind of systems is established. Secondly, based on the admissibility analysis result, the sufficient condition for static output feedback controller design is obtained to ensure the admissibility for closed-loop systems. Meanwhile, the solving method of matrix trace inequality is given to obtain the gain matrix. Different from the design method of static output feedback controller via linear matrix inequalities, the proposed method does not need the special requirement setting of output matrix. Finally, three numerical examples illustrate the feasibility and effectiveness of the proposed theoretical method, which also applies for the output feedback controller design of normal systems.
Key words: singular systemsalgebraic criteriaadmissibilitystatic output feedbackmatrix trace
奇异系统是由微分方程和代数方程共同构成, 既能够刻画系统的动态行为, 又能够刻画系统的静态行为, 区别于正常线性系统, 奇异系统具有的脉冲行为, 以及对初始状态的不相容性, 使得有关研究变得复杂而富有新颖性.相比于正常系统, 奇异系统是更具有广泛形式的一类动力系统, 存在于社会生产的众多领域中, 例如机器人系统、电力系统、经济系统、宇航系统、电子网络系统等, 故对奇异系统进行研究具有十分重要的理论意义和实用价值^[1-3].容许性(正则、无脉冲、稳定)作为奇异系统正常运行的前提, 是表征系统运动行为的一类重要结构特征.目前, 针对奇异系统容许性的分析与综合问题研究受到了控制学界的广泛关注, 并且得到了许多优秀的理论结果^[4-8].文献[4]提出一种基于干扰观测器的鲁棒控制器, 并利用李雅普诺夫稳定性理论分析了闭环奇异系统的渐近稳定性.文献[5]研究一类不完全转移率的Markov奇异系统的H_∞控制问题, 给出Markov跳变奇异系统的新型有界实引理以及状态反馈控制方法设计.文献[6]研究时滞矩形奇异系统的镇定问题, 通过引入时滞动态补偿器对系统进行反馈补偿, 给出了以严格线性矩阵不等式表示的时滞矩形奇异系统的镇定条件.文献[7]基于二次型矩阵分析方法, 给出了奇异凸多面体系统的容许性判据, 并将理论结果推广到具有时滞情形的系统.文献[8]设计基于观测器的比例导数控制器, 基于线性矩阵不等式提出模糊奇异系统容许的充分条件.
在实际系统的分析与设计时, 系统的状态变量通常是从系统外部不易直接测量获得的, 所以绝大部分情况下无法利用状态反馈控制器实现系统镇定与性能优化.同时在系统状态变量可以直接获取时, 相比于状态反馈, 对系统施加输出反馈控制更能够节约系统控制成本并提高系统可靠性.目前在输出反馈控制器设计方法中, 主要是用Lyapunov理论研究系统静态输出反馈镇定问题, 并结合线性不等式求解, 但是其可解条件通常是一个双线性矩阵不等式, 这是一个NP-hard问题^[9].文献[10]中利用Lyapunov矩阵的合同变换求得系统的静态输出反馈控制器, 其局限在于系统矩阵需要满足限定条件.文献[11]利用Finsler引理, 通过增广矩阵不等式维数, 实现静态输出反馈控制器设计, 增加了计算复杂性.文献[12]利用辅助矩阵变量方法解决一类奇异系统输出反馈控制设计问题, 但是系统输出矩阵要求是行满秩的.文献[13]通过将原系统输出变量增广为新系统的状态变量方法, 可以解除输出反馈增益矩阵与系统输入/输出矩阵耦合关系, 虽然避免出现双线性矩阵不等式, 但系统维数的扩大增加了计算的复杂度.文献[14]通过输出矩阵满足矩阵等式约束, 解决了一类随机奇异系统的有限时间输出反馈控制器设计中.
基于以上分析, 本文利用矩阵迹不等式的理论, 研究奇异系统容许性与静态输出反馈设计问题.首先给出了奇异系统容许的代数判据.并以此为基础, 设计静态输出反馈控制器保证闭环奇异系统容许, 并给出相应算法完成控制器参数求解.本文所提方法规避已有结果中利用Lyapunov稳定性理论结合线性矩阵不等式求解静态输出反馈增益矩阵面临双线性矩阵不等式的难点.同时该方法也可以应用到正常系统输出反馈设计中.
1 问题描述符号说明:
R^n×n为n×n维实矩阵集合; Rⁿ为n维实数列向量集合; I_r为r×r维复矩阵集合维单位矩阵; A^T为矩阵A的转置; A^-1为矩阵A的逆矩阵; rank(A)为矩阵A的秩; det A为矩阵A的行列式; deg(·)为多项式次数; H(A)为; tr{A}为矩阵A的迹.
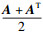
考虑如下的一类奇异系统:

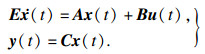(1)

其中: x(t)∈ Rⁿ是状态向量; u(t)∈ R^m是控制输入; y(t)∈ R^p是测量输出向量; E, A, B, C是给定的适维实数常矩阵, 且
定义1^[1] ??考虑如下奇异系统:

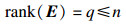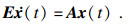(2)

1) 系统(2)被称为正则, 如果存在s∈C, 使得
2) 系统(2)被称为无脉冲, 如果
3) 系统(2)被称为稳定, 如果
其中:
4) 系统(2)被称为容许的, 如果系统是正则、无脉冲且稳定.
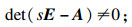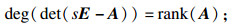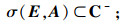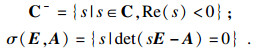引理1^[1]奇异系统(2)是无脉冲的充要条件为

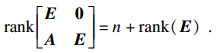(3)

引理2^[15] ??设A∈ R^n×n, 且满足

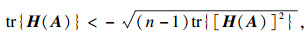(4)

则A的特征值全部分布在复平面的左半部分.
引理3 ??如果矩阵E满足rank (E)=q, 那么存在可逆矩阵U和正交矩阵V满足:

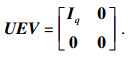(5)

证明??对矩阵E进行奇异值分解, 有

(6)

其中: P, Q∈ R^n×n是正交矩阵; E₁∈ R^q×q满足
且σ_i>0, i=1, 2, …, q是矩阵非零奇异值.然后选取
引理得证.
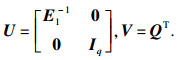引理4^[16] ??设A, B∈ R^n×n, 则有
1) tr {A+B}=tr {A}+tr{B};
2) tr{kA}=ktr{A};
3) tr{A^T}=tr{A};
4) tr {AB}=tr{BA};
5) 若矩阵U∈ R^n×n为可逆矩阵, 那么
引理5 ??如果矩阵V是正交矩阵, 那么

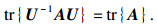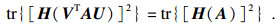(7)

证明??利用引理4中矩阵迹性质以及V为正交矩阵满足V^TV=I, 可以推出
引理得证.
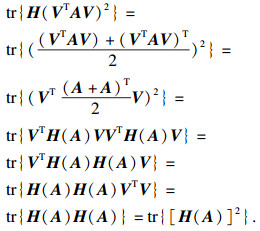本文的目的是设计静态输出反馈控制器

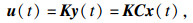(8)

使得相应的闭环系统

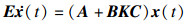(9)

是容许的.
2 主要结论给出自治奇异系统(2)容许的代数判据, 在此基础上设计输出反馈控制器实现闭环系统容许.
定理1 ??对于自治奇异系统(2), 如果满足

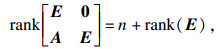(10)

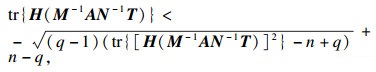(11)

则自治奇异系统(2)是容许的.
其中: q=rank (E); M=E+A-AVUE; N=E+A-EVUA; T=M+N-2E-EVUAVUE; 矩阵U和V如式(5)中所示.
证明??根据引理3, 存在可逆矩阵U和正交矩阵V满足:

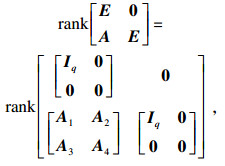(12)

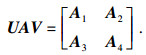(13)

由引理1, 推出系统(2)是无脉冲的.再由式(10), 结合式(12), (13), 可得

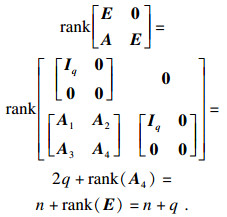(14)

这时rank(A₄)=n-q, 且A₄∈R^(n-q)×(n-q), 即A₄是可逆矩阵.
进一步, 考虑到

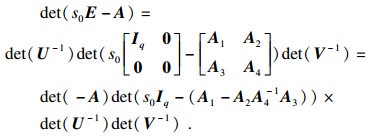(15)

由式(15)知, 当s₀不是矩阵A₁-A₂A₄^-1A₃的特征值, 此时存在s₀, 使得
因此系统(2)是正则的.
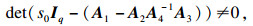下面证明系统(2)是稳定的.考虑系统状态变换如下:
然后, 对系统(2)进行受限等价变换, 可以推出

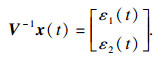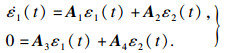(16)

考虑到是可逆的, 进行整理可得

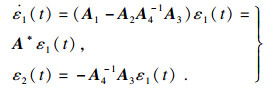(17)

接下来, 考虑到
以及
计算可得
则有

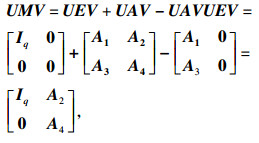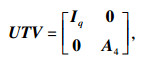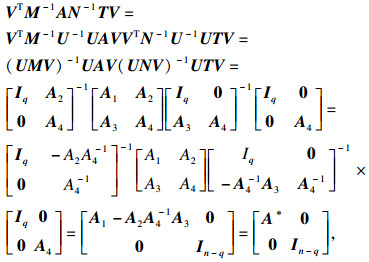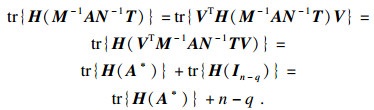(18)

再利用引理5, 可得

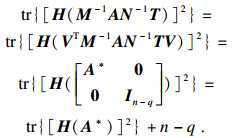(19)

利用式(11), 可以推出

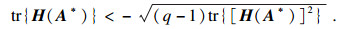(20)

所以A^* = A₁-A₂A₄^-1A₃的特征值全部分布在复平面的左半部分.再由式(15), 可以推出
det(sE-A)=0与det (sI_q-(A₁-A₂A₄^-1A₃))=0具有相同的根. 所以σ(E, A)?C^-, 可得系统(2)稳定.
综上, 系统(2)是容许的.
注1 ??利用矩阵迹的不等式, 定理1给出了奇异系统容许的代数判据.相对于文献[3]中的基于线性不等式的容许性判定定理需要寻求矩阵P满足不等式

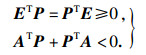(21)

定理1只需要计算系统矩阵的矩阵迹和矩阵秩来完成系统容许性判断, 所提方法更加直观简单, 易于计算.
由定理1, 直接给出闭环系统(9)的输出反馈控制器设计定理.
定理2 ??闭环系统(9)是容许的, 如果满足如下条件：

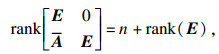(22)

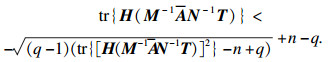(23)

其中: q=rank(E); M=E+ A-AVUE; N=E+A-EVUA; T=M+N-2E-EVUAVUE; A=A+BKC; 矩阵U和V如式(5)中所示.
注2 ??利用定理2求解输出反馈控制器时, 不需要对系统输出矩阵C进行特殊设定, 这就区别于文献[12]只能针对输出矩阵C是行满秩矩阵情况, 以及文献[14]要求C和Lyapunov矩阵P满足等式约束
也可以利用定理2设计状态反馈控制器使得闭环系统容许, 得到如下推论.
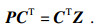推论1 ??在状态反馈控制器u(t)=Kx(t)下, 闭环系统是容许的, 如果满足
其中: q=rank (E); M=E+A-AVUE; N=E+A-EVUA; T=M+N-2E-EVUAVUE; A=A+BK; 矩阵U和V如式(5)中所示.
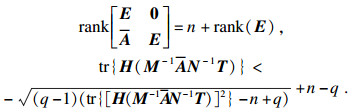当E=I, 奇异系统可以转化为正常线性系统, 系统(1)转化为

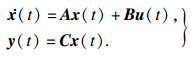(24)

又因为线性系统总是正则和无脉冲的, 定理2可以转为线性系统输出反馈控制设计定理.
推论2 ??在输出反馈控制器u(t)=Ky(t)下, 正常系统(24)是容许的, 如果满足
其中,
利用定理2求解奇异系统输出反馈控制器参数, 关键在于求解式(22), 式(23).算法的基本思路将定理条件转换为非线性规划求解问题, 并通过Matlab编程实现, 其中目标函数为最小化矩阵A+BKC的范数, 式(22), 式(23)为非线性约束条件, 通过算法求解K保证闭环系统容许性.即求解最优化问题:
式中: q=rank(E); M=E+A-AVUE; N=E+A-EVUA; T=M+N-2E-EVUAVUE; A=A+BKC.
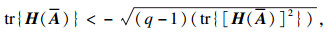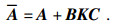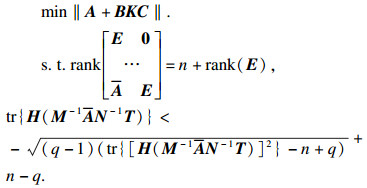3 仿真算例例1?? 含管理在内的石油催化、裂化过程非常复杂.美国Profimatics公司实现了这一过程的建模和控制, 其简化模型为

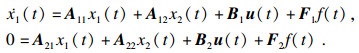(25)

且输出方程为

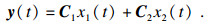(26)

其中: x₁(t)为被调节量, 如再生温度、滑阀位置、鼓风机能力等; x₂(t)是由影响过程、企业效益和反映企业管理政策的一些变量组成的, 如压力、油浆回收率、重油回收率等; u(t)为调节量; f(t)为外部干扰.
系统参数为
整理可得如下的奇异系统:
其中:
由于A₂₂=0, 系统存在脉冲行为, 不满足容许条件.通过定理2, 求解静态输出反馈控制器参数如下:
选取初态x₁(0)=2, x₂(0)=1, 该闭环系统的状态响应如图 1所示.
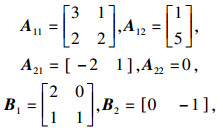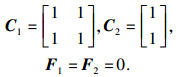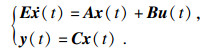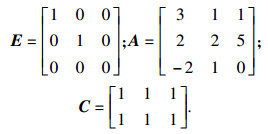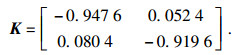图 1(Fig. 1)

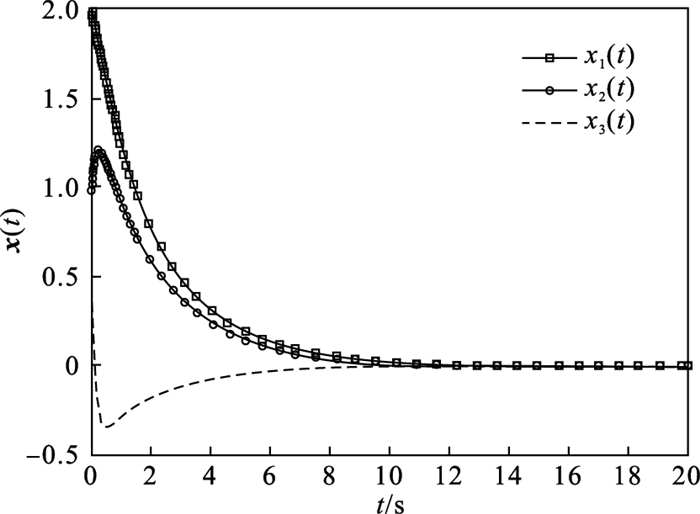图 1 闭环奇异系统状态响应(输出反馈)Fig.1 State response of closed-loop singular system (output feedback)

进一步计算系统的极点为(-2.254 3, -0.120 0), 可见闭环奇异系统是容许的.
例2^[17]?? 考虑如图 2所示的电路.此电路是由电压源、电容器、电感器和一个电流控制器组成.
图 2(Fig. 2)

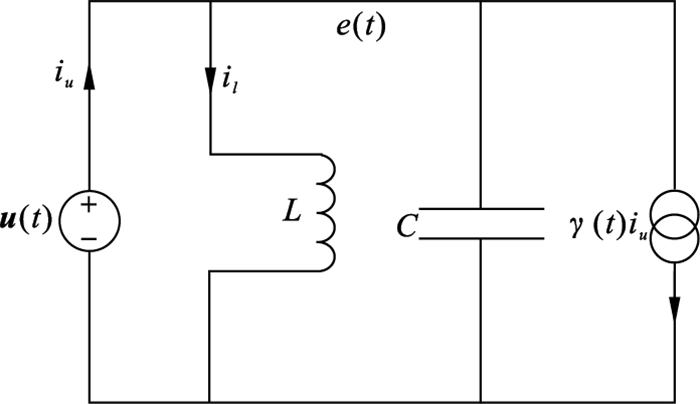图 2 电路结构图Fig.2 The structure of circuit

按照文献[17]建立系统模型:

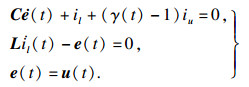(26)

选取C=1 F, L=1 H, γ(t)=2, 令
可以将式(26)表示成奇异系统为
其中:
计算
因此系统存在脉冲行为, 不满足容许条件.通过推论1, 求解得出状态反馈增益矩阵:
进一步计算
可以得出系统是无脉冲的, 同时选取初态x₁(0)=2, x₂(0)=1, 该闭环系统的状态响应如图 3所示.
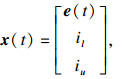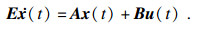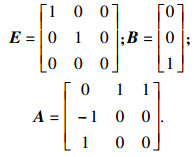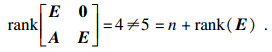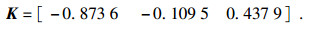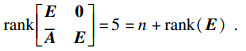图 3(Fig. 3)

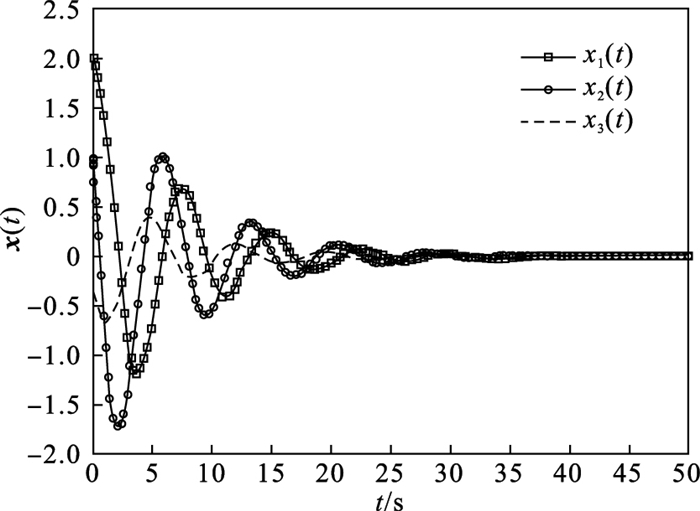图 3 闭环奇异系统状态响应(状态反馈)Fig.3 State response of closed-loop singular system (state feedback)

此时系统的极点为(-0.192 5±1.138 6i), 可见闭环奇异系统是容许的.
例3 ??考虑如下的正常线性系统:

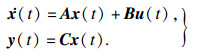(27)

其中:
取初态x₁(0)=3, x₂(0)=1, x₃(0)=-1, 该开环系统的状态响应如图 4所示.由图 4可以看出系统是不稳定的.
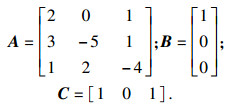图 4(Fig. 4)

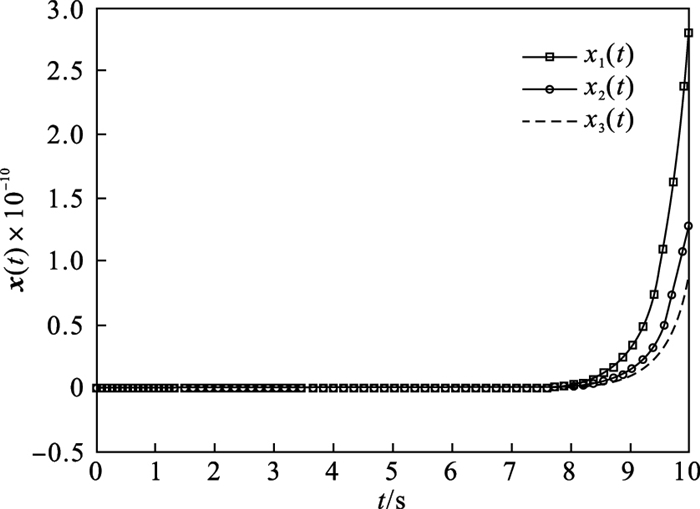图 4 开环系统状态响应Fig.4 State response of open-loop system

进一步由推论2可得输出反馈增益矩阵为
选取相同初态, 该闭环线性系统的状态响应如图 5所示.
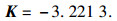图 5(Fig. 5)

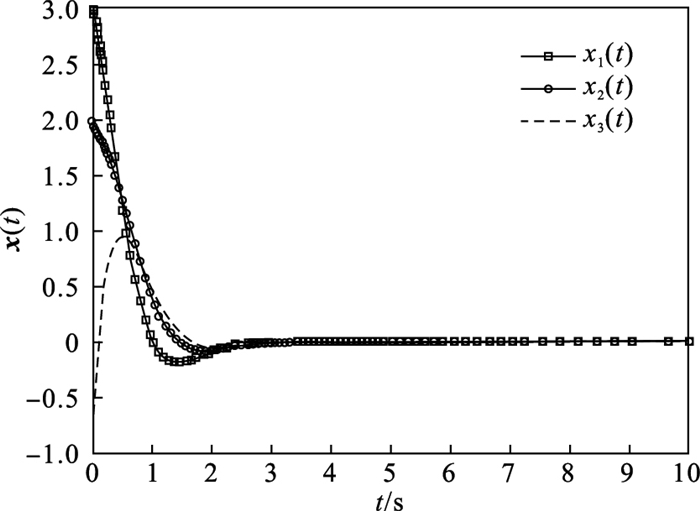图 5 闭环线性系统状态响应Fig.5 State response of closed-loop linear system

此时闭环线性系统的极点为(-0.259 6±0.270 7i, -0.153 1), 所以此系统是稳定的.
4 结语本文针对奇异系统的容许性和输出反馈设计问题展开研究.利用矩阵迹不等式理论, 提出该类系统容许性代数判据和静态输出反馈控制器设计方法.从根本上避免了已有静态输出反馈设计方法中求解双线性不等式条件的难点问题.同时, 对于奇异系统的状态反馈设计以及正常系统的输出反馈设计问题, 本文所提方法仍然有效.最后, 通过仿真例子证明了所提方法的可行性与有效性.
参考文献

[1]	杨冬梅, 张庆灵, 姚波, 等. 广义系统[M]. 北京: 科学出版社, 2004. (Yang Dong-mei, Zhang Qing-ling, Yao Bo, et al. Descriptor systems[M]. Beijing: Science Press, 2004.)
[2]	Duan G R. Analysis and design of descriptor linear systems[M]. Berlin: Springer, 2010.
[3]	Xu S Y, Lam J. Robust control and filtering of singular systems[M]. Berlin: Springer, 2006.
[4]	蔡壮, 张国良, 宋海涛, 等. 基于干扰观测器的一类奇异系统H∞控制[J]. 控制理论与应用, 2017, 34(4): 551-556. (Cai Zhuang, Zhang Guo-liang, Song Hai-tao, et al. H∞ control for a class of singular systems via disturbance observer based control method[J]. Control Theory and Applications, 2017, 34(4): 551-556.)
[5]	常华, 楼顺天, 方洋旺. 基于不完全转移率的连续Markov跳变奇异系统的H∞控制[J]. 控制与决策, 2014, 29(10): 1839-1844. (Chang Hua, Lou Shun-tian, Fang Yang-wang. H∞ control of continuous-time Markov jump singular systems subject to incomplete transition rates[J]. Control and Decision, 2014, 29(10): 1839-1844.)
[6]	黎婕, 林崇, 陈兵, 等. 一类时滞矩形广义系统的镇定[J]. 控制工程, 2020, 27(1): 42-48. (Li Jie, Lin Chong, Chen Bing, et al. Stabilization for time-delay rectangular descriptor systems[J]. Control Engineering of China, 2020, 27(1): 42-48.)
[7]	Yen L H, Phat V N. Stability analysis of linear polytopic descriptor systems using a novel copositive matrix approach[J]. IEEE Transactions on Automatic Control, 2019, 64(11): 4684-4690. DOI:10.1109/TAC.2019.2902717
[8]	Ku C C, Chang W J, Tsai M H, et al. Observer-based proportional derivative fuzzy control for singular Takagi-Sugeno fuzzy systems[J]. Information Sciences, 2021, 570: 815-830. DOI:10.1016/j.ins.2021.01.023
[9]	Toker O. On the NP-hardness of solving bilinear matrix inequalities and simultaneous stabilization with static output feedback[C]//Procceding of 1995 American Control Conference. Seattle: IEEE, 1995: 2525-2526.
[10]	Bara G I, Boutayeb M. Static output feedback stabilization with performance for linear discrete-time systems[J]. IEEE Transactions on Automatic Control, 2005, 50(2): 250-254. DOI:10.1109/TAC.2004.841922
[11]	Fabiano D A. New sufficient LMI conditions for static output stabilization[J]. IFAC Proceedings Volumes, 2013, 46(2): 184-189. DOI:10.3182/20130204-3-FR-2033.00137
[12]	史书慧, 张庆灵, 杨春雨, 等. 广义系统静态输出反馈控制的一个新方法[J]. 东北大学学报(自然科学版), 2010, 31(6): 761-764. (Shi Shu-hui, Zhang Qing-ling, Yang Chun-yu, et al. A new approach to static output feedback control for singular systems[J]. Journal of Northeastern University(Natural Science), 2010, 31(6): 761-764.)
[13]	Wang J, Ma S, Zhang C. Finite-time H∞ control for T-S fuzzy descriptor semi-Markov jump systems via static output feedback[J]. Fuzzy Sets and Systems, 2018, 365: 60-80.
[14]	Zhang Y, Liu C, Mu X. Robust finite-time H∞ control of singular stochastic systems via static output feedback[J]. Applied Mathematics and Computation, 2017, 218(9): 5629-5640.
[15]	马跃超, 张庆灵, 童松. 一类动力系统的稳定性及镇定[J]. 工程数学学报, 2007, 24(1): 175-178. (Ma Yue-chao, Zhang Qing-ling, Tong Song. Stability and stabilization for a class of dynamic systems[J]. Chinese Journal of Engineering Mathematics, 2007, 24(1): 175-178.)
[16]	徐常青, 杜先能. 高等代数方法与应用[M]. 合肥: 安徽大学出版社, 2002. (Xu Chang-qing, Du Xian-neng. Advanced algebra method and application[M]. Hefei: Anhui University Press, 2002.)
[17]	M?rz R, Riaza R. Linear differential-algebraic equations with properly stated leading term: A-critical points[J]. Mathematical and Computer Modelling of Dynamical Systems, 2007, 13(3): 291-314.