许家忠¹, 赵辉¹, 付天宇², 张成东¹
1. 哈尔滨理工大学 自动化学院, 哈尔滨 150080;
2. 哈尔滨理工大学 机械动力工程学院, 哈尔滨 150080
收稿日期：2021-04-25
基金项目：国家自然科学基金重点资助项目(91948202); 黑龙江省应用技术研究与开发计划项目(GA20A401)。
作者简介：许家忠(1977-)，男，黑龙江哈尔滨人，哈尔滨理工大学教授，博士生导师。

摘要：为了解决在电磁感应加热碳纤维增强复合材料(carbon fiber reinforced polymer, CFRP)过程中, 因系统抗干扰性弱、响应速度慢导致的CFRP成型质量差的问题, 提出了一种基于改进粒子群优化的模糊PID(improved particle swarm optimization fuzzy PID, IPF-PID)控制算法, 利用IPF对PID三个参数进行寻优和自调整.该算法结合PSO和Fuzzy-PID算法的优点, 在避免了陷入局部最优的同时, 保证控制精度和最佳的寻优性能.结果表明, 该算法在增强控制器的自适应能力和减小调整时间方面效果显著.比传统的PID算法具有更小超调和稳态误差, 更适用电磁感应加热CFRP温度控制系统.
关键词：感应加热粒子群算法模糊控制碳纤维增强复合材料辨识
Temperature Control Algorithm of Induction Heating CFRP
XU Jia-zhong¹, ZHAO Hui¹, FU Tian-yu², ZHANG Cheng-dong¹
1. School of Automation, Harbin University of Science and Technology, Harbin 150080, China;
2. School of Mechanical and Power Engineering, Harbin University of Science and Technology, Harbin 150080, China
Corresponding author: XU Jia-zhong, E-mail: xujiazhong@126.com.

Abstract: In order to solve the problem of poor molding quality of CFRP(carbon fiber reinforced polymer) caused by the system's weak anti-interference, slow response speed during the induction heating of CFRP, a Fuzzy-PID algorithm based on improved particle swarm optimization (IPF-PID) was proposed. IPF was used to optimize and self-adjust the three parameters of PID. The algorithm combines the advantages of PSO and Fuzzy-PID algorithm, while avoiding falling into the local optimum, it ensures the control accuracy and the best optimization performance. The results show that the algorithm used to enhance the adaptive ability of the controller and reduce the adjustment time has a significant effect. Compared with the traditional PID algorithm, it has smaller overshoot and steady-state error, and it is more suitable for induction heating CFRP temperature control system.
Key words: induction heatingparticle swarm algorithmfuzzy controlCFRP(carbon fiber reinforced polymer)identify
碳纤维增强复合材料(carbon fiber reinforced polymer, CFRP)具有密度小、比强度高、抗疲劳、耐腐蚀等优点, 在航空航天、体育器材、武器设备、风力发电、船舶、汽车上广泛使用^[1-3].感应加热具有能耗低、加热温度高、加热速度快、可以局部加热、温度易控制、清洁等优点，被众多****应用在CFRP加热固化领域^[4-5].在感应加热CFRP过程中, 温度场的升温历程、温度调整速度以及温度数值的准确性直接影响CFRP的成型质量, 因此控制算法对于感应加热CFRP的制备至关重要.传统的比例-积分-微分(PID)控制器因其结构简单和鲁棒性能而被广泛应用于工业控制中.然而, 当系统具有非线性或不确定性时(例如感应加热CFRP温度控制系统), 固定增益的PID控制器显示出局限性.
控制器的性能对参数的调谐^[6-7]有很大的依赖性.****们已经提出了几种方法来寻找合适的控制器参数集, 如齐格勒-尼科尔斯方法^[8]、蚁群优化算法^[9-10]和神经网络法^[11].但是感应加热系统模型总是随着环境、感应线圈以及目标工件而变化.因此, 神经网络没有用于预训练的数据集.在文献[6, 12-13]中发现, 嵌入了PID控制器结构和结合了FIS的人类专家知识的模糊PID控制器具有卓越的控制性能.Soyguder等^[14]提出了一种自适应模糊PID控制器, 结合暖通系统中温度误差和误差的变化量在线自适应调整PID参数, 具有最小的设置时间并且没有稳态误差.Chang等^[15]对所有的量化因子进行了深入的分析, 并设计了一个自校正模块, 使用有限元分析对自校正模糊逻辑控制器的控制能力进行了仿真, 并在感应加热系统上进行了实验, 验证了所提方法的有效性.Chowdhury等^[16]针对预热回收系统提出了模糊自矫正PID控制器, 测试了在稳态和瞬态热两种情况下的设定点跟踪和干扰抑制能力, 发现模糊自校正PID控制器大大减少了计算时间, 显著提高了控制性能.
Wang等^[17]提出了一种基于变论域模糊控制器的感应加热系统的温度控制方法, 仿真结果表明该温度控制系统的有效性和优越性.上述的研究已经证明了模糊PID在温度控制系统中的有效性, 但是对于感应加热CFRP这种速热系统, 准确的数学模型和温度控制系统的鲁棒性是十分重要的.
本文以COMSOL为平台, 对双线圈感应加热CFRP温度控制系统进行温度场分析计算, 采集感应加热系统从初态到稳态的温度输出数据; 并利用粒子群算法对感应加热CFRP系统进行系统数学模型辨识; 通过比较模型与实际系统的输出, 验证了所辨识的数学模型精确度; 在精确的数学模型基础上, 采用了改进的粒子群优化算法对模糊PID进行参数优化, 同时对比了PID, Fuzzy- PID在动态性能、自适应等方面的优劣.
1 基于粒子群算法的系统辨识为了对未知过程进行预测, 分析感应加热温度控制系统在不同操作条件下的行为, 就需要辨识出合适的数学模型.在本文中辨识问题被描述为一个优化问题, 当系统的实际物理测量响应与参数化模型的模拟响应之间的误差最小时, 表示此时的辨识效果最好.因此系统参数辨识可以看作是通过粒子群算法最小化绝对误差积分(integral absolute error, IAE)来实现的.动态非线性系统的辨识如图 1所示.x(n)，y(n)，，e(n)分别表示系统的输入、系统的真实输出、模型输出和误差, 其中e(n)=y(n)-.
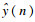
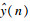
图 1(Fig. 1)

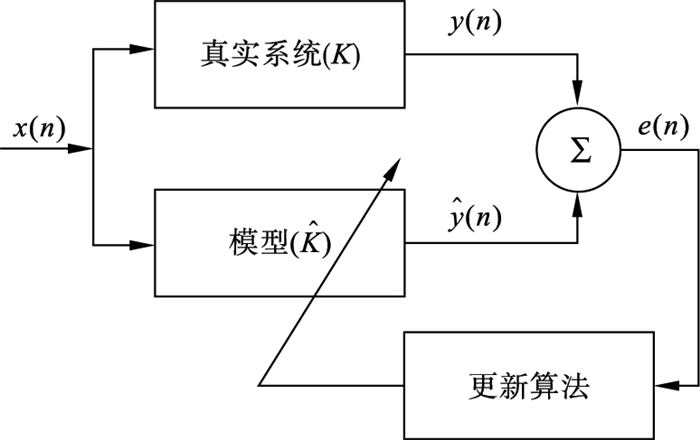图 1 动态系统辨识Fig.1 Dynamic system identification

在感应加热CFRP温度系统辨识过程中, 系统模型结构的选择直接影响到最终辨识结果模型的精度.因此在确定模型结构之前, 需要通过先验知识(如非线性程度、时间常数、纯滞后环节等)作为模型选择的指导, 并以此为基础来提高模型的精度.在感应加热CFRP温度控制系统中传递函数最常用的数学模型如下:

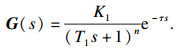(1)

其中: G(s)为系统传递函数; K₁为惯性增益; T₁为惯性时间常数; τ为滞后时间常数; n为系统的阶数, s为时域标志.
以COMSOL为有限元仿真平台, 建立双线圈感应加热CFRP有限元模型.文献[18]已经证明此有限元仿真的准确性, 见图 2.每隔0.5 s采集一次温度数据, 共计3 000个数据.利用PSO算法对感应加热CFRP温度系统模型参数在给定范围内反复地寻优, 使得由模型计算得到的数值结果能最好地拟合采样数据.所得的双温区传递函数如式(2)所示^[19-20], 图 3为感应加热系统辨识曲线.

(2)

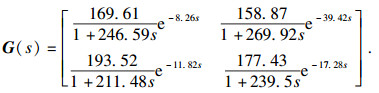图 2(Fig. 2)

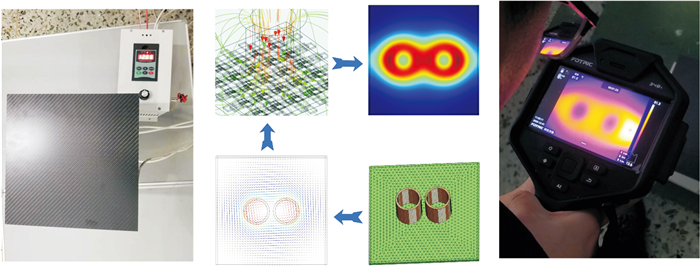图 2 有限元模型建立及验证Fig.2 Establishment and verification of finite element model

图 3(Fig. 3)

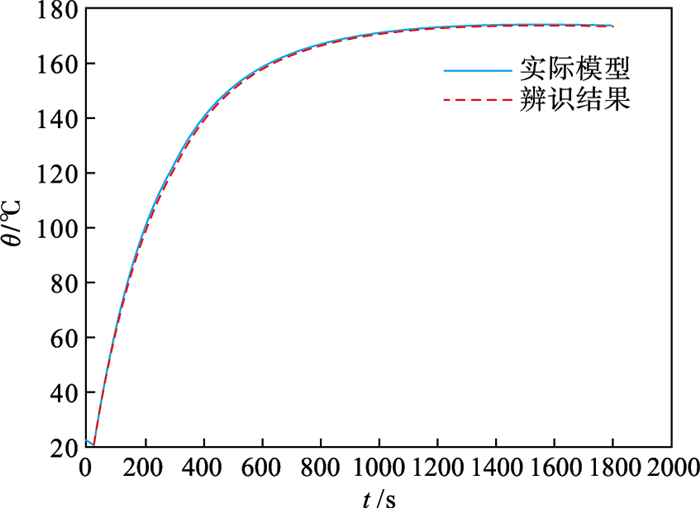图 3 感应加热系统辨识曲线Fig.3 Identification curve of induction heating system

2 改进的粒子群模糊PID算法2.1 Fuzzy-PIDPID控制算法是连续系统中技术最为成熟、应用最为广泛的一种控制算法.PID控制器的传递函数有以下形式:

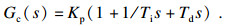(3)

式中: K_p是比例增益；T_i和T_d分别是积分和微分时间常数.本文使用的PID控制的离散时间等效表达式如下:

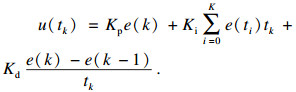(4)

其中: u(t_k)是第k次采样时间的输出; t_k是第k次采样时间步长; e(k)是输入与输出之间的误差; K_p，K_i，K_d分别是比例增益、积分增益和微分增益.
感应加热CFRP温控系统的模糊PID控制系统如图 4所示.
图 4(Fig. 4)

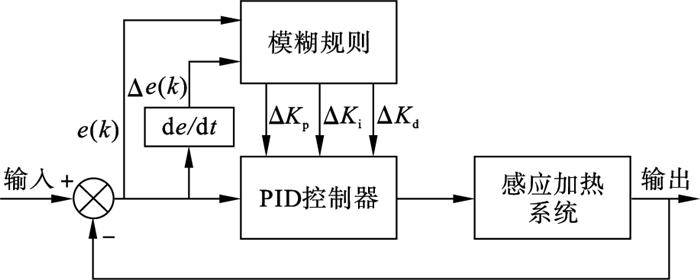图 4 模糊PID原理图Fig.4 Fuzzy PID schematic diagram

图中模糊系统输入语言变量e(k)和误差变化量Δe(k)，输出语言变量ΔK_p，ΔK_i，ΔK_d.为了方便, 将ΔK_p和ΔK_d通过归一化线性变换到[0, 1], 积分时间常数参照微分时间常数确定: T_i=αT_d, 用于计算ΔK_i.
参数整定的模糊规则可以按以下方式表示:
If e(k) is M_i and Δe(k) is N_i，then ΔK_p is H_i, ΔK_d is J_i and α=α_i，i=1, 2, 3, …, m.
其中：M_i，N_i，H_i和J_i代表对应的模糊集; α_i是常数; e(k)，Δe(k)选择高斯形状隶属函数, 如图 5所示, NB, NM, NS, ZO, PS, PM, PB分别代表负大、负中、负小、零、正小、正中、正大.
图 5(Fig. 5)

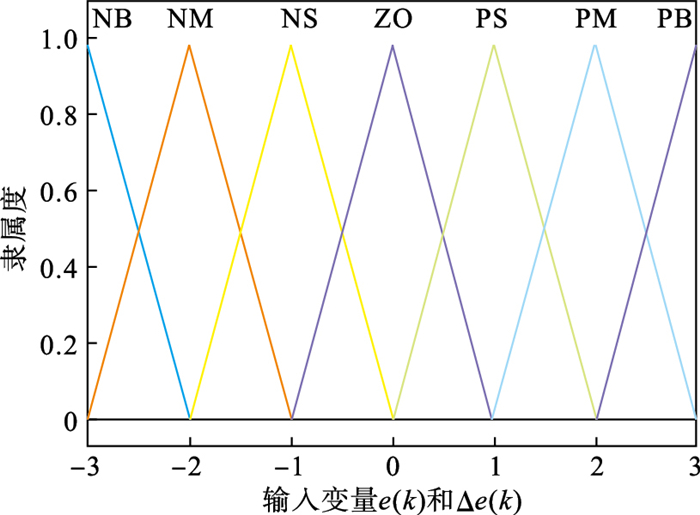图 5 e(k)和Δe(k)隶属度函数Fig.5 Membership function of e(k) and Δe(k)

模糊集H_i和J_i由隶属函数来表征, 其中隶属函数的等级μ和变量x(ΔK_p，ΔK_d)关系很小时, 服从等式μ_small(x)=- ; 两者关系很大时, 服从等式μ_big(x)=- .因此, 采用以下模糊规则:
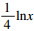
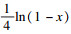
If e(k) is NB and Δe(k) is NS，
then ΔK_p is big, ΔK_d is small and α=4.
以此类推, 系统采用Mamdani法进行模糊推理, 模糊PID控制器有7个语言术语, 其中使用了49个规则, ΔK_p和ΔK_d模糊规则见表 1, 参数关系见图 6.
表 1(Table 1)

表 1 ΔKp和ΔKd模糊规则Table 1 Fuzzy rule of ΔKp and ΔKd Δe(k) e(k) NB NM NS ZO PS PM PB NB B/S/2 B/S/2 B/S/2 B/S/2 B/S/2 B/S/2 B/S/2 NM S/B/3 B/B/3 B/S/2 B/S/2 B/S/2 B/S/3 B/S/3 NS S/B/4 S/B/3 B/B/3 B/S/2 B/B/3 S/B/3 S/B/4 ZO S/B/5 S/B/4 S/B/3 B/S/3 S/B/3 S/B/4 S/B/5 PS S/B/4 S/G/3 B/B/3 B/S/2 B/B/3 S/B/3 S/B/4 PM S/B/3 B/B/3 B/S/2 B/S/2 B/S/2 B/B/3 S/B/3 PB B/S/2 B/S/2 B/S/2 B/S/2 B/S/2 B/B/2 B/B/2 注：B表示big, S表示small, 数字表示α.

表 1 ΔKp和ΔKd模糊规则 Table 1 Fuzzy rule of ΔKp and ΔKd

图 6(Fig. 6)

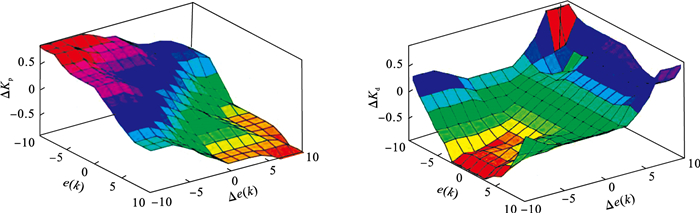图 6 ΔKp和ΔKd表面示意图Fig.6 Surface schematic representations for ΔKp and ΔKd

第i条规则的隶属度μ_i由式(5)确定：

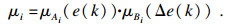(5)

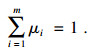式中：μ_Ai是误差e(k)模糊集合A_i的隶属度；μ_Bi是误差变化量Δe(k)模糊集合B_i的隶属度.图 6中的隶属度函数满足:

(6)

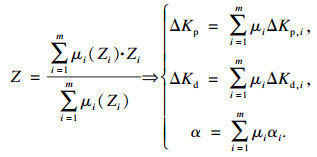然后, 去模糊化则可以使用式(7)：

(7)

式中, ΔK_p，i与ΔK_{d, i}分别对应于第i条规则中隶属度μ_i对应的K_p和K_d的值.采用重心法去模糊化, 虽然计算量更大, 但是防止了快速变化, 保证了控制面的平滑和连续.
2.2 改进粒子群优化的模糊PID传统的模糊PID控制器, 偏差量化因子、偏差变化量化因子、PID参数等都是人为选择的, 依赖于经验知识和模拟调试的参数, 可能无法达到预期的效果.因此, 采用改进的粒子群优化算法对模糊PID进行优化.这是一个实现系统最优控制的优化过程.对于感应加热CFRP温度控制系统, 改进的粒子群优化算法优化了PID控制器中的参数K_p，K_i，K_d.IPF-PID控制器的系统结构如图 7所示, 其中K_e，K_ec是误差和误差变化量的增益.
图 7(Fig. 7)

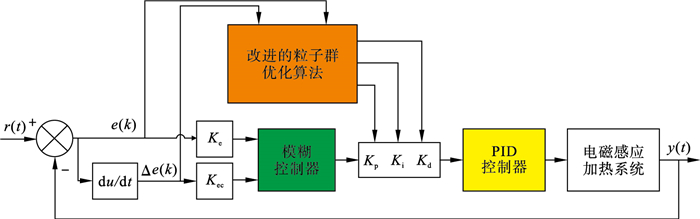图 7 IPF-PID控制原理图Fig.7 Control schematic diagram for IPF-PID

IPF-PID控制过程由粒子群生成、适应度函数、位置和速度更新以及最终终止准则5个步骤组成.流程示意图见图 8.
图 8(Fig. 8)

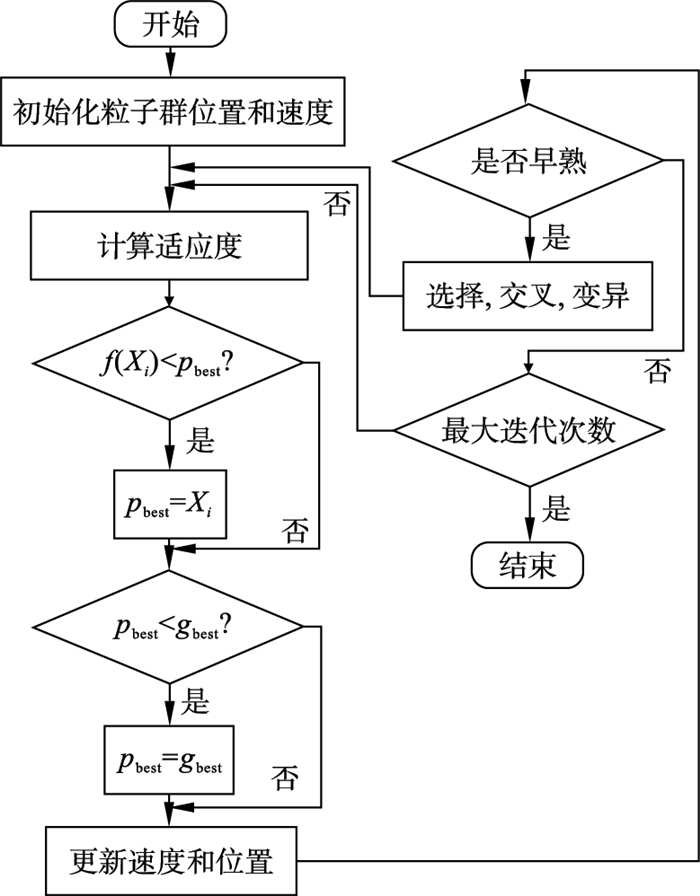图 8 改进粒子群优化流程图Fig.8 Flow chart of improved particle swarm optimization

步骤1 ??初始化粒子群的随机位置x_i和速度v_i.给定粒子数M=100和空间维数N=3, 迭代次数100, 惯性因子ω∈[0.4, 0.9]并在范围上线性变化, 学习因子c₁, c₂∈[0, 3].变异概率p_m∈[0.001, 0.4], 交叉概率p_c∈[0.9, 0.97].
步骤2 ??计算每个粒子的当前适应度值f(X_i), 适应度函数定义为.当且仅当一个特定粒子符合ITAE(时间乘以误差绝对值积分)条件时, 它才被认为是合适的, 否则, 粒子将被自动忽略和移除.
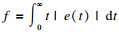
步骤3 ??粒子在每次迭代中更新个体极值p_best和全局极值g_best.当更新个体极值时, 将第i个粒子的当前适应值f(X_i)与该粒子经历的个体极值p_best的适应值进行比较.如果前者更好, 那么更新f(X_i), 否则保持f(X_i)不变.更新全局极值与个体极值操作方式一样.
步骤4 ??更新粒子的速度和位置.当更新当前速度和位置时, 通过式(8)和式(9)更新每个粒子的速度和位置.如果粒子越界, 则在指定范围内随机产生新的位置和速度来替换当前位置和速度.

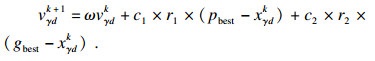(8)

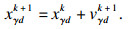(9)

式中: γ=1, 2, …, M, M为粒子总数, 为100;r₁, r₂∈[0, 1], 通常服从正态分布；v_γd^k为粒子在k时刻的速度；x_γd^k为粒子在k时刻的位置，d=1, 2, …, N，表示在第γ个组合中，第d个待寻优的参数.
步骤5 ??如果粒子群优化过程中出现过早收敛于局部最优时, 调用遗传算法进行交叉操作, 重新返回步骤2计算粒子适应度; 否则, 判断迭代次数是否达到100, 如果达到, 新的g_best被认为是最优的PID控制器参数.否则, 循环到步骤2, 直到达到最大迭代次数.
3 仿真分析在本研究中针对一个温区, 利用Matlab/Simulink作为仿真平台建立感应加热CFRP温度控制系统的控制模型.利用IPF-PID算法将需要优化的参数输入到模糊PID控制器仿真模型中, 并绘制适应度值和各参数变化曲线，如图 9所示.从图中可以看出, K_p，K_i，K_d在适应度值较大时变化较剧烈, 在适应度减小时趋于稳定.证明了改进的粒子群算法具有较好的自适应能力和抗干扰特性.伴随温度的变化，PID参数会自动调整.
图 9(Fig. 9)

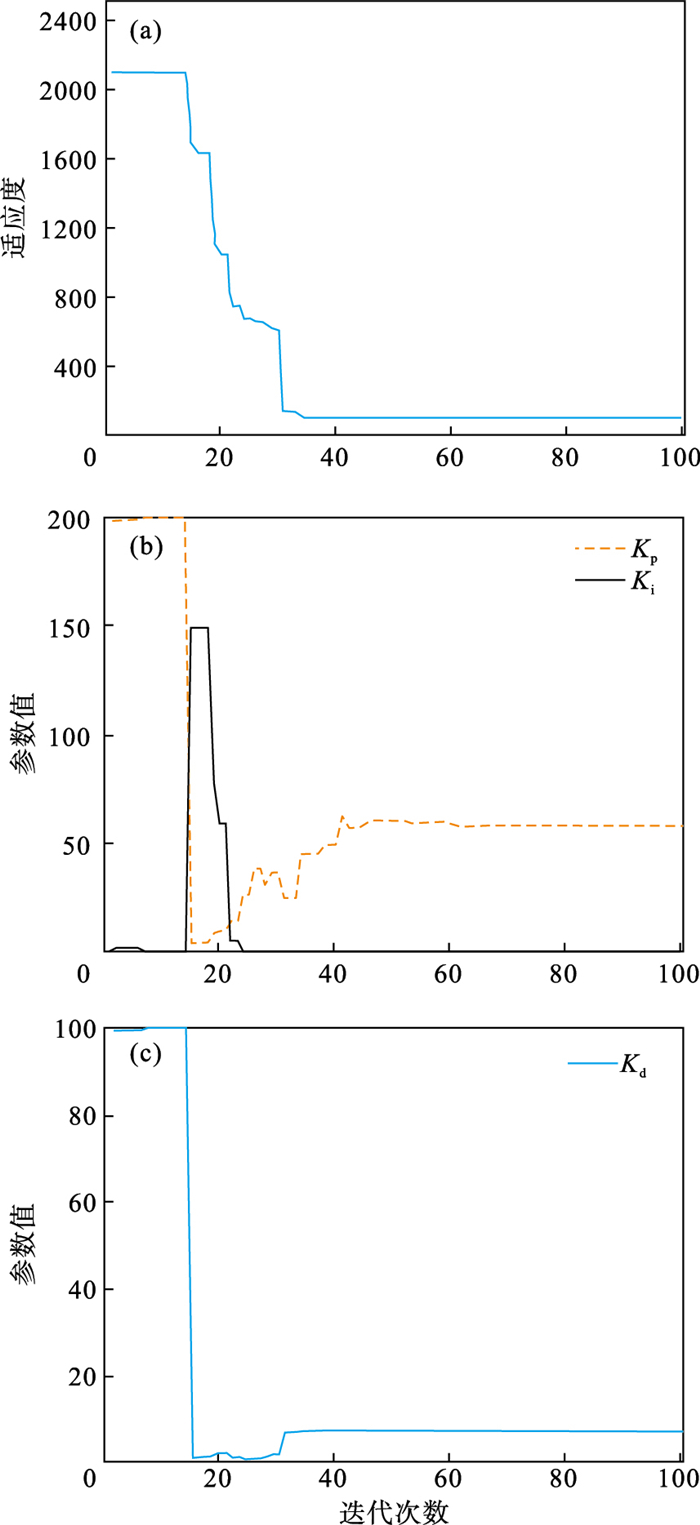图 9 参数值和适应度值随迭代次数变化曲线Fig.9 Values of parameters and fitness (a)—适应度值；(b)—Kp和Ki优化曲线；(c)—Kd优化曲线.

从图 10中可以看到针对感应加热CFRP系统, 三种算法最后都能达到稳定控制.其中IPF-PID控制器的系统呈现最小的上升时间、最小的超调量、最短的调节时间和稳态误差; 而PID控制系统和Fuzzy-PID控制系统响应时间长、超调大、系统调整过渡过程时间较长.可见IPF-PID控制性能显著提高, 超调量小, 调节时间更短, 动态性能更好.
图 10(Fig. 10)

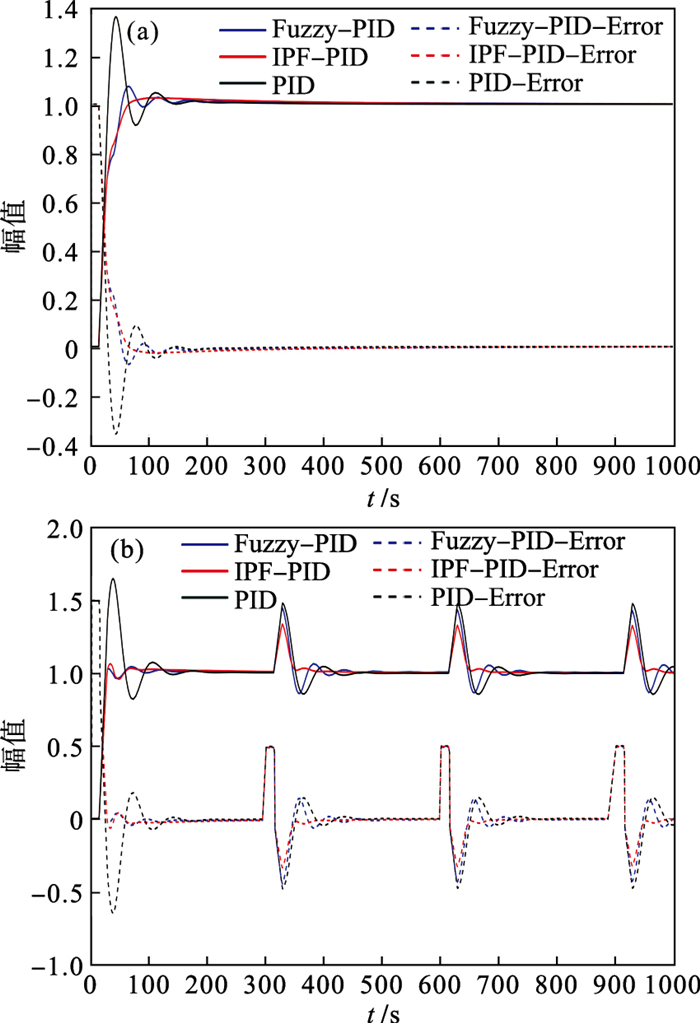图 10 三种算法的自适应性Fig.10 Adaptability of three algorithms (a)—无干扰信号的阶跃响应；(b)—有干扰信号的阶跃响应.

为了评估IPF-PID在感应加热CFRP系统中的鲁棒性和自适应性, 每隔200 s插入一个80 % 参考值的干扰信号, 如图 10b所示.IPF-PID模型稳定性和抗干扰性最佳, 即在施加干扰信号后, 控制器能够保持系统稳定的运行, 在参考值小范围的振荡, 能快速恢复到稳定状态.传统的PID控制器在每次干扰施加点上都会在参考值上下出现较大波动, 其控制性能最差; 而Fuzzy-PID的控制效果居中.证明IPF-PID对对象参数的突然干扰具有很好的抑制效果.
4 实验验证为了验证所提算法的效果, 对感应加热CFRP进行了实验验证.图 11中ADC采用的是8位的ADC0809模数转换器, 处理器采用数字电源专用DSP芯片, 温度传感器输出为4~20 mA, 对应温度范围为0~300 ℃, 感应加热电源采用可编程的HR-5000, CFRP的尺寸为300 mm×300 mm×1.5 mm, 环境温度为20 ℃, 感应加热线圈由利兹线制成, 以减少集肤效应和邻近效应.
图 11(Fig. 11)

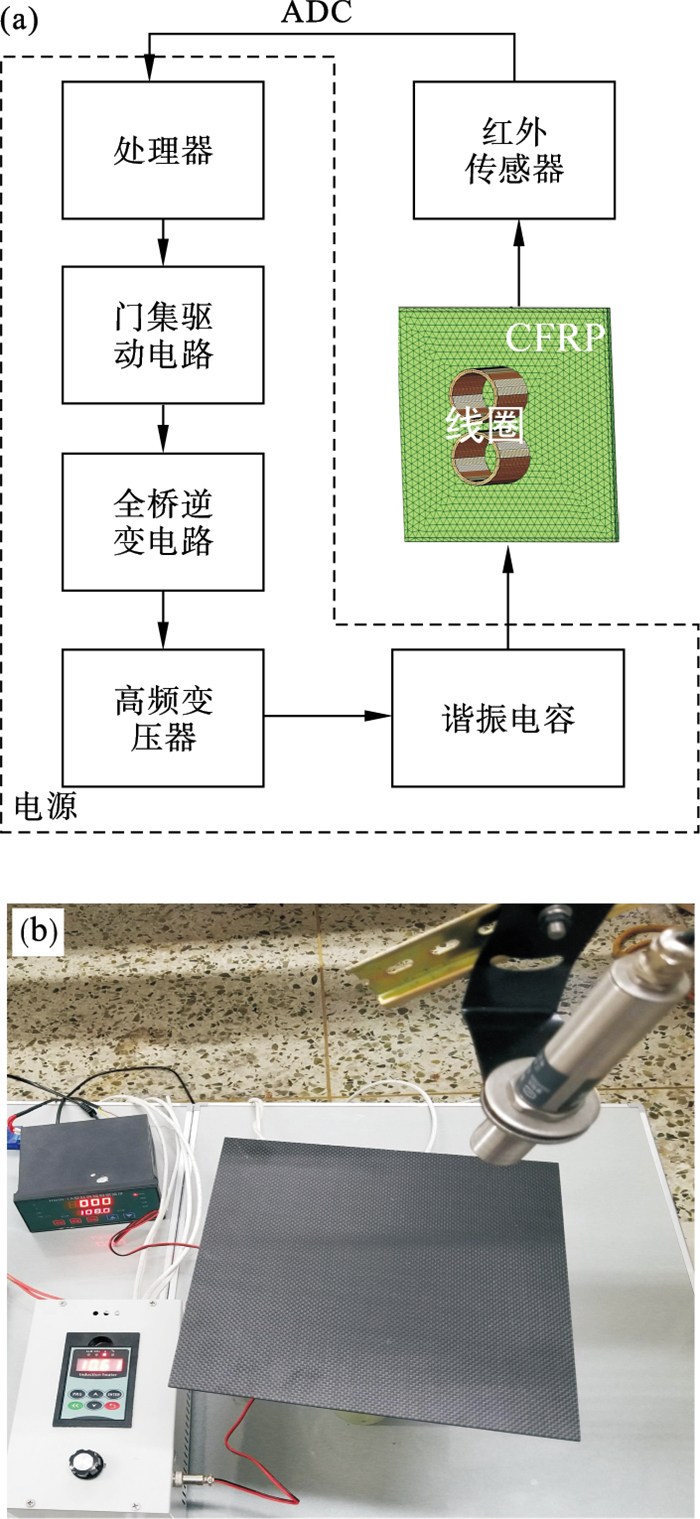图 11 电磁感应加热CFRP实验Fig.11 Induction heating CFRP experiment (a)—实验示意框图；(b)—实验系统.

图 12为所提出的系统在三种算法作用下的升温曲线, 从图中可以看出, 传统PID算法在感应加热系统中的控制效果并不理想, 始终沿着设定的温度数值大幅度的波动.而IPF-PID的曲线尽管也有浮动, 但其上下浮动的数值均在误差允许范围内, 具有较好的控制效果，且此算法具有较小的调节时间, 在实际生产中能极大地缩短加热时间.实验结果和模拟结果吻合得较好, 证实了所提出的IPF-PID算法在感应加热系统中的适用性和有效性.
图 12(Fig. 12)

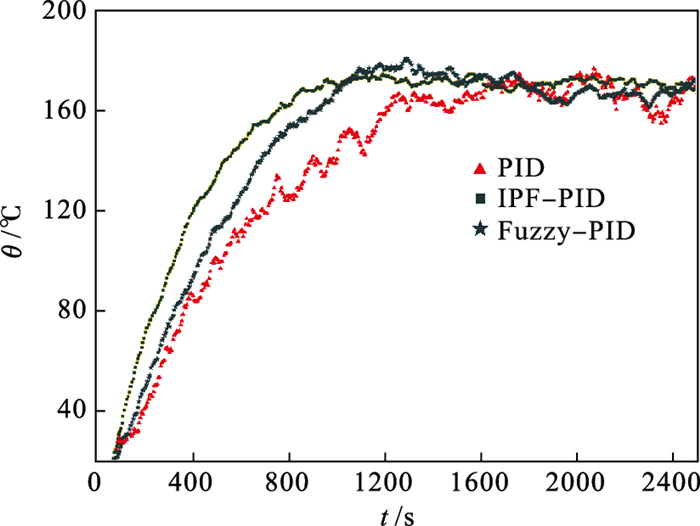图 12 三种算法升温历程曲线Fig.12 Three algorithms heating history curves

5 结论1) 本文利用PSO算法对感应加热CFRP温度控制进行数学模型辨识, 把IAE指标当作评判误差大小的指标.并比较模型输出与实际输出的拟合曲线, 确定PSO算法能够精确地辨识出数学模型的具体参数.
2) 通过对PID, Fuzzy-PID和IPF-PID三种算法的仿真结果对比分析, 得到IPF-PID控制器具有良好的性能, 获得最小的超调量、最短的上升时间和最小的调节时间.通过实验验证此算法的效果, 结果表明模拟结果和实验具有高度的吻合性.
3) 在感应加热CFRP系统中插入扰动信号, 系统没有失去稳定性, 而是在参考点周围呈现小的振荡, 提高了系统的自适应性和跟踪精度.证明了该控制器对外部干扰的容错性.
参考文献

[1]	Karatas M A, G?kkaya H. A review on machinability of carbon fiber reinforced polymer (CFRP) and glass fiber reinforced polymer (GFRP) composite materials[J]. Defence Technology, 2018, 14(4): 318-326. DOI:10.1016/j.dt.2018.02.001
[2]	Das T K, Ghosh P, Das N C. Preparation, development, outcomes, and application versatility of carbon fiber-based polymer composites: a review[J]. Advanced Composites and Hybrid Materials, 2019, 2(2): 214-233.
[3]	Schieler O, Beier U, Mitschang P. Control of the through thickness temperature distribution in carbon composite aerospace parts during induction welding[J]. Journal of Thermoplastic Composite Materials, 2017, 31(12): 1587-1608.
[4]	Frogner K, Cedell T, Andersson M. Induction heating using a 2-phase travelling wave setup[J]. International Journal of Applied Electromagnetics & Mechanics, 2014, 44(2): 217-226.
[5]	Lundstr?m F, Frogner K, Andersson M. A numerical model to analyse the temperature distribution in cross-ply CFRP during induction heating[J]. Composites Part B: Engineering, 2020, 202: 108419. DOI:10.1016/j.compositesb.2020.108419
[6]	Ravari A R N, Taghirad H D. A novel hybrid fuzzy-PID controller for tracking control of robot manipulators[C]//IEEE International Conference on Robotics and Biomimetics. Bangkok, Thailand, 2009: 1625-1630.
[7]	Howell M N, Best M C. On-line PID tuning for engine idle-speed control using continuous action reinforcement learning automata[J]. Control Engineering Practice, 2000, 8(2): 147-154. DOI:10.1016/S0967-0661(99)00141-0
[8]	Meshram P M, Kanojiya R G. Tuning of PID controller using Ziegler-Nichols method for speed control of DC motor[C]// International Conference on Advances in Engineering, Science and Management (ICAESM). Nagapattinam: IEEE, 2012: 117-122.
[9]	Duan H B, Wang D B, Yu X F. Novel approach to nonlinear PID parameter optimization using ant colony optimization algorithm[J]. Journal of Bionic Engineering, 2006, 3(2): 73-78. DOI:10.1016/S1672-6529(06)60010-3
[10]	Varol H A, Bingul Z. A new PID tuning technique using ant algorithm[C]// Proceedings of the 2004 American Control Conference. Boston, 2004: 2154-2159.
[11]	Boubertakh H, Tadjine M, Glorennec P Y. Tuning fuzzy PD and PI controllers using reinforcement learning[J]. ISA Transactions, 2010, 49(4): 543-551. DOI:10.1016/j.isatra.2010.05.005
[12]	Aghaei V T, Onat A, Eksin I, et al. Fuzzy PID controller design using Q-learning algorithm with a manipulated reward function[C]// European Control Conference (ECC). Linz, Austria, 2015: 2502-2507.
[13]	Wen X, Wang J. Fuzzy PID controller based on improved neural network for satellite attitude[C]//The Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC). Qinhuangdao, 2015: 1206-1211.
[14]	Soyguder S, Alli H. Fuzzy adaptive control for the actuators position control and modeling of an expert system[J]. Expert Systems with Applications, 2010, 37(3): 2072-2080. DOI:10.1016/j.eswa.2009.06.071
[15]	Chang C J, Chiang T H, Tai C C. A modified self-tuning fuzzy logic temperature controller for metal induction heating[J]. Review of Scientific Instruments, 2020, 91(6): 064905. DOI:10.1063/5.0006019
[16]	Chowdhury J I, Thornhill D, Soulatiantork P. Control of supercritical organic rankine cycle based waste heat recovery system using conventional and fuzzy self-tuned PID controllers[J]. International Journal of Control, Automation and Systems, 2019, 17(11): 2969-2981.
[17]	Wang Y, Cao F. Induction heating power supply temperature control based on a novel fuzzy controller[C]// 2008 International Conference on Computer and Electrical Engineering. Phuket: IEEE Computer Society, 2008: 615-618.
[18]	Fu T Y, Xu J Z, Zhao H. Analysis of induction heating temperature field of plain weave CFRP based on finite element meso model[J]. Applied Composite Materials, 2021, 28(1): 149-163.
[19]	Qiao J F, Han G T, Han H G, et al. Decoupling control for wastewater treatment process based on recurrent fuzzy neural network[J]. Asian Journal of Control, 2019, 21(3): 1270-1280.
[20]	王爽. 基于PCC的多变量温度控制与智能算法研究[D]. 广州: 华南理工大学, 2012. (Wang Shuang. Research on multivariable temperature control and intelligent algorithm based on PCC[D]. Guangzhou: South China University of Technology, 2012. )