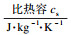张晓虎, 张晟, 赵亮, 董辉
东北大学 冶金学院, 辽宁 沈阳 110819
收稿日期：2021-05-26
基金项目：辽宁省"兴辽英才计划"项目(XLYC1802122)。
作者简介：张晓虎(1995-)，男，内蒙古呼和浩特人，东北大学博士研究生;
董辉(1969-)，男，辽宁锦州人，东北大学教授，博士生导师。

摘要：以年产5×10⁴ t烧结镁砂竖炉为研究对象, 基于多孔介质理论, 建立竖炉内三维稳态气固流动传热模型, 并模拟研究竖炉热工参数对床层内气固传热过程的影响.研究结果表明: 冷却风流量每增加10%, 出口烟气温度降低50 ℃, 出口球团温度降低80 ℃; 冷却段长度每增加5%, 出口球团温度降低25 ℃.以竖炉出口烟气温度和球团温度为优化目标函数, 得到竖炉最适宜结构和操作参数, 即煅烧风流量为2 606.67 m³/h, 冷却风流量为2 203.34 m³/h, 预热煅烧段长度为6.64 m, 冷却段长度为11.70 m.在此竖炉运行工况下, 出口球团温度为288.75 ℃, 出口烟气温度为414.32 ℃.
关键词：氧化镁球团煅烧竖炉气固传热数值模拟参数优化
Numerical Analysis of Gas-Solid Heat Transfer Characteristics in Shaft Furnace for Calcination of Sintered Magnesia
ZHANG Xiao-hu, ZHANG Sheng, ZHAO Liang, DONG Hui
School of Metallurgy, Northeastern University, Shenyang 110819, China
Corresponding author: DONG Hui, E-mail: dongh@mail.neu.edu.cn.

Abstract: Based on the theory of porous media, a three-dimensional heat transfer model for steady gas-solid flow was established for a shaft furnace of sintered magnesia with annual output of 5×10⁴ t. The influences of thermal parameters of the shaft furnace on the gas-solid heat transfer process in the bed were simulated. The results show that, with increasing the cooling air flow by 10%, the outlet flue gas temperature decreases by 50 ℃, and the outlet pellet temperature decreases by 80 ℃. When the cooling section length increases by 5%, the outlet pellet temperature decreases by 25 ℃. Taking the flue gas temperature and pellet temperature at the shaft furnace outlet as the optimization objective functions, the optimum structure and operation parameters of shaft furnace are obtained, including the calcination air flow of 2 606.67 m³/h, the cooling air flow of 2 203.34 m³/h, the preheating calcination section of 6.64 m, and the cooling section of 11.70 m. Under this working condition of the shaft furnace, the outlet pellet temperature is 288.75 ℃, and the outlet flue gas temperature is 414.32 ℃.
Key words: magnesia pelletsshaft furnace for calcinationgas-solid heat transfernumerical simulationparameter optimization
菱镁矿是我国的优势矿产资源之一, 广泛应用于冶金、建材、化工等领域.近20年来, 在高温行业快速发展的推动下, 我国镁质耐火材料取得了长足的发展和进步.镁质耐火原料的主要产品是轻烧氧化镁、烧结镁砂、电熔镁砂, 其产量分别占镁质耐火原料年产量的43 %, 40 %, 17 % ^[1].竖炉作为烧结镁砂生产所需的核心设备, 大多采用实际经验进行生产设计, 缺乏理论性指导.其规格较小, 生产能力低, 多为120~150 t/d; 排料温度较高, 最高可达400 ℃; 能耗大, 国内烧结竖炉单位产品热耗为2 000~2 500 MJ/t, 热耗值高出国外先进生产技术40 % ^[2]; 同时烧结镁砂生产中大气污染问题严重, 炉内最高温度在1 500 ℃以上, 导致热力型NO_x生成速度呈指数增长, 根据企业现有运行参数估算, 全国每年因生产烧结镁砂产生的氮氧化物约为2.2×10⁵~ 2.5×10⁵ t.
目前, 针对烧结镁砂竖炉内气固流动及换热相关研究甚少.Rasul等^[3]基于多孔介质模型, 利用Fluent对2D烧结镁砂竖炉的热力学过程进行了模拟, 讨论了气体和颗粒层温度随炉高的变化.Huang^[4]基于Matlab一维区域分析原理, 耦合求解了竖炉内燃烧、气体和颗粒流动以及炉内传热等过程.肖奋飞等^[5]建立三维重烧竖炉煅烧模型, 采用κ-ε湍流和有限速率反应模型, 同时加入气体辐射传热过程, 获得了气体温度和浓度场分布情况.丛伟^[6]定量分析了辽南地区某机械化新型镁砂竖炉热工行为, 通过热平衡分析了竖炉能量利用情况, 得到了其热效率, 同时指出了生产中存在的不足.
就床层本质而言, 烧结镁砂煅烧竖炉属于颗粒移动床范畴, 其内部流动及传热研究可借鉴现有的颗粒填充床和移动床研究.Karimipour-Fard等^[7]借助多孔介质双能量方程, 研究了气固运动速度比、雷诺数Re、空隙率等参数对逆流式换热床中气固之间换热的影响.Ghadi等^[8]基于多孔介质模型建立Midrex竖炉二维稳态数学模型, 研究了不同气流喷口数量对炉内温度分布和化学反应程度的影响变化规律.Yaman等^[9]通过建立颗粒填充床实验平台研究床层气固传热特性, 发现颗粒密度和直径为气固传热系数主要影响因素.Mahmoudi^[10]以填充有多孔材料的管道为研究对象, 研究了固体热辐射效应对多孔介质内的流体和固体温度场的影响以及对努塞尔数Nu的影响，结果表明, 固相热辐射对固体和流体温度场分布影响较大.Hajipour等^[11]通过数值与解析结合的方法, 探究动量方程中惯性项和黏性耗散对气固换热的影响, 获得了床层内流体的速度场及两相的温度场.Saberinejad等^[12]基于局部热平衡模型, 研究了达西数Da和雷诺数Re等对多孔介质管道内部气固流动及换热的影响, 结果表明传热效果和压力损失都随着达西数的降低而增强.Dickson等^[13]基于局部热非平衡理论, 研究了纳米流体流经多孔介质时热量交换过程, 分析了颗粒浓度对努塞尔数和熵的影响.Al-Sumaily等^[14]对比局部热平衡模型和非平衡模型, 分析粒径对气体流动和气固传热的影响, 同时发现局部热非平衡模型更适合填充床研究.
针对颗粒移动床的研究仍基于局部热平衡模型, 且采用传统Ergun公式计算料层阻力损失, 计算结果与实际情况有所偏差.为解决竖炉煅烧过程中竖炉规模小、余热损失量大、污染重等问题, 本研究基于局部热非平衡模型, 借鉴炉窑三类变量关系^[15], 即竖炉的结构参数和操作参数影响着炉内的传热与流动过程, 进而影响着球团的质量和产量, 开展烧结镁砂煅烧竖炉内气固流动及传热过程的研究, 借此初步解决现有生产设备中存在的热工问题.
1 模型的建立1.1 物理模型及其假设条件参照辽宁某地实际运行的竖炉, 烧结镁砂煅烧竖炉结构形式如图 1所示.菱镁矿经破碎、浮选、压球后, 氧化镁生球团由煅烧竖炉顶部进入炉内, 在重力作用下向下运动, 先后经过预热段及煅烧段, 煅烧完成的熟球团继续下行, 在冷却段冷却后由炉底旋转卸料阀排出.天然气与助燃空气通过布置在竖炉煅烧段的喷嘴喷入炉内, 燃烧产生高温烟气加热生球团.冷却风由炉底侧面通入, 在冷却段冷却熟球团后上行, 经过煅烧段与高温煅烧烟气混合后预热生球团, 最后由炉顶排出.模型中采用非结构化网格, 并对煅烧风入口、冷却风入口，以及烟气出口处网格进行加密.
图 1(Fig. 1)

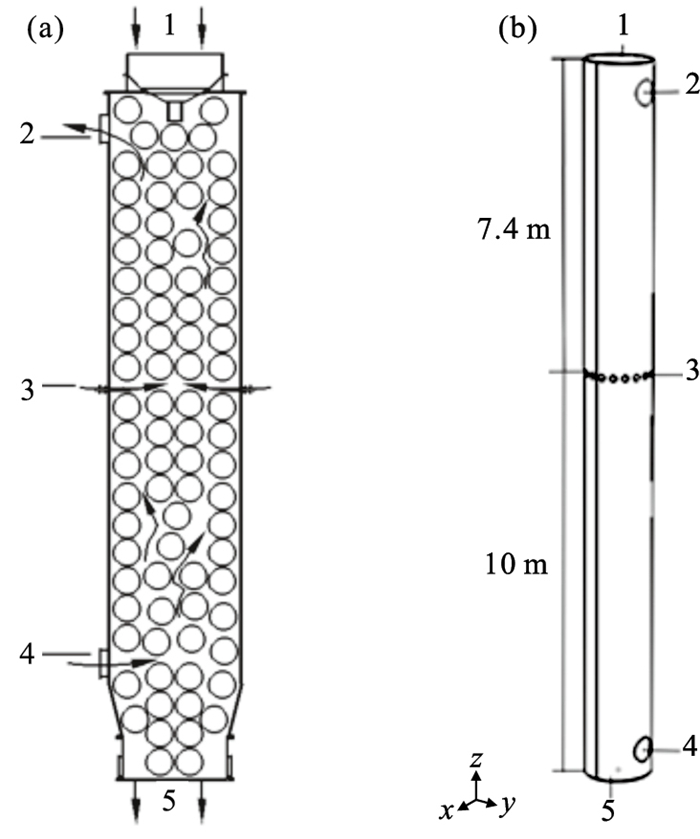图 1 烧结镁砂煅烧竖炉Fig.1 Shaft furnace for calcination of sintered magnesia 1—球团入口; 2—烟气出口; 3—煅烧风入口; 4—冷却风入口; 5—球团出口. (a)—结构示意图；(b)—三维物理模型.

图 1b所示为竖炉三维物理模型, 该竖炉总高17.4 m, 其中煅烧风入口以上长7.4 m; 煅烧风入口以下长10 m; 竖炉直径为1.6 m.
考虑到竖炉内煅烧风、冷却风以及烟气等多种气体同时存在的情况会使炉内气固流动及传热更加复杂, 在保证计算精度的同时对竖炉物理模型做出简化:
1) 运行工况稳定, 各参数在容许范围内视为恒定;
2) 炉内气体视作不可压缩流体, 忽略密度随压力变化情况;
3) 炉内球团为各向同性多孔介质, 在煅烧过程中球团状态和形状保持不变;
4) 炉壁装有保温层, 忽略热损失.
1.2 控制方程本文所采用的各控制方程如下.
1) 连续性方程:

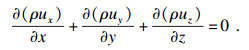(1)

式中: u_x, u_y, u_z为三个方向的速度分量, m/s; ρ为气体密度, kg/m³.
2) 动量方程

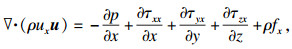(2)

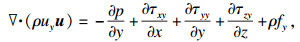(3)

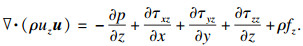(4)

式中: p为流体微元上的压强, Pa; τ为由于黏性作用产生的黏性应力, Pa，下标x, y, z代表方向；f_x, f_y, f_z为体积力, N/m³.
在动量方程中添加源项S_i, 用以描述气体流经多孔介质床层时动量传输过程.

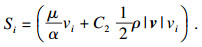(5)

式中: S_i为i方向上动量方程中的源项, i为x, y, z方向之一; 1/α为黏性阻力系数; C₂为惯性阻力系数; μ为气体动力黏度, Pa·s; |v|为气体流动速度, m/s; v_i为i方向上气体流动速度, m/s.
通过自制实验台获得适用于氧化镁球团移动床层的修正Ergun方程, 同时获得基于此方程的多孔介质区域的黏性和惯性阻力系数^[16].

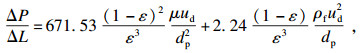(6)

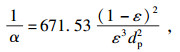(7)

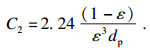(8)

式中: ΔP为气体流过料层时的压差, Pa; ΔL为料层高度, m; d_p为球团当量直径, m; ε为床层空隙率; u_d为气流通过填充层的表观流速, m/s; ρ_f为气流密度, kg/m³.
3) 能量方程
以多孔介质和局部热力学非平衡稳态双能量方程为前提, 分别建立炉内气固两相能量方程, 求解炉内换热过程^[17-18].
气相:

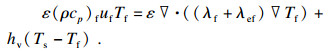(9)

固相:

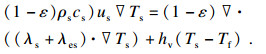(10)

式中: T_f, T_s为气、固平均温度, K; ρ_f, ρ_s为气、固密度, kg/m³; λ_f, λ_s为气、固导热系数, W/(m·K); λ_ef, λ_es为气、固等效辐射导热系数, W/(m·K); h_v为气固对流体积换热系数, W/(m³·K), 由Achenbach准则式^[19]计算.
由于烧结镁砂煅烧竖炉炉内温度整体偏高, 故须考虑炉内辐射换热, 但对于辐射换热来说, 其具体的数学描述很复杂.本文采用近似方法^[20], 将气固辐射换热项折算到等效导热系数中, 获得适用于竖炉的等效辐射换热系数:

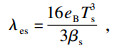(11)

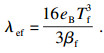(12)

式中: e_B为玻尔兹曼常数, 5.67×10^-8W/(m²·K⁴); β_f, β_s分别为气、固平均消光系数, 1/m.
1.3 边界条件的设定竖炉煅烧风和冷却风入口均设置为速度边界条件, 其速度分别根据烧结镁砂煅烧竖炉配套风机参数和煅烧风成分分析确定; 烟气出口设为压力出口; 壁面为绝热边界; 固体入口以氧化镁球团初始温度为边界条件.
1.4 模型验证模型验证采用实测值与计算结果比对的方法.测量多组烧结镁砂煅烧竖炉出口烟气温度与出口球团温度, 并与模拟结果进行对比, 验证模型的可靠性.实际生产中竖炉生球团处理量为6.7 t/h, 运行时煅烧风流量和温度分别为2 957 m³/h和1 700 K, 冷却风流量和温度分别为2 308 m³/h和298 K.氧化镁球团物性参数如表 1所示.
表 1(Table 1)

表 1 球团物性参数Table 1 Physical properties of pellets 料层空隙率ε 5 337×(T-273.15) 0.152 0.026 0.426 1 720

表 1 球团物性参数 Table 1 Physical properties of pellets

测量所用仪器为崂应烟气分析仪和CO₂便携式烟气测试分析仪(GASBOARD-3400P).对现场烟气进行采样后, 通过烟气分析仪获得烟气温度、压力、流速和流量等参数.出口球团温度通过热电偶测得.烟气温度采样点布置于排烟管道内, 球团温度采样点布置于成品球团堆场.
表 2为正常运行工况下烧结镁砂煅烧竖炉出口烟气和出口球团温度的测量值与计算值的对比.可见, 出口烟气温度和球团温度的平均相对误差分别为8.29 % 和5.94 %.由于模型存在部分简化且采样点处未采取保温手段, 计算得到的误差在允许范围内, 模型可靠.
表 2(Table 2)

表 2 测量值和计算值对比Table 2 Comparison between measured values and calculated values 出口球团温度 出口烟气温度 实测值/K 计算值/K 相对误差/% 实测值/K 计算值/K 相对误差/% 1 596.36 643.50 7.9 546.15 576.11 5.49 2 603.20 643.50 6.68 544.15 576.11 5.87 3 583.42 643.50 10.3 541.15 576.11 6.46

表 2 测量值和计算值对比 Table 2 Comparison between measured values and calculated values

2 模拟结果与分析竖炉在标准工况下运行时, 炉内球团与气体温度分布规律如图 2所示.将温度高于1 573 K的位置定义为煅烧段.由图 2可知, 竖炉煅烧段约为6.5~11 m, 70 % 的煅烧段长度位于煅烧风入口以下位置.同时由图 2可知, 竖炉出口球团温度约为600 K.其原因是70 % 的煅烧段长度位于煅烧风入口以下位置, 占据部分冷却段区域, 使得冷却段长度较短, 熟球团冷却不充分, 导致出口球团温度过高, 造成余热浪费, 同时也影响熟球团质量.
图 2(Fig. 2)

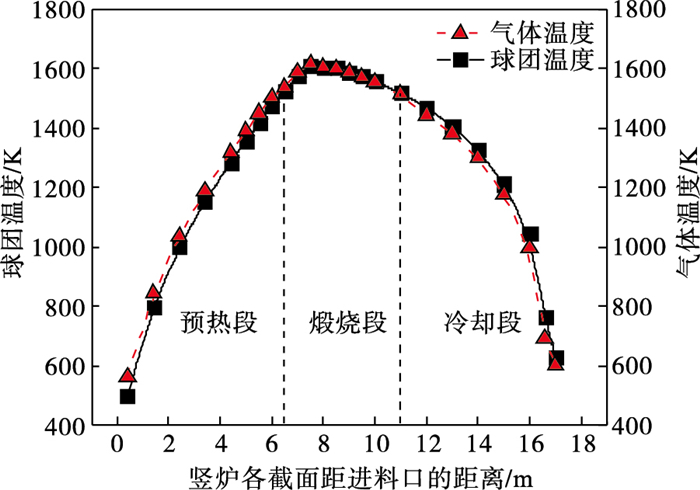图 2 烧结镁砂煅烧竖炉内气体和球团温度分布Fig.2 Temperature distributions of gas and pellets in shaft furnace for calcination of sintered magnesia

图 3及图 4分别为竖炉内气体流线及压力分布图.由图可知, 竖炉内气流分布不均, 气流由垂直于竖炉轴线的方向吹入炉内, 且由多股煅烧风及单股冷却风构成.由于竖炉直径较小, 炉侧鼓入的冷却风吹入炉内后在入口的对侧堆积, 之后盘旋向上流动, 这造成在同一截面上偏离入口一侧的压强高于入口侧, 使得炉内压强呈倾斜带状分布, 导致冷却气流不均匀.冷却风密集的一侧冷却效果好, 成品质量也较好; 冷却风稀疏的一侧冷却效果差, 成品质量差, 最终使得出料口所获得的成品质量不均匀.
图 3(Fig. 3)

图 3 流线分布Fig.3 Streamline distribution

图 4(Fig. 4)

图 4 压力分布Fig.4 Pressure distribution

由以上标准工况分析可知, 目前竖炉存在2个问题: ①出口烟气温度较低.为满足选择性催化还原(selective catalytic reduction, SCR)脱硝, 竖炉出口烟气温度应保持在643~693 K; ②熟球团冷却不充分.出口球团温度过高造成余热浪费.本文遵循炉窑三类变量原则, 针对现有生产竖炉存在的不足, 在生产可调范围内, 探究在不同煅烧风和冷却风流量以及不同煅烧段和冷却段长度下竖炉出口烟气温度和出口球团温度的变化规律, 以改进竖炉煅烧效果的方案.
2.1 煅烧风流量对气固传热过程的影响当冷却风流量一定时, 以实际工况2 957 m³/h为基准, 在可调范围内, 分别设置流量为2 069.9, 2 365.6, 2 661.3, 2 957, 3 252.7, 3 548.4, 3 844.1 m³/h, 研究煅烧风流量对竖炉出口烟气温度和出口球团温度的影响.
图 5为出口烟气温度和出口球团温度随煅烧风流量的变化规律.随着煅烧风流量逐渐增大, 出口烟气和出口球团温度逐渐升高.煅烧风流量每增加10 %, 出口烟气温度先升高20 ℃, 后升高5 ℃, 升温速率逐渐变缓; 出口球团温度变化趋势与出口烟气温度大致相同.
图 5(Fig. 5)

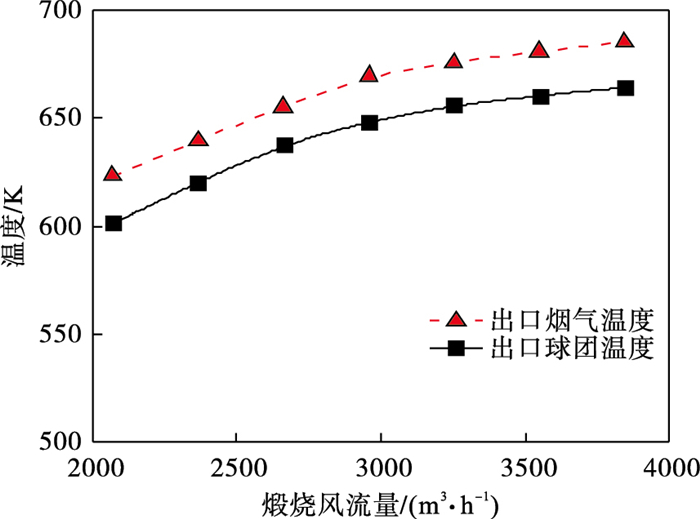图 5 出口烟气温度和出口球团温度随煅烧风流量的变化Fig.5 Temperature variations of outlet flue gas and pellet with calcination air flow

煅烧风主要在煅烧段为球团烧结提供热量, 煅烧风流量增大时单位空间供热加强, 气固换热增强, 所以出口烟气温度升高; 当冷却风一定时, 出口球团温度也随煅烧风流量增大而升高, 且增长趋势与烟气相同.基于出口烟气温度满足SCR脱硝温度前提下出口球团温度最低的原则, 确定适宜的煅烧风流量为2 430~2 960 m³/h.
2.2 冷却风流量对气固传热过程的影响取最小煅烧风流量2 430 m³/h, 同时冷却风流量取值以实际工况2 308 m³/h为基准, 在可调范围内, 分别设置流量为1 615.6, 1 846.4, 2 077.2, 2 308, 2 538.8, 2 769.6, 3 000.4 m³/h, 研究冷却风流量对竖炉出口烟气温度和出口球团温度的影响.取适宜范围内最小煅烧风流量是为了在满足炉内煅烧工艺以及球团煅烧质量的前提下, 进一步分析冷却风流量的影响.
如图 6所示, 冷却风流量对竖炉出口烟气和球团温度影响较为显著, 冷却风流量每增加10 %, 出口烟气温度降低50 ℃, 出口球团温度降低80 ℃.在冷却段, 冷却风是影响温度变化的主要因素, 在冷却风流量足够大的情况下, 出口球团温度可不断降低直至满足理想出口球团温度.但随着冷却风流量的不断增加, 在球团下移速度一定的情况下, 会一定程度降低煅烧段混合烟气的温度, 从而影响球团煅烧质量.在选取适宜冷却风流量时, 应该综合考虑出口球团温度、煅烧段温度以及煅烧时间等条件.基于出口烟气温度满足SCR脱硝温度前提下出口球团温度最低的原则, 初步确定适宜的冷却风流量范围为1 890~2 360 m³/h.
图 6(Fig. 6)

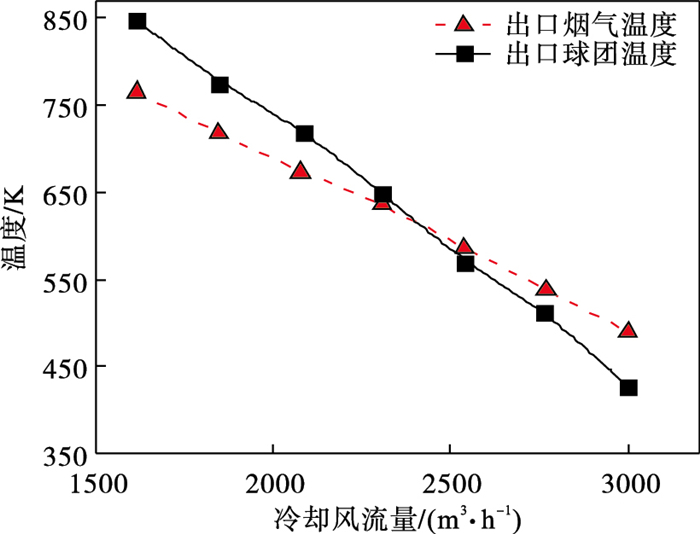图 6 出口烟气温度和出口球团温度随冷却风流量的变化Fig.6 Temperature variations of outlet flue gas and pellet with cooling air flow

2.3 预热煅烧段长度对气固传热过程的影响以煅烧风和冷却风流量适宜取值的平均值2 695和2 125 m³/h为工况, 在保证竖炉内球团煅烧质量的前提下, 探究结构参数对气固传热过程影响.以实际竖炉预热煅烧段长度为基准, 以5 % 为差值, 分别设置预热煅烧段长度为8.14, 7.77, 7.4, 7.03, 6.66, 6.29, 5.92, 5.55 m, 探究长度对出口烟气和球团温度的影响.如图 7所示, 预热煅烧段长度的增减对出口球团温度影响较小, 对出口烟气温度影响较为明显, 随着预热煅烧段长度增加, 出口烟气温度逐渐降低.预热煅烧段长度每增加5 %, 出口烟气温度降低10 ℃.
图 7(Fig. 7)

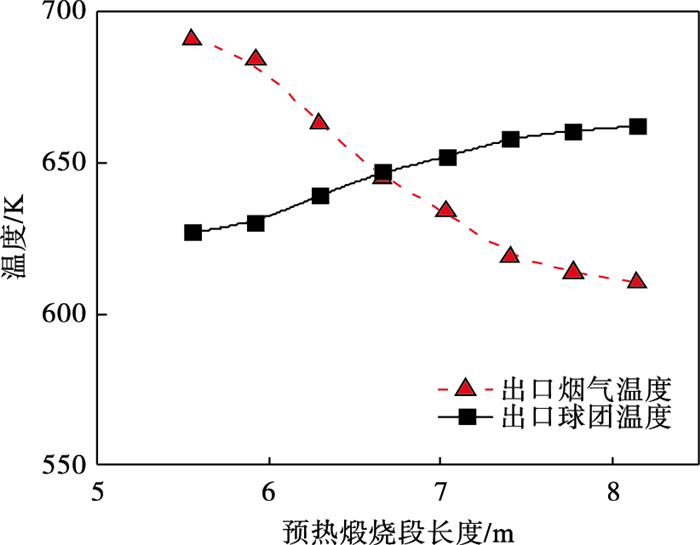图 7 出口烟气及球团温度随预热煅烧段长度的变化Fig.7 Temperature variations of outlet flue gas and pellet with the length of preheating calcination section

随着预热煅烧段长度的增加, 气固间的换热时间增加, 烟气在上行过程中冷却程度也进一步增加, 导致出口烟气温度降低.为满足脱硝温度, 得到预热煅烧段长度适宜范围为6.15~6.64 m.
2.4 冷却段长度对气固传热过程的影响竖炉冷却段长度是影响出口球团温度的最主要结构参数.以实际竖炉冷却段长度为基准, 以5 % 为差值, 分别设置长度为9, 9.5, 10, 10.5, 11, 11.5, 12, 12.5 m, 探究冷却段长度对竖炉出口烟气和球团温度的影响.如图 8所示, 冷却段长度对出口烟气温度影响不显著, 出口球团温度随着冷却段长度的增加逐渐降低.冷却段长度每增加5 %, 出口球团温度降低25 ℃.同时从图 8中可以看出, 随着冷却段长度逐渐增大, 出口球团温度降低速率逐渐变缓, 最终出口球团温度趋于280 ℃.随着冷却段长度进一步增加, 由于竖炉内部结构缺陷, 导致冷却风穿越料层阻力增大, 进而减缓了气固间换热, 使冷却能力减小.
图 8(Fig. 8)

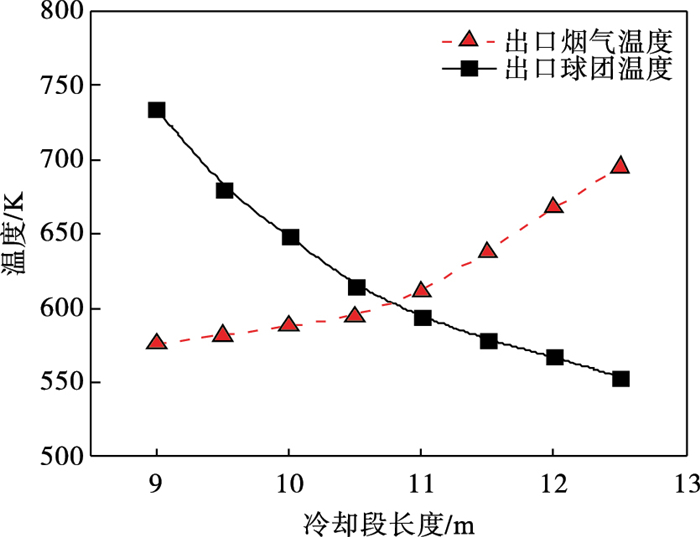图 8 出口烟气温度及球团温度随冷却段长度的变化Fig.8 Temperature variations of outlet flue gas and pellet with the length of cooling section

在考虑煅烧工艺、煅烧质量以及满足脱硝温度的基础上, 选取出口球团温度范围为280~300 ℃.得到冷却段长度适宜范围为11.7~12.5 m.
3 正交试验仿真及优化利用正交试验法对煅烧风流量、冷却风流量、预热煅烧段长度和冷却段长度4个参数进行优化分析.各参数均在其适宜范围内取值, 煅烧风流量为2 430~2 960 m³/h; 冷却风流量为1 890~2 360 m³/h; 预热煅烧段长度为6.15~6.64 m; 冷却段长度为11.7~12.5 m.表 3列出该正交试验的因素与水平.
表 3(Table 3)

表 3 正交试验因素水平表Table 3 Factors and levels of orthogonal test 水平 因素 煅烧风流量/(m3·h-1) 冷却风流量/(m3·h-1) 预热煅烧段长度/m 冷却段长度/m 1 2 430.00 1 890.00 6.15 11.70 2 2 606.67 2 046.67 6.31 11.97 3 2 783.34 2 203.34 6.47 12.24 4 2 960.00 2 360.00 6.64 12.50

表 3 正交试验因素水平表 Table 3 Factors and levels of orthogonal test

选择4参数、4水平、16工况的正交试验, 根据正交表L16(4⁴)试验不同的参数组合, 计算不同运行工况条件下竖炉的出口烟气温度及球团温度.试验方案如表 4所示.
表 4(Table 4)

表 4 多种工况试验方案Table 4 Test scheme of multiple working conditions 工况 煅烧风流量/(m3·h-1) 冷却风流量/(m3·h-1) 预热煅烧段长度/m 冷却段长度/m 1 2 430.00 1 890.00 6.15 11.70 2 2 430.00 2 046.67 6.31 11.97 3 2 430.00 2 203.34 6.47 12.24 4 2 430.00 2 360.00 6.64 12.50 5 2 606.67 1 890.00 6.31 12.24 6 2 606.67 2 046.67 6.15 12.50 7 2 606.67 2 203.34 6.64 11.70 8 2 606.67 2 360.00 6.47 11.97 9 2 783.34 1 890.00 6.47 12.50 10 2 783.34 2 046.67 6.64 12.24 11 2 783.34 2 203.34 6.15 11.97 12 2 783.34 2 360.00 6.31 11.70 13 2 960.00 1 890.00 6.64 11.97 14 2 960.00 2 046.67 6.47 11.70 15 2 960.00 2 203.34 6.31 12.50 16 2 960.00 2 360.00 6.15 12.24

表 4 多种工况试验方案 Table 4 Test scheme of multiple working conditions

对表 4中16种试验方案计算得到16组不同工况下的出口烟气温度和球团温度, 结果如表 5所示.
表 5(Table 5)

表 5 多种工况试验结果Table 5 Test results of multiple working conditions 工况 烟气温度/℃ 球团温度/℃ 工况 烟气温度/℃ 球团温度/℃ 1 350.64 416.03 9 358.31 412.45 2 370.06 325.49 10 325.52 310.08 3 376.77 320.65 11 409.80 357.89 4 346.91 283.44 12 415.51 340.39 5 357.85 431.05 13 346.05 423.27 6 337.14 412.13 14 325.76 408.46 7 414.32 288.75 15 414.42 295.02 8 408.16 332.21 16 438.57 329.91

表 5 多种工况试验结果 Table 5 Test results of multiple working conditions

为同时满足SCR脱硝和出口球团温度最低的要求, 表 5中最佳试验结果为工况7.综合分析, 该烧结镁砂煅烧竖炉最优的结构和操作参数: 煅烧风流量为2 606.67 m³/h, 冷却风流量为2 203.34 m³/h, 预热煅烧段长度为6.64 m, 冷却段长度为11.70 m.通过计算可得优化前后产品热耗分别约为1 700和1 500 MJ/t, 优化后热耗降低约11.8 %.
4 结论1) 基于多孔介质和局部热非平衡模型, 建立烧结镁砂煅烧竖炉气固传热模型, 计算得到出口烟气温度和球团温度测量值与计算值的平均相对误差分别为8.29 % 和5.94 %, 验证了数值模型的可靠性.
2) 在生产可调范围内, 煅烧风流量每增加10 %, 出口烟气温度先升高20 ℃, 后升高5 ℃, 升温速率逐渐变缓; 冷却风流量每增加10 %, 出口烟气温度降低50 ℃, 出口球团温度降低80 ℃; 预热段长度每增加5 %, 出口烟气温度降低10 ℃; 冷却段长度每增加5 %, 出口球团温度降低25 ℃.
3) 对于某产能为5×10⁴ t/a的生产竖炉, 其适宜的操作参数: 煅烧风流量为2 606.67 m³/h, 冷却风流量为2 203.34 m³/h, 预热煅烧段长度为6.64 m, 冷却段长度为11.70 m.
参考文献

[1]	陈庆明, 魏同. 中国镁质原料的发展现状和展望[J]. 耐火材料, 2013, 47(3): 210-214. (Chen Qing-ming, Wei Tong. Status and prospect of China's magnesia raw materials[J]. Refractories, 2013, 47(3): 210-214. DOI:10.3969/j.issn.1001-1935.2013.03.015)
[2]	李鑫, 罗旭东, 于忞. 我国超高温镁砂竖窑回顾及发展[J]. 硅酸盐通报, 2017, 36(2): 503-506. (Li Xin, Luo Xu-dong, Yu Min. Review and development of ultra high shaft kiln of China[J]. Bulletin of the Chinese Ceramic Society, 2017, 36(2): 503-506.)
[3]	Rasul M G, Saotayanan D. Modeling and simulation of thermodynamic processes of vertical shaft kiln used for producing deadburned magnesia[J]. International Journal of Energy and Environment, 2007, 1(1): 37-44.
[4]	Huang B. Computer model of the shaft kiln process[D]. Rockhampton: Central Queensland University, 1999.
[5]	肖奋飞, 张林进, 陈小娟. 高温竖窑煅烧区的燃烧数值模拟[J]. 工业炉, 2014, 36(6): 13-15. (Xiao Fen-fei, Zhang Lin-jin, Chen Xiao-juan. Combustion numerical simulation on calcining zone of high temperature shaft kiln[J]. Industrial Furnace, 2014, 36(6): 13-15.)
[6]	丛伟. 新型重烧氧化镁竖炉能源利用分析[J]. 冶金能源, 2019, 38(3): 61-63. (Cong Wei. Analysis of energy utilization of dead-burned magnesia shaft furnace[J]. Energy for Metallurgical Industry, 2019, 38(3): 61-63.)
[7]	Karimipour-Fard P, Afshari E, Ziaei-Rad M, et al. A numerical study on heat transfer enhancement and design of a heat exchanger with porous media in continuous hydrothermal flow synthesis system[J]. Chinese Journal of Chemical Engineering, 2017, 25(10): 1352-1359. DOI:10.1016/j.cjche.2017.01.015
[8]	Ghadi A Z, Valipour M S, Biglari M. CFD simulation of two-phase gas-particle flow in the Midrex shaft furnace: the effect of twin gas injection system on the performance of the reactor[J]. International Journal of Hydrogen Energy, 2017, 42(1): 103-118. DOI:10.1016/j.ijhydene.2016.11.053
[9]	Yaman O, Kulah G, Koksal M. Surface-to-bed heat transfer for high-density particles in conical spouted and spout-fluid beds[J]. Particuology, 2019, 42: 35-47. DOI:10.1016/j.partic.2018.03.013
[10]	Mahmoudi Y. Effect of thermal radiation on temperature differential in a porous medium under local thermal non-equilibrium condition[J]. International Journal of Heat and Mass Transfer, 2014, 76: 105-121. DOI:10.1016/j.ijheatmasstransfer.2014.04.024
[11]	Hajipour M, Dehkordi A M. Transient behavior of fluid flow and heat transfer in vertical channels partially filled with porous medium: effects of inertial term and viscous dissipation[J]. Energy Conversion and Management, 2012, 61: 1-7. DOI:10.1016/j.enconman.2012.03.001
[12]	Saberinejad H, Keshavarz A. Reciprocating turbulent flow heat transfer enhancement within a porous medium embedded in a circular tube[J]. Applied Thermal Engineering, 2016, 102: 1355-1365.
[13]	Dickson C, Torabi M, Karimi N. First and second law analyses of nanofluid forced convection in a partially-filled porous channel—the effects of local thermal non-equilibrium and internal heat sources[J]. Applied Thermal Engineering, 2016, 103: 459-480.
[14]	Al-Sumaily G F, Nakayama A, Sheridan J, et al. The effect of porous media particle size on forced convection from a circular cylinder without assuming local thermal equilibrium between phases[J]. International Journal of Heat and Mass Transfer, 2012, 55(13/14): 3366-3378.
[15]	董辉, 冯军胜, 李朋, 等. 球团竖炉结构参数影响炉内气体流动的数值模拟[J]. 东北大学学报(自然科学版), 2013, 34(7): 980-984. (Dong Hui, Feng Jun-sheng, Li Peng, et al. Numerical simulation on gas flow affected by constructional parameters of pelletizing shaft furnaces[J]. Journal of Northeastern University (Natural Science), 2013, 34(7): 980-984.)
[16]	张晟, 张晓虎, 董辉, 等. 基于Ergun方程的菱镁球团填充床层阻力特性实验[J]. 东北大学学报(自然科学版), 2021, 42(3): 347-352. (Zhang Sheng, Zhang Xiao-hu, Dong Hui, et al. Experiment of resistance characteristics for magnesite pellets packed bed based on Ergun equation[J]. Journal of Northeastern University(Natural Science), 2021, 42(3): 347-352.)
[17]	Mahmoudi Y, Maerefat M. Analytical investigation of heat transfer enhancement in a channel partially filled with a porous material under local thermal non-equilibrium condition[J]. International Journal of Thermal Sciences, 2011, 50(12): 2386-2401.
[18]	Alazmi B, Vafai K. Analysis of fluid flow and heat transfer interfacial conditions between a porous medium and a fluid layer[J]. International Journal of Heat and Mass Transfer, 2001, 44(9): 1735-1749.
[19]	Hwang K S, Jun J H, Lee W K. Fixed-bed adsorption for bulk component system: non-equilibrium, non-isothermal and non-adiabatic model[J]. Chemical Engineering Science, 1995, 50(5): 813-825.
[20]	Chen X, Xia X L, Liu H, et al. Heat transfer analysis of a volumetric solar receiver by coupling the solar radiation transport and internal heat transfer[J]. Energy Conversion and Management, 2016, 114: 20-27.