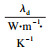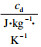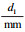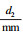杨周¹, 朴银成^1,2, 权哲优^1,3
1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 平壤交通运输大学 机械工程学院, 朝鲜 平壤 999093;
3. 朝鲜国家科学院 机械工程研究所, 朝鲜 平壤 999093
收稿日期：2021-03-16
基金项目：国家自然科学基金资助项目(52172401, U1708254); 中央高校基本科研业务费专项资金资助项目(N2003022)。
作者简介：杨周(1979-)，女，辽宁鞍山人，东北大学副教授，博士。

摘要：为了解决盘式制动器由于摩擦温度过高而导致可靠性降低的问题, 以某种汽车的通风盘式制动器为例, 进行了热-机耦合渐变可靠性灵敏度分析.利用Workbench的“Coupled Field Transient”模块进行热-机耦合分析, 得到了在紧急制动工况下制动器瞬态温度场分布, 然后通过与实验结果对比分析, 确定有限元模型的准确性.根据制动器最高温度不能超过许用温度的关系推测, 利用自适应Kriging代理模型理论建立制动器热-机耦合可靠性功能函数模型.采用自适应Kriging-Monte Carlo模拟(adaptive Kriging-Monte Carlo simulation, AK-MCS)方法进行热-机耦合渐变可靠性灵敏度分析, 确定设计参数对可靠性的影响程度, 并用Monte Carlo法进行结果的验证.结果表明: 制动盘单侧厚度对可靠性的影响最为明显, 制动盘的导热系数、比热容和散热加强筋厚度次之, 制动盘密度影响最小.
关键词：盘式制动器热-机耦合分析自适应Kriging代理模型热-机耦合渐变可靠性可靠性灵敏度分析
Gradual Reliability Sensitivity Analysis of Thermal-Mechanical Coupling of Disc Brakes
YANG Zhou¹, PAK Un-song^1,2, KWON Chol-u^1,3
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. School of Mechanical Engineering, Pyongyang Transportation University, Pyongyang 999093, Democratic People's Republic of Korea;
3. Institute of Mechanical Engineering, State Academy of Sciences, Pyongyang 999093, Democratic People's Republic of Korea
Corresponding author: YANG Zhou, E-mail: yangzhou@mail.neu.edu.cn.

Abstract: In order to solve the problem of reliability decrease due to high friction temperatures, the thermal-mechanical coupling gradual reliability sensitivity analysis is carried out. Taking a car disc brake for example, "Coupled Field Transient" module of Workbench is used to conduct the thermal-mechanical coupling analysis, and transient temperature field distribution of the brake under emergency braking condition is obtained. The accuracy of the finite element model is confirmed by comparing with the experimental results. The adaptive Kriging surrogate model theory is used to establish the reliability performance function model, and the AK-MCS method is used to conduct the gradual reliability sensitivity analysis of thermal-mechanical coupling, and then Monte Carlo method is used to verify calculation results. The results show that the thickness of brake discs has the most obvious influence on the reliability, followed by the thermal conductivity and the specific heat of brake discs, and the thickness of heat-dissipation stiffeners, while influence of the density of brake discs on the reliability is the smallest.
Key words: disc brakethermal-mechanical coupling analysisadaptive Kriging surrogate modelthermal-mechanical coupling gradual reliabilityreliability sensitivity analysis
随着科学技术的发展, 汽车制造水平及汽车安全性能的要求也越来越高，制动器的性能优劣直接决定着车辆的安全性.据统计, 汽车交通事故当中45 % 都是由制动系统失效引起的^[1], 而制动器热衰退是造成事故的主要原因之一.汽车制动是将动能转换为热能的过程, 并且其转换比例为0.9, 由摩擦片和制动盘之间所产生的大部分热能都被制动盘吸收, 使制动盘与摩擦片的温度升高^[2], 一旦温升超过摩擦片的最高温度很容易导致热衰退与制动失效, 甚至可能发生重大的交通事故, 因此盘式制动器热-机耦合失效分析对制动器可靠性以及汽车安全性的提升具有重要的理论和现实意义.
针对盘式制动器温度场问题, 很多****已经作了一些研究.Adamowicz等^[3]在不同初始速度下进行了温度场分析, 并将其与二维模型的计算结果进行对比, 确定采用制动器的三维模型来进行计算能够更好地体现制动盘瞬态温度场的变化情况.Meresse等^[4]对制动盘在制动过程中所产生的局部热流密度进行了实验研究, 采用了逆向热传导法和遥感测温技术来获得制动盘工作时的热量和温度.Belhocine等^[5]利用ANSYS软件对通风盘式制动器进行热-机耦合分析, 并获得在制动阶段制动器的温度场、应力场分布特性, 为相关研究提出了有指导性的建议.周凡华等^[6]利用有限差分法进行了实车计算, 并提出了15次循环制动的温升热力学模型，利用有限元分析方法进行制动器温度场分析.张方宇等^[7]针对制动过程中摩擦副的热负荷-接触应力-磨损耦合行为, 研究应力-磨损耦合分析的数值计算方法.初亮等^[8]针对制动器热衰退而导致制动效能不足的问题, 根据摩擦生热计算热功率, 并建立了制动器升温模型.孙冬野等^[9]在制动器温度场和应力场耦合情况下, 提出了多工况下湿式制动器热可靠性分析方法.虽然制动器温度场以及多场耦合问题的研究取得了重要的进展, 也解决了热衰退及热应力而导致制动失效的问题, 并提出优化方案, 但是将热-机耦合分析与可靠性分析方法相结合, 在所建立的实用和有效的概率可靠性功能函数模型基础上, 通过可靠性灵敏度分析方法, 获得盘式制动器制动性能的重要影响因素的研究还不多见.
本文对盘式制动器进行了热-机耦合渐变可靠性灵敏度分析.首先对汽车在紧急制动工况下进行热-机耦合分析, 得到瞬态温度场分布.为了验证模型的准确性, 与实验进行对比；然后采用自适应Kriging代理模型建立制动器热-机耦合可靠性功能函数模型, 并采用自适应Kriging-Monte Carlo模拟(adaptive Kriging-Monte Carlo simulation, AK-MCS)方法进行可靠性灵敏度分析.利用Monte Carlo方法对分析结果进行了验证, 进一步揭示了影响盘式制动性能的重要参数的可靠性渐变特性.
1 盘式制动器热-机耦合模型1.1 热-机耦合有限元模型与鼓式制动器相比, 通风盘式制动器具有良好的散热性能与稳定的制动性能, 因此被广泛应用.盘式制动器由制动盘、摩擦衬块(包括摩擦片)和制动钳等组成.
本文以文献[2]中的通风盘式制动器为例, 建立参数化模型.盘式制动器零部件的结构参数如表 1~表 3所示.材料参数包括密度、弹性模量、泊松比、导热系数、比热容和热膨胀系数.
表 1(Table 1)

表 1 盘式制动器结构参数Table 1 Structure parameters of disc brakes 零部件 外半径/mm 内半径/mm 厚度/mm 包角/(°) 制动盘 147 88 25 360 摩擦片 145 100 8 52

表 1 盘式制动器结构参数 Table 1 Structure parameters of disc brakes

表 2(Table 2)

表 2 制动盘材料参数Table 2 Material parameters of brake discs 参数 均值 ρd/(kg·m-3) 7 220 Ed/MPa 1.05×105 υd 0.3 λd/(W·m-1·K-1) 48.46 cd/(J·kg-1·K-1) 503 Kd×10-6/K-1 4.39

表 2 制动盘材料参数 Table 2 Material parameters of brake discs

表 3(Table 3)

表 3 摩擦片材料参数Table 3 Material parameters of friction plate 参数 温度/℃ 20 100 200 300 ρp/(kg·m-3) 1 550 1 550 1 550 1 550 Ep/MPa 2 200 1 300 530 320 υp 0.25 0.25 0.25 0.25 λp/(W·m-1·K-1) 0.9 1.1 1.2 1.15 cp/(J·kg-1·K-1) 1 200 1 250 1 295 1 320 Kp×10-6/K-1 10 18 30 32

表 3 摩擦片材料参数 Table 3 Material parameters of friction plate

为了提高仿真计算效率, 在不影响有限元分析精度的前提下, 对制动器进行简化处理.
1.2 制动工况及边界条件的确定为了验证所建立的有限元模型的正确性, 制动工况与文献[2]中的实验工况一样设置.假设汽车以初始速度v₀=100 km/h进行一次紧急制动直到汽车停止, 制动时间为3.1 s, 根据文献[2]可知汽车滚动半径R=0.4 m.车轮的初始角速度ω₀=v₀/R=69.44 s^-1, 汽车在紧急制动时摩擦片上的制动压力为4 MPa.
由于制动时间短且摩擦热量大, 不考虑热辐射的影响.将确定三种对流换热系数, 包括制动盘表面的对流换热系数、摩擦片的对流换热系数和制动盘通风孔的对流换热系数.首先属于受迫对流散热形式的制动盘表面的对流换热系数为

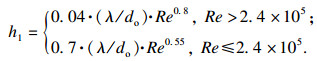(1)

式中: λ为空气导热系数; d_o为制动盘的外径; Re为雷诺数, Re=ω·R·ρ·d_o/μ; ρ为空气的密度; ω为制动器角速度; μ为空气的黏度; R为车轮的滚动半径.
随制动器角速度而变化的制动盘表面对流换热系数为

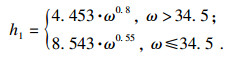(2)

摩擦片安装在制动钳内, 因此可以认为不变.摩擦片的对流换热系数设置为

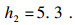(3)

制动盘通风孔的对流换热系数为

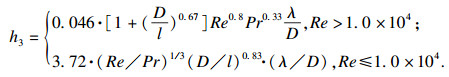(4)

式中: , D为流体力学直径; Re=v·ρ·D/μ，v为风孔中气流的平均速度, v=0.026·ω·(d_o²-d_i²)^0.5·(1+d_o/d_i); Pr为普朗特数, Pr=c_d·μ/λ, c_d为制动盘比热容; l为制动盘长度, l=(d_o-d_i)/2;b为通风槽的宽度; d_o, d_i为制动盘的外径和内径; θ为摩擦片包角; A为摩擦片的面积.
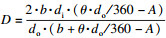
随制动器角速度而变化的通风孔对流换热系数为

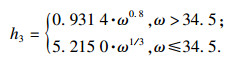(5)

2 仿真结果和实验对比2.1 制动器热-机耦合分析为了更接近实验结果, 除了边界条件的设置外, 还需要设置施加位移约束和初始温度.初始温度设置为与实验环境初始温度相同, 均为30 ℃.
制动盘设置为除了Z方向的旋转自由度外其他自由度都约束, 摩擦片只允许Z方向的位移自由度.运用Workbench “Coupled Field Transient”模块进行热-机耦合分析, 获取在紧急制动工况下制动器瞬态温度场分布.分析结果得知制动时间1.86 s时制动器达到最高温度, 其温度场分布云图见图 1.如图所示汽车在紧急制动工况下制动时间1.86 s时制动器的温度达到230.94 ℃.文献[2]中制动时间为1.9 s时最高温度达到227.12 ℃.本文建立的有限元模型的最高温度与文献[2]中有限元分析结果很接近, 误差可能是网格密度和初始温度设置不同而引起的.
图 1(Fig. 1)

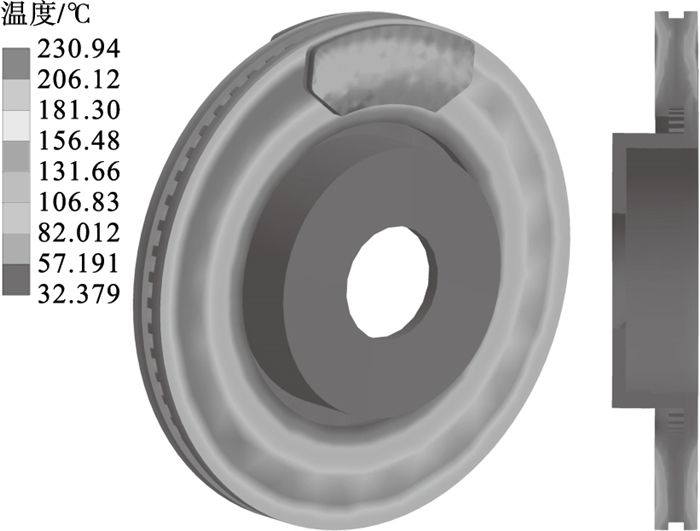图 1 制动时间为1.86 s时制动器温度场Fig.1 Brake temperature field at the braking time 1.86 s

2.2 对比分析本文制动器最高温度与文献[2]的有限元分析结果很相似, 但本文为了更加精确验证模型的正确性, 与实验数据进行对比分析.文献[2]中设计了13个采温点, 其中制动盘周向上布置了8个, 径向方向上设置了5个.由于温度采集方法采用预埋热电偶技术, 因此采集的温度与制动盘表面的温度存在一定的差距.根据文献[2]确定台架试验的采温点的位置.
本文运用Workbench后处理User Defined Result中Surface选项, 在预埋热电偶的平面上获取不同制动时刻的制动盘周向上8个采温点的温度, 而且与实验对比分析.图 2表示不同制动时间的瞬态温度场分布云图.表 4表示在不同制动时刻热-机耦合有限元分析得到的温度和文献[2]中的台架实验获取的温度对比.通过对比分析可知, 有限元分析结果与实验结果比较吻合, 误差都在可接受范围之内, 据此确定本文所建立的制动器有限元分析模型的正确性.
图 2(Fig. 2)

图 2 不同制动时间周向上的8个采温点的温度场分布Fig.2 Temperature field distribution of 8 temperature collecting points in the circumferential direction at different braking time (a)—制动时间为0.75 s; (b)—制动时间为1.3 s; (c)—制动时间为1.9 s; (d)—制动时间为2.5 s; (e)—制动时间为3.1 s.

表 4(Table 4)

表 4 不同制动时间周向上8个采温点的仿真温度和台架实验温度对比Table 4 Temperatures at 8 temperature collecting points in the circumferential direction at different braking time 采温点 仿真温度/℃ 文献[2]中台架实验温度/℃ 0.75 s 1.3 s 1.9 s 2.5 s 3.1 s 0.75 s 1.3 s 1.9 s 2.5 s 3.1 s 周向1 43.198 55.317 65.106 69.901 71.497 43 56 65 70 72 周向2 45.682 59.212 70.209 75.390 76.163 44 59 69 76 79 周向3 47.562 61.448 70.557 76.677 78.714 46 61 71 78 80 周向4 49.633 63.096 75.493 79.525 79.844 49 65 74 80 81 周向5 53.506 65.096 78.274 82.400 83.814 52 68 79 83 85 周向6 47.571 67.220 79.545 84.268 84.857 48 67 78 84 86 周向7 54.352 69.228 80.641 84.170 85.343 53 69 80 84 86 周向8 53.569 65.514 76.990 80.928 82.308 50 65 76 81 83

表 4 不同制动时间周向上8个采温点的仿真温度和台架实验温度对比 Table 4 Temperatures at 8 temperature collecting points in the circumferential direction at different braking time

2.3 参数的不确定性对盘式制动器温升的影响分析由于技术条件、制造安装误差、制造环境、材料特性等因素影响, 使得盘式制动器的材料属性和几何尺寸具有随机性.为了提高计算效率和降低可靠性分析的复杂性, 忽略有限元分析获得的对温度场影响较小的参数.根据有限元分析结果, 确定对温度场影响较大的参数为制动盘密度(ρ_d)、制动盘导热系数(λ_d)、制动盘比热容(c_d)、制动盘单侧厚度(d₁)、制动盘散热加强筋厚度(d₂).由于热-机耦合时间较长, 为了提高效率, 每个参数只选取了3个不同的均值, 并组合建立243组不同设计参数的制动器模型.然后进行热-机耦合分析, 获取相应的制动器最高温度, 如表 5所示.
表 5(Table 5)

表 5 随设计参数变化的制动器最高温度Table 5 Maximum temperature of disc brake varying with design parameters 序号 设计参数 最高温度/℃ 1 6 859 46.037 477.85 7 5 252.17 2 6 859 46.037 477.85 7 6 251.76 3 6 859 46.037 477.85 7 7 251.29 4 6 859 46.037 477.85 8 5 246.50 5 6 859 46.037 477.85 8 6 246.21 ? ? ? ? ? ? ? 239 7 581 50.883 528.15 8 6 215.48 240 7 581 50.883 528.15 8 7 215.43 241 7 581 50.883 528.15 9 5 214.30 242 7581 50.883 528.15 9 6 214.40 243 7 581 50.883 528.15 9 7 214.19

表 5 随设计参数变化的制动器最高温度 Table 5 Maximum temperature of disc brake varying with design parameters

3 制动器热-机耦合可靠性灵敏度分析3.1 盘式制动器热-机耦合可靠性功能函数模型根据可靠性干涉理论, 制动器热-机耦合可靠性功能函数可以表示为

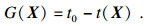(6)

式中: 随机向量X=[ρ_d, λ_d, c_d, d₁, d₂]^T; t(X)为制动器有限元分析得到的制动器最高温度; t₀为制动器最高温度阈值.
传统可靠性分析方法对实际工程可靠性问题计算效率低, 因此基于代理模型的可靠性方法被广泛应用.常用的代理模型包括Kriging模型^[10-14]、神经网络模型^[15-16]、多项式响应面模型^[17]等.这些方法可以通过少量运算得到在概率上代替真实隐式函数的功能函数模型.
Kriging代理模型作为一种估计方差最小的无偏估计模型, 可以近似表达为一个随机分布函数和一个多项式之和^[10], 即

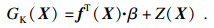(7)

式中: f(X) =[f₁(X), f₂(X), …, f_n-1(X), f_n(X)]^T为随机向量X的基函数，n为基函数个数; β=[β₁, β₂, …, β_n-1, β_n]^T为回归函数的待定系数; Z(X)为服从正态分布N(0, σ²)的随机过程, 其协方差为

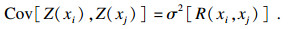(8)

式中: i, j=1, 2, …, m; m表示任意两个训练样本个数; R(x_i, x_j)表示任意两个样本点的相关函数, 常用高斯型相关函数.
根据Kriging理论, 未知点X^*处的功能函数估计值、方差估计值为

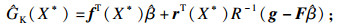(9)

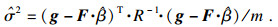(10)

式中: 为β的估计值; g为训练样本的响应值构成的列向量; r(X^*)为训练样本点和预测点之间的相关函数向量; R^-1为相关函数R(x_i, x_j)的反函数；F为由m个样本点处的回归模型组成的m×n阶矩阵.
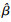
3.2 AK-MCS可靠性灵敏度分析方法采用AK-MCS可靠性分析方法求解结构失效概率的基本思路是：先产生随机变量的MCS样本池, 然后利用自适应学习函数(本文利用U函数)在样本池里不断地挑选对提高失效面拟合精度贡献较大的点来更新Kriging模型, 最终确保模型在一定置信水平下识别MCS样本池内样本的功能函数值.AK-MCS可靠性灵敏度分析方法的流程图如图 3所示.
图 3(Fig. 3)

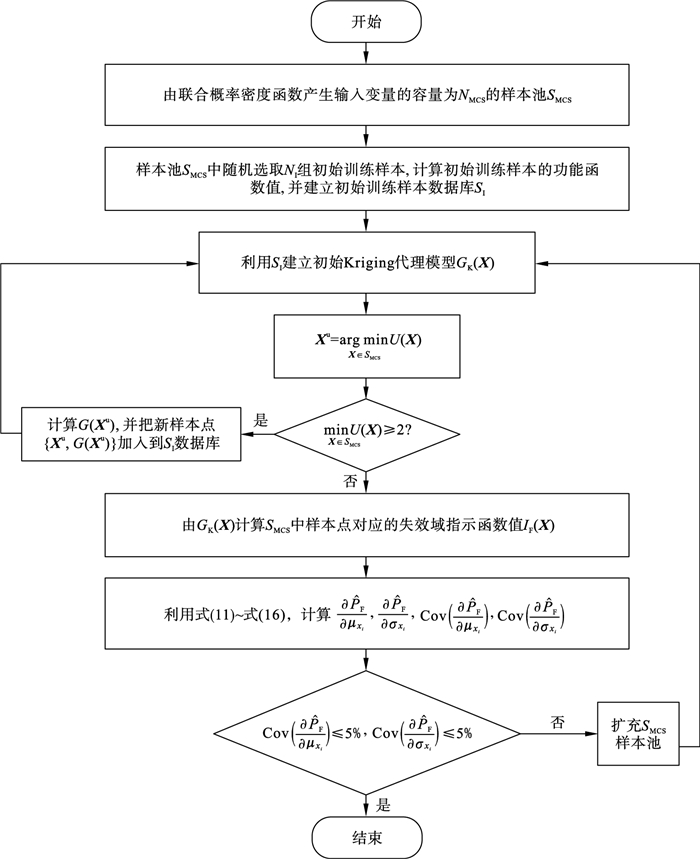图 3 AK-MCS可靠性灵敏度分析方法流程图Fig.3 Flowchart of the AK-MCS reliability sensitivity analysis method

AK-MCS可靠性灵敏度分析方法具体步骤如下:
步骤1 ??根据输入变量的联合概率密度函数产生MCS样本池.该样本池S_MCS由N_MCS组的输入变量组成.
步骤2 ??样本池S_MCS中随机选取N_I组初始训练样本, 计算初始训练样本的功能函数值, 并建立初始训练样本数据库S_I.
步骤3 ??利用S_I建立初始Kriging代理模型G_K(X).
步骤4 ??判别自学习过程是否满足收敛条件.当minU(X)≥2时, 停止自适应学习过程并执行步骤5, 否则利用U学习函数在S_MCS中选取更新的样本点(X^u), 并计算功能函数值.然后把新样本点加入到S_I数据库, 返回步骤3.
步骤5 ??利用当前Kriging代理模型计算S_MCS中样本点对应的失效域指示函数值I_F(X).
步骤6 ??计算均值灵敏度及标准差灵敏度, 其估计值分别为

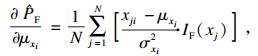(11)

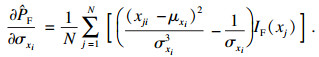(12)

式中：μ_xi为x_i的均值；σ_xi为x_i的标准差；N为输入变量的样本数.
步骤7 ??计算均值灵敏度方差和标准差灵敏度方差, 其估计值分别为

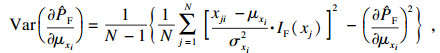(13)

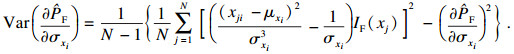(14)

步骤8 ??计算均值灵敏度变异系数和标准差灵敏度的变异系数, 其估计值分别为

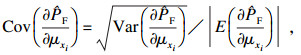(15)

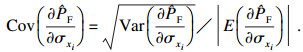(16)

步骤9 ??判别AK-MCS方法的收敛性.当变异系数, <5%时, 即认为可靠性灵敏度的估计值可以被接受, 结束求解可靠性灵敏度的AK-MCS过程, 否则扩充样本池S_MCS并返回步骤3.
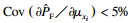
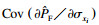
3.3 制动器热-机耦合可靠性灵敏度分析本文利用AK-MCS方法选取5个均值独立变化的设计参数对制动器进行可靠性及可靠性灵敏度分析.图 4所示为不同方法得到的制动器失效概率计算结果, 两种方法的计算结果近似一致.本文利用Monte Carlo法的模型调用次数为10⁶, 而AK-MCS方法的模型调用150次就取得了相近的分析结果.图 5和图 6分别是随参数均值变化的均值灵敏度和标准差灵敏度曲线, 其中图 5a~5e和图 6a~6e是利用AK-MCS方法得到的灵敏度曲线, 图 5f和图 6f是AK-MCS方法与Monte Carlo法的对比.
图 4(Fig. 4)

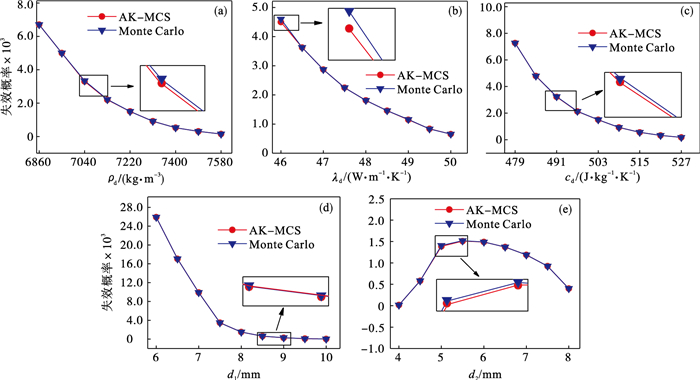图 4 随参数均值变化的失效概率曲线Fig.4 Failure probability curves with the change of parameter mean value (a)—制动盘密度; (b)—制动盘导热系数; (c)—制动盘比热容; (d)—制动盘单侧厚度; (e)—散热加强筋厚度.

图 5(Fig. 5)

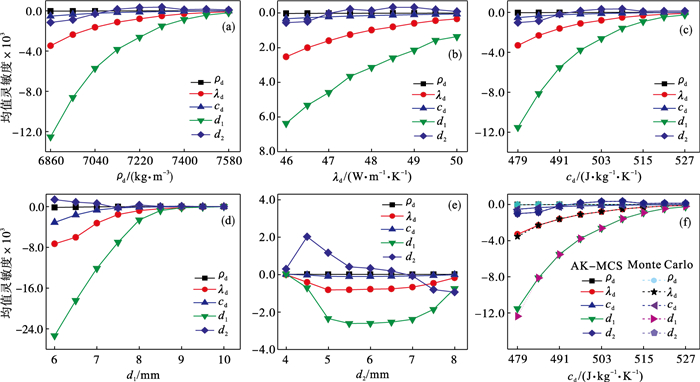图 5 随参数均值变化的均值灵敏度曲线Fig.5 Mean sensitivity curves as the design parameter mean value changes (a)—制动盘密度; (b)—导热系数; (c)—比热容; (d)—制动盘单侧厚度; (e)—散热加强筋厚度; (f)—AK-MCS与Monte Carlo法对比.

图 6(Fig. 6)

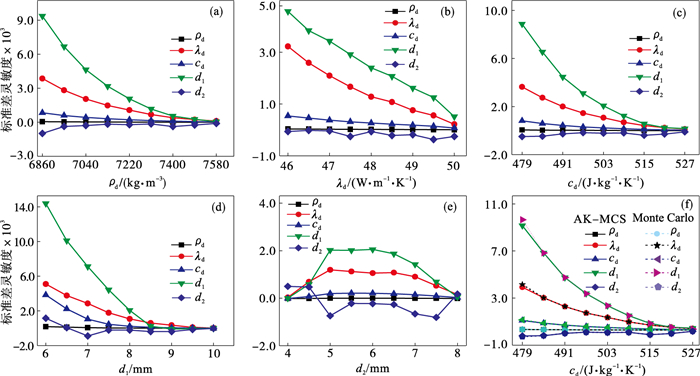图 6 随参数均值变化的标准差灵敏度曲线Fig.6 Standard deviation sensitivity curves as the design parameter mean value changes (a)—制动盘密度; (b)—导热系数; (c)—比热容; (d)—制动盘单侧厚度; (e)—散热加强筋厚度; (f)—AK-MCS与Monte Carlo法对比.

由此可知AK-MCS可靠性分析方法运算效率明显更高.通过可靠性及可靠性灵敏度分析结果可知设计参数的均值和标准差对失效概率的影响程度: 制动器制动盘单侧厚度(d₁)最为明显, 导热系数(λ_d)、比热容(c_d)、散热加强筋厚度(d₂)次之, 制动盘密度(ρ_d)影响最小.
4 结论1) 汽车在紧急制动工况下, 利用Workbench“Coupled Field Transient”模块进行了制动器热-机耦合分析, 将仿真结果与实验结果对比, 确定了有限元模型的精确性.
2) 为了提高计算效率, 确定了对制动器温度场影响较大的5个参数, 对参数在选取3个不同的均值下进行热-机耦合分析.利用自适应Kriging理论建立了温度可靠性功能函数模型.
3) 利用AK-MCS方法进行了与温度阈值为关联的渐变可靠性及可靠性灵敏度分析, 并用Monte Carlo法验证计算结果, 两种方法的计算结果近似一致.AK-MCS方法的模型调用次数为150, Monte Carlo法的模型调用次数为10⁶.AK-MCS方法与Monte Carlo法相比, 为利用Monte Carlo法所调用模型次数的0.015 %.由此可知, AK-MCS可靠性分析方法运算效率明显更高.
4) 通过可靠性灵敏度分析可知, 制动盘单侧厚度的均值和标准差对制动器温度可靠性的影响最为明显, 制动盘的导热系数、比热容和散热加强筋厚度次之, 制动盘密度影响最小.为制动器可靠性稳健优化设计提供理论与定量的依据.
参考文献

[1]	刘献栋, 尚可, 万志帅, 等. 盘式制动器温度模型构建与温度场仿真[J]. 汽车工程, 2016, 38(4): 453-458. (Liu Xian-dong, Shang Ke, Wan Zhi-shuai, et al. Temperature modeling and temperature field simulation for disc brakes[J]. Automotive Engineering, 2016, 38(4): 453-458. DOI:10.3969/j.issn.1000-680X.2016.04.010)
[2]	吴昊. 汽车通风盘式制动器热-结构耦合分析及结构的优化设计[D]. 广州: 华南理工大学, 2016. (Wu Hao. Thermal-structure coupled analysis and structural optimization design of vehicle ventilated disc brake[D]. Guangzhou: South China University of Technology, 2016. )
[3]	Adamowicz A, Grzes P. Analysis of disc brake temperature distribution during single braking under non-axisymmetric load[J]. Applied Thermal Engineering, 2011, 31(6/7): 1003-1012.
[4]	Meresse D, Harmand S, Siroux M, et al. Experimental disc heat flux identification on a reduced scale braking system using the inverse heat conduction method[J]. Applied Thermal Engineering, 2012, 48(5): 202-210.
[5]	Belhocine A, Bouchetara M. Thermal-mechanical coupled analysis of a brake disk rotor[J]. Heat and Mass Transfer, 2013, 49(8): 1167-1179. DOI:10.1007/s00231-013-1161-8
[6]	周凡华, 吴光强, 沈浩, 等. 盘式制动器15次循环制动温度计算[J]. 汽车工程, 2001, 23(6): 411-413. (Zhou Fan-hua, Wu Guang-qiang, Shen Hao, et al. Calculation of disc brake temperature in 15-cycle braking[J]. Automotive Engineering, 2001, 23(6): 411-413. DOI:10.3321/j.issn:1000-680X.2001.06.013)
[7]	张方宇, 桂良进, 范子杰. 盘式制动器热-应力-磨损耦合行为的数值模拟[J]. 汽车工程, 2014, 36(8): 984-988. (Zhang Fang-yu, Gui Liang-jin, Fan Zi-jie. Numerical simulation on the coupling behavior between thermal load, contact stress and wear in a disc brake[J]. Automotive Engineering, 2014, 36(8): 984-988.)
[8]	初亮, 马文涛, 蔡健伟, 等. 基于车速的实时盘式制动器温度模型[J]. 汽车工程, 2016, 38(1): 61-64. (Chu Liang, Ma Wen-tao, Cai Jian-wei, et al. Realtime disc brake temperature model based on vehicle speed[J]. Automotive Engineering, 2016, 38(1): 61-64.)
[9]	孙冬野, 刘升, 郝允志, 等. 高强度制动轮边湿式制动器总成多场耦合下热可靠性分析[J]. 汽车工程, 2019, 41(2): 161-169. (Sun Dong-ye, Liu Sheng, Hao Yun-zhi, et al. Thermal reliability analysis of in-wheel wet brake assembly under high-intensity braking with multi-field coupling[J]. Automotive Engineering, 2019, 41(2): 161-169.)
[10]	Yuan K, Xiao N C, Wang Z L, et al. System reliability analysis by combining structure function and active learning Kriging model[J]. Reliability Engineering and System Safety, 2020, 195: 106734. DOI:10.1016/j.ress.2019.106734
[11]	Cheng K, Lu Z Z. Structural reliability analysis based on ensemble learning of surrogate models[J]. Structural Safety, 2020, 83: 101905. DOI:10.1016/j.strusafe.2019.101905
[12]	Xiao S, Oladyshkin S, Nowak W. Reliability analysis with stratified importance sampling based on adaptive Kriging[J]. Reliability Engineering and System Safety, 2020, 197: 106852. DOI:10.1016/j.ress.2020.106852
[13]	Zhang X F, Wang L, Sorensen J D. AKOIS: an adaptive Kriging oriented importance sampling method for structural system reliability analysis[J]. Structural Safety, 2020, 82: 101876. DOI:10.1016/j.strusafe.2019.101876
[14]	Guo Q, Liu Y S, Chen B Q, et al. An active learning Kriging model combined with directional importance sampling method for efficient reliability analysis[J]. Probabilistic Engineering Mechanics, 2020, 60: 103054. DOI:10.1016/j.probengmech.2020.103054
[15]	Wang Q, Fang H. Reliability analysis of tunnels using an adaptive RBF and a first-order reliability method[J]. Computers and Geotechnics, 2018, 98: 144-152. DOI:10.1016/j.compgeo.2018.02.011
[16]	Yang Z, Pak U, Kwon C. Vibration reliability analysis of drum brake using the artificial neural network and important sampling method[J]. Complexity, 2021, 2021: 5517634.
[17]	Zhang T, Zhou X P, Liu X F. Reliability analysis of slopes using the improved stochastic response surface methods with multicollinearity[J]. Engineering Geology, 2020, 271: 105617.