
 , 董天阔1, 戴卫兵1, 战明3
, 董天阔1, 戴卫兵1, 战明3 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 辽宁省机械装备动力学可靠性 重点实验室, 辽宁 沈阳 110819;
3. 东北大学 信息科学与工程学院, 辽宁 沈阳 110819
收稿日期:2021-01-07
基金项目:国家自然科学基金资助项目(51705068);中央高校基本科研业务费专项资金资助项目(N180703009,N170302001)。
作者简介:姜世杰(1985-),男,辽宁营口人,东北大学副教授。
摘要:由于熔丝成型(fused filament fabrication, FFF)技术逐层沉积的制造工艺特点, 其产品的拉伸性能存在着明显的局限性.为了能够提出切实有效的改进措施, 需要明确FFF产品相应的机理, 即建立本构关系理论模型.基于经典弹性力学理论, 对FFF薄板试件的本构关系进行了理论建模, 完成了试件拉伸性能的解析研究; 然后利用拉伸实验机获得了试件拉伸性能的实验结果; 最后, 分别将X和Z方向打印试件的理论与实验的应力-应变曲线结果相对比, 发现二者吻合度较好, 验证了理论模型的正确性与准确性.
关键词:熔丝成型拉伸性能本构模型应力-应变拉伸实验
Theoretical and Experimental Study on Tensile Properties of Fused Filament Fabrication Thin Plates
JIANG Shi-jie1,2

 , DONG Tian-kuo1, DAI Wei-bing1, ZHAN Ming3
, DONG Tian-kuo1, DAI Wei-bing1, ZHAN Ming3 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Dynamics Reliability of Mechanical Equipment, Shenyang 110819, China;
3. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: JIANG Shi-jie, E-mail: jiangsj@me.neu.edu.cn.
Abstract: Due to the manufacturing layer-by-layer deposition process of the fused filament fabrication (FFF) technology, the tensile properties of the products have obvious limitations. In order to put forward effective improvement measures, the corresponding mechanism of FFF products should be clarified, that is, establishing theoretical constitutive model. Based on the classical elastic mechanics theory, the constitutive model of FFF thin plate samples is set up, and the theoretical analysis on the tensile properties of the samples are completed. Then, the experimental tensile properties of the samples were obtained by using the tensile testing machine.Finally, by comparing the theoretical and experimental results of stress-strain curves of the samples built in both X and Z direction, it is shown that they are in good consistence, verifying the correctness and accuracy of the theoretical model.
Key words: fused filament fabrication (FFF)tensile propertyconstitutive modelstress-straintensile test
3D打印技术是一种累积制造技术, 它以数字模型文件为基础, 运用粉末状金属或塑料等可黏合材料, 通过打印一层层的黏合材料来制造三维的物体[1-2].其中熔丝成型(fused filament fabrication, FFF)技术因其操作简单、成本低廉且环境友好等特点, 成为普及范围最广的快速成型技术之一[3-4].FFF技术的工作原理是利用送丝机构将丝状的原材料送入热熔喷头使其融化, 然后喷头通过设计好的路径和轨迹进行运动, 同时将熔融状态的材料挤出到指定的位置并最终凝固成型, 逐层打印, 层层叠加, 最终堆积成实体, 形成产品[5-7].
FFF技术虽然已经研究了很长一段时间, 但其加工的产品仍然存在明显的缺陷, 如气孔、夹杂物、层间分离等.与传统技术制造的产品相比, FFF产品机械性能较低, 限制了其发展及应用, 因此, 提高成型产品的机械性能是该技术发展的关键方向之一.而要达到提高FFF产品机械性能的目的, 首先就需要明确其相应的机理, 因此需要对FFF产品进行本构关系分析.王富伟等[8]通过拉伸和压缩实验分析了3D打印聚乳酸(polylactic acid, PLA)杆件的应力与应变之间的关系, 得出了PLA杆件的拉伸、压缩强度极限.刘静毅等[9]通过实验以及仿真相结合的方法对3D打印的不同夹芯板结构进行力学性能测试, 得到了夹芯板结构各主要部位的极限应力、应变值.Melenka等[10]通过评估Kevlar纤维增强尼龙复合材料来评估材料的拉伸力学性能, 同时, 采用体积平均法对纤维增强3D打印产品的弹性参数进行了预测, 对高纤维含量的样品预测效果较好.Li等[11]提出了一种连续碳纤维增强3D打印方法和匹配路径控制方法, 通过拉伸试验、三点弯曲试验和动态力学试验, 获得了连续碳纤维增强复合材料的拉伸性能和动态热力学性能.董骏杰等[12]利用MTS疲劳试验机对试件开展拉伸试验, 揭示了具有内部孔洞的3D打印PLA试样的机械性能.然而, 上述研究都是基于实验测试开展的, 缺乏理论支撑; 而相关的理论研究也多为经验公式, 不具有普适性(应用范围局限).
本文针对FFF薄板的本构关系进行了理论模型研究, 得到了试件拉伸性能的理论分析结果; 然后利用拉伸实验机, 对试件完成了实验研究, 获得了试件拉伸性能的实验结果; 最后将理论和实验结果相对比, 验证了理论模型的正确性.本模型将为FFF技术的进一步发展提供一定的理论基础和技术支持.
1 FFF薄板本构关系模型本文所研究的薄板为6层PLA材料黏结而成的FFF薄板, 具有正交各向异性的特点, 因此在研究其本构模型时, 首先作出如下假设: ①层与层之间黏结牢固, 无滑移, 无相对位移, 不考虑层间耦合效应; ②薄层之间黏结良好, 可作为一个整体结构板, 并且黏结层很薄, 其本身不发生变形, 即各单层板之间变形连续; ③薄板虽由多层单层板叠合而成, 但其总厚度仍符合薄板假定[13].基于经典弹性力学理论[14], 考虑正交各向异性特点, FFF薄板的本构关系遵循胡克定律, 广义的胡克定律为
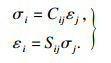 | (1) |
在弹性变形范围内, 应力与应变呈正比例关系, 其比例系数为弹性模量, 单位体积弹性体应变能U为
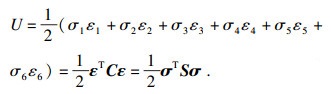 | (2) |
 |
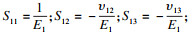
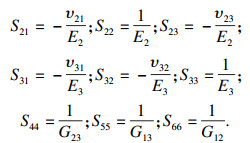 |
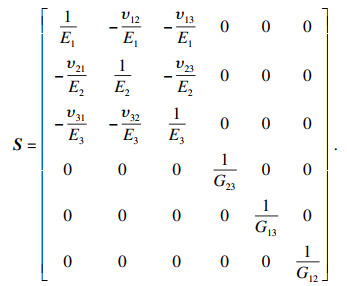 |
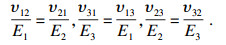 |
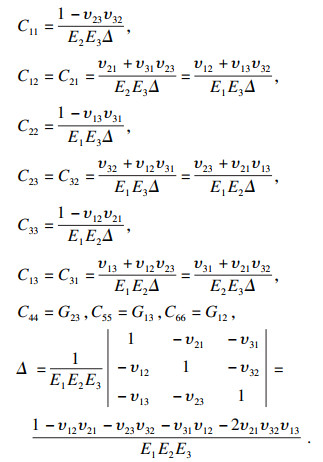 |
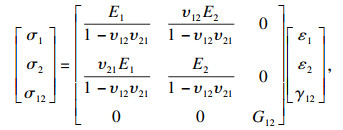 |
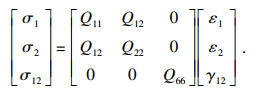 | (3) |
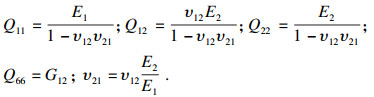 |
1) 应力在任意方向上的转换. 图 1为两种坐标之间的关系, 表示从x轴转向1轴的角度, 以逆时针转向为正.
图 1(Fig. 1)
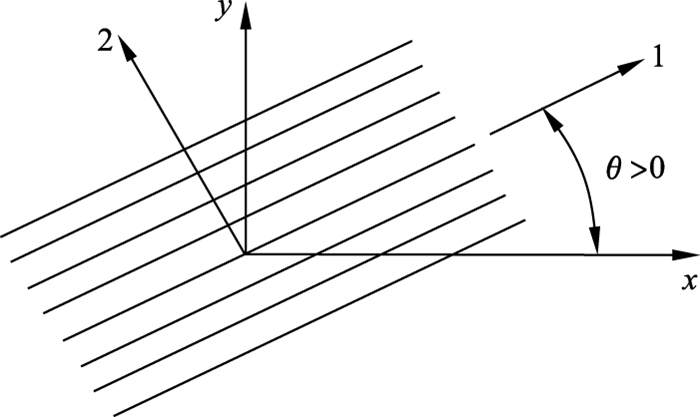 | 图 1 两种坐标间的关系Fig.1 Relationship between the two coordinates |
图 2表示单元体在x方向上的平衡, 得出x方向上的应力关系:
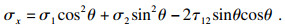 | (4) |
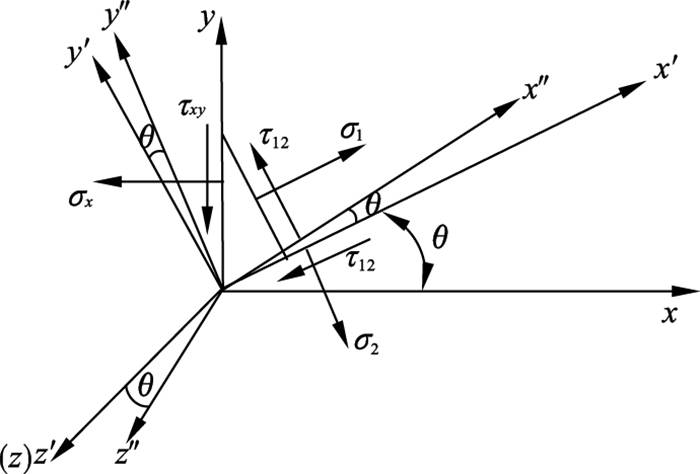 | 图 2 单元体平衡Fig.2 Balance of the element |
同理可以得出
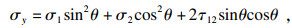 | (5) |
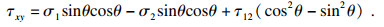 | (6) |
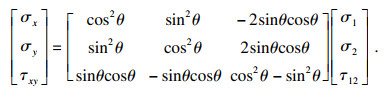 | (7) |
2) 应变在任意方向上的转换. 平面应力状态下单层板在x, y坐标中应变分量为εx, εy, γxy, 主方向与x轴夹角为θ, 主方向应变分量为ε1, ε2, γ12.当单层板边长增量分别为Δx和Δy时,其对角线长度增量Δl可表示为
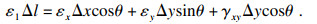 |
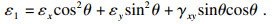 | (8) |
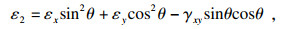 | (9) |
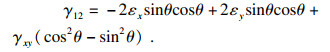 | (10) |
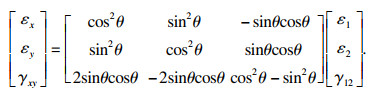 |
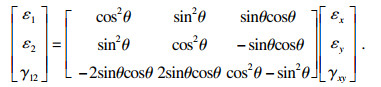 | (11) |
3) 任意方向上的应力-应变关系. 将主轴方向应力-应变关系矩阵,即式(1),代入式(7)与式(11), 并化简后可以得到
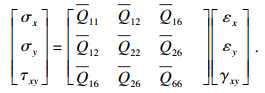 | (12) |
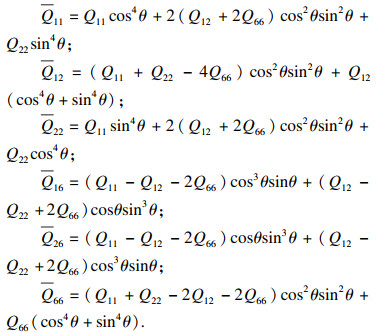 |
2 实验研究2.1 试件准备为了验证理论模型, 本文根据ISO 527-2—2012标准, 利用D-FORCE V2型快速成型设备制备了外形尺寸如图 3所示的拉伸实验试件.其中试件长度、测试宽度及厚度分别为158, 10和2.4 mm.试件材料为PLA, 一种公认的环境友好材料, 具有良好的生物可降解性, 因此得到了广泛应用[15].
图 3(Fig. 3)
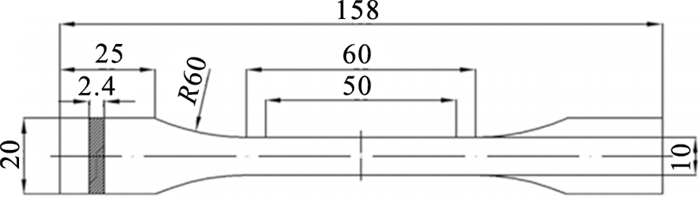 | 图 3 拉伸实验试件(单位: mm)Fig.3 Tensile test specimen(unit: mm) |
实验试件共有两种类型: ①X方向打印试件(X0i, i=1~5);②Z方向打印试件(Z0i, i=1~5).在制备试件时, 采用部分析因设计方法[16], 即所制备的试件除了打印方向不同以外(如图 4所示), 其他的过程参数如打印层高度(0.15 mm)、挤出宽度(0.4 mm)、打印速度(60 mm/s)、挤出温度(200 ℃)等的数值均相同.
图 4(Fig. 4)
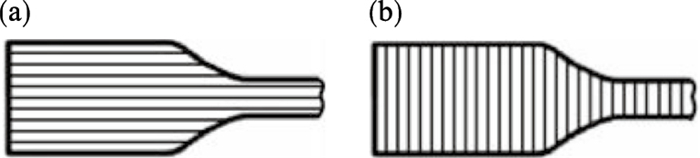 | 图 4 打印方向Fig.4 Printing direction (a)—X方向;(b)—Z方向. |
2.2 实验过程根据ISO 527-2—2012标准, 利用型号为SHIMADZU EHF-EV200K2-040的拉伸实验机对全部试件进行拉伸实验.该设备的测量精度为±0.5 %, 负载力范围为0~200 kN, 设置的加载速率为5 mm/min.
在设置拉伸实验机对试件的夹紧力时, 考虑到PLA材料的机械性能远小于钢铁等金属材料, 因此数值设置不宜过大, 仅设置为5 MPa, 以防止损坏试件而影响实验结果.
3 结果分析为了验证本文所提出的FFF薄板本构关系模型的正确性, 对比分析了试件应力-应变关系的理论与实验结果.
3.1 X方向试件图 5为X方向试件的理论模型与实验结果的应力-应变曲线对比, 可见, X方向试件理论预测与实验结果吻合度较好, 所以理论模型正确可靠, 具体数值如表 2所示.表 2中相对误差的公式为er=(X0i-X预测)/X预测×100%.由表 2可知, X预测的抗拉强度为52.74 MPa, 而通过实验确定的试件X0i的平均抗拉强度为53.85 MPa, 利用相对误差公式计算得到二者相对误差仅为2.10%.在极限应变方面, X预测的理论数值为3.8%, 试件X平均的实验结果为3.63%, 计算得到相对误差为4.47%.可见, 利用该理论模型可以准确地预测出X方向试件的应力-应变关系.
图 5(Fig. 5)
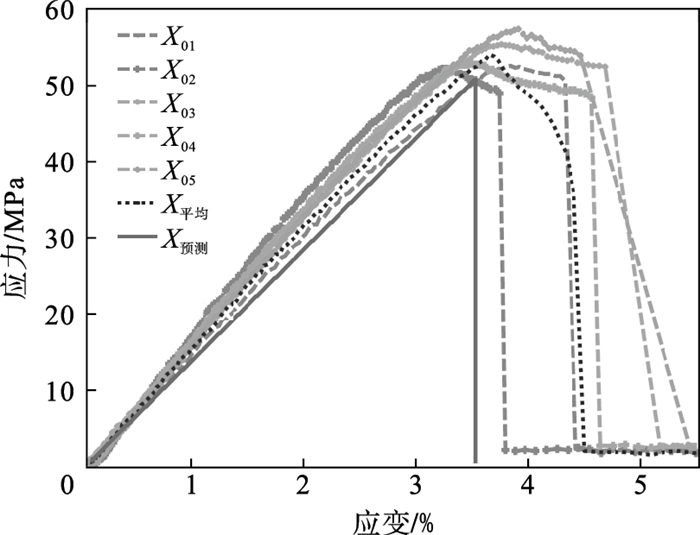 | 图 5 X方向试件应力-应变曲线Fig.5 Stress-strain curves of specimens in X direction |
表 2(Table 2)
| 表 2 X方向试件测试结果 Table 2 Test results of X direction specimens |
3.2 Z方向试件图 6为Z方向试件的理论模型与实验结果的应力-应变曲线对比, 同样可见Z方向试件理论预测与实验结果吻合度较好, 验证了理论模型的正确性, 具体数值如表 3所示.表 3中相对误差的公式为er=(Z0i-Z预测)/Z预测×100%.
图 6(Fig. 6)
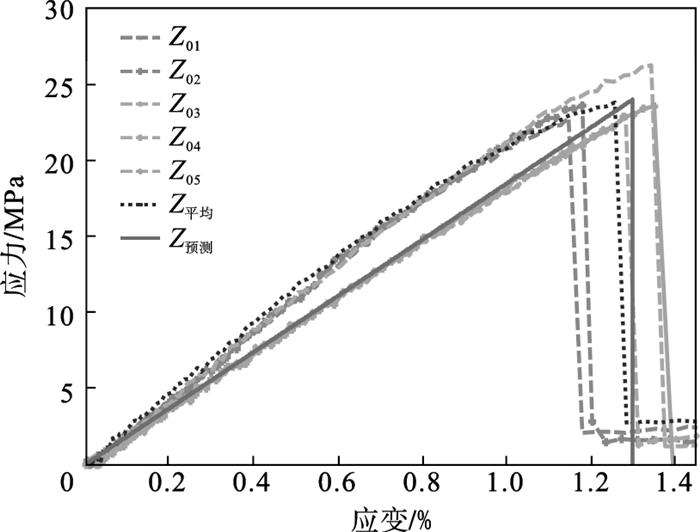 | 图 6 Z方向试件应力-应变曲线Fig.6 Stress-strain curves of specimens in Z direction |
表 3(Table 3)
| 表 3 Z方向试件测试结果 Table 3 Test results of Z direction specimens |
由表 3可以看出, Z预测的抗拉强度为23.86 MPa, 而通过实验确定的试件Z0i的平均抗拉强度为23.68 MPa, 二者相对误差仅为0.75%.在极限应变方面, Z预测的理论数值为1.30%, 试件Z平均的实验结果为1.26%, 相对误差仅为3.08%.可见, 利用该理论计算方法可以较为准确地预测出Z方向试件的应力-应变关系.
虽然理论与实验结果吻合度较好, 但仍有必要对上述结果误差产生的原因进行分析.误差主要来自理论建模和实验测试两个方面, 如模型忽略了各层之间的应力应变情况、薄板纤维排列不规则、残余应力、实验过程中边界条件不一致(夹具夹紧程度不同)、测试仪器灵敏度漂移等问题.
4 结论1) 基于经典弹性力学理论对FFF薄板拉伸性能进行了理论建模, 预测了FFF薄板本构关系.该方法同样适用于同类型多层无滑移的复合薄板的本构关系分析.
2) 对比分析了FFF薄板的本构关系的理论与实验结果, 两者吻合度良好, 验证了理论模型的正确性.
3) 本文的研究有助于提高FFF产品的拉伸性能, 为FFF技术的进一步发展提供一定的参考和技术支持.
参考文献
| [1] | Hu D P, Wen Z J, Chen Y H, et al. Surface-molding accuracy of FDM thin plastic parts molded by 3D printing[J]. China Plastics, 2017, 31(2): 82-87. |
| [2] | 唐通鸣, 张政, 邓佳文. 基于FDM的3D打印技术研究现状与发展趋势[J]. 化工新型材料, 2015, 43(6): 228-230. (Tang Tong-ming, Zhang Zheng, Deng Jia-wen. Research status and development trend of 3D printing technology based on FDM[J]. New Chemical Material, 2015, 43(6): 228-230.) |
| [3] | Boparai K S, Singh R, Singh H. Development of rapid tooling using fused deposition modeling: a review[J]. Rapid Prototyping Journal, 2016, 22: 281-99. DOI:10.1108/RPJ-04-2014-0048 |
| [4] | Cuan-Urquizo E, Barocio E, Tejada-Ortigoza V, et al. Characterization of the mechanical properties of FFF structures and materials: a review on the experimental, computational and theoretical approaches[J]. Materials, 2019, 12(6): 895. DOI:10.3390/ma12060895 |
| [5] | Hesamodin J S H, Masood W Q. Dynamic response of FDM made ABS parts in different part orientations[J]. Advanced Materials Research, 2013, 748: 291-294. DOI:10.4028/www.scientific.net/AMR.748.291 |
| [6] | Shi Q J, Xiao J J, Cheng G Y, et al. Process optimization of mechanical properties for PLA material via 3D printing[J]. Green Packaging, 2018(8): 54-61. |
| [7] | Arivazhzgan A, Masoodsh R. Dynamic mechanical properties of ABS material processed by fused deposition modelling[J]. International Journal of Applied Engineering Research, 2012, 2(3): 2013-2014. |
| [8] | 王富伟, 朱书桓, 韦明帝, 等. 3D打印PLA杆件的拉压力学性能实验研究[J]. 中阿科技论坛, 2018(4): 34-36. (Wang Fu-wei, Zhu Shu-huan, Wei Ming-di, et al. Experimental study on tension and compression properties of 3D printed PLA levers[J]. China-Arab States Science and Technology Forum, 2018(4): 34-36.) |
| [9] | 刘静毅, 龙连春. 3D打印的不同夹芯板结构的力学性能分析[C]// 北京力学会第二十五届学术年会. 北京, 2019: 652-653. (Liu Jing-yi, Long Lian-chun. Analysis of mechanical properties of 3D printed sandwich panels[C]// The 25th Annual Conference of Beijing Dynamic Society. Beijing, 2019: 652-653. ) |
| [10] | Melenka G W, Cheung B K O, Schofield J S. Evaluation and prediction of the tensile properties of continuous fiber-reinforced 3D printed structures[J]. Composite Structures, 2016, 153: 866-875. DOI:10.1016/j.compstruct.2016.07.018 |
| [11] | Li N, Li Y, Liu S. Rapid prototyping of continuous carbon fiber reinforced polylactic acid composites by 3D printing[J]. Journal of Materials Processing Technology, 2016, 238: 218-225. DOI:10.1016/j.jmatprotec.2016.07.025 |
| [12] | 董骏杰, 刘宇杰. 具有内部孔洞的3D打印PLA试样力学性能研究[J]. 四川理工学院学报(自然科学版), 2018, 31(2): 50-54. (Dong Jun-jie, Liu Yu-jie. Study on mechanical properties of 3D printing PLA specimens with inner hole[J]. Journal of Sichuan University of Science and Technology (Natural Science Edition), 2018, 31(2): 50-54.) |
| [13] | Domingo-Espin M, Borros S, Agullo N, et al. Influence of building parameters on the dynamic mechanical properties of polycarbonate fused deposition modeling parts[J]. 3D Printing and Additive Manufaturing, 2014, 1(2): 70-77. DOI:10.1089/3dp.2013.0007 |
| [14] | 王震鸣. 复合材料力学和复合材料结构力学[M]. 北京: 机械工业出版社, 1991. (Wang Zhen-ming. Mechanics of composite materials and structural mechanics of composite materials[M]. Beijing: China Machine Press, 1991.) |
| [15] | Farah S, Anderson D G, Langer R. Physical and mechanical properties of PLA, and their functions in widespread applications — a comprehensive review[J]. Advanced Drug Delivery Reviews, 2016, 107: 367-392. |
| [16] | 姜世杰, 史银芳, SIYAJEU Yannick, 等. FDM薄板振动特性的理论与实验研究[J]. 东北大学学报(自然科学版), 2019, 40(4): 516-520. (Jiang Shi-jie, Shi Yin-fang, Siyajeu Yannick, et al. Theoretical and experimental study on vibration characteristics of FDM thin plates[J]. Journal of Northeastern University(Natural Science), 2019, 40(4): 516-520.) |
