
 , 唐挺1
, 唐挺1 1. 重庆大学 机械传动国家重点试验室, 重庆 400044;
2. 重庆科技学院 机械与动力工程学院, 重庆 401331
收稿日期:2021-01-06
基金项目:国家重点研发计划项目(2018YFB1304800);广东省重点研发计划项目(2020B090926002)。
作者简介:石崟(1996-),男,安徽滁州人,重庆大学硕士研究生;
李俊阳(1982-),男,浙江绍兴人,重庆大学副教授,博士生导师。
摘要:为提高谐波减速器的机器人关节控制精度, 适应其在复杂工况下的使用需求, 对谐波减速器摩擦力矩特性进行了研究.通过引入弹流润滑关系、非线性刚度关系和柔轮弹性变形耗散关系模型, 建立了速度、负载转矩和温度等参数耦合的谐波减速器摩擦力矩模型.使用遗传算法对SHF-20-80-2UJ型谐波减速器的试验数据进行处理, 得到了待辨识参数的识别结果, 验证了模型的准确性, 摩擦力矩的仿真值与试验值间的最大和平均偏差分别为8.05%, 4.26%;满载且输入转速为2 000 r/min时, 不同温度下摩擦力矩的仿真值与试验值间的最大偏差为1.12%.该模型有效地反映了谐波减速摩擦力矩关于转速、负载转矩和温度变化的非线性关系, 测得弹性变形能量损失在空载与满载时分别约占总能量损失的20%, 50%.
关键词:机械摩擦谐波减速器摩擦模型多参数耦合弹流润滑关系弹性变形耗散
Modeling and Parameter Identification of Friction Characteristics of Harmonic Reducer
SHI Yin1, YIN Hua-chuan2, LI Jun-yang1

 , TANG Ting1
, TANG Ting1 1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;
2. School of Mechanical and Power Engineering, Chongqing University of Science and Technology, Chongqing 401331, China
Corresponding author: LI Jun-yang, E-mail: Lijunyang1982@sina.com.
Abstract: In order to improve the control precision of the robot joint of the harmonic reducer(HD)and adapt to its use under complex working conditions, the friction torque characteristics of HD are studied. By introducing the models of elastohydrodynamic lubrication relationship, the nonlinear stiffness relationship and equivalent dissipation relationship of flexspline elastic deformation, a friction torque model of HD coupled with parameters such as speed, load torque and temperature is established. The genetic algorithm is used to process the test data of the SHF-20-80-2UJ harmonic reducer, the identification results of the parameters to be identified are obtained, and the accuracy of the model is verified. The maximum and average deviations between the simulated and experimental values of friction torque are 8.05% and 4.26% respectively; with full load and input speed being 2 000 r/min, the maximum deviation between the simulated value and the experimental value of the friction torque at different temperatures is 1.12%. The model effectively reflects the nonlinear relationship between the friction torque of the harmonic reducer with respect to the rotating speed, load torque and temperature changes. The measured elastic deformation energy loss accounts for about 20% and 50% of the total energy loss at no-load and full-load respectively.
Key words: mechanical frictionharmonic reducerfriction modelmulti-parameter couplingelastohydrodynamic lubrication relationshipelastic deformation and dissipation
随着谐波减速器在工业机器人、空间飞行器等领域的大规模应用, 由于其动力学特性复杂、难以获得较高的控制精度, 限制了其进一步推广.谐波减速器动力学特性中存在的三大非线性因素为非线性摩擦、非线性刚度和迟滞.其中非线性摩擦对其动力学特性影响最为显著, 所以对谐波减速器摩擦进行精确建模具有重大的工程意义.
谐波减速器的非线性摩擦产生机理决定了其存在非线性程度高、耦合的时变参量多、观测及参数辨识困难等特点.迄今为止, 国内外****对谐波减速器的非线性摩擦展开了一些研究.Tuttle[1]提出的高次多项式摩擦模型在早期的谐波动力学模型研究中被广泛使用, 但是其参数辨别过于困难, 后快速被Gandhi等[2]的基于Lugre摩擦模型的改进模型取代.Gandhi等[3]在不同的简化后的谐波减速器动力学模型下分别进行了控制器的设计.Iwan[4]和Lampaert等[5]在Lugre模型的基础上, 提出了使用广义的Maxwell模型对摩擦进行更加准确的描述, 但因为其中存在较多的动态参数,所以未能得到广泛的应用.Wolf等[6]对谐波减速器黏滞摩擦力进行了建模, 但仅仅是使用三次多项式进行拟合, 这种方法既不利于参数辨识, 也缺乏通用性.现阶段使用最为广泛的Lugre模型可以捕捉到低速阶段Stribeck现象, 但无法反映谐波减速器运行过程中的其他非线性特性.
在航空航天领域谐波减速器运行工况复杂, 转速、负载转矩和温度变化范围大.谐波减速器负载转矩、温度对于摩擦力矩的影响都呈现出极强的非线性特性.谐波减速器通过弹性变形传动的方式产生极高的能量损耗, 这部分能量损失无法直接测量, 会在输出端与摩擦过程中的能量损耗耦合, 严重影响了谐波减速器摩擦力矩测量精度.而目前谐波减速器的摩擦模型集中于研究转速对摩擦力矩的影响, 建模方法通常为数学关系的拟合, 并且忽略了弹性变形能量损耗, 无法准确反映谐波减速器摩擦力矩特性.所以急需建立可精确反映转速、负载转矩和温度对谐波减速器摩擦力矩影响并且对弹性变形能量损耗解耦的摩擦模型.
本文对谐波减速器运行过程中各非线性因素加以考虑, 从摩擦产生机理出发, 对谐波减速器摩擦特性进行建模.首先分析谐波减速器摩擦力矩产生机理, 建立整体的模型框架, 再对各非线性因素分别建模, 从而建立起谐波减速器摩擦模型.使用遗传算法对SHF-20-80-2UJ型谐波减速器的试验数据进行处理, 并进行参数辨识, 验证模型的准确性和有效性.利用所建立模型, 分析了负载转矩对谐波减速器摩擦力矩影响的非线性特性, 对弹性变形能量耗散与摩擦力矩解耦.
1 谐波减速器摩擦建模谐波减速器主要由柔轮、刚轮和波发生器三部分组成, 其结构如图 1所示.其传动原理是通过波发生器的转动强迫柔轮发生弹性形变, 柔轮齿在绕定点平动的过程中与刚轮齿啮合, 刚轮与柔轮存在一定的齿数差, 从而实现变速传动.
图 1(Fig. 1)
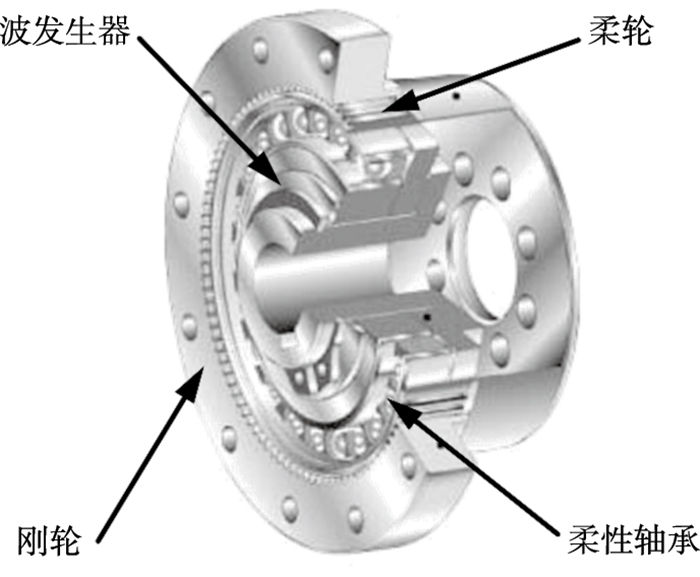 | 图 1 谐波减速器结构Fig.1 Harmonic reducer structure |
谐波减速器中的效率损失主要来源于柔轮与刚轮啮合时的摩擦损失和柔轮变形时的弹性变形能量损失.柔轮与刚轮啮合时的摩擦又可分为边界与混合阶段的接触摩擦力矩和黏滞阶段的黏滞摩擦力矩.弹性变形能量损失在建模时, 将其等效为一种特殊的摩擦力矩造成的能量损失.
接触摩擦力矩和黏滞摩擦力矩本身就存在极强的非线性关系, 而谐波减速器传动特性中的空载啮合压力、非线性刚度、啮合齿对数量变化和润滑油黏温、黏压关系等非线性因素与摩擦的非线性特性耦合, 加强了其非线性特性, 如图 2所示.
图 2(Fig. 2)
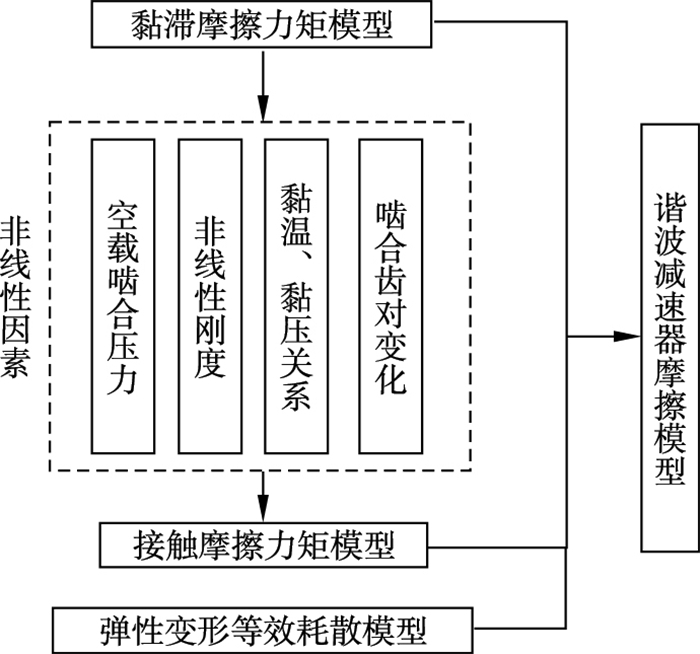 | 图 2 建模方法Fig.2 Modeling method |
1.1 接触摩擦力矩模型根据Lugre模型, 接触摩擦力矩TN可表示为
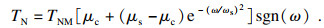 | (1) |
1.2 黏滞摩擦力矩模型谐波减速器速度变化范围较大的情况下, 摩擦力矩表现出明显的黏滞特性[7], 引入弹流润滑黏滞摩擦力表达式FV[8]:
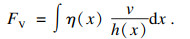 | (2) |
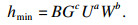 | (3) |
将式(2)整理为转动与摩擦力矩的形式, 所有常参量为待定系数, 引入权重项以消除黏滞摩擦力矩在低速时对边界摩擦力矩辨识时的干扰, 结合式(3)可得黏滞摩擦力矩TV:
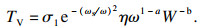 | (4) |
1.3 弹性变形等效耗散摩擦力矩模型在柔轮中线不伸长的假设下, 柔轮的变形是径向的弹性变形, 将柔轮作为一系列沿径向变形的连续金属弹性体考虑.由Goo [12]的理论单次应变中能量耗散D为
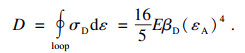 | (5) |
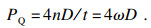 | (6) |
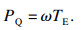 | (7) |
1.4 非线性因素建模图 3给出了谐波减速器空载时的刚轮与柔轮的啮合位置关系, 显然柔轮与刚轮在某些啮合位置存在微小的干涉变形[15], 产生了一定的啮合压力.齿面啮合产生的等效摩擦力矩TNM可以近似描述为
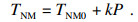 | (8) |
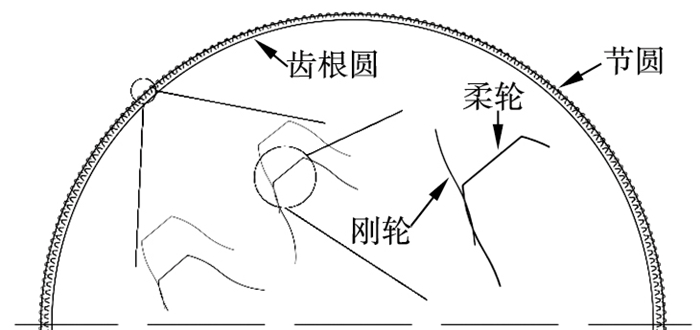 | 图 3 谐波减速器空载啮合情况Fig.3 No-load meshing of harmonic reducer |
式中: TNM0为空载啮合压力等效力矩, 为待定常量; P为输出端负载转矩; k为负载转矩系数, 待定常量.
式(1)中的ωs在Lugre模型中被作为待识别常参量处理.根据Lu等[16]的研究, ωs可表示为
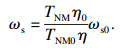 | (9) |
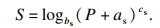 | (10) |
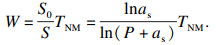 | (11) |
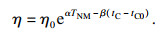 | (12) |
1.5 谐波减速器摩擦力矩模型谐波减速器摩擦力矩Tf:
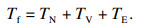 | (13) |
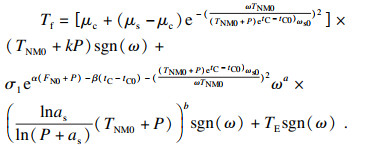 | (14) |
2 试验与参数识别为了对该模型的参数进行辨识, 并对准确性进行验证, 对哈默纳科公司生产的SHF-20-80-2UJ型谐波减速器进行了试验测量.
2.1 试验设备与试验对象试验在一体式多功能谐波减速器测试试验台上进行, 其结构如图 4所示.驱动力矩测量精度为0.001 N·m, 负载力矩测量精度为0.1 N·m, 输入转速测量精度为1 r/min, 输出转速测量精度为0.01 r/min, 采样间隔为0.1 s.
图 4(Fig. 4)
 | 图 4 一体式多功能谐波减速器测试试验台Fig.4 Integrated multifunctional harmonic reducer test bench |
哈默纳科公司生产的SHF-20-80-2UJ型谐波减速器基本参数见表 1.
表 1(Table 1)
| 表 1 SHF-20-80-2UJ型谐波减速器基本参数 Table 1 Basic parameters of SHF-20-80-2UJ type harmonic reducer |
2.2 试验流程试验环境温度为20 ℃, 为准确观察到谐波减速器运行中的Stribeck现象和黏滞摩擦现象, 并且不使试验工作量过大, 选择某些转速作为速度观测点, 每个速度观测点都以2 N·m的负载转矩间隔逐渐由空载加载至满载, 每个工况都进行一定时间的持续观测, 以消除驱动及加载电机造成的惯性力误差, 具体试验参数见表 2.每个观测点的摩擦力矩Texp通过对观测时间内驱动力矩Tin与输出力矩Tout之差的平均值求得
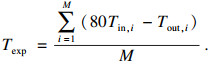 | (15) |
| 表 2 试验参数 Table 2 Experimental parameters |
式中, M为对应观测点内采样点数目.
2.3 试验结果本次试验所得数据较多, 所以只选择具有代表性的部分数据进行展示.不同负载转矩时的摩擦力矩随速度变化情况如图 5所示.在转速由0升至50 r/min的过程中, 发生了非常明显的Stribeck现象.
图 5(Fig. 5)
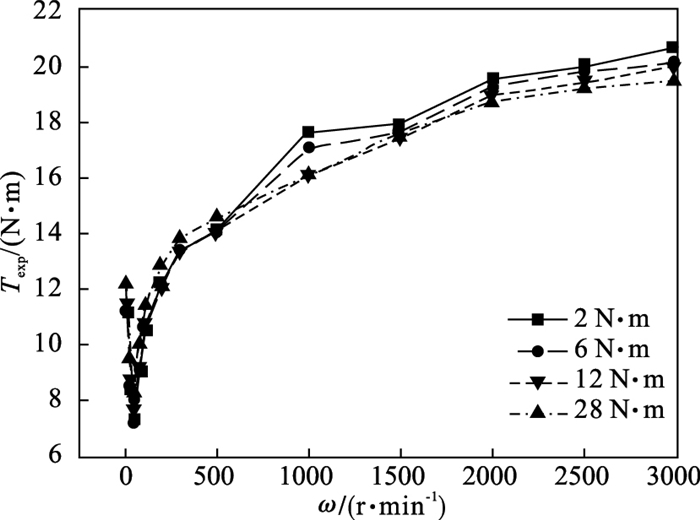 | 图 5 不同负载转矩时转速-摩擦力矩曲线Fig.5 Rotating speed-friction torque curves under different load torques |
从图 5中很明显地看出,在任何转速下负载转矩对摩擦力矩的影响都不占主导作用.这证明了在第1节中提出的关于谐波减速器在空载的情况下, 存在一定的齿对间啮合压力的推论.
图 6给出了在不同转速下的摩擦力矩随负载转矩变化的情况.很明显, 转速增加, 摩擦力矩关于负载转矩的变化率?Texp/?P逐渐由正值减至负值.该现象将在3.3节中给予解释.
图 6(Fig. 6)
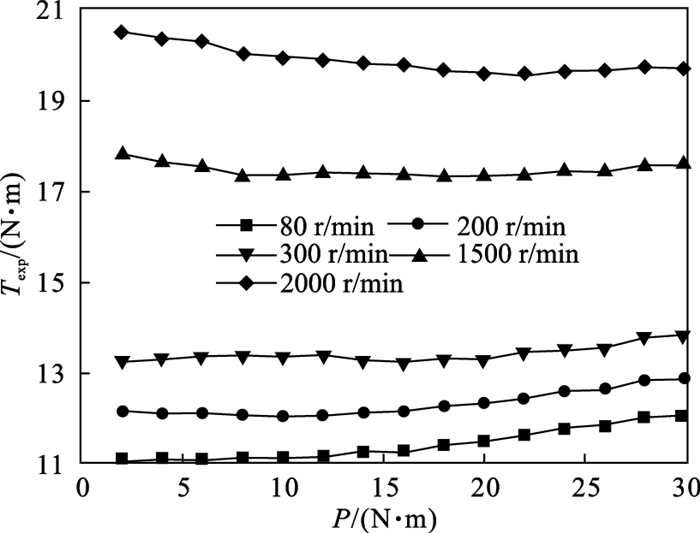 | 图 6 不同转速时负载转矩-摩擦力矩曲线Fig.6 Load torque-friction torque curves at different rotating speeds |
2.4 参数识别该模型待辨识参数较多, 所有参数皆为静态参数, 且具有明确的物理意义, 可大致确定参数范围, 所以在参数识别时的难度并不高.在这里使用遗传算法对所有待识别参数进行识别, 并且将a, b也作为待识别参数, 以验证模型的理论基础是否合理.由于试验台无法对谐波减速器运行温度进行控制、观测, 所以先不对β进行识别, 而将黏温项并入常系数σ1处理.
适应度函数的自变量向量Us:
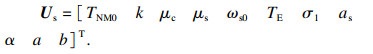 | (16) |
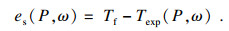 | (17) |
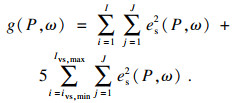 | (18) |
根据文献[18]可知, SHF-20-80-2UJ型谐波减速器室温20 ℃、满载且转速为2 000 r/min时, 效率为69%.将识别后的参数代入模型后, 计算出满载、输入转速2 000 r/min时的效率为66.45%, 与文献[18]中的结果相近.使用文献[18]中满载时温度-效率关系图作为目标数据对黏温系数β、基准温度tC0进行参数识别.将σ1分解为新的常数项σ1new与黏温项的形式:
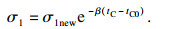 | (19) |
 | (20) |
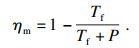 | (21) |
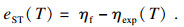 | (22) |
表 3(Table 3)
| 表 3 参数辨识结果 Table 3 The results of parameter identification |
3 模型验证与参数讨论3.1 模型验证图 7给出了该模型在不同负载转矩下的仿真效果与试验数据的对比.在2, 12 N·m的负载转矩下, 模型仿真效果与试验数据基本一致; 在28 N·m的负载转矩下, 仿真曲线在过临界Stribeck速度后增长相对于试验曲线略有滞后, 这可能是由参数辨识方法不足够精确导致的.
图 7(Fig. 7)
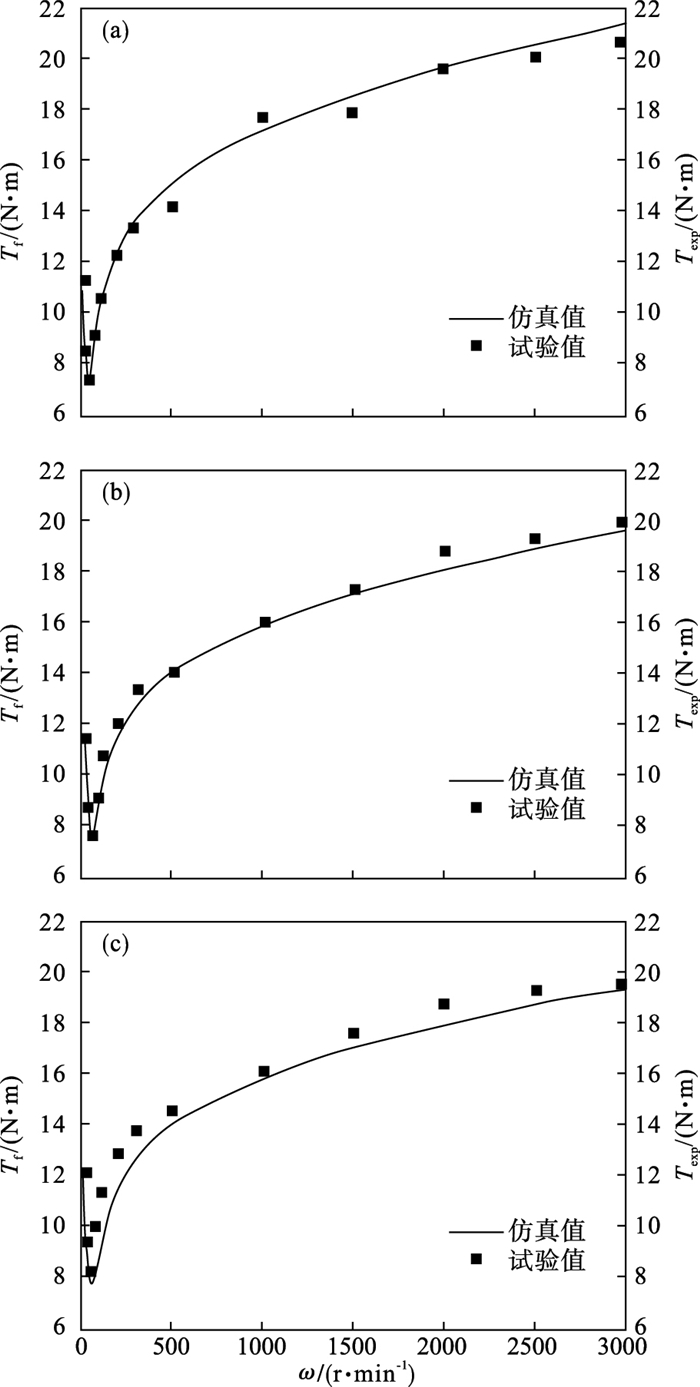 | 图 7 不同负载转矩时转速-摩擦力矩关系对比Fig.7 Comparison of the relationship between rotating speed and friction torque under different load torques (a)—2 N·m; (b)—12 N·m; (c)—28 N·m. |
图 8为模型在不同转速下的摩擦力矩与负载转矩关系.该模型非常明显地表现了负载转矩P对摩擦力矩的影响, 即随着转速的增加负载转矩与摩擦力矩间的关系逐渐由正相关变为负相关.模型仿真时, 转速升至70 r/min时, 摩擦力矩几乎不随负载转矩的变化而变化, 略早于图 6的试验数据中300 r/min.摩擦力矩的仿真值与试验值间的最大和平均偏差分别为8.05%, 4.26%.说明该模型可以有效反映转速、负载转矩与摩擦力矩的关系.
图 8(Fig. 8)
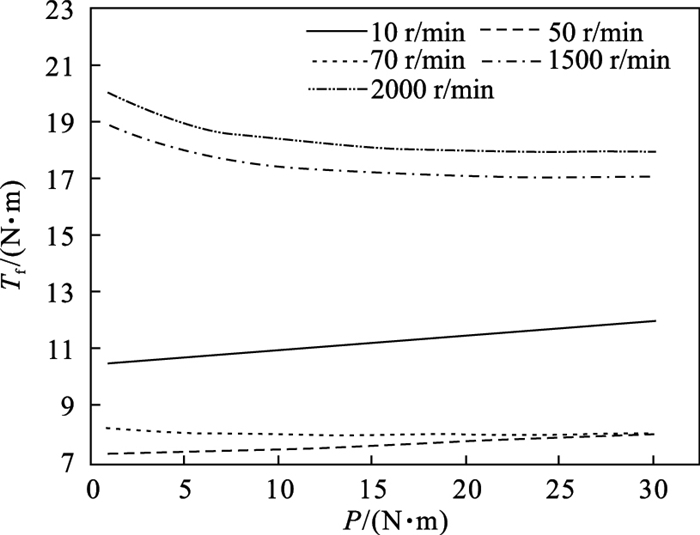 | 图 8 不同转速时负载转矩-摩擦力矩关系的仿真结果Fig.8 Simulation results of relationship of load torqueand friction torque at different speeds |
图 9给出了满载且输入转速为2 000 r/min时, 谐波减速器效率的仿真与试验结果对比.可以看到满载且2 000 r/min工况下仿真结果与试验结果几乎一致, 最大偏差为1.12%.
图 9(Fig. 9)
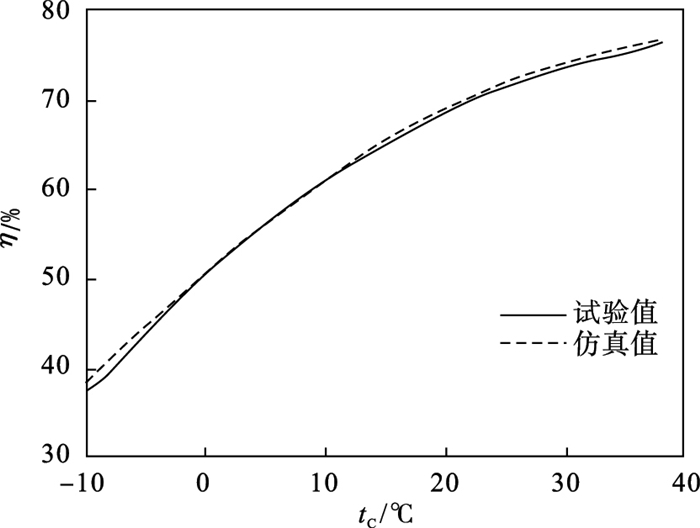 | 图 9 温度-效率的仿真与试验结果对比Fig.9 Comparison of simulation and test results of temperature-efficiency |
从图 10模型仿真效果与试验数据的对比表明, 该模型具有较高的预测精度.
图 10(Fig. 10)
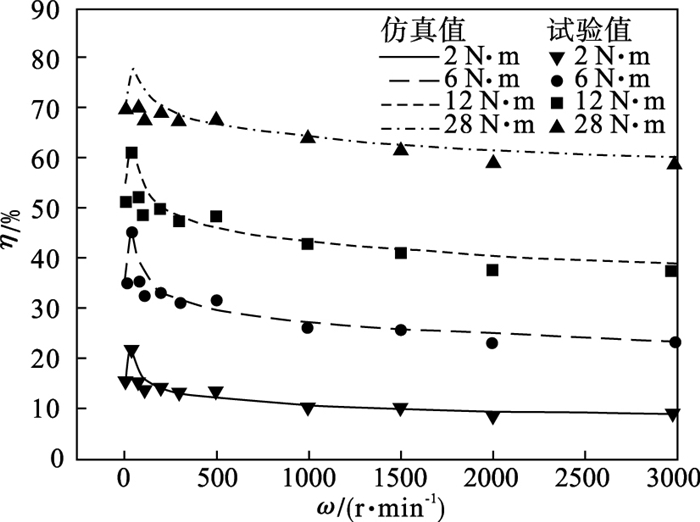 | 图 10 不同负载转矩时转速-效率的仿真与试验结果对比Fig.10 Comparison of simulation and test results of rotating speed-efficiency under different load torques |
从节省能量的角度来说, 谐波减速器的使用工况应维持在重载、临界Stribeck速度下; 但在临界Stribeck速度下摩擦力矩对转速变化非常敏感, 在对精度需求较高的场合下, 反而应避开该工作范围, 以重载、高速段作为优先选择工况.
3.2 参数讨论在无约束条件下使用遗传算法寻优时, 由于TMN0, k, μc, μs, α, σ1可能存在一定的非线性的耦合关系, 在收敛至最优时, 其值会在一个解空间中变化, 但始终满足TMN0=(3~5)kPmax.这说明SHF-20-50-2UJ型谐波减速器满载时齿面啮合压力约为空载时齿面啮合压力的1.2~1.3倍.
将as的辨识值代入式(10)和式(11), 算得满载时齿对接触面积为空载时的1.8倍.假设谐波减速器每对接触齿对间的接触面积相等且不会发生变化, 齿对间接触面积变化完全是由接触齿对数量变化造成的,那么满载时有效啮合齿对数量约为空载时啮合齿对数量的1.8倍.单侧初始啮合齿对数量为10时, 负载转矩对啮合齿对数量的影响如图 11所示.因为试验台为封闭仓, 所以无法直接观察啮合齿对数量, 并且目前领域内对负载转矩与啮合齿对数量影响的定量研究非常少, 暂时没有可靠的计算方法, 无法验证该推论的准确性, 但数据符合以往试验的经验.众所周知, 负载转矩对啮合齿对数量的影响是由柔轮杯壁刚度与齿对啮合刚度两因素耦合而成, 若将as与柔轮杯壁刚度、齿对啮合刚度解耦, 则可以实现对谐波减速器非线性刚度关系的动态辨识, 该问题还有待进一步的研究.
图 11(Fig. 11)
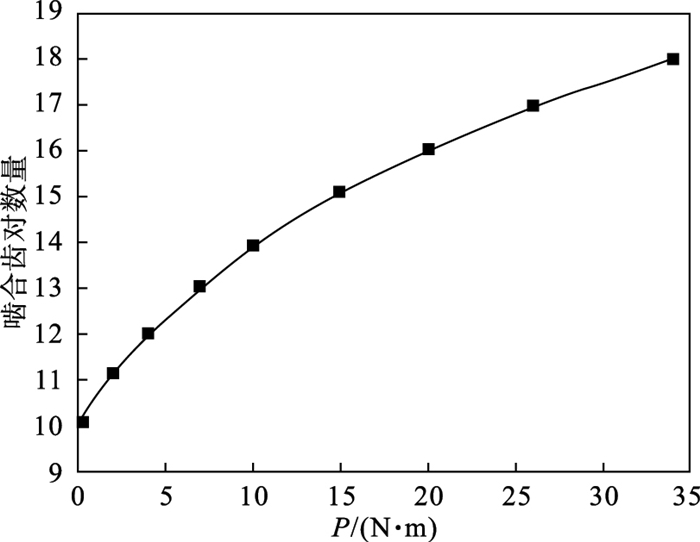 | 图 11 负载转矩对啮合齿对数量的影响Fig.11 Influence of load torque on the number of tooth pairs |
弹性变形能量耗散等效力矩TE稳定收敛于3.812 3 N·m, 试验测得全转速、全负载转矩范围内摩擦力矩的变化范围是7.237~20.57 N·m, 算得弹性变形造成能量损耗占总的能量损失约为20%~50%.忽略柔轮变形能量耗散的传统谐波减速器效率计算方法中的啮合效率计算可能存在较大误差.
通过遗传算法求得弹流润滑指数速度和压力指数系数a, b稳定收敛于0.302 0和0.133 1, 这一组数据非常接近于文献[9]由逆解法求得的弹流润滑系数代入关系式后解出的值0.3和0.13.文献[9]求得的弹流润滑系数在轻载与中载情况下与试验结果一致性极好, 可以推测谐波减速器柔轮与刚轮啮合齿对间的啮合压力应该属于轻载或中载情况.
3.3 负载转矩对摩擦力矩非线性影响的机理解释图 12分别给出模型中分离出的接触摩擦力矩TN与黏滞摩擦力矩TV在不同输入转速下随负载转矩的变化关系.
图 12(Fig. 12)
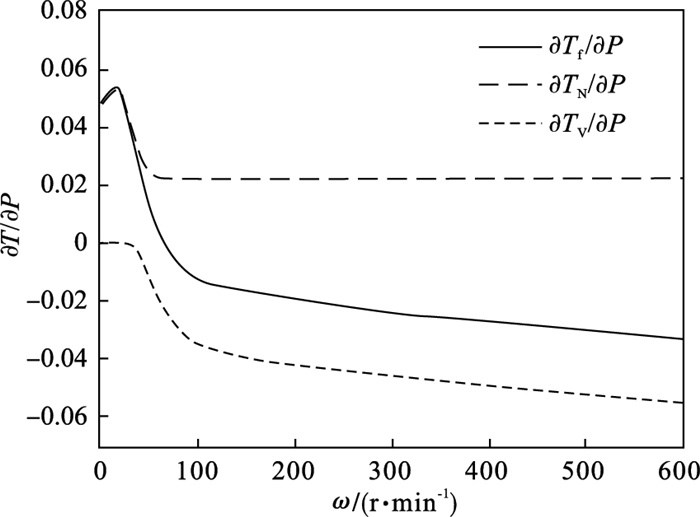 | 图 12 摩擦力矩、接触摩擦力矩和黏滞摩擦力矩随转速变化率仿真结果Fig.12 Simulation results of friction torque, contact friction torque and viscous friction torque change rate with rotating speed |
已知TE为常量, 由式(13)可知谐波减速器摩擦力矩Tf随负载转矩P的变化率?Tf/?P为
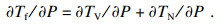 | (23) |
从图 13可知, 转速越大, 接触摩擦力矩越小, 其随负载转矩增大的速度越慢; 黏滞摩擦力矩先减小再增大, 其随负载转矩减小的速度更快.在接触摩擦力矩和黏滞摩擦力矩的共同作用下, 谐波减速器摩擦力矩呈现出图 6所示的非线性特性.
图 13(Fig. 13)
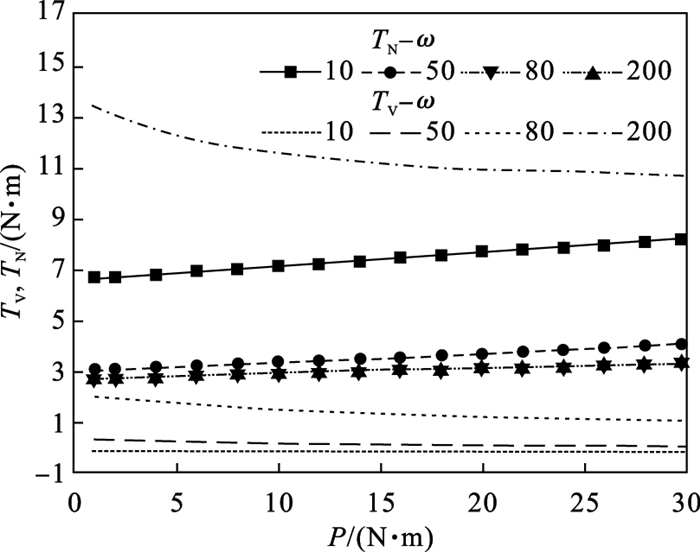 | 图 13 不同转速时负载转矩、接触摩擦力矩与黏滞摩擦力矩关系Fig.13 Relationship between load torque, contact friction torque and viscous friction torque at different rotating speeds |
as是由谐波减速器刚度决定的, 不同型号的谐波减速器刚度差别极大.根据一般的试验经验, 波发生器几何形状、材料弹性模量、不同的齿廓形状(渐开线齿廓刚度 < IH型齿廓刚度 < 双圆弧齿廓刚度)都对刚度有极大影响.SHF-20-80-2UJ型谐波减速器使用的是IH型齿形, 在使用其他刚度更高的齿形的情况下, 在对其测量过程中出现的高速段摩擦力矩随负载转矩减小的情况并不具有普遍性.当as=30,其他参数仍为表 3所示时, 不同转速下的负载转矩对摩擦力矩的影响如图 14所示.相比于图 8所示的as值为8.132 8时, 显然Tf随P增加仍然表现出极强的非线性关系, 但P增大, 高转速Tf减小的情况已经消失.
图 14(Fig. 14)
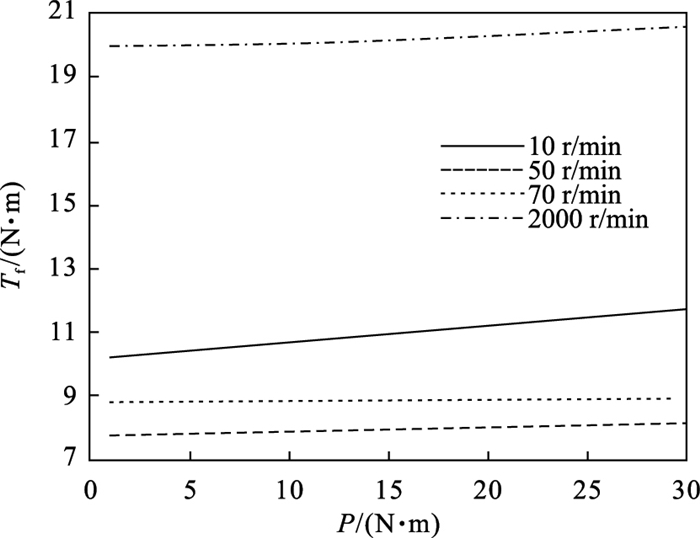 | 图 14 as为30时,不同转速下负载转矩-摩擦力矩关系Fig.14 Relationship of load torque and friction torque under different rotating speed when as is 30 |
而根据式(4), 式(11), 式(12)和图 11可知, 负载转矩与摩擦力矩非线性关系的产生机理: 负载转矩较低时, 当负载转矩增加, 啮合齿对数量快速增加, 单位面积承担负载转矩减小, 润滑条件快速改善, 黏滞摩擦力矩减小; 负载转矩较高时, 啮合齿对数量增加较慢, 对润滑条件改善不明显; 接触摩擦力矩与负载转矩的关系始终成正比.负载转矩对接触摩擦力矩与黏滞摩擦力矩的影响最终表现为谐波减速器摩擦力矩与负载转矩关系的非线性.
4 结论1) 提出一种转速、负载转矩和温度耦合的谐波减速器摩擦模型.该模型可反映各耦合参数对谐波减速器摩擦力矩的影响, 捕捉到临界Stribeck速度变化、高转速时摩擦力矩出现黏滞特性等现象, 并对柔轮弹性变形造成的能量损失与摩擦损失进行了解耦.为谐波减速器高精度动力学模型的建立提供了一定的理论基础.
2) 负载转矩对摩擦力矩非线性影响是由柔轮的非线性刚度造成的.较小的柔轮刚度可以使谐波减速器高速运行时的润滑情况得到极大的改善, 能够减小摩擦损失, 提高传动效率与性能, 但增大了控制算法的设计难度.
3) SHF-20-80-2UJ型谐波减速器处在临界Stribeck转速(50 r/min)且满载时效率达到最高, 但摩擦力矩对转速非常敏感, 在精度需求较高的场合, 应避开该工况.
参考文献
| [1] | Tuttle T D. Understanding and modeling the behavior of a harmonic drive gear transmission[D]. Cambridge: Massachusetts Institute Technology, 1992. |
| [2] | Gandhi P S, Ghorbel F H, Dabney J. Modeling, identification, and compensation of friction in harmonic drives[C]// Conference on Decision & Control. Las Vegas: IEEE, 2002: 160-166. |
| [3] | Gandhi P S, Ghorbel F H. Control of hysteresis and kinematic error nonlinearities in harmonic drives for high speed precision control applications[C]//American Control Conference. Boston: IEEE, 2004: 5760-5765. |
| [4] | Iwan W D. A distributed-element model for hysteresis and its steady-state dynamic response[J]. Journal of Applied Mechanics, 1966, 33(4): 893-900. DOI:10.1115/1.3625199 |
| [5] | Lampaert V, Al-Bender F, Swevers J. A generalized Maxwell-slip friction model appropriate for control purposes[C]// International Workshop on Workload Characterization. Saint Petersburg: IEEE, 2003: 1170-1177. |
| [6] | Wolf S, Iskandar M. Extending a dynamic friction model with nonlinear viscous and thermal dependency for a motor and harmonic drive gear[C]// Zelinsky A. International Conference on Robotics and Automation. Brisbane: IEEE, 2018: 783-790. |
| [7] | Zou C, Tao T, Jiang G D, et al. A harmonic drive model considering geometry and internal interaction[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2017, 231(4): 728-743. DOI:10.1177/0954406215621097 |
| [8] | Xu H, Kahraman A, Anderson N E, et al. Prediction of mechanical efficiency of parallel-axis gear pairs[J]. Journal of Mechanical Design, 2007, 129(1): 58-68. DOI:10.1115/1.2359478 |
| [9] | Hamrock B J, Dowson D. Isothermal elastohydrodynamic lubrication of point contacts: part Ⅲ—fully flooded results[J]. Journal of Tribology, 1977, 99(2): 275-276. |
| [10] | Christensen H. The variation of film thickness in highly loaded contacts[J]. Tribology Transactions, 1964, 7(3): 219-226. |
| [11] | 温诗铸, 杨沛然. 弹性流体动力润滑[M]. 北京: 清华大学出版社, 1992: 122-126. (Wen Shi-zhu, Yang Pei-ran. Elastohydrodynamic lubrication[M]. Beijing: Tsinghua University Press, 1992: 122-126.) |
| [12] | Goo K. A model of the hysteresis loop caused by internal friction[J]. Pressure Vessels and Piping, 1993, 54(3): 429-434. DOI:10.1016/0308-0161(93)90015-L |
| [13] | 徐芝纶. 弹性力学[M]. 5版. 北京: 高等教育出版社, 2016: 65-80. (Xu Zhi-lun. Mechanics of elasticity[M]. 5th ed. Beijing: Higher Education Press, 2016: 65-80.) |
| [14] | 沈允文, 叶庆泰. 谐波齿轮传动理论设计[M]. 北京: 机械工业出版社, 1985. (Shen Yun-wen, Ye Qing-tai. Theoretical design of harmonic gear transmission[M]. Beijing: China Machine Press, 1985.) |
| [15] | Zou C, Tao T, Jiang G, et al. Deformation and stress analysis of short flexspline in the harmonic drive system with load[C]// Guo S X. International Conference on Mechatronics and Automation. Takamatsu: IEEE, 2013: 4-7. |
| [16] | Lu X, Khonsari M M. On the lift-off speed in journal bearings[J]. Tribology Letters, 2005, 20(3): 299-305. |
| [17] | Ma J, Li C, Luo Y, et al. Simulation of meshing characteristics of harmonic reducer and experimental verification[J]. Advances in Mechanical Engineering, 2018, 10(3): 1-9. |
| [18] | 哈默纳科. 产品目录-组合型-1603版[EB/OL]. (2016-03-01)[2020-05-10]. http://www.harmonicdrive.net.cn/Download.aspx?id=5. (Hamonic Drive. Product catalog-combination type-1603[EB/OL]. (2016-03-01)[2020-05-10]. http://www.harmonicdrive.net.cn/Download.aspx?id=5. ) |
