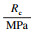赵文, 金陈, 路博, 杨楠
东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期：2021-04-19
基金项目：国家自然科学基金资助项目(51878127)。
作者简介：赵文(1962-), 男, 辽宁沈阳人, 东北大学教授, 博士生导师。

摘要：《工程岩体分级标准》(GB/T 50218—2014)修改了原标准GB 50218—1994中的BQ(basic quality)分级指标计算公式, 但其两个限定条件(岩石饱和单轴抗压强度和岩体完整性系数)没有进行同步修正.通过大量数据研究发现, 直接用受岩石饱和单轴抗压强度(R_c)和岩体完整性系数(K_v)限定条件折减后的数据进行定量计算, 多会导致定性与定量计算结果不吻合.本文对限定条件进行修正, 并基于简化的图解法进行分析, 得出R_c限定条件的影响范围较广泛, 则以数据库中新增54组数据为样本, 由R_c限定条件折减的数据进行回归分析建立新的计算公式.将得到的修正后的限定条件和新的区段计算公式, 依托实际工程数据进行验证.结果表明, 本文修正的限定条件和提出的计算公式提高了定性分级与定量分级的吻合度, 得到了更准确的分级结果.
关键词：BQ分级计算公式限定条件图解法分段函数
Study on Limited Conditions and Calculation Formula of BQ Classification Based on Graphic Method
ZHAO Wen, JIN Chen, LU Bo, YANG Nan
School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: JIN Chen, E-mail: JinChen_316@163.com.

Abstract: The calculation formula of BQ (basic quality) classification index in GB 50218—1994 is modified in the revised Standard for Engineering Classification of Rock Mass(GB/T 50218—2014), but its two limiting conditions(saturated uniaxial compressive strength of rock and rock mass integrity coefficient)were not modified simultaneously. Through a large number of data studies, it is found that the calculation results are inconsistent with the qualitative and quantitative calculation results when the data are directly reduced by R_c and K_v constraints. Therefore, the limited conditions are modified and analyzed based on simplified graphical method. According to the analysis results that are widely affected by R_c constraints, 54 sets of new data in the database are taken as samples, and a new calculation formula is established by regression analysis of the data reduced by R_c constraints. The revised limit conditions and new section calculation formula obtained are analyzed and demonstrated on the basis of actual engineering data. The results show that the revised limited conditions and the calculation formula proposed in this study improve the agreement between the qualitative classification and the quantitative classification, and a more accurate classification result is obtained.
Key words: BQ (basic quality) classificationcalculation formulalimited conditionsgraphic methodpiecewise function
《工程岩体分级标准》GB/T50218—2014^[1]对分级方式进行了统一的规定, 为相关施工提供了依据, 经过实际工程验证, 其合理性在众多岩体分级^[2-4]中得到广泛的认可.基本质量(basic quality, BQ)分级与Deere提出的RQD分类法^[5]、Wickham等^[6]提出的RSR分类方法、文献[7-11]提出的半定量半定性RMR分类系统及其优化, 及Barton^[12-14]提出的Q分类系统等相比存在一定的联系^[15], 区别在于BQ分级中计算公式由大量代表数据经逐步回归分析得到, 随着数据库的变化其精度必然会受影响, 所以要进行不断更新改进才能满足当前应用的需要.
在BQ分级中, 由于选用直线型的公式, 会有约30 % 的工程被判断失误, 基于此又增加了2个限定条件来配合共同应用.通过直线形式原理来建立回归公式, 在拟合中直线的两端会出现非常明显的偏差与散点图工程数据点, 这是造成直线形式相对于其他形式建立回归公式的吻合率低的主要原因.基于此情况, 标准中在分级计算时附加两个限定条件用来对数据散点图中岩石的抗压强度值R_c以及岩体的完整性系数K_v值进行修正^[16].
现有标准中, 对单轴饱和抗压强度R_c的限定条件是, 当R_c>90K_v+ 30时, 以R_c=90K_v+30来替换实际测试到的R_c值.当岩石的R_c值过大, 而岩体的K_v值非常小, 这类岩体硬度大但完整性差，其稳定性也是较差的, 尽管R_c值很大能够增大分级计算结果，但其并不利于岩体的稳定性.而应用这一限定条件, 对参数R_c的值进行修正.例如, 当K_v=0.65, 实际获得的R_c值比88.5 MPa大时应该取88.5 MPa, 相反的，代入实测值进行计算.
对于岩体的完整性系数K_v的限定条件, 当K_v>0.04R_c+0.4时, 以K_v=0.04R_c+0.4来替换实际测得的K_v值.当岩体的结构是非常完整的但是硬度极软时, 依然不会具有良好的稳定性.通过这一限定条件, 进行修正后可得到K_v修正值.比如, 当R_c= 5 MPa时, 当实际测得的K_v值比0.6大时仍然取0.6进行计算, 相反以实测值进行计算.
2014年修改了现有的国家标准^[1], 对标准中定量分级计算公式中的常数项进行了更改, 然而与更新后的计算公式相匹配的限定条件并没有与之共同修正.限定条件的确定是以分级定量公式为基础应用作图法计算获得, 故随着数据库的不断更新, 工程岩体质量分级公式的限定条件需作进一步研究.通过大量的分级数据验证发现, R_c限定条件折减后的数据, 导致公式计算的结果与定性分级结果不吻合, 同时R_c限定条件相对于K_v限定条件的影响范围要大很多, 计算公式对此部分数据的适用性需要进一步研究.
新的限定条件应用必然会对分级结果有影响.文献[17]通过作图法得到与新修订公式相匹配的限定条件, 并研究其应用对分级结果的影响.在BQ图解法分级方面, 申艳军等^[18]、陈曦等^[19]提出的图解方法适用性更广, 分级结果更加准确.故本文将先通过作图法对限定条件进行修正, 后在文献[18]提出的BQ分级图解法基础上对其进行改进优化, 使分级结果更加准确, 并依据实际工程数据验证修正后限定条件的合理性和图解法的应用效果.对分级计算过程引入分段函数的思想, 以数据库新增54组数据为依托, 对R_c限定条件折减后的数据建立新的计算公式, 修正此类数据计算结果, 并以工程实例验证公式的适用性和准确性, 有利于降低力学参数值差异引起的局限性^[20], 为后续的BQ法的研究及修正^[21]提供一定的借鉴参考作用.
1 限定条件的计算现有《工程岩体分级标准》GB/T 50218—2014中限定条件为

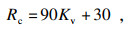(1)

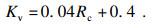(2)

限定条件公式的建立需要根据岩体分级界限、岩石单轴饱和抗压强度及完整性系数的定量划分原则进行计算, 通过作图法的方式求得.
岩体的分级、岩体的定性特征描述对应的分级结果以及分级界限参照表 1确定^[1].
表 1(Table 1)

表 1 岩体质量分级Table 1 Rock mass quality classification 基本质量级别 定性特征 质量指标(BQ) Ⅰ 坚硬岩, 岩体完整 ＞550 Ⅱ 坚硬岩, 岩体较完整; 较坚硬岩, 岩体完整 550~451 Ⅲ 坚硬岩, 岩体较破碎; 较坚硬岩, 岩体较完整; 较软岩, 岩体完整 450~351 Ⅳ 坚硬岩, 岩体破碎; 较坚硬岩, 岩体较破碎—破碎; 较软岩, 岩体较完整; 破碎软岩, 岩体完整—较完整 350~251 Ⅴ 较软岩, 岩体破碎; 软岩, 岩体较破碎—破碎; 全部软岩及全部较破碎岩 ＜250

表 1 岩体质量分级 Table 1 Rock mass quality classification

岩石单轴饱和抗压强度(R_c)与定性划分的岩石坚硬程度的对应关系可按表 2确定^[17].
表 2(Table 2)

表 2 Rc与岩石坚硬程度的对应关系Table 2 Correspondence between Rc and rock hardness ＞60 60~30 30~15 15~5 ≤5 坚硬程度 坚硬岩 较坚硬岩 较软岩 软岩 极软岩

表 2 Rc与岩石坚硬程度的对应关系 Table 2 Correspondence between Rc and rock hardness

岩体完整性系数(K_v)与定性描述时岩体的完整程度所对应的关系依据表 3确定^[17].
表 3(Table 3)

表 3 岩体完整程度描述与Kv取值对应关系Table 3 Correspondence between rock mass integrity description and Kv value Kv ＞0.75 0.75~ 0.55 0.55~ 0.35 0.35~ 0.15 ≤0.15 完整程度 完整 较完整 较破碎 破碎 极破碎

表 3 岩体完整程度描述与Kv取值对应关系 Table 3 Correspondence between rock mass integrity description and Kv value

应用作图方法建立新分级公式对应的限定条件, 其步骤如下^[17]:
1) 在R_c-K_v图上(图 1), 按分级界限(Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ)分别作出BQ=100 + 3R_c + 250K_v的4条直线A, B, C, D, 即
图 1(Fig. 1)

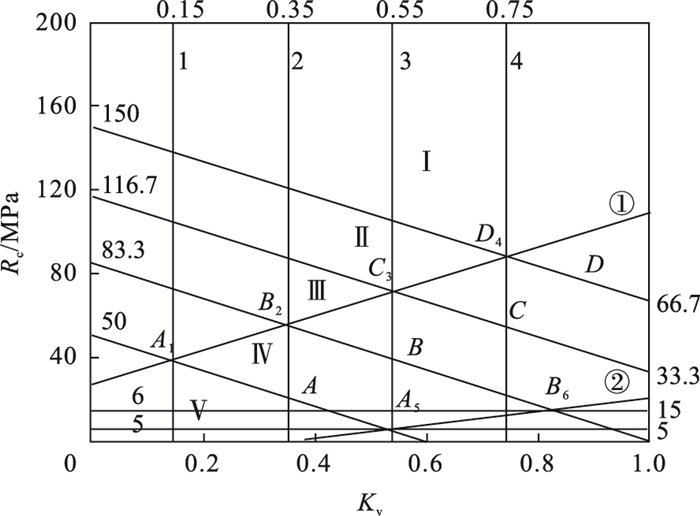图 1 BQ分级限定条件作图计算Fig.1 Drawing calculation of BQ classification limited conditions

A: 250=100 + 3R_c + 250K_v;
B: 350=100 + 3R_c + 250K_v;
C: 450=100 + 3R_c + 250K_v;
D: 550=100 + 3R_c + 250K_v.
2) 作K_v=0.15, 0.35, 0.55和0.75四条平行于R_c轴的直线1, 2, 3, 4;分别与A, B, C, D线交于A₁, B₂, C₃, D₄这4点(两点即可确定一条直线), 这4点回归成的直线即为上限的限定条件.
得出的交点坐标为A₁(0.15, 37.5), B₂(0.35, 54.17), C₃(0.55, 70.83), D₄(0.75, 87.5).其中任意两点确定的直线为R_c=83.35K_v+24.998;经验证, 4个点A₁, B₂, C₃, D₄全在确定的直线上.
3) 作R_c=5 MPa与15 MPa的2条平行线5和6平行于K_v轴, 分别相交于直线A与B上的A₅, B₆两点, 并以交点构建下限的限定条件.得出交点坐标为A₅(0.54, 5), B₆(0.82, 15)两点确定的直线为K_v=0.028R_c+0.4.计算结果为便于实际应用, 对于限定条件进行取整, 直线①公式为R_c=85K_v+25，直线②公式为K_v=0.03R_c+0.4.
限定条件的作图法计算分析过程见图 1.
根据图 1所示, 对直线①限定条件, 令K_v=0, 则R_c=25;令K_v=1, 则R_c=110.对直线②限定条件, 令R_c=0, 则K_v=0.4;令K_v=1, 则R_c=20.根据图示的面积占比经计算可得直线①限定条件的作用范围为66.66 %; 直线②限定条件的作用范围为3.21 %.限定条件综合作用范围为69.87 %，直线①限定条件的作用范围远远大于直线②限定条件.
2 应用图解法表示BQ分级结果2.1 图解法计算过程图解法计算过程的步骤如下:
1) 对于分级计算公式：

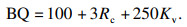(3)

令K_v=1, 计算公式变为BQ=350+3R_c, 式中无需考虑完整性系数的影响, 且BQ=350+3R_c≥350恒成立.在此情况下BQ对应岩体质量等级为Ⅰ, Ⅱ, Ⅲ级, 同时令BQ=550, 450, 350, 代入计算可得, R_c分别为66.667, 33.333, 0 MPa.
2) 令R_c= 85K_v+25, 需计算求解出对R_c值进行折减的上限值, K_v值满足0≤K_v≤1, 由此可知当R_c≥110 MPa时, 参数R_c值均需要进行折减计算, 此时的R_c值可以由85K_v+25进行代替, 故式(3)转化为BQ=100+3(85K_v+25)+250K_v=175+505K_v.
令BQ分别为550, 450, 350, 250, 对应在R_c≥110 MPa情况下, 求解岩体的不同级别所对应的K_v值, 经过求解可得, K_v值分别为0.743, 0.545, 0.347, 0.149.
3) 令K_v= 0.743, 0.545, 0.347, 0.149, 分别将K_v的值代入式(3)计算, 此时令BQ分别为550, 450, 350, 250, 计算求解出对R_c值进行折减的下限值分别为88.083, 71.25, 54.417, 37.583 MPa.
4) 令K_v= 0.03R_c+0.4, 需求解进行折减后K_v值的上限值, 已知K_v= 0.03R_c+0.4, K_v取值区间为[0.4, 1], 求解得R_c取值区间为[0, 20] MPa, 则R_c≥20 MPa时, 无需对K_v值进行折减.
考虑R_c取值区间为[0, 20] MPa时, K_v可由0.03R_c+0.4代替, 代入式(3)后, BQ=100+3R_c+250(0.03R_c+0.4)=200+10.5R_c.之后, 分别令BQ= 350, 250, 计算得到Ⅳ~Ⅴ级岩体K_v值折减后所得R_c上限值, 结果为14.286, 4.762 MPa.
5) 令R_c分别取14.286, 4.762 MPa, 代入式(3)，需求解出对Ⅳ~Ⅴ级K_v值进行折减的下限值, 结果分别为0.829, 0.543.
基于以上分析计算过程, 可以实现定量指标计算公式BQ=100+3R_c+250K_v的图解化.
2.2 定量指标BQ应用图解法表示根据2.1节分析计算中建立的分级定量指标公式BQ=100+3R_c+250K_v，以及附属的两个限定条件对应的图解法, 在计算过程中, 无限定条件的详细图解结果见图 2.以应用规范限定条件进行图解的结果见图 3^[18]; 应用本文中求解得到的限定条件进行图解的结果见图 4.
图 2(Fig. 2)

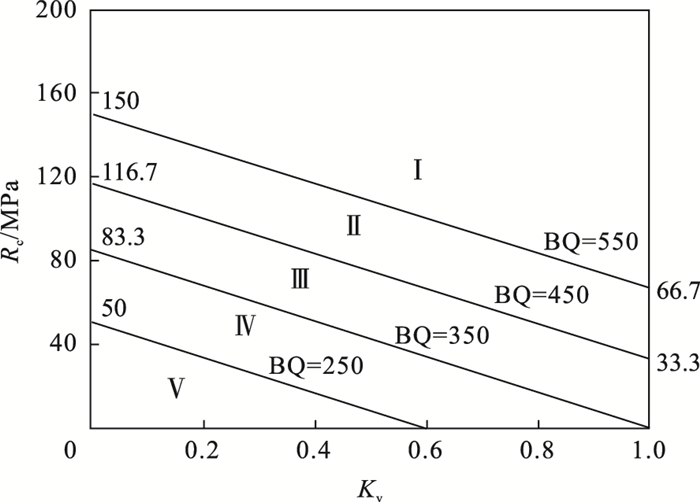图 2 无限定条件的图解Fig.2 Diagram without considering the limited conditions

图 3(Fig. 3)

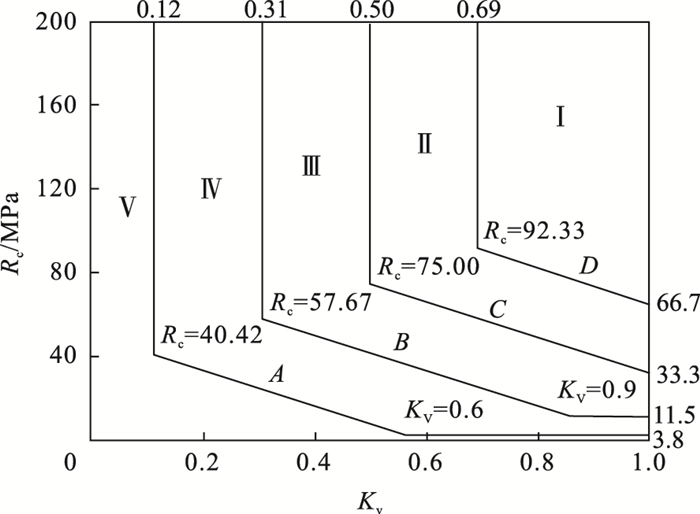图 3 应用规范限定条件的图解Fig.3 Diagram considering existing constraints

图 4(Fig. 4)

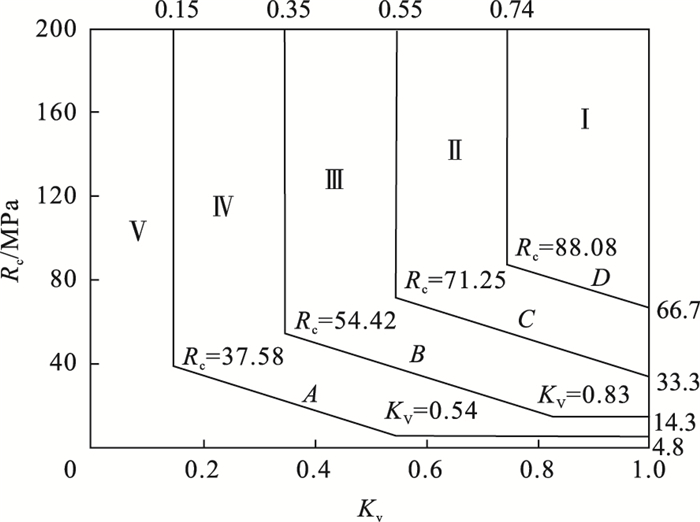图 4 应用本文限定条件的图解Fig.4 Diagram considering the proposed calculation limited conditions

限定条件优化后根据图解结果经计算可得, 应用规范限定条件的图解Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ级区域面积占比分别为18.68 %, 17.79 %, 22.22 %, 23.71 %, 17.61 %; 应用本文计算限定条件的图解Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ级区域面积占比分别为15.94 %, 17.30 %, 22.30 %, 24.23 %, 20.24 %; 两者对比结果为Ⅰ, Ⅱ级区域范围减小，而Ⅲ, Ⅳ, Ⅴ级区域范围逐渐增大.
3 工程实例验证新的限定条件下图解法的准确性以及合理性需进行验证, 选取实际工程和已发表成果中的BQ分级采集数据进行分析.表 4和表 5中定量1和图解1为当前规范中所应用的计算公式和限定条件下的分级结果, 定量2和图解2为现有计算公式以及应用作图法新计算出的限定条件下的分级结果, 通过采用在图上描点的方式能够更加快捷和准确地确定分级结果.
表 4(Table 4)

表 4 国内水电地下岩体工程BQ分级结果Table 4 BQ classification results of domestic hydropower underground rock mass engineering 项目名称 Rc/MPa Kv 定性 定量1 图解1 定量2 图解2 白山 126.0 0.72 Ⅱ Ⅰ Ⅰ Ⅱ Ⅱ 鲁布革 80.0 0.81 Ⅰ Ⅱ Ⅱ Ⅱ Ⅱ 东风 108.9 0.50 Ⅲ Ⅲ Ⅱ、Ⅲ Ⅲ Ⅲ 龙潭 107.1 0.42 Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ

表 4 国内水电地下岩体工程BQ分级结果 Table 4 BQ classification results of domestic hydropower underground rock mass engineering

表 5(Table 5)

表 5 西华岭隧道岩体BQ分级结果Table 5 BQ classification results of rock mass in Xihualing tunnel 洞段 Rc/MPa Kv 定性 定量1 图解1 定量2 图解2 K106+760 ~790(左) 62.1 0.31 Ⅳ Ⅲ Ⅲ Ⅳ Ⅳ K106+790 ~820(左) 61.5 0.25 Ⅳ Ⅳ Ⅳ Ⅳ Ⅳ K107+776 ~806(右) 72.3 0.63 Ⅱ Ⅱ Ⅱ Ⅱ Ⅱ K106+806 ~836(右) 77.6 0.71 Ⅱ Ⅱ Ⅱ Ⅱ Ⅱ

表 5 西华岭隧道岩体BQ分级结果 Table 5 BQ classification results of rock mass in Xihualing tunnel

3.1 国内水电地下岩体工程分级赖勇等^[22]列出了国内和国外的相关工程数据统计表, 因BQ分级是国内的统一分级方式, 现选取其研究国内实际岩体工程中的数据进行验证.相关的数据及计算结果见表 4.
通过表 4的对比分析结果可知, 白山工程定性结果为Ⅱ级，与定量2和图解2的分级结果是一致的, 而未进行更新的定量1和图解1的分级结果为Ⅰ级, 不同的分级结果对指导施工存在较大区别.
3.2 西华岭隧道工程岩体分级西华岭隧道^[18]属于诸永高速公路项目的金华段部位的工程, 隧道行车方式为双车道单向行车的分离式结构.本研究对其隧道中左右各两部分区段的围岩进行分级评价.隧道中左洞洞段的岩体性质属于火山凝灰岩, 此岩体整体比较破碎, 完整性较差.有发育程度较高的节理裂隙, 存在的节理严重切割围岩结构, 是导致其整体较破碎的主要原因.工程中右洞里程部分围岩是火山凝灰岩，受到轻微风化, 工程中无地下水发育, 岩体稳定性一般, 节理未出现延展性.分析结果如表 5所示.
通过表 5的对比分析结果可知, 西华岭隧道工程中洞段K106+760~790(左), 分级定性结果为Ⅳ级，与定量2和图解2的分级结果是一致的, 而未进行改进的定量1和图解1的分级结果为Ⅲ级, 不同的分级结果对指导施工存在较大区别.
4 公式优化及验证4.1 分段公式的建立经以上研究发现, 对于分级结果定性与定量不吻合的数据多为由限定条件折减后的数据, 现以国标计算公式更新时数据库新增54组数据^[17]为例, 以分段函数的思想对折减部分数据重新进行回归分析, 建立新的分级公式, 并对所得公式的准确性进行验证.
林韵梅^[16]总结发现二元多项式更适用于分级的5个级别, 与这5个等级都具有较好的相关性, 同时其在使用性以及推广性等方面的优势巨大, 在公式的推广上也更容易被使用者接受, 因此选定二元直线型函数来确定计算公式.在进行回归分析时, 其公式为

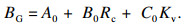(4)

式中：B_G为岩体等级；A₀, B₀, C₀为待定系数.
以实际工程数据中的R_c以及K_v代入式(4), 对应的计算结果可能会出现小数, 此情况应按照四舍五入的标准将岩体的分级结果划归为靠近BQ值的级别, 即数值比1.5小时为Ⅰ级, 数值在1.5~2.5时定为Ⅱ级, 在2.5~3.5时定为Ⅲ级, 在3.5~4.5时定为Ⅳ级, 数值大于4.5时取Ⅴ级.
式(4)中计算结果B_G的值越小, 则分级级数越小, 对应的岩体稳定性越好.且划分的级别区间在1~5之间, 会导致利用回归法求得式(4)中的系数较小.考虑到工程实际使用效果及具体计算时过程简便, 且在工程实例中其稳定性越好对应的BQ计算数值越大, 同时分级计算结果数据较小时, 轻微的变化会导致级别的跨越, 并且直接计算分级结果会增大计算误差, 所以建立公式时依然以BQ计算数值为标准并参照表 1岩体质量分级表来确定最终分级结果.
数据库中新增54组数据, 经计算分析发现其中包括33组数据无法用现有BQ分级计算公式直接计算, 需要先经过限定条件折减.现对这33组数据以二元直线型函数进行拟合新的计算公式.将数值代入进行拟合分析, 按照样本回归得到的直线型公式为

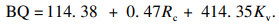(5)

在此条件下分级界限依然与表 1岩体质量分级对应.
式(5)的拟合相关程度为0.92, 曲线的拟合程度较好, 数据分析拟合过程如图 5所示.
图 5(Fig. 5)

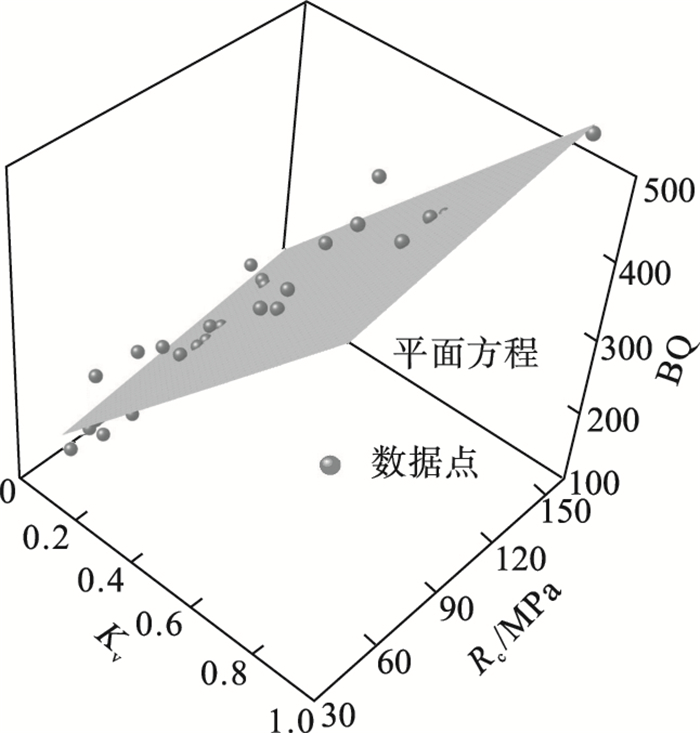图 5 二元直线型回归分析Fig.5 Binary linear regression analysis

4.2 公式的验证选取不同的行业公开发表的分级工程实例数据, 新公式计算分级结果与专家定性分级结果和原有分级计算公式计算的分级结果进行对比, 查验吻合度, 来验证新建立公式的准确性与适用性.
1) 对上文提到的西华岭公路隧道工程及国内的相关工程的实例数据进行验证, 结果见表 6.
表 6(Table 6)

表 6 新公式实例工程数据验证Table 6 Engineering data verification of new formula 隧道名称 Rc/MPa Kv 定性 原定量 新定量 K106+760 ~790(左) 62.1 0.31 Ⅳ Ⅲ Ⅳ 白山 126.0 0.72 Ⅱ Ⅰ Ⅱ

表 6 新公式实例工程数据验证 Table 6 Engineering data verification of new formula

2) 选取来自文献[13]的相关数据进行验证新公式的适用性, 结果见表 7.
表 7(Table 7)

表 7 部分实例工程数据Table 7 Some examples of engineering data 标号 Rc/MPa Kv 定性 原定量 新定量 A8-9 122 0.51 Ⅲ Ⅱ Ⅲ A121-140 91.9 0.53 Ⅲ Ⅱ Ⅲ A217-218 50.9 0.12 Ⅴ Ⅳ Ⅴ A222-225 89.3 0.31 Ⅳ Ⅲ Ⅳ

表 7 部分实例工程数据 Table 7 Some examples of engineering data

结合表 6, 表 7的数据计算结果, 分析得到由R_c限定条件折减的数据建立新公式计算的定量分级结果与定性分级结果完全吻合, 进一步说明所建立新公式的可行性.
5 结论1) 利用作图法获得了基于现有BQ计算公式的新限定条件, 以岩石抗压强度R_c和完整性系数K_v为参数作图, 使分级计算结果更加精确.
2) 通过实际工程数据以图解法验证新的限定条件应用效果, 提高了定性与定量分级结果的匹配程度, 使得吻合度提高了4 % ~15 %.
3) 限定条件优化后根据图解结果经计算可得, Ⅰ, Ⅱ级区域范围减小, 而Ⅲ, Ⅳ, Ⅴ级区域范围逐渐增大.
4) 研究验证了BQ分级中定性与定量分级结果不一致多由于R_c限定条件折减数据后计算导致, 并提出了分段函数思想, 对折减部分数据单独建立公式用于计算受限定条件影响的数据, 经验证计算结果与定性分级的结果完全一致.
5) 本文以现有分级公式计算了对应的限定条件, 通过研究分析得出限定条件的变化对部分工程数据对应的分级结果产生了较大影响; 针对限定条件影响数据单独建立公式计算, 应用效果较好.由于数据有限, 在此建议结合更广泛的实际工程数据来进行优化研究.
参考文献

[1]	中华人民共和国住房和城乡建设部. 国标《工程岩体分级标准》GB/T50218—2014[S]. 北京: 中国计划出版社, 2015. (Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for engineering classification of rock mass(GB/T50218—2014)[S]. Beijing: China Planning Press, 2015. )
[2]	Ootsuka Y, Ishikawa T, Tajima K, et al. Rock mass property evaluation based on the borehole wall images taken by using an ultrasonic scanner(USS)[J]. Journal of Nepal Geological Society, 2018, 55(1): 1-6. DOI:10.3126/jngs.v55i1.22782
[3]	Hou F J, Xie X K, Shi S S, et al. Dynamic optimization classification model for submarine tunnel surrounding rocks and its application in engineering[J]. Journal of Coastal Research, 2019, 94(sup1): 311-315.
[4]	Saroglou C, Qi S W, Guo S F, et al. ARMR: a new classification system for the rating of anisotropic rock masses[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(5): 3611-3626. DOI:10.1007/s10064-018-1369-4
[5]	Chen Q F, Yin T C, Niu W J. Replacing RQD and discontinuity spacing with the modified blockiness index in the rock mass rating system[J]. Archives of Mining Sciences, 2018, 63(2): 353-382.
[6]	Wickham G E, Tiedemann H R, Skinner E H. Support determinations based on geologic predictions[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1975, 12(7): 95.
[7]	Bieniawski Z T. Engineering rock mass classification—a complete manual for engineers and geologists in mining, civil and petroleum engineering[M]. Hoboken: Wiley, 1989.
[8]	Bieniawski Z T. Geomechanics classification of rock masses and its application in tunneling[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1975, 12(10): 141.
[9]	Bieniawski Z T. Rock mass classification in rock engineering[C]//Proceedings of Symposium for Rock Engineering. Johannesburg: [s. n. ], 1976: 97-106.
[10]	Khatik V M, Nandi A K. A generic method for rock mass classification[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2018(10): 102-116.
[11]	Mohammad M, Mohammad F H. Modification of rock mass rating system: interbedding of strong and weak rock layers[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017(9): 1165-1170.
[12]	Barton N. Some new Q-value correlations to assist in site characterization and tunnel design[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(2): 185-216. DOI:10.1016/S1365-1609(02)00011-4
[13]	Barton N. Analysis of rock mass quality and support practice in tunneling and a guide for estimating support requirements[J]. Rock Mechanics, 1974, 6(4): 189-236. DOI:10.1007/BF01239496
[14]	Barton N. Rock mass classification and tunnel reinforcement selection using the Q-system[M]//Kirkaldie L. Rock Classification Systems for Engineering Purposes. West Conshohocken: ASTM International, 1988: 59-88.
[15]	Chen L X, Chen S G, Tu P, et al. Study on mutual relationships between surrounding rock classifications by Q value, RMR and BQ method for underground cavern[J]. Subgrade Engineering, 2017(6): 107-112.
[16]	林韵梅. 岩体基本质量定量分级标准BQ公式的研究[J]. 岩土工程学报, 1999(4): 481-485. (Lin Yun-mei. Study on BQ formula of basic quality grading standard of rock mass[J]. Chinese Journal of Geotechnical Engineering, 1999(4): 481-485. DOI:10.3321/j.issn:1000-4548.1999.04.018)
[17]	王小江. 工程岩体基本质量指标和分级档次的研究[D]. 沈阳: 东北大学, 2011. (Wang Xiao-jiang. Study on basic quality index and classification grade of engineering rock mass[D]. Shenyang: Northeastern University, 2011. )
[18]	申艳军, 徐光黎. 国标岩体分级标准BQ的图解法表示[J]. 岩石力学与工程学报, 2012, 31(sup2): 3659-3665. (Shen Yan-jun, Xu Guang-li. Graphical representation of national rock mass classification standard BQ[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(sup2): 3659-3665.)
[19]	陈曦, 曾亚武, 刘伟. 岩体基本质量指标BQ图解法讨论[J]. 铁道标准设计, 2018, 62(11): 155-160. (Chen Xi, Zeng Ya-wu, Liu Wei. Discussion on graphic method of rock mass basic quality index BQ[J]. Railway Standard Design, 2018, 62(11): 155-160.)
[20]	周宗青, 李术才, 李利平, 等. 岩体质量等级分类预测方法及其工程应用[J]. 中南大学学报(自然科学版), 2017, 48(4): 1049-1056. (Zhou Zong-qing, Li Shu-cai, Li Li-ping, et al. Classification method of rock mass quality and its engineering application[J]. Journal of Central South University(Natural Science Edition), 2017, 48(4): 1049-1056.)
[21]	Chen K D, Song Y H, Zhang Y L, et al. Modification of the BQ system based on the Lugeon value and RQD: a case study from the Maerdang hydropower station, China[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(4): 2979-2990. DOI:10.1007/s10064-021-02151-3
[22]	赖勇, 张永兴. 细观损伤理论确定岩体参数的方法研究[J]. 岩石力学与工程学报, 2008, 27(sup1): 2617-2623. (Lai Yong, Zhang Yong-xing. Analytical method of rock mass parameters with micromechanical damage theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(sup1): 2617-2623.)