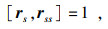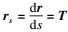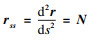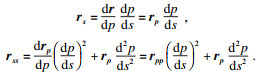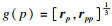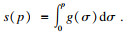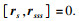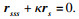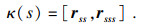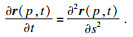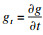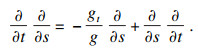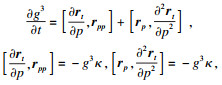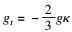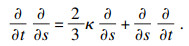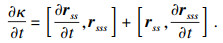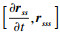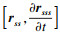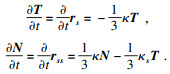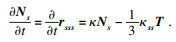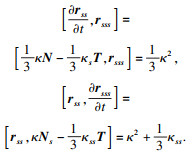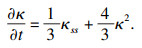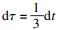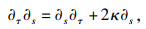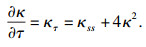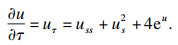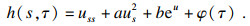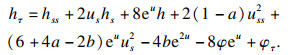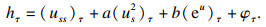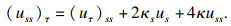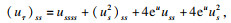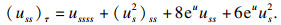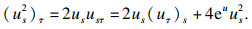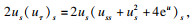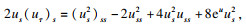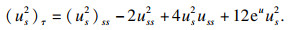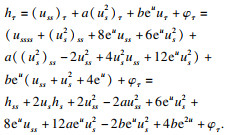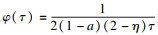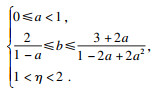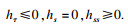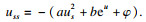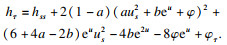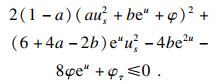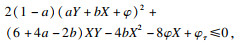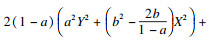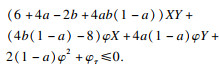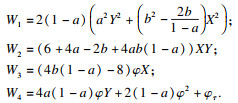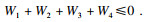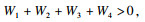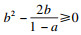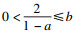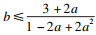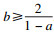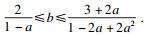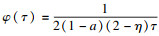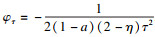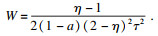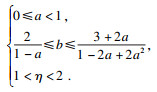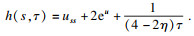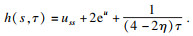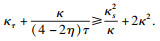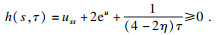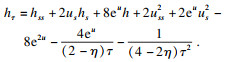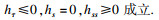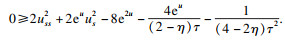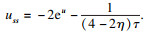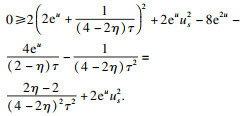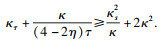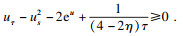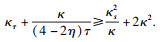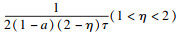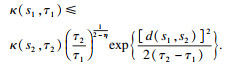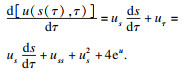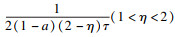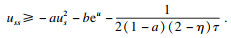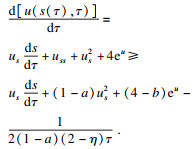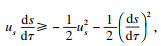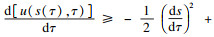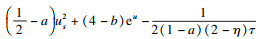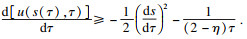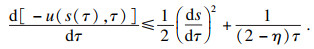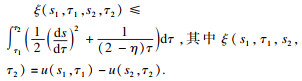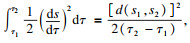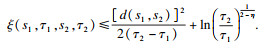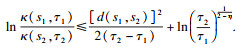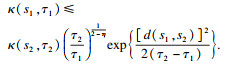于延华, 金伶


东北大学 理学院, 辽宁 沈阳 110819
收稿日期:2021-05-07
基金项目:国家自然科学基金资助项目(61773110)。
作者简介:于延华(1978-),女,湖北荆门人,东北大学副教授。
摘要:在仿射空间中研究了基于等仿射曲线收缩流的一族闭凸等仿射曲线的Harnack不等式.首先, 根据仿射空间中等仿射曲线的几何演化性质定义一类新的闭凸等仿射曲线Harnack量, 进而得到该Harnack量满足的几何演化方程.其次, 利用最大值原理证明Harnack量为非负, 即给出闭凸等仿射曲线的Harnack不等式, 并得到Harnack量中参数的相应约束条件.然后, 利用新定义的Harnack量进一步研究了闭凸等仿射曲线的Hamilton’s Harnack不等式.最后基于闭凸等仿射曲线Harnack不等式和柯西-施瓦兹(Cauchy-Schwarz)不等式推导出了经典的Harnack不等式.
关键词:仿射空间等仿射曲线曲线收缩流Harnack不等式
Harnack Inequality for Equi-Affine Curve Shortening Flow
YU Yan-hua, JIN Ling


School of Sciences, Northeastern University, Shenyang 110819, China
Corresponding author: JIN Ling, E-mail:
1391034570@qq.com.
Abstract: The Harnack inequalities of a family of closed convex equi-affine curves based on equi-affine curve shortening flow were studied. Firstly, according to the geometric evolution property of the equi-affine curve, a new type of Harnack quantity on the closed convex equi-affine curve was defined, then the evolution equation about the Harnack quantity of the closed convex equi-affine curve was discovered. Secondly, by the maximum principle, the non-negativity of the Harnack quantity, i.e., the Harnack inequality of the closed convex equi-affine curve, was investigated. Moreover, the constraint conditions of parameters in the Harnack quantity were found. Then, the Hamilton's Harnack inequality of the closed convex equi-affine curve was further explored using the newly defined Harnack quantity.Finally, the classical Harnack inequality was derived based on Harnack inequality of the closed convex equi-affine curve and Cauchy-Schwarz inequality.
Key words: affine spaceequi-affine curvecurve shortening flowHarnack inequality
在几何分析领域, 微分Harnack不等式是一个重要的研究课题.20世纪60年代初, Moser
[1]首次引入了线性抛物型微分方程正解的Harnack不等式.此后, Li和Yau
[2]研究了完备黎曼流形上的抛物型方程, 并利用最大值原理得到了黎曼流形上热方程
ut=Δ
u正解的梯度估计和Harnack不等式.Hamilton
[3-5]用同样的方法进一步证明了Ricci流上的Harnack不等式以及一些非线性方程的平均曲率流上的Harnack不等式.以上研究奠定了微分Harnack不等式的基础, 故此类微分估计也被称为“Li-Yau-Hamilton”型(LYH型)估计.近几十年来, 微分Harnack不等式成为了几何分析领域中主要的研究对象之一, 许多****在这领域作出了重大贡献
[6-7].
同时, 几何流在近些年来也逐渐成为了几何研究的热点内容
[8-9], 而且发展迅速.Gage等
[10]证明了当初始嵌入曲线是平面简单闭凸曲线时, 凸曲线在有限时间内收缩到一个点.1987年, Grayson
[11]证明了嵌入平面中的任何闭合曲线在有限时间内变为凸曲线, 并最终收缩到一个点.1994年, Sapiro等
[12]对凸曲线考虑了欧几里得曲线收缩流的仿射模拟,在此情况下, 演化曲线的速度是由仿射法向量给出.此后, Andrews
[13]将上述结果推广到了根据其仿射法线移动的凸超曲面.此外, Angenent等
[14]研究了关于非凸曲线的仿射热方程.
基于上述的研究成果, 本文将等仿射曲线收缩流和微分Harnack不等式问题相结合, 旨在研究等仿射曲线收缩流的微分Harnack不等式性质.
1 预备知识在二维实平面
ω上, 等仿射变换被定义为
x=
Gx+
y, 其中
x,
x,
y为二维实向量,
G∈ SL
2+ (
R).
设
C(
p):
S1→
R2 (
S1表示单位圆)为光滑嵌入曲线, 其中
p为一般参数.取参数
s使得曲线
C的表达式为
r =
r (
s),且满足条件:
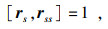 | (1) |
则参数
s被称为等仿射弧长, 并且称
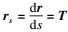
为等仿射切向量,
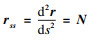
为等仿射法向量
[12].
文中[·, ·]表示2×2阶矩阵的行列式, 其中,
令等仿射度量
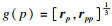
, 那么等仿射弧长
s可表示为
除非特殊说明, 本文均假设曲线以
s为参数, 映射都是充分光滑的, 且等仿射度量
g在曲线的每一点都不等于零.
在式(1)两边同时对
s求导, 可得
即存在函数
κ=
κ(
s)使得
则等仿射曲率可定义为
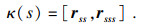 | (2) |
此时等仿射曲线演化方程有如下形式:
本文假设等仿射曲线均为严格凸曲线, 即为具有严格正曲率的曲线,且初始曲线记为
r (·, 0)=
r0(·).
在等仿射曲线收缩流下, 由等式d
s=
gd
p,
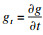
,可知
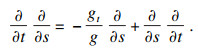 | (3) |
另一方面, 由
可以得到
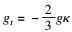
, 将其代入式(3), 易得
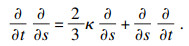 | (4) |
由式(2)可得
κ(
s)对时间
t的变化为
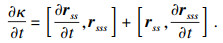 | (5) |
下面分别计算
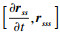
,
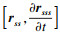
,并代回式(5).首先, 计算等仿射切向量和等仿射法向量的演化方程, 即
更进一步地, 计算
Ns的演化方程得
故易知,
因此, 等仿射曲率的演化方程为
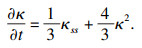 | (6) |
2 主要结论2.1 微分Harnack不等式令
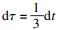
, 则式(4)和式(6)可分别表示为
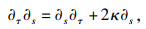 | (7) |
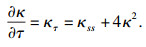 | (8) |
若令
u=
u(
s,
τ)=ln
κ(
s,
τ), 则式(8)可改写为
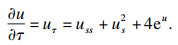 | (9) |
借鉴式(9)的表达形式, 定义一类新的Harnack量为
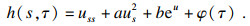 | (10) |
其中:
a,
b∈
R;
φ(
τ)为关于变量
τ的函数.
假设本文所研究的闭凸等仿射曲线的Harnack量均用表达式(10).下面先研究该Harnack量的演化方程.
定理1??设
C为等仿射曲线收缩流下的一族闭凸等仿射曲线, 且其Harnack量为
h(
s,
τ)=
uss+
aus2+
be
u+
φ(
τ), 其中
a,
b∈
R,
u为关于变量
s和
τ的函数,
φ(
τ)为关于变量
τ的函数, 则其演化方程为
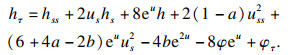 | (11) |
证明??在计算Harnack量的演化方程前, 作如下说明: 由式(10)可知Harnack量与函数
φ(
τ)相关, 当
φ(
τ)已知时, 为保证Harnack量为正值, 利用最大值原理进行下述讨论: 在
τ→0时,
φ(
τ)必须取非常大的值以保证Harnack量为正值.在上述假定下, 开始计算Harnack量的演化方程.
对式(10)关于
τ求导得
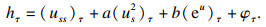 | (12) |
由此, 分别计算(
uss)
τ和(
us2)
τ, 并代回式(12).首先计算(
uss)
τ, 由于
?τ和
?s不可互换, 故由式(7)可知
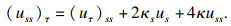 | (13) |
另一方面, 易知
将其代入式(13)有
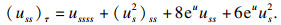 | (14) |
则(
us2)
τ可进一步化简为
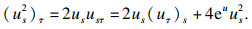 | (15) |
又由于式(9), 因此可得
即
将其代入式(15), 可得
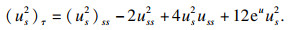 | (16) |
将式(14)和式(16)代入式(12), 可以得到Harnack量的演化方程的具体表达式为
定理1得证.
得到上述Harnack量的演化方程后, 进一步研究Harnack量的非负性.将
φ(
τ)取具体函数形式后, 可以得到如下结论.
定理2??设
C为等仿射曲线收缩流下的一族闭凸等仿射曲线, 且其Harnack量为
h(
s,
τ)=
uss+
aus2+
be
u+
φ(
τ),
u为关于变量
s和
τ的函数,
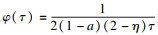
为关于变量
τ的函数, 其中
a,
b,
η∈
R, 则有
h(
s,
τ)≥0. 若
τ满足
τ>0, 则
h(
s,
τ)的系数满足
证明??用反证法证明该定理.假设存在某一时间使得
h(
s,
τ)≤0成立.
由于在定理1的证明过程中, 已假设
φ(
τ)→+∞(
τ→0), 即
a < 1,
η < 2时,
h(
s,
τ)>0. 因此, 必然存在某一时间
τ=
τ0>0,使min
h(
s,
τ)=0. 不妨假设
h(
s0,
τ0)=0, 由最大值原理可得在(
s0,
τ0)处有
由于
h(
s0,
τ0)=0, 则
因此, 在(
s0,
τ0)处, 式(11)可表示为
从而, 易得不等式:
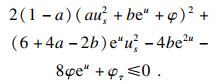 | (17) |
让
X=e
u,
Y=
us2, 那么式(17)可被写为
即
将不等式的左端分解为如下4项:
即有如下不等式:
因此, 只需证明存在参数使得
即可产生矛盾.
下面分别讨论
W1,
W2,
W3,
W4的非负性.
对
W1, 不失一般性, 假设0≤
a < 1.若存在
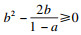
, 即
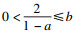
或
b≤0, 那么
W1是非负的.
对
W2, 由于
X>0,
Y≥0, 若多项式6+4
a-2
b+4
ab(1-
a)是非负的, 即
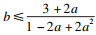
.而当
b≤0时, 该不等式必然成立.故
b≤0,
W2是非负的.
对
W3, 由于
X>0, 若假设
φ为正, 则
W3的非负性取决于4
b(1-
a)-8.如果4
b(1-
a)-8为非负的, 则
W3≥0, 此时
b满足
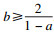
.
由上述对
W1,
W2,
W3的分析可得,
b满足如下不等式时,
W1,
W2,
W3均为非负,
对
W4, 由于0≤
a < 1,
Y≥0,
φ为正, 则4
a(1-
a)
φY≥0.记
W=2(1-
a)
φ2+
φτ.从而有
W4≥
W.
又因为
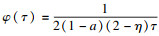
, 其中0≤
a < 1,
η < 2, 则显然有
τ→0时,
φ(
τ)→+∞, 此时,
h(
s,
τ)在等仿射曲线收缩流开始时是非负的, 且
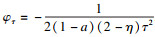
.
将
φ(
τ),
φτ代入
W, 可得
当
η满足1 <
η < 2时,
W中的所有项均为正, 即
W4≥
W>0.
由以上分析可知, 确实存在条件使
W1+
W2+
W3+
W4>0.故假设不成立, 即不存在使
h(
s,
τ) < 0的某一时间
τ. 又因假设
φ(
τ)→+∞(
τ→0), 故Harnack量在任意时刻始终为非负值.
与此同时, 由上述证明过程易知
τ>0时,
h(
s,
τ)的系数满足
定理2得证.
在定理2的结论下, 将闭凸等仿射曲线的Harnack量中的参数取定值, 即令
a=0(0≤
a < 1),
b=2, 故闭凸等仿射曲线Harnack量可以写为
其中1 <
η < 2.
将上述表达形式的闭凸等仿射曲线的Harnack量称为闭凸等仿射曲线的Hamilton's Harnack量, 并用该Harnack量研究闭凸等仿射曲线的Hamilton's Harnack不等式.
定理3??设
C为等仿射曲线收缩流下的一族闭凸等仿射曲线, 其Harnack量为
其中1 <
η < 2, 且
u=ln
κ, 则有
h(
s,
τ)≥0, 且等仿射曲率
κ满足不等式
证明??首先, 证明Harnack量为非负, 即
由定理1易知, 上述闭凸等仿射曲线的Harnack量演化方程为
在该演化方程下, 与定理2类似, 用反证法证明该推论, 即先假设存在某一时间使得
h(
s,
τ)≤0成立, 再寻找矛盾, 从而证明
h(
s,
τ)≥0.由定理2的证明过程可知, 必然存在
τ=
τ0>0使min
h(
s,
τ)=0.若
h(
s0,
τ0)=0, 则由最大值原理可得在(
s0,
τ0)处
故在(
s0,
τ0)处, Harnack量的演化方程可写为
另一方面, 由于
h(
s0,
τ0)=0, 故有
因此, 在(
s0,
τ0)处, 易得以下不等式:
由于1 <
η < 2,
τ>0, 显然假设并不成立, 即不存在使
h(
s,
τ) < 0的某一时间
τ. 所以, 闭凸等仿射曲线的Harnack量在任意时刻始终满足
h(
s,
τ)≥0.
下面证明等仿射曲率
κ满足不等式:
由于已经证明闭凸等仿射曲线的Harnack量满足
h(
s,
τ)≥0,且
uss=
uτ-
us2-4e
u, 故下列不等式成立,
此外,
u=ln
κ, 从而经过简单计算和变换, 可得上述不等式的等价形式如下:
定理3得证.
2.2 经典Harnack不等式在2.1节中, 已经得到了闭凸等仿射曲线的Harnack不等式.下面沿时空路径积分Harnack不等式, 可推导出经典的Harnack不等式.
定理4??设
C为等仿射曲线收缩流下的一族闭凸等仿射曲线, 且其Harnack量为
h(
s,
τ)=
uss+
aus2+
be
u+
φ(
τ), 其中
a,
b∈
R,
u(
s,
τ)=ln
κ(
s,
τ)为关于变量
s和
τ的函数,
φ(
τ)=
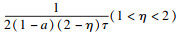
为关于变量
τ的函数.若
C为仿射空间内连接(
s1,
τ1), (
s2,
τ2)的任意时空曲线, 其中
τ2>
τ1>0, 且Harnack量中的参数满足2
a≤1,
b≤4, 则(
s1,
τ1)和(
s2,
τ2)处的曲率将满足以下不等式:
其中: 1 <
η < 2;
d(
s1,
s2)为
s1与
s2之间的距离.
证明??由微分Harnack不等式的内容可知, 若令
u(
s,
τ)=ln
κ(
s,
τ),
u的演化方程可写为
uτ=
uss+
us2+4e
u. 计算
u沿着
C的演化方程可得
不失一般性, 将形如式(10)的Harnack量中的函数
φ(
τ)固定为一类具体函数, 即令
φ(
τ)=
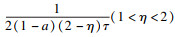
, 则可得
因此, 结合
u沿着
C的演化方程可得
又由柯西-施瓦兹(Cauchy-Schwarz)不等式, 可知
于是, 易得
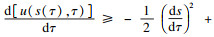
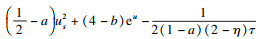
.
若令Harnack量中参数
a,
b分别满足2
a≤1,
b≤4, 则上述不等式可化简为
即式(18)成立:
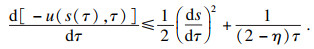 | (18) |
将式(18)沿着
C作积分, 易得
由于
C(
s,
τ)是仿射空间内连接(
s1,
τ1), (
s2,
τ2)的任意时空曲线, 故沿着时空路径积分, 速度不变, 那么有
故可得
又由于
u(
s,
τ)=ln
κ(
s,
τ), 则
因此, 上述不等式等价于:
定理4得证.
3 结语本文将等仿射曲线收缩流和微分Harnack不等式问题相结合, 研究了等仿射曲线收缩流下一族闭凸等仿射曲线的Harnack不等式.首先, 寻找到了闭凸等仿射曲线Harnack量的演化方程, 并在该演化方程下证明了闭凸等仿射曲线Harnack量的非负性, 即证明了闭凸等仿射曲线的Harnack不等式.其次, 在闭凸等仿射曲线Harnack量的非负性的基础上进一步证明了闭凸等仿射曲线的Hamilton’s Harnack不等式.最后基于闭凸等仿射曲线Harnack不等式研究了经典的Harnack不等式.本文提供了微分Harnack不等式研究的一个新的方向, 在此基础上还可以研究等仿射曲线收缩流下一族闭凸等仿射曲线的弱Harnack不等式等.
参考文献 | [1] | Moser J. A Harnack inequality for parabolic differential equations[J]. Communications on Pure and Applied Mathematics, 1964, 17(1): 101-134. DOI:10.1002/cpa.3160170106
|
| [2] | Li P, Yau S T. On the parabolic kernel of the Schrodinger operator[J]. Acta Mathematica, 1986, 156(3/4): 153-201.
|
| [3] | Hamilton R S. Matrix Harnack estimate for the heat equation[J]. Communications in Analysis and Geometry, 1993, 1(1): 113-126. DOI:10.4310/CAG.1993.v1.n1.a6
|
| [4] | Hamilton R S. The Harnack estimate for the Ricci flow[J]. Journal of Differential Geometry, 1993, 37(1): 225-243.
|
| [5] | Hamilton R S. Harnack estimate for the mean curvature flow[J]. Journal of Differential Geometry, 1995, 41(1): 215-226.
|
| [6] | Barlow M T, Chen X. Gaussian bounds and parabolic Harnack inequality on locally irregular graphs[J]. Mathematische Annalen, 2016, 366(3/4): 1677-1720.
|
| [7] | Qian B. Remarks on differential Harnack inequalities[J]. Journal of Mathematical Analysis and Applications, 2014, 409(1): 556-566. DOI:10.1016/j.jmaa.2013.07.043
|
| [8] | Bryan P, Louie J. Classification of convex ancient solutions to curve shortening flow on the sphere[J]. The Journal of Geometric Analysis, 2016, 26(2): 858-872. DOI:10.1007/s12220-015-9574-x
|
| [9] | Viado-Lereu F. The curve shortening flow with density of a spherical curve in codimension two[J]. Journal of Evolution Equations, 2020(2): 1-30.
|
| [10] | Gage M, Hamilton R S. The heat equation shrinking convex plane curves[J]. Journal of Differential Geometry, 1986, 23(1): 69-96.
|
| [11] | Grayson M A. The heat equation shirnks embedded plane curves to round points[J]. Journal of Differential Geometry, 1987, 26(2): 285-314.
|
| [12] | Sapiro G, Tannenbaum A. On affine plane curve evolution[J]. Journal of Functional Analysis, 1994, 119(1): 79-120. DOI:10.1006/jfan.1994.1004
|
| [13] | Andrews B. Contraction of convex hypersurfaces by their affine normal[J]. Journal of Differential Geometry, 1996, 43(2): 207-230.
|
| [14] | Angenent S, Sapiro G, Tannenbaum A. On the affine heat equation for non-convex curves[J]. Journal of the American Mathematical Society, 1998, 11(3): 601-634. DOI:10.1090/S0894-0347-98-00262-8
|