
 , 刘平凡, 张石, 许方晗
, 刘平凡, 张石, 许方晗 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期:2021-02-01
基金项目:中央高校基本科研业务费专项资金资助项目(N182410001)。
作者简介:佘黎煌(1980-),男,福建莆田人,东北大学讲师,博士;
张石(1963-),男,辽宁抚顺人,东北大学教授,博士生导师。
摘要:针对目前多数低复杂度Root-MUSIC算法的精度损失问题, 研究并提出了一种具备精度补偿能力的低复杂度Root-MUSIC算法.该算法依据有限快拍数得到的近似数据观测矩阵首行重构具有Toeplitz形态的自相关矩阵, 使重构的自相关矩阵具备Hermitian性; 对重构的自相关矩阵特征值分解后获得噪声子空间, 并将噪声子空间翻转拆分, 重构新的求根多项式, 进而通过求根方法得到DOA估计值.本文算法通过Toeplitz矩阵重构及求根多项式降阶, 不但有效提高了改进Root-MUSIC算法的DOA估计精度, 同时改进算法的时间复杂度不高于前人算法; 在不同的入射信源及采样快拍数下, 本文算法表现出更强的鲁棒性和稳定性.
关键词:Root-MUSIC算法精度损失重构Toeplitz矩阵噪声子空间翻转拆分求根多项式降阶鲁棒性和稳定性
An Improved Root-MUSIC Algorithm with High Precision and Low Complexity
SHE Li-huang

 , LIU Ping-fan, ZHANG Shi, XU Fang-han
, LIU Ping-fan, ZHANG Shi, XU Fang-han School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: SHE Li-huang, E-mail: shelihuang@ise.neu.edu.cn.
Abstract: Aiming at the precision loss problem of most low-complexity Root-MUSIC algorithms at present, a low-complexity Root-MUSIC algorithm with precision compensation ability is studied and proposed. The algorithm reconstructs the autocorrelation matrix with Toeplitz shape according to the first row of the approximate data observation matrix obtained by finite snapshots, so that the reconstructed autocorrelation matrix has Hermitian property. After decomposing the reconstructed autocorrelation matrix, the noise subspace is obtained, the noise subspace is flipped and split, a new root-finding polynomial is reconstructed, and then the DOA estimated value is obtained by the root-finding method. The algorithm proposed in this paper using Toeplitz matrix reconstruction and root polynomial reduction effectively improves the DOA estimation accuracy of the improved Root-MUSIC algorithm. And the time complexity of the improved algorithm is no higher than that of previous algorithms. Under different incident sources and sampling snapshots, the algorithm proposed in this paper also shows stronger robustness and stability.
Key words: Root-MUSIC algorithmprecision lossreconstructing Toeplitz matrixnoise subspaceflip and splitroot polynomial reductionrobustness and stability
阵列信号处理技术包括DOA估计技术及波束形成技术, 广泛应用于空间信号探测、雷达及水声信号探测等诸多领域[1].其中DOA估计技术作为获得信号波达方向角度的重要技术, 如何使DOA估计算法获得更高的估计精度和更低的时间复杂度一直是科研人员的主要研究方向.
在众多DOA估计算法中, Root-MUSIC算法以其较高的估计精度、较低的复杂度受到众多科研人员的重视[2], 大量基于Root-MUSIC算法的改进算法被提出.传统Root-MUSIC算法存在的最大问题在于随着阵列规模的增大, 算法的运算负担成倍增加.在较低阵列规模时, 多项式求根使算法运行效率较高, 而当阵列规模增大后, 其求根多项式阶数快速升高, 算法运行耗时甚至超过谱峰搜索类算法[3].目前众多基于Root-MUSIC算法的改进算法都着重针对求根多项式进行降维操作, 通过较低的数据规模实现DOA估计.Ren等[4]提出了一种快速Root-MUSIC算法, 通过将噪声子空间进行拆分, 构造新的数据向量, 使得求根多项式阶数降低至仅为信号源个数, 大大降低了算法运行复杂度.由于噪声子空间信息利用率较低, 算法精度损失严重, 王新贺等[5]在Ren等[4]拆分噪声子空间矩阵的基础上重构数据向量, 充分利用噪声子空间, 算法精度有了大幅度提升, 但运算复杂度也随之增大, 同时算法在阵列规模较大时完全失效, 不具备鲁棒性.Yan等[6]将均匀线阵拆分为两个相等子阵列, 利用两个子阵列采集的数据构造3个无噪声互相关矩阵, 用处理后的新数据矩阵进行DOA估计, 并将此DOA估计数据作为参考值, 重复以上方法,进行二次估计得到最终DOA估计值[7].算法通过拆分子阵构造新互相关矩阵的方法避免了特征分解运算, 降低了求根运算的复杂度, 但在低阵列规模时算法精度损失严重.探测阵列必须为偶数, 可估计信源个数较少, 鲁棒性较差.本文在Toeplitz矩阵重构及求根多项式降阶的基础上, 提出了一种改进的Root-MUSIC算法, 算法依据数据观测矩阵首行重构Toeplitz矩阵.特征值分解后得到噪声子空间, 并将噪声子空间翻转拆分, 重构新的求根多项式向量, 进而通过求根方法得到DOA估计值.算法通过重构Toeplitz矩阵使得新自相关矩阵具备Hermitian性质, 相比于传统自相关矩阵特征值分解算法, 本文算法拥有更高的DOA估计精度.噪声子空间的翻转拆分重构了新的低阶求根多项式, 有效降低了算法的时间复杂度.
1 阵列信号模型设存在M个满足远场条件的各向同性阵元所组成的均匀线阵模型, 同时有q个远场窄带目标信号源, 其入射角为θk(k=1, 2, …, q), 并且满足M>q.选择首个阵元作为参考阵, 阵元间距设为d, 则此时阵列响应向量为
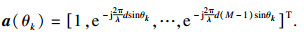 | (1) |
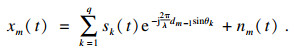 | (2) |
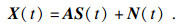 | (3) |
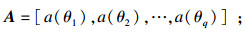 | (4) |
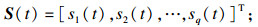 | (5) |
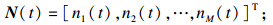 | (6) |
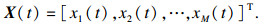 | (7) |
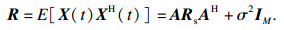 | (8) |
2 本文方法描述2.1 Toeplitz矩阵重构算法由于硬件设备采样快拍数的限制, 由数据观测矩阵获得的自相关矩阵并不能满足理想的Hermitian性质, 仅能保证对角占优, 因此存在估计误差.Toeplitz矩阵重构算法通过将数据观测矩阵的第一行即首个阵元获得的数据作为参考向量, 构造新的自相关矩阵使得新矩阵具备Hermitian性质.相较于原始自相关矩阵更加逼近理想值, DOA估计精度更高, 同时不会产生阵列孔径损失, 估计信源个数不会受到影响[8].
由式(2)可以得到数据观测矩阵第一行即首个阵元的输出为
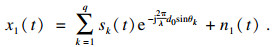 | (9) |
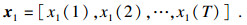 | (10) |
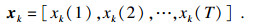 | (11) |
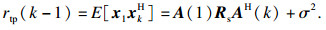 | (12) |
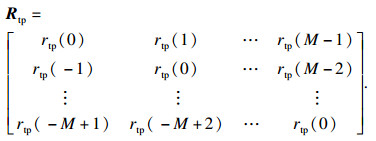 | (13) |
2.2 Root-MUSIC算法谱峰搜索算法通过全范围角度的遍历来搜索DOA估计值, 在阵元数较少时会导致算法运行耗时增大.而求根MUSIC算法(Root-MUSIC)将这一过程省去, 替代为简化的多项式求根过程.
通过式(1)可以得到阵列响应向量, 这里定义:
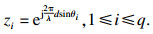 | (14) |
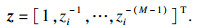 | (15) |
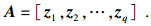 | (16) |
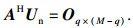 | (17) |
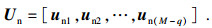 | (18) |
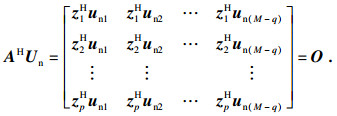 | (19) |
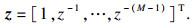 | (20) |
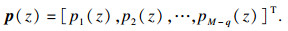 | (21) |
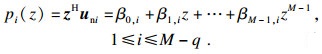 | (22) |
由式(21)可知, M-q个多项式pi(z)的阶数均为M-1, 且有q个公共根z1, z2, …, zq.
根据文献[7]构造多项式:
 | (23) |
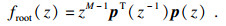 | (24) |
在实际情况下因采样快拍数的限制无法获得理想的自相关矩阵, 因此实际得到的近似协方差矩阵存在一定程度的误差, 这时只需要对式(24)求近似的q个根即可(最靠近单位圆).在均匀直线阵下的DOA估计角度计算式为
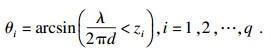 | (25) |
根据2.2节可知, 设存在多项式p1(z), p2(z), …, pM-q(z)且同时拥有q个公共根z1, z2, …, zq, 则它们之间存在线性组合Q(z):
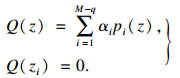 | (26) |
设存在c1, c2, …, cM-q使得Q(z)=∑cipi(x), 则将公共根r代入Q(z)可得
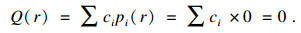 | (27) |
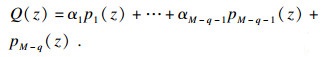 | (28) |
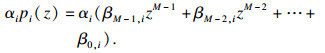 |
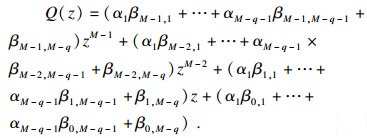 | (29) |
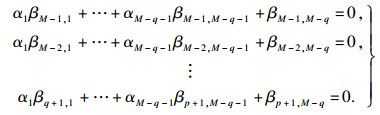 | (30) |
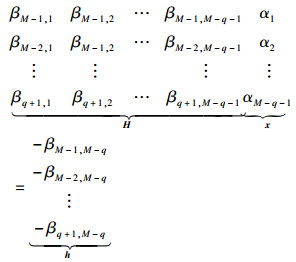 | (31) |
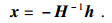 | (32) |
在2.2节的讨论中, 对自相关矩阵R进行特征值分解得到噪声子空间Un, 其列向量uni=[β0, i, β1, i, …, βM-1, i]T, 则将噪声子空间列向量翻转可得:
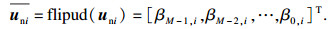 | (33) |
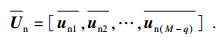 | (34) |
 | (35) |
依据式(32)及式(35)计算得到线性组合Q(z)的系数向量x, 并将式(21)代入式(25)得到一个新的求根多项式:
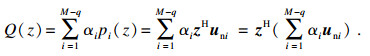 | (36) |
本文算法的整体实现过程如下:
1) 根据式(12)及式(13)构造近似数据观测矩阵下的Hermitian Toeplitz矩阵Rtp;
2) 对矩阵Rtp做特征值分解, 得到噪声子空间矩阵Un;
3) 依据式(33)~式(35), 对Un翻转拆分获得矩阵H及向量h;
4) 通过计算式(32)得到系数向量x, 并根据式(36)构造新的求根多项式Q(z);
5) 完成求根运算, 并寻找最靠近单位圆的q个根, 通过式(25)求得DOA估计角度.
3 实验验证与比较针对改进算法的DOA估计性能及算法运行耗时进行仿真测试.为验证本文算法的各项性能, 仿真实验分别对比了文献[4]的快速Root-MUSIC算法、文献[6]的无需特征分解计算的两步Root-MUSIC算法和经典Root-MUSIC算法; 同时, 对几种算法的时间复杂度进行了分析.
均方根误差计算式为
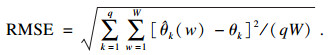 | (37) |
3.1 DOA估计精度实验实验1:两个独立入射信源角度分别为-10°和10°; 阵列为8阵元均匀直线阵列, 阵列间距为λ/2;采样快拍数为200, 信噪比以2 dB间隔从-10 dB变化至10 dB,进行1 000次蒙特卡洛实验,计算均方根误差.不同信噪比下算法的DOA估计精度对比如图 1所示.
图 1(Fig. 1)
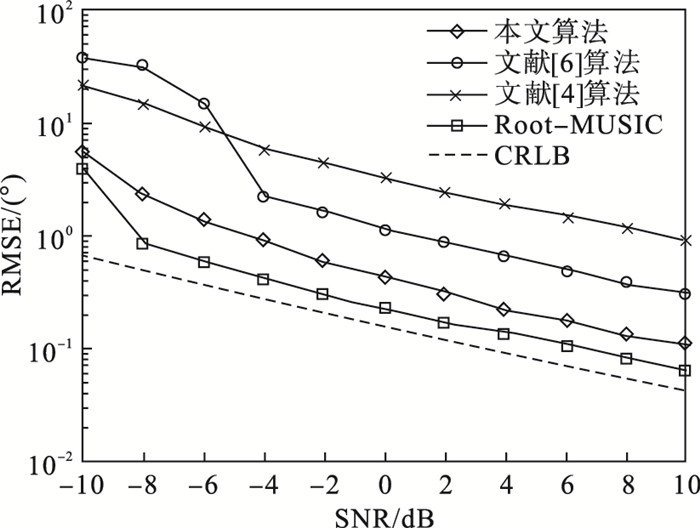 | 图 1 不同信噪比下算法的DOA估计精度对比Fig.1 Comparison of DOA estimation accuracy of algorithms under different signal-to-noise ratios |
由图 1可知, 随着信噪比的增加, 4种算法的均方根误差均有所下降, 而本文算法的估计误差最接近经典Root-MUSIC算法, 低于文献[4]及文献[6]所提算法; 同时可以发现, 本文算法及经典算法更加接近算法的无偏估计量下界(克拉美罗下界)CRLB, 拥有更高的估计精度.
实验2: 独立入射信源数量为3个, 分别为-10°, 10°和20°, 其余实验条件与实验1一致, 同样使信噪比以2 dB间隔从-10 dB变化至10 dB进行1 000次蒙特卡洛实验, 计算均方根误差.
不同信噪比下算法的DOA估计精度对比如图 2所示.
图 2(Fig. 2)
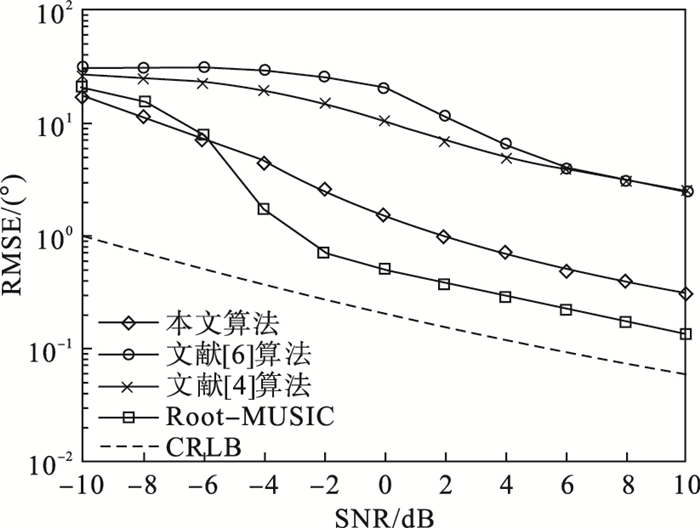 | 图 2 不同信噪比下算法的DOA估计精度对比Fig.2 Comparison of DOA estimation accuracy of algorithms under different signal-to-noise ratios |
由图 2可知, 当入射信源增加为3个时, 由于阵列规模的限制, 文献[4]和文献[6]的算法已经基本失效, 而本文算法及经典Root-MUSIC算法在低信噪比环境下效果较差, 随信噪比的增加, 均方根误差都有较大幅度的下降.受限于阵列规模, 相较于2个入射信源的情况本文算法及经典Root-MUSIC算法的DOA估计性能均有所下降.
实验3: 2个独立入射信源角度为-10°和10°, 阵列仍采用8阵元均匀直线阵列, 阵列间距为λ/2, 信噪比固定为5 dB.采样快拍数以50为间隔从100变化至600进行1 000次蒙特卡洛实验, 计算均方根误差.不同快拍数下算法的DOA估计精度对比如图 3所示.
图 3(Fig. 3)
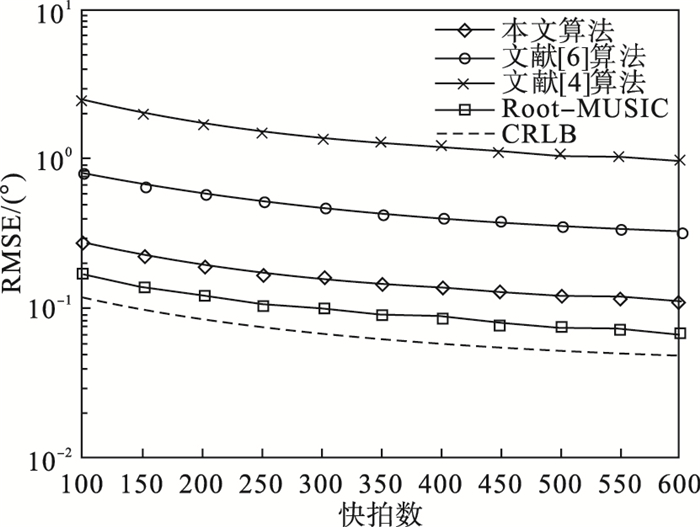 | 图 3 不同快拍数下算法的DOA估计精度对比Fig.3 Comparison of DOA estimation accuracy of algorithms under different snapshots |
由图 3可知, 采样快拍数对算法的DOA估计精度有显著影响, 随采样快拍数量的增加, 4种算法的均方根误差都呈现出减小的趋势.但从仿真图中可以清晰看出, 本文算法的整体均方根误差曲线在文献[4]和文献[6]之下, 其均方根误差曲线更加接近经典Root-MUSIC算法及无偏估计量下界CRLB, 拥有更高的DOA估计精度及更强的鲁棒性.
实验4:独立入射信源数量变为3个, 分别为-10°, 10°和20°, 其余实验条件与实验3一致.采样快拍数同样以50为间隔从100变化至600进行1 000次蒙特卡洛实验, 计算均方根误差.不同快拍数下算法的DOA估计精度对比如图 4所示.
图 4(Fig. 4)
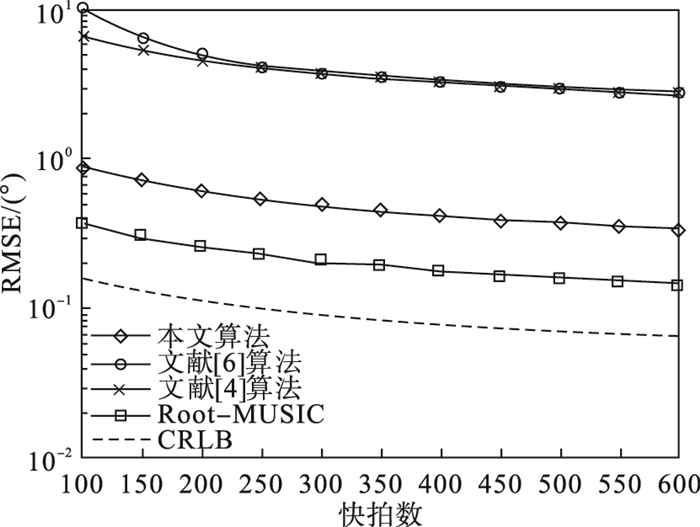 | 图 4 不同快拍数下算法的DOA估计精度对比Fig.4 Comparison of DOA estimation accuracy of algorithms under different snapshots |
由图 4可知, 算法的均方根误差均随着快拍数的增加而下降.但在入射信源个数增加至3个时, 由于阵列规模的限制, 文献[6]由于算法自身需要拆分阵元进行互相关矩阵重构, 其可利用阵元数量严重下降, DOA估计精度损失严重; 文献[4]则由于算法本身利用噪声子空间信息较少, DOA估计精度同样不足; 本文算法及经典Root-MUSIC算法的均方根误差相较于2个入射信源时同样有所上升, 但总体更加趋近于无偏估计量下界CRLB, 算法的DOA估计精度更高.
3.2 时间复杂度分析本文算法的目的旨在解决目前多数低复杂度Root-MUSIC算法的DOA估计精度不足问题, 那么所提算法自身的时间复杂度也不能有明显提升, 对3.1节中的4种算法的时间复杂度进行分析(其中T为采样快拍数).算法各主要运算部分时间复杂度对比如表 1所示.
表 1(Table 1)
| 表 1 算法各主要运算部分时间复杂度对比 Table 1 Comparison of time complexity of main operation parts of algorithm |
由表 1可知, 文献[4]算法的求根运算时间复杂度最低; 本文算法在求根多项式运算部分的时间复杂度上高于文献[4], 但低于文献[6]及经典Root-MUSIC算法; 本文算法的协方差矩阵运算时间复杂度最低; 在阵元规模较小时, 本文算法及文献[4]算法的子空间提取时间复杂度略高于文献[6]算法, 但随着阵元规模的增大, 本文及文献[4]算法的子空间提取时间复杂度将低于文献[6]算法.整体看, 本文算法的综合时间复杂度略高于文献[4]算法, 但低于文献[6]及经典Root-MUSIC算法.下面通过实验5来验证这一结果.
实验5:两个独立入射信源角度分别为-10°和10°, 信噪比固定为5 dB, 采样快拍数为200, 阵元间距为λ/2.阵元数量以2为间隔从6变化至40, 每种算法运行1 000次计算耗时.算法运行1 000次的耗时对比如图 5所示.
图 5(Fig. 5)
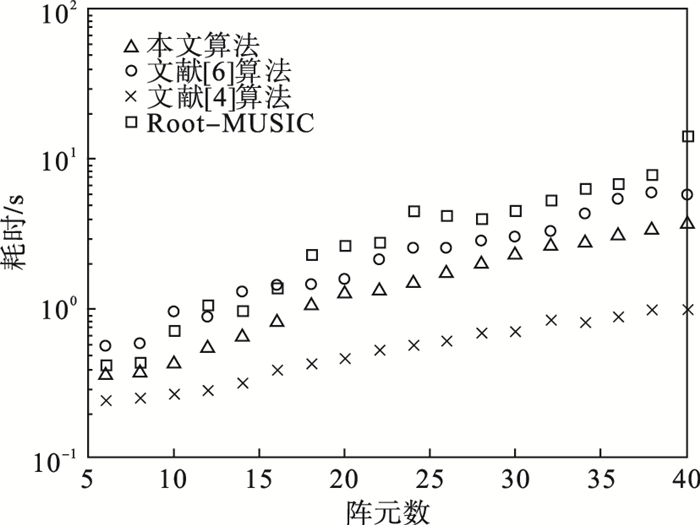 | 图 5 算法运行1 000次的时间耗时对比Fig.5 Comparison of the time consumption of algorithm running 1 000 times |
由图 5可知, 随着阵元数量的增加, 算法的运行耗时均有所增加.其中文献[4]的算法耗时始终最低, 这也说明了多项式求根运算是整个算法运行过程中耗时占比最高的部分; 本文算法耗时高于文献[4]算法, 但始终低于文献[6]算法及经典Root-MUSIC算法, 从表 1的时间复杂度分析也可以验证这一点.多项式求根运算的时间复杂度决定了算法整体的时间复杂度, 而本文算法在不提高其他运算部分时间复杂度的同时, 降低了多项式求根运算的时间复杂度, 使得算法整体运行耗时降低.
4 结论针对多数低复杂度Root-MUSIC算法的DOA估计精度损失问题, 本文提出了一种高精度低复杂度的改进Root-MUSIC算法.算法通过近似数据观测矩阵首行重构具有Hermitian性质的Toeplitz矩阵, 并将其作为新的自相关矩阵做特征值分解运算得到噪声子空间; 对噪声子空间作翻转拆分处理, 重构新的求根多项式; 最终通过求根运算得到DOA估计值.仿真实验结果表明, 相较于部分前人算法, 本文算法拥有更高的DOA估计精度, 其均方根误差更接近于经典Root-MUSIC算法及无偏估计量下界, 同时拥有更高的鲁棒性及稳定性,其时间复杂度则基本不高于前人算法.
参考文献
| [1] | Xu K J, Nie W K, Feng D Z, et al. A multi-direction virtual array transformation algorithm for 2D DOA estimation[J]. Signal Processing, 2016, 125: 122-133. DOI:10.1016/j.sigpro.2016.01.011 |
| [2] | Yan F G, Shen Y, Jin M, et al. Computationally efficient direction finding using polynomial rooting with reduced-order and real-valued computations[J]. Journal of Systems Engineering and Electronics, 2016, 27(4): 739-745. DOI:10.21629/JSEE.2016.04.01 |
| [3] | Yan F G, Jin M, Zhou H J, et al. Low-degree Root-MUSIC algorithm for fast DOA estimation based on variable substitution technique[J]. Science China: Information Sciences, 2020, 63(5): 218-220. |
| [4] | Ren Q S, Willis A J. Fast Root-MUSIC algorithm[J]. IEEE Electronics Letters, 1997, 33(6): 450-451. DOI:10.1049/el:19970272 |
| [5] | 王新贺, 周围. 改进的Root-MUSIC算法的DOA估计[J]. 通信技术, 2015, 48(12): 1354-1357. (Wang Xin-he, Zhou Wei. DOA estimation of modified Root-MUSIC algorithm[J]. Communications Technology, 2015, 48(12): 1354-1357. DOI:10.3969/j.issn.1002-0802.2015.12.007) |
| [6] | Yan F G, Liu S, Wang J, et al. Two-step Root-MUSIC for direction of arrival estimation without EVD/SVD computation[J]. International Journal of Antennas and Propagation, 2018[2021-02-01]. https://doi.org/10.1155/2018/9695326. |
| [7] | Shaghaghi M, Vorobyoy S A. Subspace leakage analysis and improved DOA estimation with small sample size[J]. IEEE Transactions on Signal Processing, 2015, 63(12): 3251-3265. DOI:10.1109/TSP.2015.2422675 |
| [8] | Tang L, Song H, Hu L J. Blind separation of coherent signals based on Toeplitz matrix reconstruction[J]. Applied Mechanics and Materials, 2012, 1511: 331-335. |
