

1. 吉林大学 计算机科学与技术学院, 吉林 长春 130012;
2. 吉林大学符号计算与知识工程教育部重点实验室, 吉林 长春 130012
收稿日期:2021-06-17
基金项目:国家自然科学基金资助项目(61976050); 吉林省自然科学基金资助项目(20190103005JH)。
作者简介:韩淑婷(1998-), 女, 河南博爱人, 吉林大学硕士研究生;
赖永(1985-), 男, 江西萍乡人, 吉林大学副教授。
摘要:模型计数是求给定命题公式的模型数, 是人工智能领域的一个基本问题.在贝叶斯网络、有界模型检测、精确集合覆盖等众多实际问题中, 存在许多exactly-one约束.常见的处理方法是将exactly-one约束编码为CNF公式, 再调用模型计数器求解.这种方法扩大了命题公式的规模, 容易导致求解时间过长.本文分别提出从CNF公式中还原exactly-one约束的ECR算法和处理exactly-one约束的ECP算法.ECR算法能明显提高C2D编译器的求解效率.基于最新的模型计数器ExactMC, 本文改进了能识别和单独处理exactly-one约束的模型计数器ECMC.实验结果表明, ECMC的时间效率相比ExactMC有显著提高.
关键词:exactly-one约束模型计数二元约束传播合取范式C2D
Research on Model Counting with Mixed Exactly-One Constraints
HAN Shu-ting1, LAI Yong1, LIU Jie1


1. College of Computer Science and Technology, Jilin University, Changchun 130012, China;
2. Key Laboratory of Symbolic Computation and Knowledge Engineering, Ministry of Education, Changchun 130012, China
Corresponding author: LIU Jie, E-mail: liu_jie@jlu.edu.cn.
Abstract: Model counting is the number of models for a given proposition formula, which is a basic problem in the field of artificial intelligence. There are many exactly-one constraints in many practical problems such as Bayesian networks, bounded model detection, and accurate set coverage. A common processing method is to encode exactly-one constraints as CNF formulas, and then call the model counter to solve them. This method expands the scale of the proposition formula and easily leads to too long solution time. This paper respectively proposes the ECR algorithm that restores exactly-one constraints from the CNF formula and the ECP algorithm that handles exactly-one constraints. The ECR algorithm can significantly improve the solution efficiency of the C2D compiler. Based on the latest model counter ExactMC, this paper improves the model counter ECMC that can recognize and handle exactly-one constraints separately. The experimental results show that the time efficiency of ECMC is significantly improved compared to ExactMC.
Key words: exactly-one constraintmodel countingbinary constraint propagationconjunctive normal formC2D
命题可满足性(satisfiability, SAT)问题是判定给定命题公式是否可满足的问题, 是第一个被证明的NP完全问题[1].模型计数(#SAT)是求给定命题公式的可满足的解数,即模型数[2], 计算复杂度是#P完全的[3].模型计数在概率推理[4-5]、规划[6]、量化信息流[7]、神经网络验证[8]等方面有广泛应用.
精确的模型计数按求解方式分为直接求解和编译求解.精确计数求出的模型数是精确的.Sang等[9]提出组件缓存技术并与SAT问题中的CDCL架构相结合实现了精确计数器Cachet. Thurley[10]在他的sharpSAT求解器中提出改进的组件缓存方案和隐式BCP算法.Sharma等[11]的Ganak求解器使用概率组件缓存技术进一步改进了sharpSAT求解器.以上3种求解器都是精确的直接求解器.编译求解的主要思想是通过知识编译将原命题公式编译为更易处理的目标语言, 再使用模型计数算法进行计数. Darwiche[12-13]提出的C2D求解器将给定命题公式编译为d-DNNF再计数, C2D求解器是基于编译的精确求解器[14]. Lai等[15]提出利用文字等价的新目标语言CCDD, 并将直接求解和编译求解相结合设计了精确求解器ExactMC, 其性能优于Ganak和C2D.
合取范式(conjunctive normal form, CNF)是模型计数常用命题公式, 公式中变量的取值只有0和1两种.但在贝叶斯网络、精确集合覆盖、图着色问题等实际问题中, 多值变量的使用更为常见.多值变量在命题逻辑知识库中用exactly-one约束表示.对包含多值变量的问题进行模型计数时, 通常需要将exactly-one约束转化为只包含二值变量的CNF公式[16].对于包含大量exactly-one约束的复杂问题, 在转化时就需要引入大量的二元子句.Exactly-one约束越多越复杂, 转化得到的CNF公式越庞大, 求解时间呈指数增长.显然, 需要更好的方法来解决上述问题.本文从还原CNF公式中exactly-one约束和直接处理exactly-one约束两方面, 对模型计数算法进行改进.目标是缩小CNF公式的规模, 提高模型计数器求解效率.
本文提出的算法ECR(exactly-one constraint recognition)能从CNF公式中识别exactly-one约束.目前C2D是唯一能直接处理exactly-one约束的求解器, 将算法ECR应用于C2D求解器能明显提升其求解效率.模型计数器ExactMC相较C2D求解器使用了多种先进的模型计数算法, 求解效率也更高.然而ExactMC目前不能直接处理exactly-one约束.因此, 本文提出对exactly-one约束进行单独处理的算法ECP(exactly-one constraint propagation).为了让本文提出的技术可用于加权模型计数, 屏蔽了ExactMC中的内核化技术.基于ExactMC改进得到可处理exactly-one约束的模型计数器ECMC.大量实验结果表明, 改进后的求解器ECMC时间效率明显优于ExactMC求解器.
1 基础知识1.1 Exactly-one约束命题公式由命题变量(x, y, z)、布尔常量(0或1)和逻辑连接词(?、∧、∨)组成.本文用F表示CNF公式, Var(F)和Cl(F)分别表示F的变量集和子句集.CNF公式F由子句C的合取组成, 子句由文字l的析取组成.文字包括正文字(变量x)和负文字(变量的否定?x).其他任意命题公式都可以等价转化为CNF公式.当一组定义在Var(F)上的真值指派使F评估为真时, 称该真值指派为一个可满足的解或模型.CNF公式可理解为n个变量的二元赋值到二元结果的映射{0, 1}n→{0, 1}.模型计数就是计算使F可满足的真值指派数.
Exactly-one约束在贝叶斯网络、图着色问题、有界模型检测、精确集合覆盖等多值问题上有广泛应用. CNF公式中的子句都是at-least-one约束, 即子句中至少有一个变量被满足.而exactly-one约束是有且只有一个变量被满足的子句, 因此可以用来表示多值变量.例如多值变量有m个取值, 其对应的exactly-one约束就会包含m个变量.
定义1?? at-least-one约束: 给定文字集(l1 , …, ln)上的布尔公式是at-least-one约束当且仅当满足以下条件: ∑i=1nli≥1, 其中文字li被满足时本文记为1, 反之为0.
定义2?? exactly-one约束: 给定文字集(l1, …, ln)上的布尔公式是exactly-one约束当且仅当满足以下条件: ∑i=1nli=1, 其中文字li被满足时本文记为1, 反之为0.
给定文字集(l1, …, lk), 其上的exactly-one约束记为l1∨l2∨…∨lk.文字集中有且只有一个文字被满足时, exactly-one约束被满足.将exactly-one约束转换为at-least-one约束, 需要保证任意两个文字都不同时为真.当k=2时, 二元exactly-one约束l1∨l2可等价转换为(l1∨l2)∧(?l1∨?l2), 从而没有大幅增大公式规模.本文所研究的exactly-one约束可用于表示多值变量, 因此无特殊说明下文中所提到的k均大于2, 识别和处理exactly-one约束时不考虑单元子句(长度为1)和二元子句(长度为2), 只考虑长子句(长度大于2).
基于exactly-one约束任意两文字不同时为真的性质, 包含k个变量的exactly-one约束能等价转换成
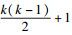
例1 ??

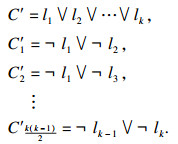 |
N皇后问题是指在n×n格的棋盘上摆放n个皇后, 任意两个皇后不能处于同一横纵行或斜线上, 求共有多少种摆法.棋盘上共有2n条横纵行(格数为n), 4n-6条斜线(格数大于1). 将棋盘上每个格都看作一个变量, n×n格对应变量集(x1, …, xn2).同一横纵行或斜线上至多有一个变量被满足, 因此N皇后问题共需6n-6条exactly-one约束表示.其中每条横纵行有且只有一个变量被满足, 共编码为2n条exactly-one约束, 每条约束包含n个变量.每条斜线上至多一个变量被满足, 编码为exactly-one约束需要为每条斜线增加一个新变量, 以保证斜线上有0或1个变量被满足.N皇后问题使用n2+4n-6个变量编码为6n-6条exactly-one约束, 再调用模型计数器即可快速求出摆法数.
将多值变量编码为exactly-one约束再进行模型计数求解的方法应用广泛, 提升混合exactly-one约束的模型计数求解效率对快速解决多值问题至关重要.
1.3 模型计数C2D是一个经典的基于编译的精确模型计数器, 可以直接处理exactly-one约束, 但由于C2D未开源无法应用许多更先进的模型计数新技术, 其求解效率受到极大限制.最新的精确求解器ExactMC相较于C2D采用了多种已被证明对编译有效的模型计数优化方法, 包括组件缓存、子句学习、两文字监视法和变量排序启发式VSIDS(variable state independent decaying sum)等.
组件缓存技术将给定布尔公式分解为若干不相交的子公式, 在模型计数搜索过程中存储子公式的模型数以便再次遇到时不必重新求解.
BCP利用单元子句规则对已赋为真的文字l进行传播, 在包含?l的子句C中寻找更多的蕴含文字.具体蕴含方式为: 若C中有且只有一个文字l′未赋值, 其余文字均被赋为假, 则l为真.在BCP过程中, 若存在某文字同时被蕴含为真和假, 则必有某个子句不被满足, BCP出现冲突.若C中文字均被赋为假, 则C不被满足出现冲突, BCP将出现冲突的子句返回;若无冲突产生, BCP返回值为空.
当BCP返回值不为空时, 利用子句学习技术对BCP返回的冲突进行分析, 并将生成学习子句加入公式中, 从而避免搜索时再次出现同一冲突.
两文字监视法是为加速BCP过程而提出的长子句管理方法.因为单元子句规则只有在长子句中未赋值文字由2个变为1个时发挥作用, 所以对长子句前两个文字进行监视, 始终保持前两个文字未赋值或赋值为真.两文字监视法减少了单元传播过程中所需遍历的子句数, 对快速BCP有重要意义.
VSIDS是一种选择分支变量的启发式算法, 其主要思想是为每个变量设置活性积分, 每次选择排序中积分最高的变量进行赋值.当冲突分析产生的学习子句时, 学习子句中包含的变量积分增加.同时, 为避免陷入局部最优, 所有变量的积分需要定期除以一个常量.
2 Exactly-one约束识别算法面对包含复杂多值变量的实际应用问题时, exactly-one约束编码为CNF公式, 往往要引入大量二元子句, 从而导致CNF公式规模过大, 求解时间过长.一条包含m个文字的exactly-one约束编码时需要引入o(m2)的二元子句.因此本文提出exactly-one约束识别算法ECR.通过算法ECR还原给定F中的exactly-one约束, 能大大减少F中的二元子句数, 缩小公式规模.同时对识别出的exactly-one约束进行标记, 以便之后对其单独处理.
从CNF公式中识别exactly-one约束和将exactly-one约束编码为CNF公式互为逆过程.因此ECR识别算法主要思想是判断子句中任意两个文字是否都不同时为真.在CNF公式F中, 判断一个普通长子句C=l1∨… li… lj…∨ln(i, j∈(1, …, n))是否为exactly-one约束, 需要判断C中任意两个文字的否定组成的二元子句(?li, ?lj)是否都被F蕴含.若C需要判断的所有二元子句都在F中显式存在或者隐式蕴含, 则C是exactly-one约束, 若存在某个二元子句不被蕴含, 则C不是exactly-one约束.
判断二元子句(?li, ?lj)是否被F蕴含是一个co-NP完全问题, 因此采取一种近似判断方法, 将li, lj赋值为真后进行BCP, 若产生冲突则说明li, lj不能同时赋值为真, 二元子句(?li, ?lj)被F蕴含; 若没有产生冲突, 则不被蕴含, 即C中存在某两个文字可以同时赋值为真, C不是exactly-one约束.算法1给出exactly-one约束识别算法ECR的算法描述,见表 1.
表 1(Table 1)
| 表 1 1 000 s内4种方法能求解出的实例数 Table 1 The number of instances that can be solved by the 4 methods in 1 000 s |
在算法ECR中, 第1行遍历F中所有长子句. 2 ~3行判断C是否是已标明的exactly-one约束.第4行用numbi记录子句C需要判断的二元子句个数.5~9行遍历所有需要判断的二元子句.第6行判断二元子句是否被F蕴含, 若被蕴含则进入第7行将numbi减1, 若不被蕴含则转到第9行判断出C不是exactly-one约束, 返回第1行继续遍历下一子句. 10~11行numbi=0说明已经遍历完所有需要判断的二元子句且均未出现冲突, 因此C是exactly-one约束.第12行函数返回F中exactly-one约束比例.对于识别出的exactly-one约束, 算法ECR删除其蕴含的所有二元子句, 大大缩小了识别后CNF公式的大小规模.
表 1(Table 1)
| 表 1 算法1 Table 1 Algorithm 1 |
ECR算法第6行判断某二元子句是否被蕴含时设置了两个判断条件, 分别是显式查询和BCP蕴含.本文将只判断是否为F中二元子句而不进行BCP蕴含的exactly-one约束识别算法记为ECR-wo-BCP.与ECR-wo-BCP相比, ECR算法能更彻底地挖掘CNF公式中存在的exactly-one约束, 识别能力也会更高.
3 Exactly-one约束处理算法ECR算法完成了对exactly-one约束的识别, 若将exactly-one约束视为CNF公式中的普通子句来处理, 模型计数得到的结果将偏大.C2D是目前唯一能直接处理exactly-one约束的求解器.然而C2D中未采用目前很多先进的模型计数求解技术, 大大影响其求解效率.因此本节提出对exactly-one约束进行单独处理的算法ECP.
Exactly-one约束在BCP时拥有比普通子句更强的蕴含和剪枝能力.具体表现为, exactly-one约束除了具有普通子句BCP时的性质, 还具有任意两文字不同时为真的性质.当exactly-one约束中某文字被满足时, 其余所有文字都只能赋值为假.若exactly-one约束其余文字中仍存在已经赋值为真的文字, 则exactly-one约束不被满足, 出现冲突.此时BCP返回由这两个同时为真的文字的否定构成的二元子句.与普通子句相比, exactly-one约束在BCP时能蕴含出更多的文字, 出现冲突情况也多了一种.更强大的文字蕴含能力意味着更快的剪枝能力.因此, 直接处理exactly-one约束能减少模型计数的求解时间.下面给出exactly-one约束处理算法ECP的算法描述, 见表 2.
表 2(Table 2)
| 表 2 算法2 Table 2 Algorithm 2 |
ECP算法是exactly-one约束的传播算法.ECP算法的输入包括CNF公式F和文字集L, 其中文字集L是当前传播过程中已被赋为真的所有文字的集合.ECP算法的输出和BCP算法一致, 都是int型的冲突原因.算法第1行将返回值reason初始化为0, 第2行开始对文字集L中的文字l进行传播.第3~4行找出包含l的exactly-one约束.第5~9行检验exactly-one约束中所有非l的文字, 将未赋值文字的赋值为假.若存在已赋值为真的文字, 将l作为冲突文字左移一位记录到冲突原因reason中.第10行中若reason为0, 则进入11行对文字l进行BCP.第12行返回冲突原因.ECP算法对exactly-one约束是否存在两文字同时为真的冲突进行检测, 对已满足即存在文字为真的exactly-one约束进行文字蕴含, 实现了对exactly-one约束的单独处理.
4 实验结果为验证本文所提出的算法ECR和算法ECP在模型计数问题上的有效性, 本文通过多个实验来分析测试算法的性能.本节依次介绍实验所用测试集、测试集中exactly-one约束比例、对测试集进行模型计数的实验结果.
4.1 测试集为确保实验结果具有普遍性, 本文依据CNF公式中exactly-one约束比例分别选取部分包含exactly-one约束和只包含exactly-one约束两类测试集进行测试.
测试集1中的CNF公式exactly-one约束占比小于100%, 具体包括Planning, Bayesian Network-Ace, bmc, Handmade-Latin Square, circuit-iscas, qif共350个CNF公式, 这些测试用例来源于人工智能领域的许多重要问题:规划、贝叶斯网络、有界模型检测、拉丁方等.
测试集2是由精确集合覆盖问题编码得到的CNF公式,exactly-one约束占比100%.精确集合覆盖问题在人工智能和运筹学领域有重要应用, 包括数独、N皇后难题、图着色问题、完美匹配问题等.精确集合覆盖问题是指P=(X, S), P是一个二元组, X是有限元素的集合, S是由X的子集构成的集合.P的解S*是S的子集, 且满足X中的元素在S*中恰好出现一次.因此精确集合覆盖问题编码得到的CNF公式将只包含exactly-one约束.目前已知的将精确集合覆盖问题转化为CNF公式的方法有很多, 本文使用Junttila等[16]的编码方式得到CNF公式作为实验的测试集2, 包括bell, Latin6, Latin7, doublefact共40个CNF公式.
4.2 exactly-one约束比例测试集1中的测试用例部分包含exactly-one约束, 测试集2的测试用例全由exactly-one约束组成.使用第3节中提出的识别算法对测试集1中exactly-one约束的比例进行统计, 以分析算法的有效性.设计了两种exactly-one约束识别算法, 分别是算法ECR和ECR-wo-BCP.由于测试集2全部由exactly-one约束组成, 两种识别算法在测试集2上计算出的比例均为100%.图 1对比了两种识别算法在测试集1上的识别效果.测试集1中CNF公式的exactly-one约束比例在0~100%之间均有分布, exactly-one约束比例的随机性说明本文选取的测试集具有普遍性.图 1中红色曲线代表算法ECR在测试集1上识别exactly-one约束的结果, 绿色曲线代表算法ECR-wo-BCP的识别结果.由实验结果可知, 算法ECR识别出的exactly-one约束明显更多, 识别能力更强.
图 1(Fig. 1)
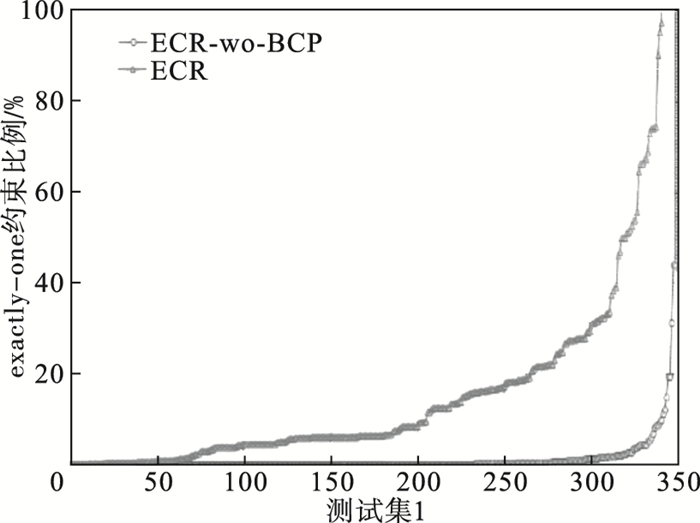 | 图 1 算法ECR与ECR-wo-BCP在测试集1上识别exactly-one约束的比例Fig.1 The exactly-one constraint proportion of CNF identified by ECR and ECR-wo-BCP in testset 1 |
4.3 实验结果C2D是经典的基于编译的精确模型计数器, 也是目前唯一能够直接处理exactly-one约束的求解器.算法ECR识别exactly-one约束之后的测试用例可由C2D编译器求解.ExactMC是目前最先进的精确模型计数器.基于算法ECR和算法ECP将模型计数器ExactMC改进为可处理exactly-one约束的模型计数器ECMC.
采用4种不同方法对比测试本文提出的算法ECR和算法ECP的性能.其中方法1和方法2分别使用C2D和ExactMC直接对测试集进行模型计数; 方法3使用算法ECR识别exactly-one约束后再调用C2D求解器进行模型计数, 将该方法记为C2D_E; 方法4使用本文改进得到的求解器ECMC进行模型计数.方法3和方法4使用了算法ECR和ECP, 因此与方法1和方法2进行对比可验证本文算法的有效性.
图 2对比了4种方法在测试集1上的实验结果.横坐标表示数据集1中的测试用例, 纵坐标表示模型计数时间, 纵坐标时间上限为1 000 s.由图 2可知, 由于ExactMC求解器采用了许多模型计数的新技术, 因此ExactMC求解效率比C2D更高; C2D_E的求解时间明显少于C2D, 说明算法ECR能显著提升C2D的求解效率; ECMC的求解效率是4种方法中最高的, 说明算法ECR和算法ECP大大提高了模型计数求解效率.
图 2(Fig. 2)
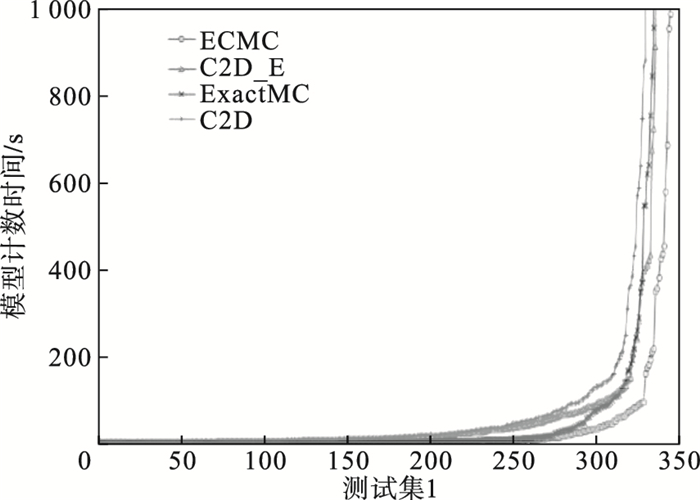 | 图 2 C2D_E,C2D,ExactMC,ECMC在测试集1上的模型计数时间Fig.2 Model counting time of C2D-E, C2D, ExactMC and ECMC on testset 1 |
图 3对比了4种模型计数方法在测试集2上的实验结果.横坐标表示数据集2中的测试用例, 纵坐标表示模型计数时间, 纵坐标时间上限为1 000 s.图 3中4种求解方法在精确集合覆盖问题上的求解速度由快到慢排序分别是: ECMC>ExactMC>C2D_E>C2D.ECMC求解效率最优, 表明本文提出的对exactly-one约束识别并单独处理的策略对模型计数求解效率有显著提升.
图 3(Fig. 3)
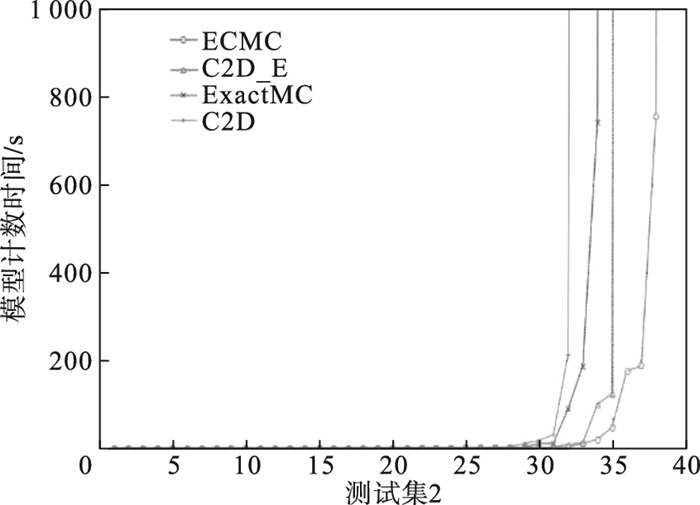 | 图 3 C2D_E, C2D, ExactMC, ECMC在测试集2上的模型计数时间Fig.3 Model counting time of C2D-E, C2D, ExactMC and ECMC on testset 2 |
表 1统计了1 000 s内4种模型计数方法在测试集1和测试集2上求解出的实例数目.测试集1共包含350个测试用例, 测试集2共包含40个测试用例.观察表 1可知, 在测试集1和测试集2上, 从左到右4列数据是递增的, 即4种方法求出的实例数目是递增的.C2D_E和ECMC求出的实例数均大于C2D和ExactMC求出的实例数, 这说明使用算法ECR和算法ECP能求解出更多的实例.
综合上述实验结果, C2D_E总是优于C2D, ECMC总是优于ExactMC.这说明本文算法ECR和ECP无论是单独使用还是同时使用, 都能有效提升模型计数问题的求解效率.相较于直接求解的模型计数方法, 识别并单独处理exactly-one约束的策略是有效的, 且求解效率更高.
5 结论1) 针对模型计数方法处理多值变量时, 数据量大、求解时间过长的问题, 提出从CNF公式中还原并单独处理exactly-one约束策略.该策略包含两个算法: 识别exactly-one约束的ECR算法; 处理exactly-one约束的ECP算法.
2) 实验结果表明, 将算法ECR应用于C2D求解器能显著提升C2D的求解效率, exactly-one约束的模型计数器ECMC求解效率明显高于改进前的求解器ExactMC.
参考文献
| [1] | Cook S. The complexity of theorem-proving procedures[C]// Proceedings of the Third Annual ACM Symposium on Theory of Computing. Nork York: Association for Computing Machinery, 1971: 151-158. |
| [2] | 贺甫霖, 刘磊, 吕帅, 等. 基于格局检测的模型计数方法[J]. 软件学报, 2020, 31(2): 395-405. (He Fu-lin, Liu Lei, Lyu Shuai, et al. Model counting methods based on configuration checking[J]. Journal of Software, 2020, 31(2): 395-405.) |
| [3] | Valiant L G. The complexity of enumeration and reliability problems[J]. SIAM Journal on Computing, 1979, 8(3): 410-421. DOI:10.1137/0208032 |
| [4] | Bacchus F, Dalmao S, Pitassi T. Algorithms and complexity results for #SAT and Bayesian inference[C]// Proceedings of the 44th Annual IEEE Symposium on Foundations of Computer Science. Cambridge: IEEE Press, 2003: 340-351. |
| [5] | Roth D. On the hardness of approximate reasoning[J]. Artificial Intelligence, 1996, 82(1/2): 273-302. |
| [6] | Domshlak C, Hoffmann J. Probabilistic planning via heuristic forward search and weighted model counting[J]. Journal of Artificial Intelligence Research, 2011, 30(1): 565-620. |
| [7] | Biondi F, Enescu M A, Heuser A, et al. Scalable approximation of quantitative information flow in programs[M]. Los Angeles: Springer-Verlag, 2018: 71-93. |
| [8] | Baluta T, Shen S, Shinde S, et al. Quantitative verification of neural networks and its security applications[C]//Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. New York: Association for Computing Machinery, 2019: 1249-1264. |
| [9] | Sang T, Beame P, Kautz H. Heuristics for fast exact model counting[C]// International Conference on Theory & Applications of Satisfiability Testing. Berlin: Springer-Verlag, 2005: 226-240. |
| [10] | Thurley M. SharpSAT: counting models with advanced component caching and implicit BC[C]// International Conference on Theory and Applications of Satisfiability Testing. Berlin: Springer-Verlag, 2006: 424-429. |
| [11] | Sharma S, Roy S, Soos M, et al. GANAK: a scalable probabilistic exact model counter[C]//Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. Macao: IJCAI Press, 2019: 1169-1176. |
| [12] | Darwiche A. New advances in compiling CNF into decomposable negation normal form[C]// Proceedings of the 16th European Conference on Artificial Intelligence. Amsterdam: IOS Press, 2004: 328-332. |
| [13] | Darwiche A. Decomposable negation normal form[J]. Journal of the Association for Computing Machinery, 2001, 48(4): 608-647. DOI:10.1145/502090.502091 |
| [14] | 吕帅, 张桐搏, 王强, 等. 两种新的基于扩展规则#SAT问题求解算法[J]. 东北大学学报(自然科学版), 2019, 40(5): 630-634, 646. (Lyu Shuai, Zhang Tong-bo, Wang Qiang, et al. Two novel algorithms based on extension rule for solving #SAT problem[J]. Journal of Northeastern University(Natural Science), 2019, 40(5): 630-634, 646.) |
| [15] | Lai Y, Meel K S, Yap R H C. The power of literal equivalence in model counting[C]// Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence. California: AAAI Press, 2021: 3851-3859. |
| [16] | Junttila T A, Kaski P. Exact cover via satisfiability: an empirical study[C]// Principles and Practice of Constraint Programming-CP 2010. Berlin: Springer-Verlag, 2010: 297-304. |
