徐礼胜^1,2, 苏宇剑¹, 谭浚宜¹, 方喜冬¹
1. 东北大学 医学与生物信息工程学院, 辽宁 沈阳 110169;
2. 沈阳东软智能医疗科技研究院有限公司, 辽宁 沈阳 110167
收稿日期：2021-06-11
基金项目：国家自然科学基金资助项目(61773110)；沈阳市科学技术计划项目(20-201-4-10)；中央高校基本科研业务费专项资金资助项目(N2119008)；沈阳东软智能医疗科技研究院有限公司会员课题基金资助项目(MCMP062002)。
作者简介：徐礼胜(1975-)，男，安徽安庆人，东北大学教授，博士生导师。

摘要：心电P波蕴含了人体丰富的生理、病理信息, 但P波幅值较小、形态多变, 检测十分困难.本文提出一种双边长短窗能量差法来检测多形态P波边界, 并使用粒子群算法优化其参数.从LUE数据库和QT数据库中分别选取4 363个和1 936个心电节拍, 其中70%作为训练集, 30%作为测试集, 并与基于动态规划的参数混合高斯拟合法和无相位平稳小波变换法对比, 正向与负向P波的结果误差明显小于上述两种方法, 该算法可检测出双向P波, 同时还具有一定抗噪能力.
关键词：心电信号P波检测多形态心电P波双边长短窗能量差法粒子群
ECG P Wave Detection Combining Particle Swarms and Energy Difference Between Bilateral Long and Short Windows
XU Li-sheng^1,2, SU Yu-jian¹, TAN Jun-yi¹, FANG Xi-dong¹
1. College of Medicine and Biological Information Engineering, Northeastern University, Shenyang 110169, China;
2. Neusoft Research of Intelligent Healthcare Technology Co., Ltd., Shenyang 110167, China
Corresponding author: XU Li-sheng, E-mail: xls@bmie.neu.edu.cn.

Abstract: The ECG P wave contains abundant physiological and pathological information of the human body, but the P wave amplitude is small and the shape is changeable, which is very difficult to detect. This paper proposes a bilateral long-short-window energy difference method to detect multi-modal P wave boundaries, and uses the particle swarm algorithm to optimize its parameters. 4363 and 1936 ECG beats are selected from the LUE database and QT database respectively, with 70% and 30% of them used as the training set and the test set, respectively. Compared with the parameter-mixed Gaussian fitting method based on dynamic programming and the phase-free stationary wavelet transform method, the error of the results of positive and negative P waves is significantly smaller than the above two methods, and the algorithm can detect bidirectional P waves, and it also has anti-noise ability.
Key words: ECG signalP wave detectionpolymorphic ECG P wavebilateral long-short-window energy difference methodparticle swarm
心电图分析可用于诊断心血管疾病, 大多数诊断所需数据都可以从心电图波形的间隔、幅度和形状中获得^[1], 所以准确且可靠提取心电图特征十分重要.心电信号是在皮肤表面获得的由心脏极化和去极化产生的电信号, 这种电信号具有周期性, 每个心电周期按照前后顺序分为P波、QRS波群、T波和U波.其中: P波代表心房去极化, QRS波群代表心室去极化, T波代表心室去极化后再极化^[1].虽然心电图中P波幅值小、时长短, 但P波蕴含了丰富的病理信息.P波是判断室性早搏和正常心拍的主要判据之一, 是心房功能能否正常的主要判断依据.P波起点到QRS波群的起点间的时长是判断窦性心动过速、预激综合征等的重要指标^[2], 因此, 心电P波的准确提取对生理健康判断具有重要意义.
P波幅值较低, 在不同导联中的形态也有所不同, 心电P波按照波峰的形态可分为正向、倒置与双向三种^[3].目前较好的P波提取方法有自适应滤波法、高斯拟合法、神经网络法等, 但这些检测方法都以正向P波为主^[4-6].Mohamed等^[4]对心电波形首先采用带通滤波, 然后使用两个移动的平均滤波器检测P波和T波, 该方法的缺点是滤波器需要精准参数, 而且参数无法自适应^[4].Rao等^[5]使用基于动态规划的参数混合高斯拟合法, 先预设一种与P波类似的高斯模型, 并与心电信号对比, 与其模型最相近的部分为心电P波.这种方法只能检测出正向P波, 对于双向P波则无法检测.Lenis等^[6]运用了无相位小波变换对心电P波进行提取分析, 并取得良好结果, 但未考虑到P波有正向、负向和双向三种形态.目前检测P波的方法都是从波形时域形态或频域方面检测, 但P波波形有三种不同形态, 很难使用一种方法同时检测所有形态的P波.因为心电低频噪声与P波在频域重合, 所以频域法需要心电信号有非常好的质量.本文提出了一种融合粒子群和双边长短窗能量差检测多形态心电P波的算法, 此算法通过能量变换检测出所有形态的心电P波, 并具有一定的抗噪能力.
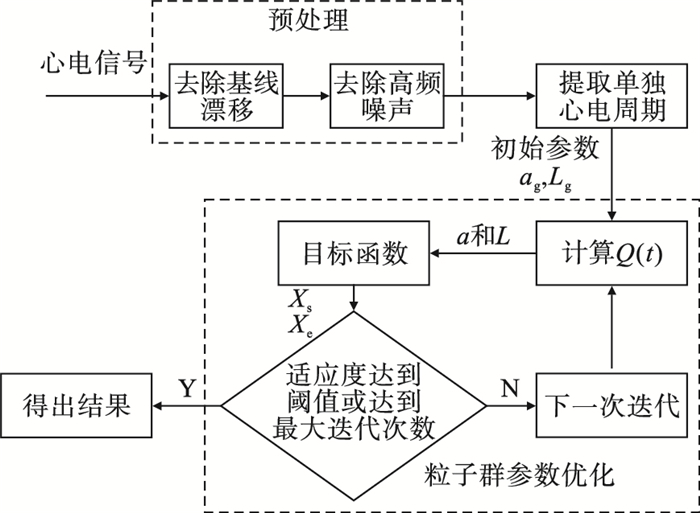
1 方法与步骤本文算法主要通过双边长短窗能量差法提取心电P波起点与终点的特征, 并使用粒子群来优化其参数, 最终确定P波的起点与终点.算法具体步骤如图 1所示.
图 1(Fig. 1)

图 1 算法具体步骤Fig.1 Algorithm specific steps

首先对信号进行预处理, 包括去除基线漂移和高频噪声; 再根据R波波峰将心电信号分离为单个心电周期, 并找出预选区域.根据Q(t)找到P波的起点与终点, 在计算过程中使用粒子群算法得到最优解.在图 1中, a_g, L_g分别代表粒子群算法的初始解, 其中a_g为短窗长, L_g为长窗长比短窗长的倍数.a和L分别为每次通过粒子群算法迭代所得的短窗长、长窗长比短窗长的倍数.X_s和X_e分别为通过双边长短窗平均能量差法计算所得心电P波的起点与终点.图 1中的目标函数是使用当前迭代所得参数提取P波的起点与终点, 将其结果与金标准对比, 计算标准差, 其结果越小则参数优越性越高.
1.1 双边长短窗平均能量差法在双边长短窗平均能量差法的基础上, 对长短时窗能量差法加以改进, 基础的长短时窗能量差法广泛用于微地震波起点的检测^[7-8].微地震波是指在山体施工、土木建设、能源开发或汽油采集等过程中引起地下应力场变化, 导致岩体破裂, 发生微小震动而产生的地震波, 其幅值低、频率低、含有大量高频噪声, 与人体心电类似^[9].本研究将基础的长短时窗平均能量差法加以改进, 用于检测心电P波的起点与终点.
双边长短时窗平均能量差法的原理是通过能量变化来判断信号的边界.基础的长短时窗平均能量差法通过计算, 将起点前没有信号的部分判断为低能量区, 将起点后含有信号的部分判断为高能量区.当长短窗都位于起点前, t点位于起点前时由于长窗和短窗的区域都为噪声, 能量值偏低, 长窗与短窗的平均能量差值接近于0;继续向后滑动, 一部分长窗包含信号, 进入了高能量区, 差值开始减少; 继续滑动, 全部长窗进入高能量区, 短窗在低能量区达到极小值; 再继续滑动, 短窗进入高能量区, 长窗不变, 差值变大.具体计算方式如下:
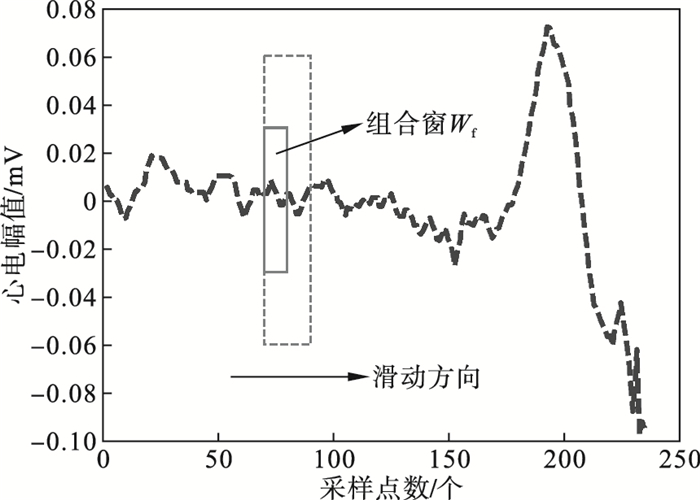
1) 先选定一组长短窗, 短窗包含l个采样点, 长窗包含L个采样点, 短窗在长窗的内部前侧, 长、短窗交界处为一个采样点, 此点既存在于长窗内, 又存在于短窗内, 长窗与短窗组合成组合窗W_f.W_f的移动方式如图 2所示, 图中虚线为长窗, 实线为短窗, 共同组成组合窗W_f.
图 2(Fig. 2)

图 2 Wf移动方式示意图Fig.2 Schematic diagram of sliding Wf

2) 以信号第1个点为起点, 计算短窗与长窗内采样点的平均能量差Q_f:

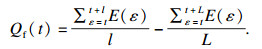(1)

式中: E(ε)为采样点的能量值, 数值上等于采样点数值的平方; Q_f为t点的平均能量差.向后移动时窗, 步长为一个采样点, 计算下一个采样点的平均能量差值, 遍历信号中所有采样点, 得到Q_f(t).Q_f(t)的变化过程分为3个阶段: ①初始点没有进入到组合窗内, 所以Q_f(t)的变化是噪声的变化, 其幅值改变很小; ②初始点到达组合窗内, 长窗能量值逐渐增加, Q_f(t)减小; ③组合窗的起点与信号初始点重合, Q_f(t)成为极小值, 随组合窗向后移动, Q_f(t)逐渐恢复至第一阶段的状态, Q_f(t)与P波起点的关系如图 3所示, 可知Q_f(t)的极小值点与心电P波初始点的对应关系.
图 3(Fig. 3)

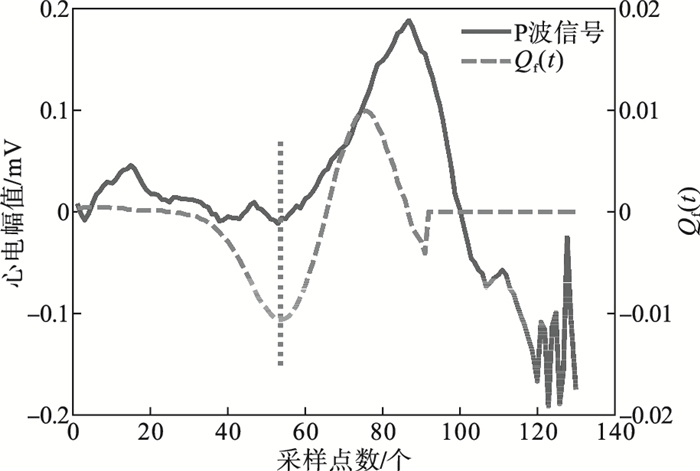图 3 Qf(t)与P波起点的关系示意图Fig.3 Schematic diagram of the relationship between Qf(t)and the starting point of the P wave

基础的长短时窗能量差法可以检测出波形的初始点, 但由于算法本身限制, 基础的长短时窗能量差法无法计算P波最后长为L的部分, 导致P波的终点无法识别, 这是算法中的缺点.本研究将组合窗的位置改变, 将短窗放置在长窗内部后侧, 长度不变, 创造一组新的长短组合窗W_b, 新的组合窗中长短窗终点重合, 具体放置位置如图 4所示.此组合窗内平均能量的计算过程与基础长短时窗能量差法类似, 也是将短窗内采样点的平均能量减去长窗内采样点的平均能量, 计算结果为Q_b，如图 5所示.此组合窗只可以从信号的第L个点开始计算, 同样向后滑动, 每次滑动一个采样点至P波结束.计算式为
图 4(Fig. 4)

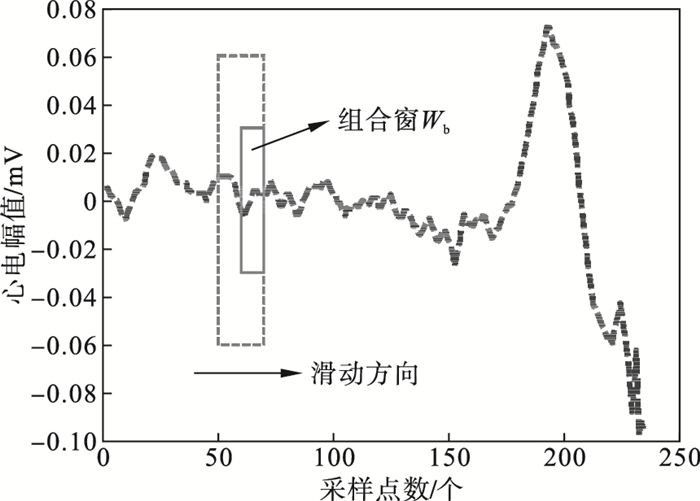图 4 Wb移动方式示意图Fig.4 Schematic diagram of sliding Wb

图 5(Fig. 5)

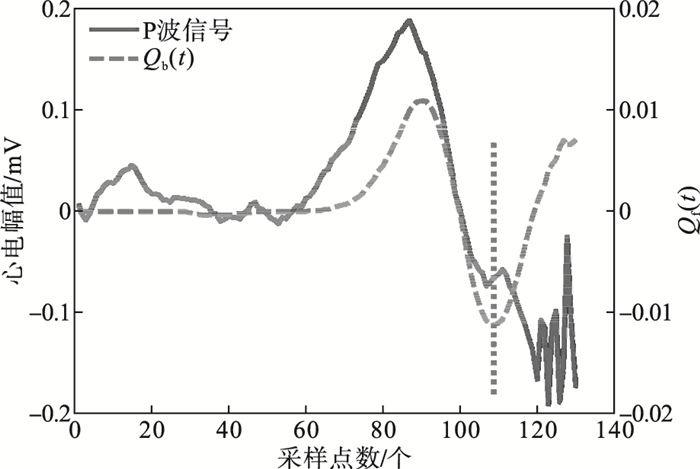图 5 Qb(t)与P波终点的关系示意图Fig.5 Schematic diagram of the relationship between Qb(t)and the ending point of the P wave

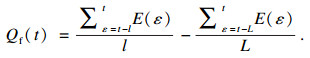(2)

在W_b的移动过程中, 经历起点时和基础长短时窗W_f不一样, W_b的短窗与长窗同时接触信号的起点, 在此之前新长短时窗W_b内的平均能量差Q_b是噪声的变化, 其值几乎不变.在W_b接触信号初始点后, Q_b的数值会增加, 因为短窗大部分位于高能量区内, 而长窗大部分位于低能量区内, 随组合窗W_b向后滑动, 短窗逐渐退出高能量区域, 长窗依旧保持在高能量区内, Q_b开始下降.当W_b的终点与P波截止点重合时, Q_b达到极小值.再向后滑动长窗逐渐退出高能量区, Q_b开始增加.
Q_b可以将心电P波的截止点和起始点都标记出来, P波的起点即为Q_b开始变化的起点, P波的终点即为Q_b的极小值点.但Q_b开始变化的起点不容易测量, 而且, P波前可能存在一定量噪声, 会干扰Q_b开始变化的起点, 导致检测结果不准确.
将Q_b与Q_f组合在一起, 先将P波的预选区域通过W_f遍历一遍得到Q_f(t), 再使用新的组合窗W_b遍历一次P波预选区域得到Q_b(t), 最后将其结果融合，得Q(t)=Q_b(t)-Q_f(t)，将W_f和W_b的结果融合在一起.Q_f(t)在P波起点时是极小值, Q_b(t)在起点之后有上升趋势, 所以P波的起点在Q(t)为波峰的极大值点; Q_f(t)在P波终点时因公式与算法中的缺陷为0, 而P波终点在Q_b(t)中表示为波谷的极小值点.依据Q(t)的计算过程, P波的起点Q(t)表示为极大值点, P波的终点Q(t)表示为极小值点, 这使P波的边界提取十分简单.
采集得到的心电信号通常会有不同程度的噪声, 即使通过之前的去噪手段, 也无法将噪声完全去除, 因此, 在所有的原波形上直接判断P波的边界是不现实的.依据能量变化速度将P波起点与终点检测的困难变换为检测波峰与波谷的问题, 这不仅降低了检测P波的难度, 还可以同时检测出正向、负向和双向3种不同形态的P波.基于被初步处理后的心电信号的噪声能量低及信号能量高的特点, 将信号分为有信号的高能量区和没信号的低能量区.低能量区在Q(t)中体现为接近基线, 高能量区在Q(t)中体现为较规律的波形, 这样就可以据此来判断P波的起点与终点.
1.2 粒子群参数优化原理及具体步骤粒子群算法具有进化计算和群体智能的特点, 主要过程是通过个体间的协同与竞争, 实现复杂空间中最优解的搜索^[10].算法具体步骤如下: 首先确定粒子的初始解和初速度.初始解是将粒子均匀分布在可选择解的范围内, 每个粒子的初速度都是随机的.通过目标函数计算每个粒子的适应度, 目标函数使用当前解提取P波的起点与终点.将结果与金标准对比, 计算标准差, 结果越小则参数越优.在解空间内选取适应度最小的解, 作为当前迭代的全局最优解.每个粒子的结果与上一次迭代结果进行对比, 选出粒子本身的历史最优解.当找到足够好的最优解或达到了最大迭代次数时, 算法完成^[11].迭代式为

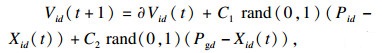(3)

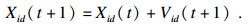(4)

式中: ?为惯性因子, 其值为非负; V_id(t)和X_id(t)分别为第i个粒子在第t次迭代中第d维的速度和位置; C₁和C₂为加速度常数, 通常设置为2;rand(0, 1)为[0, 1]区间上的随机数; P_id为第i个粒子中第d维度的个体最优解; P_gd为第d维度全局最优解^[12].粒子维度指的是有多少个参数需要优化, 在本文中粒子维度为2.根据实验经验将粒子数设为36, 最大迭代次数为500.
使用手动标注的金标准(g_n)与本文方法估计的位置(x_n)之间的误差的方差作为粒子群算法的目标函数:

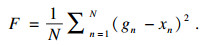(5)

2 实验及结果2.1 实验数据使用两个数据库, 分别为Lobachevsky University Electrocardiography Database(LUE)^[13]和QT Database(QT)^[14], 分割出共含有6 299个心动周期的心电波形, 进行P波提取算法的训练和验证.LUE中心电数据为12导联, 采样频率为500 Hz, 在此数据库中, P波的形态包括正向、负向和双向.QT数据库中心电数据包括2个导联, P波包括正向与负向.文献[5-6]的检测方法新颖, 检测结果误差小.在LUE数据库中使用了1 892个含正向P波的单周期心电波形, 1 397个含负向P波的单周期心电波形, 1 074个含双向P波的单周期心电波形.从QT数据库中使用了1 936个周期的单周期心电波形, 将数据的70%作为训练集, 30%作为测试集, 具体如表 1所示.
表 1(Table 1)

表 1 实验数据集Table 1 Experimental data sets? 个 数据库 训练集 测试集 QT 1 352 584 LUE 3 064 1 299

表 1 实验数据集 Table 1 Experimental data sets?

2.2 实验结果使用手动标注的金标准(g_n)与本文方法估计的位置(x_n)之间的误差标准差S来评估精度.S是所有标记出的起点及终点的标准差, p_e是数据采样周期, S_t为以时间为单位的误差.金标准由高级医生和两个初级医生共同标注.误差式为

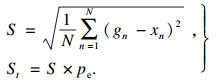(6)

2.2.1 双边长短窗平均能量差法计算结果图 6~图 8分别为3种不同形态的心电P波样本及其对应的Q(t), 心电P波的起点与Q(t)的第一个波峰对应, P波终点与Q(t)最后一个波谷对应.
图 6(Fig. 6)

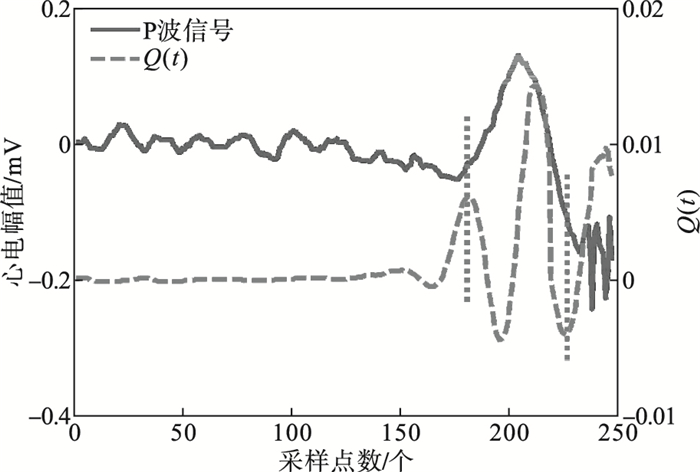图 6 正向P波检测结果Fig.6 Result of detecting positive P wave

图 7(Fig. 7)

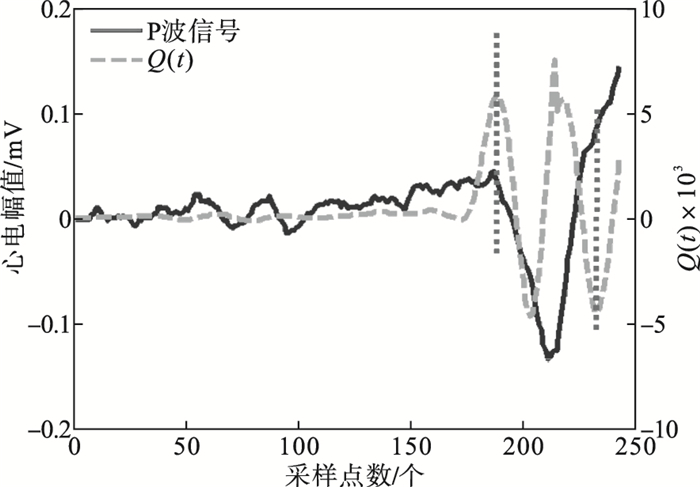图 7 负向P波检测结果Fig.7 Result of detecting negative P wave

图 8(Fig. 8)

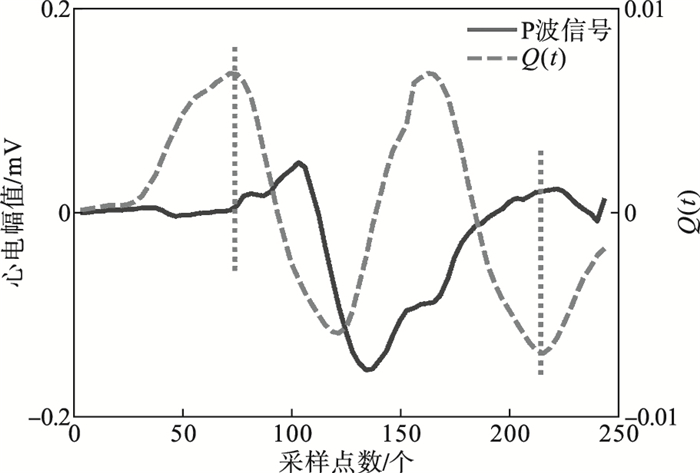图 8 双向P波检测结果Fig.8 Result of detecting bidirectional P wave

2.2.2 粒子群算法迭代结果在粒子群算法中, 粒子数为36, 最大迭代次数为500, 每次迭代选用全局最优解作为本研究的最优参数, 图 9为每次迭代所得最优参数计算得到的结果与金标准的误差标准差, 本文算法在100次左右取得最优解, 并保持稳定.
图 9(Fig. 9)

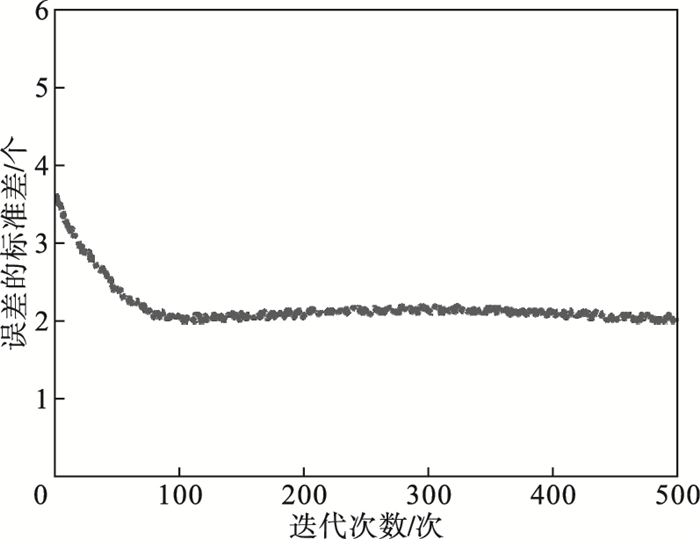图 9 粒子群迭代结果Fig.9 Iteration results of particle swarm

2.2.3 不同形态心电P波检测结果在QT数据库中使用了584个心电周期对算法进行测试, 数据均为正向心电, QT数据库中的数据采样频率为250 Hz, S_t为7.80 ms.本文算法检测结果与金标准之间的误差直方图如图 10所示, 在采样频率为250 Hz时, 误差最大值是16 ms, 大部分在[-8, 8]ms以内.
图 10(Fig. 10)

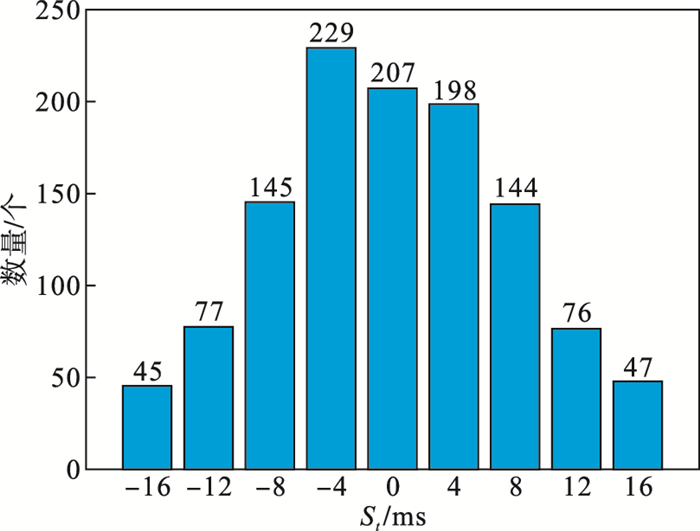图 10 QT数据库P波检测结果Fig.10 Results of QT database for detecting P wave

在LUE数据库中使用了1 299个心电周期对算法进行测试, 综合误差标准差为6.26.其中, 569个心电周期含有正向P波, S_t为6.18 ms; 421个心电周期含有负向P波, S_t为6.21 ms; 309个心电周期含有双向P波, S_t为6.52 ms.结果如图 11~图 13所示.
图 11(Fig. 11)

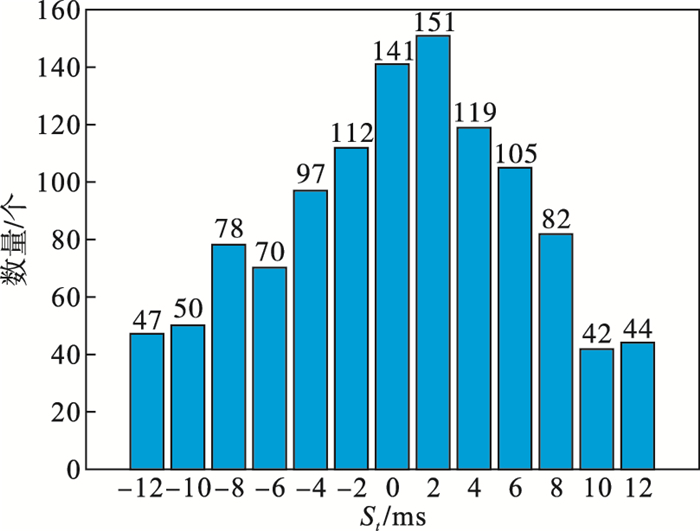图 11 正向P波检测结果Fig.11 Results of detecting positive P wave

图 12(Fig. 12)

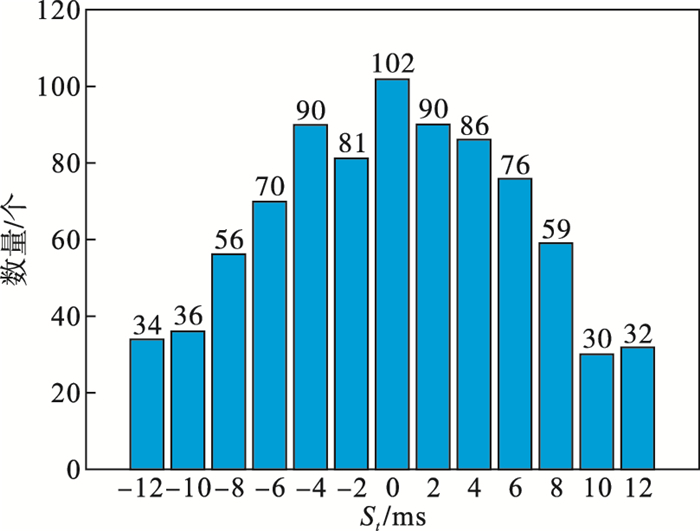图 12 负向P波检测结果Fig.12 Results of detecting negative P wave

图 13(Fig. 13)

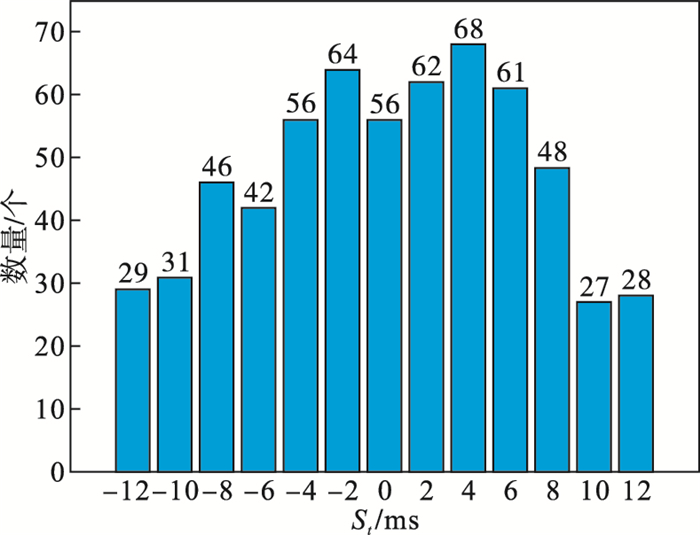图 13 双向P波检测结果Fig.13 Results of detecting bidirectional P wave

本文算法与文献[5-6]的检测结果对比如表 2所示, P波起点和终点的检测结果皆优于其他两种算法.
表 2(Table 2)

表 2 P波的起点与终点检测结果对比Table 2 Comparison of detection results of starting point and ending point of P wave 算法 P波起点 P波终点 S/个 St/ms S/个 St/ms 本文 1.88 7.52 2.02 8.07 文献[5] 1.99 7.96 2.29 9.12 文献[6] 2.44 9.77 2.55 10.19

表 2 P波的起点与终点检测结果对比 Table 2 Comparison of detection results of starting point and ending point of P wave

图 11~图 13分别为正向P波、负向P波和双向P波的误差直方图, 在采样频率为500 Hz时, 误差最大值为12 ms, 大部分在[-8, 8]ms.将本文算法与文献[5]中基于动态规划的参数混合高斯拟合法和文献[6]中无相位平稳小波变换法进行比较, 所得统计结果如表 3所示.由表 3可知本文方法检测结果误差较小, 可以检测出双向P波的位置.
表 3(Table 3)

表 3 P波检测标准差Table 3 Standard deviation of P wave detection 数据 采样频率/Hz P波形态 St/ms 本文方法 文献5 文献6 QT 250 正向 7.80 8.96 9.76 LUA 500 正向、负向、双向 6.26 8.34(不包括双向) 8.78(不包括双向)

表 3 P波检测标准差 Table 3 Standard deviation of P wave detection

2.3 不同强度噪声下本算法的精度将LUE数据库中心电分别加入信噪比为10, 20, 30 dB噪声检测本算法的鲁棒性.在正向P波与负向P波中加入30, 20 dB的噪声, 可以辨认出P波的形状.当噪声强度为10 dB时, 由于P波的幅值较小, 已无法从信号整体判断出P波的准确位置.在双向P波中加入30 dB的噪声时, 可以辨别P波的大致形状, 当噪声强度为20, 10 dB时, 噪声覆盖信号, 已辨别不出P波的准确位置.本文使用P波位置的检测准确率(Acc)与检测P波误差的标准差S代表本算法对噪声的鲁棒性.
P波位置的准确率为

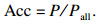(7)

式中: P为检测出P波的数量; P_all为每种形态P波的数量.
图 14~图 16分别为算法在正向、负向和双向P波加入仿真白噪声后检测结果误差的变化趋势.随机白噪声用来模拟心电信号采集过程中的高频随机噪声.该随机白噪声是均值为0、方差为1的高斯随机序列.双向P波在信噪比为10 dB噪声强度下准确率降低为0, 正向与负向P波在信噪比为10 dB时仍可检测出P波位置; S与信噪比具有明显的负相关性, 且变化趋势相似, 在信噪比提升至20 dB时, S减小缓慢.
图 14(Fig. 14)

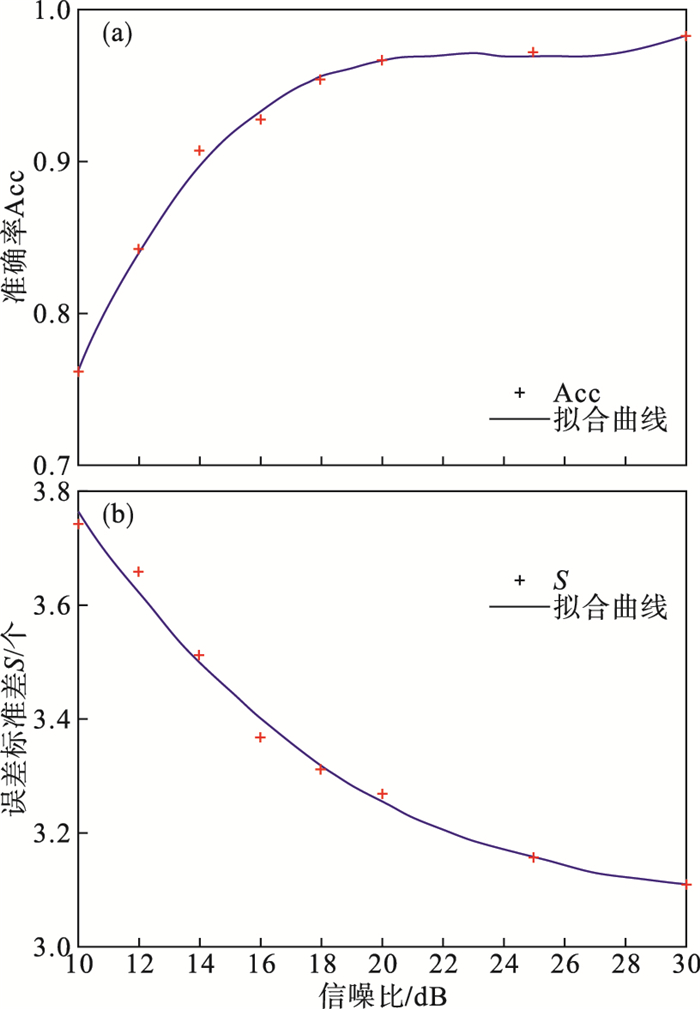图 14 噪声对算法检测正向P波的影响Fig.14 The influence of noise on the algorithm to detect positive P wave (a)—噪声对检测准确率的影响；(b)—噪声对检测误差标准差的影响.

图 15(Fig. 15)

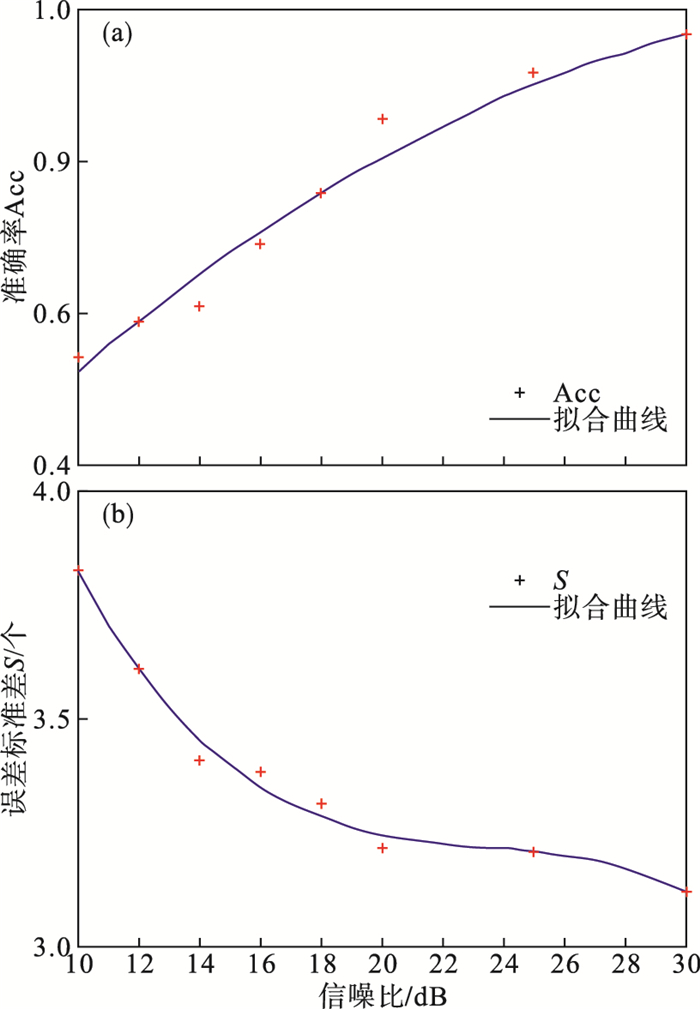图 15 噪声对算法检测负向P波的影响Fig.15 The influence of noise on the algorithm to detect the negative P wave (a)—噪声对检测准确率的影响；(b)—噪声对检测误差标准差的影响.

图 16(Fig. 16)

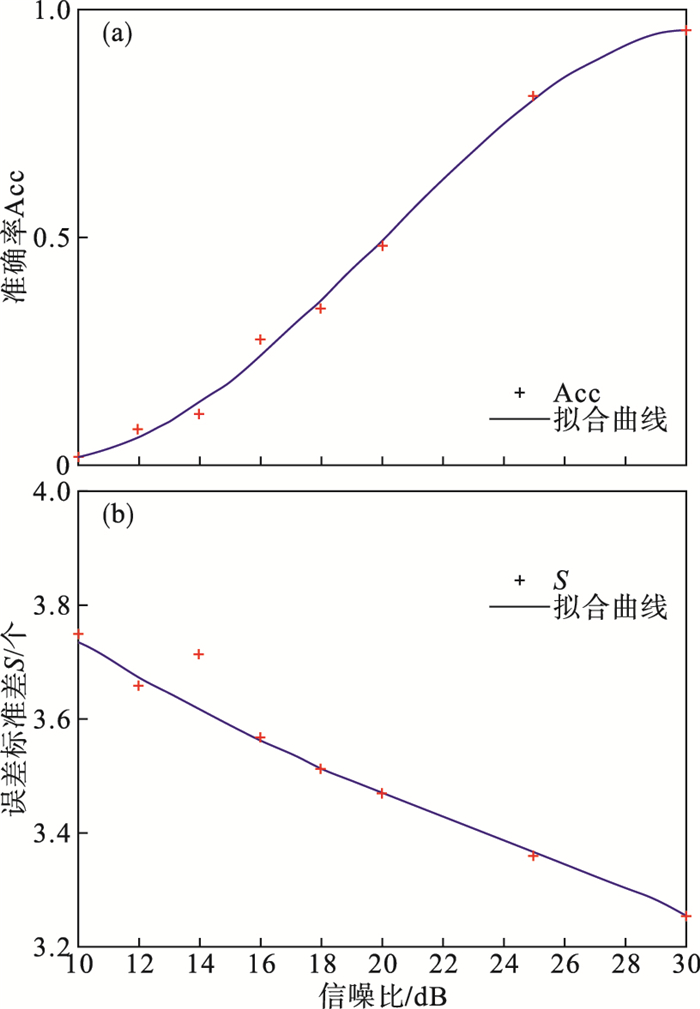图 16 噪声对算法检测双向P波的影响Fig.16 The influence of noise on the algorithm to detecting the bidirectional P wave (a)—噪声对检测准确率的影响；(b)—噪声对检测误差标准差的影响.

2.4 不同采样频率下本算法的精度对LUE和QT数据进行重采样, 将信号的采样频率提高到1 000, 2 000, 3 000, 4 000, 5 000 Hz, 并重新计算结果.重采样后并没有对P波峰值检测的准确率造成影响, 起点与终点的检测结果采样点误差有所提高, 但时间误差逐渐降低.本文算法的检测结果误差随采样频率的升高不断减少, 并趋于平稳, 在采样频率为5 000 Hz时检测结果误差降为1.1 ms.重采样后不同方法检测结果对比如表 4所示, 采样频率对P波检测的误差随采样频率的增加而降低.本文方法在高采样频率的情况下, 性能要优于文献[5-6].
表 4(Table 4)

表 4 重采样后不同方法检测结果对比Table 4 Comparison of detection results of different methods after resampling 采样频率/Hz St/ms 本文方法 文献[5] 文献[6] 1 000 3.93 4.52 5.07 2 000 2.21 2.57 4.32 3 000 1.41 2.44 3.03 4 000 1.25 2.31 2.79 5 000 1.1 2.27 2.63

表 4 重采样后不同方法检测结果对比 Table 4 Comparison of detection results of different methods after resampling

3 结论1) 改进了基础的长短窗平均能量差法, 利用其对信号微小变化的敏感性, 设计一种新的多形态心电P波提取算法, 检测多种心电P波.
2) 将本文算法与其他算法相比, 本文算法的检测结果相对较好, 但不能完全准确检测P波, 绝大部分误差在4个采样点内.
3) 对于不同形态心电P波, 本文算法检测结果的误差明显不同, 而且在相同噪声下, 不同形态P波检测的准确性有很大差别.在后续工作中, 需改进以上问题.
参考文献

[1]	Pourhassan M, Cuvelier I, Gehrke I, et al. Methodology of ECG interpretation in the Dalhousie program; NOVACODE ECG classification procedures for clinical trials and population health surveys[J]. Methods of Information in Medicine, 1990, 29(4): 362-374. DOI:10.1055/s-0038-1634798
[2]	Hisazaki K, Miyazaki S, Hasegawa K, et al. The P wave morphology in lead V7 on the synthesized 18-lead ECG is a useful parameter for identifying arrhythmias originating from the right inferior pulmonary vein[J]. Heart and Vessels, 2019, 35(2): 246-251.
[3]	王珏, 刘素云. 室性早搏体表心电图的定位方法[J]. 中国心脏起搏与心电生理杂志, 2020, 34(5): 429-434. (Wang Jue, Liu Su-yun. The location method of body surface electrocardiogram of ventricular premature contraction[J]. Chinese Journal of Cardiac Pacing and Electrophysiology, 2020, 34(5): 429-434.)
[4]	Mohamed E, Marianna M, Derek A. A proof-of-concept study: simple and effective detection of P and T waves in arrhythmic ECG signals[J]. Bioengineering, 2016, 3(4): 32-46. DOI:10.3390/bioengineering3040032
[5]	Rao A M V, Gupta P, Ghosh P K. P-and T-wave delineation in ECG signals using parametric mixture Gaussian and dynamic programming[J]. Biomedical Signal Processing and Control, 2019, 51(5): 328-337.
[6]	Lenis G, Pilia N, Oesterlein T, et al. P wave detection and delineation in the ECG based on the phase free stationary wavelet transform and using intracardiac atrial electrograms as reference[J]. Biomedical Engineering Biomedicines Technik, 2016, 61(2): 164-170.
[7]	Zheng J L, Xu J. The research of first break time picking based on energy D-value[J]. Chinese Journal of Engineering Geophysics, 2013, 10(6): 834-839.
[8]	叶根喜, 姜福兴, 杨淑华. 时窗能量特征法拾取微地震波初始到时的可行性研究[J]. 地球物理学报, 2008(5): 1574-1581. (Ye Gen-xi, Jiang Fu-xing, Yang Shu-hua. The feasibility study of picking up the initial arrival time of the microseismic wave by the time-window energy feature method[J]. Chinese Journal of Geophysics, 2008(5): 1574-1581. DOI:10.3321/j.issn:0001-5733.2008.05.033)
[9]	郑江龙, 许江. 能量差法拾取直达波初至的应用研究[J]. 工程地球物理学报, 2013, 10(6): 834-839. (Zheng Jiang-long, Xu Jiang. Research on the application of energy difference method to pick up the first arrival of direct wave[J]. Chinese Journal of Engineering Geophysics, 2013, 10(6): 834-839.)
[10]	Hd A, Chao C A, Gm B, et al. Energy-aware scheduling of virtual machines in heterogeneous cloud computing systems[J]. Future Generation Computer Systems, 2017, 74: 142-150. DOI:10.1016/j.future.2016.02.016
[11]	Yang Y, Wang Y, Yuan X. Bidirectional extreme learning machine for regression problem and its learning effectiveness[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(9): 1498-1505. DOI:10.1109/TNNLS.2012.2202289
[12]	Chakraborty T, Banik S K, Bhadra A K, et al. Dynamically learned PSO based neighborhood influenced fuzzy C-means for pre-treatment and post-treatment organ segmentation from CT images[J]. Computer Methods and Programs in Biomedicine, 2021, 202(2): 105971.
[13]	Goldberger A, Amaral L, Glass L. PhysioBank, PhysioToolkit, and Physionet: components of a new research resource for complex physiologic signals. 2000. http://dx.doi.org/10.1161/01.cir.101.23.e215.
[14]	Kalyakulina A, Yusipov I, Moskalenko V, et al. Lobachevsky university electrocardiography database(version1.0.1). 2020. https://www.physionet.org/content/ludb/1.0.1/.