杨博文, 霍军周, 张伟, 张占葛
大连理工大学 机械工程学院, 辽宁 大连 116024
收稿日期：2021-06-10
基金项目：国家自然科学基金资助项目(51875076)；国家重点研发计划项目(2018YFB1306701)；辽宁百千万人才计划项目(2020921006)；国家自然科学基金辽宁省联合基金资助项目(U1708255)。
作者简介：杨博文(1992-)，女，辽宁本溪人，大连理工大学博士研究生;
霍军周(1979-)，男，山西运城人，大连理工大学教授，博士生导师。

摘要：为保证关键结构疲劳寿命的实时监测, 以动态随机载荷为监测条件, 准确预测超前载荷谱对实际工程分析十分重要.针对服役设备难以实时监测并准确反应载荷真实规律等问题, 提出一种基于数值分析的概率密度预测方法, 结合机器学习BP神经网络智能算法建立预测模型.应变传感器采集随机载荷进行预处理得到随机载荷谱, 利用蒙特卡洛法分析模型载荷波形走势及波动范围的预测精度.结果表明: 超前预测载荷谱的核密度拟合曲线与真实数值相似性较大, 为大型复杂服役结构件的超前载荷监测提供了理论支持与实际工程应用.
关键词：超前载荷预测BP神经网络蒙特卡洛法核密度估计实时预测
Research on Real-Time Overload Prediction Method of in-Service Structures
YANG Bo-wen, HUO Jun-zhou, ZHANG Wei, ZHANG Zhan-ge
School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China
Corresponding author: HUO Jun-zhou, E-mail: huojunzhou@dlut.edu.cn.

Abstract: In order to ensure the real-time monitoring of the fatigue life of key structures, the dynamic random load is used as the monitoring condition to accurately predict the importance of the advanced load spectrum for actual engineering analysis.Aiming at the difficulty of real-time monitoring of in-service equipment and accurately responding to the real laws of load, a probability density prediction method based on numerical analysis is proposed, combined with machine learning BP neural network intelligent algorithm to establish a prediction model. The random load is collected by the strain sensor for preprocessing to obtain random load spectra, and the Monte Carlo method is used to analyze the model load waveform trend and the prediction accuracy of the fluctuation range. The results show that the nuclear density fitting curve of the advanced prediction load spectrum has a high similarity to the real value, which provides theoretical support and practical engineering application for the advanced load monitoring of large and complex in-service structures.
Key words: advanced load predictionBP neural networkMonte Carlo methodkernel density estimationreal-time prediction
智能节点监测技术采用智能方式实时监测^[1], 通过传感网络^[2]及驱动模块集成监测系统^[3], 实时采集传感器信号.结合数字信号处理算法, 提取数据相关参数, 对结构危险点的疲劳萌生及扩展趋势进行监测与评估, 实时预测结构的疲劳寿命^[4].智能节点监测能够实现实时获取关键结构的损伤状态及变化规律, 对设备停机维护及服役寿命预测提供重要支持.通过智能节点技术对结构危险部位的损伤状态、外部载荷冲击及服役环境等监测获取服役期间的疲劳载荷^[5].预测超前载荷谱并计算剩余疲劳寿命, 保证降低制造使用成本的同时提高设备使用寿命, 通过预测疲劳寿命并及时预警, 为设备停机维护提供依据.传感器网络^[6]是一种微型、智能、系统的多特性检测设备, 将被测物体相关信息转化为载荷、电压等信号输出.一般常见的传感器包括应变片、压电片、光纤传感器^[7]等, 集成在设备结构上的传感器网络可对设备结构的应力应变、外部冲击及疲劳损伤进行实时监测, 通过载荷超前预测模型、物理失效模型等计算剩余疲劳寿命^[8].
TBM是一种集掘进、出渣和支护于一体的高端隧道掘进装备, 越来越多的隧道工程采用TBM施工.TBM工作环境恶劣, 常面临极端高压、极端硬岩、涌水、破碎带等复杂地质环境, 掘进过程中刀盘易遭受强冲击突变载荷, 导致主机系统关键结构的疲劳失效问题经常发生.由于TBM主机系统结构紧凑, 关键部件损坏时难以维修和更换, 严重时有可能造成TBM整机报废, 将会大大延长工程周期.因此, 对服役结构超前载荷实时预测方法的研究具有十分重要的工程意义.
在循环载荷作用下, 持续加载高应力会导致结构材料出现疲劳累积损伤现象^[9], 循环载荷引起的局部损伤是由裂纹萌生、扩展及断裂组成的累积过程.为了实现在役设备的疲劳载荷评估, 需实时监测载荷历程^[10], 确保关键设备使用的安全性.对结构长期载荷进行外推, 载荷外推方法的优劣直接决定超前载荷谱的预测精度, 同时影响后期疲劳寿命分析和评估.李凡松等^[11]基于多载荷时间历程的外推法编制设备承载结构疲劳试验载荷谱, 通过载荷数据与实际测试数据进行对比, 证明KDE外推载荷计算的损伤比线性外推载荷计算法真实可靠.万一品等^[12]为了研究装载机工作装置疲劳性能, 提出一种考虑分段载荷均值特性的工作装置及疲劳试验程序载荷谱的编制方法, 实现二维载荷谱的编制.宫海彬等^[13]提出一种基于极值理论与非参数密度估计相结合的载荷数据统计方法, 建立了高速列车齿轮传动装置程序的载荷谱，但难以检测全寿命周期可能发生对部件寿命影响较大的极值载荷.Gong等^[14]通过对参数雨流外推、极限雨流外推和非参数雨流外推三种外推法的优势和局限性展开对比分析, 发现非参数外推法与其他方法相比, 具有基于数据驱动、不依赖样本母体分布的独特优势.针对现有外推法存在的局限性, 建立了全带宽非参数外推模型.Pei等^[15]发现机器学习具有强大的数据处理能力, 无需确切的物理模型和专家经验理论, 基于机器学习理论的剩余疲劳寿命预测方法是未来研究的主要方向.董青等^[16]针对载荷谱的随机性、不确定性及数据样本有限的问题, 提出自适应双层果蝇相关向量机(ADRVM)的起重机当量载荷谱预测方法, 提高了载荷谱预测精度与鲁棒性.EL-Sagheer等^[17]基于渐进应力加速寿命试验模型(PRO-II-C), 获得威布尔指数分布(WED)参数点和区间估计, 使用最大似然估计和贝叶斯估计方法估计未知参数和加速因子, 获得近似置信区间和渐近方差矩阵.采用蒙特卡洛法对加速模型参数进行估计, 通过实例分析设计加速寿命试验中数据统计优化方案.Paraforos等^[18]基于加速结构耐久性试验方法计算累积疲劳损伤, 通过雨流循环计数外推法计算未测量的高振幅载荷, 结合蒙特卡洛分析法及实际载荷编制载荷谱, 对结构的加速耐久性试验方法进行优化设计.Kim等^[19]基于Weibull方程的加速理论模型, 对载荷计算结果与实际工况下的试验结果进行了分析比较, 建立一套寿命试验系统, 将加速模型进行优化设计.Shafiullah等^[20]通过分析冲击响应谱及疲劳损伤谱从而得到载荷历程, 利用有限元仿真软件建立悬臂梁模型, 并采用频域S-N曲线得到结构的疲劳寿命, 优化了模型的加速耐久性.
通过采集服役期间的历史累积载荷, 预测未来载荷谱尤为重要, 目前国内外对原位结构的疲劳载荷预测模型研究尚少.本文根据在线服役设备的实时监测数据和历史数据, 探究不同工况下的载荷规律, 通过深度学习算法预测载荷变化趋势, 设计超前载荷预测的核心算法.
1 超前载荷谱预测模型1.1 神经网络模型理论机器学习是利用计算机编程手段对样本数据或以往的经验积累进行建模, 使用实例数据训练计算机模型, 优化性能标准解决复杂问题.机器学习的BP神经网络预测方法可以针对历史载荷进行评估, 对随机性及不确定性的载荷预测具有优势.传统的时间序列按照时间顺序记录一系列观测值, 是参量在不同时刻形成的随机数据, 反映了参量的变化规律.时间序列预测是根据有限的历史数据, 建立反映时间序列中所包含的动态依存关系的数学模型, 并利用该模型对系统未来的行为进行预测.神经元结构如图 1所示, 神经元主要由三种基本元素组成: 连接权值、加法器和激活函数.神经元的连接权值用于表示各个神经元之间的连接强度; 加法器则用于将各个神经元的信号按照相应权值进行加权求和; 激活函数主要用来限制神经元的输出.为了增强或减弱神经元的网络输出, 神经元结构有时会引入一个偏置b, 人工神经元的数学模型为

(1)

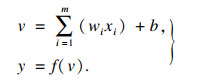图 1(Fig. 1)

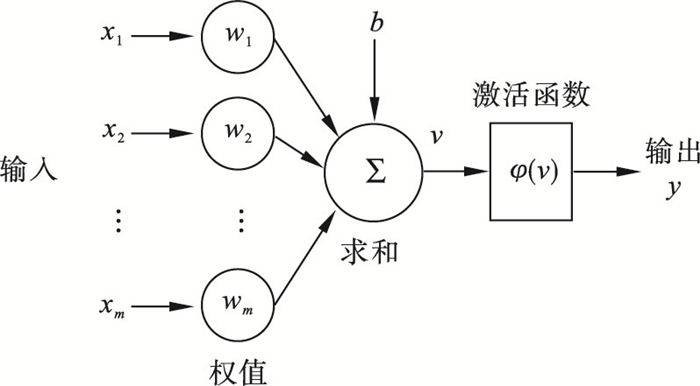图 1 神经元结构Fig.1 Structure of neurons

式中: x_i为神经元的输入信号; w_i为输入信号与神经元之间的连接权值; v为神经元加法器的输出; b为神经元阈值; f为激活函数; y为神经元的输出信号.
在图 1中，φ(v)为神经元激活函数, 即式(1)中的f常用的激活函数包括阈值函数、线性函数及非线性转移函数. 其中, Sigmoid函数(S型函数)在构造人工神经网络中是最常用的激活函数, 能够在线性和非线性之间保持较好平衡, S型函数曲线如图 2所示, S型函数的输出如式(2)所示.

(2)

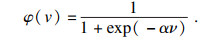图 2(Fig. 2)

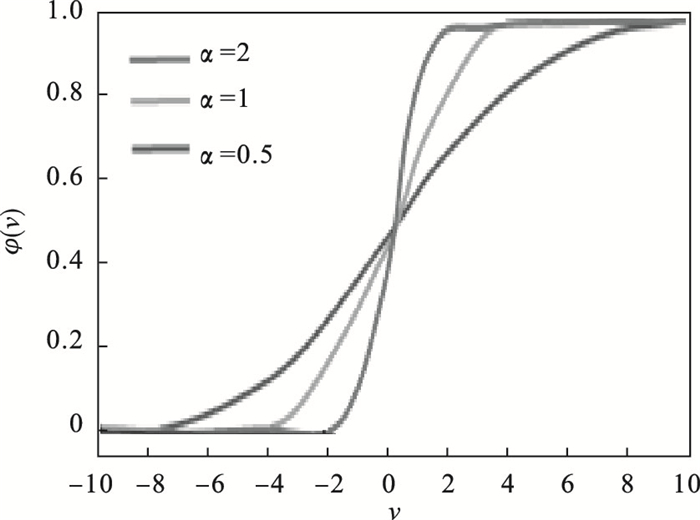图 2 S型函数Fig.2 Sigmoid function

式中: α表示激活函数的类型, 当α=1时, S型函数为对数S型激活函数; 当α=2时, S型函数为正切S型激活函数.
神经网络由输入层、输出层、若干层及隐藏层神经元组成, 神经元之间通过权值和阈值的相互作用可以实现各种强大功能, 神经网络连接图如图 3所示.神经网络预测模型如图 4所示.
图 3(Fig. 3)

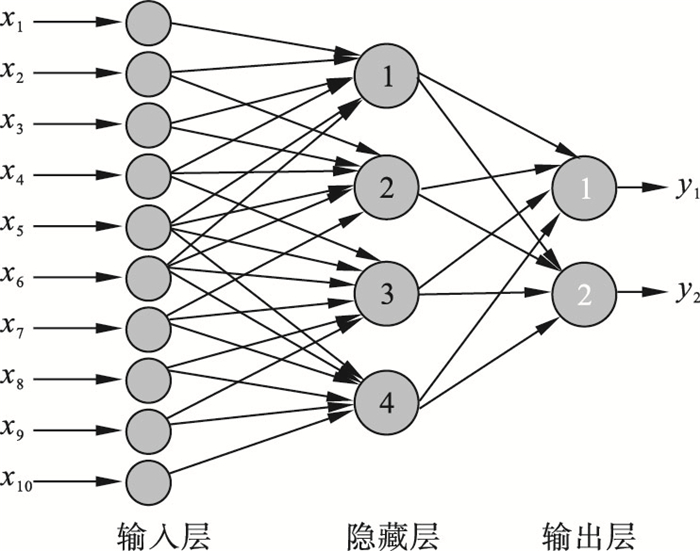图 3 神经网络连接图Fig.3 Neural network connection diagram

图 4(Fig. 4)

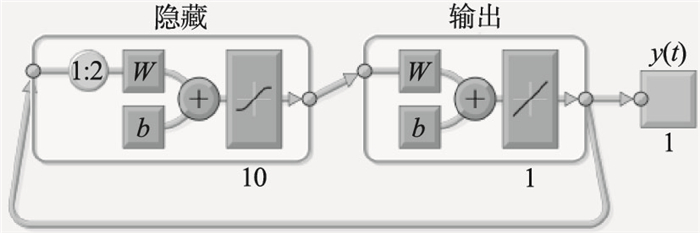图 4 神经网络预测模型结构示意图Fig.4 Schematic diagram of the structure of the neural network

人工神经网络具备良好的非线性处理能力, 擅于处理非线性和时变性问题.神经网络又称非线性自回归神经网络模型, 是一种应用于时间序列预测的典型神经网络模型, 利用历史时刻随机变量的线性组合来描述以后某时刻的随机变量, 其关系表达式为

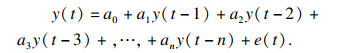(3)

式中: e(t)为白噪声.由式(3)可知下一时刻的输出y(t+1)取决于前n个时刻的数据y(t), 基于自回归原理, NAR神经网络模型可表示为

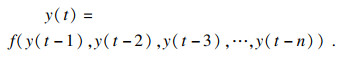(4)

在图 4中: y(t)为神经网络的输出; 1∶ 2为延时阶数; W为神经网络的连接权值; b为阈值.神经网络具体神经元的连接图如图 5所示.其输出表达式为

(5)

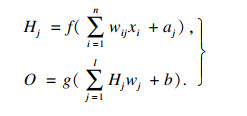图 5(Fig. 5)

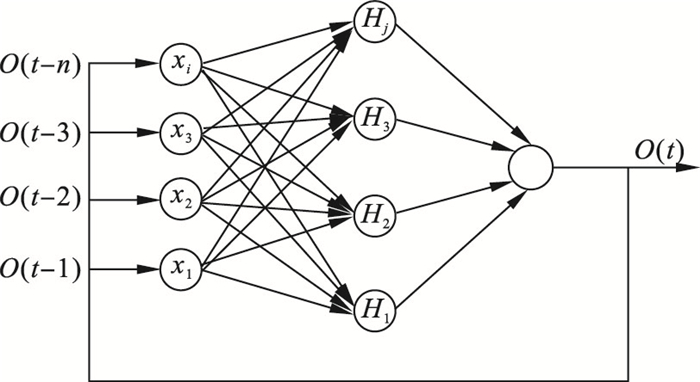图 5 NAR神经网络连接图Fig.5 NAR neural network connection diagram

式中: H_j为隐藏层神经元的输出值; f为隐藏层神经元的激活函数; x_i为神经网络的输入层神经元的值; w_ij为输入层神经元与隐藏层神经元之间的连接权值; a_j为隐藏层神经元的阈值; O为输出层神经元的输出值; b为输出层神经元阈值; w_j为隐藏层神经元与输出层神经元之间的连接权值; g为相应的激活函数.
神经网络是基于自身历史数据的回归模型, 模型输出的延时输出值y(t)为神经网络的输入.在网络训练时, 神经网络的输出值为已知数据, 为提高训练精度, 采用开环方式进行神经网络训练, 用真实值替代预测值作为神经网络的输入.由于BP神经网络有强大的非线性拟合能力, 以及成熟的训练算法, 可以采用BP算法进行训练, 以提高预测精度.
1.2 概率密度参数外推法根据实时监测的累积载荷数据与当前服役结构状态, 利用本文建立的概率密度参数外推法载荷预测模型预测未来载荷的超前载荷谱.
采用应变片实时采集应变载荷谱数据, 利用预处理技术得到峰谷应变数据.通过四峰谷雨流计数法得到三维雨流域载荷数据, 将载荷谱由时域转化为频域进行分析.根据Goodman等寿命载荷法将三维数组转化为二维载荷谱数据, 实时监测关键结构件, 应变载荷谱滚动更新.经过处理的应变载荷谱, 利用最大似然估计理论计算载荷谱, 通过K-S检验判断数据分布模式.
如果载荷谱分布为规律性载荷谱, 可转化为威布尔分布、正态分布等模式继续进行预测.确定分布模式后提取载荷谱数据, 得到阶段载荷特征值方差与期望等参数.每一段都得到一组方差与期望值, 将得到的若干数据组成特征值矩阵, 根据机器学习的BP神经网络预测载荷谱的特征参数.利用抽样模拟法将预测得到的特征值参数, 根据预测的特征值参数进行反推得到超前载荷谱.
载荷谱不能保证每次滚动更新均服从概率分布模式, 当载荷谱不符合分布模式时则提取参数对载荷进行预测, 无法保证预测的精准性, 因此对随机载荷谱进行预测时需要判断及扩充修正.
对大量数据累积进行数据序列切片分析, 将实时传输的载荷数据分成若干等分区间, 分别对每个子区间进行相同处理, 确保数据精确、完整, 提高预测精度的准确性.对区间进行统计, 经过筛选提取出阶段载荷极限值, 根据机器学习的BP神经网络预测超前载荷谱的极限值.利用核密度估计法将切片得到的区间载荷谱分别归一化处理得到载荷概率密度函数, 通过机器学习的BP神经网络预测超前核密度载荷谱的若干组区间载荷谱.利用反归一化法将预测的超前核密度载荷谱处理至幅值极限范围内, 得到超前核密度估计曲线, 通过多项式拟合得到超前载荷预测的概率密度函数; 利用舍选抽样法提取得到最终预测的超前随机载荷谱.概率密度外推法载荷预测具体流程图如图 6所示.
图 6(Fig. 6)

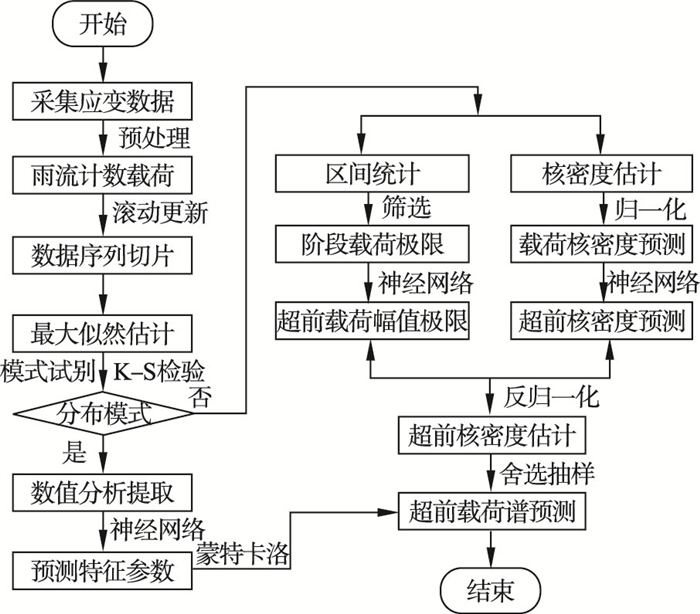图 6 概率密度参数外推法载荷预测流程图Fig.6 Flow chart of load prediction by extrapolation of probability density parameters

1.3 神经网络预测超前载荷谱通过雨流计数及等寿命载荷法对载荷谱数据进行处理, 得到二维载荷谱后进行预测分析, 为了精准预测实时滚动更新载荷谱, 根据机器学习的BP神经网络方法预测提取不同参数及数据, 最终得到超前预测载荷谱.优化BP神经网络算法流程如图 7所示.
图 7(Fig. 7)

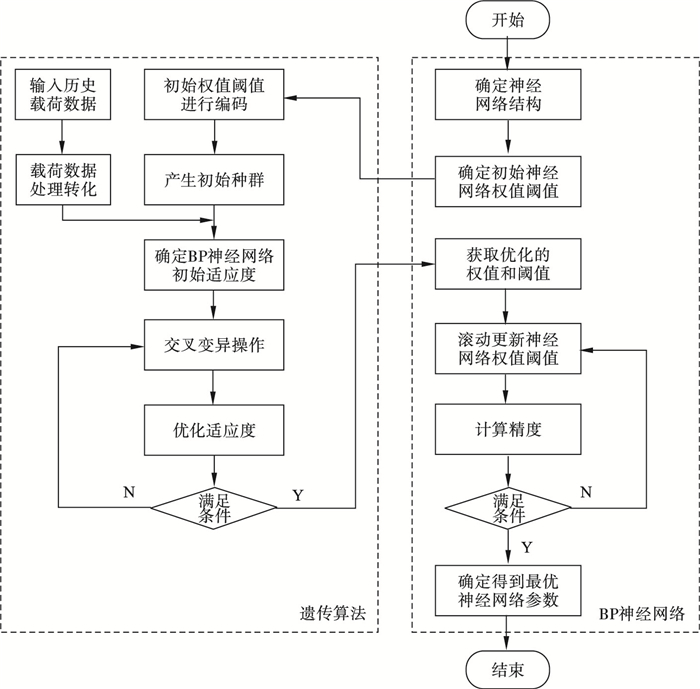图 7 优化BP神经网络算法流程图Fig.7 Optimized BP neural network algorithm flow chart

通过载荷预测模型确定神经网络结构、神经网络初始值、权值与阈值.引入遗传算法对权值及阈值进行优化, 通过设定的初始权值与阈值对信息进行编码, 产生初始种群信息.输入监测的历史载荷数据, 根据处理方法对数据进行转化, 最终确定BP神经网络的初始自适应度.通过选择操作、交叉操作及变异操作对初始值进行适应度优化, 判断是否满足设定的精度条件, 如果不满足条件, 循环返回至交叉变异操作, 进行进一步优化, 直至满足条件即可输出.利用遗传算法优化获得的权值与阈值, 滚动输入至神经网络, 通过计算预测精度, 判断是否符合超前预测的误差阈值, 如果满足则继续滚动更新神经网络参数, 直至满足预测精度, 确定最优的神经网络参数模型, 并计算预测超前载荷谱及优化预测精度.
BP神经网络工作时, 输入信号从输入层经隐层传向输出层, 表示正向传播, 若输出与期望相同, 则训练结束; 否则转至反向传播.将输出与期望的误差信号按原连接通路反向计算, 由梯度下降法调整各层神经元的权值, 使误差信号减小.经过不断反复学习, 最终使网络输出达到要求.
神经网络具有极强的映射能力, 通过有限学习训练, 以高精度实现从输入空间到输出空间的映射关系, 确定映射算子是载荷预测的关键.神经网络是一种比较重要的网络预测模型, 具有极强的非线性拟和能力.理论研究证明一个隐藏层为三层神经网络模型, 通过学习可以实现从输入到输出空间复杂的非线性映射关系.神经网络作为确定函数的逼近算法, 将前X个状态值作为神经网络的输入值, 下一时刻的状态值作为输出Y.输入端为前X个时刻的状态参量值, 输出值为下一个时刻的状态值.在预测过程中, 当得到X+1时刻的值后, 将输入最早的一个状态值剔除, 预测值作为输入值以预测下一个时刻的状态值.由于多次迭代误差会因为积累而不断增大, 为保证预测精度, 预测的整个工作过程按时间顺序进行预测, 用前X个时刻的状态值预测后Y个时刻的状态值, 随着时间的推移不断用新获得的Y信号值来训练神经网络系统参数.
概率密度外推法载荷预测模型的优点是细化载荷谱区间统计，优化预测方法提高了对随机复杂载荷谱的预测能力.对预处理转化后的载荷谱进行数据切片, 根据核密度估计法得到载荷的概率密度, 同时为了确定载荷谱的区间范围, 需对载荷幅值的极限进行预测, 确保预测准确性.根据若干段载荷极值及载荷概率密度进行输入, 假定输入X, 通过神经网络预测出超前载荷谱的预测极值及预测概率密度, 得到输出Y, 根据舍选抽样法确定预测超前载荷谱.这种方式的优点在于可以准确预测大型复杂服役结构的超前载荷谱, 对实时监测结构的疲劳载荷及计算疲劳寿命有重大意义.概率密度外推法的载荷预测模型如图 8所示.
图 8(Fig. 8)

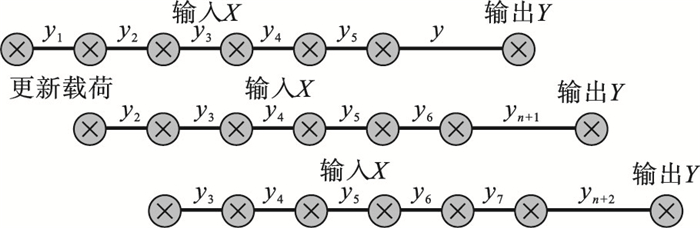图 8 概率密度外推法载荷预测模型示意图Fig.8 Schematic diagram of load prediction model of probability density extrapolation method

部分参数主要通过神经网络进行预测, 将载荷谱输入神经网络模块, 进行循环训练, 通过改变权值和阈值最终确定隐藏层的节点个数.假定第一段载荷谱的训练集输入数据为1~6, 则输出7, 将输出7作为下一层的输入数据进行滚动预测得到输出8, 以此类推, 通过n此训练、测试及预测, 最终得到输出数据x.相同方式对若干组区间载荷谱进行预测, 最终得到超前预测载荷谱.
通过BP神经网络预测模型的优化分析, 其预测方法相对于传统时序预测方法更精确, 可对规律性及非规律性载荷谱进行预测, 具有通用普适性.在进行服役设备关键结构疲劳寿命实时监测预警时, 需疲劳载荷谱超前预测模型随载荷的监测实时更新预测结果, 因此就需要预测模型在实时监测系统中能够高效、精确进行数据预测.机械设备在服役期间载荷具有高度复杂性与时变性, 需要载荷预测模型能够拥有强大非线性处理能力及可随工况变化自动调整预测策略.由于BP神经网络具有强大的非线性拟合能力, 相对其他回归模型更适合处理非线性与随机性问题.
2 计算实例分析以辽西北工程为依托, 建立TBM远程振动监测平台, 对相同工况下TBM主机系统关键部件的载荷数据进行现场采集.基于该工程对敞开式TBM在实际掘进过程中的主驱动系统数据进行现场实测.测试使用高精度三向应变传感器, 以及相关传感器及数据接收网关的技术参数.其中载荷测点选择主驱动单元内部支撑壳体结构体位置, 主梁前段靠近支撑壳体部位及撑靴油缸上部三处.
传感器信号采集系统设置在主梁末端处, 以保证测试信号稳定可靠接受.监测平台主要包括无线应变传感器、无线网关及上位机组成.应变传感器采用Beetech公司的A302无线应变传感器, 通过网关将多个应变传感器的载荷数据传递至上位机, 在上位机端对采集的载荷数据进行保存、分析等处理.在刀盘和主梁前段的合适位置上布置载荷传感器, 主梁后段安装网关, 对现场的载荷进行实测, 如图 9所示.
图 9(Fig. 9)

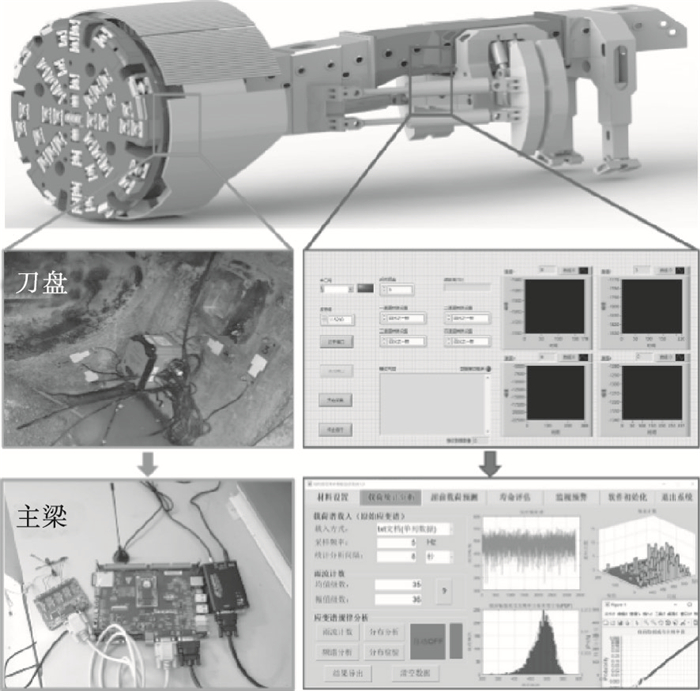图 9 无线载荷监测系统Fig.9 Wireless load monitoring system

2.1 载荷采样点对比分别选取不同工况下三种载荷谱, 分析建立超前载荷预测模型.选取具有代表性的三类载荷谱, 分别为一般随机载荷谱、趋势上升载荷谱、周期函数载荷谱, 如图 10所示.
图 10(Fig. 10)

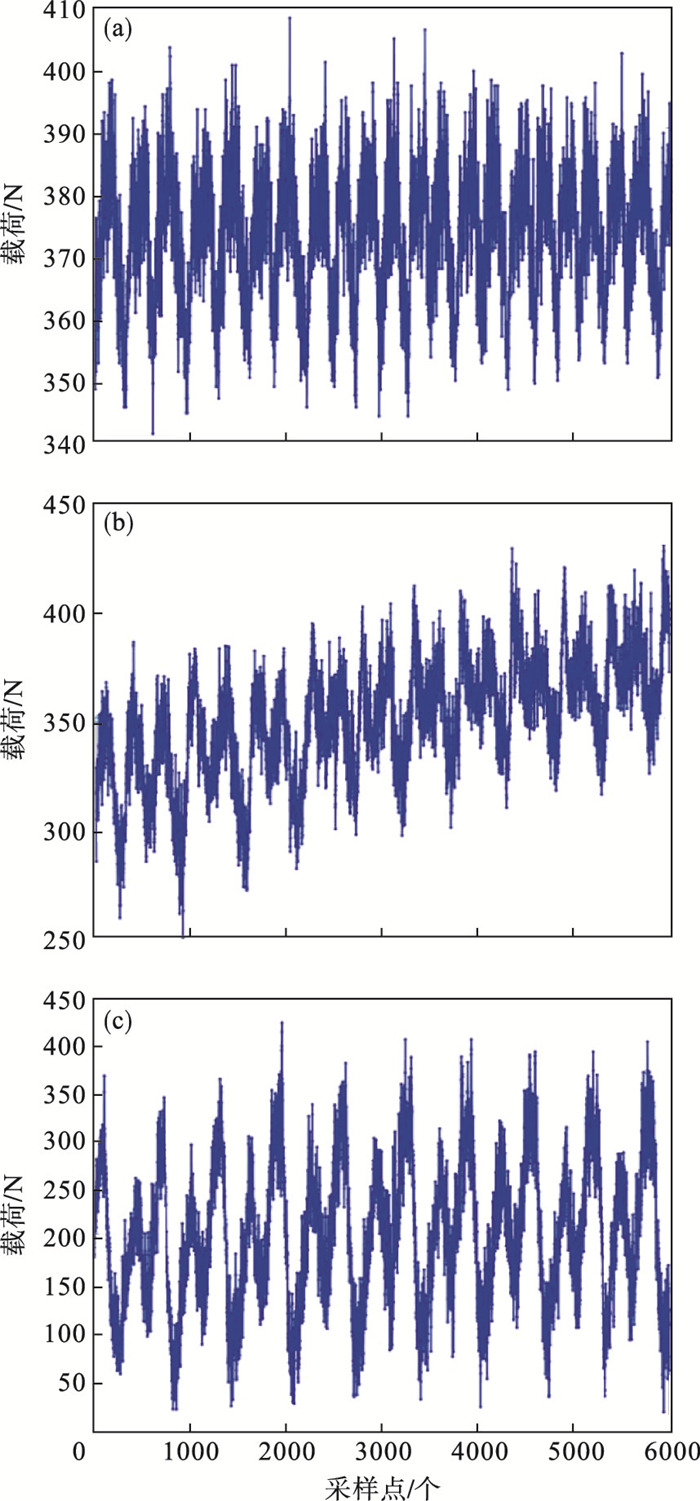图 10 不同工况数据采集载荷谱Fig.10 Data collection load spectrum under different working conditions (a)—一般随机载荷谱; (b)—趋势上升载荷谱; (c)—周期函数载荷谱.

通过随机选取连续的6 000个实测载荷采样点绘制形成载荷谱, 根据测量历史载荷谱预测未来的300个超前载荷谱, 与实际测量的300个载荷采样点进行对比分析, 确定误差值, 根据载荷的规律特性选取不同方法的超前载荷预测算法.超前预测载荷采样点与真实载荷采样点的绘制曲线如图 11所示.
图 11(Fig. 11)

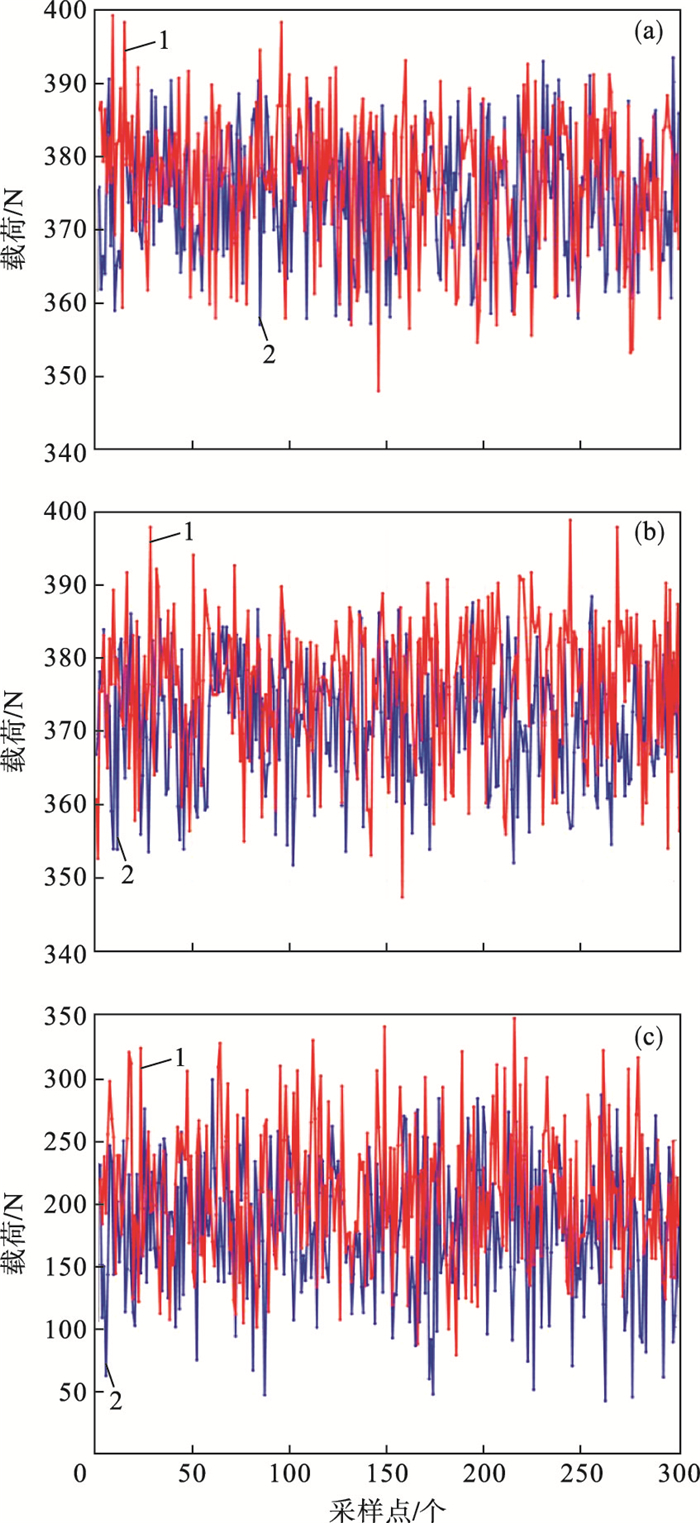图 11 不同工况载荷谱采样点对比Fig.11 Comparison of sampling points of load spectrum under different working conditions (a)—一般随机载荷谱; (b)—趋势上升载荷谱; (c)—周期函数载荷谱.

通过对比观察载荷谱极值, 载荷预测值的波动均在真实值上下浮动, 拟合的超前载荷预测波形呈阶跃性变化.概率密度外推法载荷预测模型对不同工况下的载荷谱预测较为精准, 采样点的波形走势与真实载荷谱大体一致, 载荷波动幅值范围相同, 预测精度高.预测结果较为理想, 预测数据与实际数据相吻合.建立的概率密度外推法载荷预测模型拟合的超前载荷谱波形分布形式和波动区间相似性高, 预测精度准确.
不同工况下, 超前预测载荷采样点与真实载荷采样点的核密度估计曲线如图 12所示.通过对比不同工况下核密度估计曲线, 可知预测值与真实值的概率密度最大值的误差较小, 载荷波动范围一致, 波形走势相同、预测准确.
图 12(Fig. 12)

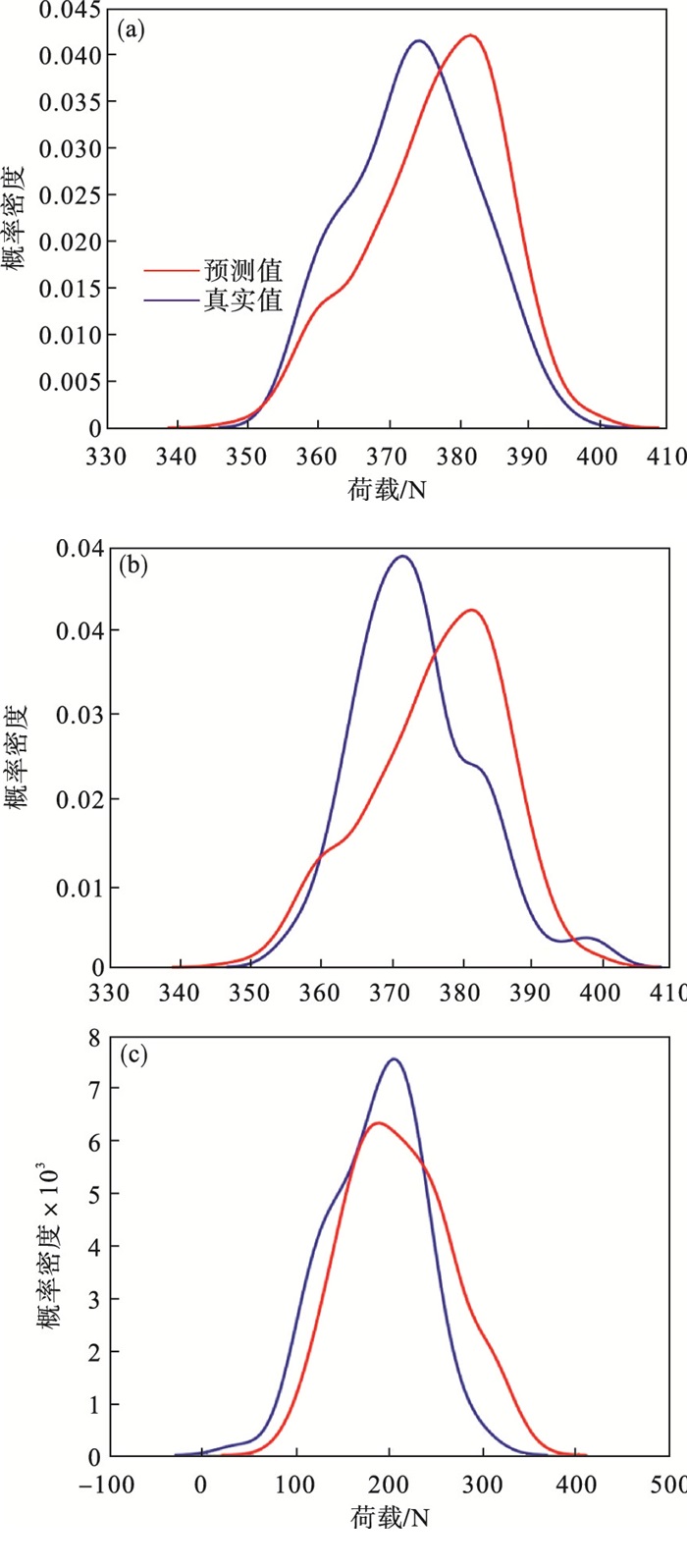图 12 不同工况载荷谱核密度估计曲线对比Fig.12 Comparison of load spectrum nuclear density estimation curves under different working conditions (a)—一般随机载荷谱; (b)—趋势上升载荷谱; (c)—周期函数载荷谱.

为了对比不同预测方法的准确度, 通过分析载荷谱核密度曲线的方式, 得到预测曲线与载荷曲线走势相似, 宽带大致相同, 可以对预测部分进行评定.利用蒙特卡洛法可以更加精准评估不同区间内的载荷预测精度.蒙特卡洛法是根据实际问题的特点, 构造简单而又便于实现的概率统计模型, 使所求的解恰好是所求问题的概率分布或数学期望.给出模型中各种不同分布随机变量的抽样方法, 统计处理模拟结果, 给出问题解的统计估计值和精度估计值.优势在于其方法的误差与问题的维数无关, 对于具有统计性质的问题可以直接进行解决, 对于连续性的问题不必进行离散化处理等优势.
2.2 载荷数据区间对比为了进一步验证预测载荷波形各个区间的数值占比情况, 利用蒙特卡洛方法^[21]，在相同条件下选取载荷真实数值及预测数值的300个采样点, 分别将数据按载荷幅值等分成11个区间, 比较分析预测的超前载荷谱数据与随机真实数值在不同区间里的占比, 根据区间密度绘制载荷谱区间对比曲线, 根据波形走势对比预测精度, 如图 13所示.
图 13(Fig. 13)

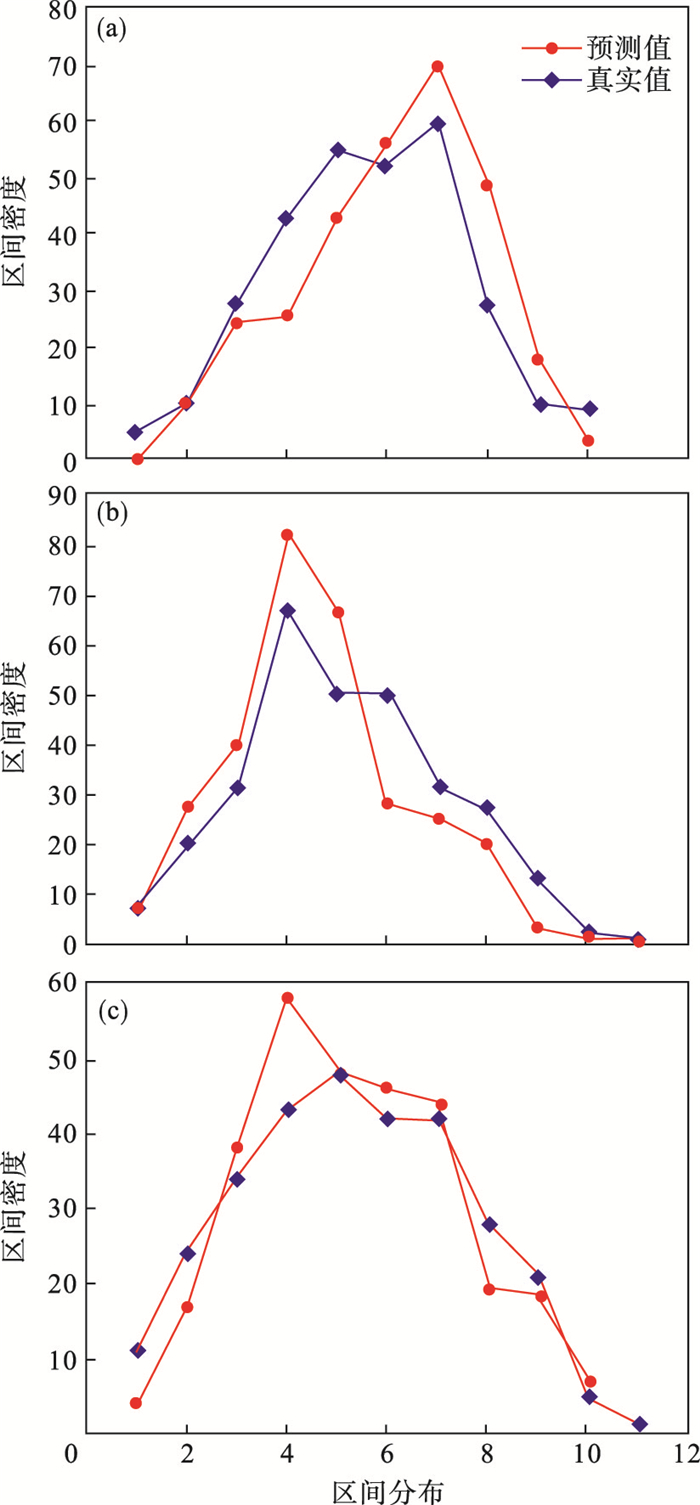图 13 载荷区间对比Fig.13 Comparison of load intervals (a)—一般随机载荷谱; (b)—趋势上升载荷谱; (c)—周期函数载荷谱.

对采样数据进行区间分布统计分析, 结果如表 1~表 3所示.真实值占比通过该真实区间数值个数占整体采样点的百分比确定, 预测值占比通过该预测区间数值个数占整体采样点的百分比确定, 误差占比通过真实占比与预测占比的差值计算所得.超前载荷预测模型的区间密度波形走势及重合度高度相似, 预测精度高.随机真实数据与超前载荷预测数据的占比最大差值均在10 % 之内, 其可信度高达90 %, 因此通过超前载荷预测模型得到的载荷符合要求且精度高.
表 1(Table 1)

表 1 一般随机载荷谱区间占比Table 1 Proportion of general random load spectrum intervals 区间 真实值 真实值占比/% 预测值 预测值占比/% 误差 个 个 个 % 1 6 2.00 0 0.00 2.00 2 10 3.33 10 3.33 0.00 3 28 9.33 24 8.00 1.33 4 43 14.33 25 8.33 6.00 5 55 18.33 43 14.33 4.00 6 52 17.33 57 19.00 -1.67 7 60 20.00 70 23.33 -3.33 8 27 9.00 49 16.33 -7.33 9 10 3.33 18 6.00 -2.67 10 9 3.00 4 1.33 1.67 11 0 0.00 0 0.00 0.00

表 1 一般随机载荷谱区间占比 Table 1 Proportion of general random load spectrum intervals

表 2(Table 2)

表 2 趋势上升载荷谱区间占比Table 2 Proportion of trend increasing load spectrum intervals 区间 真实值 真实值占比/% 预测值 预测值占比/% 误差 个 个 个 % 1 6 2.00 6 2.00 0.00 2 19 6.33 26 8.67 -2.33 3 30 10.00 40 13.33 -3.33 4 68 22.67 84 28.00 -5.33 5 50 16.67 68 22.67 -6.00 6 51 17.00 26 8.67 8.3 7 31 10.33 24 8.00 2.33 8 27 9.00 19 6.33 2.67 9 14 4.67 4 1.33 3.33 10 3 1.00 2 0.67 0.33 11 1 0.33 1 0.33 0

表 2 趋势上升载荷谱区间占比 Table 2 Proportion of trend increasing load spectrum intervals

表 3(Table 3)

表 3 周期函数载荷谱区间占比Table 3 Proportion of periodic function load spectrum intervals 区间 真实值 真实值占比/% 预测值 预测值占比/% 误差 个 个 个 % 1 11 3.67 4 1.33 2.33 2 24 8.00 17 5.67 2.33 3 35 11.67 38 12.67 -1.00 4 44 14.67 59 19.67 -5.00 5 48 16.00 48 16.00 0.00 6 42 14.00 46 15.33 -1.33 7 42 14.00 44 14.67 -0.67 8 28 9.33 19 6.33 3.00 9 19 6.33 18 6.00 0.33 10 6 2.00 7 2.33 -0.33 11 1 0.33 0 0.00 0.33

表 3 周期函数载荷谱区间占比 Table 3 Proportion of periodic function load spectrum intervals

3 结论1) 针对服役设备难以实时监测并准确反应载荷真实规律等问题, 提出一种基于数值分析概率密度预测方法, 结合机器学习算法建立预测模型, 通过实际工程数据运用蒙特卡洛方法验证预测模型的准确性.
2) 基于数值分析概率密度预测方法结合机器学习的神经网络智能算法, 对采集的随机载荷进行处理, 得到随机载荷谱.利用神经网络预测得到超前载荷谱, 通过真实数据与超前载荷谱预测数据进行对比分析, 得到采样点及预测载荷谱的关系.
3) 通过对比预测模型载荷谱的波形走势及波动范围等确定预测精度, 利用蒙特卡洛方法验证预测数据与真实数据在置信区间内的误差, 本文建立的超前预测载荷模型的拟合曲线与真实数值相似, 且计算精度最高.
4) 提出复杂工况下实时监测服役结构, 利用随机载荷预测超前载荷谱的方法, 为实时监测结构疲劳寿命提供算法与依据.
参考文献

[1]	Lewandowski M, Placzek B. An event-aware cluster-head rotation algorithm for extending lifetime of wireless sensor network with smart nodes[J]. Sensors, 2019, 19(19): 4060-4071. DOI:10.3390/s19194060
[2]	Ma X, Wang B, Li L, et al. A communication method between high-speed uuv and distributed intelligent nodes[J]. Mobile Networks and Applications, 2019, 25(4): 1528-1536.
[3]	Vahabi S, Eslaminejad M, Dashti S E. Integration of geographic and hierarchical routing protocols for energy saving in wireless sensor networks with mobile sink[J]. Wireless Networks, 2019, 25(5): 2953-2961. DOI:10.1007/s11276-019-02015-5
[4]	Wang Y, Liu J, Hu J, et al. Fatigue strength of EH36 steel welded joints and base material at low-temperature[J]. International Journal of Fatigue, 2020, 122: 105-117.
[5]	Zhao X, Su S, Wang W, et al. Metal magnetic memory inspection of q345b steel beam in four point bending fatigue test[J]. Journal of Magnetism and Magnetic Materials, 2020, 514: 155-167.
[6]	Costilla-Reyes A, Erbay C, Carreon-Bautista S, et al. A time-interleave-based power management system with maximum power extraction and health protection algorithm for multiple microbial fuel cells for Internet of things smart nodes[J]. Applied Sciences, 2018, 8(12): 113-125.
[7]	石松芳. 高可靠光纤布拉格光栅传感器网络传输风险预测[J]. 激光杂志, 2020, 41(5): 167-171. (Shi Song-fang. High-reliability fiber Bragg grating sensor network transmission risk prediction[J]. Laser Magazine, 2020, 41(5): 167-171.)
[8]	Li F. Compilation method of fatigue test load spectrum for underfloor equipment bearing structure[J]. Journal of Mechanical Engineering, 2016, 52(24): 99-110. DOI:10.3901/JME.2016.24.099
[9]	郑何妍. 高速列车车体加速寿命试验载荷谱编制及疲劳寿命预测仿真[D]. 成都: 西南交通大学, 2019. (Zheng He-yan. Load spectrum compilation and fatigue life prediction simulation of accelerated life test of high-speed train body[D]. Chengdu: Southwest Jiaotong University, 2019. )
[10]	翟新婷. 基于外推改进的工程机械载荷谱编制方法研究[D]. 长春: 吉林大学, 2018. (Zhai Xin-ting. Research on the compilation method of construction machinery load spectrum based on extrapolation improvement[D]. Changchun: Jilin University, 2018. )
[11]	李凡松, 邬平波, 曾京. 车下设备承载结构疲劳试验载荷谱编制方法[J]. 机械工程学报, 2016, 52(24): 99-106. (Li Fan-song, Wu Ping-bo, Zeng Jing. Compilation method of fatigue test load spectrum of undercarriage equipment bearing structure[J]. Journal of Mechanical Engineering, 2016, 52(24): 99-106.)
[12]	万一品, 宋绪丁, 员征文. 装载机工作装置疲劳试验载荷谱编制方法[J]. 中国机械工程, 2017, 28(15): 1806-1811. (Wan Yi-pin, Song Xu-ding, Yuan Zheng-wen. Compilation method of fatigue test load spectrum of loader working device[J]. China Mechanical Engineering, 2017, 28(15): 1806-1811. DOI:10.3969/j.issn.1004-132X.2017.15.007)
[13]	宫海彬, 苏建, 王兴宇. 基于极值外推的高速列车齿轮传动装置载荷谱编制[J]. 吉林大学学报(工学版), 2014, 174(5): 1264-1269. (Gong Hai-bin, Su Jian, Wang Xing-yu. Compilation of load spectrum of high-speed train gear transmission based on extreme value extrapolation[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 174(5): 1264-1269.)
[14]	Gong H B, Su J, Wang X Y. Compiling method of load spectrum of high-speed train gear drive system base on extreme value extrapolation[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(5): 1365-1377.
[15]	Pei H, Hu C H, Si X S, et al. Review of machine learning based remaining useful life prediction methods for equipment[J]. Journal of Mechanical Engineering, 2019, 55(8): 98-109.
[16]	董青, 徐格宁. 自适应双层果蝇相关向量机起重机当量载荷谱预测方法[J]. 机械设计, 2017(2): 86-93. (Dong Qing, Xu Ge-ning. Adaptive double-layer fruit fly correlation vector machine crane equivalent load spectrum prediction method[J]. Machine Design, 2017(2): 86-93.)
[17]	El-Sagheer R M, Mahmoud M A W, Nagaty H. Inference for Weibull-exponential distribution based on progressive type-Ⅱ censoring under step-stress partially accelerated life test model[J]. Journal of Statistical Theory and Practice, 2018, 13(1): 32-41.
[18]	Paraforos D S, Griepentrog H W, Vougioukas S G. Methodology for designing accelerated structural durability tests on agricultural machinery[J]. Biosystems Engineering, 2016, 149: 24-37. DOI:10.1016/j.biosystemseng.2016.06.004
[19]	Kim D W, Kim S H, Chu C N, et al. A new life model of tripod type constant velocity joint using accelerated life test[J]. Tribology International, 2019, 132: 130-141. DOI:10.1016/j.triboint.2018.12.005
[20]	Shafiullah A K M, Wu C Q. Generation and validation of loading profiles for highly accelerated durability tests of ground vehicle components[J]. Engineering Failure Analysis, 2013, 33: 8-16.
[21]	Fridman E, Huo X. Dynamic simulation of the CEFR control rod drop experiments with the Monte Carlo code Serpent[J]. Annals of Nuclear Energy, 2020, 148: 52-66.