
 , 彭霞3, 刘劲军4
, 彭霞3, 刘劲军4 1. 重庆大学 机械传动国家重点实验室, 重庆 400044;
2. 重庆大学 机械与运载工程学院, 重庆 400044;
3. 石河子大学 机械电气工程学院, 新疆 石河子 832000;
4. 洛阳矿山机械工程设计研究院有限公司, 河南 洛阳 471039
收稿日期:2021-11-29
基金项目:国家重点基础研究发展计划项目(2014CB049403);石河子大学高层次人才科研启动项目(RCZK2018C05)。
作者简介:葛建兵(1976-),男,新疆奎屯人,重庆大学博士研究生;
龚宪生(1956-),男,重庆人,重庆大学教授,博士生导师。
摘要:为揭示多层缠绕卷筒的振动特性及矿井提升系统相关参数对其动力学响应的影响, 以矿井提升机实验台的双折线卷筒为研究对象, 利用变质量完整力学系统Lagrange方程建立圈间过渡激励下质量慢变卷筒的含耦合项振动方程.对所建模型进行了数值分析和实验验证.结果表明: 推导出的方程较好地反映了卷筒的振动特性; 卷筒两个方向的加速度幅值略有差异, 卷筒两方向的振动加速度幅值都存在波动, 且具有同步性; 讨论了卷筒转速、卷筒非对称角、卷筒折线区圆心角、钢丝绳直径、密度等系统参数对卷筒振动加速度幅值的影响规律.研究成果有利于优化卷筒结构, 对系统安全运行具有一定参考价值.
关键词:多层缠绕圈间过渡质量慢变加速度响应系统参数
Vibration Characteristics of Multi-layer Winding Drum of Mine Hoists
GE Jian-bing1,2,3, GONG Xian-sheng1,2

 , PENG Xia3, LIU Jin-jun4
, PENG Xia3, LIU Jin-jun4 1. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;
2. College of Mechanical and Transportation Engineering, Chongqing University, Chongqing 400044, China;
3. Mechanical and Electrical Engineering College, Shihezi University, Shihezi 832000, China;
4. Luoyang Mining Machinery Engineering Design Institute Co., Ltd., Luoyang 471039, China
Corresponding author: GONG Xian-sheng, E-mail: cqxsgong@cqu.edu.cn.
Abstract: In order to reveal the vibration characteristics of the multi-layer winding drum and the influence of relevant parameters of the mine hoisting system on its dynamic response, a double folding line drum of the mine hoist experimental platform was taken as the research object, the vibration equations with coupling terms of the drum with slowly varying mass under rope transiting excitation were established by using Lagrange equation of variable mass holonomic mechanical system. The numerical analysis and experimental verification of the model were carried out. The results showed that the deduced equation reflects the vibration characteristics of the drum well. The acceleration amplitude of the two directions of the drum is slightly different. The amplitude of vibration acceleration in both directions of the drum fluctuates and is characterized by synchronization. The effects of such system parameters as drum speed, drum asymmetric angle, center angle of the crossover arc, wire rope diameter and density on drum vibration acceleration were discussed. The research results are helpful to optimize the drum structure, and have some reference value for the safe operation of the system.
Key words: multi-layer windingrope transitingslowly changing massacceleration responsesystem parameter
随矿井深度不断增加, 多层缠绕式提升机有望成为超深矿井的主要提升装备[1].多层缠绕式提升机的运行速度高、载荷大, 存在多种扰动.钢丝绳振动大, 系统工作不平稳, 影响钢丝绳的寿命和矿井生产安全及乘坐人员的舒适性.在多层缠绕式提升机工作过程中, 受到的扰动主要包括: 钢丝绳圈间过渡形成的周期性振动、卷筒偏心、制造误差、罐道对罐笼扰动等.这些因素的共同作用对提升系统安全运行构成了严重影响[2-3].其中, 钢丝绳圈间过渡对钢丝绳动张力、钢丝绳摩擦磨损、振动冲击等影响明显.为使钢丝绳在缠绕过程中无滑动冲击, 文献[4-5]基于微分几何测地线理论提出钢丝绳平稳过渡的力学条件.卷筒在钢丝绳平稳过渡下的振动, 不仅与提升系统的运动状态有关, 还与卷筒绳槽的结构形式及钢丝绳参数等相关, 其相关研究尚未见报道.
针对缠绕式提升系统的振动问题, 早期研究以单层缠绕式提升系统为研究对象, 在天轮、提升容器等多种因素的影响下, 分析钢丝绳的振动特性、动张力、摩擦磨损等问题[6-12].文献[13-14]应用Hamliton原理建立变长度提升系统钢丝绳运动微分方程, 研究了提升系统钢丝绳的纵向振动特性.Peng等[15]利用Galerkin方法研究多层缠绕卷筒布置形式对钢丝绳振动特性的影响.卷筒自身刚度大, 在钢丝绳缠绕过程中质量缓慢增加, 因此, 可以把卷筒看作滚动轴承支撑的刚性质量慢变转子.在刚性转子的振动研究中: 张学宁等[16]研究了含双频时变的三自由度转子-轴承系统响应特征.于涛[17]基于渐近解析法获得质量慢变转子系统的解析解, 并讨论了具有单一质量慢变模型的转子系统非线性动力学响应.王宗勇[18]利用渐近法研究激励幅值慢变转子系统的动力学特征.Pesce等[19]分析了变质量振动问题的相关理论.Cveticanin[20]研究了卷筒下放钢丝绳时的定轴转子振动问题.
多层缠绕的卷筒振动与上述研究不同在于钢丝绳圈间过渡形成的振动, 这种振动不但与运行参数有关, 还与提升机卷筒的结构参数如折线区圆心角、折线区非对称角、钢丝绳与卷筒的直径比、钢丝绳的直径、线密度等多个参数有关.
在钢丝绳平稳过渡的前提下, 以矿井提升机实验台的双折线卷筒为研究对象, 在分析其多层缠绕模型的基础上, 利用变质量完整力学系统Lagrange方程, 建立卷筒匀速转动条件下多层缠绕卷筒的无阻尼振动方程.利用数值方法分析卷筒的振动加速度响应, 并通过实验验证振动方程的正确性.研究提升系统部分参数对振动加速度的影响规律.
1 双折线卷筒钢丝绳的多层缠绕1.1 双折线卷筒的结构超深井提升设备采用双绳缠绕式提升系统, 如图 1所示.双折线绳槽结构如图 2所示.卷筒装配特有的双折线平行绳槽, 整个绳槽分为两个折线区和两个直线区, 绳槽两边缘各有一个层间过渡装置,如图 2a所示.1~2层层间过渡装置须布置到出绳口另一侧, 2~3层层间过渡装置与出绳口同侧.折线区对应的圆心角为β, 两折线区之间的较小夹角为非对称角κ, 如图 2b所示.
图 1(Fig. 1)
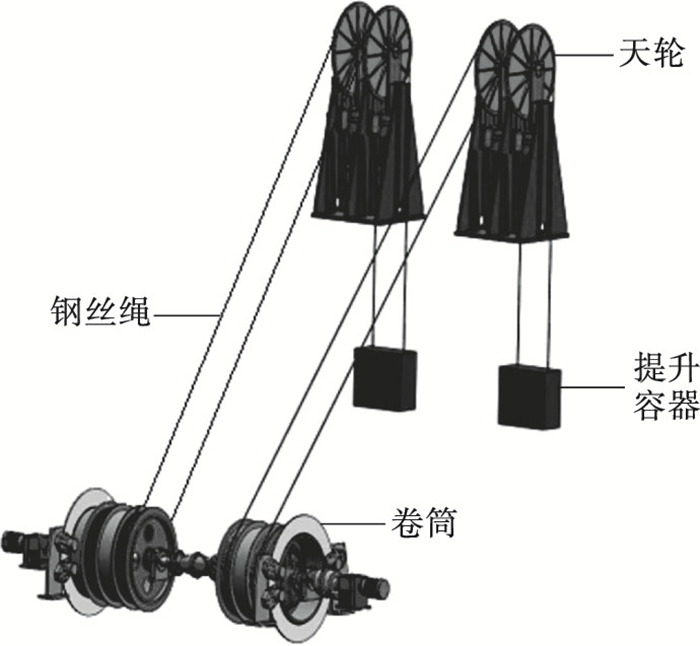 | 图 1 缠绕式双绳双卷筒提升系统Fig.1 Double rope double winding drum hoisting system |
图 2(Fig. 2)
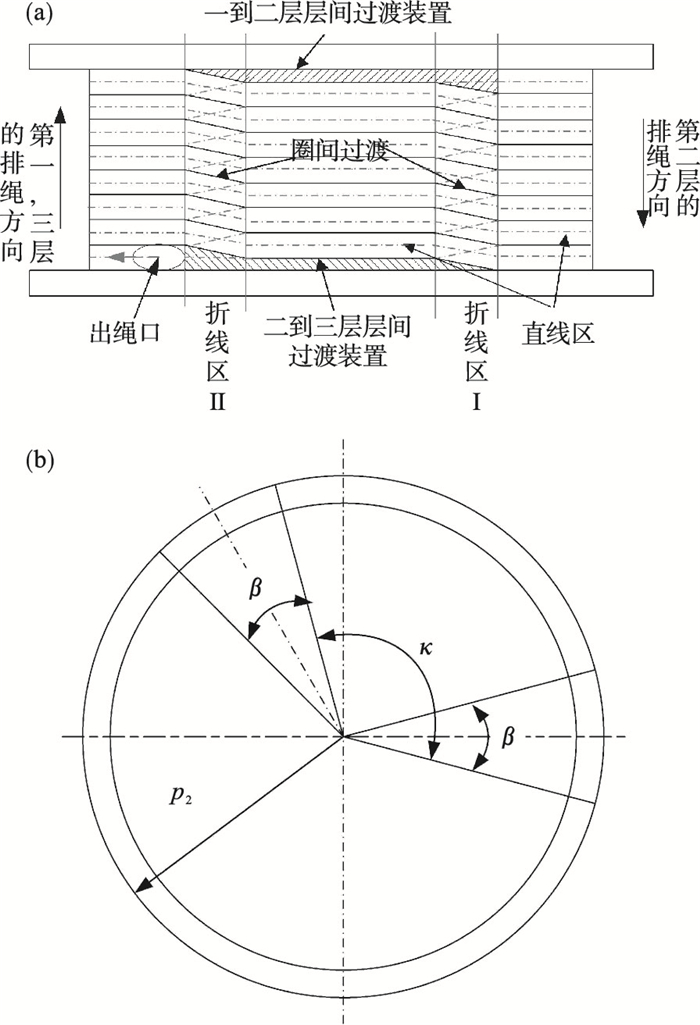 | 图 2 双折线绳槽结构Fig.2 Double folding line rope groove structure (a)—双折线绳槽展开图;(b)—双折线绳槽布置图. |
为了更好研究钢丝绳过度运动及其振动特性, 本文提出以下基本假设:
1) 钢丝绳轴线在变形前后均为3阶以上光滑曲线;
2) 矿井提升机卷筒刚度大、转速低, 简化为刚性转子;
3) 钢丝绳在圈间、层间过渡时不发生相对滑动和冲击;
4) 忽略由于钢丝绳平稳过渡引起的质量偏心;
5) 假设卷筒作匀速转动, 在分析系统振动过程中忽略系统阻尼.
1.2 钢丝绳多层缠绕模型钢丝绳多层缠绕模型如图 3所示.设钢丝绳半径为rr, 上下两层接触钢丝绳轴线距离为r, 螺旋升角为α1=arctan(rr/Rβ), R为卷筒半径.卷筒的角速度为ω1, 钢丝绳上升速度为v1, 以时间t为参数即可得到过渡区内的第一层螺旋线在坐标系M′中的方程:
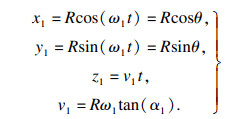 | (1) |
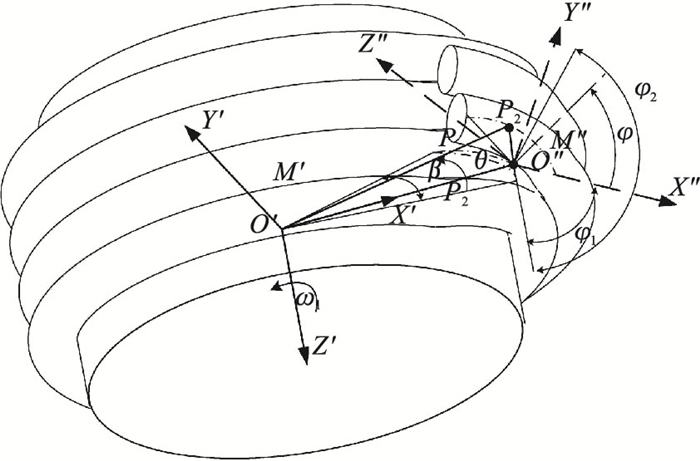 | 图 3 钢丝绳圈间过渡模型Fig.3 Transition model between wire rope loops |
式中: θ为第一层钢丝绳在折线区的转角; ω1为第一层钢丝绳绕下层钢丝绳轴线角速度; v1为上升速度.第一层钢丝绳的螺旋角α1=arctan(r/2R), 以时间t为参数即可得第二层钢丝绳轴线在坐标系M″中的方程:
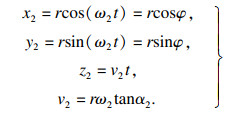 | (2) |
第一层钢丝绳线长度为
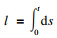
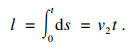 | (3) |
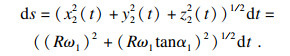 | (4) |
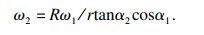 |
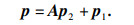 | (5) |
当卷筒转动时, 自动带动钢丝绳上升, 所以上层钢丝绳相对速度为零. 把式(1)~式(4)代入式(5)可得上层钢丝绳轴线方程:
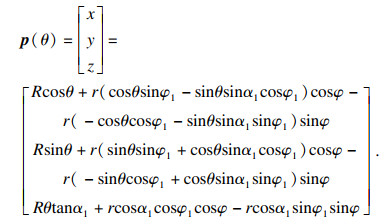 | (6) |
图 4(Fig. 4)
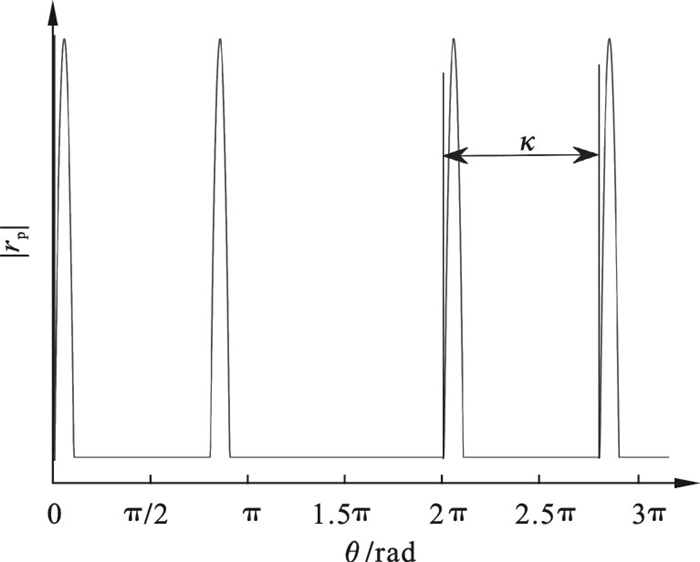 | 图 4 多层缠绕钢丝绳的矢径模与转角关系Fig.4 Relationship between vector modulus of multi- layer winding wire rope and rotation angle |
对式(6)前两项分别求二阶导数, 得到钢丝绳圈间过渡形成的激励.由于激励函数的表达式较复杂, 在工程中, R> >rr, α1 < < 1, 可以得到简化整理后的钢丝绳圈间过渡激励计算式:
 | (7) |
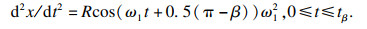 | (8) |
2.2 质量慢变卷筒的振动方程质量慢变卷筒的振动模型如图 5所示.设多层缠绕提升机卷筒的广义坐标为qi=[ux, uy, θ]T, 是无阻尼系统.其中ux, uy是卷筒质心的坐标, θ是卷筒的转角.
图 5(Fig. 5)
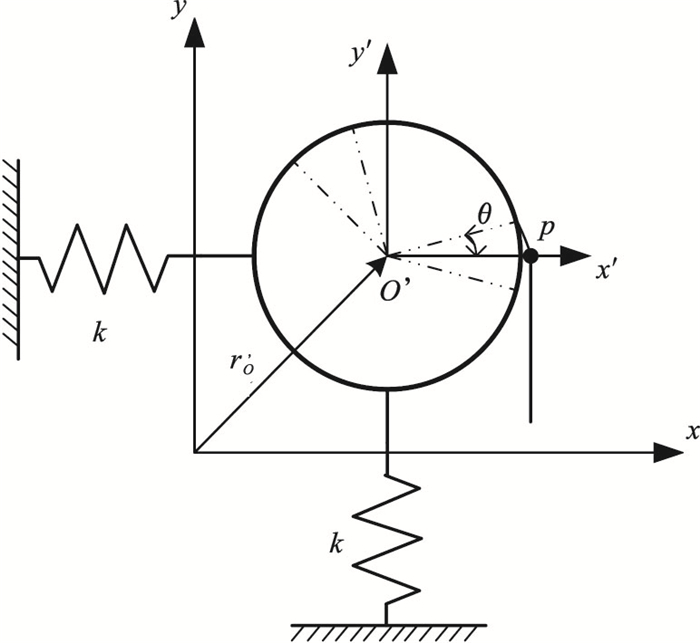 | 图 5 多层缠绕卷筒振动模型Fig.5 Vibration model of Lebus drums |
根据变质量完整力学系统Lagrange方程, 提升机卷筒的动力学方程为
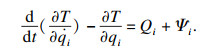 | (9) |
向心力:
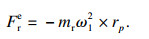 | (10) |
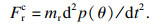 | (11) |
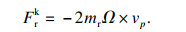 | (12) |
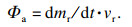 | (13) |
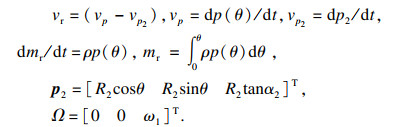 |
卷筒动能为
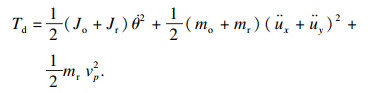 |
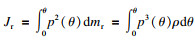
把式(10)~式(13)代入Largange方程, 钢丝绳在圈间平稳过渡时的振动方程为
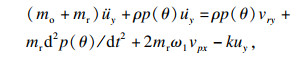 | (14) |
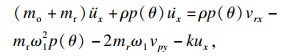 | (15) |
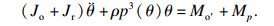 | (16) |
2.3 实验验证与数值仿真对比卷筒加速度响应的数值仿真与实验结果, 验证在圈间平稳过渡激励下变卷筒的振动模型的正确性, 为多层缠绕的卷筒振动、冲击、摩擦磨损等相关问题提供理论基础和实验依据.
实验在“国家安全生产洛阳矿山机械检测检验中心”的双折线双绳缠绕式提升机试验台进行, 实验现场如图 6所示.采用基于LabView平台的测试系统, 利用压电式加速度传感器采集振动信号, 采样频率为5.12 kHz.实验提升系统相关参数如表 1所示.左、右卷筒通过齿式联轴器连接, 左卷筒下出绳, 右卷筒上出绳, 即右卷筒提升时左卷筒下放.提升实验时, 钢丝绳在第一层缠2圈开始向第二层过渡, 第二层缠11圈后向第三层过渡, 第三层缠约1圈后停车.在轴承座处沿卷筒径向方向的振动信号更好地反映了钢丝绳圈间过渡情况.实测曲线如图 7所示.
图 6(Fig. 6)
 | 图 6 实验现场Fig.6 Experimental site (a)—双折线双绳缠绕式提升机试验台;(b)—振动测试现场. |
表 1(Table 1)
| 表 1 实验提升系统相关参数 Table 1 Parameters of the test hoisting system |
图 7(Fig. 7)
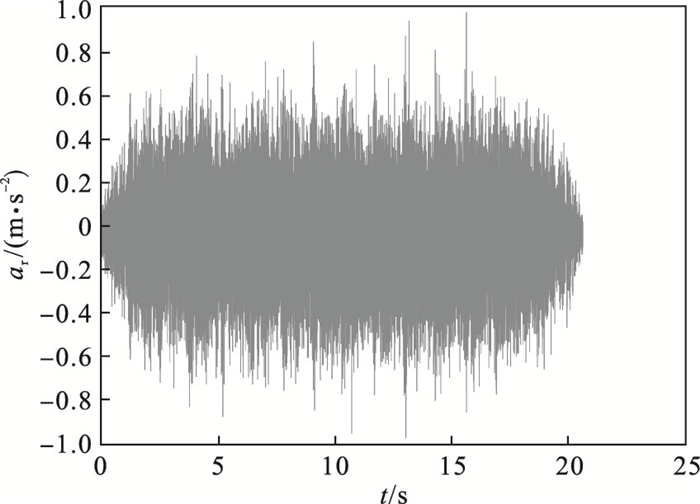 | 图 7 卷筒径向振动加速度实测曲线Fig.7 Measured curve of drum radial vibration acceleration |
采集的时域信号采用快速傅里叶变换并经低通滤波处理得到幅频特性曲线, 如图 8所示.第一阶振动响应频率为2.308 Hz, 幅值为0.001 01 m · s-2; 第二阶振动响应频率均为4.617 Hz, 幅值为0.000 69 m · s-2; 第三阶振动响应频率均为6.143 Hz, 幅值为0.000 46 m · s-2.振动响应仿真曲线分别如图 9, 图 10所示.
图 8(Fig. 8)
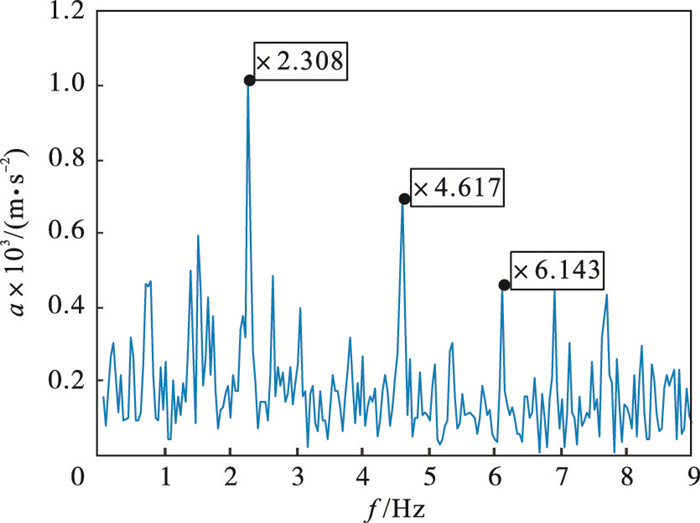 | 图 8 卷筒径向振动频谱图Fig.8 Spectrogram of dram radial vibration response of vibration |
图 9(Fig. 9)
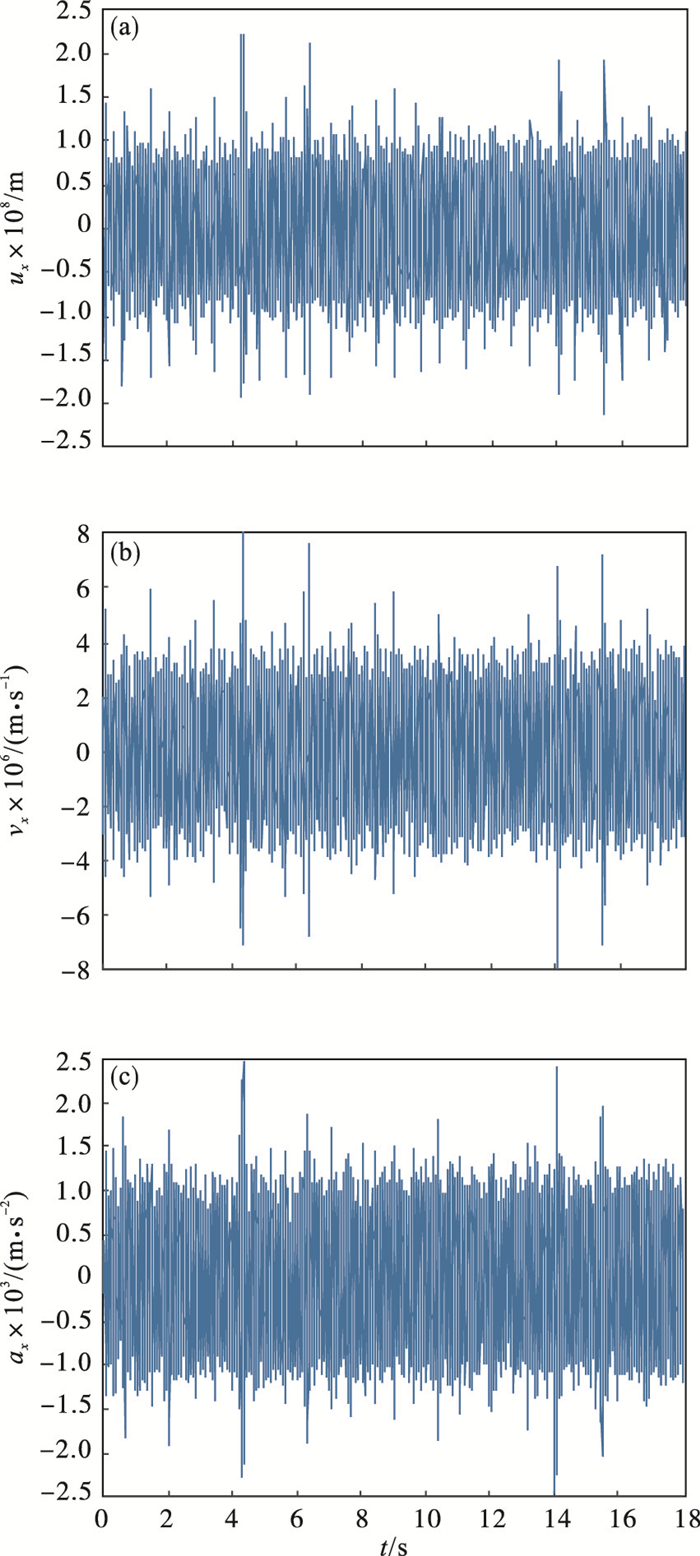 | 图 9 卷筒x向振动仿真曲线Fig.9 Simulation curve of drum x-direction vibration |
图 10(Fig. 10)
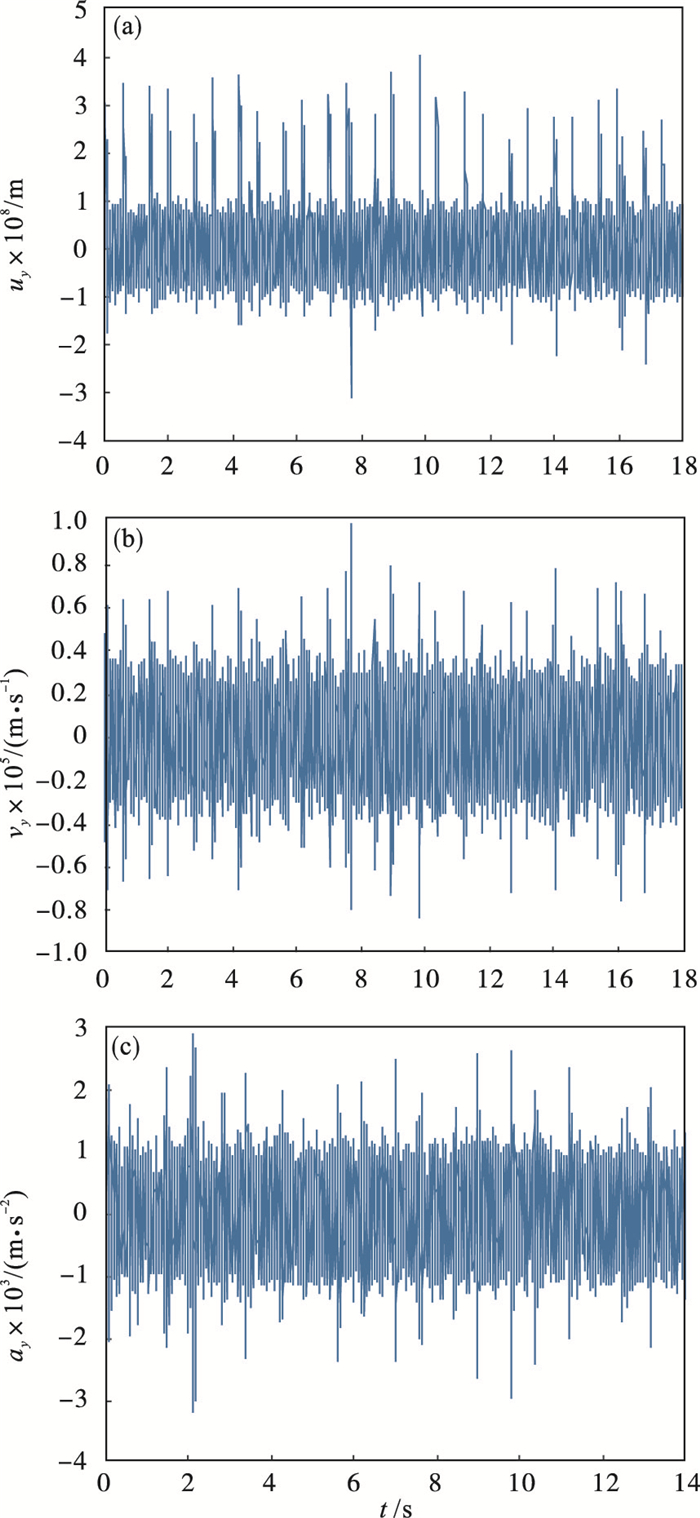 | 图 10 卷筒y向振动仿真曲线Fig.10 Simulation curve of drum y-direction vibration |
从数值仿真曲线可知: 卷筒两方向的振动加速度幅值存在波动, 且具有同步性, 这是多层缠绕钢丝绳平稳过渡的反映; 卷筒x向加速度幅值比卷筒y向加速度幅值略小.由式(14)、式(15)可知, 其主要原因是这两式中含圈间过渡激励项及耦合项的差异; 卷筒的两个方向加速度幅值对加速度响应起到同等作用; 由数值仿真和实测可知: 振动加速度的幅值较小且有波动.其主要原因: ①钢丝绳缠绕约14圈, 虽然时间比较短, 但其时变特性体现较明显; ②圈间过渡钢丝绳的质量远远小于卷筒质量, 其激励的幅值相对很小, 导致其响应振幅也很小.
对比双折线卷筒缠绕的实验与仿真结果可知: 卷筒加速度曲线值和实测幅值存在小幅误差.可能原因: ①数值仿真在多个假设条件下进行; ②没有考虑两方向支撑刚度的差别及载荷对支撑刚度等的影响; ③没有考虑系统运行状态、滚动轴承运动过程中引起的噪声, 以及钢丝绳的层间过渡、制造误差等对振动的影响.
3 提升机系统部分参数对振动特性的影响质量慢变卷筒的振动响应包括位移、速度、加速度响应, 由于实验测试得到的是加速度信号, 为了具有直观的可比性, 通过数值模拟分析卷筒振动系统参数对卷筒加速度幅值的影响规律.为了确定某个参数对加速度振幅的影响, 在其余参数不变的条件下进行相应分析计算.
3.1 非对称角对加速度幅值的影响钢丝绳在折线区不同布置形式的绳槽上缠绕, 将形成边界激励的相位差异, 产生不同的动态响应.非对称角表示两个折线区的相对位置关系, 对卷筒的加速度幅值影响如图 11所示.由图可知, y向加速度幅值比x向加速度略大, 两方向加速度幅值都在较小范围内波动: 当非对称角κ=0.4π时, x向加速度最小值为0.001 71 m · s-2; 当κ=π时, x向加速度最大值为0.001 99 m · s-2, y向加速度最大值为0.003 05 m · s-2.当κ=0.8π时, y向加速度最小值为0.002 33 m · s-2.考虑减小卷筒的振动, 可以初步选定非对称角为0.4π或0.8π.
图 11(Fig. 11)
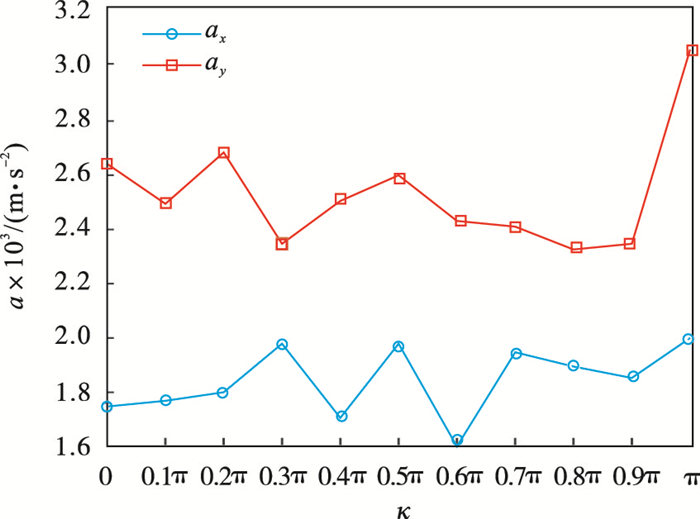 | 图 11 卷筒的非对称角与加速度幅值关系Fig.11 Relationship between asymmetric angle of drum and acceleration amplitude |
3.2 卷筒角速度对加速度幅值的影响根据实验条件, 卷筒角速度选定为2.5~4.5 rad · s-1.卷筒角速度与加速度幅值的关系如图 12所示.由图可知, x向加速度幅值比y向加速度幅值均稍小, 说明两个正交方向的加速度幅值对加速度幅值起相同主要作用; 随卷筒角速度从2.5 rad · s-1逐步增大到4.5 rad · s-1, x向加速度幅值从0.001 45 m · s-2逐步增大到0.001 90 m · s-2; y向加速度幅值则从0.001 84 m · s-2逐步增大到0.002 23 m · s-2.实际测量得到第一阶频率的振幅从0.000 56 m · s-2逐步增大到0.001 01 m · s-2.实验值与仿真值的变化趋势一致, 进一步说明了方程的正确性.减小卷筒振动, 应在满足工作要求的前提下, 降低卷筒角速度.
图 12(Fig. 12)
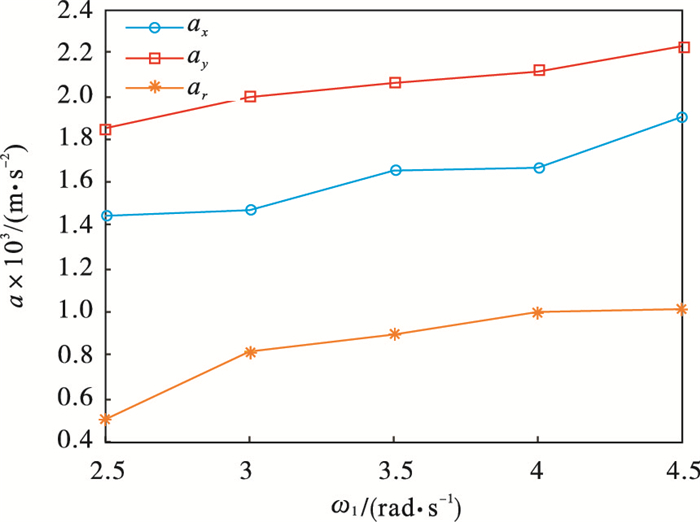 | 图 12 卷筒角速度与加速度幅值关系曲线Fig.12 Relationship curves between drum angular velocity and vibration acceleration |
3.3 折线区圆心角对加速度幅值的影响在卷筒直径和钢丝绳直径均不改变的情况下, 通过钢丝绳节距的方式微调折线区圆心角.综合考虑行业标准, 折线区圆心角限定在0.2~0.4 rad.折线区圆心角与加速度幅值的关系如图 13所示, 可知, y向加速度幅值均略大于x向加速度幅值, 说明两方向加速度幅值作用相似.圆心角为0.2~0.4 rad时, x向加速度幅值从0.001 78 m · s-2缓慢增大到0.002 12 m · s-2; y向加速度幅值则在0.002 07 m · s-2缓慢增大到0.002 27 m · s-2.随折线区圆心角的增大, 振动加速度幅值逐渐增大.为了减小卷筒振动, 在满足平稳过渡的前提下, 选取较小的圆心角.
图 13(Fig. 13)
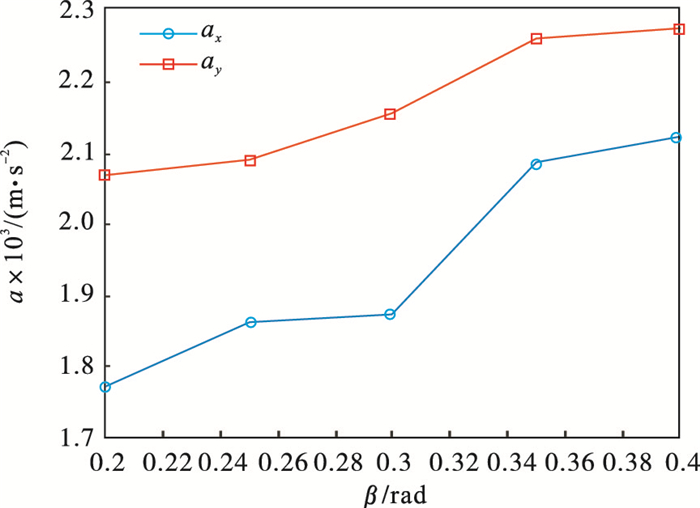 | 图 13 折线区圆心角与加速度幅值关系Fig.13 Relationship between center angle of the crossover arc and acceleration amplitude |
3.4 钢丝绳直径对加速度幅值的影响当卷筒直径一定时, 矿井提升机的钢丝绳直径选取主要受卷筒与钢丝绳的直径比范围限制.根据试验台的卷筒直径, 选定钢丝绳直径范围为10~30 mm.钢丝绳直径与加速度幅值的关系如图 14所示.由图可知, y向加速度幅值略大于x向加速度幅值.钢丝绳直径为10~30 mm时, x向加速度幅值从0.001 90 m · s-2逐步减小到0.001 52 m · s-2, y向加速度幅值由0.002 23 m · s-2逐渐减小到0.001 61 m · s-2. 因此, 可以认为随着钢丝绳直径的增大, 振动加速度的幅值逐渐减小.
图 14(Fig. 14)
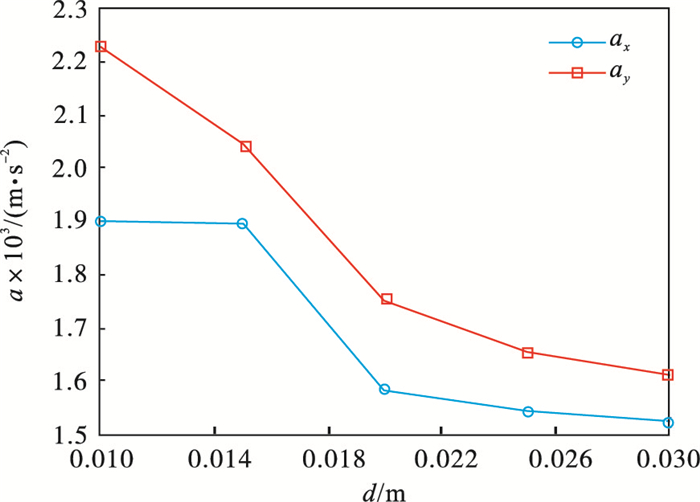 | 图 14 钢丝绳直径与加速度幅值关系Fig.14 Relationship between wire rope diameter and acceleration amplitude |
3.5 钢丝绳线密度对加速度幅值的影响钢丝绳的密度主要与钢丝绳的直径有关, 钢丝绳直径为10~30 mm时, 其相应钢丝绳密度的范围为0.41~2.81 kg · m-1, 钢丝绳线密度与加速度的幅值关系如图 15所示.由图可知, x向加速度幅值比y向加速度幅值略小, 随钢丝绳线密度的增加, 两者的差距逐渐增大.随钢丝绳线密度从0.41 kg · m-1增大到2.81 kg · m-1, x向加速度幅值从0.001 90 m · s-2逐渐增大到0.006 57 m · s-2, y向加速度幅值在由0.002 23 m · s-2逐渐增大到0.011 83 m · s-2的范围内波动.因此, 可以认为钢丝绳线密度与振动加速度的幅值成正比关系.
图 15(Fig. 15)
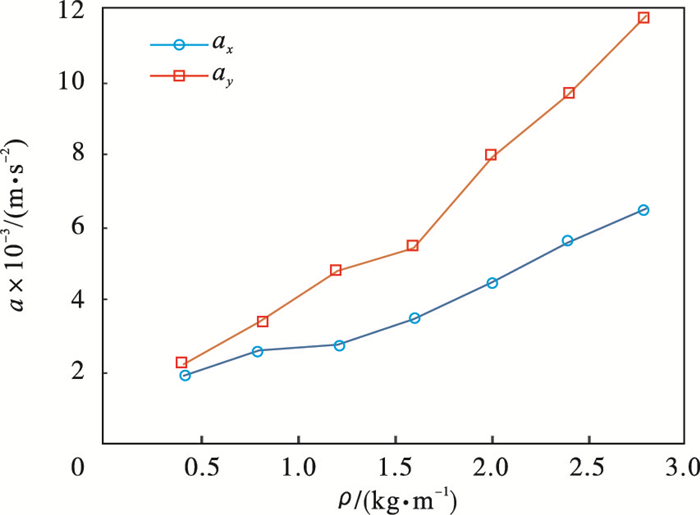 | 图 15 钢丝绳线密度与加速度幅值关系Fig.15 Relationship between wire rope density and acceleration amplitude |
为了减小卷筒振动, 在满足安全运行的前提下, 应首先选取线密度小, 直径大的钢丝绳.
4 结论1) 本文将钢丝绳看作连续的弹性体, 运用变质量完整力学系统Lagrange方程建立了圈间过渡激励下双折线卷筒的振动控制方程.
2) 通过对比缠绕式钢丝绳提升机卷筒的振动信号与数值仿真分析的振动信号, 可知卷筒的振动加速度幅值与实测值相近, 表明本文质量慢变卷筒振动方程的正确性.数值仿真表明: 卷筒两方向的振动加速度幅值都存在波动, 且具有同步性; 卷筒x向加速度幅值比卷筒y向加速度幅值略小, 对振动幅值贡献大致相同.
3) 在其余参数不变的条件下, 非对称角在0~π时, 卷筒振动的加速度幅值在较小范围内波动; 卷筒振动加速度幅值随着角速度的增加逐渐增大; 卷筒振动加速度幅值随着折线区圆心角增加而缓慢增大; 钢丝绳直径增大, 卷筒振动的加速度幅值逐渐减小; 钢丝绳线密度与振动加速度的幅值成正比关系.
参考文献
| [1] | 刘劲军, 邹声勇, 张步斌, 等. 我国大型千米深井提升机械的发展趋势[J]. 矿山机械, 2012, 40(7): 1-5. (Liu Jin-jun, Zou Sheng-yong, Zhang Bu-bin, et al. Discussion trend of domestic large hoisting equipments for deepshafts of thousands meters[J]. Mining & Processing Equipment, 2012, 7(40): 1-5.) |
| [2] | Chang X D, Peng Y X, Zhu Z C, et al. Experimental investigation of mechanical response and fracture failure behavior of wire rope with different given surface wear[J]. Tribology International, 2018, 119: 208-221. DOI:10.1016/j.triboint.2017.11.004 |
| [3] | Singh R P, Mallick M, Verma M K. Studies on failure behaviour of wire rope used in underground coal mines[J]. Engineering Failure Analysis, 2016, 70: 290-304. DOI:10.1016/j.engfailanal.2016.09.002 |
| [4] | 葛建兵, 龚宪生, 彭霞, 等. 新型双折线绳槽结构设计与实验研究[J]. 东北大学学报(自然科学版), 2019, 40(7): 997-1001, 1027. (Ge Jian-bing, Gong Xian-sheng, Peng Xia, et al. Structural design and experimental research of new double-folded groove[J]. Journal of Northeastern University(Natural Science), 2019, 40(7): 997-1001, 1027.) |
| [5] | Peng X, Gong X S, Liu J J, et al. Vibration control on multilayer cable moving through the crossover zones on mine hoist[J]. Shock and Vibration, 2016, 2016: 1-7. |
| [6] | Kaczmarczyk S, Ostachowicz W. Transient vibration phenomena in deep mine hoisting cables.Part 1:mathematical model[J]. Journal of Sound & Vibration, 2003, 262(2): 219-244. |
| [7] | Kaczmarczyk S, Ostachowicz W. Transient vibration phenomena in deep mine hoisting cables.Part 2:numerical simulation of the dynamic response[J]. Journal of Sound & Vibration, 2003, 262(2): 245-289. |
| [8] | Kaczmarczyk S, Ostachowicz W. Modeling of vibrations and prediction of failure in mine hoisting cables[J]. Key Engineering Materials, 1999(167/168): 281-290. |
| [9] | Chen L Q, Wang J J, Han Q K, et al. Nonlinear dynamic modeling of a simple flexible rotor system subjected to time-variable base motions[J]. Journal of Sound and Vibration, 2017, 404: 58-83. DOI:10.1016/j.jsv.2017.05.032 |
| [10] | Chen L Q, Tang Y Q, Jean W Z. Nonlinear transverse vibration of axially accelerating strings with exact internal resonances and longitudinally varying tensions[J]. Nonlinear Dynamics, 2014, 76(2): 1443-1468. DOI:10.1007/s11071-013-1220-1 |
| [11] | Wang J, Pi Y J, Hu Y M, et al. Modeling and dynamic behavior analysis of a coupled multi-cable double drum winding hoister with flexible guides[J]. Mechanism and Machine Theory, 2017, 108: 191-208. DOI:10.1016/j.mechmachtheory.2016.10.021 |
| [12] | Srinil N, Rega G, Chucheepsakul S. Large amplitude three-dimensional free vibrations of inclined sagged elastic cables[J]. Nonlinear Dynamics, 2003, 33: 129-154. DOI:10.1023/A:1026019222997 |
| [13] | Bao J H, Zhang P, Zhu C M. Transverse vibration of flexible hoisting rope with time-varying length[J]. Journal of Mechanical Science and Technology, 2014, 28(2): 457-466. DOI:10.1007/s12206-013-1110-y |
| [14] | 包继虎, 张鹏, 朱昌明. 变长度提升系统钢丝绳纵向振动特性[J]. 振动与冲击, 2018, 32(15): 173-177. (Bao Ji-hu, Zhang Peng, Zhu Chang-ming. Longitudinal vibration of rope hoisting systems with time-varying length[J]. Journal of Vibration and Shock, 2018, 32(15): 173-177.) |
| [15] | Peng X, Gong X S, Liu J J. The study on crossover layouts of multi-layer winding grooves in deep mine hoists based on transverse vibration characteristics of catenary rope[J]. Journal of Systems and Control Engineering, 2019, 233(2): 118-132. |
| [16] | 张学宁, 韩勤锴, 褚福磊. 含双频时变滚动轴承刚度的转子-轴承系统响应特征研究[J]. 振动与冲击, 2017, 36(13): 116-121. (Zhang Xue-ning, Han Qin-kai, Chu Fu-lei. Response characteristics of a rotor-bearing system with double frequency time-varying bearing stiffness[J]. Journal of Vibration and Shock, 2017, 36(13): 116-121.) |
| [17] | 于涛, 王娇, 李英杰, 等. 基于时频分析的质量慢变转子系统非线性动力学特性研究[J]. 振动与冲击, 2014(20): 105-110. (Yu Tao, Wang Jiao, Li Ying-jie, et al. Nonlinear dynamics characteristics of rotor system with slowly-varying mass based on time-frequency analysis[J]. Journal of Vibration and Shock, 2014(20): 105-110.) |
| [18] | 王宗勇, 龚斌, 闻邦椿. 激励幅值慢变转子系统的动力学研究[J]. 中国机械工程, 2007, 18(24): 2969-2973. (Wang Zong-yong, Gong Bin, Wen Bang-chun. Study on dynamics of rotor systems with slowly varying excitation magnitude[J]. China Mechincal Enigneering, 2007, 18(24): 2969-2973. DOI:10.3321/j.issn:1004-132x.2007.24.016) |
| [19] | Pesce C P. The application of Lagrange equations to mechanical systems with mass explicitly dependent on position[J]. Journal of Applied Mechanics, 2003, 70: 751-755. DOI:10.1115/1.1601249 |
| [20] | Cveticanin L, Djukic D. Dynamic properties of a body with discontinual mass variation[J]. Nonlinear Dynamics, 2008, 52(3): 249-261. DOI:10.1007/s11071-007-9275-5 |
