
 , 宋新潮, 邵欣然
, 宋新潮, 邵欣然 东北大学 工商管理学院, 辽宁 沈阳 110169
收稿日期:2021-03-15
基金项目:国家自然科学基金资助项目(71871048)。
作者简介:姜艳萍(1968-), 女, 辽宁沈阳人, 东北大学教授, 博士生导师。
摘要:共享经济的兴起为解决城市“停车难”提供了思路.针对既在目的地附近有车位需求, 又拟将自有车位共享出去的这类双角色主体间的私人闲置车位和需求者匹配问题进行了研究.根据匹配主体的可接受价格、时间窗和最大允许步行距离, 分别计算其作为私人闲置车位供应者和需求者的区域热度优先级; 构建了以平台收益最大、主体匹配数量最大和主体优先级最高为目标的多目标优化模型.通过改进的NSGA-Ⅱ算法对该多目标优化模型求解, 确定了私人闲置车位和需求者的匹配方案, 并通过算例说明了所提方法的可行性.本文研究结果对开展私人闲置车位与需求者匹配问题的研究提供了参考.
关键词:共享经济私人闲置车位匹配优先级双角色主体NSGA-Ⅱ改进算法
Matching Model for Private Idle Parking Spaces and Demanders Between Dual-Role Agents
JIANG Yan-ping

 , SONG Xin-chao, SHAO Xin-ran
, SONG Xin-chao, SHAO Xin-ran School of Business Administration, Northeastern University, Shenyang 110169, China
Corresponding author: JIANG Yan-ping, E-mail: ypjiang@mail.neu.edu.cn.
Abstract: Sharing economy provides a new way to solve the problem of "parking difficulty". A matching problem between private idle parking spaces agents and demanders of dual-role agents was studied. A dual-role agent not only needs parking spaces near the destination, but also intends to share its own parking spaces. According to the acceptable price, time window and maximum allowable walking distance of the matching subjects, the regional heat priority as a supplier and demander of private parking spaces was calculated respectively. A multi-objective optimization model is constructed with the goal of maximizing platform revenue, maximizing the number of subject matches and the highest subject priority.The multi-objective optimization model was solved by the improved NSGA-Ⅱ algorithm, the matching plan between private idle parking spaces and demanders was determined, and the feasibility of the proposed method was illustrated by a calculation example. The research results may provide reference for the research on matching between private parking spaces and demanders.
Key words: sharing economyprivate idle parking spacematchingprioritydual-role agentimproved NSGA-Ⅱ algorithm
随私家车保有量的不断增加, 停车难成为城市中普遍存在的问题, 受到社会广泛关注.我国城市中的停车资源总体呈供不应求的趋势, 在大城市中, 停车位与私家车的数量比为0.8∶1, 而在中小城市仅为0.5∶1, 均远低于发达国家1.3∶1的比例[1].停车资源供需矛盾导致诸如乱停车、长时间寻找停车位、交通拥堵、环境污染等问题的产生.在停车资源捉襟见肘的情形下, 城市中却还有大量私人拥有的停车位经常被闲置.据统计, 我国停车位的平均空置率高达50%, 即使在一线城市北京、上海、广州、深圳, 车位平均空置率也达到了44.6%[1].因此, 通过共享私人闲置车位来提高车位利用率从而解决停车难问题具有很大潜力.
随互联网技术的快速发展, 为私人闲置车位和需求者提供共享服务的电子共享平台应运而生[2].电子共享平台根据私人闲置车位的位置、价格、供应时间和需求者的停车位置、价格、停车时间、可接受步行距离等信息, 统一为需求者匹配私人闲置车位.
现实中有一类人, 称之为具有双角色特点的主体: 他们驾车前往目的地附近停车资源供不应求, 而在外出期间他们的私人车位被闲置, 这类人既有停车资源的使用需求, 又有能力提供车位.如果这类主体之间交换使用私人车位, 则可以达到通过鼓励车位拥有者进行车位共享, 从而达到降低车位空置率, 满足更多司机停车需求的目的.因此, 本文研究了主体具有双角色特点的私人闲置车位和需求者的匹配问题.Xu等讨论了在大城市工作时间内的私人停车位匹配问题.通过既有车位需求又能提供车位的主体之间相互交换车位、只提供车位的主体出租其私人闲置车位和只有车位需求的主体租用车位, 提出了顶部交易循环与交易机制、价格兼容的顶部交易循环与链机制[3].根据主体偏好得到一个主体之间帕累托最优匹配方案, 使匹配方案稳定, 但没有考虑平台收益和主体目的地及车位所处区域的供需差异.
Zhang等针对如何对可共享的私有车位进行再分配问题, 在考虑供需时间差异的基础上, 建立了以最大化共享车位利用率和最大化停车需求者满意度为目标的多目标优化模型[4].Shao等提出了使车位拥有者和需求者在工作时间共享小区停车位的整数线性规划模型, 并得到使共享平台利润最大的匹配方案[5].Guo等针对在一天的特定时间段内临时回购一些私人停车位的停车场运营公司, 提出了一种描述司机到达/离开行为的高斯混合模型, 通过指导公司选择回购金额和停止时间, 使运营公司利润最大化[6].Huang等针对居住区空置停车位, 考虑停车用户的超时停车行为, 建立了以停车效益最大化为目标的共享停车分配模型.根据停车效益最大化原则, 确定最优预留车位比例和需要向居民购买的共享车位数量[7].Zou等提出了一种公共停车位的分配机制, 针对不同司机对车位收益感知不同, 以社会福利最大化为目标构建优化模型, 并通过设计支付规则激励司机在参与分配的过程中如实报告自己的私人信息[8].段满珍等建立了居住区共享停车泊位分配的双层规划模型, 通过对高峰泊位空闲指数差异均值和司机停车后步行距离目标的双重约束实现了停车资源的有效利用[9].王艳等综合考虑了动态多时段的停车需求, 提出了一个最小化所有用户的总步行距离的公共停车场布局优化模型[10].Xiao等采用周期性的双边拍卖得到一个社会福利最大化的匹配结果, 保证了共享停车位主体匹配结果的公平性, 并考虑了如何防止主体退出共享市场[11].林小围等运用合作博弈理论研究了完全信息静态停车博弈问题, 给出了一个成本合理、公平的分配机制.基于合作博弈的车位分配结果, 系统引导先到的车辆将车停在远处, 后到车辆转移支付给先到车辆, 以补偿其因让出近处车位而增加的直接停车成本[12].
从已有研究结果可知, 大多考虑的是匹配主体只作为需求者或只作为车位供应者的情形.因此, 本文针对主体具有双角色特点的私人闲置车位和需求者的匹配问题, 通过参与车位共享的主体之间交换车位, 在考虑平台收益、主体匹配数量、主体优先级等条件下, 给出一种能提高车位资源利用率的私人闲置车位与需求者匹配方法.
1 问题描述基于电子共享平台, 本文研究具有双角色特点的主体之间的私人闲置车位和需求者匹配问题, 主体既有车位需求又能提供私人车位, 例如拥有私家车和私人车位的上班族.他们将自己的私人车位在闲置时间内通过平台共享出去, 并换得一个位于其目的地附近的可接受车位.
匹配示意图如图 1所示, 4名匹配主体U1, U2, U3, U4作为需求者U1d, U2d, U3d, U4d有各自的目的地


图 1(Fig. 1)
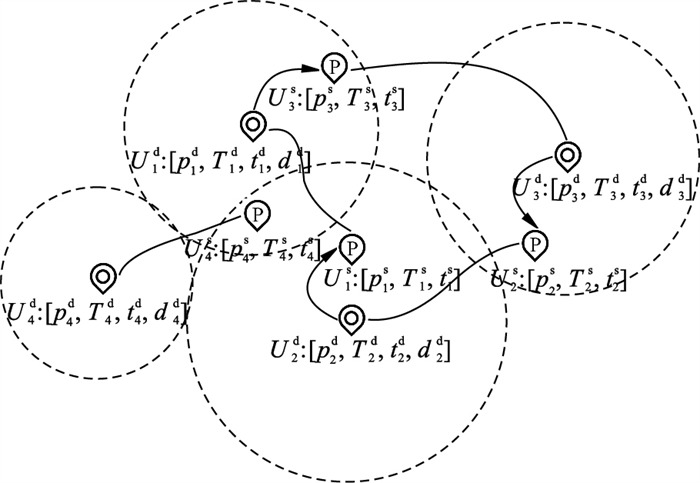 | 图 1 匹配示意图Fig.1 Matching diagram |
1.1 符号描述为了描述本文所研究的问题, 给出以下量的解释:
U=(U1, U2, …, UM)为参与私人闲置车位共享的主体集合, 其中Ui={Uid, Uis}表示第i个主体, Ui既是需求者又是供应者, 其中Uis表示Ui的角色是供应者, Uid表示Ui的角色是需求者;(Ais, Bis)为Uis提供的私人闲置车位的位置坐标;pis为Uis可接受的单位时间车位的最低出租价格;Tis为Uis共享车位的最早开始时刻;tis为Uis共享车位的最晚结束时刻;(Aid, Bid)为Uid目的地的位置坐标;pid为Uid可接受的单位时间车位的最高租用价格;Tid为Uid需要停车的最早开始时刻;tid为Uid需要停车的最晚结束时刻;did为Uid可以接受的车位到其目的地之间的最大步行距离.
1.2 优先级分析和计算区域热度优先级是衡量主体在本次匹配中优先程度的一个指标, 受主体目的地所处区域的车位供需情况和其私人闲置车位所处区域的车位供需情况两方面的影响.优先级越高的主体越优先被匹配.以主体Ui作为车位供应者为例, 当Uis提供车位的所处区域供不应求时, 该车位的重要性较高, 主体Ui的区域热度优先级随之上升; 如果可以接受Uis提供车位的需求者有充足的其他选择, 则会导致该车位的重要性下降, 主体Ui的区域热度优先级也随之下降.同理可分析主体作为需求者对主体的区域热度优先级的影响.令wis, wid分别表示主体Ui作为车位供应者Uis和作为需求者Uid的区域热度优先级:
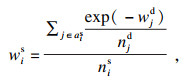 | (1) |
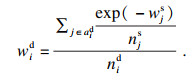 | (2) |
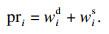 | (3) |
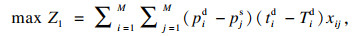 | (4) |
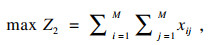 | (5) |
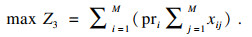 | (6) |
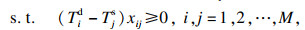 | (7) |
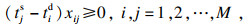 | (8) |
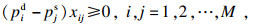 | (9) |
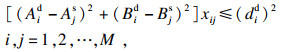 | (10) |
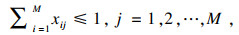 | (11) |
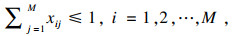 | (12) |
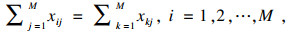 | (13) |
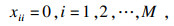 | (14) |
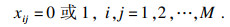 | (15) |
由于目标函数式(4)、约束条件式(11)、式(12)和式(15)经简化后构成的模型式(16)~式(19)是经典的TSP问题, 因此本文建立的多目标优化模型式(4)~式(15)也是一个NP-hard问题.
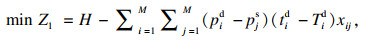 | (16) |
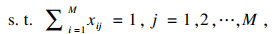 | (17) |
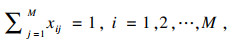 | (18) |
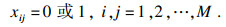 | (19) |
2.2 算法设计式(4)~式(15)是一个多目标的0-1整数规划模型, 当主体数量较大时, 可采用粒子群算法(PSO)、声搜索算法(DHS)、NSGA-Ⅱ算法等启发式算法求解.考虑到私人闲置车位与需求者匹配优化模型只有3个目标函数, 纬度较低, 而NSGA-Ⅱ算法已被证实在求解低维优化问题的速度和效率上具有优良性能[13-14], 因此本文选择NSGA-Ⅱ算法求解该模型.
考虑到式(4)~式(15)是离散问题, 且约束条件使所建模型的可行解空间具有稀疏性, 直接应用NSGA-Ⅱ算法生成可行解的概率很低, 为此对NSGA-Ⅱ算法进行了改进: ①根据研究问题特点, 采用整数编码的方式对染色体进行编码; ②为了快速生成初始种群, 提出了可行解快速生成方案; ③为了保障交叉变异后的染色体依然是可行的, 重新设计了染色体变异规则.本文改进的NSGA-Ⅱ算法的流程如图 2所示.
图 2(Fig. 2)
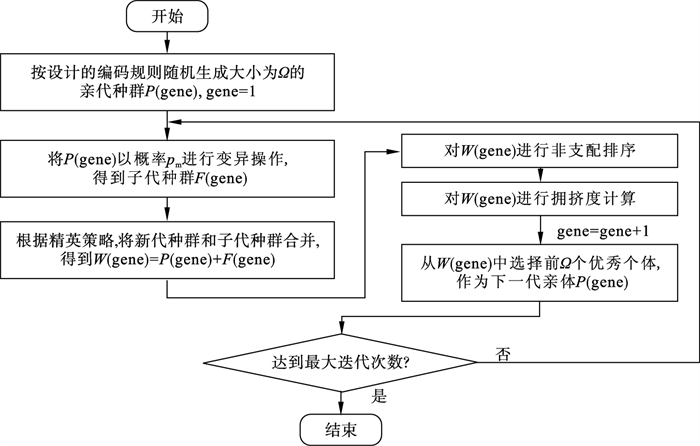 | 图 2 算法流程图Fig.2 Flow chart of the algorithm |
具体说明如下:
1) 染色体编码方式: 采用整数编码方式为染色体进行编码.一条染色体代表模型的一个解, 用变量match_list表示.一条染色体最多有M+1个基因, 每个基因可取整数1, 2, …, M, 代表一个主体编号, 相邻的两个基因表示前一个主体占用后一个主体的车位.若match_list对于式(4)~式(15)是可行解, 其最后一个元素和第一个元素相同且前M个互不相同, 意味着被分配到车位的主体, 他自己的车位也必被分配给其他主体; 车位被分配出去的主体, 也必然会被分配给一个来自其他主体的车位.
2) 快速生成可行解: 由于式(4)、式(15)可行解空间比较稀疏, 随机赋值的方式会产生大量不可行解.为了提高生成可行解的速度, 本文设计了如下快速生成可行解方案的规则:
步骤1 ??找到每个主体作为需求者的可接受车位列表(定义为初始状态), 初始化空数组match_list, 随机选择一个有可接受车位的主体, 添加到数组match_list的末尾, 转步骤2;
步骤2 ??如果match_list为空数组, 转步骤9;否则转步骤3;
步骤3 ??如果match_list最后一个主体i没有可接受车位, 将i从match_list倒数第二个主体的可接受车位列表中删除, 将i的可接受车位列表恢复至初始状态, 将i从match_list中删除, 转步骤2;否则转步骤4;
步骤4 ??将match_list最后一个主体i作为需求者的可接受车位中随机选择一个主体j;
步骤5 ??如果j恰好是match_list中的第一个主体, 将j添加到数组match_list的末尾, 转步骤8;否则转步骤6;
步骤6 ??如果j存在于match_list中, 将j从i的可接受车位列表中删除, 转步骤2;否则转步骤7;
步骤7 ??将j添加到数组match_list的末尾, 将j的可接受车位列表恢复到初始状态, 转步骤2;
步骤8 ??成环, 匹配结果为主体match_list[i]作为需求者匹配主体match_list[i+1]的车位, i=1, …, longth(match_list)-1, 结束;
步骤9 ??匹配方案为空, 结束.
3) 变异算子: 由于约束条件式(7)~式(15)使可行解空间比较稀疏, 所以按照传统NSGA-Ⅱ算法随机进行0-1变换容易产生不可行解, 因此需要对算法的变异操作进行改进, 即选定亲代个体后, 识别其中未匹配成功的主体, 将其对应信息作为输入, 重新运行快速生成可行解算法, 得到一个新的可行匹配环R, 将R以概率pm直接作为子代新个体, 以概率(1-pm)添加到亲代个体中, 生成子代新个体.
4) 选择优秀可行解: 首先根据约束条件式(7)~式(15)筛选掉新生成的子代个体中的不可行解, 然后将剩余的可行子代与亲代采用快速非支配排序和拥挤度[13]进行比较, 选择其中表现优良的个体作为下一代亲体, 继续迭代运算.
3 算例分析假设有20个主体U1, U2, …, U20提交共享信息, 具体如表 1所示.
表 1(Table 1)
| 表 1 主体信息 Table 1 Subject information |
首先根据表 1中步行距离、价格、时间窗等信息筛选出需求者的可接受车位列表和可接受某车位的需求者列表.利用式(1)、式(2)分别计算主体作为供应者和作为需求者的区域热度优先级, 如表 2所示.
表 2(Table 2)
| 表 2 可接受对象和优先级 Table 2 Acceptable objects and priority |
为了确定私人闲置车位与需求者的匹配方案, 以MATLAB 2018b为编程环境, 在Inter Core i5-8250处理器、内存为8 GB的Windows10计算机上实现文中所涉及的算法.经过10次实验, 确定算法参数设计如下: N=13, P=6, 种群规模Ω=100, 最大迭代次数50, 交叉概率pc=0.9, 变异概率pm=0.1.为了避免单次实验出现的偶然误差, 运行算法10次, 剔除重复解后出现次数最多的Pareto优化结果如图 3所示, 对应的Pareto解的私人闲置车位与需求者匹配方案和目标函数值如表 3所示.
图 3(Fig. 3)
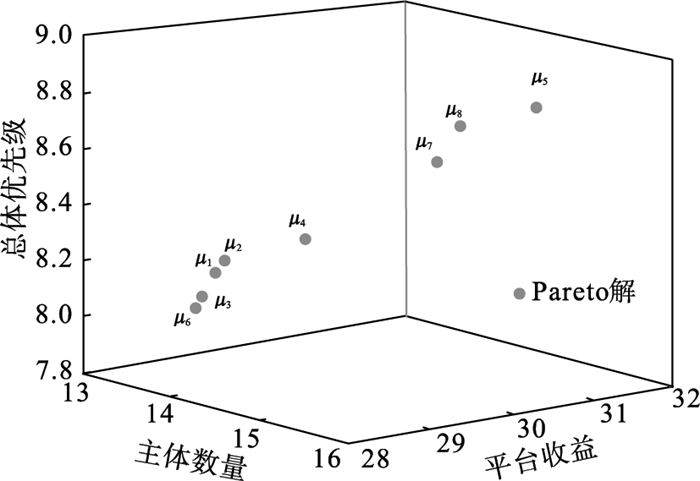 | 图 3 可行解分布散点图Fig.3 Scatter diagram of feasible solution |
表 3(Table 3)
| 表 3 私人闲置车位与需求者匹配方案及目标函数值 Table 3 Matching scheme and objective function value of private idle parking spaces and demanders |
根据图 3和表 3可以看出, 通过本文所提算法求解模型共获得了8组Pareto最优解.在图 3中, X轴、Y轴和Z轴分别对应目标函数Z1, Z2和Z3.Z1越大表示平台收益越高, Z2越大表示匹配成功的主体越多, Z3越大表示有更多的优先级、较高的主体匹配成功.由图 3可知, 如果共享平台只考虑最大化平台收益, 可能会导致匹配成功的主体数量较少或优先级较高的主体匹配失败, 这类主体要么其目的地附近的车位资源供过于求, 要么其私人闲置车位附近的车位资源供不应求, 如图 3中的μ6点所示.虽然该方案平台收益最高, 但无论是主体匹配数量还是总体优先级都比较低.如果只考虑最大化总体优先级, 可能会影响平台收益, 如图 3中的μ5点所示.虽然该方案主体的总体优先级较高, 但相较于其他方案, 平台收益却处于较低水平.因此, 共享平台在制定主体匹配方案时, 既要保障平台收益, 还需要兼顾考虑匹配成功的主体数量和主体的优先级水平.
为了验证算法的优良性, 将改进的NSGA-Ⅱ算法、粒子群优化(PSO)算法与离散和声邻域搜索(DHS)算法进行仿真对比.比较本文的快速生成初始解与随机生成初始解的生成时间.为了减少单次实验误差, 每组实验重复10次, 实验结果如表 4所示.
表 4(Table 4)
| 表 4 快速生成初始解与随机生成初始解的时间 Table 4 Time for quickly generating initial solution and randomly generating initial solutions ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 4可知, 本文的快速生成初始解在4种算例中均明显优于随机方案, 特别是在20×20和40×40算例规模下, 在随机方案中每个有效解的生成时间都超过了1 h.表 4中的算例规模越大, 本文的快速生成初始解的优势越明显.因此, 利用随机方案生成初始解集的PSO算法和DHS算法不能有效求解私人闲置车位与需求者匹配模型.
基于本文的快速生成初始解, 引入Elarbi等[14]提出的两个性能指标N(Si)和R(Si)对算法性能进行比较.Si为本文提出的改进NSGA-Ⅱ算法、PSO算法和DHS算法, ΨSi表示由算法Si得到的非支配解集, |ΨSi|表示算法Si得到的解集中的解的个数, N(Si)表示ΨSi中的解不被ΨS1∪ΨS2∪ΨS3中的解占优的解的个数, R(Si)表示算法Si得到的ΨSi中解的质量, N(Si)和R(Si)分别为
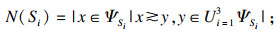 | (20) |
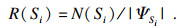 | (21) |
改进的NSGA-Ⅱ相关参数设置: Ω=100, 最大迭代次数100, 变异概率pm=0.9.DHS相关参数: 和声库的规模HMS=50, 最大迭代次数Tmax=500, 和声记忆库保留概率HMCR=0.85, 记忆库扰动概率PAR=0.3, 音调微调带宽BW=1.PSO相关参数设置: 种群规模N=50, 学习因子C1=C2=2, 惯性权重ω=0.7, 最大速度Vmax=0.8.对比结果如表 5所示.
表 5(Table 5)
| 表 5 算法性能对比 Table 5 Algorithm performance comparison | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 5可知, 本文算法与PSO算法和DHS算法相比, 在求解小规模私人闲置车位与需求者匹配问题时, 本文算法求得的非支配解与PSO算法和DHS算法求得的非支配解基本一致, 而在求解大规模算例时, 本文算法求得的非支配解的N(Si)和R(Si)明显优于PSO算法和DHS算法, 而大规模的私人闲置车位与需求者匹配问题更贴近现实.在求解小规模和大规模的私人闲置车位与需求者匹配问题时, 本文提出的算法运行时间明显优于PSO算法和DHS算法.综上所述, 本文算法与其他方法相比能够快速有效地求解私人闲置车位与需求者匹配问题.
4 结语1) 将私人闲置车位通过平台共享给车位需求者可以提高车位利用率, 是缓解停车困难的重要思路.针对主体具有双角色特点的私人闲置车位与需求者匹配问题, 构建了以平台收益最高、主体匹配数量最大和主体优先级最高为目标的多目标优化模型.
2) 与已有研究成果相比, 考虑了具有双角色特点的主体之间的匹配及主体的区域热度优先级, 在局部区域供需不平衡的情况下, 通过提高区域热度优先级较高主体的匹配成功率, 吸引这类主体留在共享平台上.
3) 为了求解多目标优化模型, 优化了NSGA-Ⅱ算法, 优化后的NSGA-Ⅱ算法在要求较高的约束条件下, 呈现出求解时间更快和全局寻优的特点.在未来研究工作中, 进一步考虑一个车位允许与多个需求者匹配或者一个需求者可以先后占用不同车位的问题.
参考文献
| [1] | Lin X W, Zhou J, Lu K. Dynamic reservation and allocation in private parking slot sharing[J]. Systems Engineering: Theory & Practice, 2018, 38(11): 2907-2917. |
| [2] | Jiang Y P, Shao X R, Song X C. Matching model between private idle parking slots and demanders for parking slot sharing[J]. Journal of Transportation Engineering.Part A: Systems, 2021, 147(6): 347-351. |
| [3] | Xu S X, Cheng M, Kong X, et al. Private parking slot sharing[J]. Transportation Research.Part B: Methodological, 2016, 93: 596-617. DOI:10.1016/j.trb.2016.08.017 |
| [4] | Zhang Y, Wen H, Zhao M, et al. How does bilateral preference affect shared parking in sharing economy?[J]. Mathematical Problems in Engineering, 2020, 2020(24): 1-13. |
| [5] | Shao C, Yang H, Zhang Y, et al. A simple reservation and allocation model of shared parking lots[J]. Transportation Research.Part C: Emerging Technologies, , 2016, 71: 303-312. DOI:10.1016/j.trc.2016.08.010 |
| [6] | Guo W, Zhang Y, Xu M, et al. Parking spaces repurchase strategy design via simulation optimization[J]. Journal of Intelligent Transportation Systems, 2016, 20(3): 255-269. DOI:10.1080/15472450.2015.1063424 |
| [7] | Huang X, Long X, Wang J, et al. Research on parking sharing strategies considering user overtime parking[J]. PLOS One, 2020, 15(6): 1-22. |
| [8] | Zou B, Kafle N, Wolfson O, et al. A mechanism design based approach to solving parking slot assignment in the information era[J]. Transportation Research.Part B: Methodological, 2015, 81: 631-653. DOI:10.1016/j.trb.2015.05.015 |
| [9] | 段满珍, 杨兆升, 张林, 等. 个性化诱导下的居住区共享停车泊位分配模型[J]. 东北大学学报(自然科学版), 2017, 38(2): 174-179. (Duan Man-zhen, Yang Zhao-sheng, Zhang Lin, et al. Parking spaces allocation model of residential areas sharing parking based on personalized guidance[J]. Journal of Northeastern University(Natural Science), 2017, 38(2): 174-179. DOI:10.3969/j.issn.1005-3026.2017.02.005) |
| [10] | 王艳, 彭忠益, 陈群. 基于动态多时段停车需求的公共停车场布局优化[J]. 系统管理学报, 2019, 28(2): 347-353. (Wang Yan, Peng Zhong-yi, Chen Qun. Optimization model for planning public car parks considering multi-periodic parking demands[J]. Journal of Systems & Management, 2019, 28(2): 347-353. DOI:10.3969/j.issn.1005-2542.2019.02.017) |
| [11] | Xiao H, Xu M. How to restrain participants opt out in shared parking market? a fair recurrent double auction approach[J]. Transportation Research.Part C: Emerging Technologies, 2018, 93: 36-61. DOI:10.1016/j.trc.2018.05.023 |
| [12] | 林小围, 周晶, 卢珂, 等. 基于合作博弈的停车位分配模型[J]. 系统管理学报, 2019, 28(1): 62-66, 85. (Lin Xiao-wei, Zhou Jing, Lu Ke, et al. Parking slot assignment model based on cooperative game theory[J]. Journal of Systems & Management, 2019, 28(1): 62-66, 85. DOI:10.3969/j.issn.1005-2542.2019.01.007) |
| [13] | Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [14] | Elarbi M, Bechikh S, Gupta A, et al. A new decomposition-based NSGA-Ⅱ for multi-objective optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(7): 1191-1210. DOI:10.1109/TSMC.2017.2654301 |
