

东北大学 计算机科学与工程学院, 辽宁 沈阳 110819
收稿日期:2021-03-29
基金项目:国家自然科学基金资助项目(62072085);辽宁省科技厅兴辽英才计划项目(XLYC1902017)。
作者简介:林宇晗(1988-),男,福建福清人,东北大学博士研究生;
邓庆绪(1970-), 男, 河南南阳人, 东北大学教授, 博士生导师。
摘要:由于多核处理器争用共享缓存导致的不确定性为实时系统带来极大的挑战.为解决这个问题,现代处理器引入了缓存划分技术, 通过隔离处理器核对缓存的访问从而提高了时间可预测性.但是, 这种隔离技术可能导致实时任务因缓存分区的数量不足而被阻塞, 而传统的实时调度算法与分析方法无法有效应对这种情况.因此, 提出了支持缓存划分的可抢占全局最早截止期优先(EDF)实时调度算法gEDFca, 并结合最新的缓存敏感调度理论针对这种调度算法进行了可调度性分析, 提出了一种基于线性规划的可调度性判定条件.还提出了一种具有线性时间复杂度的优化算法, 进一步提高了分析方法的性能.随机生成任务的仿真实验表明, 提出的可调度性判定方法具有较高的效率.同时, 优化算法提高了算法可调度性.
关键词:资源管理实时嵌入式系统最早截止期优先多核缓存划分
Scheduling and Analysis of Global EDF for Multi-core Real-time Systems with Cache Partitioning
LIN Yu-han, YAN Jian, WANG Kan-kan, DENG Qing-xu


School of Computer Science and Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: DENG Qing-xu, E-mail: dengqx@mail.neu.edu.cn.
Abstract: Multi-core real-time systems are significantly challenging to analyze due to the unpredictability from extensive contention over shared caches. Therefore, an efficient method, cache partitioning, is introduced into modern multi-core platforms to avoid cache access from co-executing cores, by which the timing predictability are improved. However, the cache space isolation technique may result in unbounded blocking because of the insufficient number of cache partitions. Unfortunately, the existing scheduling and analysis techniques cannot be applied to this situation. gEDFca, a cache-aware preemptive global earliest deadline first(EDF)scheduling algorithm was proposed for multi-core systems. And its analysis method was presented based on linear programming. Besides, a novel optimization algorithm was introduced for further improving schedulability. Evaluations using generation tasks show the proposed analysis method is highly efficient. It also shows that the optimization algorithm yields a significant improvement in schedulability.
Key words: resource managementreal-time embedded systemsearliest deadline firstmulti-corecache partition
近年来, 现代多核处理器技术日趋成熟, 其在实时嵌入式系统领域的应用也逐渐普及.为了提高系统平均性能, 大部分多核处理器都支持共享缓存(Cache)技术.然而由于多核处理器对共享缓存的争用, 在各个核上并行执行的实时任务可能会显著延迟[1].特别是在缓存资源紧张的嵌入式系统中, 缓存争用导致的延迟发生的时刻, 次数和持续时间都是不确定的, 因此严重影响了实时系统的时间可预测性.传统上, 为了保证调度的时间正确性, 系统设计人员通常假设所有实时任务都受到最大的争用延迟作为最差执行时间(WCET)的一部分从而为任务预留足够的系统资源.但是这种基于悲观假设的方法不仅造成极大的系统资源浪费, 而且抵消甚至降低了共享缓存对系统性能的提升.
解决多核处理器间缓存干扰的一种有效方法是缓存划分(cache partition)技术[2], 通过页着色(page coloring)[3]或通路划分(way partitioning)[4]的方法将缓存划分成多个缓存分区, 并将任务映射到这些分区上执行, 比如ARM的LbM技术[5-6], Intel的CAT技术[1, 7]等.这样并行执行的任务总是可使用不同的分区, 实现了对共享缓存的隔离.由于并行执行的任务无法访问别的任务的缓存分区, 因此避免了并发的缓存访问造成的缓存干扰, 从而降低了处理器核之间的互相干扰导致的额外开销并减少了任务的最坏响应时间[2].然而在实时系统中, 这种技术需要根据不同任务的实际需求分配缓存分区, 而且由于缓存空间有限, 还需要保证任意时刻没有缓存分区重叠.这种约束可能导致任务因缓存空间不足而被阻塞.因此, 传统的实时调度算法与分析方法无法有效地应对缓存共享带来的难题.
最近研究者们提出了一种缓存敏感的全局调度策略.这种策略允许在系统运行时根据任务的需求将共享缓存动态地分配给各个处理器核, 同时还能允许任务在各个核上迁移以充分利用系统资源.文献[2]提出了一种缓存敏感的不可抢占全局固定优先级调度策略(FPca)和分析方法.由于不允许任务抢占, 这种策略虽然避免了抢占带来的开销, 但是可能导致优先级反转使得高优先级任务受到过长的阻塞而错失截止期.在此基础上, 文献[1]提出了一种缓存敏感的可抢占全局固定优先级调度策略(gFPca)并分析了抢占造成的开销.然而, 以上工作都是基于固定优先级的调度(即任务的优先级是静态分配的), 并不适用于动态优先级调度, 特别是全局EDF(earliest deadline first)调度.
可抢占全局EDF调度策略允许系统在运行中根据最早截止期优先的规则动态生成任务的优先级.因此这种调度策略相比于固定优先级更适用于开放系统(open system).文献[8-11]针对可抢占全局EDF调度研究了基于时间窗口和干涉量估计相结合的分析方法.然而这些方法都没有考虑缓存划分技术带来挑战.
本文针对可抢占全局EDF采用缓存划分技术的问题进行研究.结合已有的缓存敏感全局调度及分析的思想[2, 5, 12], 本文提出了一种支持缓存划分技术的可抢占全局EDF调度算法(gEDFca)及其可调度性分析方法.不同于现有的工作,本文首先提出了一种新的缓存敏感调度算法;在此基础上分别讨论了只考虑处理器和只考虑缓存的可调度条件;并且针对现有分析的缺陷, 提出了一个优化算法;综合以上提出了一个基于线性规划的可调度条件;最后通过实验验证了调度分析的有效性.
1 系统模型本文研究一个支持共享缓存划分的多核处理器.这种处理器包含M个相互独立的同构处理器核(以下简称核)以及A个大小相等相互独立的缓存分区.所有核都可以访问这些缓存分区.
考虑一个相互独立的偶发性(sporadic)任务集τ={τ1, τ2, …, τn}.任务τi由一个四元组(ei, di, pi, ai)表示, 其中, ei表示任务的最差执行时间(worst-case execution time, WCET), di表示任务的相对截止期(relative deadline), 即任务释放后必须完成的时间长度, pi表示任务的周期, 即两个连续释放的任务实例之间的最小时间间隔, ai表示的是任务需要占用的缓存分区的个数.任务的松弛时间为Sk=dk-ek.需要注意的是, 本文仅考虑限制截止期(constrained deadline)任务, 即0<ci≤di≤pi.单个任务占用的缓存分区不大于处理器缓存分区的总个数, 即0≤ai≤A.
每个偶发任务τi都会释放一个无限的作业(Job)序列, 每个作业的到达时刻都至少间隔pi个时间单位.其中, 第j个作业用τij表示, 因此该作业序列可以用{τi1, τi2, …, τij, …}表示.作业τij的释放时刻记为rij, 完成时刻记为fij, 绝对截止期记为dij, 它的最晚开始时间记为lij, 其中dij=rij+di, lij=rij+Si.本文中, 一个任务为就绪(ready)任务当且仅当该任务释放后且没有执行完成.本文中, 一个作业τij满足截止期, 当且仅当fij≤dij.
2 调度算法上节讨论了系统的模型与定义, 本节给出一种支持缓存划分的可抢占全局EDF调度算法(gEDFca).这种算法将EDF策略应用到缓存敏感的全局调度中: 绝对截止期越早的作业被分配的优先级越高.与经典的全局EDF(gEDF)策略[11]不同, 在gEDF中系统总是可以并行执行M个就绪任务, 而在gEDFca中系统还需要考虑可用缓存分区数量的限制.
具体来说, gEDFca总是在有作业完成或释放的时刻做调度决策: 在有足够的缓存分区和核的前提下总是选择优先级最高(绝对截止期最早)的任务执行(包括抢占其他低优先级任务所占用的缓存分区和处理器).对于任意一个作业τij, 如果它满足以下条件就可以被调度执行:
1) 除了高优先级的任务占用的, 当前至少有一个处理器核可用;
2) 除了高优先级的任务占用的, 当前至少有Ai个缓存空间可用;
3) τij是当前所有满足以上条件任务中优先级最高的.
由于本文只考虑限制截止期任务, 即di≤pi, 因此每个任务在任意时刻最多只有一个作业正在执行.算法的伪代码如下所示.
算法1??gEDFca算法.
输入: Qready
输出: Qrun
1: Qrun←?; Qready←All ready tasks
2: while Qready≠? do
3: ???τi←first(Qready)
4:???if (1+|Qrun|≤M)∧(Ai+∑τk∈QrunAk≤A) then
5:??????Qrun←Qrun∪{τi}
6:???end if
7:???Qready←Qready\{τi}
8: end while
9: return schedule(Qrun)
算法1的输入为就绪任务队列Qready, 该队列包含所有已释放但还未完成的任务, 且按最早绝对截止期优先排序.算法的输出为执行队列Qrun.其中, 函数first(Qready)返回的是队列Qready中优先级最高(绝对截止期最早)的任务.函数schedule(Qrun)表示的是让系统调度执行任务队列Qrun: 如果当前正在执行的任务在队列Qrun, 那么保持执行; 如果当前正在执行的任务不在队列Qrun, 那么释放所占用的核和缓存分区(即被抢占); 最后让在队列Qrun中且当前不在执行的任务占用剩下的核和资源并开始执行.
算法的第1行首先初始化了队列Qrun和Qready.算法的第2~8行循环是算法生成执行队列Qrun的主要过程.在每次循环中, 找到当前就绪任务中具有最早截止绝对期的任务(第3行), 并检查是否满足当前核和缓存分区的约束(第4行), 如果满足就将该任务加入执行队列Qrun中(第5行), 循环最后将该任务从就绪队列Qready中移除(第7行).算法重复执行上述循环直到Qready为空.算法结束时就可以得到当前的执行队列.
需要注意, 虽然算法采用了最早截止期优先的策略, 有些缓存需求较大的高优先级任务可能会由于缓存空间的限制而被阻塞.为了减少系统资源的浪费, 算法允许其他具有较晚截止期却满足缓存空间约束的任务在这种情况下利用空闲资源优先执行.
例子1. 如表 1所示, 一个任务集τ包含有三个互相独立的限制截止期任务.假设任务集τ中所有任务在0时刻释放.图 1展示了任务集τ被gEDFca调度算法调度的一个具体例子.图 1中, 在0时刻, τ11, τ21, τ31同时释放.虽然τ21的绝对截止期(为2)早于τ31(绝对截止期为3)而获得了较高的优先级, 然而由于具有最高优先级τ11占用了2个缓存分区, 使得τ21因缓存无法满足需求而被阻塞.因此, 较晚截止期的τ31利用了剩余的缓存与处理器资源而优先执行.在第1时刻, τ11执行完成, 释放了原本占用的核和缓存.因此被阻塞的τ21得以执行.同样, 在第2时刻, τ12释放.由于τ21的绝对截止期(为3)早于τ12(绝对截止期为4), 同时τ12占用了2个缓存分区使得τ12即使在有空闲的处理器(核2)的情况下仍然被阻塞, 直到τ21在第3时刻完成并释放资源.
表 1(Table 1)
| 表 1 一个任务集例子 Table 1 A task set example |
图 1(Fig. 1)
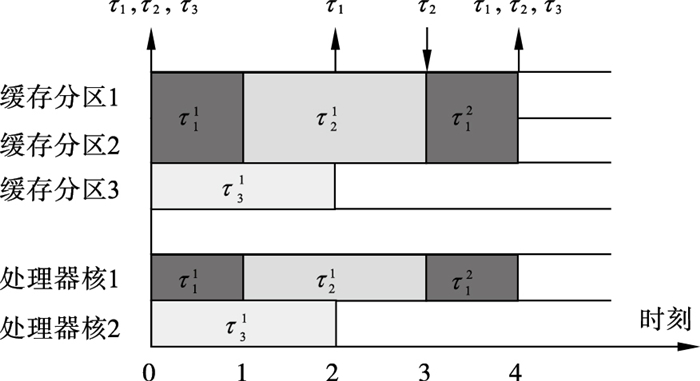 | 图 1 gEDFca调度实例示意图Fig.1 Illustration of gEDFca scheduling |
3 可调度分析结合gEDF和FPca调度分析方法的思想[2, 12]对gEDFca的可调度性问题进行分析, 并针对已有方法的缺陷, 提出一种优化算法, 最后结合优化算法提出一种基于线性规划的gEDFca的可调度条件.
3.1 问题窗口分析在介绍关于gEDFca的问题窗口分析技术之前,需要引入几个有用的概念.
定义1??在时间长度为t的时间段内, 任务τi对任务τk的干涉Ii, k(t)表示为: 任务τi在该时间段内使得τk就绪后无法执行所累积的最长执行时间.
定义2??在时间长度为t的时间段内, 任务的工作负载表示为: 该任务在该时间段内需要的计算量.
引理1[2]??不针对具体的调度算法, 一个任务τi在长度为t的时间段内的工作负载上界为Wi(t):
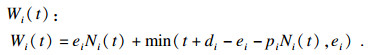 | (1) |
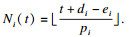
因此根据引理1, 可以很容易得到干涉Ii, k(t)一个安全的上界:
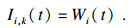 | (2) |
注意由于gEDFca允许任务间抢占, τk的问题窗口可能包含许多子区间, 其总长度为Sk.根据缓存敏感调度的问题窗口分析框架理论[1-2], 分析一个任务是否能被调度, 首先可以讨论两种极端的情况: 1)假设总是有足够的缓存空间; 2)假设总是有足够的处理器核, 然后放松上述约束综合出一个一般性的可调度条件.本文结合了类似文献[1-2]中的思想, 引入gEDFca问题窗口分析方法.
3.1.1 假设总是有足够的缓存空间在这种情况下gEDFca等同于经典的gEDF调度, 具有非主动空闲(work-conserving)的性质, 即当有等待执行的作业时, 不存在空闲的处理器核.因此可以得到引理2.
引理2??假设总是有足够的缓存空间, 一个任务τk∈τ一定可调度如果满足:
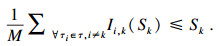 | (3) |
3.1.2 假设总是有足够的处理器核在这种情况下, 只考虑缓存分区对任务的影响.根据gEDFca算法中作业被调度执行的三个条件, 易得如下引理.
定义4??在长度为t时间段内的任务τi缓存负载为: 缓存分区数ai乘以时间段长度t.
引理3??假设总是有足够的处理器核, 一个任务τk就绪后无法被gEDFca调度执行, 仅当有至少A-ak+1个缓存分区被高优先级任务占用.
证明: 假设一个任务τk无法执行, 且存在最多A-ak个缓存分区被高优先级任务占用.那么存在至少有A-A+ak=ak个缓存分区空闲或被低优先级任务占用.由于有足够的处理器核, 那么任务τk满足被gEDFca调度执行的条件而被调度执行, 与假设矛盾.证毕.
引理4??假设总是有足够的处理器核, 一个任务τk∈τ一定可调度如果满足:
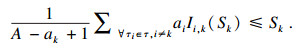 | (4) |
3.2 优化算法根据观察发现, 引理4的调度条件之所以能成立关键在于引理3的结论, 即一个任务无法执行, 仅当有至少A-ak+1个缓存分区被高优先级任务占用.虽然引理3的估计是安全的, 但是却过于悲观.实际上, 高优先级任务占用的缓存空间大于或等于1, 所以由这些使得任务τk无法执行的高优先级任务占用缓存空间的组合之和的最小值大于或等于A-ak+1, 即至少有A′个缓存被高优先级任务占用, 其中A-ak+1≤A′≤A.直观上意味着在τk恰好满足截止期时系统实际可以利用更多的缓存空间.具体可以参考以下的例子.
例子2.考虑一个处理器包含3个核和10个缓存分区, 一个任务集τ包含3个相互独立的限制截止期任务: τ={τ1, τ2, τ3}, τ1(2, 8, 8, 4), τ2(2, 8, 8, 4), τ3(3, 8, 8, 6).根据引理1, 其他任务对任务τ3的干涉I1, 3(5)=4, I2, 3(5)=4.可得∑?τi∈τ, i≠kaiIi, k(Sk)=4·4+4·4=32, 同时,(A-a3+1)=5.根据引理4,
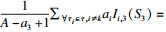
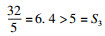
在例子2中, 处理器核的个数等于任务的个数, 因此核的个数总是足够的.缓存分区总数大于每个任务的需求, 而且任务集τ的所有任务执行时间之和都小于其中任何一个任务的截止期, 因此显然是可调度的.然而却被判定为不可调度, 说明引理4的条件确实过于悲观了.特别是如果τ3就绪后无法执行, τ1和τ2必须同时执行, 保证了8个缓存分区被占用, 而引理3的估计只有至少5个缓存空间忙碌, 低估了系统实际的缓存负载.如果例子2按真实情况计算, 即存在8个缓存分区被高优先级任务占用,
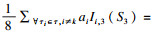
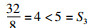
定义5??假设总是有足够的处理器核, 如果一个任务τk就绪后无法被gEDFca调度执行, 被高优先级任务占用缓存分区的最小值为A′k, 其中A-ak+1≤A′k≤A.
根据定义5, 发现A′k必须满足等于除了任务τk外的一个或者多个任务所需缓存分区ai的和.因此求解A′k, 至少相当于求解一个NP难的问题: 子集和问题.通过动态规划方法给出多项式复杂度算法.
算法2??A′k优化算法.
输入: k, τ, A
输出: A′k
1:????x∈[1, A], v[x]←False; v[0]←True; τ′←τ/{τk};
2:???for i←0 to |τ′|-1 do
3:??????for j←A to ai do
4:?????????v[j]←v[j]∨v[j-ai]
5:??????end for
6:??end for
7:??for A′k ← A-ak+1 to A do
8:????if v[A′k]=True then
9:????return A′k
10:??end if
11: end for
12: return A′k not exists
在算法2中, 引入了一个布尔数组v, v[x]表示缓存分区的数量x是否等于除τk之外其他任务所需的缓存分区ai的和.算法2的输入包含一个正整数k, 一个任务集τ和处理器缓存分区的总数A.算法第1行的作用初始化, 令布尔数组v除v[0]之外所有的值为假, 且v[0]为真, 并由于τ是限制性任务, 在任务每个周期内只存在一个作业, τk对自己的干涉为0, 因此只需算法考虑除自身之外的干涉任务集τ/{τk}.算法的第2~7行是寻找A′k的主要过程, 二重循环利用动态规划的方法求解数量j能否等于任务缓存分区的和; 另外第8~12行循环是从A-ak+1直到A升序遍历A′k, 判断当前A′k是否等于任务缓存分区的和: 如果是, 则返回当前的A′k.如果不存在A′k, 那么任务τk无法被阻塞而一定可调度.由于A′k≥A-ak+1, 且1≤ak≤A, 因此可知1≤A′k≤A.
算法2最多有二重循环, 其中第2~6行的外层循环最多遍历n次, 第3~5行的内层循环最多遍历A次, 因此算法2的时间复杂度是O(An), 其中处理器缓存分区总数A是常数, 因此算法2是线性复杂度的.
引理5??假设总是有足够的处理器核, 一个任务τk∈τ一定可调度如果满足:
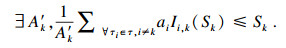 | (5) |
定义6??在某个时刻, 处理器处于τk忙碌状态(非忙碌状态)如果所有(不是所有)M个处理器核都在执行τk的高优先级任务.在某个时间段内, 如果该时间段内所有时刻处理器核都处于忙碌状态(非忙碌状态), 那么这个时间段定义为忙碌期(非忙碌期).
根据定义6, 易知对于任意时刻t要么处于忙碌状态, 要么处于非忙碌状态, 不存在其他中间状态或者t既处于忙碌状态又处于非忙碌状态.因此, 可以安全地将τk问题窗口划分为两个部分: 核忙碌区间和缓存忙碌区间.
定义7??任务τk的核忙碌区间为τk问题窗口中的忙碌期, 任务τk的缓存忙碌区间为τk问题窗口中的非忙碌期.
定义8任务τi在任务τk的核忙碌区间的工作负载为αi, k, 在任务τk的缓存忙碌区间的工作负载为βi, k.
根据定义8, 任务集τ在τk的核忙碌区间工作负载之和为∑τi∈ταi, k.根据定义6, 在τk的核忙碌区间, 所有的处理器都在忙碌, 因此τk问题窗口中的忙碌期长度的上界Xk为
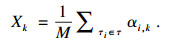 | (6) |
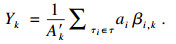 | (7) |
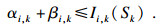 | (8) |
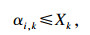 | (9) |
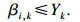 | (10) |
引理6??τk的问题窗口长度上界为Bk, 其中Bk是如下线性规划的最优解:
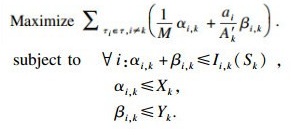 | (11) |
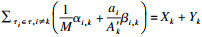
定理1??任务集τ可被gEDFca调度, 如果?τk∈τ都满足:
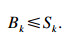 | (12) |
4 实验为验证本文提出的可调度分析方法的有效性与效率, 使用随机生成数据集进行大量的仿真实验对分析方法的可调度性和可延展性进行评估.首先进行可调度性实验来评估可调度条件的性能,然后进行可延展性实验来评估方法的效率.
4.1 实验设置本文采用随机生成的任务集, 参数设置如下: 首先设置任务集的任务周期均匀分布在[10, 20]内, 任务资源利用率(任务的最差执行时间与周期之比)根据任务类型分为三类: 轻型任务, 均匀分布在[0.05, 0.1]内;中型任务, 均匀分布在[0.1, 0.2]内;重型任务,均匀分布在[0.2, 0.4]内.任务的最差执行时间由利用率与任务周期的乘积求得.任务所需的缓存均匀分布在[8, 10]内.处理器核的个数M设为4, 处理器缓存分区的个数A设为20.任务集通过迭代的方式生成, 将每次迭代生成1个满足设置的随机任务加入到任务集中直到任务集的利用率之和大于目标值为止.最后降低最后一个任务的利用率使得任务集利用率之和等于目标值.
实验采用开源的整数规划求解工具Python-MIP工具集进行求解.实验运行在Intel Xeon 4110处理器(2.6 GHz), 32 GB主存的Linux PC上.
4.2 可调度性实验图 2中横坐标表示任务集利用率之和, 纵坐标表示任务集接受率(可调度的任务集数与所有任务集的个数之比).为曲线上每个点都生成了1 000个随机任务集.其中, opt中A′k采用的是由算法2生成的值, 而nopt中A′k采用的是A-ak+1.实验结果表明,算法2对不同任务类型可调度性的结果都有较大幅度的提高.
图 2(Fig. 2)
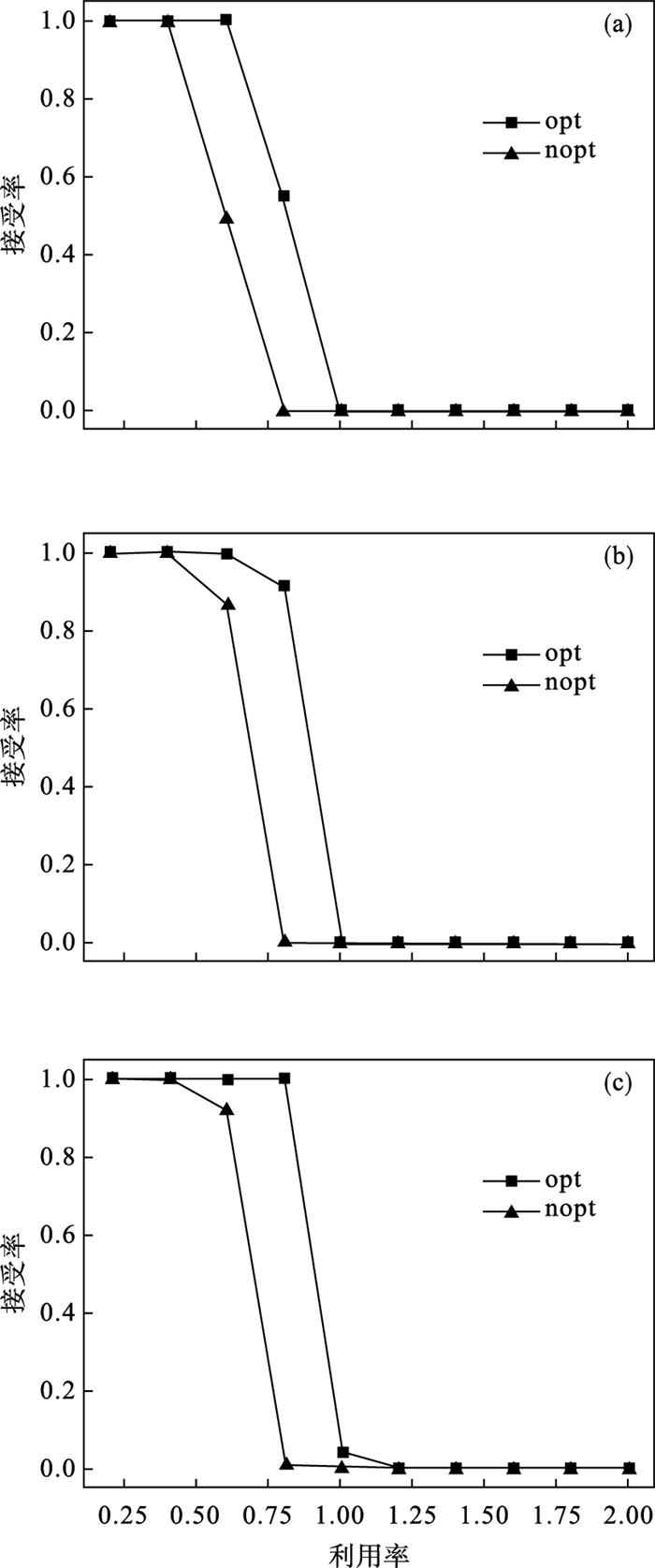 | 图 2 调度接受率结果Fig.2 Results of acceptance ratio (a)—轻型任务;(b)—中型任务;(c)—重型任务. |
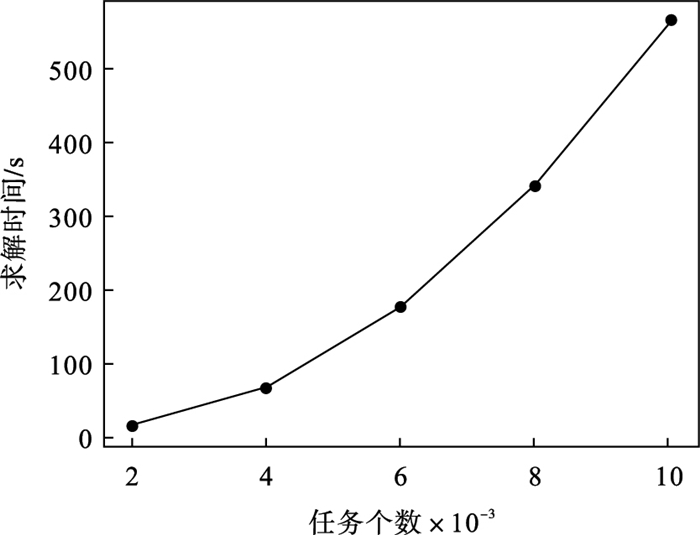
4.3 可延展性实验图 3中横坐标表示任务集中任务个数, 纵坐标表示引理6中线性规划的求解时间.2 000个任务的求解时间为15 s, 10 000个任务的求解时间为563 s.实验结果表明,在实验平台上, 一个具有数千个任务的任务集也能在数分钟内求得解, 具有较高的效率.
图 3(Fig. 3)
 | 图 3 求解时间结果Fig.3 Results of execution time |
5 结语共享缓存划分技术提供了一种减少任务执行时间不确定性的手段.本文提出一种支持缓存划分的全局EDF调度算法, 并针对该算法提出了一种可调度性分析技术.通过线性规划的方法判断任务集的可调度性来保证系统的可预测性.本文还提出了一种分析优化算法, 进一步提高了可调度性.随机实验显示本文的分析方法具有较高的效率和性能.
参考文献
| [1] | Xu M, Phan L, Choi H, et al. Analysis and implementation of global preemptive fixed-priority scheduling with dynamic cache allocation[C]// IEEE Real-Time and Embedded Technology and Applications Symposium. Vienna, 2016: 1-12. |
| [2] | Guan N, Stigge M, Yi W, et al. Cache-aware scheduling and analysis for multicores[C]// Proceedings of the 7th ACM International Conference on Embedded Software. New York: ACM Press, 2009: 245-254. |
| [3] | Kessler R, Hill M. Page placement algorithms for large real-indexed caches[J]. ACM Transactions on Computer Systems, 1992, 10(4): 338-359. |
| [4] | Mancuso R, Dudko R, Betti E, et al. Real-time cache management framework for multi-core architectures[C]// IEEE Real-Time and Embedded Technology and Applications Symposium. Philadelphia, 2013: 45-54. |
| [5] | Xu M, Phan L, Choi H, et al. Holistic resource allocation for multicore real-time systems[C]// IEEE Real-Time and Embedded Technology and Applications Symposium. Montreal, 2019: 345-356. |
| [6] | Ward B C, Herman J L, Kenna C J, et al. Making shared caches more predictable on multicore platforms[C]// Euromicro Conference on Real-Time Systems. Paris, 2013: 157-167. |
| [7] | Xu M, Phan L, Choi H, et al. vCAT: Dynamic cache management using CAT virtualization[C]//IEEE Real-Time and Embedded Technology and Applications Symposium. Pittsburgh, 2017: 211-222. |
| [8] | Bertogna M, Cirinei M. Response-time analysis for globally scheduled symmetric multiprocessor platforms[C]// IEEE Real-Time Systems Symposium. Tucson, 2007: 149-160. |
| [9] | Baruah S, Fisher N. Global deadline-monotonic scheduling of arbitrary-deadline sporadic task systems[C]// Proceedings of the 11th International Conference on Principles of Distributed Systems. Berlin: Springer, 2007: 204-216. |
| [10] | Sun Y, Lipari G. Response time analysis with limited carry-in for global earliest deadline first scheduling[C]// IEEE Real-Time Systems Symposium. San Antonio, 2015: 130-140. |
| [11] | 韩美灵, 邓庆绪, 张天宇, 等. 多核处理器限制性可抢占G-EDF调度策略研究[J]. 计算机学报, 2019, 42(11): 2355-2367. (Han Mei-ling, Deng Qing-xu, Zhang Tian-yu, et al. Limited preemption for G-EDF scheduling on multiprocessors[J]. Chinese Journal of Computers, 2019, 42(11): 2355-2367.) |
| [12] | Baker T P. Multiprocessor EDF and deadline monotonic schedulability analysis[C]// IEEE Real-Time Systems Symposium. Cancun, 2003: 120-129. |
