李占山, 姚鑫, 刘兆赓, 张家晨
吉林大学 计算机科学与技术学院, 吉林 长春 130012
收稿日期：2021-04-09
基金项目：国家自然科学基金资助项目(61802056)；吉林省自然科学基金资助项目(20180101043JC)；吉林省发展和改革委员会产业技术研究与开发项目(2019C053-9)。
作者简介：李占山(1966-)，男，吉林公主岭人，吉林大学教授，博士生导师;
张家晨(1969－)，男，吉林德惠人，吉林大学教授。

摘要：为解决过滤式和基于演化学习的包裹式两类特征选择算法的缺陷, 提出一种新型包裹式特征选择算法LGBFS(LightGBM feature selection).首先引入LightGBM对原始特征构建迭代提升树模型并对特征重要度进行度量; 随后结合提出的LR序列前向搜索策略LRSFFS对特征进行选择; 最后将所提出算法与9种对比算法在21个标准数据集上进行对比, 结果显示LGBFS在21个标准数据集中的16个取得最优分类精度、18个取得最优维度缩减率和最优CPU运行时间.还进行了时间复杂度分析与显著性检验, 检验表明LGBFS相较6种对比算法具有显著性差异, 也说明LGBFS能够同时兼顾特征子集的计算效率和分类精度.
关键词：特征选择LightGBM迭代提升树包裹式序列搜索
Feature Selection Algorithm Based on LightGBM
LI Zhan-shan, YAO Xin, LIU Zhao-geng, ZHANG Jia-chen
College of Computer Science and Technology, Jilin University, Changchun 130012, China
Corresponding author: ZHANG Jia-chen, E-mail: zhangjc@jlu.edu.cn.

Abstract: In order to solve the shortcomings of the following two types of feature selection algorithms, filtering and wrapping based on evolutionary learning, a new wrapping feature selection algorithm LGBFS(LightGBM feature selection) was proposed. First, LightGBM was introduced to construct an gradient boosting tree model for the original features and measure the importance of features; then the proposed LR sequential forward search strategy LRSFFS was combined to select features; finally, the proposed algorithm was compared with nine algorithms in 21 standard datasets. The results show that 16 of the 21 standard data sets of LGBFS have achieved the best classification accuracy, and 18 standard data sets have achieved the best dimensionality reduction rate and the best CPU running time. In addition, time complexity analysis and significance test were carried out. The test shows that LGBFS is significantly different from the six comparison algorithms, and it also shows that LGBFS can balance the calculation efficiency and classification accuracy of feature subsets.
Key words: feature selectionLightGBMboosting treewrapped methodsequential search
特征选择是数据挖掘、机器学习等领域中的重要方向, 其主要通过减少冗余与不相关特征、使用合适的搜索策略来寻找最优特征子集, 力求在减小特征维度的情况下减少运行时间、提高模型精度.特征选择的目标是在满足给定某种泛化误差的条件下挑选最小特征子集; 或选择指定个数的特征子集, 并使其在原始样本上产生最小的泛化误差^[1].依据方法自身与构建模型的关系, 特征选择主要分为过滤式方法和包裹式方法^[2].
过滤式方法对数据特征按照一定标准进行排序并选择表现较好的特征, 由于这些标准独立于学习过程且单独评价每个特征的重要度, 不考虑对结果的影响, 因而过滤式方法通常具有较高的计算效率，却很难得到具有较高分类准确率的特征子集^[3-4].
为克服过滤式的缺点, 包裹式方法一般会引入学习器来评估所选的特征子集, 并根据评估结果来选择特征子集, 进而找到最优特征子集.该方法引入与学习器的交互后虽然增加了计算量, 但通过不断交互通常能得到满足给定泛化误差的优秀特征子集^[3-4].
过滤式方法运行效率较高, 但由于其选择特征的过程并没有考虑到后续学习, 因而得到的特征子集的分类精度一般低于包裹式, 经常不能满足后续任务的需求; 包裹式方法虽然能够得到具有较高分类精度的特征子集, 但引入的交互过程降低了计算效率, 增加了算法复杂度, 故包裹式对要求短时间内求解的任务适应性较差.
在现有研究工作中, 过滤式研究着力于采用某种度量标准在较低时间复杂度内得到特征子集, 包裹式的研究力求通过不断的交互得到更高分类精度的特征子集.以上两类研究缺乏对特征子集计算效率和分类精度的协调与平衡.
为克服这两类方法的缺陷, 本文采用LightGBM中两种特征重要度指标作为数据特征间的度量依据, 并在此基础上提出一种包裹式的特征选择算法LGBFS(LightGBM feature selection), 并将提出算法与对比算法在通用的21个UCI标准数据集上对分类精度、维度缩减率和CPU时间三种指标进行了对比, 随后又进行了显著性分析与时间复杂度分析.
1 LightGBM系统LightGBM^[5]是由微软提供的一个迭代提升树系统, 它是梯度提升决策树(GBDT, gradient boosting decision tree)经过改进后的一种变体.经典GBDT一般只采用损失函数的一阶负梯度, 而它却同时使用损失函数的一二阶负梯度计算当前树的残差, 并以此结果去拟合下一轮的新树.此外, 它还采用了基于Histogram的决策树算法使得GBDT算法的执行可以节省一半时间, 而且其采用最大深度限制的叶子生长策略使得算法的整体执行更加具有效率.
1.1 利用直方图算法构建决策树模型相比原始数据的浮点形式, 直方图数据占用内存更少、数据分隔复杂度更低, 因而LightGBM处理数据采用直方图算法(Histogram算法).
直方图算法的思想为: 将数据中每列特征值都转化为一个直方图, 转化方法是对每个直方图都按照数据所在整数区间生成k个bin, 随后将连续的浮点特征值按照所在的整数区间放入对应的bin中, 以此对每个特征的所有特征值进行转换, 即得到原始数据的直方图表示形式.
经过直方图算法计算后, 原始的每个特征都转换为直方图, 而原始的特征值也以整数的形式存储在每个直方图的所有bin中, 因而LightGBM只需遍历每个直方图, 并将每一直方图作为分割点计算分割收益, 即可寻得最优分割直方图作为分割节点.在计算中, LightGBM使用了整数(每个离散值在直方图中的累计统计量, 也就是某一直方图中某个bin的高度)代替原始数据的浮点值, 这样有两个好处: 一是起到了正则化的效果来防止树模型的过拟合, 二是可以通过父节点与子节点中的一个做差来得到另一个子节点, 从而节省了一半的计算量.
对于分割点的增益Gain, 可定义如下:

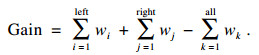(1)

式(1)说明对每一分割点而言, 其增益表示为分割后的左、右叶节点的总权重减去分割前原节点的权重.
1.2 构建迭代树LightGBM算法中的梯度提升决策树由给定的训练数据集多轮迭代得到, 并在每一次迭代的时候都会使用梯度信息重新拟合一棵新树来加入前续迭代树, 而这在函数空间上可以视作一种不断更迭的线性组合过程, 形式化描述如下:

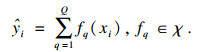(2)

式中: χ是迭代树的函数空间; f_q(x_i)表示第i个样例在第q棵树中的预测值.
树的每一层分裂节点采用的都是最佳分割点, 构建树模型时实际采用贪心方法.LightGBM通过综合所有叶子节点的权重作为构建树的参照, 继而确定分割点并计算一阶梯度和二阶梯度.
1.3 特征重要度指标根据Guyon等的研究^[6], 迭代树的启发信息可以作为特征的重要衡量标准, 因此, 基于树结构的度量将直接影响候选特征子集的质量, 也最终决定了原始机器学习算法的实验效果.
对于任意给定的树形结构, LightGBM定义了每个特征在迭代树中被分割的总次数T_Split及特征在所有决策树中被用来分割后带来的增益总和T_Gain作为衡量特征重要性的度量标准, 它们的具体定义如下:

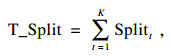(3)

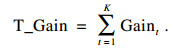(4)

其中, K为K轮迭代产生的K棵决策树.
2 LGBFS算法本文主要采用LightGBM构建迭代树的过程来计算样本的特征重要性度量，提出了一种包裹式的特征选择算法LGBFS.
LGBFS采用一种适应LightGBM做启发式的序列浮动前向搜索方法^[7]进行特征选择, 并把分类准确率最高的特征集合作为特征选择的结果.特征选择问题从本质而言, 可分为评估原始特征与搜索特征子集的两阶段算法.因此本文将LGBFS算法拆分为评估原始特征阶段与搜索特征子集阶段.
2.1 LGBFS评估原始特征在评价阶段开始前, 要将其构造为迭代树模型从而利用树形结构对特征进行评价, 迭代树是由K轮迭代生成的K棵决策树分步迭加而成, 每棵决策树生成方式相同, 故本处仅给出构建单棵决策树的伪代码.
首先, 采用直方图算法将原始转化为直方图.在转换过程中, 一个叶子节点的Histogram可以直接由父节点和兄弟节点的Histogram做差得到, 称为差加速, 体现在算法2中.随后, 确定分割点时利用一阶梯度g_i和二阶梯度h_i进行计算, 每次都选取具有最大Gain的特征进行分割并在每层分裂时都贪心选取最佳分割点.
而对于给定的训练集X, 上述步骤具体细节如算法1和算法2伪代码所示, 其中算法2是算法1的支撑代码.
观察上述模型, 可以得到结论: 一个特征可能被多次分割; 特征被分割次数越多, 整棵树的增益也越多.这两个结论说明: 某些特征应在子集选择阶段被优先考虑.
利用DecisionTree算法构建决策树模型后, 可得到上文所描述的某一特征的重要性度量Split和Gain.而利用LightGBM构建整体的迭代提升树后, 可用式(3), (4)算出所有特征的T_Split和T_Gain, 就得到了所需的经过树形结构评价后的原始特征集及重要度集合.
算法1??DecisionTree
Input: X: training data, C: number of leaf, l: loss function
Output: Split, Gain
T₁(X)← X //Put all data on root
for m in(2, C)
(Gain, p_m, f_m, v_m)←FindBestSplit(X, T_m-1, l)
T_m←T_m-1(X).split(p_m, f_m, v_m) /* Perform split */
Split←Split+1
end for
算法2??FindBestSplit
Input: X: training data, T_m-1(X): current model H: histogram data, g: first order gradient, h: second order gradient
Output: p_m: leaf on split point, f_m: feature of certain dimension, v_m: value of maximum gain of f_m，Gain
for all Leaf p in T_m-1(X) do
???for all f in X.Features do
???H ← new Histogram()
???for i in usedRows do /*Go through all the data row*/
????H[f.bins[i]].g← H[f.bins[i]].g+g_i
????H[f.bins[i]].h← H[f.bins[i]].h+h_i
???end for
???for i in len(H) do /* Go through all the bins*/
????S_L←S_L+H[i].g
????h_L←h_L+H[i].h
????S_R←S_P- S_L??/*Difference
acceleration*/
????h_R←h_P-h_L
????Gain←S_L²/h_L+S_R²/h_R-S_P²/h_P
????if Gain＞(p_m, f_m, v_m) then
?????(p_m, f_m, v_m)←(p, f, H[i].value)
????end if
???end for
??end for
end for
2.2 LGBFS搜索特征子集在子集搜索阶段, 首先按照得到的重要度特征索引重新对原始数据集进行排序, 随后采用一种基于LightGBM重要性度量的序列浮动前向搜索方法LRSFFS对特征子集进行浮动搜索, 即每次加入L个特征使得特征子集性能更加优异; 此外, 在每次循环时也尝试去除R个特征使得特征子集的性能更加稳定优异.
LRSFFS搜索策略的优势在于能够交叉浮动的选择特征, 从而较好避免特征子集陷入局部最优, 而浮动思想也能够尽可能地兼顾特征之间的相关性, 具体伪代码给出如下.
算法3??LRSFFS
Input: S₁: feature subset from sorting according to T_Split in descending order, S₂ feature subset from sorting according to T_Gain in ascending order
Output: Y: objective feature set
Y←?
while S₁≠? do
??i, j← 0
??while S₁≠? do
???x⁺← S₁.top
????if J(Y+x⁺)＞J(Y) then
??????Y←Y+x⁺
??????i← i+1
????end if
????if i==L then
??????break
????end if
??end while
??while j≠R do
????x^-←S₂.top
????if J(Y-x^-)＞J(Y) then
??????Y←Y-x^-
??????j←j+1
????end if
??end while
end while
实验结果表明, LRSFFS策略能在一定程度上减少这些特征子集搜索问题的局限性, 故取得了优于其他方法的更好结果, 其时间复杂度将在第4章讨论.
3 实验及分析讨论3.1 数据集与对比算法本文从UCI^[8]数据库中选择了21个数据集对算法进行测试.表 1中列出了这些数据集的名称、特征数和实例数.
表 1(Table 1)

表 1 数据集详细信息Table 1 Specific information of the selected datasets 序号 数据集 特征数 样本数 1 Breastcancer 9 699 2 BreastEW 30 569 3 Clean1 166 476 4 Clean2 166 6598 5 CongressEW 16 435 6 Exactly 13 1000 7 Exactly2 13 1000 8 HeartEW 13 270 9 IonosphereEW 34 351 10 KrvskpEW 36 3196 11 Lymphography 18 148 12 M-of-n 13 1000 13 PenglungEW 325 73 14 Semion 265 1593 15 SonarEW 60 208 16 SpectEW 22 267 17 Tic-tac-toe 9 958 18 Vote 16 300 19 WaveformEW 40 5000 20 WineEW 13 178 21 Zoo 16 101

表 1 数据集详细信息 Table 1 Specific information of the selected datasets

为说明LGBFS算法性能的优越性, 选择9种近年来具有代表性的算法(表 2)进行对比.
表 2(Table 2)

表 2 对比算法的详细信息Table 2 Details of compared algorithms 算法 描述/发表年份 BMBO 帝王蝶特征选择[9]/2020 HGSA 万有引力特征选择[10]/2019 BOA 蝴蝶特征选择[11]/2019 RcBBFA 萤火虫特征选择[12]/2017 BGWO 灰狼特征选择[13]/2016 BALO 蚁狮特征选择[14]/2015 BPSO 粒子群特征选择[15]/2014 JMI 联合互信息[16]/2014 MIM 最大互信息[16]/2014

表 2 对比算法的详细信息 Table 2 Details of compared algorithms

3.2 实验参数设置及实验环境给出本文所提算法LGBFS与9种对比算法的参数设置(表 3).全部算法均采用30次独立重复实验, 数据集划分方法统一为80 % 作为训练集, 20 % 作为测试集.用于验证特征子集分类性能的分类器为KNN(K近邻, K=5)分类器, 因为KNN本身实现简便、稳定、参数少, 在特征选择领域得到了广泛认可, 许多工作^{[10-11, 13-14]}仅把KNN作为唯一的基分类器.
表 3(Table 3)

表 3 实验参数设置Table 3 Parameter setting for experiments 参数 算法 值 Max_step BMBO 1 Partition BMBO 5/12 Period BMBO 1.2 Cross_rate, HGSA 0.5 Mutation_rate HGSA 0.5 Gmin, Gmax HGSA 0, 10 α BOA 0.1 Cmin, Cmax BOA 0.01, 0.25 σ Rc-BBFA 0.1-0.09×t/T Amin, Amax BGWO 0, 2 Rmin, Rmax BALO 0, 0.9 C1, C2 BPSO 2, 2 Wmin, Wmax BPSO 0.6, 0.9 L, R LGBFS 1, 1/2, 2/4, 4

表 3 实验参数设置 Table 3 Parameter setting for experiments

LGBFS采用的参数L, R分为3组, 其具体含义为: 当数据集的特征维度小于50时采用第一组参数, 特征维度在50至200时采用第二组参数, 特征维度大于200时采用第三组参数.此外, 所有基于演化学习的特征选择算法粒子数设为10, 迭代次数设置为100.
算法的实现环境为Python语言在PyCharm下的3.7.6版本, 使用公开包LightGBM和scikit-learn.计算机配置为: CPU I7-7300K, 内存8 GB, 硬盘1 TB.
3.3 实验结果分析与检验为表述实验结果, 使用分类准确率(classification accuracy, CA)、维度缩减率(dimensionality reduction, DR)和CPU时间(CPU time)三种指标用于检验特征选择算法的性能, CA与DR的具体定义如下.

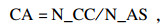(5)

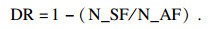(6)

式中：N_CC(number of correct classification)为正确的分类数; N_AS(number of all samples)为数据集的实例数; N_SF(number of selected feature)为选择的特征数; N_AF(number of all features)为特征总数.
表 4, 表 5给出21个数据集上LGBFS与9种算法在分类准确率和维度缩减率上的对比结果.最后一行的W, S, L代表所提算法与对比算法胜、平、负的统计量.表 6给出CPU运行时间的对比结果.表 4~表 6中下划线代表最优结果.
表 4(Table 4)

表 4 LGBFS与9种算法在平均分类准确率上的对比Table 4 Comparison between the LGBFS and nine approaches based on average CA? % 数据集 BMBO HGSA BOA RcBBFA BGWO BALO BPSO JMI MIM LGBFS Breastcancer 97.40 98.54 97.86 97.86 97.37 97.32 97.71 97.62 97.15 97.59 BreastEW 94.77 95.35 95.35 95.30 94.74 94.36 95.15 93.39 93.12 95.41 Clean1 90.31 90.80 91.08 94.55 97.19 92.22 96.18 86.35 85.48 97.92 Clean2 96.84 97.02 96.68 97.14 97.61 96.31 97.54 96.28 95.73 97.80 CongressEW 96.55 97.20 96.59 97.20 96.32 96.48 97.05 96.70 96.03 98.26 Exactly 77.58 88.30 92.65 99.23 78.73 76.65 84.05 83.00 70.68 81.50 Exactly2 75.60 74.32 75.78 75.75 75.60 75.58 75.60 75.61 75.20 75.61 HeartEW 82.96 84.51 85.99 87.47 84.26 83.09 85.93 69.20 67.74 87.96 IonosphereEW 92.25 92.21 92.58 95.12 96.10 93.38 95.31 86.81 83.84 95.83 KrvskpEW 94.03 96.25 95.92 97.43 95.81 95.73 97.14 95.62 94.79 97.40 Lymphography 88.44 89.33 90.56 92.44 89.44 87.78 91.00 81.11 77.78 92.63 M-of-n 91.13 96.92 98.40 99.88 98.30 95.73 99.18 97.53 96.22 98.66 PenglungEW 89.56 91.11 90.89 92.89 97.11 92.00 92.89 85.78 84.09 96.59 Semion 91.76 91.58 91.47 92.96 93.70 92.63 94.96 89.64 89.07 95.01 SonarEW 89.84 90.24 91.11 94.84 95.24 91.19 95.71 80.40 80.05 95.74 SpectEW 87.84 88.89 89.44 90.99 89.07 86.11 90.31 83.77 82.02 91.02 Tic-tac-toe 79.17 82.05 81.06 80.59 79.11 79.15 80.35 79.27 80.09 79.27 Vote 96.78 97.11 97.00 97.83 97.00 96.44 97.28 96.11 95.30 98.28 WaveformEW 81.88 82.21 82.05 84.07 83.14 82.37 84.15 83.08 83.28 85.53 WineEW 96.48 97.87 98.52 98.79 97.04 97.04 98.06 91.20 92.59 98.79 Zoo 96.03 96.98 97.94 98.89 95.71 96.19 97.46 88.57 84.84 97.38 W|S|L 21|0|0 18|0|3 17|0|4 16|1|4 19|0|2 21|0|0 18|0|3 18|1|2 21|0|0 ——

表 4 LGBFS与9种算法在平均分类准确率上的对比 Table 4 Comparison between the LGBFS and nine approaches based on average CA?

表 5(Table 5)

表 5 LGBFS与9种算法在平均维度缩减率上的对比Table 5 Comparison between the LGBFS and nine approaches based on average DR? % 数据集 BMBO HGSA BOA RcBBFA BGWO BALO BPSO JMI MIM LGBFS Breastcancer 67.04 51.48 71.85 72.59 71.48 69.26 72.22 31.48 24.81 59.78 BreastEW 71.89 59.44 68.56 84.22 90.78 86.00 84.00 47.33 49.78 86.93 Clean1 55.96 51.85 53.88 55.72 83.31 58.61 59.48 38.96 35.66 94.85 Clean2 58.84 51.47 59.18 64.60 86.77 85.58 65.22 37.45 45.68 95.24 CongressEW 73.96 63.33 77.29 83.75 88.96 82.92 81.67 78.96 83.13 93.00 Exactly 52.05 39.74 43.08 52.82 78.72 71e-5 67.18 41.03 52.56 86.15 Exactly2 76.67 49.23 88.46 91.03 92.31 90.26 92.31 76.92 75.64 89.92 HeartEW 63.08 61.79 62.05 67.69 72.56 64.87 65.64 62.31 45.90 73.69 IonosphereEW 61.67 62.75 63.33 74.71 84.51 75.10 74.90 71.47 54.22 87.32 KrvskpEW 54.26 45.93 53.52 64.35 80.74 52.87 60.74 38.98 36.67 81.92 Lymphography 57.22 57.59 57.59 64.81 69.26 57.96 63.33 71.48 73.89 81.39 M-of-n 45.13 35.38 41.03 53.85 55.13 36.41 51.28 43.33 41.54 70.69 PenglungEW 58.26 53.36 56.33 62.72 95.58 81.03 66.36 47.53 48.34 97.89 Semion 52.97 49.28 52.59 51.58 72.55 53.46 53.07 23.99 22.24 91.13 SonarEW 57.89 54.61 57.11 65.33 85.56 66.78 69.22 48.33 67.89 90.93 SpectEW 62.42 57.27 57.73 67.73 75.61 76.97 66.21 44.70 42.42 90.82 Tic-tac-toe 43.33 19.63 45.56 48.89 47.41 47.78 46.67 21.11 19.63 57.11 Vote 68.96 61.46 71.88 80.42 84.38 76.88 76.88 74.17 82.50 89.50 WaveformEW 50.67 44.08 51.67 56.42 71.92 51.50 54.08 46.08 45.33 75.60 WineEW 66.92 58.21 63.33 72.31 75.90 61.54 73.33 65.13 76.92 78.31 Zoo 62.29 61.67 63.96 70.63 75.63 64.79 72.92 63.75 63.33 80.75 W|S|L 20|0|1 21|0|0 20|0|1 19|0|2 18|0|3 19|0|2 19|0|2 21|0|0 21|0|0 ——

表 5 LGBFS与9种算法在平均维度缩减率上的对比 Table 5 Comparison between the LGBFS and nine approaches based on average DR?

表 6(Table 6)

表 6 LGBFS与9种算法在平均CPU时间上的对比Table 6 Comparison between the LGBFS and nine approaches based on average CPU time 数据集 BMBO HGSA BOA RcBBFA BGWO BALO BPSO JMI MIM LGBFS Breastcancer 14.57 10.47 9.67 31.23 10.73 26.57 41.17 1e-5 1e-5 0.35 BreastEW 14.20 11.40 9.10 30.70 10.03 66.40 39.00 1e-5 1.00 1e-5 Clean1 23.30 27.67 14.87 48.40 17.43 316.10 63.47 24.33 21.90 1.00 Clean2 649.73 707.30 468.93 1352.10 160.57 491.27 1494.90 331.90 288.00 13.02 CongressEW 12.23 8.30 7.50 24.93 8.67 37.50 33.80 1e-5 1e-5 1e-5 Exactly 20.63 14.20 11.53 38.30 13.43 34.87 54.70 1e-5 1e-5 1e-5 Exactly2 19.20 14.33 11.83 37.67 11.80 33.37 49.80 1e-5 1e-5 1e-5 HeartEW 9.93 5.37 5.83 19.30 6.87 29.30 27.53 1e-5 1e-5 1e-5 IonosphereEW 11.90 8.93 6.87 23.93 8.30 68.07 31.80 0.73 1e-5 1e-5 KrvskpEW 81.27 73.80 49.80 162.67 43.30 119.70 211.17 5.27 4.60 1.46 Lymphography 7.53 4.20 4.70 15.83 5.50 36.10 21.07 1e-5 1e-5 0.02 M-of-n 17.73 13.77 10.97 36.30 12.67 34.70 48.17 1e-5 1e-5 1e-5 PenglungEW 14.70 28.00 9.93 32.73 15.60 570.03 36.67 14.87 12.70 1.02 Semion 145.90 156.10 98.20 314.57 73.63 551.13 406.70 148.57 134.03 18.16 SonarEW 9.83 10.43 6.97 22.93 7.60 122.23 25.67 1.00 2.00 1e-5 SpectEW 9.03 7.00 6.67 22.17 6.63 48.73 25.17 1e-5 1e-5 1e-5 Tic-tac-toe 16.50 14.40 11.73 39.40 12.03 30.10 46.20 1e-5 1e-5 1e-5 Vote 8.97 6.83 6.67 22.07 6.37 37.37 25.17 1e-5 1e-5 1e-5 WaveformEW 214.03 236.77 158.63 497.30 94.33 245.00 559.00 17.77 17.47 13.61 WineEW 9.10 5.10 5.67 19.50 6.43 30.63 24.97 1e-5 1e-5 1e-5 Zoo 8.13 4.60 4.83 17.13 5.67 35.57 22.63 1e-5 1e-5 1.00

表 6 LGBFS与9种算法在平均CPU时间上的对比 Table 6 Comparison between the LGBFS and nine approaches based on average CPU time

首先, 观察表 4的分类准确率结果, LGBFS在16个数据集的分类准确率均达到最高, 而在未达到最高的5个数据集上相较最优结果也未存在明显差距.因此, 可以认定LGBFS在多数数据集上效果达到最优或次优.再观察未能到达最优的5个数据集, 可以发现这5个数据集均为20维以下的低维数据集, 而LGBFS在构建树模型时需要构建较深的树形结构才能平衡掉贪心选取最优节点所带来的局部最优性, 因而LGBFS算法更适合处理中高维度, 实验结果也对此进行了验证.
再对表 5的维度缩减率进行观察, LGBFS在被选中的21个数据集中的18个数据集上达到最优, 2个数据集上达到近似最优.简而言之, 可以认为LGBFS在近似全部数据集上有着更高效的维度缩减率.进一步观察, 发现在维度超过100的高维数据集上, LGBFS相对其他算法总能在满足较高的维度缩减率的前提下获得同样较高的分类准确率, 这也再次说明利用LightGBM评估特征的合理性和有效性, 充分印证了LGBFS能够通过特征之间的内在关联找到更相关的特征并进行维度缩减, 而并非仅以分类准确率的提高作为算法运行的第一要义.
随后对表 6的CPU运行时间进行观察, 可以发现LGBFS虽然是包裹式的特征选择算法, 却并未像基于演化学习的特征选择算法需要复杂的计算量和较长的计算时间, 而这是由LGBFS设计理念的完整性和设计结构的精简性所决定的.LGBFS力求在演化式包裹特征选择算法和过滤式算法中做出平衡, 既希望能够得到具有优秀分类性能的特征子集, 又希望能够用较少的计算时间和较小的计算量完成特征选择这一阶段的任务, 从表 6中可以看出, LGBFS在全部数据集上的运行时间都远优于传统的演化特征选择算法.粗略计算, LGBFS比每种演化包裹式特征选择算法快100倍以上, 即使与公认计算效率最优的过滤式算法相比, LGBFS在大部分数据集的CPU运行时间指标依然处于平手, 甚至在个别数据集上超过了过滤式的JMI和MIM算法的运行时间.LGBFS出色地在特征选择的计算量和特征子集的最优性间做出了平衡.
最后, 为定量讨论LGBFS算法相较对比算法的有效性与显著性, 本文采用了非参数的威尔森秩和检验^[17](Wilcoxon rank-sum test)来确认9种对比算法与LGBFS是否有统计学上的差异(显著性水平设置为0.05), 威尔森秩和检验定义如式(7)所示:

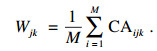(7)

其中: CA为分类准确率; M为所使用数据集的数量; i代表 21个数据集中第i个数据集; j表示9种对比算法中第j个算法; k代表 30次独立重复实验的第k次实验; W_jk代表第j个对比算法相较LGBFS在第k次实验在全部数据集上的威尔森秩和检验结果.
9种对比算法的检验结果于表 7给出.其中6种算法相较LGBFS的p值小于或近似等于0.05, 这在统计学上表示测试拒绝默认值5 % 显著性水平下的中位数相等的零假设, 证明了无论初始解决方案和整个搜索过程中采用的随机决策如何, LGBFS总能够找到相较其他6种算法更优异的特征子集.
表 7(Table 7)

表 7 LGBFS相较9种算法在分类准确率上的威尔森检验结果Table 7 The Wilcoxon test results for the CA obtained by nine approaches 算法名称 BMBO HGSA BOA RcBBFA BGWO BALO BPSO JMI MIM LGBFS 0.045 6 0.025 7 0.140 4 0.520 5 0.705 2 0.005 7 0.000 2 0.000 6 0.025 7

表 7 LGBFS相较9种算法在分类准确率上的威尔森检验结果 Table 7 The Wilcoxon test results for the CA obtained by nine approaches

通过威尔森秩和检验, 既定性地分析了LGBFS的准确性与高效性, 又定量地验证了LGBFS显著性与有效性.
4 时间复杂度分析分析算法LGBFS的时间复杂度, 对数据集给定如下假设: 给定无缺失值的具有N个样本、M个特征的数据集X, 设D为树模型最大树深、T为决策树的棵数且非零重要性特征的比例为β, 则m=βM, 对于数据处理阶段的直方图算法, 每一特征的N个特征值被分配进k个bin中(k?N), 则直方图算法时间扫描数据的复杂度为O(kM).
得到每个特征对应的直方图后, 树节点的分裂对应直方图的分裂, 在遍历每层特征的直方图后就确定了最佳分割点, 时间复杂度仍为O(kM), 对于建立最大深度为D、数量为T的迭代树模型的总计时间复杂度为O(kMDT).采用快速排序对度量后的子集排序时间复杂度为O(mlogm).
最后考虑搜索策略LRSFFS算法, 由于L, R均为常数, 故向项添加与后向去除的时间复杂度均为O(m), 而浮动的过程导致迭代的前向交叉浮动, 所以浮动算法时间复杂度为O(m²×KNN), 而KNN的时间复杂度可近似表示为O(mN logN), 所以LRSFFS的总时间复杂度为O(m³N logN).
故LGBFS算法总时间复杂度可近似表示为O(kM+mlogm+kMDT+m³NlogN).
5 结语本文提出了基于LightGBM的包裹式特征选择算法LGBFS, 该算法利用树形信息度量特征集合, 提出一种新型的序列浮动前向选择策略用于特征选择.经过21个数据集和9种特征选择算法的对比实验, 验证了LGBFS算法的良好性能, 对L与R参数的自适应化将是下一步的研究内容.
参考文献

[1]	Guyon I, Elisseeff A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3: 1157-1182.
[2]	Liu H, Motoda H, Setiono R, et al. Feature selection: an ever evolving frontier in data mining[J]. Journal of Machine Learning Research, 2010, 10: 4-13.
[3]	Kohavi R, John G H. Wrappers for feature subset selection[J]. Artificial Intelligence, 1997, 97(1/2): 273-324.
[4]	Dash M, Liu H. Feature selection for classification[J]. Intelligent Data Analysis, 1997, 1(3): 131-156. DOI:10.3233/IDA-1997-1302
[5]	Ke G L, Meng Q, Finley T, et al. LightGBM: a highly efficient gradient boosting decision tree[C]//Conference on Neural Information Processing Systems. Long Beach, 2017: 569-577.
[6]	Guyon I, Elisseeff A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3(6): 1157-1182.
[7]	Hall M A. Feature selection for discrete and numeric class machine learning[C]// Proceedings of the Seventeenth International Conference on Machine Learning. Stanford: Morgan Kaufmann, 2000: 359-366.
[8]	Guyon I, Elisseeff A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research, 2003, 3(6): 1157-1182.
[9]	Alweshah M, Khalaileh S A, Gupta B B, et al. The monarch butterfly optimization algorithm for solving feature selection problems[EB/OL]. [2021-04-05]. https://doi.org/10.1007/s00521-020-05210-0.
[10]	Taradeh M, Mafarja M, Heidari A, et al. An evolutionary gravitational search-based feature selection[J]. Information Sciences, 2019, 49(7): 219-239.
[11]	Arora S, Anand P. Binary butterfly optimization approaches for feature selection[J]. Expert Systems with Applications, 2019, 116: 147-160.
[12]	Zhang Y, Song X, Gong D. A return-cost-based binary firefly algorithm for feature selection[J]. Information Sciences, 2017, 418/419: 561-574. DOI:10.1016/j.ins.2017.08.047
[13]	Emary E, Zawbaa H M, Hassanien A E. Binary grey wolf optimization approaches for feature selection[J]. Neurocomputing, 2016, 172: 371-381. DOI:10.1016/j.neucom.2015.06.083
[14]	Emary E, Zawbaa H M, Hassanien A E. Binary ant lion approaches for feature selection[J]. Neurocomputing, 2016, 213: 54-65. DOI:10.1016/j.neucom.2016.03.101
[15]	Xue B, Zhang M, Browne W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(4): 606-626. DOI:10.1109/TEVC.2015.2504420
[16]	Bennasar M, Hicks Y, Setchi R. Feature selection using joint mutual information maximisation[J]. Expert Systems with Applications, 2015, 42(22): 8520-8532. DOI:10.1016/j.eswa.2015.07.007
[17]	Wilcoxon F. Individual comparisons by ranking methods[J]. Biometrics Bulletin, 1945, 1(6): 80-83. DOI:10.2307/3001968