
 , 刘平凡
, 刘平凡 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期:2020-10-12
基金项目:中央高校基本科研业务费专项资金资助项目(N182410001)。
作者简介:张石(1963-),男,辽宁抚顺人,东北大学教授,博士生导师。
摘要:传统DOA(direction of arrival)估计算法无法处理相干信号, 因此提出一种基于重构噪声子空间的高精度DOA估计算法.该算法利用阵元接收数据的自协方差与互协方差信息构造成增广矩阵作为新的协方差矩阵, 对该矩阵进行奇异值分解得到相应的噪声子空间和特征值矩阵.为了获得更精确的信号向量, 重构一个由新特征值矩阵对应的特征向量所组成的噪声子空间.最后通过谱峰搜索得到DOA估计值.算法不影响对非相干信号估计的效果, 并且比IMMUSIC(improved multiple signal classification)算法具有更高的估计精度, 在低信噪比及信号入射间隔较小的情况下也有良好的准确性.仿真结果表明, 提出的改进算法在低信噪比及低采样快拍数的条件下, 能有效估计出相干信号的波达方向.
关键词:波达方向估计相干信号增广矩阵重构噪声子空间MUSIC算法
DOA Estimation of Coherent Signals Based on Reconstructed Noise Subspace
ZHANG Shi, XU Fang-han, SHE Li-huang

 , LIU Ping-fan
, LIU Ping-fan School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: SHE Li-huang, E-mail: shelihuang@ise.neu.edu.cn.
Abstract: Traditional DOA(direction of arrival) estimation algorithms often fail to deal with coherent signals, so a new DOA estimation method with high accuracy based on reconstructed noise subspace is proposed. This method constructs an augmented matrix as a new covariance matrix by using the auto-covariance and cross-covariance information of uniform liner array, and then, the corresponding noise subspace and the eigen value matrix can be obtained through singular value decomposition on the augmented matrix. To obtain more accurate signal vectors, a new noise subspace can be reconstructed by the eigenvectors associated with the new eigen value matrix. Finally, DOA estimation is completed through spectral peak searching. The proposed algorithm doesnot affect the estimation effect of independent signals. Compared with the IMMUSIC(improved multiple signal classification) algorithm, the proposed algorithm has higher estimation accuracy, especially under the conditions of low signal-to-noise ratio and small signal incidence interval. The simulation results show that even for the conditions of low signal-to-noise ratio and low sampling snapshot number, the improved algorithm can effectively estimate the DOA.
Key words: DOA(direction of arrival) estimationcoherent signalsaugmented matrixreconstructionnoise subspaceMUSIC(multiple signal classification) algorithm
DOA(direction of arrival)估计是一种重要的阵列信号处理技术, 广泛应用于雷达、通信及医疗领域[1-2].随着通信环境的日益复杂, 到达天线阵的信号通常是相干的, 传统DOA估计算法的性能会逐渐下降甚至完全失效[3-4].因此, 相干信源的波达方向估计是当前空间谱估计领域的一个热点问题[5].
目前解相干有两种方法: 一种是降维处理[6-8], 例如前后向空间平滑(FBSS)算法, 它具有较好的解相干性能[6], 但会损失阵列孔径[7]; 另一种则没有进行降维处理, 此类方法主要利用接收数据矩阵来构造Toeplitz矩阵从而实现解相干[9], 但计算复杂度也会随之增加.
针对传统的多信号分类(multiple signal classification, MUSIC)算法对相干信源不能进行正确的施密特正交化[10], 文献[11]提出了IMMUSIC(improved MUSIC)算法.IMMUSIC算法使重构的协方差矩阵具有Toeplitz矩阵的特征, 可以得到相干信源的DOA估计; 但如果信号信噪比较低或信号间隔较小时则无法准确地分辨信号, DOA估计的性能将明显下降[12].对于相干信号而言, 本文充分利用阵元接收数据来构造一个新的增广矩阵, 提出一种基于重构噪声子空间的相干信源DOA估计算法.
1 信号模型假设角度分别为θi(i = 1, 2, …, D)的D(D<M)个远场窄带信号入射到由M个阵元组成的均匀等距线阵上, 以首个阵元作为参考, 第k个阵元接收到的信号可以表示为
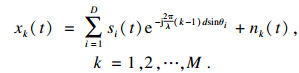 | (1) |
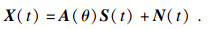 | (2) |
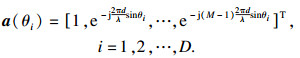 | (3) |
2 新型高精度DOA估计算法2.1 MUSIC算法对于解决非相干信号的DOA估计, MUSIC算法可以达到高分辨率估计的效果[10].接收数据矩阵X(t)的协方差矩阵RX可表示为
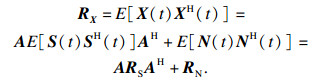 | (4) |
对矩阵RX进行特征分解, 得
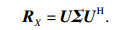 | (5) |
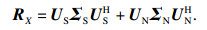 | (6) |
由于矩阵A(θ)中的每个导向矢量与噪声子空间UN正交, 故UNHa(θi)=0, (i=1, 2, …, D).通过谱峰搜索函数的最大峰值来估计入射信号源的DOA:
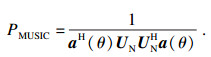 | (7) |
2.2 修正MUSIC(MMUSIC)算法在MUSIC算法中接收信号模型表达式为
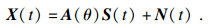 | (8) |
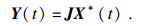 | (9) |
 | (10) |
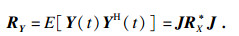 | (11) |
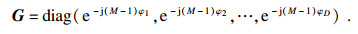 | (12) |
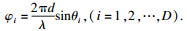
通过推导可以得到
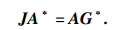 | (13) |
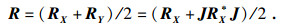 | (14) |
2.3 IRNSMUSIC算法为了解决DOA估计数组中相干信源的问题, 本文提出一种基于重构噪声子空间(IRNS)的算法.IRNS算法的推导如下.
在IMMUSIC算法[11]中, 只利用了X(t)和Y(t)的自协方差信息; 而本文算法则充分利用X(t)和Y(t)的互协方差信息去构造一个新的増广矩阵, 其表达式为
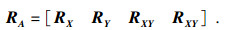 | (15) |
通过对增广矩阵RA进行奇异值分解, 可以得到对应的噪声子空间和特征值为
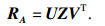 | (16) |
将式(14)作奇异值分解, 得
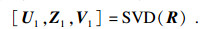 | (17) |
在RWNS算法[14]中, 将Σ和Z按序对比其特征值, 选择较大特征值重构对应的特征向量矩阵; 但本文经过多次参数修改和仿真测试, 发现其仿真结果在低信噪比及入射信源为相干的情况下并不理想.本文借鉴RWNS算法的思想, 将同为接收相干信源的协方差矩阵R和RA分别进行奇异值分解, 将得到的矩阵Z1和矩阵Z按顺序比较对应的特征值.例如, 如果λ′1>η1, 那么λ′1被选择作为λn, 1以构成新的特征值矩阵, 因此新的特征值矩阵表达式被构造为
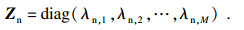 | (18) |
选择Zn的特征值关联的特征向量以构造一个新的特征向量矩阵:
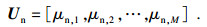 | (19) |
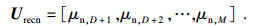 | (20) |
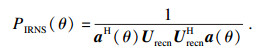 | (21) |
1) 根据式(15)构造接受数据的增广协方差矩阵;
2) 对式(16)的RA执行奇异值分解;
3) 对式(14)的R执行奇异值分解;
4) 根据式(20)重构新的噪声子空间;
5) 求PIRNS的D个最大峰值, 得到相干信号的DOA估计.
3 仿真和分析为解决相干信源DOA估计的问题, 仿真分析了新算法的性能.性能分析的主要指标包括不同算法的空间分辨率及算法的稳健性随着信噪比和采样快拍数的变化关系等.实验条件为8个间距为d(d=λ/2)的传感器组成的均匀等距线阵, 噪声为理想高斯白噪声.
3.1 验证IRNSMUSIC算法的有效性实验一.3个远场窄带信号的入射角分别为-20°, 40°, 60°, 其中前两个信号为相干信号, 第3个信号为非相干信号.图 1显示了信噪比为0 dB时IMMUSIC算法、MMUSIC算法和IRNSMUSIC算法的DOA估计结果.
图 1(Fig. 1)
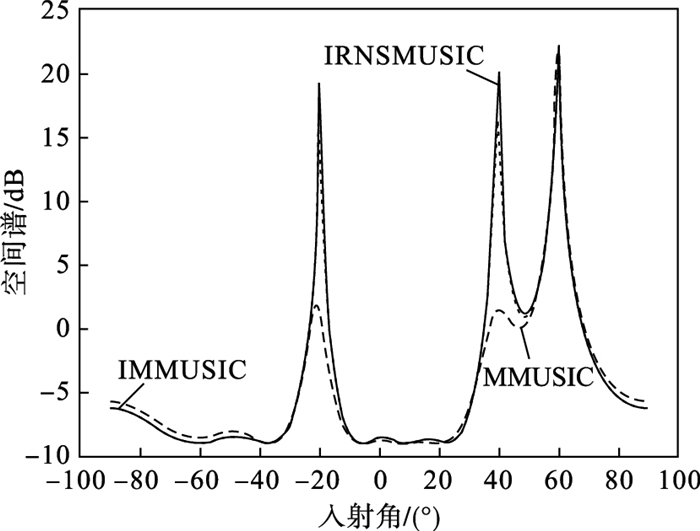 | 图 1 低信噪比3种算法的DOA估计Fig.1 DOA estimation of three algorithms with low SNR |
由图 1的仿真曲线可知, 当信噪比较低时, MMUSIC算法对相干信源的估计性能严重下降, 而IMMUSIC算法与本文的IRNSMUSIC算法在信噪比较低时均具有较好的估计性能, 并且IRNSMUSIC算法的谱峰更尖锐.
实验二.3个远场窄带信号的入射角分别为0°, 5°, 60°, 其中前两个信号为相干信号, 第3个信号为非相干信号.图 2显示了信噪比为5 dB时所提IRNSMUSIC算法与IMMUSIC算法的DOA估计结果.
图 2(Fig. 2)
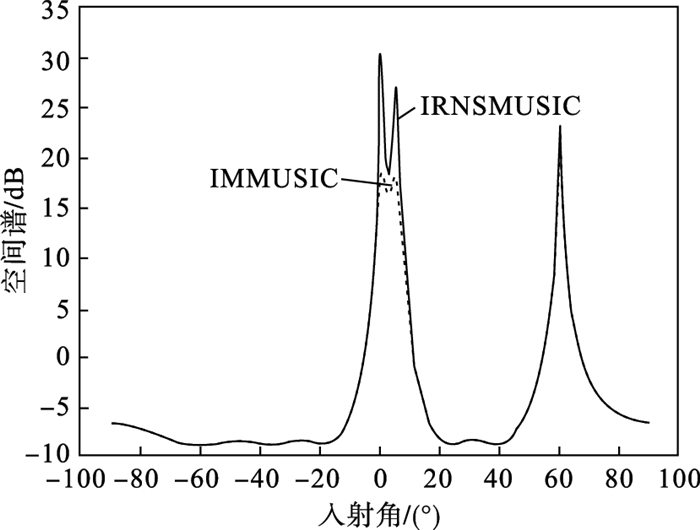 | 图 2 低信噪比及入射信号间隔较小时的DOA估计Fig.2 DOA estimation with low SNR and small interval |
由图 2的仿真曲线可得, IRNSMUSIC算法在低信噪比及信源入射间隔较小时也能够准确估计这两个相干信号且谱峰较尖锐.
3.2 验证IRNSMUSIC算法的准确性为了验证IRNSMUSIC算法的DOA估计精度, 以均方根误差(RMSE)衡量算法准确性的标准:
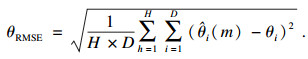 | (22) |
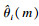
实验三.采用MMUSIC算法、IMMUSIC算法及本文的IRNSMUSIC算法进行性能对比仿真实验.采样快拍数为1 024.两组相干信源的入射角分别为0°和10°, 测试信噪比从-10 dB变化到10 dB, 每间隔2 dB进行500次蒙特卡洛实验, 结果如图 3所示.
图 3(Fig. 3)
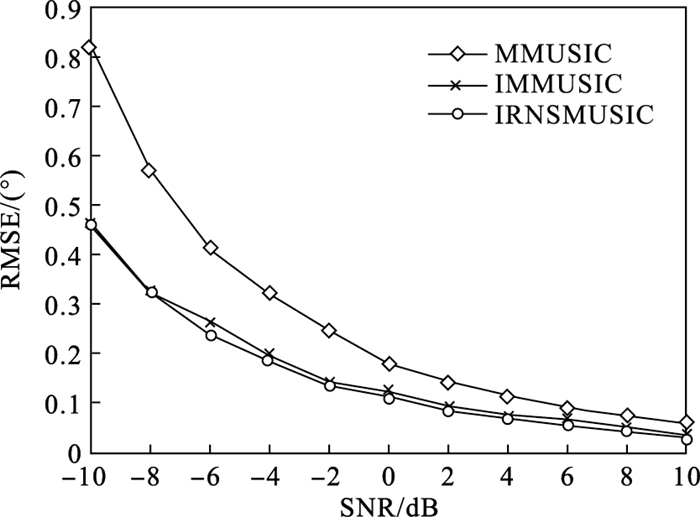 | 图 3 均方根误差与信噪比之间的关系Fig.3 Relationship between RMSE and SNR |
从图 3的仿真曲线可知, 在采样快拍数一定的条件下, 随着信噪比的增加, 3种算法的均方根误差都呈现减小的趋势, 说明估计性能随信噪比的增加而逐渐提升.IMMUSIC算法和IRNSMUSIC算法的RMSE曲线位置比MMUSIC算法更低, 即估计性能更好; 而IRNSMUSIC算法的RMSE曲线位置不仅略低于IMMUSIC算法而且曲线较为平滑, 说明IRNSMUSIC算法具有更好的估计性能.
实验四.采用MMUSIC算法、IMMUSIC算法及本文的IRNSMUSIC算法进行性能对比仿真实验.信噪比为0 dB.两组相干信源的入射角分别为0°和10°, 测试采样快拍数的范围100~1 000, 每间隔100个快拍数进行500次蒙特卡洛实验, 结果如图 4所示.
图 4(Fig. 4)
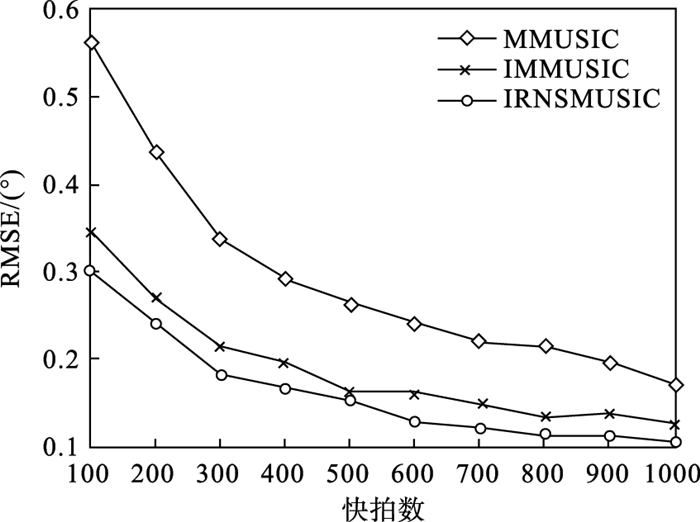 | 图 4 均方根误差与快拍数之间的关系Fig.4 Relationship between RMSE and snapshots |
从图 4的仿真曲线可知, 在信噪比一定的条件下, 随着采样快拍数的增加, 3种算法的均方根误差都呈现减小的趋势, 说明估计性能随着快拍数的增加而逐渐提升.本文IRNSMUSIC算法的RMSE曲线位置低于MMUSIC和IMMUSIC算法, 说明IRNSMUSIC算法具有更好的DOA估计性能.
4 结语传统的MUSIC等谱估计算法在对相干信源进行估计时可能失效, 针对这一问题, 本文提出一种基于重构噪声子空间的相干信源DOA估计算法.该算法充分利用接收到的数据信息构造成增广矩阵作为新的协方差矩阵, 对该矩阵进行奇异值分解得到对应的噪声子空间和特征值矩阵.按序比较两个特征值矩阵对应的特征值, 重构一个由较大特征值对应的特征向量所组成的噪声子空间.最后通过谱峰搜索完成相干信源的DOA估计.
仿真结果表明, 本文提出的算法无孔径损耗, 能区分较小间隔的相干信号, 在信噪比较低及采样快拍数较少的情况下DOA估计精度优于MMUSIC算法和IMMUSIC算法.
参考文献
| [1] | Liu L T, Liu H. Joint estimation of DOA and TDOA of multiple reflections in mobile communications[J]. IEEE Access, 2016, 4: 3815-3823. |
| [2] | Gorcin A, Arslan H. A two-antenna single RF front-end DOA estimation system for wireless communications signals[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(10): 5321-5333. DOI:10.1109/TAP.2014.2346197 |
| [3] | Jeong S H, Son B K, Lee J H. Asymptotic performance analysis of the MUSIC algorithm for direction-of-arrival estimation[J]. Applied Sciences, 2020, 10(6): 1-25. |
| [4] | Mao W P, Li G L, Xie X, et al. DOA estimation of coherent signals based on direct data domain under unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13: 1525-1528. DOI:10.1109/LAWP.2014.2343671 |
| [5] | Zamani H, Zayyani H, Marvasti F. An iterative dictionary learning-based algorithm for DOA estimation[J]. IEEE Communications Letters, 2016, 20(9): 1784-1787. DOI:10.1109/LCOMM.2016.2587674 |
| [6] | Pillai S U, Kwon B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8-15. DOI:10.1109/29.17496 |
| [7] | 石要武, 陈淼, 单泽涛, 等. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报(工学版), 2017, 47(1): 268-273. (Shi Yao-wu, Chen Miao, Shan Ze-tao, et al. Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 268-273.) |
| [8] | Qian C, Huang L, So H C. Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J]. IEEE Signal Process Letters, 2014, 21(2): 140-144. DOI:10.1109/LSP.2013.2294676 |
| [9] | Chen H, Hou C P, Wang Q, et al. Cumulants-based Toeplitz matrices reconstruction method for 2-D coherent DOA estimation[J]. IEEE Sensors Journal, 2014, 14(8): 2824-2832. DOI:10.1109/JSEN.2014.2316798 |
| [10] | Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 |
| [11] | 周小军, 谭薇, 冯大政, 等. 基于解相干的改进MUSIC算法DOA估计[J]. 无线电工程, 2014, 44(12): 18-21. (Zhou Xiao-jun, Tan Wei, Feng Da-zheng, et al. DOA estimation of improved MUSIC algorithm based on decorrelation signal[J]. Radio Engineering, 2014, 44(12): 18-21. DOI:10.3969/j.issn.1003-3106.2014.12.06) |
| [12] | Liu G H, Chen H, Sun X Y, et al. Modified MUSIC algorithm for DOA estimation with Nystr?m approximation[J]. IEEE Sensors Journal, 2016, 16(12): 4673-4674. DOI:10.1109/JSEN.2016.2557488 |
| [13] | Kundu D. Modified MUSIC algorithm for estimating DOA of signals[J]. Signal Processing, 1996, 48: 85-89. DOI:10.1016/0165-1684(95)00126-3 |
| [14] | Liu X Z, Song M Y, Yang Y H. An effective DOA estimation method of coherent signals based on reconstruct weighted noise subspace[C]// 29th Chinese Control and Decision Conference(CCDC). Chongqing, 2017: 2218-2222. |
