
 , 李佳其, 刘子傲, 于佳月
, 李佳其, 刘子傲, 于佳月 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期:2021-03-29
基金项目:国家自然科学基金资助项目(U1602232)。
作者简介:康玉梅(1973-),女,辽宁灯塔人,东北大学副教授。
摘要:为提高装配式箱涵构件可靠度分析的计算精度和效率, 依托实际工程, 基于概率密度演化方法对其进行了研究.首先, 建立了装配式箱涵构件的功能函数, 推导出功能函数的广义概率密度演化方程, 并采用有限差分法进行求解; 其次, 对求解得到的概率密度函数进行积分, 得到构件的失效概率, 进而获得相应的可靠指标; 最后, 与蒙特卡罗法进行对比, 分析概率密度演化方法的适用性.研究表明: 概率密度演化方法在装配式箱涵构件可靠度的求解过程中, 从物理系统与随机系统联系的角度出发, 更加充分地考虑了构件参数的随机性和样本点之间的概率联系.该方法与蒙特卡罗法相比可以有效避免随机收敛性, 在保证结果唯一的前提下, 提高了计算精度和效率.
关键词:概率密度演化方法装配式箱涵构件可靠度蒙特卡罗法功能函数
Reliability Study of Prefabricated Box Culvert Components Based on Probability Density Evolution Method
KANG Yu-mei

 , LI Jia-qi, LIU Zi-ao, YU Jia-yue
, LI Jia-qi, LIU Zi-ao, YU Jia-yue School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: KANG Yu-mei, E-mail: kangyumei@mail.neu.edu.cn.
Abstract: The calculation accuracy and efficiency of reliability analysis of prefabricated box culvert components are studied using the probability density evolution method based on the actual project. Firstly, the function of prefabricated box culvert is established, the generalized probability density evolution equation of the function is derived, and the finite difference method is used to solve the problem. Secondly, the probability density function is integrated to get the failure probability of components, and then the corresponding reliability index is obtained. Finally, it is compared with Monte Carlo method to analyze the applicability of probability density evolution method. The results show that: in the process of solving the reliability of prefabricated box culvert components, the probability density evolution method fully considers the randomness of component parameters and the probability relationship between sample points based on the relationship between physical system and stochastic system. Compared with Monte Carlo method, probability density evolution method can avoid random convergence effectively, and improve the accuracy and efficiency of calculation under the premise of guaranteeing the unique result.
Key words: probability density evolution methodprefabricated box culvertreliability of componentsMonte Carlo methodfunction
装配式箱涵是一种常见的工程结构, 具有良好的场地适应能力和整体受力性能, 现已被广泛应用于公路和铁路工程中[1-2].如何精确高效地分析装配式箱涵各个构件在设计和使用过程中的可靠性[3]是一个非常值得研究的问题.国内外****多采用蒙特卡罗方法[4]、随机摄动方法[5]和正交多项式展开理论[6]等可靠度求解方法分析地下结构[7]和边坡[8]的可靠度.蒙特卡罗法基于大数定律, 在求解过程中需要多次迭代, 计算量极大, 花费时间较长, 且计算结果具有随机收敛性, 难以适用于实际工程.验算点法则存在计算精度不足的问题, ****们为了提高验算点法的精度, 提出了基于验算点法的改进方法, 例如, Chen等[9]依据在验算点处相似概率密度函数导数相等的原则, 提出了三参数正态尾区近似的原则; Guo等[10]给出了结构功能函数的三阶与四阶可靠指标.虽然已经在改进验算点法方面取得了一些进展, 但是改进后的验算点法在分析实际工程可靠度时的精度尚有待提高.Li等[11]提出了概率密度演化方法, 该方法基于概率守恒原理, 能够充分考虑参数随机性和样本点之间的概率联系, 弥补了传统可靠度分析方法中存在的不足[12].目前, 概率密度演化方法已经被应用于部分地上和地下结构的可靠度分析[13].
本文依托“双辽至洮南高速公路03A设计段”装配式箱型涵洞工程项目, 基于概率密度演化方法分析装配式箱涵构件的可靠度, 并与蒙特卡罗法的计算结果进行对比, 验证概率密度演化方法的计算效率和精度, 以期为装配式箱涵构件可靠度研究提供一种新的途径和方法.
1 概率密度演化理论在随机物理系统中, 概率密度演化理论可以描述任意状态量的概率分布和演化过程.其为分析结构受力的物理过程和考察随机性的传播规律, 从概率角度求解结构可靠度提供了理论依据.概率密度守恒原理是概率密度演化理论的基础, 具有两种描述方式, 分别为状态空间描述和随机事件描述[14].
状态空间描述可表示为
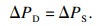 | (1) |
随机事件描述可表示为
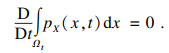 | (2) |
随机动力系统可表示为
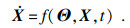 | (3) |
根据概率守恒原理:
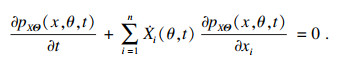 | (4) |
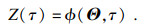 | (5) |
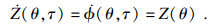 | (6) |
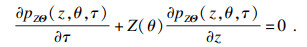 | (7) |
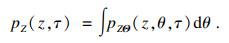 | (8) |
2 基于概率密度演化方法的装配式箱涵构件可靠度研究2.1 功能函数根据装配式箱涵的受力情况来确定箱涵构件的功能函数.对于箱涵顶板、侧墙及底板组成的整体需要重点关注其抗弯可靠度, 对于铰缝构造处(上下各取0.5 m作为研究对象)需要重点关注其抗剪可靠度, 实际的结构受力形式如图 1所示.其中: g1为顶板自重力(kN);q1为上部填土体重力(kN);p为车辆荷载(kN);q2, q3, q4分别为不同位置侧向土压力(kN);q5为撑脚土体重力(kN);g2为结构整体自重力(kN).
图 1(Fig. 1)
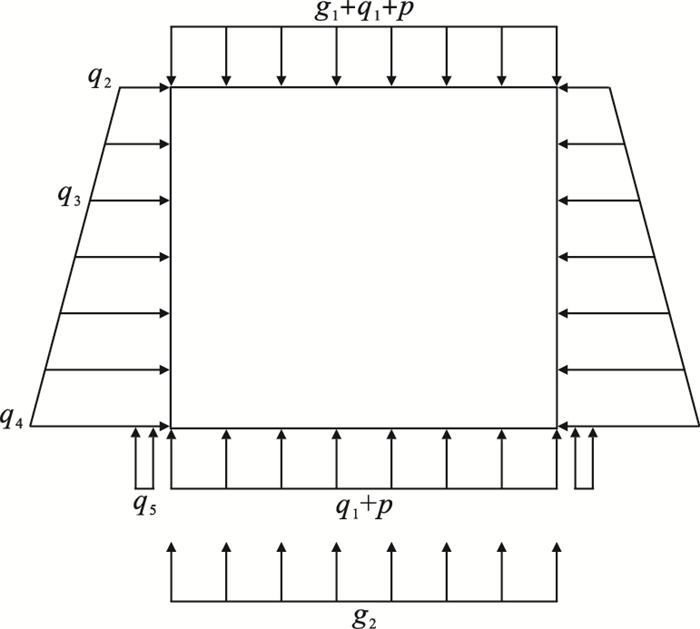 | 图 1 结构受力示意简图Fig.1 Schematic diagram of structural force |
装配式箱涵构件有两种极限状态方程[15]:
1) 箱涵构件抗弯承载能力极限状态设计式为
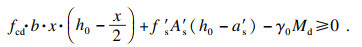 | (9) |
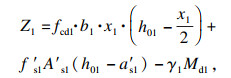 | (10) |
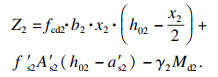 | (11) |
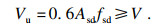 | (12) |
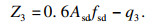 | (13) |
2.2 概率密度演化方程箱涵构件的抗力与荷载效应可以分别表示为
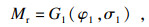 | (14) |
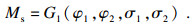 | (15) |
箱涵构件的功能函数可以表示为
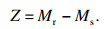 | (16) |
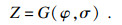 | (17) |
当σ取某一特定值μ时, 随机变量H的概率为?(φ, σ, t), 可得
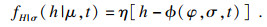 | (18) |
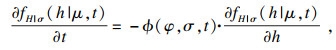 | (19) |
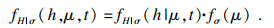 | (20) |
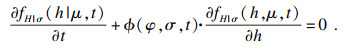 | (21) |
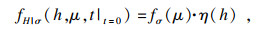 | (22) |
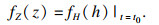 | (23) |
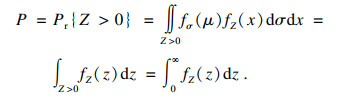 | (24) |
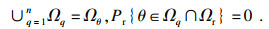 | (25) |
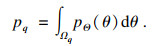 | (26) |
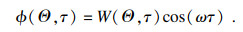 | (27) |
3) 根据步骤2)的选点结果, 对于给定的θ=θq, q=1, 2, …, n, 求解式(17), 获得所需物理量的时间导数(速度状态量)
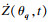
4) 根据上述步骤得到初始条件和速度状态量
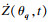
5) 以Z>0为积分区间, 对概率密度函数积分求得可靠概率:
 | (28) |
图 2(Fig. 2)
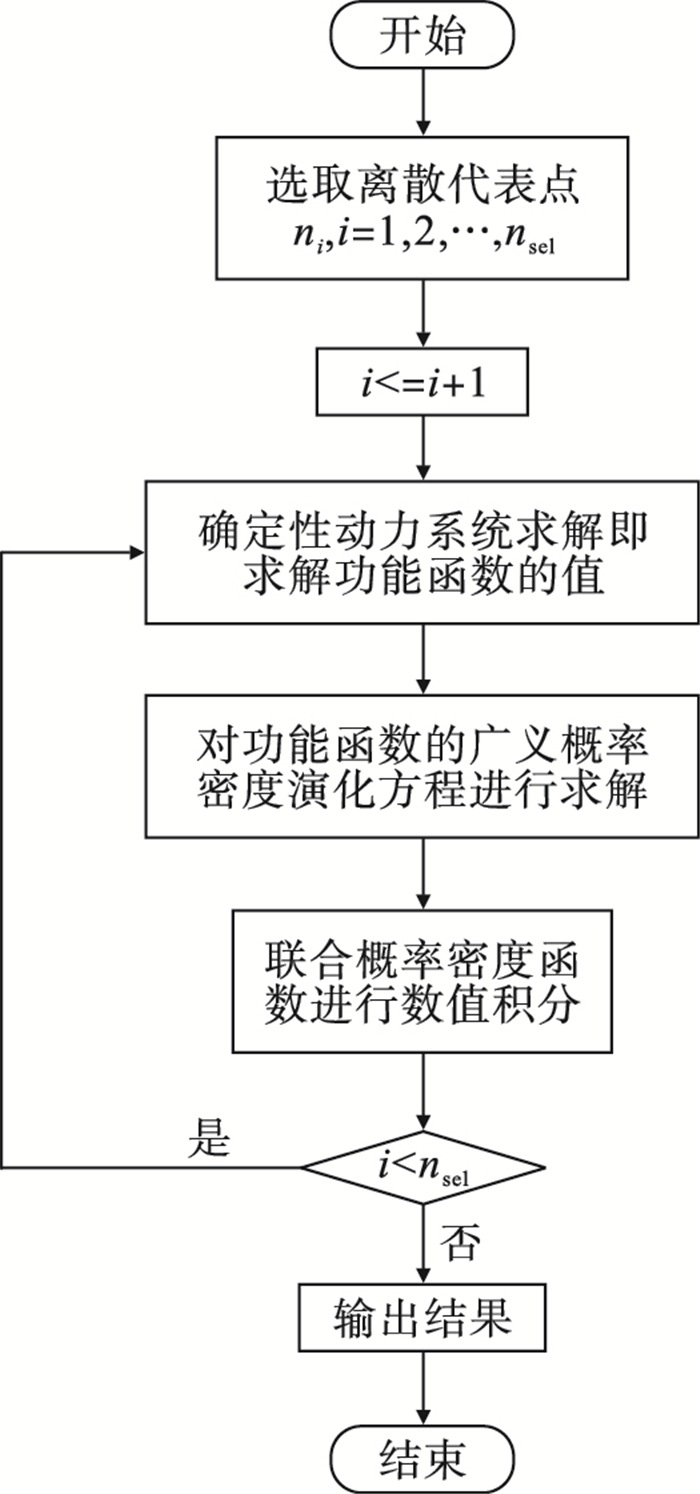 | 图 2 构件可靠度分析步骤流程Fig.2 Flow chart of component reliability analysis |
3 概率密度演化方法在装配式箱涵构件可靠度分析中的应用3.1 工程概况“双辽至洮南高速公路03A设计段”路线全长25.702 km, 周围土体主要是泥岩和粉质黏土, 具体的土层参数如表 1所示, 其中涵洞共有22道, 均采用预制装配式钢筋混凝土箱涵, 其结构形式分为三种, 标准节段均为3 m.以四构件组合结构箱涵为例, 顶板和侧墙为铰接, 侧墙采用混凝土现浇的方式和底板连接(见图 3和图 4).
表 1(Table 1)
| 表 1 土层基本参数 Table 1 Basic parameters of soil layer |
图 3(Fig. 3)
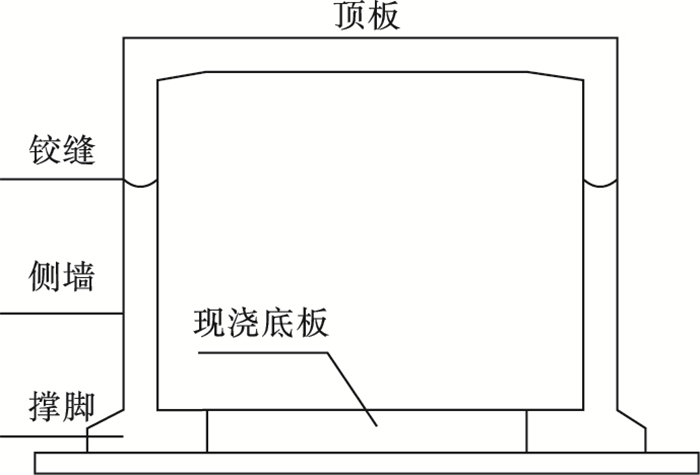 | 图 3 装配式箱涵结构示意图Fig.3 Structural diagram of prefabricated box culvert |
图 4(Fig. 4)
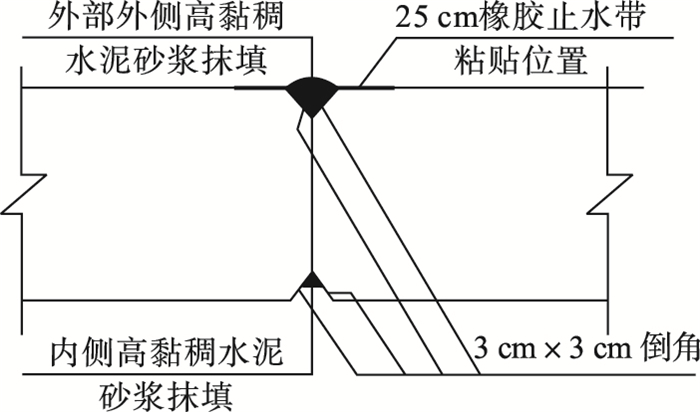 | 图 4 铰缝构造处示意图Fig.4 Schematic diagram of hinge joint structure |
3.2 有限元模型通过现场勘察资料得到箱涵构件钢筋和混凝土的材料参数, 采用等效弹性模量和容重来代替钢筋混凝土的弹性模量和容重.利用ABAQUS软件建立箱涵构件三维模型, 如图 5所示.箱涵顶板、侧墙和底板组成的整体采用铰接形式, 对于铰缝构造处, 取其上下0.5 m范围的计算单元作为研究对象, 上下两端均采用固接形式.网格划分采用四边形单元, 在易破坏区域细密划分, 其余区域的网格划分可以较为稀疏, 这样有利于提高计算效率.箱涵各构件均采用8节点实体单元, 进行力学性能分析, 得到箱涵顶板、侧墙及底板整体的跨中弯矩和铰缝构造处的剪力值, 为后续的可靠度分析提供确定性的依据.当所有参数均作为确定性值考虑的时候, 数值分析和采用截面法计算得到的内力响应结果相近, 误差在允许的范围内, 验证了本模型的正确性.
图 5(Fig. 5)
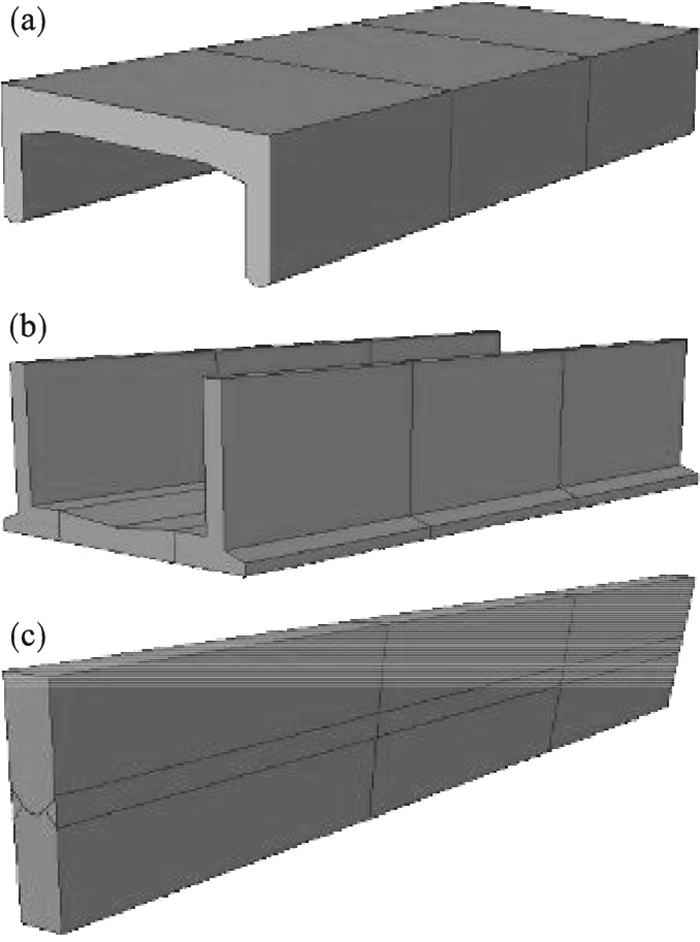 | 图 5 构件三维模型图Fig.5 Three dimensional model of components (a)—顶板;(b)—侧墙及底板组成的整体;(c)—铰缝. |
3.3 随机变量的确定及特性统计定义箱涵构件的钢筋抗拉强度设计值、构件钢筋直径、混凝土保护层厚度、截面宽度、计算跨度、回填土重力密度、钢筋混凝土结构重力密度、内摩擦角、车辆荷载、铰缝钢筋直径和钢筋抗拉强度设计值为随机变量, 通过参考现场实测资料与相关文献[17]可知, 各个随机变量均服从正态分布[18], 随机变量的具体分布参数如表 2所示.
表 2(Table 2)
| 表 2 箱涵随机参数特性统计[17-18] Table 2 Statistics of random parameters of the box culvert[17-18] |
3.4 随机变量的敏感性分析随机变量的敏感性会对箱涵构件的可靠度分析产生影响, 因此在进行箱涵构件可靠性研究之前, 需要对随机变量进行敏感性分析.将对可靠度分析影响程度较大的随机变量继续作为随机变量考虑, 影响程度较小的随机变量作为确定性值考虑, 敏感性系数如表 3所示.
表 3(Table 3)
| 表 3 随机变量的敏感性系数 Table 3 Sensitivity coefficients of random variables |
由表 3可知: 在进行箱涵顶板、侧墙和底板构成的整体的可靠度研究时, 钢筋的抗拉强度设计值、内摩擦角、钢筋直径、土的重力密度以及计算跨度的敏感程度较大, 需要作为随机变量考虑.对于铰缝构造处的可靠度分析, 计算跨度的敏感程度较小, 因此仅将钢筋的抗拉强度设计值、内摩擦角、钢筋直径、土的重力密度这四个参数作为随机变量, 其他参数均作为确定性值考虑.
3.5 构件可靠度分析结合随机变量敏感性的分析结果, 利用数论选点法对各构件的随机变量选取2 000组代表点进行确定性分析, 得到构件的荷载效应如图 6所示, 顶板荷载效应的均值为130.029 kN · m, 标准差为7.967 1, 变异系数为0.061 3;侧墙及底板组成的整体均值为87.161 8 kN · m, 标准差为9.437 3, 变异系数为0.108 3;铰缝构造处的均值为43.161 1 kN, 标准差为3.015 7, 变异系数为0.069 9.
图 6(Fig. 6)
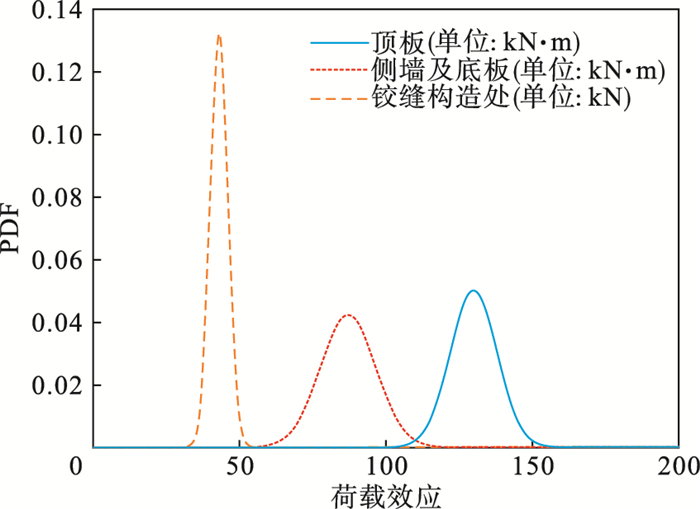 | 图 6 构件荷载效应概率密度函数Fig.6 Probability density function of component load effect |
当构件的随机参数均服从正态分布时, 其荷载效应也基本服从正态分布, 且荷载效应的变异系数要大于单个随机变量的变异系数, 因此, 在构件可靠度的研究过程中, 需要充分考虑参数的随机性.将有限元软件中确定性分析得到的效应值以及相应的抗力值代入式(27), 构造虚拟随机过程, 各构件的虚拟随机过程如图 7所示.
图 7(Fig. 7)
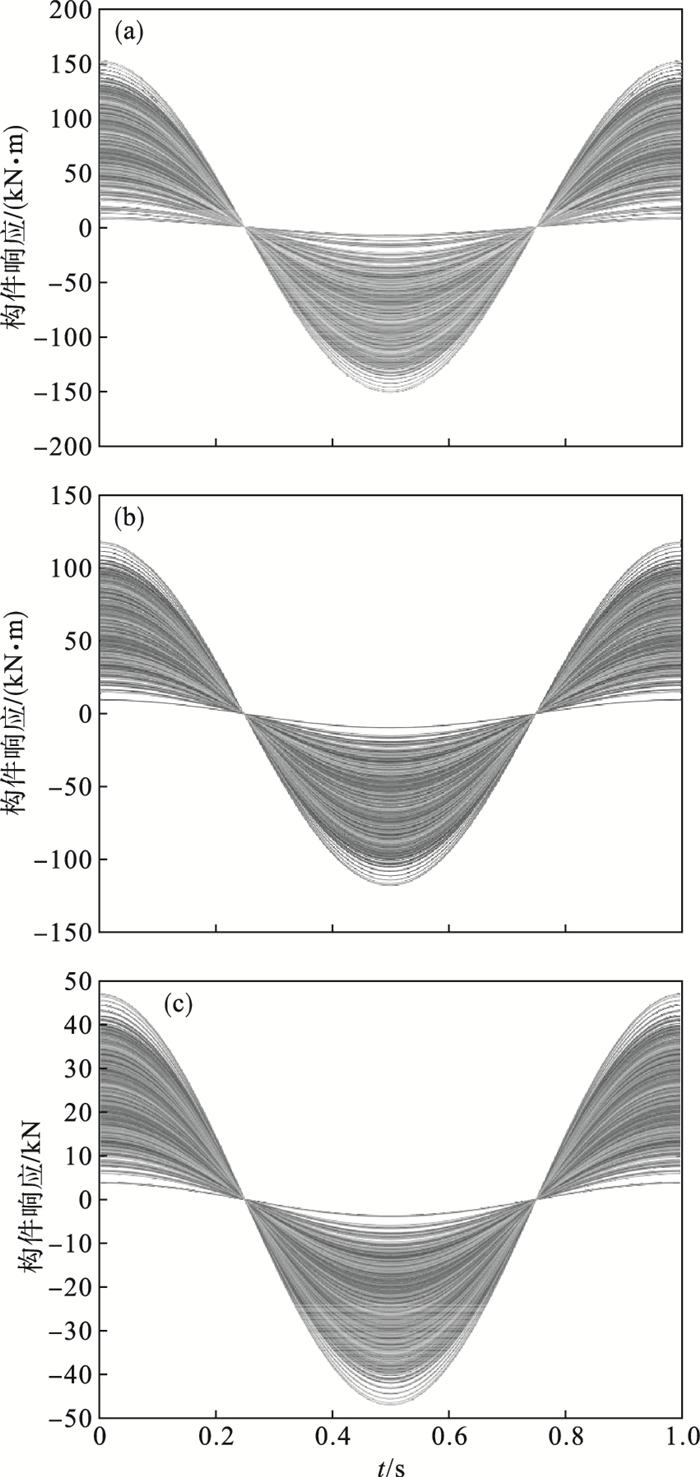 | 图 7 各构件的虚拟随机过程Fig.7 Virtual stochastic process of the component (a)—顶板;(b)—侧墙及底板整体;(c)—铰缝构造处. |
构造虚拟随机过程需要引入时间向量, 将结构受到的静力转化为动态过程.在虚拟随机过程中, 箱涵构件响应的概率密度演化过程如图 8所示.在构件可靠度的分析过程中, 经过概率密度演化, 构件响应的变异性会增大, 需要充分考虑参数的随机性和样本点之间的概率联系.
图 8(Fig. 8)
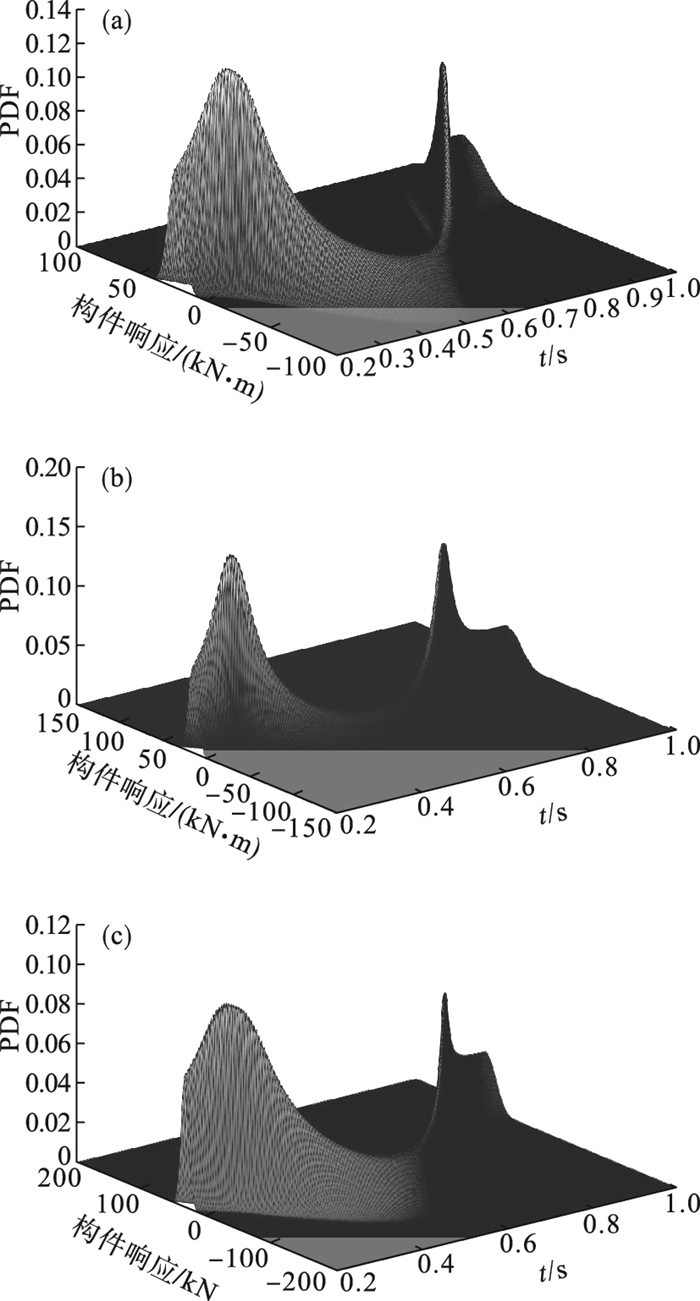 | 图 8 构件响应的概率密度演化曲面图Fig.8 Probability density evolution curved surface of component response (a)—顶板;(b)—侧墙及底板整体;(c)—铰缝构造处. |
采用MATLAB编程的方法, 依次得到顶板、侧墙及底板组成的整体和铰缝构造处的最后时刻响应截口概率密度函数的图像, 如图 9所示.对最后时刻截口概率密度函数在失效域上积分, 即可得到构件的失效概率, 进而求得可靠指标.其中, 顶板的可靠指标为4.281 4, 侧墙及底板构成的整体的可靠指标为4.328 2, 铰缝构造处的可靠指标为4.399 9, 均符合规范要求.
图 9(Fig. 9)
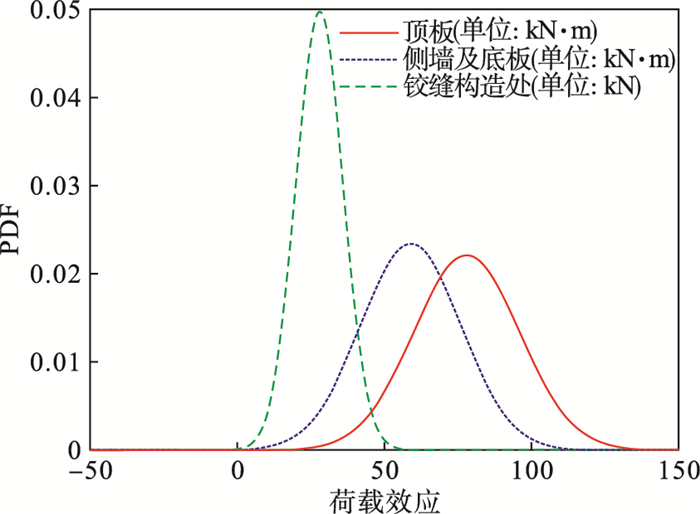 | 图 9 构件响应最后时刻的截口概率密度函数Fig.9 The cut-off probability density function of the component response at the last moment |
3.6 两种方法对比分析采用蒙特卡罗法对不同抽样次数下箱涵构件可靠度进行计算, 计算结果均满足规范要求.当给定抽样次数为800万次时, 求得箱涵顶板的可靠指标为4.307 6, 侧墙及底板构成的整体的可靠指标为4.428 3, 铰缝构造处的可靠指标为4.391 6.随着抽样次数的增加, 构件可靠度的计算结果出现了明显的随机收敛性.800万次到2 000万次抽样下失效概率的变化情况如图 10所示.
图 10(Fig. 10)
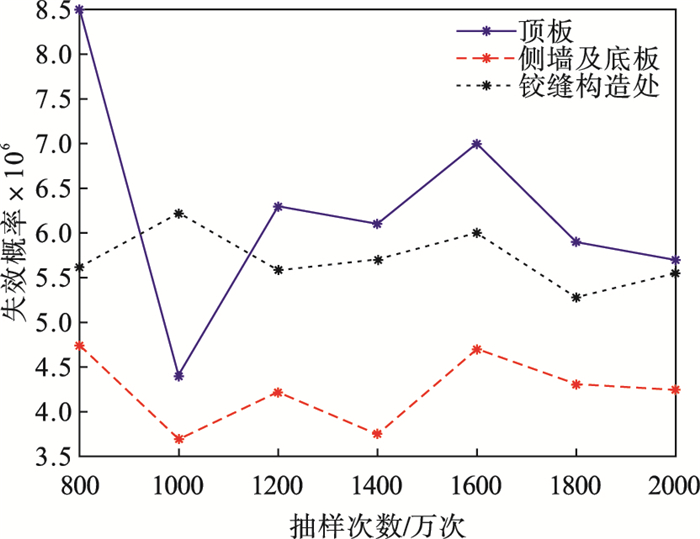 | 图 10 构件失效概率随抽样次数变化趋势图Fig.10 Trend chart of component failure probability with sampling times |
将两种方法求得的箱涵构件可靠指标进行对比, 其结果如表 4所示, 可以看出: 两种方法的计算结果基本一致, 均能较为精确地求出箱涵构件的可靠指标.表 5给出了两种方法的计算效率, 可见, 同样的计算精度, 蒙特卡罗法的选点次数是概率密度演化方法的4 000倍, 所需要的计算时间为概率密度演化方法的5倍, 且无法避免随机收敛性.
表 4(Table 4)
| 表 4 可靠指标计算结果 Table 4 Calculation results of reliability index |
表 5(Table 5)
| 表 5 计算效率对比 Table 5 Comparison of calculation efficiency |
综上所述, 蒙特卡罗法以抽样理论为基础, 其结果的准确性受到抽取样本数量的影响, 且求解过程耗时较长, 结果具有明显的随机收敛性.概率密度演化方法则充分考虑了构件参数的随机性, 所需选取的代表点集数量较小, 计算速度较快, 具有较高的准确性, 可以有效避免蒙特卡罗法在求解过程中的弊端.
4 结语1) 对装配式箱涵构件可靠度分析的概率密度演化方法进行了研究, 确定了装配式箱涵构件的功能函数, 并基于此求解出概率密度演化方程; 给出了相应的构件可靠度求解步骤.
2) 分别采用蒙特卡罗法和概率密度演化方法对装配式箱涵构件的可靠度进行求解; 概率密度演化方法可以有效避免计算结果的随机收敛性, 在保证计算结果唯一和较高精度的同时, 能够极大地提高计算效率.
3) 概率密度演化方法充分考虑了装配式箱涵构件参数的随机性和样本点之间的概率联系, 对于求解装配式箱涵构件可靠度具有良好的适用性, 是一种高效、适用范围广的可靠度分析方法.
参考文献
| [1] | Das S. Application of diagnostic load testing and 3D-FEA in load rating of RC box culverts[J]. Bridge Structures—Assessment, Design and Construction, 2013, 9(4): 155-167. |
| [2] | Peng Q, Jin D I, Feng J Q. Shear stress in the webs of single-box multi-cell composite box girders with corrugated steel webs[J]. Engineering Mechanics, 2017, 34(7): 97-107. |
| [3] | 康玉梅, 刘子傲, 吴鹏飞. 考虑荷载作用顺序的结构可靠度分析方法[J]. 东北大学学报(自然科学版), 2019, 40(11): 1648-1653. (Kang Yu-mei, Liu Zi-ao, Wu Peng-fei. Structural reliability analysis method considering load sequence[J]. Journal of Northeastern University(Natural Science), 2019, 40(11): 1648-1653. DOI:10.12068/j.issn.1005-3026.2019.11.023) |
| [4] | Nie J S, Ellingwood B R. Directional methods for structural reliability analysis[J]. Structural Safety, 2000, 22: 233-249. DOI:10.1016/S0167-4730(00)00014-X |
| [5] | Kleiber M, Hien T D. The stochastic finite element method: basic perturbation technique and computer implementation[M]. New York: John Wiley & Sons, 1992: 198-235. |
| [6] | Ghanem R, Spanos P D. Polynomial chaos in stochastic finite elements[J]. Journal of Applied Mechanics, 1990, 57(1): 197-202. DOI:10.1115/1.2888303 |
| [7] | Bhargava K, Mori Y, Ghosh A K. Time-dependent reliability of corrosion-affected RC beams.Part 1:Estimation of time-dependent strengths and associated variability[J]. Nuclear Engineering and Design, 2011, 241(5): 1371-1384. DOI:10.1016/j.nucengdes.2011.01.005 |
| [8] | 唐小松, 李典庆, 曹子君, 等. 有限数据条件下边坡可靠度分析的Bootstrap方法[J]. 岩土力学, 2016, 37(3): 893-911. (Tang Xiao-song, Li Dian-qing, Cao Zi-jun, et al. Bootstrap method for slope reliability analysis with limited data[J]. Geotechnical Mechanics, 2016, 37(3): 893-911.) |
| [9] | Chen X, Lind N C. Fast probability integration by three-parameter normal tail approximation[J]. Structural Safety, 1982, 1(4): 269-276. DOI:10.1016/0167-4730(82)90003-0 |
| [10] | Guo J, Zhao J, Zeng S. Structural reliability analysis based on analytical maximum entropy method using polynomial chaos expansion[J]. Structural and Multidisciplinary Optimization, 2018, 58(3): 1187-1203. DOI:10.1007/s00158-018-1961-z |
| [11] | Li J, Chen J B. Stochastic dynamics of structures[M]. Singapore: John Wiley & Sons, 2009: 568-593. |
| [12] | Li J, Chen J B. The principle of preservation of probability and the generalized density evolution equation[J]. Structural Safety, 2008, 30(1): 65-77. DOI:10.1016/j.strusafe.2006.08.001 |
| [13] | Chen J B, Chen J P. Error estimate of point selection in uncertainty quantification of nonlinear structures involving multiple nonuniformly distributed parameters[J]. International Journal for Numerical Methods in Engineering, 2019, 118(9): 536-560. DOI:10.1002/nme.6025 |
| [14] | Li J, Yan Q, Chen J B. Stochastic modeling of engineering dynamic excitations for stochastic dynamics of structures[J]. Probabilistic Engineering Mechanics, 2012, 27(1): 19-28. DOI:10.1016/j.probengmech.2011.05.004 |
| [15] | 中交公路规划设计院. 公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG3362—2018[M]. 北京: 人民交通出版社, 2018: 483-579. (Highway Planning and Design Institute. Code for design of highway reinforced concrete and prestressed concrete bridges and culverts: JTG3362—2018[M]. Beijing: China Communications Publishing, 2018: 483-579.) |
| [16] | Li J, Chen J B. The number theoretical method in response analysis of nonlinear stochastic structures[J]. Computer Mechanics, 2007, 39(6): 693-708. DOI:10.1007/s00466-006-0054-9 |
| [17] | Meng Z, Zhou H L, Hu H, et al. Enhanced sequential approximate programming using second order reliability method for accurate and efficient structural reliability-based design optimization[J]. Applied Mathematical Modelling, 2018, 62(6): 562-579. |
| [18] | 王茜. 开裂在役钢筋混凝土梁加卸载刚度与正常使用可靠度分析[D]. 成都: 西南交通大学, 2017. (Wang Xi. Analysis of loading and unloading stiffness and normal service reliability of cracked reinforced concrete beams in service[D]. Chengdu: Southwest Jiaotong University, 2017. ) |
