近地表30m的等效剪切波速Vs(30)是地震动预测方程和建筑规范中的一个关键参数，由于技术的限制、或环境的问题、或超过预先设定的速度阈值、或经费预算的限制，实测的剪切波速剖面的深度往往未能达到30m。如何基于深度不足30m的剪切波速剖面合理地估计Vs(30)是一个非常重要、而且迫切需要解决的问题。

为了估计Vs(30)，以Boore为代表的研究人员（例如，Boore, 2004; Cadet and Duval, 2009; Boore et al., 2011）使用回归分析方法建立了一系列由某一较浅深度的等效剪切波速Vs(z)（z<30m）估计Vs(30)之间的经验关系式，简称为一点法；深度z越接近于30m，估计的Vs(30)越接近于实测值，但这些经验关系式受到区域的限制。

王海云和王苏阳（2015）提出用一个钻孔中实测的剪切波速剖面中两个较浅的、不同深度的等效剪切波速估计目标深度等效剪切波速的新方法（式1，2），简称为两点法。



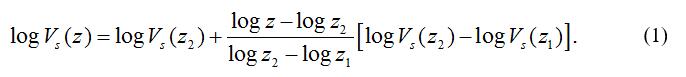
其中，Vs(z₁)，Vs(z₂)，Vs(z)分别为较浅深度z₁，z₂和目标深度z（z₁2


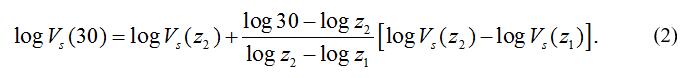
他们利用实测剪切波速剖面大于30m的两组数据，即日本Kik-Net强震动台网中594个钻孔和美国加利福尼亚135个钻孔的剪切波速剖面数据，通过实测和估计的目标深度的等效剪切波速之间的相关性，用估计的相应的目标深度的等效剪切波速划分的场地类别的准确率，验证新方法的可靠性。结果表明：新方法估计的目标深度的等效剪切波速的精度较高，而且选择的两个深度越接近目标深度，估计的等效剪切波速的精度越高(图1，2)。与Boore（2004）和Boore等（2011）利用某个地区大量钻孔的剪切波速剖面通过回归分析方法求取经验关系式的方法相比较，（1）新方法是一个简单的内插/外推函数，简单、方便、实用；（2）新方法估计的目标深度的等效剪切波速的精度更高，即使是剪切波速剖面变化非常复杂的场地；（3）新方法不受区域的影响，具有更好的适用性，可用于任何一个场地目标深度等效剪切波速的估计。




王苏阳和王海云（2017）提出另一种可供选择的两点法（式3，4）。



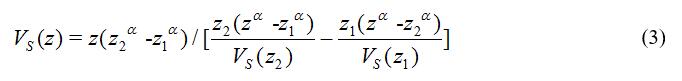
其中，a是一个调整参数，取0.6时最优。取目标深度为30m，得：



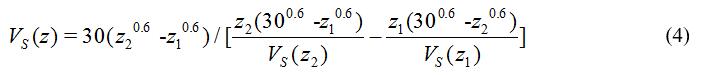
他们利用日本Kik-Net强震动台网中643个钻孔和美国加利福尼亚135个钻孔实测的剪切波速剖面大于30m的两组数据，采用王海云和王苏阳（2015）相同的方式，验证新两点法的可靠性。结果表明：新两点法估计的目标深度的等效剪切波速的精度较高，而且选择的两个深度越接近目标深度，估计的等效剪切波速的精度越高(图3，4)。与王海云和王苏阳（2015）的传统两点法相比较，在精度和划分场地类别的准确率方面均有所提高。






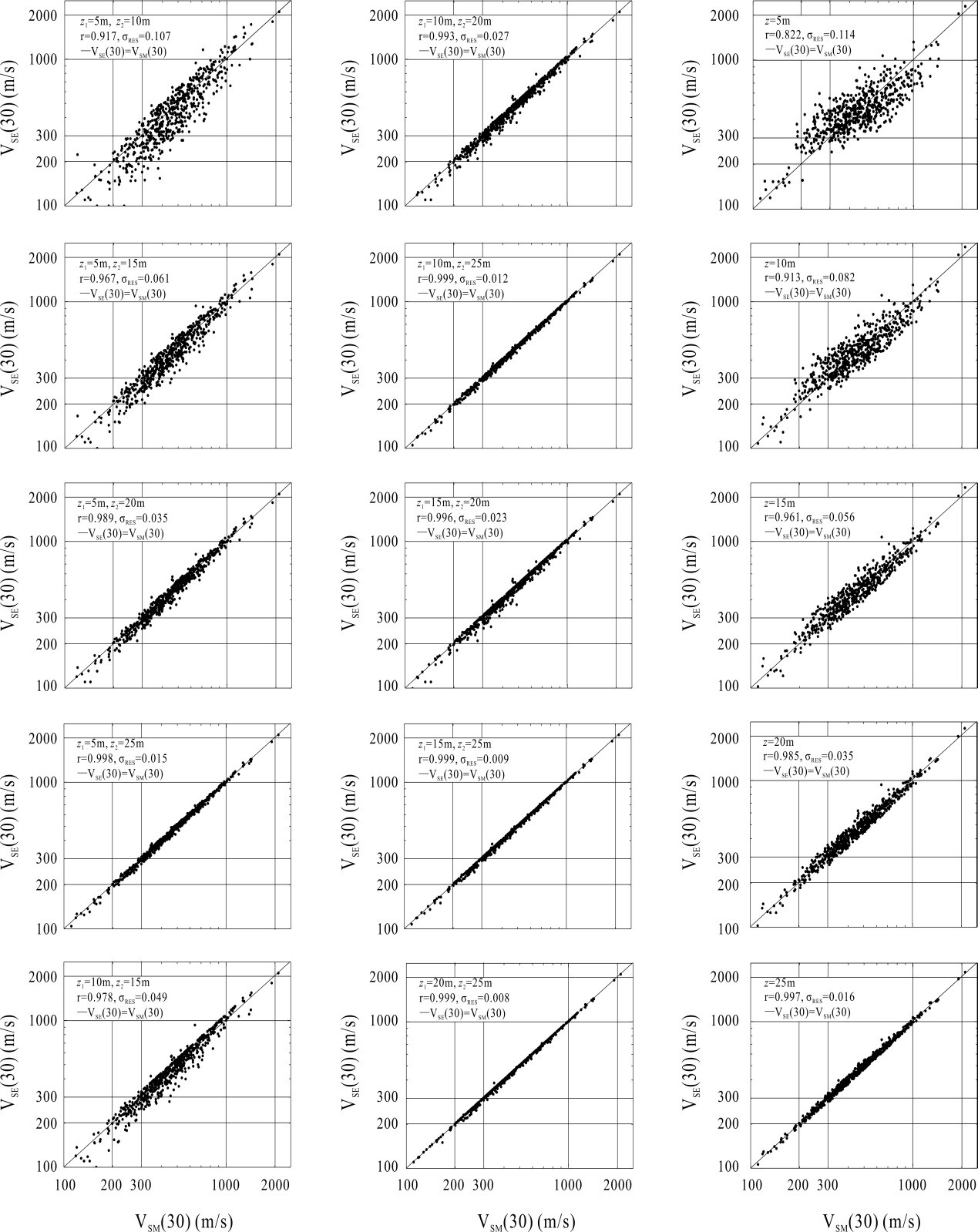
Figure 1. Correlations between V_SM(30) and V_SE(30) for the KiK-net sites in Japan using the new method of Wang and Wang (2015)(left and middle column) and the method of Boore et al. (2011) (right column), respectively. The Pearson correlation coefficient r and the standard deviations of residuals ?between V_SM(30) and V_SE(30) are presented in each graph.






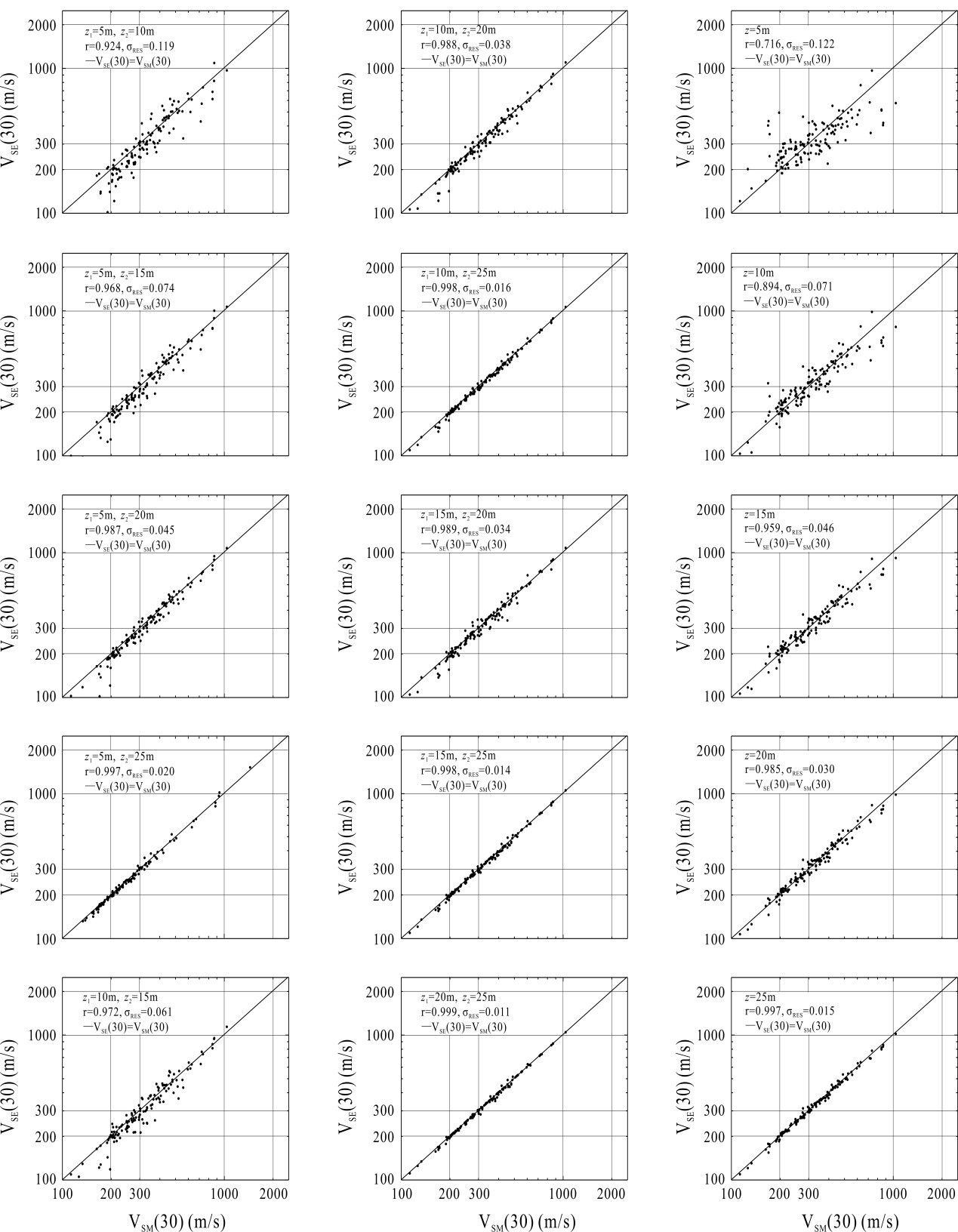
Figure 2. Correlations between V_SM(30) and V_SE(30) for the sites in California using the new method Wang and Wang (2015) (left and middle column) and the method of Boore et al. (2004) (right column), respectively. The Pearson correlation coefficient r and the standard deviations of residuals ?between V_SM(30) and V_SE(30) are presented in each graph.






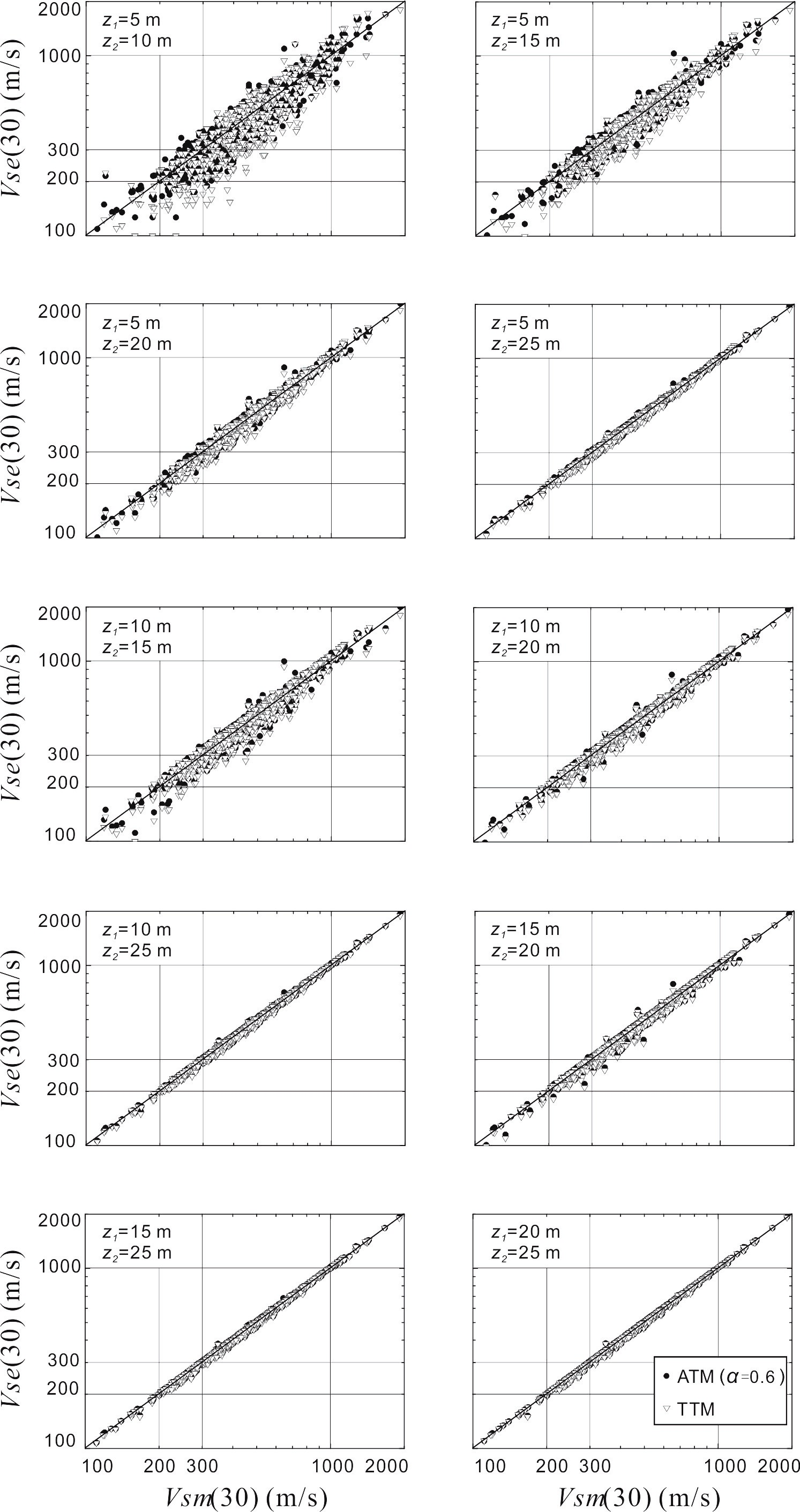
Fig.3 Correlations between measured and estimated Vs(30) for sites in Japan by the alternative two-point method (ATM) of Wang and Wang (2017) (solid round) and? the traditional two-point method (TTM) of Wang and Wang (2015) (hollow triangle), respectively.






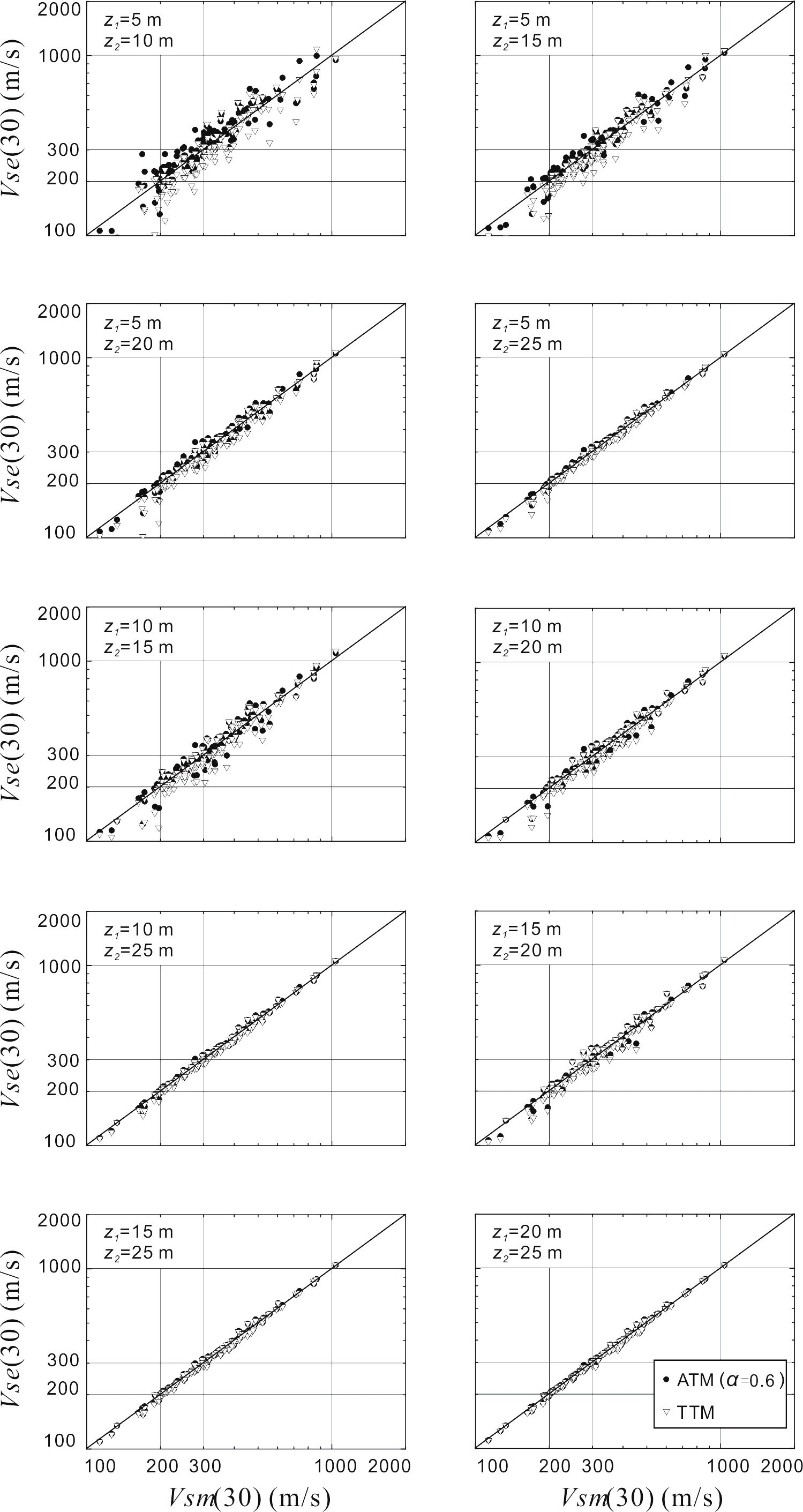
Fig.4 Correlations between measured and estimated Vs(30) for sites in California by the alternative two-point method (ATM) of Wang and Wang (2017) (solid round) and? the traditional two-point method (TTM) of Wang and Wang (2015) (hollow triangle), respectively.

该成果分别发表在国际重点权威杂志Bulletin of the Seismological Society of America和Soil Dynamics and Earthquake Engineering上。

1. Hai-Yun Wang and Su-Yang Wang. A New Method for Estimating V_S(30) from a Shallow Shear-Wave Velocity Profile (Depth< 30 m). Bulletin of the Seismological Society of America. 2015, 105( 3): 1359–1370.

2. Su-Yang Wang, Hai-Yun Wang and Qiang Li. An alternative method for estimating Vs(30) from a shallow shear-wave velocity profile (depth<30m), Soil Dynamics and Earthquake Engineering, 2017, 99:68-73.