单奇峰1,童科挺1,丁静姝1,李玉顺2
(1.宁波大学 土木工程与地理环境学院,浙江 宁波 315211;2.青岛农业大学 建筑工程学院,山东 青岛 266109)
摘要:
为研究张弦式钢竹组合工字形梁的受弯性能,以预应力水平、张弦及加载方式为基本参数,设计制作了12根张弦式钢竹组合工字形梁进行受弯试验,观察分析了加载过程中组合梁的试验现象、破坏特征,探究了各参数对组合梁承载能力、应变分布、变形性能等的影响规律,并推导得出了张弦式组合梁承载力的近似计算公式。结果表明:张弦式组合梁的整体性能优良、组合效应突出,具有良好的变形性能及承载能力；张弦试件的破坏形态主要为翼缘竹材撕裂、局部钢材屈曲等破坏；施加预应力及提高预应力水平能有效增加组合梁的变形性能,以及在相同挠度控制条件下的承载能力,且采用二点张弦布置预应力筋时可获得更好的效果；张弦式组合梁跨中截面应变分布符合平截面假定,且随着预应力水平提高而中性轴下移；最后,基于理论计算得出的承载力与试验值较为接近且相对保守,近似计算公式具有较好的适用性。
关键词: 组合结构 张弦式钢竹组合梁 受弯性能 张弦方式 承载力计算
DOI：10.11918/202303003
分类号:TU366.3
文献标识码:A
基金项目:国家自然科学基金(5,4)
Short-term bending performance of prestressed steelbamboo composite I-shaped beams
SHAN Qifeng1,TONG Keting1,DING Jingshu1,LI Yushun2
(1.School of Civil & Environmental Engineering and Geography Science, Ningbo University, Ningbo 315211, Zhejiang,China; 2.College of Civil Engineering & Architecture, Qingdao Agricultural University, Qingdao 266109, Shandong, China)
Abstract:
To study the bending performance of prestressed steelbamboo composite I-shaped beams, 12 prestressed composite I-shaped beams were designed and manufactured for bending tests, considering prestress loads, prestressing schemes, and loading schemes as basic parameters. The experimental phenomenon was observed, and failure characteristics were analyzed during the test. The influences of different parameters on the load-bearing capacity, strain distribution, and deformation performance were explored, and an approximate formula for the bearing capacity of the prestress composite beam was proposed. The results indicated that the prestressed composite beams have relatively good performances from the perspectives of combination effect, deformation characteristic, and bearing capacity. Failure modes of tested specimens were mainly owing to the bamboo flanges damage and the local buckling of steel plates. With the technique of prestress and the increase of prestress level, the deformation performances can be improved effectively, as well as the load-bearing capacity considering the same deflection situation. Moreover, the improvements can be more significant with the two-point prestressing scheme. The mid-span strain distribution of prestressed composite beams conforms to the plane section assumption, and the neutral axis moves down with the increase of the prestressing level. Finally, the bearing capacities based on the theoretical calculation matched well with the experimental results, which showed the applicability of the proposed methods.
Key words: composite structure prestressed steelbamboo composite beam bending performance prestressing scheme, calculation of load-bearing capacity
单奇峰, 童科挺, 丁静姝, 李玉顺. 张弦式钢-竹组合工字形梁的短期受弯性能[J]. 哈尔滨工业大学学报, 2024, 56(1): 93-102. DOI: 10.11918/202303003.
SHAN Qifeng, TONG Keting, DING Jingshu, LI Yushun. Short-term bending performance of prestressed steel-bamboo composite I-shaped beams[J]. Journal of Harbin Institute of Technology, 2024, 56(1): 93-102. DOI: 10.11918/202303003.
基金项目 国家自然科学基金(51978345，52278264) 作者简介 单奇峰(1990—)，男，博士研究生;
李玉顺(1968—)，女，教授，博士生导师 通信作者 李玉顺，lys0451@163.com 文章历史 收稿日期: 2023-03-01
Abstract Full text Figures/Tables PDF
张弦式钢-竹组合工字形梁的短期受弯性能
单奇峰1, 童科挺1, 丁静姝1, 李玉顺2
1. 宁波大学 土木工程与地理环境学院，浙江 宁波 315211;
2. 青岛农业大学 建筑工程学院，山东 青岛 266109
收稿日期: 2023-03-01; 录用日期: 2023-03-23; 网络首发日期: 2023-06-27
基金项目: 国家自然科学基金(51978345，52278264)
作者简介: 单奇峰(1990—)，男，博士研究生; 李玉顺(1968—)，女，教授，博士生导师
通信作者: 李玉顺，lys0451@163.com
摘要: 为研究张弦式钢-竹组合工字形梁的受弯性能，以预应力水平、张弦及加载方式为基本参数，设计制作了12根张弦式钢-竹组合工字形梁进行受弯试验，观察分析了加载过程中组合梁的试验现象、破坏特征，探究了各参数对组合梁承载能力、应变分布、变形性能等的影响规律，并推导得出了张弦式组合梁承载力的近似计算公式。结果表明：张弦式组合梁的整体性能优良、组合效应突出，具有良好的变形性能及承载能力；张弦试件的破坏形态主要为翼缘竹材撕裂、局部钢材屈曲等破坏；施加预应力及提高预应力水平能有效增加组合梁的变形性能，以及在相同挠度控制条件下的承载能力，且采用二点张弦布置预应力筋时可获得更好的效果；张弦式组合梁跨中截面应变分布符合平截面假定，且随着预应力水平提高而中性轴下移；最后，基于理论计算得出的承载力与试验值较为接近且相对保守，近似计算公式具有较好的适用性。
关键词: 组合结构 张弦式钢-竹组合梁 受弯性能 张弦方式 承载力计算
Short-term bending performance of prestressed steel-bamboo composite I-shaped beams
SHAN Qifeng1, TONG Keting1, DING Jingshu1, LI Yushun2
1. School of Civil & Environmental Engineering and Geography Science, Ningbo University, Ningbo 315211, Zhejiang, China;
2. College of Civil Engineering & Architecture, Qingdao Agricultural University, Qingdao 266109, Shandong, China
Abstract: To study the bending performance of prestressed steel-bamboo composite I-shaped beams, 12 prestressed composite I-shaped beams were designed and manufactured for bending tests, considering prestress loads, prestressing schemes, and loading schemes as basic parameters. The experimental phenomenon was observed, and failure characteristics were analyzed during the test. The influences of different parameters on the load-bearing capacity, strain distribution, and deformation performance were explored, and an approximate formula for the bearing capacity of the prestress composite beam was proposed. The results indicated that the prestressed composite beams have relatively good performances from the perspectives of combination effect, deformation characteristic, and bearing capacity. Failure modes of tested specimens were mainly owing to the bamboo flanges damage and the local buckling of steel plates. With the technique of prestress and the increase of prestress level, the deformation performances can be improved effectively, as well as the load-bearing capacity considering the same deflection situation. Moreover, the improvements can be more significant with the two-point prestressing scheme. The mid-span strain distribution of prestressed composite beams conforms to the plane section assumption, and the neutral axis moves down with the increase of the prestressing level. Finally, the bearing capacities based on the theoretical calculation matched well with the experimental results, which showed the applicability of the proposed methods.
Keywords: composite structure prestressed steel-bamboo composite beam bending performance prestressing scheme calculation of load-bearing capacity
预应力技术经过长期研究和快速发展，在国内外土木工程中的应用已越来越广，尤其在混凝土结构中的应用更为广泛。受到预应力混凝土结构的启发，不少中外学者为改善竹、木梁的受力性能，提出了预应力竹、木梁这一新型结构构件[1-3]。
文献[4-5]研究了体内预应力胶合木梁的短期受弯性能，结果表明预应力梁在受弯承载力、刚度、延性、变形能力等方面与普通梁相比都有较大程度提高；通过极限应变法得出的承载力计算值与试验值吻合较好。文献[6-8]对预应力胶合木梁试件进行受弯性能试验，研究表明以CFRP筋作为预应力筋的增强胶合木梁，其承载力和刚度均有较大幅度提升。文献[9-10]针对新型预应力配筋胶合木梁，分析了预应力水平、张弦及加载方式对梁力学性能的影响。文献[11-12]以FRP筋直径和预应力水平为参数，对预应力FRP筋增强竹梁进行力学性能试验，并采用复合梁理论预测了截面刚度。
此外，文献[13]在胶合木梁的黏合层间添加高性能预应力纤维来改善构件的受弯性能。文献[14]通过三维非线性有限元模型对GFRP预应力胶合木梁进行了模拟分析，模拟得到的荷载-挠度曲线与试验结果能较好地吻合。
钢-竹组合结构作为一种新型的高性能结构体系，集竹材低碳环保、钢材轻质高强等优良性能于一体[15]。通过一系列研究表明钢-竹组合梁的整体性能良好，组合效应突出[16-17]。然而，由于钢材和竹材的弹模相差较大，仍存在竹材抗压强度无法充分发挥等不足[18]。因此，本文借鉴预应力木梁，提出了对钢-竹组合梁实施体外张拉预应力这一新思路，并以张弦方式、加载方式、预应力水平为参数，设计12根组合梁试件并开展受弯试验研究。通过分析张弦梁的试验现象、破坏形态及受力特征，探究不同参数对张弦梁承载能力、变形性能的影响，提出并验证张弦式组合梁的承载力近似计算公式。
1 试验概况 1.1 试件设计试验设计制作了12根截面尺寸一致的钢-竹组合工字形梁试件(图 1)，其中10根为进行预应力筋张弦的梁试件(L-3~L-12)，2根为未配置预应力筋的对照试件(L-1、L-2)。组合梁的总长度均为3.8 m，计算跨度为3.5 m。二点张弦试件示意图、截面尺寸及组合梁制作方法见图 2。组合梁试件的具体设计参数见表 1：P为对两根预应力筋施加预应力值的总和；一点张弦指跨中截面下部设置一个预应力筋转向装置，实现预应力筋双折线布置，二点张弦指对称设置二个转向装置，实现预应力筋三折线布置；加载方式中，四点弯加载指通过分配梁对试件二点施加集中力(各集中力作用点到临近支座的水平距离为1 200 mm)。
Fig. 1
图 1 钢-竹组合工字形梁试件 Fig. 1 Steel-bamboo composite I-shaped beam Fig. 2
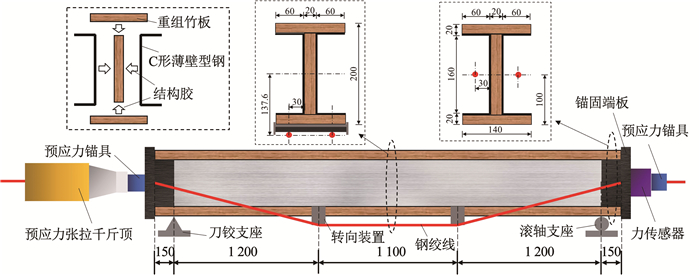图 2 二点张弦组合梁示意(mm) Fig. 2 Diagram of two-point prestressed composite beams(mm) 表 1
表 1 试件参数 Tab. 1 Parameters of specimens 试件 P/kN 张弦方式 加载方式 L-1 跨中集中加载
L-2 四点弯加载
L-3 40 一点张弦 跨中集中加载
L-4 60 一点张弦 跨中集中加载
L-5 40 一点张弦 四点弯加载
L-6 60 一点张弦 四点弯加载
L-7 40 二点张弦 跨中集中加载
L-8 60 二点张弦 跨中集中加载
L-9 40 二点张弦 四点弯加载
L-10 60 二点张弦 四点弯加载
L-11 80 二点张弦 四点弯加载
L-12 0 二点张弦 四点弯加载
表 1 试件参数 Tab. 1 Parameters of specimens
1.2 材料力学性能根据GB/T 17657—2013《人造板及饰面人造板理化性能试验方法》，对6个20 mm厚重组竹板试样进行强度和弹性模量测定，结果见表 2。冷弯薄壁C形薄壁型钢的厚度均为2 mm，根据GB/T 228.1—2010《金属材料拉伸试验第1部分：室温试验方法》，对6个试样进行抗拉试验，取平均值得到钢材屈服强度、极限强度、弹性模量及泊松比，见表 3。
表 2
表 2 重组竹板力学性能试验结果 Tab. 2 Test results of bamboo plywood 厚度/mm 抗压强度/MPa 抗拉强度/MPa 弹性模量/MPa 20.0 93.47
(0.91) 124.04
(4.88) 15 673.40
(1 108.55)
注：括号内为材性参数的标准差。
表 2 重组竹板力学性能试验结果 Tab. 2 Test results of bamboo plywood
表 3
表 3 钢材力学性能 Tab. 3 Test results of steel 厚度/mm 屈服强度/MPa 极限强度/MPa 弹性模量/105 MPa 泊松比 2.0 284.43
(3.44) 378.39
(8.73) 2.04
(0.27) 0.31
(0.05)
注：括号内为材性参数的标准差。
表 3 钢材力学性能 Tab. 3 Test results of steel
1.3 预应力设计 1.3.1 锚具及转向装置本试验组合梁为工字形截面，为能有效地锚固预应力筋，自行设计并制作了端部垫板和锚固装置。该锚固装置主要由转换钢板、带有外螺纹的锚具、预应力筋夹片和防松盖板组成，见图 3(a)。
Fig. 3
图 3 试验加载装置 Fig. 3 Loading scheme in the test 试件预应力筋设置了一点张弦(图 3(a))和二点张弦(图 3(b))两种不同形式。为使预应力筋呈折线形布置，参考混凝土梁体外预应力筋折线布置形式，并结合本试验工字形截面梁的实际情况，设计了制作简单、使用方便、安全可靠的转向装置，用以改变预应力筋的线型，见图 3(a)。
1.3.2 预应力加载预应力筋的张拉工序可大致分为3步：
1) 试件一端作为锚固端(图 3(a))，另一端作为张拉端，按顺序放置压力传感器及锚固装置，并进行预紧。
2) 使用穿心千斤顶进行张拉，对试件施加预应力；鉴于预应力筋沿梁中心左右两侧对称布置，采用两个穿心千斤顶同时加载(图 3(b))，准确控制两侧预应力筋的预应力同步上升。
3) 张拉至控制应力后，撤掉千斤顶，盖上防松盖板，并待压力传感器示数稳定后，核查预应力施加值是否达到预设水平。
1.4 加载及量测方案本试验采用两种不同的加载方式(跨中集中加载和四点弯加载)，在100 t反力架上进行试验，并通过自带力传感器的高压千斤顶施加竖向荷载。其中跨中集中加载为千斤顶通过加载支点施加荷载于梁跨中处(图 3(b))，两点加载采用刚性分配梁实现两点对称荷载(图 3(a))。试验采用力控制分级加载，并以预估极限荷载的10%为一级，每加载一级持荷3 min进行试验现象观察与数据采集。
试验前，在组合梁跨中处、两点加载时集中力作用点处、支座与集中力作用点的中点处共设置5个位移计，用以测量试件的整体变形情况；在组合梁跨中截面或距跨中300 mm处截面(跨中集中加载或一点张弦试件)共粘贴11个应变片，具体沿截面高度布置见图 4。
Fig. 4
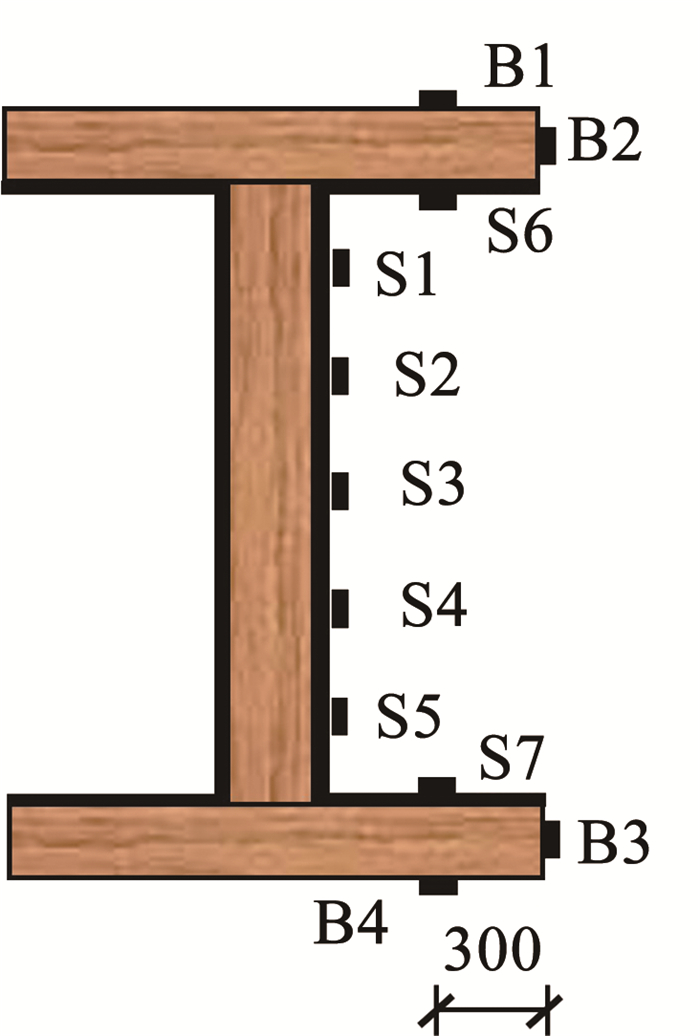图 4 应变片布置 Fig. 4 Layout of strain gagues 2 试验结果及分析 2.1 试验现象及破坏特征因设置的预应力值、加载及张弦方式不同，各组合梁在加载过程中表现出不同的破坏现象。
2.1.1 未配置预应力筋的梁试件未配置预应力筋的普通梁主要因下翼缘竹板发生纵向撕裂或横向断裂而发生破坏。未配置预应力筋的普通梁试件为L-1和L-2，在加载初期无明显现象；荷载增加至95 kN时，跨中挠度已超过梁跨度的1/50，上翼缘加载点附近钢材出现局部轻微屈曲，但仍能继续承受荷载；随着荷载继续增加，钢-竹界面脱胶加剧，钢材局部屈曲严重，跨中位置的下翼缘竹板出现细微纵向裂缝；最终，下翼缘竹板中部出现锯齿状断裂而破坏，见图 5(a)。
Fig. 5
图 5 钢-竹组合梁破坏形态 Fig. 5 Failure modes of steel-bamboo composite beams 2.1.2 一点加载的张弦梁试件一点加载的张弦梁主要因下翼缘竹板产生裂纹、层间撕裂等而发生破坏。一点加载的张弦梁试件L-3、L-4、L-7和L-8，虽预应力水平和张弦方式不同，但其破坏现象较为类似。主要特征为：在加载到85%破坏荷载时，钢-竹界面开始出现细微开胶；随着荷载增加，跨中位置的下翼缘竹板出现细微纵向裂缝(图 5(b))，并不断向两端延伸与横向扩展；临近破坏荷载时，跨中处竹板发生层间撕裂(图 5(c))，加载点处钢材局部屈曲严重(图 5(d))，组合梁失效。
2.1.3 两点加载的张弦梁试件两点加载的张弦梁主要因界面脱胶、翼缘及腹板钢材局部屈曲鼓起而发生破坏。两点加载的张弦梁试件L-5、L-6，以及L-9~L-12，其主要破坏特征为：翼缘钢-竹界面严重脱胶，加载点处上翼缘及腹板钢材明显屈曲外鼓，使组合梁无法有效保持荷载而结束试验，此时竹板尚无明显的撕裂、断裂等现象，见图 5(e)、图 5(f)。
从整个试验过程来看，是否设置预应力筋及加载方式改变对破坏形式影响较明显；预应力水平和张弦方式的变化对组合梁破坏形态的影响较小，但会改变荷载的大小。此外，未配置预应力筋的普通梁，破坏较突然，具有一定的脆性破坏特征；张弦组合梁在破坏前则具有较明显的征兆，相对而言具有更好的变形能力。
2.2 影响因素分析试验以施加预应力值、加载方式和张弦方式为主要参数变量，由试验现象及破坏特征分析可见，所设置参数的变化对组合梁受弯性能有一定的影响，现以上述参数为因素对组合梁受弯性能进行分析。
2.2.1 预应力水平不同预应力水平下各组合梁的受弯试验结果见表 4。随着施加预应力P增加，反拱挠度δ也随之增加。根据规范定义梁挠度限值为l/250，其对应的荷载为梁挠度限制荷载Fs。与普通梁L-2相比，仅增设预应力筋但预应力为0的L-12，其Fs有小幅度的提升。施加预应力并随着预应力值的增加，试件L-9~L-11的承载力有了较为显著的提高，其挠度限值对应的荷载水平相比较普通梁L-2的增幅分别为65.49%、100.61%、126.57%。可见施加预应力能改善组合梁的受力性能，使组合梁在产生相同挠度时可承受更高的荷载。
表 4
表 4 不同预应力水平下组合梁试验结果 Tab. 4 Test results of composite beams under different prestress levels 试件 P/kN δ/mm Fs/kN Fs增幅/% EIeq/(kN·m2) EIeq增幅/% L-2 0 26.31 1 497
L-9 40 4.77 43.54 65.49 1 934 22.51
L-10 60 7.57 52.78 100.61 1 941 29.66
L-11 80 9.54 59.61 126.57 1 976 31.99
L-12 0 0 29.43 11.86 1 621 8.28
表 4 不同预应力水平下组合梁试验结果 Tab. 4 Test results of composite beams under different prestress levels
图 6的荷载-跨中挠度曲线及表 4中的数据显示：增设预应力筋能提高组合梁的等效抗弯刚度EIeq，最高可达31.99%，但增加预应力值并不能明显提高组合梁的等效抗弯刚度。试件L-12由于初始未施加预应力，预应力筋锚固后仍有空隙，故预应力筋在梁加载变形过程中需先被张紧后才能发挥效果，其等效刚度值介于未加预应力筋梁和施加预应力梁之间。
Fig. 6
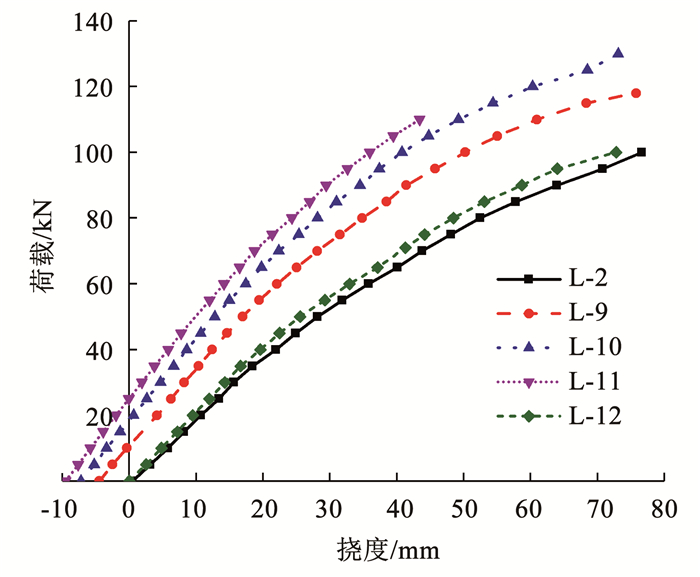图 6 不同预应力水平下组合梁荷载-跨中挠度曲线 Fig. 6 Load-midspan deflection curves of composite beam under different prestress levels 2.2.2 加载方式表 5对比了一点加载和两点加载试件的承载力试验结果。由表 5可得，两点加载试件无论是正常使用挠度限值对应的荷载水平Fs还是极限荷载Fu，较一点加载试件均有一定幅度的提升。其中，挠度限值对应的荷载水平提升了7.2%~21.7%，极限荷载提升了20.5%~50.0%。但与此同时，正常使用及承载能力极限状态下，两点加载时跨中截面的弯矩值多数小于一点加载试件。
表 5
表 5 不同加载方式下组合梁试验结果 Tab. 5 Test results of composite beams under different loading schemes 试件 加载方式 Fs/kN Fs增幅/% Ms/(kN·m) Fu/kN Fu增幅/% Mu/(kN·m) L-1 跨中集中加载 24.5 7.3 21.5 72.0 50.0 63.0
L-2 四点弯加载 26.3 15.8 108.0 64.8
L-3 跨中集中加载 35.0 12.6 30.6 95.0 24.2 83.1
L-5 四点弯加载 39.4 23.6 118.0 70.8
L-4 跨中集中加载 40.6 17.2 35.5 88.0 20.5 77.0
L-6 四点弯加载 47.6 28.5 106.0 63.6
L-7 跨中集中加载 38.3 13.6 33.5 100.0 30.0 87.5
L-9 四点弯加载 43.5 26.1 130.0 78.0
L-8 跨中集中加载 43.4 21.7 37.9 105.0 27.6 91.9
L-10 四点弯加载 52.8 31.7 134.0 80.4
表 5 不同加载方式下组合梁试验结果 Tab. 5 Test results of composite beams under different loading schemes
进一步地，以一组典型试件为例(图 7)，对比不同加载方式作用下的荷载-跨中挠度曲线。加载初期，跨中挠度随荷载呈线性增加；随着荷载增加，一点加载试件的(L-4)挠度增加速率更快。相同荷载作用下，一点加载试件会产生更大的变形量，会先一步进入弹塑性阶段，并较早出现竹材撕裂、界面胶层开裂等破坏现象。
Fig. 7
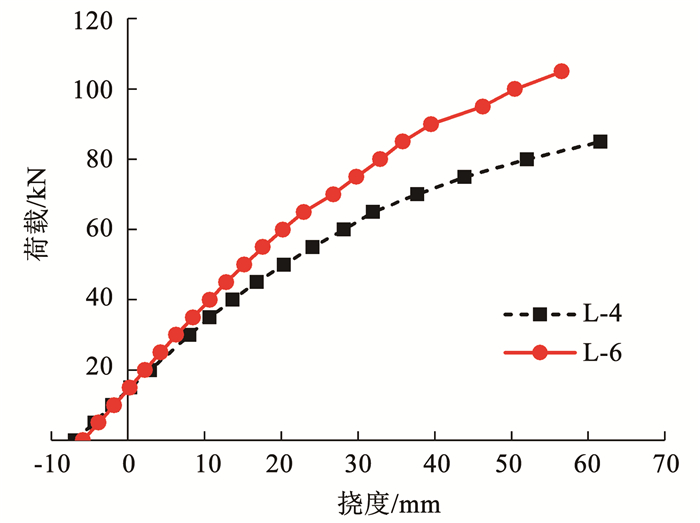图 7 试件L-4、L-6荷载-跨中挠度曲线 Fig. 7 Load-midspan deflection curves of L-4 and L-6 2.2.3 张弦方式预应力筋张弦方式的改变，会使组合梁的受力状态发生变化，从而影响其受弯性能。以试件L-4和L-8为例(图 8)，加载前期，跨中挠度基本呈线性增长；随着荷载增加，两点张弦试件呈现出更好的变形性能和更高的承载能力。结合表 6中的试验结果，由于两点张弦时，能够获得更高的预应力等效竖向荷载，反拱挠度δ均高于一点张弦试件，从而可有效提高挠度限值对应的荷载水平Fs(较一点张弦试件提高6.77%~10.99%)和受弯极限承载力Fu(较一点张弦试件提高5.26%~26.42%)，且使试件具有更好的变形能力。
Fig. 8
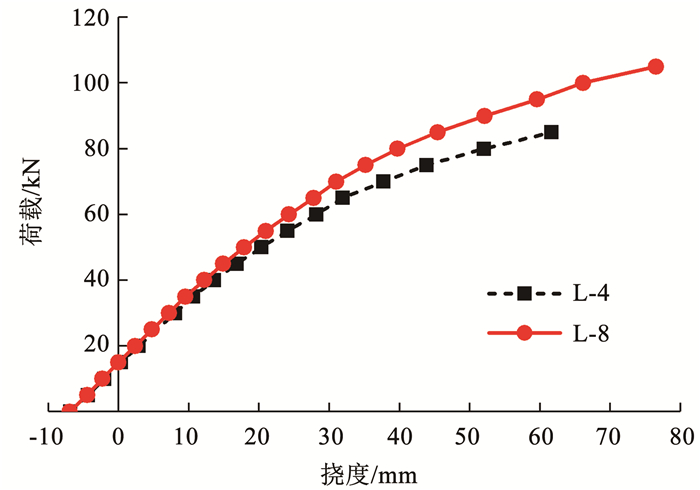图 8 试件L-4、L-8荷载-跨中挠度曲线 Fig. 8 Load-midspan deflection curves of L-4 and L-8 表 6
表 6 不同张弦方式下组合梁试验结果 Tab. 6 Test results of composite beams under different prestressing schemes 试件 张弦方式 δ/mm δ增幅/% Fs/kN Fs增幅/% Fu/kN Fu增幅/% L-3 一点张弦 4.09 19.3 35.01 9.5 95 5.3
L-7 二点张弦 4.88 38.32 100
L-4 一点张弦 6.95 1.4 40.61 6.8 88 19.3
L-8 二点张弦 7.05 43.36 105
L-5 一点张弦 3.90 22.3 39.36 10.6 118 10.2
L-9 二点张弦 4.77 43.54 130
L-6 一点张弦 5.88 28.7 47.55 11.0 106 26.4
L-10 二点张弦 7.57 52.78 134
表 6 不同张弦方式下组合梁试验结果 Tab. 6 Test results of composite beams under different prestressing schemes
2.3 应变曲线 2.3.1 跨中截面应变各组合梁跨中截面应变沿高度方向的分布情况较为相似(图 9)。荷载较小时，型钢与竹板黏结较好、界面无滑移，且截面应变沿高度基本呈线性分布，符合平截面假定；随着荷载继续增加，钢-竹界面逐渐脱胶、发生相对滑移，应变曲线在界面处出现一定突变，全截面不再符合平截面假定，但腹板和翼缘各自的应变在后续加载过程中沿高度仍呈现线性分布特征。
Fig. 9
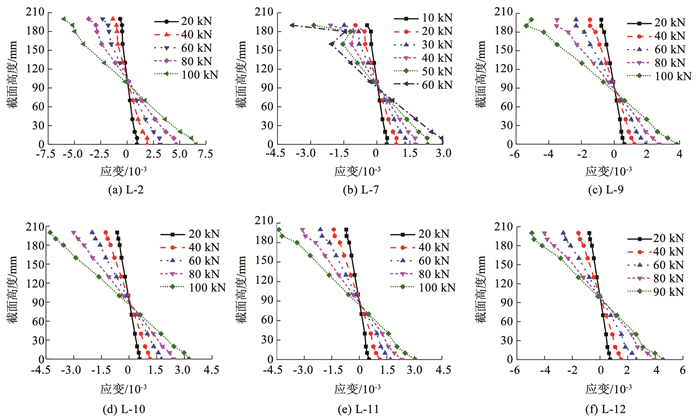图 9 组合梁跨中截面应变分布 Fig. 9 Strain distribution of composite beam at the mid-span section 未配置预应力筋的组合梁，如图 9(a)所示，在加载过程中，中性轴位置基本保持在截面1/2高度处。由于体外预应力筋与组合梁的竖向变形之间存在耦合关系，且随着竖向变形增加，预应力筋的应力增量亦不断提高。因此，如图 9(b)~(e)所示，各张弦组合梁在持续加载过程中，随着荷载增加，中性轴位置会沿截面高度方向发生一定的下移，且初始预应力水平较高的试件，中性轴下移更为明显。这一现象说明，施加预应力可增加组合梁的受压区高度，从而更为有效地发挥受压区竹材的强度。此外，对于配置预应力筋但未施加初始预应力的试件(图 9(f))，其中性轴位置与对照组试件(L-2)类似，在整个加载过程中始终保持在截面1/2高度附近，说明试件中预应力筋并未按预期发挥作用。
2.3.2 翼缘应变图 10为翼缘荷载-应变曲线，在加载初期翼缘应变基本呈线性增长，由于上、下翼缘的重组竹板处于受压、受拉外侧，其应变会略大于薄壁型钢的应变；随着荷载增加，薄壁钢板应变超过约1.4×10-3后进入屈服阶段，组合梁表现出弹塑性变形特征，荷载-应变呈曲线变化；到了加载后期，界面胶层出现细微裂缝，导致重组竹材与薄壁钢板之间的应变差增加，但两者荷载-应变曲线的发展趋势保持一致。由此可见，竹板与钢材能保持较好的协同性，两者可以整体工作、共同受力、协调变形。
Fig. 10
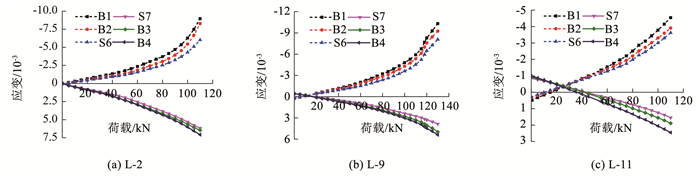图 10 翼缘荷载-应变曲线 Fig. 10 Load-strain curves of flanges 由图 10(b)、(c)可见，在施加预应力后，受压翼缘应变明显高于受拉翼缘，且随着初始预应力水平的提高，二者差值亦不断增加。与对照组试件相比，在相同荷载条件下，预应力张弦梁的受压、受拉翼缘应变均有一定的下降。这一现象再次说明，施加预应力后，竹材强度可进一步有效利用，从而节约材料。
2.4 整体变形曲线图 11反映了组合梁在各级荷载作用下整体变形情况，不同参数条件下的试件，其变形曲线均较为相似。加载初期，组合梁表现出弹性特征，每一级荷载作用下整体挠度变化呈线性增加，变形基本呈对称分布，近似为正弦半波曲线；荷载超过40%~60%破坏荷载后，每一级的变形增加越来越快，其中一点加载的试件(L-7)，在加载后期其整体变形曲线逐渐由正弦半波形转变为倒三角形。张弦方式和预应力值的变化对梁整体变形趋势无明显影响。
Fig. 11
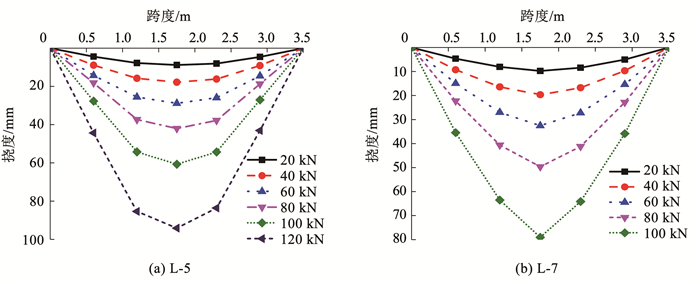图 11 梁整体变形曲线 Fig. 11 Overall deformation curves of beams 3 理论分析 3.1 预应力增量张弦式钢-竹组合梁可看做由体外预应力筋和钢-竹组合梁组成的一次超静定结构，可采用柔度法求解预应力筋的应力增量[19-21]。为简便计算过程，引入如下基本假设：
1) 组合梁受弯后截面变形符合平截面假定。
2) 不考虑端部锚固装置的微小变形。
3) 不考虑转向装置与组合梁之间的细微滑移。
4) 预应力筋处于弹性工作，且各截面上的应力均匀分布。
由力法典型方程得
$\Delta T=-\frac{\varDelta_{1 \mathrm{P}}}{\delta_{11}}$ (1)
式中：ΔT为预应力筋的应力增量；δ11为组合梁在单位应力增量作用下的位移；Δ1P为组合梁在外荷载作用下的位移。其中δ11、Δ1P可由虚功原理按以下方法计算：
$\delta_{11}=\int_0^L \frac{M_1^2}{E I} \mathrm{d} x+\int_0^L \frac{N_1^2}{E A} \mathrm{d} x+\int_0^{L_1} \frac{N_{1 \mathrm{P}}^2}{E_{\mathrm{P}} A_{\mathrm{P}}} \mathrm{d} x$ (2)
$\varDelta_{1 \mathrm{P}}=\int_0^L \frac{M_1 M_{\mathrm{P}}}{E I} \mathrm{d} x$ (3)
式中：EI和EA分别为组合梁抗弯刚度和抗压刚度，可按叠加原理分别计算薄壁型钢部分和重组竹部分；EP和AP分别为预应力筋的弹性模型和截面面积；L、L1分别为组合梁和预应力筋的总长度；MP为外荷载对组合梁产生的弯矩；M1、N1分别为单位预应力增量作用下组合梁产生的弯矩和轴力；N1P为单位预应力增量。
故外荷载作用下预应力筋的总拉力TP为
$T_{\mathrm{P}}=T_0+\Delta T$ (4)
式中T0为初始预应力施加值。
3.2 承载力考虑预应力筋的作用，钢-竹组合梁正截面抗弯承载力Mu可通过以下方法近似计算：
$M_{\mathrm{u}}=M_{\mathrm{s}}+M_{\mathrm{b}}+M_{\mathrm{sp}}$ (5)
$M_{\mathrm{s}}=\gamma_{\mathrm{s}} f_{\mathrm{u}} W_{\mathrm{s}}$ (6)
$M_{\mathrm{b}}=\gamma_{\mathrm{b}} \sigma_{\mathrm{b}} W_{\mathrm{b}}$ (7)
$M_{\mathrm{sp}}=a T_{\mathrm{p}} \sin \alpha$ (8)
式中：Ms、Mb和Msp分别为组合梁中薄壁型钢的受弯承载力，竹材的受弯承载力和预应力筋总拉力TP对组合梁产生的弯矩；Ws和Wb为薄壁型钢的抗弯截面系数和竹材的抗弯截面系数；γb为竹材截面强度的折减系数，γs为薄壁型钢截面的塑性发展系数，根据文献[22]建议，对于工字形截面，取γb=0.85，γs=1.05；a为转向点至临近支座水平距离，α为预应力筋与水平夹角。
3.3 计算结果与试验结果对比由上述方法求得组合梁承载力计算值Nu与承载力试验值Nue的对比结果见表 7。除L-6、L-11、L-12由于试件加工、材料缺陷等原因提前结束加载，导致承载力试验值偏小外，其余试件计算值与试验值吻合较好，其相对误差可基本控制在10%以内，平均误差为5.8%。鉴于上述理论公式得出的承载力偏高于试验结果, 可偏于安全的考虑5%~10%的折减系数后，用于实际工程的计算分析。
表 7
表 7 承载力试验值与计算值对比 Tab. 7 Comparison of test value and calculated value for bearing capacity 试件 Nue/kN Nus/kN Nub/kN Nup/kN Nu/kN 误差/% L-1 72 16.01 55.70 71.71 0.40
L-2 108 23.35 81.23 104.58 3.17
L-3 95 16.01 55.70 13.20 84.91 10.62
L-4 88 16.01 55.70 15.93 87.64 0.41
L-5 118 23.35 81.23 11.43 116.01 1.69
L-6 106 23.35 81.23 14.16 118.74 12.02
L-7 100 16.01 55.70 16.22 87.93 12.07
L-8 105 16.01 55.70 20.07 91.78 12.59
L-9 130 23.35 81.23 22.76 127.34 2.05
L-10 134 23.35 81.23 26.61 131.19 2.10
L-11 122 23.35 81.23 30.46 135.04 10.69
L-12 110 23.35 81.23 10.57 115.15 15.15
注：Nus、Nub和Nup分别为钢材、竹材和预应力筋理论计算的承载力。
表 7 承载力试验值与计算值对比 Tab. 7 Comparison of test value and calculated value for bearing capacity
4 结论1) 张弦式钢-竹组合梁的整体性能良好，组合效应突出。普通梁试件主要表现为下翼缘竹板断裂破坏；一点加载试件表现为翼缘竹板产生裂纹、发生层间撕裂破坏；二点加载试件表现为界面局部脱胶、翼缘及腹板钢材局部屈曲。
2) 钢-竹界面发生明显滑移前，组合梁跨中截面符合平截面假定；持续加载过程中，中性轴明显向受拉侧偏移，有利于竹材抗压强度充分发挥；组合梁整体变形可近似为正弦半波曲线，在加载后期，截面中部出现集中塑性变形，整体变形曲线呈倒三角形发展。
3) 预应力水平对组合梁影响显著，随预应力提高，组合梁挠度限值对应的荷载和抗弯刚度均提升显著；加载方式上，二点加载时挠度限值对应荷载与极限荷载较一点加载均有提升，而相应的跨中截面弯矩低于一点加载试件；张弦方式上，二点张弦试件在反拱挠度、挠度限值对应荷载和极限承载力上较一点张弦试件有一定幅度提升。
4) 基于理论分析求得的张弦式钢-竹组合梁承载力估计值与试验值吻合较好，相对误差基本在10%以内，平均误差为5.85%。
参考文献
[1] 张晋, 许清风, 张鸣, 等. 拱形张弦胶合木梁结构受力性能试验研究[J]. 建筑结构学报, 2014, 35(5): 104.
ZHANG Jin, XU Qingfeng, ZHANG Ming, et al. Experimental research on mechanical performance of arched glulam beam string structure[J]. Journal of Building Structures, 2014, 35(5): 104. DOI:10.14006/j.jzjgxb.2014.05.017
[2] BORRI A, CORRADI M, GRAZINI A. A method for flexural reinforcement of old wood beams with CFRP materials[J]. Composites Part B: Engineering, 2005, 36(2): 143. DOI:10.1016/j.compositesb.2004.04.013
[3] DE LUCA V, MARANO C. Prestressed glulam timbers reinforced with steel bars[J]. Construction and Building Materials, 2012, 30: 206. DOI:10.1016/j.conbuildmat.2011.11.016
[4] 张晋, 王卫昌, 仇荣根, 等. 体内预应力胶合木梁短期受弯性能试验研究[J]. 土木工程学报, 2019, 52(5): 23.
ZHANG Jin, WANG Weichang, QIU Ronggen, et al. Experimental study on short-term flexural behavior of internal prestressed glulam beams[J]. China Civil Engineering Journal, 2019, 52(5): 23. DOI:10.15951/j.tmgcxb.2019.05.003
[5] 张晋, 沈浩, 高森, 等. 体内预应力胶合木梁抗弯承载能力研究[J]. 湖南大学学报(自然科学版), 2018, 45(5): 134.
ZHANG Jin, SHEN Hao, GAO Sen, et al. Study on flexural capacity of internal prestressed glulam beams[J]. Journal of Hunan University (Nature Sciences), 2018, 45(5): 134. DOI:10.16339/j.cnki.hdxbzkb.2018.05.016
[6] 杨会峰, 朱文祥, 郝建东, 等. 体外预应力胶合木梁抗弯性能试验研究[J]. 南京工业大学学报(自然科学版), 2016, 38(5): 68.
YANG Huifeng, ZHU Wenxiang, HAO Jiandong, et al. Experimental study on the flexural behaviors of external prestressed glulam beams[J]. Journal of Nanjing University of Technology (Nature Sciences Edition), 2016, 38(5): 68. DOI:10.3969/j.issn.1671-7627.2016.05.011
[7] YANG Huifeng, LIU Weiqing, LU Weidong, et al. Flexural behavior of FRP and steel reinforced glulam beams: Experimental and theoretical evaluation[J]. Construction and Building Materials, 2016, 109: 550. DOI:10.1016/j.conbuildmat.2015.12.135
[8] YANG Huifeng, JU Dongdong, LIU Weiqing, et al. Prestressed glulam beams reinforced with CFRP bars[J]. Construction and Building Materials, 2016, 109: 73. DOI:10.1016/j.conbuildmat.2016.02.008
[9] 左宏亮, 宋鑫, 郭楠, 等. 张弦及加载方式对预应力胶合木梁受弯性能的影响[J]. 东北林业大学学报, 2017, 45(2): 65.
ZUO Hongliang, SONG Xin, GUO Nan, et al. Effect of jacking and loading methods on the bending performance of prestressed glue-lumber beams[J]. Journal of Northeast Forestry University, 2017, 45(2): 65.
[10] GUO Nan, WANG Wenbo, ZUO Hongliang. Flexural property of string beam of pre-stressed glulam based on influence of regulation and control[J]. Structural Durability & Health Monitoring, 2019, 13(2): 143. DOI:10.32604/sdhm.2019.04640
[11] WEI Yang, YAN Shaocong, ZHAO Kang, et al. Experimental and theoretical investigation of steel-reinforced bamboo scrimber beams[J]. Engineering Structures, 2020, 223: 111179. DOI:10.1016/j.engstruct.2020.111179
[12] ZHAO Kang, WEI Yang, YAN Shaocong, et al. Experimental and analytical investigations on flexural behavior of bamboo beams strengthened with steel bars[J]. Advances in Structural Engineering, 2021, 24(14): 3338. DOI:10.1177/13694332211026230
[13] DOLAN C W, GALLOWAY T L, TSUNEMORI A. Prestressed glued-laminated timber beam-pilot study[J]. Journal of Composites for Construction, 1997, 1(1): 10. DOI:10.1061/(ASCE)1090-0268(1997)1:1(10)
[14] GUAN Z W, RODD P D, POPE D J. Study of glulam beams pre-stressed with pultruded GRP[J]. Computers and Structures, 2005, 83(28/29/30): 2476. DOI:10.1016/j.compstruc.2005.03.021
[15] 李玉顺, 张家亮. 钢-竹组合构件及其结构体系研究进展[J]. 工业建筑, 2016, 46(1): 1.
LI Yushun, ZHANG Jialiang. State of the art of steel-bamboo composite components and structural system[J]. Industrial Construction, 2016, 46(1): 1. DOI:10.13204/j.gyjz201601001
[16] 邬沛, 李玉顺, 许达, 等. 基于遗传算法的钢-竹组合工字形梁截面优化设计[J]. 建筑结构学报, 2020, 41(1): 149.
WU Pei, LI Yushun, XU Da, et al. Multi-objective optimal section design of I-shaped section steel-bamboo composite beam using genetic algorithm[J]. Journal of Building Structure, 2020, 41(1): 149. DOI:10.14006/j.jzjgxb.2018.0018
[17] 李玉顺, 单炜, 黄祖波, 等. 压型钢板-竹胶板组合楼板的力学性能试验研究[J]. 建筑结构学报, 2008, 29(1): 96.
LI Yushun, SHAN Wei, HUANG Zubo, et al. Experimental study on mechanical behavior of profiled steel sheet-bamboo plywood composite slabs[J]. Journal of Building Structure, 2008, 29(1): 96. DOI:10.14006/j.jzjgxb.2008.01.014
[18] WU Mingtao, MEI Lidan, GUO Nan, et al. Mechanical properties and failure mechanisms of engineering bamboo scrimber[J]. Construction and Building Materials, 2022, 344: 1. DOI:10.1016/j.conbuildmat.2022.128082
[19] 许锋. CFRP筋体外预应力加固钢筋混凝土梁受弯性能研究[D]. 武汉: 武汉大学, 2014: 71
XU Feng. Flexural performance of reinforced concrete beams strengthend by external prestressing CFRP tendons[D]. Wuhan: Wuhan University, 2014: 71
[20] 姚辉瑞. 预应力钢-混凝土组合梁挠度变形分析和计算理论研究[D]. 西安: 长安大学, 2005: 50
YAO Huirui. Deflection analysis and calculation theory research of prestressed steel-concrete composite beam[D]. Xi'an: Chang'an University, 2005: 50
[21] 詹界东, 张文福, 王娜, 等. 预应力组合梁的弹性性能分析[J]. 大庆石油学院学报, 2004(1): 112.
ZHAN Jiedong, ZHANG Wenfu, WANG Na, et al. Elastic behavior analysis of prestressed composite beam[J]. Journal of Daqing Petroleum Institute, 2004(1): 112.
[22] LI Yushun, SHAN Wei, SHEN Huangying, et al. Bending resistance of I-section bamboo-steel composite beams utilizing adhesive bonding[J]. Thin-Walled Structures, 2015, 89: 17. DOI:10.1016/j.tws.2014.12.007
