魏文军1,2,张轩铭1,杨立本1
(1.兰州交通大学 自动化与电气工程学院,兰州 730070; 2.兰州交通大学 光电技术与智能控制教育部重点实验室,兰州 730070)
摘要:
针对实际中轴承的故障数据少难以满足深度学习数据大量训练模型的要求,利用卷积神经网络的微小特征提取优势和模糊聚类不需要训练即可完成分类的特点,提出了一种基于模糊聚类和改进Densenet网络的小样本轴承故障诊断方法。首先将预训练微调的Densenet网络去掉分类只保留特征提取层,设计一个维度自适应全局均值池化层（GAP）代替全连接层（FC）,其次利用模糊聚类代替Densenet网络的softmax分类层,不需要训练即可完成分类。实验结果表明:该算法利用小样本数据训练网络中的GAP参数,模型需要的训练样本大大减少,诊断时将轴承时域图像输入到网络中,在GAP层输出1 920个特征数据,不同故障状态的特征数据构建特征向量矩阵,利用模糊聚类方法求得模糊相似矩阵和模糊等价矩阵,当置信因子从大到小变化时,由对应布尔矩阵得到动态聚类图,从而实现轴承故障分类。
关键词: 小样本 全局均值池化层 迁移学习 模糊聚类 故障诊断
DOI：10.11918/202206075
分类号:TP391;U298
文献标识码:A
基金项目:国家自然科学基金(52162050)；光电技术与智能控制教育部重点实验室(兰州交通大学)开放课题(KFKT2020-11)
Fault diagnosis of small sample bearings based on fuzzy clustering and improved Densenet network
WEI Wenjun1,2,ZHANG Xuanming1,YANG Liben1
(1.School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2.Key Laboratory of Opto-Technology and Intelligent Control of Ministry of Education (Lanzhou Jiaotong University), Lanzhou 730070, China)
Abstract:
In practice, the scarcity of failure data for bearings makes it challenging to meet the extensive training requirements of deep learning models. This paper leverages the fine-grained feature extraction capabilities of Convolutional Neural Networks and the classification ability of fuzzy clustering without the need for training, proposing a small-sample bearing fault diagnosis method based on fuzzy clustering and an improved Densenet network. Initially, the pretrained Densenet network is modified by removing the classification layer and retaining only the feature extraction layers, and designing an Adaptive Global Average Pooling (GAP) layer to replace the Fully Connected (FC) layer. Subsequently, fuzzy clustering is utilized instead of the Densenet networks softmax classification layer, eliminating the need for training to achieve classification. Experimental results demonstrate that by training the GAP layer parameters with small-sample data, the model significantly reduces the requirement for training samples. During diagnosis, bearing time-domain images are input into the network, outputting 1 920 feature data at the GAP layer. Feature vectors matrices are constructed from the feature data of different fault states. Fuzzy similarity matrices and fuzzy equivalence matrices are obtained using fuzzy clustering methods. As the confidence factor changes from high to low, dynamic clustering diagrams are derived from the corresponding Boolean matrices, thereby achieving bearing fault classification.
Key words: small sample global mean pooling layer transfer learning fuzzy clustering fault diagnosis
魏文军, 张轩铭, 杨立本. 基于模糊聚类和改进Densenet网络的小样本轴承故障诊断[J]. 哈尔滨工业大学学报, 2024, 56(3): 154-163. DOI: 10.11918/202206075.
WEI Wenjun, ZHANG Xuanming, YANG Liben. Fault diagnosis of small sample bearings based on fuzzy clustering and improved Densenet network[J]. Journal of Harbin Institute of Technology, 2024, 56(3): 154-163. DOI: 10.11918/202206075.
基金项目 国家自然科学基金(52162050)；光电技术与智能控制教育部重点实验室(兰州交通大学)开放课题(KFKT2020-11) 作者简介 魏文军(1971—)，男，教授，硕士生导师 通信作者 张轩铭，1224742542@qq.com 文章历史 收稿日期: 2022-06-18
Abstract Full text Figures/Tables PDF
基于模糊聚类和改进Densenet网络的小样本轴承故障诊断
魏文军1,2, 张轩铭1
, 杨立本1 1. 兰州交通大学 自动化与电气工程学院，兰州 730070;
2. 兰州交通大学 光电技术与智能控制教育部重点实验室，兰州 730070
收稿日期: 2022-06-18; 录用日期: 2022-06-01; 网络首发日期: 2024-03-27
基金项目: 国家自然科学基金(52162050)；光电技术与智能控制教育部重点实验室(兰州交通大学)开放课题(KFKT2020-11)
作者简介: 魏文军(1971—)，男，教授，硕士生导师
通信作者: 张轩铭，1224742542@qq.com
摘要: 针对实际中轴承的故障数据少难以满足深度学习数据大量训练模型的要求，利用卷积神经网络的微小特征提取优势和模糊聚类不需要训练即可完成分类的特点，提出了一种基于模糊聚类和改进Densenet网络的小样本轴承故障诊断方法。首先将预训练微调的Densenet网络去掉分类只保留特征提取层，设计一个维度自适应全局均值池化层(GAP)代替全连接层(FC)，其次利用模糊聚类代替Densenet网络的softmax分类层，不需要训练即可完成分类。实验结果表明：该算法利用小样本数据训练网络中的GAP参数，模型需要的训练样本大大减少，诊断时将轴承时域图像输入到网络中，在GAP层输出1 920个特征数据，不同故障状态的特征数据构建特征向量矩阵，利用模糊聚类方法求得模糊相似矩阵和模糊等价矩阵，当置信因子从大到小变化时，由对应布尔矩阵得到动态聚类图，从而实现轴承故障分类。
关键词: 小样本 全局均值池化层 迁移学习 模糊聚类 故障诊断
Fault diagnosis of small sample bearings based on fuzzy clustering and improved Densenet network
WEI Wenjun1,2, ZHANG Xuanming1
, YANG Liben1 1. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;
2. Key Laboratory of Opto-Technology and Intelligent Control of Ministry of Education (Lanzhou Jiaotong University), Lanzhou 730070, China
Abstract: In practice, the scarcity of failure data for bearings makes it challenging to meet the extensive training requirements of deep learning models. This paper leverages the fine-grained feature extraction capabilities of Convolutional Neural Networks and the classification ability of fuzzy clustering without the need for training, proposing a small-sample bearing fault diagnosis method based on fuzzy clustering and an improved Densenet network. Initially, the pretrained Densenet network is modified by removing the classification layer and retaining only the feature extraction layers, and designing an Adaptive Global Average Pooling (GAP) layer to replace the Fully Connected (FC) layer. Subsequently, fuzzy clustering is utilized instead of the Densenet network's softmax classification layer, eliminating the need for training to achieve classification. Experimental results demonstrate that by training the GAP layer parameters with small-sample data, the model significantly reduces the requirement for training samples. During diagnosis, bearing time-domain images are input into the network, outputting 1 920 feature data at the GAP layer. Feature vectors matrices are constructed from the feature data of different fault states. Fuzzy similarity matrices and fuzzy equivalence matrices are obtained using fuzzy clustering methods. As the confidence factor changes from high to low, dynamic clustering diagrams are derived from the corresponding Boolean matrices, thereby achieving bearing fault classification.
Keywords: small sample global mean pooling layer transfer learning fuzzy clustering fault diagnosis
轴承作为机械设备的重要旋转部件，也是旋转机械设备重要的故障源之一，复杂的结构和严酷的工作条件，容易出现故障而造成较大的事故和经济损失[1-2]，据统计机械设备中30%的故障由轴承引起[3]。为确保机械设备的长期稳定运行，有效的轴承故障诊断显得尤为重要。传统的故障诊断主要分为数据的特征提取和故障分类，对采集的振动信号进行时频域分析并提取特征，然后利用分类器进行特征分类[4-5]，特征提取方法主要包括傅里叶变换[6]、小波变换(WT)[7]、局部均值分解(LMD)[8]以及经验模态分解(EMD)[9-10]等；故障分类主要包括支持向量机(SVM)、隐马尔可夫模型[11]和人工神经网络[12]等。但此类方法存在一定弊端，数据处理往往需要一定的专业知识及人工经验，存在数据利用不足以及早期微弱故障特征提取不充分等问题，其次机器学习需要手动挖掘特征，算法架构过于浅薄难以处理复杂的非线性故障问题。
随着大数据时代的到来，以“数据驱动”为基础的深度学习[13]在图像处理[14]和故障诊断[15-16]展现了独特的优势。文献[15]在传统CNN激活函数的基础上提出了STAC-tach自适应激活函数，通过改进残差网络ResNet建立ResNet-STAC-tanch模型实现对轴承的非线性特征自适应提取，文献[16]提出了一种基于热成像的轴承故障诊断，利用不同工况下的热成像结合ANN和CNN实现故障诊断。上述文献中存在一个问题，利用卷积神经网络进行故障诊断需要大量数据训练，但在实际应用的过程中故障数据难以获得，数据量少难以满足训练的要求，在数据不足的情况下容易发生过拟合现象严重影响分类结果。文献[16-17]将CNN与SVM结合提出了小样本情况下的故障诊断，文献[17]利用迁移学习建立了故障样本特征计算模型，将源域中学习到的故障信息迁移到目标域，映射模型的输出作为SVM的输入，借助迁移学习和SVM分类器实现小样本下的燃气机故障诊断，文献[18]以轴承时域图像为输入，训练CNN模型，通过softmax层输出的分类结果判断是否满足SVM最终分类条件，通过多次训练提取出最适合SVM分类的特征实现故障诊断。上述文献中采用SVM作为最终分类器，SVM本质上为二分类器，当故障种类繁杂和样本多时，需要构建多分类器，运算量大耗时长，实现多分类情况较困难，同时上述文献CNN模型中全连接层中存在大量参数，全连接层与softmax在整个卷积神经网络中起到“分类器”作用，全连接层将卷积池化提取的特征映射到样本空间，但在训练CNN网络时多数数据用于训练全连接层参数，如果分类层使用不需要训练的方法实现分类，将可大大减少训练数据，简化卷积神经网络结构。
预训练微调可以将源域学习到的知识迁移到目标域[19]，由于源域中已经学习到大量基础知识，在目标域中仅训练部分特殊特征数据，即可完成网络训练。文献[20]根据源域与目标域间数据分布不同，建立域自适应神经网络模型，实现轴承不同工况间的故障诊断，文献[21]使用与目标域近似的辅助数据，利用LSSVM迁移学习算法实现变工况下的轴承故障诊断，上述文献在在变工况情况下可用数据充足，但实际大部分变工况情况下数据较少，同时上述文献利用迁移学习对不同轴承型号情况下的故障诊断识别率提升程度较小，达不到实用化程度。
本文研究发现训练数据中有相当数据用于训练CNN网络中的全连接层和softmax层，而全连接层和softmax层主要用于分类，如果减少全连接层网络参数和使用不需要训练的分类算法则可以显著减少训练数据。模糊聚类(fuzzy clustering means, FCM)作为一种无监督分类方法，利用模糊数学原理可以实现不需要训练即可实现多种故障分类，广泛应用于故障诊断[22]和图像处理[23]，为此本文针对以上不足借助凯斯西储大学[24]，提出了一种基于模糊聚类的改进CNN-模型的轴承故障诊断，首先设计一维度自适应的全局均值池化层(global average pooling, GAP)替换卷积神经网络的全连接层网络，缩减网络结构和参数量，减少所需训练样本，同时以模糊聚类代替softmax函数分类，将轴承时域图像输入到改进后的网络中，在网络的GAP层输出特征，不同轴承时域图像的特征构建特征向量矩阵，采用模糊聚类分析算法求该矩阵的模糊等价矩阵，在模糊等价矩阵中，当λ(可变阈值)在[0, 1]上变动时，模糊等价矩阵转化为等价的布尔矩阵，由布尔矩阵可以得到动态聚类图并得到故障分类结果，从而实现轴承的故障诊断。最后在凯斯西储大学轴承公开数据集的基础上假设源域数据充足目标域数据较少的情况下对同型号同工况和同型号跨工况进行实验验证，实验结果表明该算法在配合少量目标域数据的情况下能够准确识别轴承故障。
1 理论基础 1.1 CNN传统的卷积神经网络(CNN)主要由卷积层、池化层、激活函数、全连接层和Softmax层组成[25]。卷积层作为CNN网络的核心，通过Relu激活函数获得非线性特征，池化层可以保持数据的显著特征，降低特征的维度，卷积层通过池化层进入一个或多个全连接层，然后进入Softmax层分类。
Densenet神经网络在2017年由Gao Huang等提出，Densenet以前馈的方式将每个层连接在一起，相比于传统卷积神经网络中n层对应n个连接，其在n层的输出为xn=Hn(xn－1)，而Densenet网络n层中有(n+1)/2个连接，其在n层的输出为xn=Hn([x0, x1, …, xn－1])，这大大减轻了梯度消失，增强了特征的传递和利用，减少了参数量，提高了网络的整体特征提取能力。
在现有的机器学习理论下，要训练出一个鲁棒性强的深度学习模型，需要大量的数据支撑，这在实际应用中很难满足。迁移学习将预训练好的网络模型进行迁移，在新应用场合用少量数据进行再训练，不需要大量数据即可建立精确的深度学习模型。
迁移学习由域和任务组成，一个域D由一个特征空间X和特征空间上总体概率分布P(X)构成，X=x1, x2, …, xn，其中已有的知识叫源域，要学习的新知识叫目标域，给定一个有标记的源域 Ds={xi, yi}i=1n和一个无标记目标域Dt={xj}j=n+1n+m，这两个领域数据分布在P(xs)和P(xt)，P(xs)≠P(xt)。迁移学习目的是借助Ds知识，来学习目标域Dt的标签。当目标数据远小于源数据时可以采用微调，固定较浅层网络参数，使用少量数据训练深层参数。
1.2 全局均值池化层全连接层(fully connected layer, FC)中参数量占了整个网络的80%~90%，降低了训练速度且容易发生过拟合现象，本文提出使用全局均值池化层代替FC, 利用池化层的降维，图 1为GAP与FC结构对比，传统的方法经过卷积层特征提取后, 经全连接层将特征展开逐过程降维分类，而GAP替代FC可以将任意维度的特征以一维特征输出，增强卷积层特征提取能力的同时又保留了卷积层和池化层提取的空间信息，减少了模型中的参数量，一方面减少数据训练量，另一方面防止过拟合。本文算法拟设计维度自适应的GAP代替卷积神经网络模型中的全连接网络部分。
Fig. 1
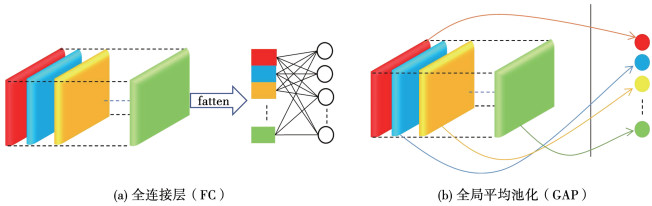图 1 FC与GAP结构对比 Fig. 1 Comparison of FC and GAP structures 1.3 模糊聚类算法模糊聚类作为一种无监督分类算法，利用模糊数学原理，对所研究的事物按一定标准分类，本文采用基于模糊关系矩阵的聚类算法代替卷积神经网络中的softmax分类层分类，基于模糊关系的聚类分析如下。
设被分类轴承健康状态共n种，其论域表示为U=(x1, x2, x3, …, xn)，每种健康状态有m个特征指标Xi=(xi1, xi2, …, xim), i=1, 2, …, n，由此可得相应的数据矩阵：
$\boldsymbol{X}=\left[\begin{array}{cccc}x_{11} & x_{12} & \cdots & x_{1 m} \\x_{21} & x_{22} & \cdots & x_{1 m} \\\vdots & \vdots & \vdots & \vdots \\x_{n 1} & x_{n 2} & \cdots & x_{n m}\end{array}\right]$ (1)
1) 为消除特征指标之间量纲不同的问题，满足模糊聚类算法要求需对上述矩阵作标准化处理，采用平移· 标准差和平移· 极差变换将区间压缩到[0, 1]。
平移· 标准差:
$x_{i k}^{\prime}=\frac{x_{i k}-\bar{x}_k}{s_k}$ (2)
$s_k=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(x_{i k}-\bar{x}_k\right)^2}$ (3)
平移· 极差：
$x_{i k}^{\prime \prime}=\frac{x_{i k}^{\prime}-\min\limits_{1 \leqslant i \leqslant n}\left\{x_{i k}^{\prime}\right\}}{\max\limits_{1 \leqslant i \leqslant n}\left\{x_{i k}^{\prime}\right\}-\min\limits_{1 \leqslant i \leqslant n}\left\{x_{i k}^{\prime}\right\}}$ (4)
式中：i=1, 2, …, n，k=1, 2, …, m。
2) 根据分类对象m个特征指标得到的标准化数据，利用距离法计算分类对象样本间的相似程度rij，建立模糊模糊相似矩阵R，其中rij=1－cd(xi, xj)。
欧几里得距离：
$d\left(x_i, x_j\right)=\sqrt{\sum\limits_{k=1}^m\left(x_{i k}-x_{j k}\right)^2}$ (5)
3) 由上述得到的模糊相似矩阵，需利用传递闭包法求得传递闭包t(R), 得到模糊等价矩阵R*，对于不同的λ，当存在rij>λ时，将两个样本归为一类，对于不同的置信因子λ∈[0, 1]得到不同的聚类结果，形成动态聚类图[26]。
2 建立Densenet-GAP-FCM轴承故障诊断模型 2.1 预训练微调本文所使用预训练微调方法如图 2所示，在源域上预训练Densenet卷积神经网络后将源域中网络参数迁移到目标域，冻结网络的1到n-3层网络参数，使用新的卷积层替换Densenet最后一个可学习层，以便匹配新数据集，在目标域中使用小样本数据重新训练微调深层网络，建立TL-Densenet模型。其数学表达式如下[27]：
$\Delta w_{i j}=\left\{\begin{array}{l}0, l＜n-3 \\-\alpha\left(\hat{y}_j-y_j\right) \times f^{\prime} \times m_j, n-3＜l\end{array}\right.$ (6)
Fig. 2
图 2 预训练微调示意图 Fig. 2 Schematic diagram of fine-tuning transfer learning 式中：Δwij为两神经元之间权重的变化，α为学习率，
2.2 全局均值池化层代替全连接层传统卷积神经网络进行分类时，经过多层卷积与池化后，使用FC与softmax进行分类，但在小样本的情况下，FC层因参数多以及训练数据不足容易出现过拟合现象，导致诊断率下降，针对传统卷积神经网络CNN中参数量大、训练时间长以及需要大量数据训练等不足，在2.1节的基础上对预训练微调的Densenet网络基础上进行改进，为达到降低网络参数、加快识别分类速度的目的，本文设计一维度自适应调节维度的全局均值池化层替换Densenet网络中的全连接网络部分，降低整个网络90%以上的参数量，该全局均值池化可根据输出轴承特征维度和类别进行自适应调整，在多层感知器后为分类中的每个类别生成一个feature map，并对每个feature map进行全局平均。在GAP结构上设计一个[x, wout, n]的自适应矩阵，x代表前一层卷积输入GAP层通道数，n代表池化核的数量，wout代表前一层的卷积层输入特征图feature map尺寸：
$w_{\text {out }}=\frac{w_{\text {in }}-F}{s}+1$ (7)
式中：win为输入特征图大小，F为卷积核大小，s为步长。对于前一卷积层输入到GAP的feature map，GAP的池化核自动匹配卷积核输出的个数n和维度，并对特征图尺寸wout利用池化运算计算出一个与CNN中FC等效的全局平均值作为GAP输出的特征值，用于后续分类。GAP的运算方式为
$S_{\text {avg-pooling }}^l=\frac{1}{c} \sum\limits_{i=1}^c X_{1: h, 1: w, i}^l$ (8)
式中：Slavg－pooling为第l层卷积经GAP得到的均值, Xl1∶ h, 1∶ w, i为均值池化核对应的输出特征图映射的范围横向第一行到第h行的像素点、纵向第一列到w列的像素点。
以VggNet-16为例对改进后的参数量进行对比，如表 1所示，全局总参数减少了90.92%。其中卷积层参数量计算公式为
$P=C_0 \times\left(k_w \times k_h \times C_i+1\right)$ (9)
表 1
表 1 改进后各层参数量对比 Tab. 1 Compare the parameters of each layer VggNet-16 改进前参数量 改进后参数量 卷积层 12，351，168 12，351，168
池化层 0 0
全连接层 123，633，664 0
总参数 135，984，832 12，351，168
表 1 改进后各层参数量对比 Tab. 1 Compare the parameters of each layer
式中：C0为输出通道，Ci为输入通道，kw×kh×Ci为一个卷积核的权重数量。
2.3 模糊聚类算法代替Softmax分类采用第一节中模糊聚类算法代替TL-Densenet-GAP网络中的Softmax分类层，在GAP层中利用activations函数输出GAP层提取的特征，建立TL-Densenet-GAP-FCM模型，构建特征向量矩阵，由模糊聚类构建动态聚类图，实现轴承的故障诊断。改进后的网络模型如图 3所示，该模型由输入层、特征提取层、GAP层和模糊聚类分类层组成，采集轴承时域图像输入到卷积层自动提取特征，在网络的GAP层降维后输出特征，在实际应用中，将标准数据得到的特征向量与待测样本的特征向量构建特征向量矩阵，然后由模糊聚类形成聚类图输出诊断结果。
Fig. 3
图 3 轴承故障诊断框图 Fig. 3 Block diagram of bearing fault diagnosis 3 实验验证分析 3.1 同型号同工况情况轴承故障诊断实验采用凯斯西储大学轴承公开数据集中的驱动端数据，利用该数据集验证本文所提算法在同型号同工况下的轴承故障诊断情况，其中轴承型号为SKF6205，采样频率为12 kHz，选取电机转速为1 797 r/min工况下故障直径分别为0.177 8 mm和0.533 4 mm的外圈故障、内圈故障和滚动体故障6类故障状态，再加上正常状态共7类数据，从这7类数据的时域信号中取1 000个连续点作为一个样本，建立标准数据库。图 4为正常状态下的轴承时域信号，图 5为不同故障状态下的轴承时域信号。每组选取20个样本，共140组，以卷积神经网络DenseNet-201为例，利用预训练微调训练建立TL-Densenet-GAP-FCM模型，将源域中轴承的故障知识迁移到目标域，提高模型的特征提取能力。
Fig. 4
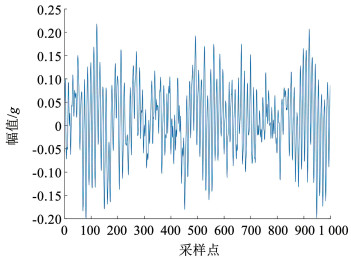图 4 轴承正常状态f0时域曲线图 Fig. 4 Time domain diagram of bearing under normal condition f0 Fig. 5
图 5 轴承各故障时域曲线图 Fig. 5 Time domain of bearing fault 图 6轴承时域图输入TL-Desenet-GAP-FCM模型中，在GAP层输出1 920个特征向量，其中图 5和图 6用于构建标准数据向量库，如表 2所示，图 6输出的向量构建待测样本特征向量，如表 3所示，其中d0为正常轴承待测样本。
Fig. 6
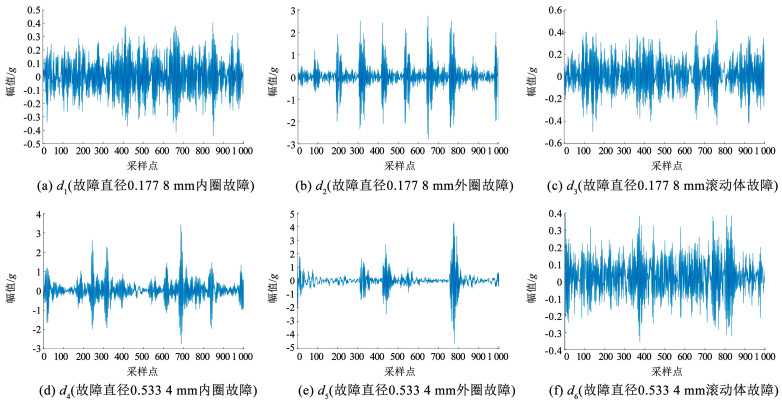图 6 测试样本轴承各故障曲线图 Fig. 6 Time domain diagram of bearing faults under test 表 2
表 2 标准数据库样本特征 Tab. 2 Standard database characteristics 标准数据库 特征1 特征2 特征3 特征4 ··· 特征1917 特征1918 特征1919 特征1920 f0 -1.811 -9.875 -1.253 -0.001 ··· 0.532 9.266 1.822 -1.161
f1 -1.835 -2.027 1.122 -0.001 ··· -0.049 -0.398 -0.175 -0.664
f2 -2.240 -9.875 -1.253 0.001 ··· -0.512 -0.293 -0.255 -0.100
f3 -2.266 0.001 9.764 6.809 ··· 0.086 -0.087 1.179 0.194
f4 -1.937 -1.710 5.369 0.002 ··· -0.221 -0.018 -0.551 0.253
f5 -1.583 -2.279 2.649 0.001 ··· 0.262 -0.247 -0.277 -0.441
f6 -3.108 3.574 1.193 5.129 ··· 0.445 -0.696 -1.491 -0.297
表 2 标准数据库样本特征 Tab. 2 Standard database characteristics
表 3
表 3 待测样本特征 Tab. 3 Characteristics of samples to be tested 待测样本 特征1 特征2 特征3 特征4 ··· 特征1917 特征1918 特征1919 特征1920 d0 -2.463 -2.507 8.235 -0.002 ··· 0.432 0.888 1.110 -0.764
d1 -2.565 -4.624 1.108 6.524 ··· 0.750 -0.332 1.142 -0.340
d2 -2.188 -4.045 -6.466 0.001 ··· -0.178 -0.063 -0.031 -0.261
d3 -2.609 9.920 0.001 0.001 ··· -0.234 0.423 0.563 0.649
d4 -1.824 0.001 1.447 7.671 ··· 0.273 -0.090 -0.091 1.111
d5 -1.776 -5.498 8.250 8.706 ··· 1.216 -0.508 -0.387 -0.436
d6 -3.245 8.929 7.922 0.001 ··· 0.521 -0.508 0.491 -0.112
表 3 待测样本特征 Tab. 3 Characteristics of samples to be tested
将表 2和表 3数据建立特征向量矩阵，为消除数据间量纲不同的影响，需对特征向量矩阵作标准化处理，使数据分布在[0, 1]内, 得到标准化矩阵 X如下所示：
$\boldsymbol{X}=\left[\begin{array}{ccccccccc}0.863\;1 & 0 & 0.433\;8 & 0.160\;8 & \cdots & 0.598\;9 & 0.440\;0 & 1 & 0 \\0.848\;4 & 0.345\;2 & 0.502\;7 & 0.302\;8 & \cdots & 0.267\;7 & 0.187\;9 & 0.158\;2 & 0.262\;6 \\0.605\;0 & 0.606\;1 & 0 & 0.773\;2 & \cdots & 0 & 0.254\;2 & 0.124\;6 & 0.466\;9 \\0.350\;8 & 1 & 0.979\;1 & 0.646\;3 & \cdots & 0.346\;5 & 0.384\;2 & 0.729\;0 & 0.596\;5 \\0.787\;2 & 0.291\;4 & 0.736\;8 & 1 & \cdots & 0.424\;4 & 0.427\;7 & 0 & 0.622\;6 \\1 & 0.344\;3 & 0.586\;8 & 0.791\;2 & \cdots & 0.448\;1 & 0.283\;3 & 0.115\;5 & 0.317\;0 \\0.082\;1 & 0.480\;0 & 0.506\;5 & 0.609\;1 & \cdots & 0.554\;0 & 0 & 0.860\;3 & 0.642\;1 \\0.470\;4 & 0.263\;0 & 0.894\;8 & 0 & \cdots & 0.546\;6 & 1 & 0.699\;9 & 0.174\;7 \\0.409\;3 & 0.517\;5 & 0.476\;3 & 0.520\;1 & \cdots & 0.730\;3 & 0.229\;8 & 0.713\;3 & 0.361\;4 \\0.636\;2 & 0.496\;9 & 0.084\;2 & 0.886\;4 & \cdots & 0.192\;9 & 0.396\;6 & 0.218\;9 & 0.626\;1 \\0.382\;6 & 0.706\;5 & 1 & 0.725\;5 & \cdots & 0.160\;9 & 0.706\;8 & 0.469\;6 & 0.796\;5 \\0.855\;1 & 0.754\;2 & 0.448\;7 & 0.665\;3 & \cdots & 0.454\;3 & 0.382\;6 & 0.193\;6 & 1 \\0.883\;7 & 0.156\;2 & 0.895\;6 & 0.688\;2 & \cdots & 1 & 0.118\;5 & 0.068\;9 & 0.318\;9 \\0 & 0.671\;1 & 0.484\;4 & 0.783\;8 & \cdots & 0.598\;1 & 0.118\;5 & 0.252\;9 & 0.461\;6\end{array}\right]$
上述矩阵共14行1 920列，从上到下依次表示f0~d6，为计算样本间的相似程度，对矩阵 X标定得到模糊相似矩阵 R，利用传递闭包法将矩阵 R改造成模糊等价矩阵 R*：
$\boldsymbol{R}^*=\left[\begin{array}{cccccccccccccccc}1 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.495\;1 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 \\0.217\;0 & 1 & 0.314\;9 & 0.379\;4 & 0.340\;9 & 0.340\;9 & 0.379\;4 & 0.217\;0 & 0.605\;4 & 0.314\;9 & 0.379\;4 & 0.340\;9 & 0.340\;9 & 0.379\;4 \\0.217\;0 & 0.314\;9 & 1 & 0.314\;9 & 0.314\;9 & 0.314\;9 & 0.314\;9 & 0.217\;0 & 0.314\;9 & 0.677\;2 & 0.314\;9 & 0.314\;9 & 0.314\;9 & 0.314\;9 \\0.217\;0 & 0.379\;4 & 0.314\;9 & 1 & 0.340\;9 & 0.340\;9 & 0.384\;6 & 0.217\;0 & 0.379\;4 & 0.314\;9 & 0.548\;9 & 0.340\;9 & 0.340\;9 & 0.384\;6 \\0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 1 & 0.350\;4 & 0.340\;9 & 0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 0.607\;2 & 0.354\;0 & 0.340\;9 \\0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 0.350\;4 & 1 & 0.340\;9 & 0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 0.354\;0 & 0.716\;6 & 0.340\;9 \\0.217\;0 & 0.379\;4 & 0.314\;9 & 0.384\;6 & 0.340\;9 & 0.340\;9 & 1 & 0.217\;0 & 0.379\;4 & 0.314\;9 & 0.384\;6 & 0.340\;9 & 0.340\;9 & 0.573\;6 \\0.495\;1 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 1 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 & 0.217\;0 \\0.217\;0 & 0.650\;4 & 0.314\;9 & 0.379\;4 & 0.340\;9 & 0.340\;9 & 0.379\;4 & 0.217\;0 & 1 & 0.314\;9 & 0.379\;4 & 0.340\;9 & 0.340\;9 & 0.379\;4 \\0.217\;0 & 0.314\;9 & 0.677\;2 & 0.314\;9 & 0.314\;9 & 0.314\;9 & 0.314\;9 & 0.217\;0 & 0.314\;9 & 1 & 0.314\;9 & 0.314\;9 & 0.314\;9 & 0.314\;9 \\0.217\;0 & 0.379\;4 & 0.314\;9 & 0.548\;9 & 0.340\;9 & 0.340\;9 & 0.384\;6 & 0.217\;0 & 0.379\;4 & 0.314\;9 & 1 & 0.340\;9 & 0.340\;9 & 0.384\;6 \\0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 0.607\;2 & 0.354\;0 & 0.340\;9 & 0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 1 & 0.354\;0 & 0.340\;9 \\0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 0.354\;0 & 0.716\;6 & 0.340\;9 & 0.217\;0 & 0.340\;9 & 0.314\;9 & 0.340\;9 & 0.354\;0 & 1 & 0.340\;9 \\0.217\;0 & 0.379\;4 & 0.314\;9 & 0.384\;6 & 0.340\;9 & 0.340\;9 & 0.573\;6 & 0.217\;0 & 0.379\;4 & 0.314\;9 & 0.384\;6 & 0.340\;9 & 0.340\;9 & 1 \end{array}\right]$
在模糊等价矩阵 R*中当置信因子λ从1到0变化时，形成动态聚类图，得到诊断结果，如图 7所示。对预训练的TL-DenseNet模型以及本文TL-DenseNet-GAP-FCM模型进行对比验证，采用12 kHz采样频率的驱动端、故障直径0.177 8mm、电机转速1 797 r/min同型号同工况轴承每种故障类型各15组数据，共105组数据，进行实验验证对比分析其结果如表 4所示，其中TL-DenseNet平均准确率为79.04%，改进后TL-DenseNet-GAP-FCM模型准确率为99.05%，实验结果表明，改进后的卷积神经网络其卷积层的具有更好的特征提取能力，在同型号同工况情况下，使用少量样本进行迁移学习并改进建立TL-Densenet-GAP-FCM模型，在此模型的基础上只需要建立标准数据库就可实现轴承故障诊断，无需新样本的数据训练。但内圈的故障检测分类存在一定误差究其原因内圈故障滚动体故障在故障机理和传递路径来说存在一定的相似性，因此在提取到内圈和滚动体故障特征时出现部分特征混合，造成一定的误差，可以通过增加预训练微调的样本来提高分类准确率。
Fig. 7
图 7 同型号同工况动态聚类图 Fig. 7 Dynamic clustering for the same model and working conditions 表 4
表 4 小样本迁移学习故障分类准确率 Tab. 4 Fault classification accuracy of small sample transfer learning 模型 不同状态下的准确率/% 平均准确率/% f0 f1 f2 f3 f4 f5 f6
TL-DenseNet 93.33 80.00 73.33 66.67 86.67 80.00 73.33 79.04
TL-DenseNet-GAP-FCM 100 93.33 100 100 100 100 100 99.05
表 4 小样本迁移学习故障分类准确率 Tab. 4 Fault classification accuracy of small sample transfer learning
将本节算法模型与各文献中基于CWRU数据集的结果进行比较，以说明本文算法的优越性，如表 5所示，在140组样本情况下，实现了和文献[28]CNN模型3 030样本相近的准确性，表明本文算法在小样本的优越性。
表 5
表 5 基于西储轴承数据集分类准确率比较 Tab. 5 Comparison of classification accuracy based on western Reserve bearing data set 方法 训练样本总数 迭代次数 测试准确率/% RBF-SVM[29] 280 — 97.26
CNN-SVM[18] 500 140 97.52
分类回归树(CART)[29] 280 — 93.56
ANN[30] 480 1 000 96.53~100
CNN[28] 3 030 — 99.8~100
TL-DenseNet-GAP-FCM 140 100 99.05
表 5 基于西储轴承数据集分类准确率比较 Tab. 5 Comparison of classification accuracy based on western Reserve bearing data set
3.2 同型号跨工况情况轴承故障诊断实验 3.2.1 零目标样本轴承故障诊断在3.1节驱动端12 kHz、电机转速1 797 r/min轴承预训练微调模型基础上，验证电机转速1 750 r/min情况下故障分类准确率。考虑在没有目标样本可用于训练的情况下，如果利用转速1 797 r/min得到的改进迁移学习模型TL-DenseNet-GAP-FCM，进行转速1 750 r/min状态下轴承故障分类验证，在目标域零样本的情况下(即没有转速1 750 r/min状态下轴承样本)，验证其不同故障直径下内圈、外圈和滚动体共6种故障分类准确率，并与其他零样本方法进行对比，迭代次数均设置100，LSVM的准确率为46.67%，ANN的准确率为41.67%，TL-DenseNet的准确率为58.33%，TL-DenseNet-GAP-FCM的准确率为84.17%，实验结果表明在零目标样本的情况下利用预训练好的TL-DenseNet-GAP-FCM模型可以对不同类型的故障进行诊断和分类，具有较高的实用参考价值，同时在今后的研究中还可以进一步完善。例如：1)可以考虑参考文献[31], 利用向量空间表述不同故障的属性描述; 2)增加预训练微调样本种类和数量，使卷积层学习到更多的轴承故障特征，提高特征提取层的提取能力。
3.2.2 小样本轴承故障诊断现在进行小样本迁移学习，1 750 r/min的每种故障各取15组，共90组数据记为数据F，将3.1节标准数据A记为源域，数据F记为目标域进行预训练，即建立A→F的迁移学习任务，以A→F建立的TL-DenseNet-GAP-FCM模型，动态聚类图如图 8所示，其中f1~f5为建立的1 772 r/min、1 750 r/min中内圈、外圈和滚动体故障数据库，d1~d5为其对应待测故障。
Fig. 8
图 8 同型号跨工况动态聚类图 Fig. 8 Cross-working dynamic clustering diagram of the same model 从上述结果可以看出去除全连接层的模型具有更好的特征提取能力，使用全局均值池化层代替全连接层避免了数据不足引起的过拟合现象，利用模糊数学的方法对样本间的特征进行定量分析，实现小样本的轴承故障诊断，仅需140组目标域样本数据，准确率可达99.05%。在零目标样本同型号跨工况情况下分类准确率为84.17%，究其原因为不同工况下数据存在一定差异，但可利用数据充足的实验室数据作为源域结合少量目标域数据利用迁移学习微调网络，在TL-DenseNet-GAP-FCM模型的基础上实现实际应用中可用数据较少而出现的过拟合现象以及分类准确率低的问题。
3.3 XITU-SY轴承数据故障诊断实验本节采用西安交通大学XJTU-SY轴承公开数据集进行实验验证，轴承型号LDK UER204，该数据集包括3种工况, 设定转速分别为2 100、2 250、2 400 r/min，每种工况包括水平和垂直振动信号，本文以工况2水平振动信号数据为例进行实验验证，以轴承2为例，如表 6所示，选取工况2中正常、内圈故障、外圈故障、保持架故障进行验证，鉴于在实际应用过程中故障数据可用较少，对于4种不同状态轴承，每种选择20组共80组训练TL-Densenet-GAP-FCM模型，从每种状态中随机选择一组数据进行验证，其结果如图 9所示，f1到f4分别为正常、内圈、外圈和保持架故障，d1到d4为随机选取的待测样本，故障分类结果均准确。
表 6
表 6 XJTU-SY工况2数据介绍 Tab. 6 Data introduction of XJTU-SY working conditions 2 数据集 样本数 基本额定寿命/h 使用寿命/min 故障位置 Bearing2_1 491 6.786~11.726 491 内圈
Bearing2_2 161 6.786~11.726 161 外圈
Bearing2_3 533 6.786~11.726 533 保持架
Bearing2_4 42 6.786~11.726 42 外圈
Bearing2_5 339 6.786~11.726 339 外圈
表 6 XJTU-SY工况2数据介绍 Tab. 6 Data introduction of XJTU-SY working conditions 2
Fig. 9
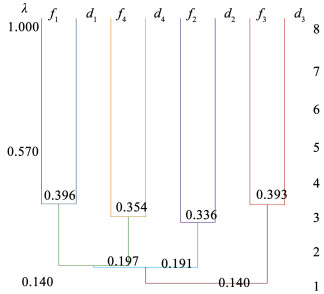图 9 XJTU-SY轴承故障诊断聚类图 Fig. 9 XJTU-SY bearing fault diagnosis cluster diagram 通过实验以及对比验证，说明改进后的模型保留了Densenet网络卷积层的特征提取能力，通过改进池化层和分类层来减少训练样本数量，提高运算速度有效地避免了过拟合现象，本文算法不仅仅适用于各类型号轴承的故障诊断，相关算法还适用于转辙机的状态诊断[32]，可根据检测目标的曲线复杂程度来适当增减训练样本的数量以此来提高卷积层特征提取能力，增加分类准确率。但在本文算法分类层使用的是模糊聚类算法，该算法需要提前收集出现的故障数据建立相应的标准数据库样本特征，利用模糊数学原理实现检测样本特征与数据库样本特征的配对，如果后续出现新的故障可以添加到数据库中。
4 结论1) 针对传统卷积神经网络全连接层参数、Softmax层参数需要大量数据进行训练，在小样本情况下容易出现过拟合等问题，本文提出了一种TL-Densenet-GAP-FCM模型用于轴承故障诊断，该模型以全局均值池化层代替全连接层和模糊聚类层代替Softmax层，包括输入层、特征提取层、全局均值池化层和模糊聚类分类层，该模型大大减少了训练样本需求，适合小样本故障诊断。
2) 利用凯斯西储大学轴承数据和西安交通大学XJTU-SY轴承数据进行实验验证，在小样本的情况下，TL-DenseNet-GAP-FCM相比TL-DenseNet模型具有更好的故障分类准确率，究其原因是全连接层存在大量参数，在数据量不足的情况下会出现过拟合现象，可有效解决实际应用中因数据量不足导致机器学习分类精度低的问题。
参考文献
[1] SHAO haidong, JIANG hongkai, ZHAO huiwei. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis[J]. Mech Syst Sig Process, 2017, 95: 187. DOI:10.1016/j.ymssp.2017.03.034
[2] LI Y, XU M, ZHAO H, et al. Hierarchical fuzzy entropy and improved support vector machine based binary tree approach for rolling bearing fault diagnosis[J]. Mech Mach Theory, 2016, 98: 114. DOI:10.1016/j.mechmachtheory.2015.11.010
[3] THOMAS M V, PULEO D A, ALSABBAGH M. Calcium sulfate: a review[J]. J Long Term Eff Med Implants, 2005, 15(6): 599. DOI:10.1615/JLongTermEffMedImplants.v15.i6.30
[4] EI-THALJI I, JANTUNEN E. A summary of fault modelling and predictive health monitoring of rolling element bearings[J]. Mechanical Systems & Signal Processing, 2015, 60-61(8): 252.
[5] LI Jimeng, WANG Hui, WANG Xiaodong, et al. Rolling bearing fault diagnosis based on improved adaptive parameterless empirical wavelet transform and sparse denoising[J]. Measurementm, 2020, 152(C): 107392.
[6] KANG M, ISLAM M R, KIM J, et al. A hybrid feature selection scheme for reducing diagnostic performance deterioration caused by outliers in data-driven diagnostics[J]. IEEE Trans Ind Electron, 2016, 63(5): 3299. DOI:10.1109/TIE.2016.2527623
[7] WANG Ziwei, ZHANG Qinghua, XIONG Jianbin, et al. Fault diagnosis of a rolling bearing using wavelet packet denoising and random forests[J]. IEEE Sens J, 2017, 17(17): 5581. DOI:10.1109/JSEN.2017.2726011
[8] WANG Lei, LIU Zhiwen, MIAO Qiang, et al. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings[J]. Mech Syst Signal Pr, 2018, 106: 24. DOI:10.1016/j.ymssp.2017.12.031
[9] LEI Yaguo, LIN Jing, HE Zhengjia, et al. A review on empirical mode decomposition infault diagnosis of rotating machinery[J]. Mech Syst Signal Pr, 2013, 35(1/2): 108.
[10] GUO Tai, DENG Zhongming. An improved EMD method based on the multi-objective optimization and its application to fault feature extraction of rolling bearing[J]. Appl Acoust, 2017, 127: 46. DOI:10.1016/j.apacoust.2017.05.018
[11] SUN L, LI Y, DU H, et al. Fault diagnosis method of low noise amplifier based on support vector machine and hidden markov model[J]. Journal of Electronic Testing, 2021, 37(2): 215. DOI:10.1007/s10836-021-05938-0
[12] SAMANTA B, NATARAJ C. Use of particle swarm optimization for machinery fault detection[J]. Engineering Applications of Artificial Intelligence, 2009, 22(2): 308. DOI:10.1016/j.engappai.2008.07.006
[13] 雷亚国, 贾峰, 周昕, 等. 基于深度学习理论的机械装备大数据健康监测方法[J]. 机械工程学报, 2015, 51(21): 49.
LEI Yaguo, JIA Feng, ZHOU Xin, et al. A deep learning-based method for machinery health monitoring with big data[J]. Journal of Mechanical Engineering, 2015, 51(21): 49.
[14] KUMAR S, PANDEY A, SATWIK K S R, et al. Deep learning framework for recognition of cattle using muzzle point image pattern[J]. Measurement, 2018, 116: 1.
[15] ZHANG Tian, LIU Shulin, WEI Yuan, et al. A novel feature adaptive extraction method based on deep learning for bearing fault diagnosis[J]. Measurement, 2021, 185: 110030. DOI:10.1016/j.measurement.2021.110030
[16] CHOUDHARY A, MIAN T, FATIMA S. Convolutional neural network based bearing fault diagnosis of rotating machine using thermal images[J]. Measurement, 2021, 176(4): 109196.
[17] ZHONG Shisheng, FU Song, LIN Lin. A novel gas turbine fault diagnosis method based on transfer learning with CNN[J]. Measurement, 2019, 137: 435. DOI:10.1016/j.measurement.2019.01.022
[18] HAN Tian, ZHANG Longwen, YIN Zhongjun, et al. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine[J]. Measurement, 2021, 177(1): 109022.
[19] PENG Z, ZHANG W, HAN N, et al. Active transfer learning[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2020, 30(4): 1022. DOI:10.1109/TCSVT.2019.2900467
[20] LU W, LIANG B, YU C, et al. Deep model based domain adaptation for fault diagnosis[J]. IEEE Transactions on Industrial Electronics, 2016, 64(3): 2296.
[21] CHEN Chao, SHEN Fei, YAN Ruqiang. Enhanced least squares support vector machine-based transfer learning strategy for bearing fault diagnosis[J]. Chinese Journal of Scientific Instrument, 2017, 38(1): 33.
[22] CHENG Jing, WANG Weiqing, FAN Xiaochao, et al. Bearing fault pattern recognition of wind turbine based on two-value bispectrum feature-fuzzy clustering method[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(4): 765.
[23] GOROKHOVATSKYI V O, TVOROSHENKO I S, VLASENKO N V. Using fuzzy clustering in structural methods of image classification[J]. Telecommunications and Radio Engineering, 2020, 79(9): 781. DOI:10.1615/TelecomRadEng.v79.i9.50
[24] LOPARO K A. Bearing vibration data set[DB/OL]. https://engineering.case.edu/bearingdatacenter/download-data-file
[25] BENGIO Y, COURVILLE A, VINCENT P. Representation learning: a review and new perspectives[J]. IEEE Trans Pattern Anal Mach Intell, 2013, 35(8): 1798. DOI:10.1109/TPAMI.2013.50
[26] 魏文军, 刘新发. 基于EEMD多尺度样本熵的S700K转辙机故障诊断[J]. 中南大学学报(自然科学版), 2019, 50(11): 2763.
WEI Wenjun, LIU Xinfa. Fault diagnosis of S700K switch machine based on EEMD multiscale sample entropy[J]. Journal of Central South University(Science and Technology), 2019, 50(11): 2763.
[27] 张西宁, 余迪, 刘书语. 基于迁移学习的小样本轴承故障诊断方法研究[J]. 西安交通大学学报, 2021, 55(10): 30.
ZHANG Xining, YU Di, LIU Shuyu. Research on fault diagnosis method of small sample bearing based on transfer learning[J]. Journal of Xi'an Jiaotong University, 2021, 55(10): 30.
[28] HOANG D T, KANG H J. Rolling element bearing fault diagnosis using convolutional neural network and vibration image[J]. Cognit Syst Res, 2019, 53: 42. DOI:10.1016/j.cogsys.2018.03.002
[29] WANG X, ZHENG Y, ZHAO Z, et al. Bearing fault diagnosis based on statistical locally linear embedding[J]. Sensors, 2015, 15(7): 16225. DOI:10.3390/s150716225
[30] MURUGANATHAM B, SANJITH M A, KRISHNAKUMAR B, et al. Roller element bearing fault diagnosis using singular spectrum analysis[J]. Mech Syst Signal Process, 2013, 35(1/2): 150.
[31] FENG Liangjun, ZHAO Chunhui. Fault description based attribute transfer for zero-sample industrial fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2020, 17(3): 1852.
[32] WEI Wenjun, ZHANG Xuanming, YANG Liben. Full-cycle state evaluation of S700K switch machine based on residual network and fuzzy clustering[J]. International Journal of Innovative Computing, Information and Control, 2022, 18(4): 1203.
