应用于姿态敏感器的SORNN微小故障诊断方法

龙弟之¹,闻新^1,2,王戬¹,战泓廷¹

(1.南京航空航天大学 航天学院,南京 210016; 2.广东省“天临空地海”复杂环境智能探测重点实验室 (北京理工大学), 广东 珠海 519088)



摘要:

为实现空间外部干扰和测量噪声存在情况下,航天器姿态敏感器微小故障的有效检测,以及方位敏感器和惯性敏感器之间的故障隔离,提出了一种基于自组织循环神经网络(self-organizing recurrent neural network,SORNN)的微小故障诊断方法。首先,设计了SORNN模型,包括网络结构自组织算法、终止条件和调整条件,实现对网络隐藏层神经元数量和循环记忆深度的自适应调节,用以提升网络的拟合性能。然后,针对姿态运动学子系统设计了基于SORNN的干扰观测器,给出网络权值更新算法并证明了状态估计误差的收敛性。将系统输出估计误差通过低通滤波器以抑制星敏感器测量噪声,推导更严格的残差和检测阈值进而提高对微小故障的检测能力。最后,针对姿态动力学子系统设计了故障隔离观测器,通过干扰解耦和干扰观测器的补偿消除未知扰动和噪声对残差的影响,利用动力学和运动学的冗余关系解决了两类敏感器故障的隔离问题。仿真结果表明,验证了所提方法对扰动和噪声掩盖下的星敏感器和陀螺微小故障检测与隔离的有效性。

关键词:  故障诊断  姿态敏感器  微小故障  循环神经网络  干扰观测器

DOI：10.11918/202303032

分类号:V44

文献标识码:A

基金项目:南京航空航天大学研究生跨学科创新基金 (KXKCXJJ202010)；南京航空航天大学“实验技术研究与开发”项目(2020051500058011)



SORNN small fault diagnosis method for attitude sensors

LONG Dizhi¹,WEN Xin^1,2,WANG Jian¹,ZHAN Hongting¹

(1.College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China; 2.Guangdong Key Laboratory of Intelligent Detection in Complex Environment of Aerospace, Land and Sea (Beijing Institute of Technology), Zhuhai 519088, Guangdong, China)

Abstract:

To achieve effective detection of small faults in spacecraft attitude sensors and fault isolation of orientation sensors and inertial sensors in the presence of disturbance and measurement noise, we proposed a self-organizing recurrent neural network (SORNN) based small fault diagnosis method. Firstly, a SORNN model, including the self-organizing algorithm, termination condition, and adjustment condition, was designed to realize the adaptive adjustment of the number of hidden layer neurons and memory depth, thereby improving the fitting performance of the network. Then, a SORNN-based disturbance observer was designed for the kinematics subsystem. The network weight update algorithm was given, and the state estimation error convergence was proved. The output estimation error was passed through a low-pass filter to suppress the measurement noise of the star sensor. More rigorous residual and detection threshold were derived to improve the detection ability of small faults. Furthermore, a fault isolation observer was designed for the dynamic subsystem. The influence of unknown disturbance and noise on residual was eliminated by disturbance decoupling and disturbance observer compensation. The problem of fault isolation of different sensors was solved by using the redundancy relationship between dynamics and kinematics. Finally, the simulation results verified the effectiveness of the proposed method for detecting and isolating small faults of star sensors and gyros under the cover of disturbance and noise.

Key words:  fault diagnosis  attitude sensor  small fault  recurrent neural network  disturbance observer


龙弟之, 闻新, 王戬, 战泓廷. 应用于姿态敏感器的SORNN微小故障诊断方法[J]. 哈尔滨工业大学学报, 2024, 56(4): 31-41. DOI: 10.11918/202303032.
LONG Dizhi, WEN Xin, WANG Jian, ZHAN Hongting. SORNN small fault diagnosis method for attitude sensors[J]. Journal of Harbin Institute of Technology, 2024, 56(4): 31-41. DOI: 10.11918/202303032.
基金项目 南京航空航天大学研究生跨学科创新基金(KXKCXJJ202010); 南京航空航天大学"实验技术研究与开发"项目(2020051500058011) 作者简介 龙弟之(1995—), 男, 博士研究生;
闻新(1961—), 男, 教授, 博士生导师 通信作者 龙弟之, longdizhi@nuaa.edu.cn 文章历史 收稿日期: 2023-03-09



Abstract            Full text            Figures/Tables            PDF


应用于姿态敏感器的SORNN微小故障诊断方法
龙弟之¹, 闻新^1,2, 王戬¹, 战泓廷¹    
1. 南京航空航天大学 航天学院, 南京 210016;
2. 广东省"天临空地海"复杂环境智能探测重点实验室 (北京理工大学), 广东 珠海 519088

收稿日期: 2023-03-09; 录用日期: 2023-04-27; 网络首发日期: 2024-03-18
基金项目: 南京航空航天大学研究生跨学科创新基金(KXKCXJJ202010); 南京航空航天大学"实验技术研究与开发"项目(2020051500058011)
作者简介: 龙弟之(1995—), 男, 博士研究生; 闻新(1961—), 男, 教授, 博士生导师
通信作者: 龙弟之, longdizhi@nuaa.edu.cn


摘要: 为实现空间外部干扰和测量噪声存在情况下, 航天器姿态敏感器微小故障的有效检测, 以及方位敏感器和惯性敏感器之间的故障隔离, 提出了一种基于自组织循环神经网络(self-organizing recurrent neural network, SORNN)的微小故障诊断方法。首先, 设计了SORNN模型, 包括网络结构自组织算法、终止条件和调整条件, 实现对网络隐藏层神经元数量和循环记忆深度的自适应调节, 用以提升网络的拟合性能。然后, 针对姿态运动学子系统设计了基于SORNN的干扰观测器, 给出网络权值更新算法并证明了状态估计误差的收敛性。将系统输出估计误差通过低通滤波器以抑制星敏感器测量噪声, 推导更严格的残差和检测阈值进而提高对微小故障的检测能力。最后, 针对姿态动力学子系统设计了故障隔离观测器, 通过干扰解耦和干扰观测器的补偿消除未知扰动和噪声对残差的影响, 利用动力学和运动学的冗余关系解决了两类敏感器故障的隔离问题。仿真结果表明, 验证了所提方法对扰动和噪声掩盖下的星敏感器和陀螺微小故障检测与隔离的有效性。
关键词: 故障诊断    姿态敏感器    微小故障    循环神经网络    干扰观测器    
SORNN small fault diagnosis method for attitude sensors
LONG Dizhi¹, WEN Xin^1,2, WANG Jian¹, ZHAN Hongting¹    
1. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
2. Guangdong Key Laboratory of Intelligent Detection in Complex Environment of Aerospace, Land and Sea (Beijing Institute of Technology), Zhuhai 519088, Guangdong, China



Abstract: To achieve effective detection of small faults in spacecraft attitude sensors and fault isolation of orientation sensors and inertial sensors in the presence of disturbance and measurement noise, we proposed a self-organizing recurrent neural network (SORNN) based small fault diagnosis method. Firstly, a SORNN model, including the self-organizing algorithm, termination condition, and adjustment condition, was designed to realize the adaptive adjustment of the number of hidden layer neurons and memory depth, thereby improving the fitting performance of the network. Then, a SORNN-based disturbance observer was designed for the kinematics subsystem. The network weight update algorithm was given, and the state estimation error convergence was proved. The output estimation error was passed through a low-pass filter to suppress the measurement noise of the star sensor. More rigorous residual and detection threshold were derived to improve the detection ability of small faults. Furthermore, a fault isolation observer was designed for the dynamic subsystem. The influence of unknown disturbance and noise on residual was eliminated by disturbance decoupling and disturbance observer compensation. The problem of fault isolation of different sensors was solved by using the redundancy relationship between dynamics and kinematics. Finally, the simulation results verified the effectiveness of the proposed method for detecting and isolating small faults of star sensors and gyros under the cover of disturbance and noise.
Keywords: fault diagnosis    attitude sensor    small fault    recurrent neural network    disturbance observer    
姿态敏感器是航天器获取自身姿态信息的重要测量部件，长期在轨运行它的内部元件会发生老化和漂移，导致测量信息不可信，若不能及时诊断并进行补偿，轻则航天器姿态控制性能下降，重则丢失姿态。因此，开展航天器姿态敏感器故障诊断研究对提升航天器在轨安全性意义重大^[1-2]。

对于姿态敏感器故障，通常基于姿态运动学模型开展故障诊断设计，相比动力学模型可认为其模型是精确已知的，不存在模型不确定性的问题^[3]。但敏感器测量噪声和空间扰动是客观存在的，会对诊断结果产生较大影响。常用的解决方案是提高诊断算法的鲁棒性。文献[4]设计自适应观测器用于敏感器故障诊断，并采用非线性几何方法解耦外部干扰对观测器输出的影响。文献[5]在传统卡尔曼滤波器基础上提出了一种自适应扩展卡尔曼滤波器(extend Kalman filter, EKF)，利用新息序列建立卡方检验实现敏感器故障诊断。文献[6-7]将神经网络用于在线学习状态方程未知函数信息，通过补偿观测器从而提高对敏感器的诊断性能。但是，当敏感器发生微小故障时，仅提高鲁棒性难以达到检测目的，如何计算合理的检测阈值也是影响故障诊断性能的关键^[8]。因此，在增强鲁棒性的同时设置更严格的阈值是解决敏感器微小故障诊断的有效途径之一。

考虑多重故障的隔离问题，文献[9-10]分别实现了对不同轴向陀螺故障的隔离以及执行器与敏感器故障之间的隔离。而航天器姿态控制系统包括方位敏感器和惯性敏感器，且均有可能发生故障。文献[11]研究了红外地球敏感器和陀螺故障的隔离问题，指出利用姿态运动学方程的解析冗余关系可以对故障进行检测，但不能定位故障出自二者中哪一个敏感器，需要额外的冗余关系辅之进行判断。在工程应用中航天器在轨资源有限，如何在现有硬件基础上设计高效诊断系统，以增强对姿态敏感器的故障检测与隔离能力还有待研究。

针对上述问题，本文提出了基于SORNN干扰观测器的姿态敏感器故障诊断方法，在干扰和测量噪声存在的情况下实现两类敏感器微小故障的检测与隔离。首先设计了具备自适应调节功能的SORNN模型解决网络结构确定问题；然后给出了SORNN干扰观测器设计方法并结合低通滤波器推导更严格的残差和检测阈值；最后利用姿态动力学和运动学冗余关系设计了故障隔离观测器实现对星敏感器和陀螺故障的隔离。

1 自组织循环神经网络模型如图 1所示，SORNN利用循环结构将上一时刻的输出反馈至隐藏层神经元作为下一时刻的输入。相比传统RNN，SORNN不仅能够根据系统输入输出自适应地调节隐藏层神经元数量m，还可以调节循环记忆深度n，将之前n个时刻记忆的输出反馈至隐藏层作为输入，强化时序数据之间的联系。

Fig. 1
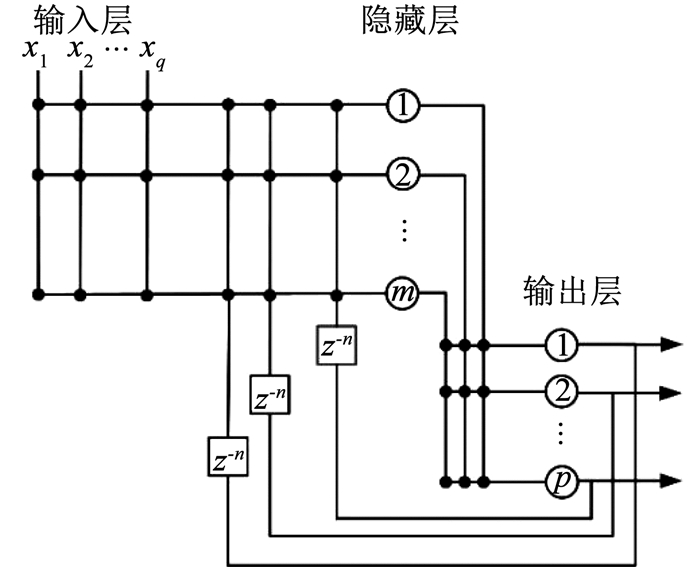图 1 自组织循环神经网络结构示意 Fig. 1 Structure of self-organized recurrent neural network


1.1 网络结构自组织算法在文献[12-13]的基础上，设计了一种适用性更广的网络结构自组织算法，使得SORNN具备自适应调节功能，能够更好地应用于复杂非线性函数的拟合。

SORNN结构自组织算法流程如图 2所示，详细步骤为：

Fig. 2
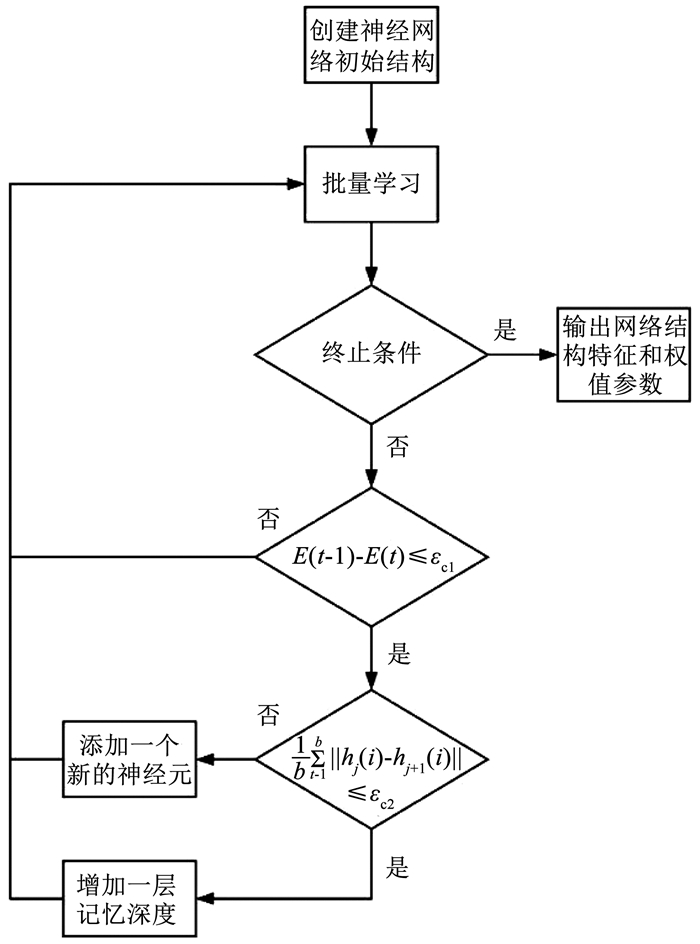图 2 自组织循环神经网络结构自组织算法流程 Fig. 2 Self-organizing algorithm flow chart of self-organizing recurrent neural network


Step1??选取一个简单的3层RNN结构。其中，隐藏层初始仅有一个神经元，输入层和输出层中的神经元个数q和p与拟合任务需要的输入输出变量维数相关。初始化SORNN连接权值，并设置批量学习大小为b，即在线学习b组采样数据为一个学习批次。

Step2??利用权值更新算法对SORNN权值进行训练，计算第ι个学习批次的训练误差E(ι)。需要注意，只训练与隐藏层新添加神经元相关的权值，已完成训练的权值保持不变。

其中，E(ι)的计算公式为

$E(\iota)=\frac{1}{p b} \sum\limits_{j=1}^{b} \sum\limits_{i=1}^{p}\left(Y_{i, j}(\iota)-Z_{i, j}(\iota)\right)^{2} $ (1)

式中：p为输出层神经元个数，Y_{i, j}、Z_{i, j}分别为输出层在一个学习批次中，第j组数据对应的第i个神经元期望与实际输出。

Step3??根据训练误差对SORNN学习进程进行终止条件判定，若满足条件则SORNN结构完成搭建，转到Step6；否则继续下一步。

Step4??计算前、后两个批次学习误差的减少量，若小于等于预定值ε_c1，则继续下一步；否则转到Step2。

Step5??判断隐藏层第m个神经元与相邻神经元是否冗余，若是则在输出层反馈至隐藏层第m个神经元的回路中增加一层记忆深度；否则在隐藏层添加一个神经元，并固定已有连接权值，将新添加的神经元对应的连接权值初始化为0，转到Step2。

Step6??输出SORNN结构特征与权值参数。

1.2 终止条件在SORNN训练过程中，利用训练误差和验证误差来设定终止条件。首先给定一个训练窗口K，通过计算D_K(ι)描述SORNN在K个学习批次的平均训练误差大于最小训练误差的程度，然后利用当前学习批次的训练误差E(ι)和验证误差E_v(ι)计算泛化损失G_L(ι)。当G_L(ι)>D_K(ι)时，停止训练。其中，D_K(ι)和G_L(ι)计算公式分别为：

$D_{\mathrm{K}}(\iota)=\left(\frac{\sum\limits_{\iota^{\prime}=-K+1}^{t} E\left(\iota^{\prime}\right)}{K \times \min\limits _{\iota^{\prime}=-K+1} E\left(\iota^{\prime}\right)}-1\right)$ (2)

$G_{\mathrm{L}}(\iota)=\left(\frac{E_{\mathrm{v}}(\iota)}{E_{\mathrm{o}}(\iota)}-1\right)$ (3)

式中E_o(ι)为最小验证误差。

1.3 调整条件当继续训练无法提高SORNN性能，即原有网络结构达到性能饱和时，为防止过拟合，可添加隐藏层神经元或反馈记忆深度来优化网络。

通常利用前、后两批次训练误差的减少量来判断是否添加新的神经元，数学描述为

$E(\iota-1)-E(\iota) \leqslant \varepsilon_{\mathrm{c} 1}$ (4)

式中：E(ι－1)为前一个学习批次的误差，ε_c1为预设的阈值。当添加过多的神经元，由于功能的相似会变得冗余，对神经网络性能提升并无作用。为解决该情况，引入如下条件定量地判断一个学习批次内两个神经元是否表现出相似的功能:

$\frac{1}{b} \sum\limits_{i=1}^{b}\left\|h_{m}(i)-h_{m-1}(i)\right\| \leqslant \varepsilon_{\mathrm{c} 2}$ (5)

式中：h_m(i)、h_m－1(i)分别为隐藏层第m个神经元和相邻神经元对应第i组训练数据的输出，ε_c2为预设的阈值。

综上所述，当只满足条件式(4)时，则在隐藏层添加新的神经元；而当同时满足条件式(4)、(5)时，则通过加深反馈记忆深度，使得第m个神经元接收更多来自先前的信号来扩展搜索空间，提升网络的拟合性能。

2 故障检测方法星敏感器和陀螺微小故障一般发生在故障初期，具有幅值小、不易发觉以及故障信息容易被干扰和噪声掩盖的特点，加之闭环控制系统本身的特性，使得微小故障在初期对航天器姿态影响并不明显。为及时发现微小故障，需要增强故障检测观测器的鲁棒性，并且计算更严格残差和阈值。

2.1 干扰观测器设计考虑陀螺和星敏感器的测量噪声以及二者故障情况，采用四元数法描述姿态运动学状态空间方程为^[14]

$\left\{\begin{array}{l}\boldsymbol{\dot{x}}_{1}=\phi\left(\boldsymbol{x}_{1}, \boldsymbol{u}_{1}+ \boldsymbol{f}_{\mathrm{g}}\right) \\\boldsymbol{y}_{1}=\boldsymbol{x}_{1}+\boldsymbol{\xi}+\boldsymbol{f}_{\mathrm{s}}\end{array}\right.$ (6)

式中：x₁=[q₀??q₁??q₂??q₃]^T为姿态四元数，u₁=[ω_x??ω_y??ω_z]^T为三轴角速度，y₁为系统输出，ξ为星敏感器测量噪声，f_g、f_s分别为陀螺故障和星敏感器故障，?(x₁, u₁)为姿态运动学非线性函数，表达式为

$\boldsymbol{\phi}\left(\boldsymbol{x}_{1}, \boldsymbol{u}_{1}\right)=\frac{1}{2}\left[\begin{array}{cccc}q_{0} & -q_{1} & -q_{2} & -q_{3} \\ q_{1} & q_{0} & -q_{3} & q_{2} \\ q_{2} & q_{3} & q_{0} & -q_{1} \\ q_{3} & -q_{2} & q_{1} & q_{0}\end{array}\right]\left[\begin{array}{l}0 \\ \omega_{x} \\ \omega_{y} \\ \omega_{z}\end{array}\right]$

不失一般性，可作以下合理假设^[15]。

假设1??航天器工作在小角度姿态机动状态下，?(x₁, u₁)满足Lipschitz条件，即

$\left\|\boldsymbol{\phi}\left(\boldsymbol{x}_{1}, \boldsymbol{u}_{1}\right)-\boldsymbol{\phi}\left(\hat{\boldsymbol{x}}_{1}, \hat{\boldsymbol{u}}_{1}\right)\right\| \leqslant \gamma_{\phi}\left\|\left[\boldsymbol{x}_{1}-\hat{\boldsymbol{x}}_{1}, \boldsymbol{u}_{1}-\hat{\boldsymbol{u}}_{1}\right]^{\mathrm{T}}\right\| $ (7)

式中：γ_?为Lipschitz常数，$\hat{\boldsymbol{x}}_{1}$为x₁的估计，$\hat{\boldsymbol{u}}_{1}$为u₁的估计。

假设2??陀螺和星敏感器不会同时发生故障。

假设3??敏感器故障和测量噪声均有界，且故障的变化速率有界。

在无故障情况下，采用SORNN对陀螺测量误差进行估计，得到基于SORNN的干扰观测器为

$\left\{\begin{array}{l}\dot{\hat{x}}_{1}=\phi\left(\boldsymbol{y}_{1}, u_{1}+\boldsymbol{b}-\hat{\boldsymbol{b}}\right) \\\hat{\boldsymbol{y}}_{1}=\hat{\boldsymbol{x}}_{1}\end{array}\right.$ (8)

式中：$\hat{\boldsymbol{y}}_{1}$为星敏感器测量估计值, b为陀螺测量误差，包括随机噪声和常值漂移；$\hat{\boldsymbol{b}}$为SORNN输出的对b的估计值。其中，第i个估计结果为

$\hat{\boldsymbol{b}}^{i}(t)=\boldsymbol{W}_{0}^{i \mathrm{~T}}(t) \sigma\left(\boldsymbol{W}_{\mathrm{R}}^{i}(t) \cdot \hat{\boldsymbol{b}}^{i}(t, n)+\boldsymbol{W}_{\mathrm{I}}^{i}(t) \cdot e_{y_{1}}^{i}(t)\right) $ (9)

式中：i=1, 2, 3分别为航天器x轴, y轴和z轴, W_Oⁱ(t)∈R^m×1，W_Rⁱ(t)∈R^m×n，W_Iⁱ(t)∈R^m×1分别为t时刻第i个估计值对应的输出权值矩阵，反馈权值矩阵和输入权值矩阵；m、n分别为隐藏层神经元数量和记忆深度，二者随训练过程可在线调节以适应动态系统；$\hat{\boldsymbol{b}}^{i}(t, n)=\left[\hat{\boldsymbol{b}}^{i}(t-\tau), \cdots, \hat{\boldsymbol{b}}^{i}(t-n \tau)\right]^{\mathrm{T}}$，其中τ为采样周期；$e_{y_{1}}^{i}(t)=y_{1}^{i}(t)-\hat{y}_{1}^{i}(t)$，对应q_i的估计误差，用以代替式(1)中期望与实际输出之差；σ(·)为隐藏层激活函数。

令$ \boldsymbol{W}_{\mathrm{RI}}^{i}(t)=\left[\boldsymbol{W}_{\mathrm{R}}^{i}(t), \boldsymbol{W}_{\mathrm{I}}^{i}(t)\right], \boldsymbol{X}=\left[\hat{b}^{i}(t, n), e_{y_{1}}^{i}(t)\right]^{\mathrm{T}}$，式(9)改写为

$\hat{b}^{i}(t)=\boldsymbol{W}_{0}^{i \mathrm{~T}}(t) \sigma\left(\boldsymbol{W}_{\mathrm{RI}}^{i}(t) \boldsymbol{X}(t)\right) $ (10)

为了快速逼近b(t)，将EKF自适应更新算法用于SORNN权值更新^[16]。针对式(10)建立的SORNN输入输出映射模型，权值参数可描述为

$\boldsymbol{\theta}^{i}(k)=\left[\boldsymbol{W}_{0}^{i}(k), \boldsymbol{W}_{\mathrm{RI}}^{i}(k)\right]^{\mathrm{T}}$ (11)

式中, k=t/τ表示第k个采样时刻。

当隐藏层添加新神经元后，不再对已训练好的权值进行更新。因此每个采样时刻只需对θⁱ(k)的最后一列，即第m列参数进行更新。基于EKF的权值更新算法为

$\left\{\begin{array}{l}\boldsymbol{\theta}_{m}^{i}(k)=\boldsymbol{\theta}_{m}^{i}(k-1)+\eta_{m}^{i} \boldsymbol{G}_{m}^{i}(k)\left[y_{1}^{i}(k)-\hat{y}_{1}^{i}(k)\right] \\\boldsymbol{G}_{m}^{i}(k)=\boldsymbol{P}_{m}^{i}(k) \boldsymbol{H}_{m}^{i}(k)\left[\boldsymbol{H}_{m}^{i \mathrm{~T}}(k) \boldsymbol{P}_{m}^{i}(k) \boldsymbol{H}_{m}^{i}(k)+R_{m}^{i}(k)\right]^{-1} \\\boldsymbol{P}_{m}^{i}(k+1)=\boldsymbol{P}_{m}^{i}(k)-\boldsymbol{G}_{m}^{i}(k) \boldsymbol{H}_{m}^{i \mathrm{~T}}(k) \boldsymbol{P}_{m}^{i}(k) \end{array}\right.$ (12)

式中：η_mⁱ为学习率，G_mⁱ∈R^(n+2)×1为卡尔曼增益矩阵，P_mⁱ∈R^(n+2)×(n+2)为状态估计误差协方差矩阵，R_mⁱ为噪声协方差，可由下式更新：

$R_{m}^{i}(k)=R_{m}^{i}(k-1)+\left[e_{y_{1}}^{i 2}(k)-R_{m}^{i}(k-1)\right] / k $ (13)

式(12)中H_mⁱ为观测器输出$\hat{y}_{1}^{i}$关于θ_mⁱ的导数，那么基于观测器方程(8)、(9)，H_mⁱ可由下式计算：

$\begin{equation*}\boldsymbol{H}_{m}^{i}(k)=\left.\frac{\partial \hat{y}_{1}^{i}(k)}{\partial \boldsymbol{\theta}_{m}^{i}}\right|_{\boldsymbol{\theta}_{m}^{i}=\boldsymbol{\theta}_{m}^{i}(k-1)}=\\\left.\frac{\partial \hat{y}_{1}^{i}(k)}{\partial \hat{x}_{1}^{i}(k)} \frac{\partial \hat{x}_{1}^{i}(k)}{\partial \hat{b}^{i}(k)} \frac{\partial \hat{b}^{i}(k)}{\partial \boldsymbol{\theta}_{m}^{i}}\right|_{\boldsymbol{\theta}_{m}^{i}=\boldsymbol{\theta}_{m}^{i}(k-1)} \end{equation*}$ (14)

式中$\frac{\partial \hat{b}^{i}(k)}{\partial \boldsymbol{\theta}_{m}^{i}}=\left[\begin{array}{lll}\frac{\partial \hat{b}^{i}(k)}{\partial \boldsymbol{W}_{0, m}^{i}} & \frac{\partial \hat{b}^{i}(k)}{\partial \boldsymbol{W}_{\mathrm{R}, m}^{i}} & \frac{\partial \hat{b}^{i}(k)}{\partial \boldsymbol{W}_{\mathrm{I}, m}^{i}}\end{array}\right]^{\mathrm{T}} $。

记$d_{x b}^{i}=\frac{\partial \hat{x}_{1}^{i}(k)}{\partial \hat{b}^{i}(k)}$，由式(8)可得

$\dot{d}_{x b}^{i}=\frac{\partial \phi^{i}}{\partial x_{1}^{i}} d_{x b}^{i}+\frac{\partial \phi^{i}}{\partial \hat{b}^{i}}$ (15)

式中?ⁱ为运动学非线性函数对应i轴的分量。最终H_mⁱ的表达式为

$\boldsymbol{H}_{m}^{i}(k)=d_{x b}^{i}\left[\begin{array}{c}\left(\sigma_{m}(\boldsymbol{Z}(k))\right)^{\mathrm{T}} \\\left(\boldsymbol{W}_{0, m}^{i \mathrm{~T}} \hat{\boldsymbol{b}}^{i}(k, n) \boldsymbol{\sigma}_{m}^{\prime}(\boldsymbol{Z}(k))\right)^{\mathrm{T}} \\\left(\boldsymbol{W}_{0, m}^{i \mathrm{~T}} e_{y_{1}}^{i}(k) \boldsymbol{\sigma}_{m}^{\prime}(\boldsymbol{Z}(k))\right)^{\mathrm{T}}\end{array}\right]$ (16)

式中：$\boldsymbol{Z}(k)=\boldsymbol{V}(k) \boldsymbol{X}(k), \hat{\boldsymbol{b}}^{i}(k, n)$为从SORNN输出层到隐藏层n个时刻的记忆反馈。

为证明基于EKF的权值更新算法收敛性，假设噪声协方差R_mⁱ满足：

$0<R_{m}^{i}(k) \ll \boldsymbol{H}_{m}^{i \mathrm{~T}}(k) \boldsymbol{P}_{m}^{i}(k) \boldsymbol{H}_{m}^{i}(k) $ (17)

定理1??如果由式(12)、(13)和式(16)描述的EKF权值更新算法的训练参数满足式(18)，那么SORNN权值更新过程将是收敛的。

$0<\eta_{m}^{i}<2+\frac{2 R_{m}^{i}(k)}{\left\|\boldsymbol{H}_{m}^{i}(k)\right\| \lambda_{\max }\left(\boldsymbol{P}_{m}^{i}(k)\right)} $ (18)

式中λ_max(·)为矩阵最大特征值。

证明??根据干扰观测器输出误差e_y1ⁱ(k)，定义Lyapunov函数为

$V_{\mathrm{d}}^{i}(k)=\frac{1}{2} e_{y_{1}}^{i \mathrm{~T}}(k) e_{y_{1}}^{i}(k)$ (19)

计算V_dⁱ(k)的差值为

$\begin{gather*}\Delta V_{\mathrm{d}}^{i}(k)=V_{\mathrm{d}}^{i}(k+1)-V_{\mathrm{d}}^{i}(k)= \\\Delta e_{y_{1}}^{i}(k)\left(e_{y_{1}}^{i}(k)+\frac{1}{2} \Delta e_{y_{1}}^{i}(k)\right) \end{gather*}$ (20)

式中Δe_y1ⁱ(k)=e_y1ⁱ(k+1)－e_y1ⁱ(k)，近似表示为

$\begin{gather*}\Delta e_{y_{1}}^{i}(k)=-\left(\frac{\partial e_{y_{1}}^{i}(k)}{\partial \boldsymbol{\theta}_{m}^{i}(k)}\right)^{\mathrm{T}} \Delta \boldsymbol{\theta}_{m}^{i}(k)= \\-\eta_{m}^{i} \boldsymbol{H}_{m}^{i \mathrm{~T}}(k) \boldsymbol{G}_{m}^{i}(k) e_{y_{1}}^{i}(k) \end{gather*}$ (21)

将Δe_y1ⁱ(k)代入式(20)可得

$\begin{align*}& \Delta V_{\mathrm{d}}^{i}(k)=\left[-\eta_{m}^{i} \boldsymbol{H}_{m}^{i \mathrm{~T}}(k) \boldsymbol{G}_{m}^{i}(k)\right] \\& {\left[1-\frac{1}{2} \boldsymbol{\eta}_{m}^{i} \boldsymbol{H}_{m}^{i \mathrm{~T}}(k) \boldsymbol{G}_{m}^{i}(k)\right] e_{y_{1}}^{i 2}(k)} \end{align*}$ (22)

根据式(17)、(18)可得

$0<\eta_{m}^{i}<2+\frac{2 R_{m}^{i}}{\boldsymbol{H}_{m}^{i \mathrm{~T}} \boldsymbol{P}_{m}^{i} \boldsymbol{H}_{m}^{i}}=2 \frac{\boldsymbol{H}_{m}^{i \mathrm{~T}} \boldsymbol{P}_{m}^{i} \boldsymbol{H}_{m}^{i}+R_{m}^{i}}{\boldsymbol{H}_{m}^{i \mathrm{~T}} \boldsymbol{P}_{m}^{i} \boldsymbol{H}_{m}^{i}}$ (23)

$因此，$0<\eta_{m}^{i} \boldsymbol{H}_{m}^{i \mathrm{~T}} \boldsymbol{P}_{m}^{i} \boldsymbol{H}_{m}^{i}\left[\boldsymbol{H}_{m}^{i \mathrm{~T}} \boldsymbol{P}_{m}^{i} \boldsymbol{H}_{m}^{i}+R_{m}^{i}\right]^{-1}<2$$ (24)

将式(12)中G_m代入式(24)可得

$0<\eta_{m}^{i} \boldsymbol{H}_{m}^{i \mathrm{~T}} \boldsymbol{G}_{m}^{i}<2 $ (25)

综上所述，当满足不等式(18)时，由式(22)和式(25)可得ΔV_dⁱ(k)＜0。因此，采用式(12)更新的权值将收敛，对应[q₁, q₂, q₃]^T输出误差收敛，根据四元数的性质可知所设计干扰观测器是稳定的，证毕。

2.2 残差与检测阈值计算为实现姿态敏感器微小故障检测，需要更灵敏的残差以及与之相匹配的更严格的检测阈值。对于前者，通常是选取观测器的输出误差作为残差，表示为r₁(t)=e_x1(t)+ξ(t)，其中e_x1(t)=x₁(t)－$\hat{\boldsymbol{x}}_{1}(t)$。虽然使用SORNN得到的估计值可以抵消陀螺测量误差b(t)，但星敏感器测量噪声ξ(t)的存在仍会影响观测器对微小故障的有效检测，出现将噪声视为故障造成误报的情况，或是将故障掩盖在噪声中造成漏检的情况。

星敏感器测量噪声一般由高频部分构成，因此可引入低通滤波器对残差信号进行处理从而抑制噪声。假设滤波器阶数为p_o，传递函数H(s)=sH_po(s)，其中

$H_{p_\rm{o}}(s)=\frac{d_{p_{\rm{o}}{-2}} s^{p_\rm{o}-2}+d_{p_{\rm{o}}{-3}} s^{p_\rm{o}-3}+\cdots+d_0}{s^{p_\rm{o}}+c_{p_\rm{o}-1} s^{p_\rm{o}-1}+\cdots+c_1 s+c_0}$ (26)

不失一般性，可用相同的H(s)对观测器每一个输出滤波。用于故障检测的残差信号r₁(k)表达式为

$\boldsymbol{r}_{1}(t)=H(s)\left[\boldsymbol{e}_{y_{1}}(t)\right]$ (27)

根据拉普拉斯变换的微分性质可得$s\left[\boldsymbol{x}_{1}(t)\right]= \dot{\boldsymbol{x}}_{1}(t)+\boldsymbol{x}_{1}(0) \delta(t)$，其中δ(t)为Dirac delta函数。将其和式(6)代入式(27)可得

$\begin{align*}\boldsymbol{r}_{1}(t)= & s H_{p_{\rm{o}}}(s)\left[\boldsymbol{x}_{1}(t)-\hat{\boldsymbol{x}}_{1}\right]+H(s)[\boldsymbol{\xi}(t)]+ \\& H(s)\left[\boldsymbol{f}_{\mathrm{s}}(t)\right]=H_{p_{\mathrm{o}}}(s)\left[\Delta \phi(t)+\phi\left(\boldsymbol{x}_{1}(t), \right.\right. \\& \left.\left.\boldsymbol{f}_{\mathrm{g}}(t)\right)-\phi\left(\boldsymbol{y}_{1}(t), \tilde{\boldsymbol{b}}(t)\right)\right]+H_{p_{\mathrm{o}}}(s)\left[\boldsymbol{x}_{1}(0) \delta(t)-\right. \\& \left.\hat{\boldsymbol{x}}_{1}(0) \delta(t)\right]+\boldsymbol{\varepsilon}_{\xi}(t)+H(s)\left[\boldsymbol{f}_{\mathrm{s}}(t)\right] \end{align*}$ (28)

式中：$\Delta \phi(t)=\phi\left(\boldsymbol{x}_{1}, \boldsymbol{u}_{1}\right)-\phi\left(\boldsymbol{y}_{1},\boldsymbol{u}_{1}\right), \tilde{\boldsymbol{b}}(t)=\boldsymbol{b}(t)- \hat{\boldsymbol{b}}(t)$, $\boldsymbol{\varepsilon}_{\xi}(t)=H(s)[\boldsymbol{\xi}(t)]$。因为滤波器H(s)是BIBO稳定，那么对于有界测量噪声，滤波后的测量噪声满足$\left|\boldsymbol{\varepsilon}_{\xi}(t)\right| \leqslant \bar{\varepsilon}_{\xi}$，其中$\bar{\varepsilon}_{\xi}$为一有界常值。

为推导系统无故障时对应的不确定性边界来计算检测阈值r₁(t)，令观测器初始值满足$\hat{\boldsymbol{x}}(0)= \boldsymbol{y}(0)$，在无故障情况下，式(28)改写为

$\begin{gathered}r_{1}^{l}(t)=H_{p_{\rm{o}}}(s)\left[\Delta \phi^{l}(t)-\phi^{l}\left(\boldsymbol{y}_{1}(t), \tilde{\boldsymbol{b}}(t)\right)\right]-\\h_{p_{\rm{o}}}(t) \xi^{l}(0)+\varepsilon_{\xi}^{l}(t)\end{gathered}$ (29)

式中：h_po(t)为H_po(s)的脉冲响应，l=1, 2, 3，对应姿态四元素的[q₁, q₂, q₃]^T。在某个时刻T_d，对于一个或多个通道，当|r₁^l(T_d)|>r₁^l(T_d)，系统发出故障警报，其中r₁^l(T_d)为对应检测阈值。

针对式(29)，定义$\varepsilon_{\phi}^{l}(t)=H_{p_{\rm{o}}}(s)\left[\Delta \phi^{l}(t)\right]=$ $H_{p_{\rm{o}}}(s)\left[\boldsymbol{\phi}^{l}\left(\boldsymbol{x}_{1}, \boldsymbol{u}_{1}\right)-\boldsymbol{\phi}^{l}\left(\boldsymbol{x}_{1}+\boldsymbol{\xi}, \boldsymbol{u}_{1}\right)\right]$，这是由于星敏感器测量噪声而产生的函数差值项的滤波形式。在无故障情况下，滤波后的$\varepsilon_{\phi}^{l}(t)$可通过一个可计算的正值函数$\bar{\varepsilon}_{\phi}^{l}(t)$来界定，即对于t>0的任意时刻，满足:

$\left|H_{p_{\rm{o}}}(s)\left[\Delta \phi^{l}(t)\right]\right| \leqslant \bar{\varepsilon}_{\phi}^{l}(t)$ (30)

根据假设1，利用$\phi\left(\boldsymbol{x}_{1}, \boldsymbol{u}_{1}\right)$的Lipschitz特性，计算出一个合适的上界，即

$\bar{\varepsilon}_{\phi}^{l}(t)=\gamma_{\phi}^{l} \bar{H}_{p_{\mathrm{o}}}(s)\left[\bar{\xi}_{\mathrm{d}}\right]$ (31)

式中：γ_?^l为Lipschitz常数，$\bar{\xi}_{\mathrm{d}}$为星敏感器测量噪声界值，满足$|\xi| \leqslant \bar{\xi}_{\mathrm{d}} ; \bar{H}_{p_{\mathrm{o}}}(s)$为具有脉冲响应$\bar{h}_{p_{\mathrm{o}}}(t)$的传递函数，使得对于t>0的任意时刻，满足$\left|h_{p_{\rm{o}}}(t)\right| \leqslant \bar{h}_{p_\rm{o}}(t)$。

根据神经网络万能近似定理，SORNN存在最优权值使得陀螺测量不确定性b(t)与SORNN输出估计值$\hat{\boldsymbol{b}}(t)$之间的误差有界，满足：

$\left|b^{l}(t)-\hat{b}^{l}(t)\right| \leqslant \bar{b}^{l}(t)$ (32)

式中$\bar{b}^{l}(t)$为一有界常值。

在姿态小角度机动情况下，$\phi^{l}\left(\boldsymbol{y}_{1}(t), \tilde{\boldsymbol{b}}(t)\right)$可通过给出的上限界定:

$\left|\phi^{l}\left(\boldsymbol{y}_{1}(t), \tilde{\boldsymbol{b}}(t)\right)\right| \leqslant \gamma_{\phi}^{l} \cdot\left|\bar{b}^{l}(t)\right|=\bar{\varepsilon}_{b}^{l}(t)$ (33)

利用三角不等式，式(29)满足:

$\begin{gather*}\left|r_{1}^{l}(t)\right| \leqslant\left|H_{p_\rm{o}}(s)\left[\phi^{l}\left(\boldsymbol{y}_{1}(t), \tilde{\boldsymbol{b}}(t)\right)\right]\right|+ \\\left|\varepsilon_{\phi}^{l}(t)\right|+\left|h_{p_{\rm{o}}}(t) \xi^{l}(0)\right|+\left|\varepsilon_{\xi}^{l}(t)\right|\end{gather*}$ (34)

已知渐近稳定的传递函数H_po(s)的脉冲响应h_po(t)呈指数衰减，即t>0时，对于特定的υ>0，ζ>0，满足|h_po(t)|≤υe^－ζt。根据上述推导的边界值，得到最终的故障检测阈值为

$\bar{r}_{1}^{l}(t)=\bar{H}_{p_{\rm{o}}}(s)\left[\bar{\varepsilon}_{b}^{l}(t)\right]+\bar{\varepsilon}_{\phi}^{l}(t)+\left|h_{p_{\rm{o}}}(t)\right| \bar{\xi}^{l}+\bar{\varepsilon}_{\xi}^{l}(t)$ (35)

式中$\bar{H}_{p_{\rm{o}}}(s)=\boldsymbol{v} /(s+\zeta)$。需要注意，ξ^l(0)即便选取较为保守的界值ξ^l也只影响初始瞬态期间的阈值，并且h_po(t)呈指数衰减，所以可以不用考虑|h_po(t)|ξ^l后续对阈值的影响。

3 故障隔离机制航天器姿态控制方程由运动学子系统和动力学子系统组成。以陀螺和星敏感器为例，运动学方程能够表述星敏感器输出角度和陀螺输出角速度之间的关系，动力学方程能够表述陀螺输出角速度和执行器输出力矩之间的关系。因此，利用两个系统之间的冗余关系可以实现对星敏感器故障和陀螺故障的隔离。故障诊断系统框架如图 3所示，首先针对运动学子系统设计基于SORNN的干扰观测器，然后针对动力学子系统设计故障隔离观测器。前者用于判断是否发生故障，后者用于判断是否为陀螺故障，实现姿态敏感器故障隔离。

Fig. 3
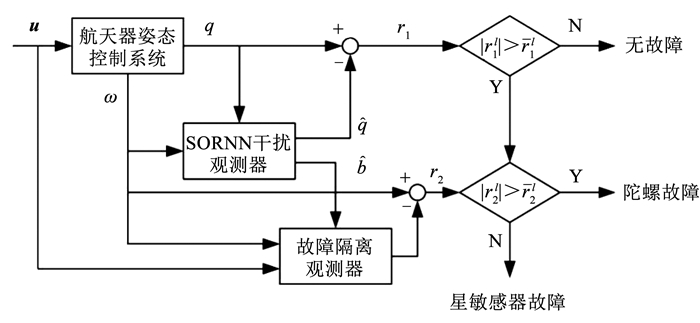图 3 航天器姿态敏感器故障检测与隔离框架 Fig. 3 Spacecraft attitude sensor fault diagnosis framework


带外部扰动和陀螺故障的姿态动力学子系统状态方程表示为^[14]

$\left\{\begin{array}{l}\dot{\boldsymbol{x}}_{2}=\varPhi\left(\boldsymbol{x}_{2}, t\right)+\boldsymbol{B} \boldsymbol{u}_{2}(t)+\boldsymbol{E d}(t) \\\boldsymbol{y}_{2}=\boldsymbol{C} \boldsymbol{x}_{2}(t)+\boldsymbol{b}(t)+\boldsymbol{f}_{\mathrm{g}}(t)\end{array}\right.$ (36)

式中：$\boldsymbol{x}_{2}=\left[\begin{array}{lll}\omega_{x} & \omega_{y} & \omega_{z}\end{array}\right]^{\mathrm{T}}$为航天器三轴角速度，$\boldsymbol{u}=\left[\begin{array}{lll}T_{x} & T_{y} & T_{z}\end{array}\right]^{\mathrm{T}}$为控制力矩，b(t)为陀螺测量误差，d(t)为外部干扰力矩，f_g(t)为陀螺故障函数，B=E=diag{1/I_x, 1/I_y, 1/I_z}，C=I₃，Φ(x, t)为动力学非线性函数，表达式为

$\varPhi(\boldsymbol{x}, t)=\left[\begin{array}{lll}\frac{I_{y}-I_{z}}{I_{x}} \omega_{y} \omega_{z} & \frac{I_{z}-I_{x}}{I_{y}} \omega_{z} \omega_{x} & \frac{I_{x}-I_{y}}{I_{z}} \omega_{x} \omega_{y} \end{array}\right]^{\mathrm{T}}$ (37)

不失一般性，假设d(t)，b(t)以及$\dot{\boldsymbol{b}}(t)$有界，并且Φ(x, t)满足Lipschitz条件:

$\left\|\varPhi\left(\boldsymbol{x}_{2}, t\right)-\varPhi\left(\hat{\boldsymbol{x}}_{2}, t\right)\right\| \leqslant \gamma_{\varPhi}\left\|\boldsymbol{x}_{2}-\hat{\boldsymbol{x}}_{2}\right\| $ (38)

式中γ_Φ为Lipschitz常数。

针对状态方程(36)设计未知输入观测器^[17]：

$\left\{ \begin{array}{l}\dot{\boldsymbol{z}}_{(t)=} \boldsymbol{F} \hat{\boldsymbol{x}}_{2}(t)+\boldsymbol{T} \boldsymbol{B} \boldsymbol{u}_{2}(t)+\boldsymbol{T} \varPhi\left(\hat{\boldsymbol{x}}_{2}, t\right)+ \\\quad\quad\quad \boldsymbol{L}\left(\boldsymbol{y}_{2}(t)-\hat{\boldsymbol{b}}(t)\right) \\\hat{\boldsymbol{x}}_{2}(t)= \boldsymbol{z}(t)+\boldsymbol{N}\left(\boldsymbol{y}_{2}(t)-\hat{\boldsymbol{b}}(t)\right) \\\hat{\boldsymbol{y}}_{2}(t)= \boldsymbol{C} \hat{\boldsymbol{x}}_{2}(t)+\hat{\boldsymbol{b}}(t)\end{array} \right.$ (39)

式中：z(t)为观测器状态变量，矩阵F, T, N, L满足:

$\left\{\begin{array}{l}\boldsymbol{T}= \boldsymbol{I}- \boldsymbol{N C } \\\boldsymbol{F}=- \boldsymbol{L C}\end{array}\right.$ (40)

定义状态估计误差$\boldsymbol{e}_{x_{2}}(t)=\boldsymbol{x}_{2}(t)-\hat{\boldsymbol{x}}_{2}(t)$，在无故障情况下，误差动态方程为

$\begin{align*}\dot{\boldsymbol{e}}_{x_{2}}(t)= & \dot{\boldsymbol{x}}_{2}(t)-\dot{\hat{\boldsymbol{x}}}_{2}(t)= \\& \boldsymbol{T}\dot{\boldsymbol{x}}_{2}(t)-\dot{\boldsymbol{z}}(t)-\boldsymbol{N}(\dot{\boldsymbol{b}}(t)-\dot{\hat{\boldsymbol{b}}}(t))-\boldsymbol{N} \dot{\boldsymbol { f }} _ { \mathrm { g } }(t)= \\& \boldsymbol{F} \boldsymbol{e}_{x_{2}}(t)+\boldsymbol{T} \Delta \varPhi(t)+\boldsymbol{T} \boldsymbol{E} \boldsymbol{d}(t)- \\& \boldsymbol{L} \tilde{\boldsymbol{b}}(t)- \boldsymbol{N}\dot{\tilde{\boldsymbol{b}}}(t) \end{align*}$ (41)

式中$\Delta \varPhi(t)=\varPhi\left(\boldsymbol{x}_{2}, t\right)-\varPhi\left(\hat{\boldsymbol{x}}_{2}, t\right)$。令TE=0，那么干扰d(t)将被解耦不会对残差产生影响，式(41)改写为

$\dot{\boldsymbol{e}}_{x_{2}}(t)=\boldsymbol{F} \boldsymbol{e}_{x_{2}}(t)+\boldsymbol{T} \Delta \varPhi(t)-\boldsymbol{L} \tilde{\boldsymbol{b}}(t)-\boldsymbol{N} \dot{\tilde{\boldsymbol{b}}}(t) $ (42)

另外，rank(CE)=rank(C)=q，根据TE=E－NCE=0可解得矩阵N=E[(CE)^T(CE)]^－1(CE)^T。当确定了矩阵L，利用式(40)容易得到其他矩阵。为此，给出如下定理求解矩阵L。

定理2??给定常数γ_Φ和δ，如果存在矩阵P₂(P₂=P₂^T>0)和U，使得

$\left[\begin{array}{cccc}-\boldsymbol{C}^{\mathrm{T}} \boldsymbol{U}^{\mathrm{T}}-\boldsymbol{U} \boldsymbol{C}+\boldsymbol{I}+\boldsymbol{C}^{\mathrm{T}} \boldsymbol{C} & -\boldsymbol{U}+\boldsymbol{C}^{\mathrm{T}} & -\boldsymbol{P}_{2} \boldsymbol{N} & \boldsymbol{P}_{2} \boldsymbol{T} \\ * & \left(1-\delta^{2}\right) \boldsymbol{I} & \mathbf{0} & \mathbf{0} \\ * & * & -\delta^{2} \boldsymbol{I} & \mathbf{0} \\ * & * & * & -\gamma_{\varPhi} \boldsymbol{I}\end{array}\right]<0$ (43)

那么所设计观测器是鲁棒稳定的，其中U=P₂L。

证明?? 根据状态估计误差e_x2(t)，定义Lyapunov函数V₂(t)=e_x2^T(t)P₂e_x2(t)，对时间求导:

$\begin{align*}\dot{V}_{2}(t)= & \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t)\left[\boldsymbol{F}^{\mathrm{T}} \boldsymbol{P}_{2}+\boldsymbol{P}_{2} \boldsymbol{F}\right] \boldsymbol{e}_{x_{2}}(t)+ \\& 2 \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t) \boldsymbol{P}_{2} \boldsymbol{T} \Delta \varPhi(t)- \\& 2 \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t) \boldsymbol{P}_{2}(\boldsymbol{L} \tilde{\boldsymbol{b}}(t)+\boldsymbol{N} \dot{\tilde{\boldsymbol{b}}}(t)) \end{align*}$ (44)

已知$\|\Delta \varPhi(t)\| \leqslant \gamma_{\varPhi}\left\|\boldsymbol{x}_{2}-\hat{\boldsymbol{x}}_{2}\right\|$，式(44)满足:

$\begin{align*}\dot{V}_{2}(t) \leqslant & \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t)\left[\boldsymbol{F}^{\mathrm{T}} \boldsymbol{P}_{2}+\boldsymbol{P}_{2} \boldsymbol{F}\right] \boldsymbol{e}_{x_{2}}(t)+ \\& \gamma_{\varPhi}^{2} \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t) \boldsymbol{P}_{2} \boldsymbol{TT}^{\mathrm{T}} \boldsymbol{P}_{2} \boldsymbol{e}_{x_{2}}(t)+ \\& \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t) \boldsymbol{e}_{x_{2}}(t)-2 \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t) \boldsymbol{P}_{2}(\boldsymbol{L} \tilde{\boldsymbol{b}}(t)+N \dot{\tilde{\boldsymbol{b}}}(t)) \end{align*}$ (45)

定义指标函数:

$J=\int_{0}^{t}\left[\dot{V}_{2}(\tau)+\boldsymbol{e}_{x_{2}}^{\mathrm{T}}(\tau) \boldsymbol{e}_{y_{2}}(\tau)-\delta^{2} \nu^{\mathrm{T}}(\tau) \nu(\tau)\right] \mathrm{d} \tau$ (46)

式中：$\boldsymbol{e}_{y_{2}}(t)=\boldsymbol{C} \boldsymbol{e}_{x_{2}}(t)+\tilde{\boldsymbol{b}}(t), \nu^{\mathrm{T}}(t)=\left[\tilde{\boldsymbol{b}}^{\mathrm{T}}(t)\right.$, $\left.\dot{\tilde{\boldsymbol{b}}}^{\mathrm{T}}(t)\right]$为新定义的变量。

将式(45)代入J可得

$\begin{aligned} J \leqslant &\int_0^t\left[\boldsymbol{e}_{x_2}^{\mathrm{T}}(\tau)\left(\boldsymbol{F}^{\mathrm{T}} \boldsymbol{P}_2+\boldsymbol{P}_2 \boldsymbol{F}+\gamma_\phi \boldsymbol{P}_2 \boldsymbol{T} \boldsymbol{T}^{\mathrm{T}} \boldsymbol{P}_2+\boldsymbol{I}\right) \boldsymbol{e}_{x_2}(\tau)-\right. \\& 2 \boldsymbol{e}_{x_2}^{\mathrm{T}}(\tau) \boldsymbol{P}_2(\boldsymbol{G} \tilde{\boldsymbol{b}}(\tau)+\dot{\boldsymbol{N}}(\tau))+\boldsymbol{e}_{x_2}^{\mathrm{T}}(\tau) \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C} \boldsymbol{e}_{x_2}(\tau)+ \\& 2 \boldsymbol{e}_{x_2}^{\mathrm{T}}(\tau) \boldsymbol{C}^{\mathrm{T}} \tilde{\boldsymbol{b}}(\tau)+\tilde{\boldsymbol{b}}^{\mathrm{T}}(\tau) \tilde{\boldsymbol{b}}(\tau)- \\& \left.\delta^2\left(\tilde{\boldsymbol{b}}^{\mathrm{T}}(\boldsymbol{\tau}) \tilde{\boldsymbol{b}}(\tau)+\dot{\boldsymbol{b}}^{\mathrm{T}}(\tau) \dot{\boldsymbol{b}}(\tau)\right)\right] \mathrm{d} \tau= \\& \int_0^t\left[\boldsymbol{X}^{\mathrm{T}}(\tau) \boldsymbol{\varXi} \boldsymbol{\chi}(\tau)\right] \mathrm{d} \tau\end{aligned}$ (47)

其中：

$\begin{gathered}\boldsymbol{\chi}^{\mathrm{T}}(t)=\left[\begin{array}{lll}\boldsymbol{e}_{x_{2}}^{\mathrm{T}}(t) & \tilde{\boldsymbol{b}}^{\mathrm{T}}(t) & \dot{\boldsymbol{b}}^{\mathrm{T}}(t)\end{array}\right] \\\boldsymbol{\varXi}=\left[\begin{array}{ccc}\boldsymbol{\varXi}_{11} & -\boldsymbol{P}_{2} \boldsymbol{L}+\boldsymbol{C}^{\mathrm{T}} & -\boldsymbol{P}_{2} \boldsymbol{N} \\* & \left(1-\delta^{2}\right) \boldsymbol{I} & 0 \\* & * & -\delta^{2} \boldsymbol{I}\end{array}\right]\end{gathered}$

式中，Ξ₁₁=F^TP₂+P₂F+γ_ΦP₂TT^TP₂+I+C^TC。

当Ξ＜0时，在零初始条件下：

$\begin{gather*}\int_{0}^{t}\left(\boldsymbol{e}_{x_{2}}^{\mathrm{T}}(\boldsymbol{\tau}) \boldsymbol{e}_{y_{2}}(\boldsymbol{\tau})-\delta^{2} \nu^{\mathrm{T}}(\tau) \nu(\tau)\right) \mathrm{d} \tau< \\J-V_{2}(0)<0 \end{gather*}$ (48)

因此，$\int_{0}^{t} \boldsymbol{e}_{x_{2}}^{\mathrm{T}}(\boldsymbol{\tau}) \boldsymbol{e}_{y_{2}}(\boldsymbol{\tau}) \mathrm{d} \tau<\delta^{2} \int_{0}^{t} \nu^{\mathrm{T}}(\boldsymbol{\tau}) \nu(\boldsymbol{\tau}) \mathrm{d} \boldsymbol{\tau}$。利用舒尔补定理，Ξ＜0等价于式(43)，证毕。

当发生陀螺微小故障时，误差动态方程(42)改写为

$\begin{gather*}\dot{\boldsymbol{e}}_{x_{2}}(t)=\boldsymbol{F} \boldsymbol{e}_{x_{2}}(t)+\boldsymbol{T} \Delta \varPhi(t)-\boldsymbol{L} \tilde{\boldsymbol{b}}(t)- \\\boldsymbol{N \dot { \tilde { b } }}(t)-\boldsymbol{L} \boldsymbol{f}_{\mathrm{g}}(t)-\boldsymbol{N} \dot{\boldsymbol{f}}_{\mathrm{g}}(t) \end{gather*}$ (49)

可以看出，陀螺故障f_g(t)对$\dot{\boldsymbol{e}}_{x_{2}}(t)$有直接影响，并且通过干扰解耦和SORNN干扰观测器补偿消除了d(t)和b(t)对状态误差的影响。为此可以定义残差为$\boldsymbol{r}_{2}=\left(\int \boldsymbol{e}_{y_{2}}^{\mathrm{T}} \boldsymbol{e}_{y_{2}} \mathrm{~d} t / \boldsymbol{\tau}\right)^{1 / 2}$，用以检测陀螺微小故障，实现故障的隔离。需要注意，某些情况下矩阵T会同时解耦执行器故障，但这并不影响该方法对敏感器的诊断。可以进一步理解为，即便在敏感器和执行器同时发生故障时，该方法依然可以实现敏感器的检测与隔离。

4 仿真分析航天器三轴转动惯量分别为I_x=18.73 kg·m²，I_y=20.77 kg·m²，I_z=23.63 kg·m²；初始角速度ω(0)=[－0.041 6??0.048 4??－0.055 6]^Trad/s, 初始角度q(0)=[0.993 6??0.047 2??－0.078 8??0.065 5]^T, 陀螺漂移1×10^－5I₃，测量噪声均方差3×10^－5, 星敏感器测量噪声均方差2×10^－5, 扰动力矩T_d(t)=$1.5 \times 10^{-5} \cdot\left[\begin{array}{c}3 \cos \omega_{0} t+1 \\ 1.5 \sin \left(\omega_{0} t\right)+3 \cos \omega_{0} t \\ 3 \sin \left(\omega_{0} t\right)+1\end{array}\right] \mathrm{N} \cdot \mathrm{m}$，其中ω₀=0.001 2 rad/s。设置仿真时长200 s，步长τ=0.1 s，针对姿态敏感器故障开展仿真实验。

4.1 陀螺测量误差估计根据式(8)设计SORNN干扰观测器。[q₁, q₂, q₃]^T对应的3个SORNN学习参数初始值和网络结构调整预设阈值见表 1。

表 1
表 1 自组织循环神经网络仿真实验参数 Tab. 1 Simulation experimental parameters of SORNN 网络 P_m R_m G_m η_m ε_c1 ε_c2

SORNN1 I_n+2 10^－8 I_(n+2)×1 1.8 2×10^－6 0.01

SORNN2 5·I_n+2 10^－8 I_(n+2)×1 1.5 2×10^－6 0.02

SORNN3 5·I_n+2 10^－8 I_(n+2)×1 1.5 2×10^－6 0.08



表 1 自组织循环神经网络仿真实验参数 Tab. 1 Simulation experimental parameters of SORNN


SORNN干扰观测器初始状态$\hat{\boldsymbol{x}}(0)=\boldsymbol{y}(0)$，选择批量学习大小b=50，训练窗口K=4。为验证SORNN干扰观测器对陀螺测量误差的估计效果，在系统无故障情况下，将其与基于改进EKF的状态估计方法^[10]进行比较，仿真结果如图 4~7所示。其中，图 4为SORNN结构自组织变化过程，3个SORNN的隐藏层神经元数量m和记忆深度n在100~150 s内均调整至一个平稳的状态。图 5~7分别给出了两种方法对3个轴向陀螺测量误差b(t)的估计情况。EKF将估计误差$\boldsymbol{b}(t)-\hat{\boldsymbol{b}}(t)$扩展为状态向量，通过对状态的更新和估计误差的累加直接获取陀螺测量误差的估计值，因此自适应能力欠佳，误差较大。而SORNN由于内部循环结构可以更好地处理时序数据，且具备隐藏层神经元和记忆深度调节能力，使得SORNN对陀螺测量误差的估计性能更优，从而能够更好地补偿观测器，消除陀螺测量误差对状态估计的影响。

Fig. 4
图 4 自组织循环神经网络隐藏层神经元和记忆深度调整过程 Fig. 4 Hidden layer neurons and memory depth adjustment process of SORNN


Fig. 5
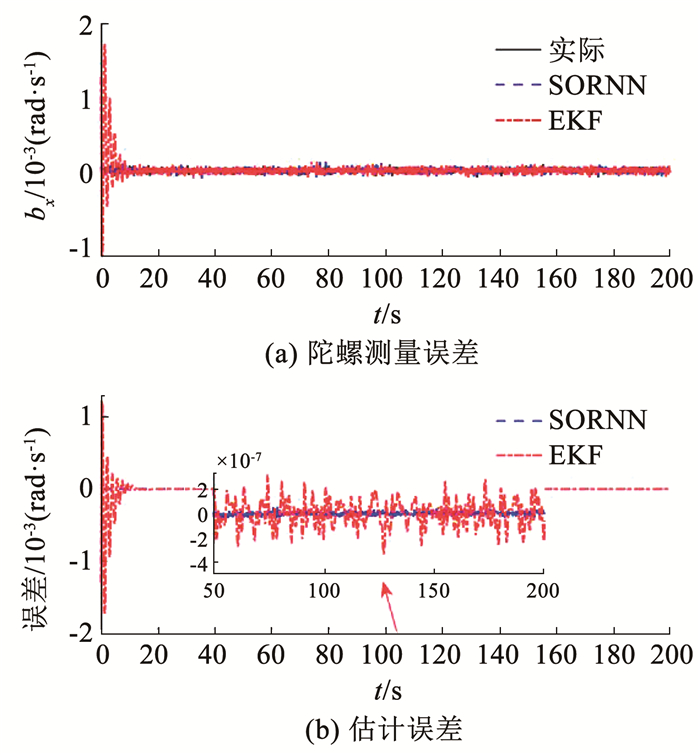图 5 x轴陀螺测量误差估计 Fig. 5 x-axis gyro measurement error estimation


Fig. 6
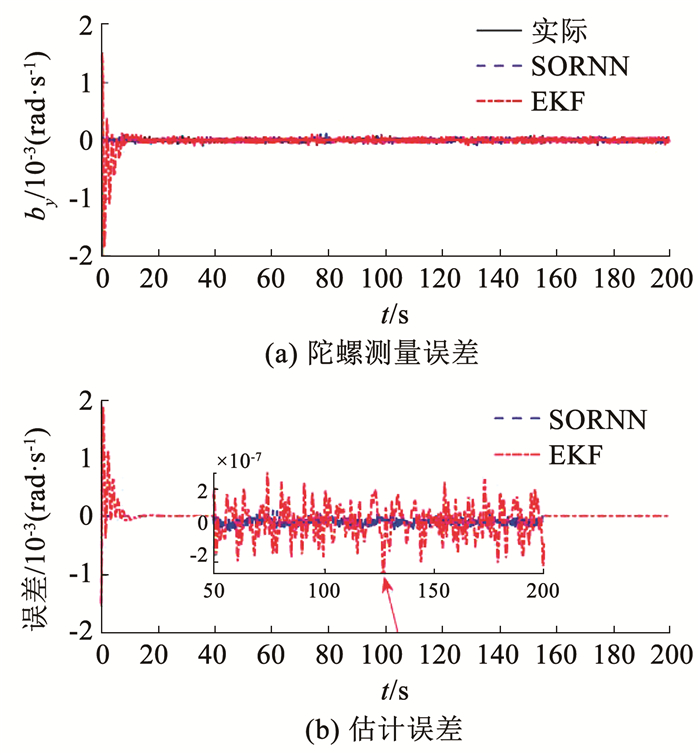图 6 y轴陀螺测量误差估计 Fig. 6 y-axis gyro measurement error estimation


Fig. 7
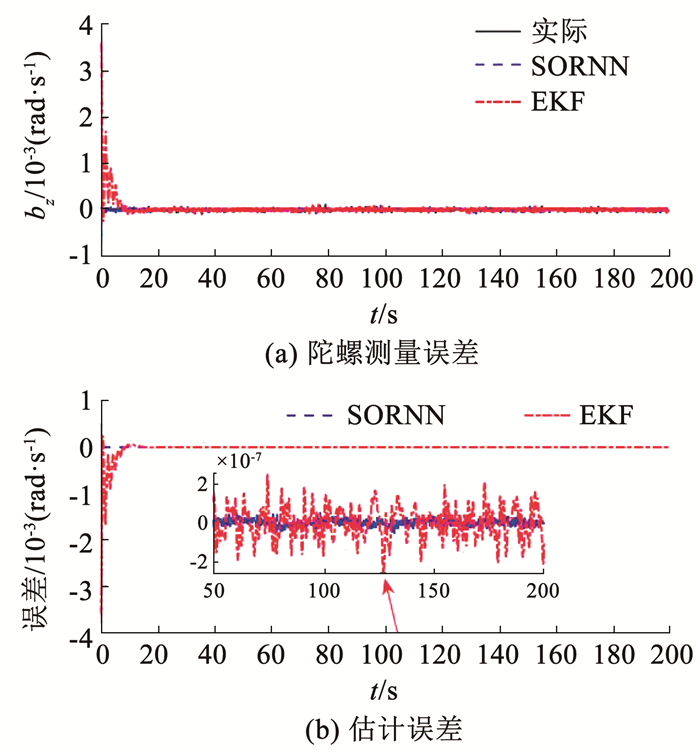图 7 z轴陀螺测量误差估计 Fig. 7 z-axis gyro measurement error estimation


4.2 故障检测设置滤波器阶数为3，传递函数H_po(s)=50/s(s+5)(s+10)。通过拉式反变换可知H_po(s)脉冲响应非负，因此计算阈值所需的滤波器传递函数H_po(s)=H_po(s)。考虑到工程上有成熟的方法对星敏感器测量噪声进行评估^[18]，为简单起见，滤波后的星敏感器测量噪声的界值从仿真结果中获取，$\bar{\varepsilon}_{\xi}^{1}(t)=\bar{\varepsilon}_{\xi}^{2}(t)=\bar{\varepsilon}_{\xi}^{3}(t)=1.4 \times 10^{-5}$。类似地，设定Lipschitz常数γ_?^l=0.2，得到滤波后的函数差值项界值$\bar{\varepsilon}_{\phi}^{l}(t) $=γ_?^lH_po(s)[ξ_d]=γ_?^lε_ξ^l(t)=2.8×10^－6。进一步利用航天器3个轴向陀螺测量误差估计值可以得到$\bar{\varepsilon}_{b}^{1}(t)=3.0658 \times 10^{-8}, \bar{\varepsilon}_{b}^{2}(t)=2.9151 \times$ $10^{-8}, \bar{\varepsilon}_{b}^{3}(t)=2.6236 \times 10^{-8}$。最终根据式(35)计算得到3个轴向阈值分别为：$\bar{r}_{1}^{1}=1.6831 \times 10^{-5}$, $\bar{r}_{1}^{2}=1.6829 \times 10^{-5}, \bar{r}_{1}^{3}=1.6826 \times 10^{-5}$。分别对陀螺和星敏感器开展故障检测实验。

1) 陀螺故障。假设航天器x轴陀螺在t=150 s时发生时变故障，故障表示为

${\mathit{\boldsymbol{f}}_{\rm{g}}} = \left\{ {\begin{array}{*{20}{l}}{{{\left[ {\begin{array}{*{20}{l}}0&0&0\end{array}} \right]}^{\rm{T}}}, }&{t < 150{\rm{s}}}\\{2 \times {{10}^{ - 5}}\sin {{\left( {\begin{array}{*{20}{l}}{0.04\pi t)}&0&0\end{array}} \right]}^{\rm{T}}}, }&{t \ge 150{\rm{s}}}\end{array}} \right.$ (50)

2) 星敏感器故障。假设航天器星敏感器y轴测量输出在t=150 s时发生突变故障，故障表示为

$\boldsymbol{f}_{\mathrm{s}}=\left\{\begin{array}{lll}{\left[\begin{array}{lll}0 & 0 & 0\end{array}\right]^{\mathrm{T}}, } & t<150 \mathrm{~s} \\{\left[\begin{array}{lll}0 & 5 \times 10^{-5} & 0\end{array}\right]^{\mathrm{T}}, } & t \geqslant 150 \mathrm{~s}\end{array}\right.$ (51)

为验证检测方法的性能，将所提方法与基于改进EKF的故障检测方法^[10]进行对比。采用3-σ法对基于改进EKF的检测方法设置阈值，陀螺故障检测结果如图 8、9所示。

Fig. 8
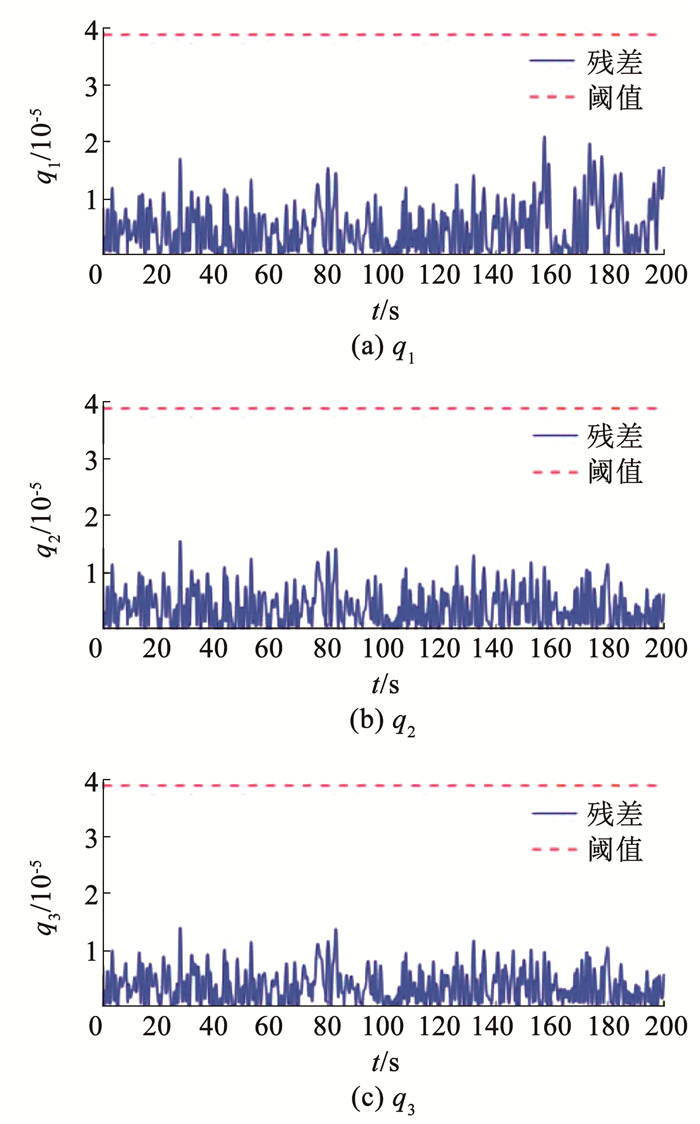图 8 基于改进EKF故障检测方法陀螺故障检测结果 Fig. 8 Fault detection results of gyro based on improved EKF fault detection method


Fig. 9
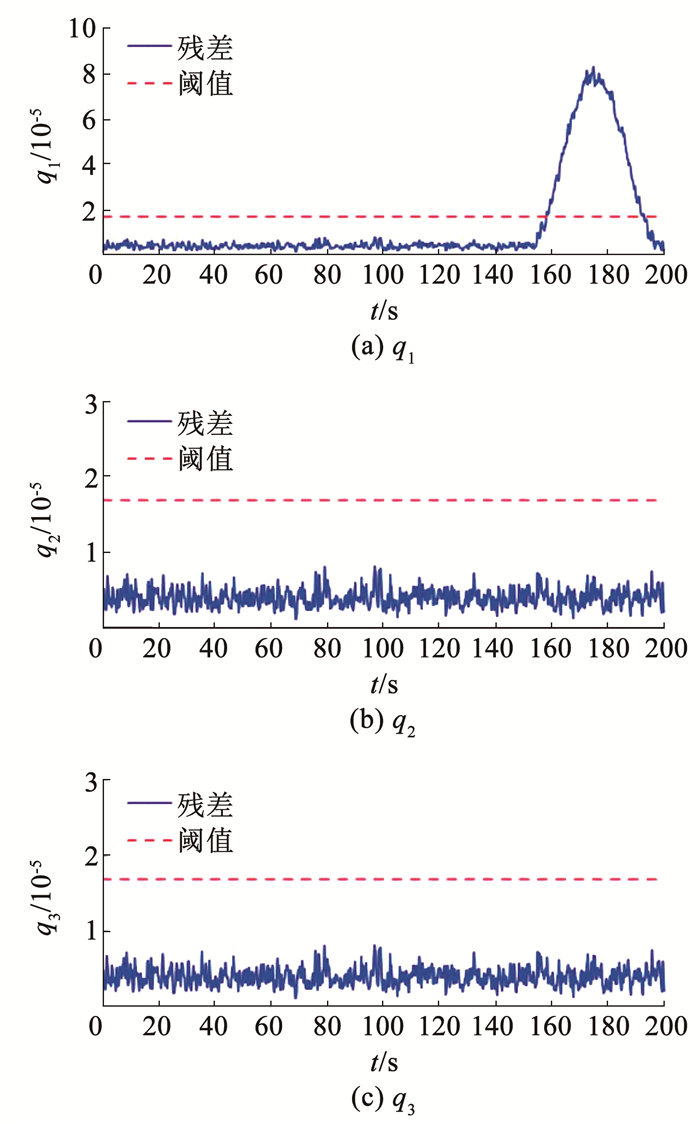图 9 所提检测方法陀螺故障检测结果 Fig. 9 Fault detection results of gyro based on the proposed detection method


星敏感器故障检测结果如图 10、11所示。从图 8和图 10的结果可以看出，基于改进EKF的故障检测方法虽然对陀螺测量误差进行了鲁棒抗干扰处理，但由于噪声的存在，对微小故障响应不明显，并且没有适配更严格的检测阈值，导致对陀螺和星敏感器微小故障的检测均出现了漏报情况。而对比图 9和图 11的结果，在陀螺测量误差补偿以及滤波处理后，很大程度上消除了陀螺测量误差和星敏感器噪声的影响，然后利用式(35)计算出的检测阈值，能够实现对陀螺和星敏感器微小故障的准确检测，从而验证了所提微小故障检测方法的有效性。

Fig. 10
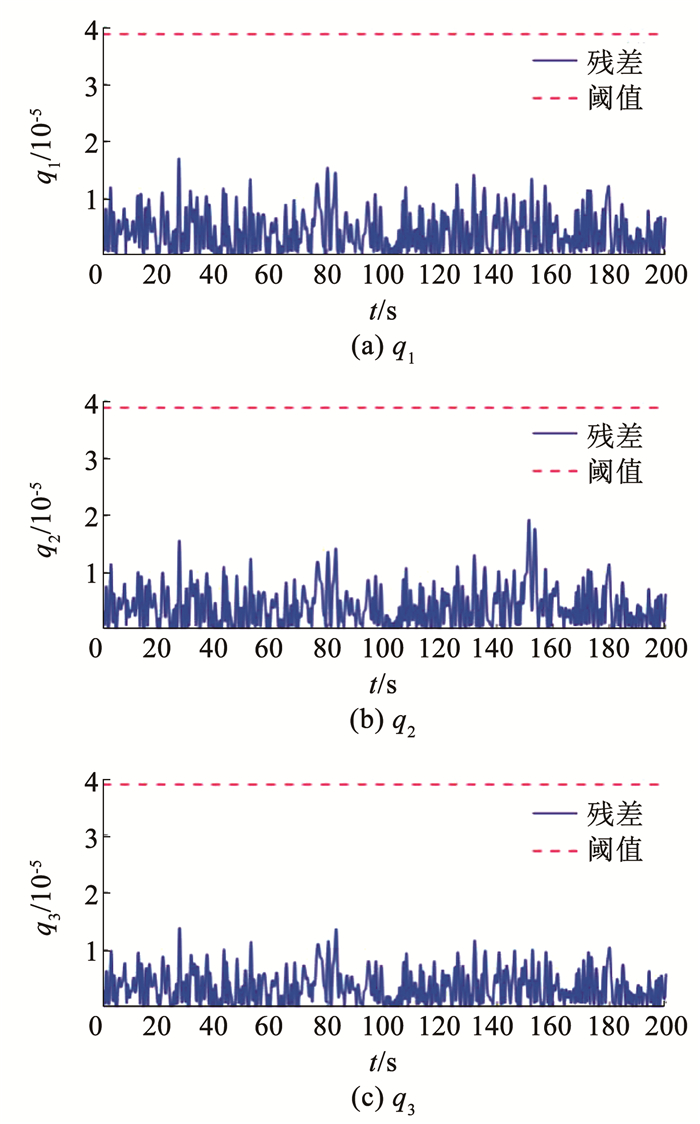图 10 基于改进EKF故障检测方法星敏感器故障检测结果 Fig. 10 Fault detection results of star sensor based on improved EKF fault detection method


Fig. 11
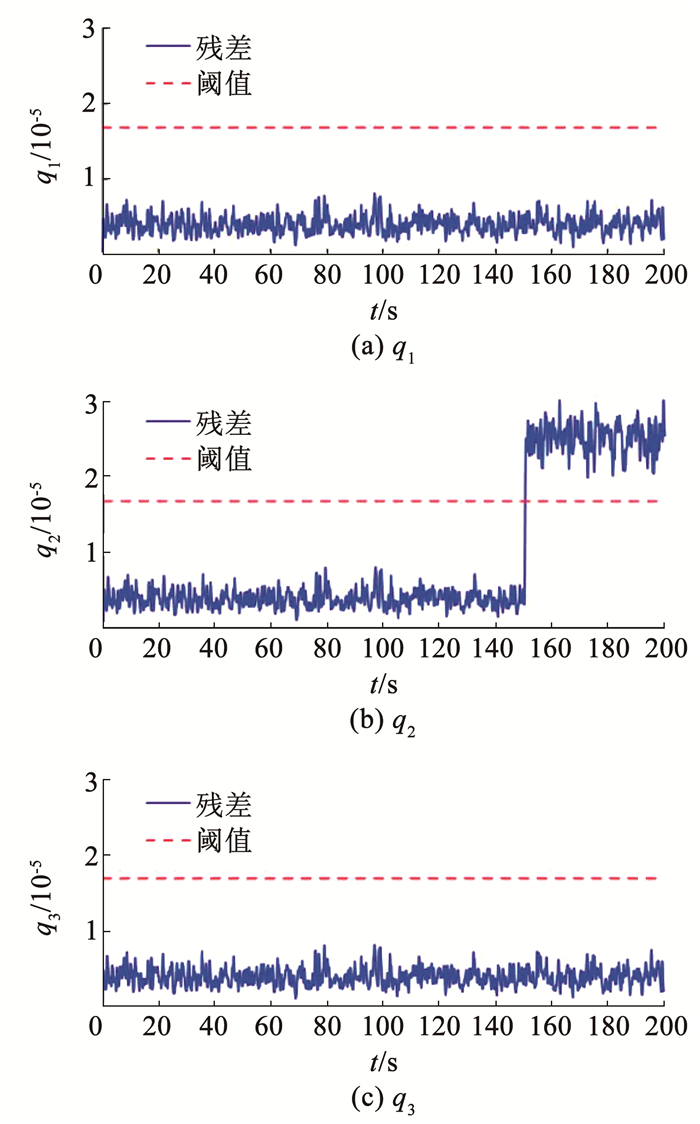图 11 所提方法星敏感器故障检测结果 Fig. 11 Fault detection results of star sensor based on the proposed detection method


4.3 故障隔离在检测出故障发生后，根据式(38)设计故障隔离观测器并利用残差来判断是否为陀螺故障，从而实现陀螺故障和星敏感器故障的二分问题。给定常数γ_Φ=0.5，δ=0.8，求解LMI(43)，得到观测器增益矩阵为

$\boldsymbol{L}=\left[\begin{array}{lll}4.2543 & 0.9901 & 0.8703 \\0.9901 & 4.0492 & 0.7848 \\0.8703 & 0.7848 & 3.8461\end{array}\right]$ (52)

为评估故障隔离观测器的检测性能，在动力学模型存在不确定性情况下，分别对式(51)、(52)所描述的陀螺故障和星敏感器故障开展故障隔离实验。将10^－7[2sin(0.3t)?3cos(0.1t)?1cos(0.2t)]^T叠加高斯白噪声加入至动力学状态方程中作为模型不确定性，设置检测阈值分别为1.250 4×10^－6、7.057 0×10^－7、1.465 5×10^－6，仿真结果如图 12、13所示(其中残差初始部分为动态调整过程，在此不作讨论)。仿真结果可以看出故障隔离观测器对模型不确性具有一定鲁棒性，并且残差只对陀螺故障敏感，当陀螺发生故障时，残差迅速越过阈值，而当星敏感器发生故障时残差并不会出现明显的响应，验证了该方法对姿控系统陀螺故障和星敏感器故障的隔离功能。

Fig. 12
图 12 陀螺故障情况下故障隔离结果 Fig. 12 Fault isolation results in case of gyro fault


Fig. 13
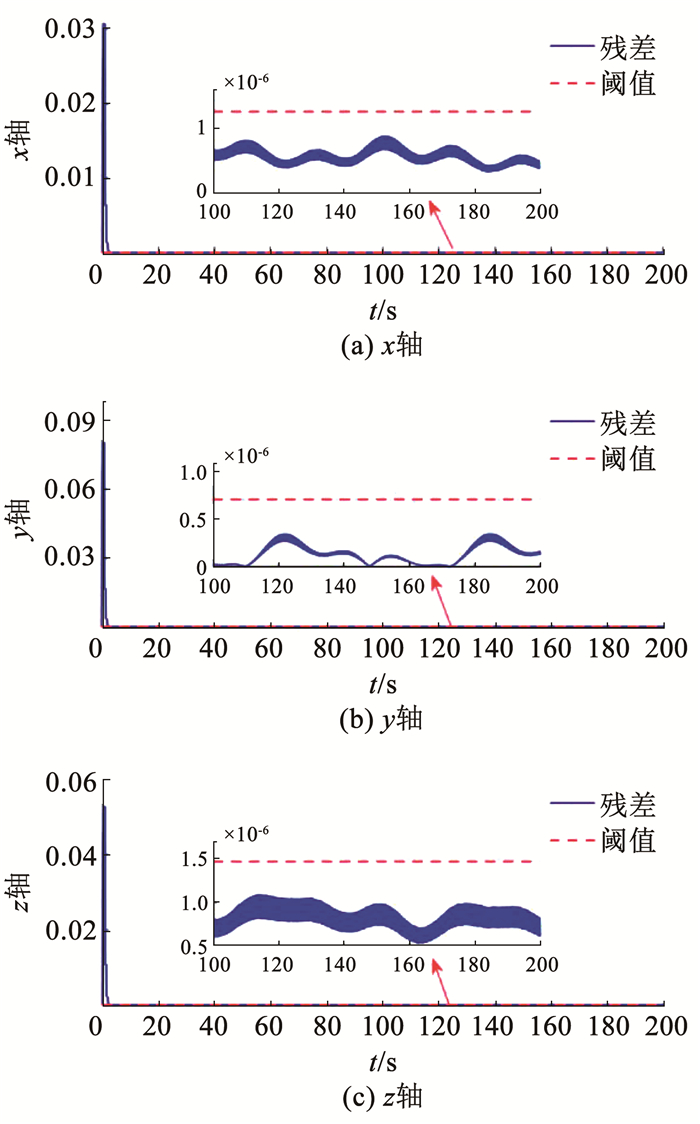图 13 星敏感器故障情况下故障隔离结果 Fig. 13 Fault isolation results in case of star sensor fault


5 结论1) 在传统RNN结构基础上设计了具备自适应调节功能的SORNN和对应的EKF自适应权值更新算法，并应用于干扰观测器中，通过估计陀螺测量误差消除其对状态估计的影响。

2) 结合低通滤波器抑制测量噪声对系统输出估计误差的影响，推导出了更严格的残差和检测阈值的计算方法，从而提高了对微小故障的检测能力。

3) 利用航天器姿态运动学和动力学冗余关系设计未知输入观测器实现对星敏感器和陀螺故障的隔离。最终通过仿真结果验证了所提出故障检测与隔离方法的可行性。


参考文献
[1] AOUAOUDA S, CHADLI M, SHI P, et al. Discrete-time H_-/H_∞ sensor fault detection observer design for nonlinear systems with parameter uncertainty[J]. International Journal of Robust and Nonlinear Control, 2015, 25(3): 339. DOI:10.1002/rnc.3089


[2] LIU Weixin, LI Shengwen, CHEN Minhua, et al. Fault diagnosis for attitude sensors based on analytical redundancy and wavelet transform[C]//2020 Chinese Automation Congress (CAC). Shanghai, China: IEEE, 2020: 6471. DOI: 10.1109/CAC51589.2020.9327370


[3] VAN EYKEREN L, CHU Q P. Fault detection and isolation for inertial reference units[C]//Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference. Reston, Virginia: AIAA, 2013: AIAA2013-4697. DOI: 10.2514/6.2013-4697


[4] BALDI P, BLANKE M, CASTALDI P, et al. Fault diagnosis for satellite sensors and actuators using nonlinear geometric approach and adaptive observers[J]. International Journal of Robust and Nonlinear Control, 2019, 29(16): 5429. DOI:10.1002/rnc.4083


[5] YUAN Zhengguo, SONG Ningfang, PAN Xiong, et al. Fault detection, isolation, and reconstruction for satellite attitude sensors using an adaptive hybrid method[J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 3522112. DOI:10.1109/TIM.2021.3097404


[6] CHEN Tianrui, ZHU Zejian, WANG Cong, et al. Rapid sensor fault diagnosis for a class of nonlinear systems via deterministic learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(12): 7743. DOI:10.1109/TNNLS.2021.3087533


[7] REPPA V, POLYCARPOU M M, PANAYIOTOU C G. Adaptive approximation for multiple sensor fault detection and isolation of nonlinear uncertain systems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(1): 137. DOI:10.1109/TNNLS.2013.2250301


[8] KELIRIS C, POLYCARPOU M M, PARISINI T. A distributed fault detection filtering approach for a class of interconnected continuous-time nonlinear systems[J]. IEEE Transactions on Automatic Control, 2013, 58(8): 2032. DOI:10.1109/TAC.2013.2253231


[9] 李利亮, 牛睿, 邵志杰, 等. 基于专用卡尔曼滤波器思想的陀螺故障诊断[J]. 控制理论与应用, 2019, 36(9): 1501.
LI Liliang, NIU Rui, SHAO Zhijie, et al. Gyroscope fault diagnosis based on dedicated Kalman filter scheme[J]. Control Theory & Applications, 2019, 36(9): 1501. DOI:10.7641/CTA.2019.80192


[10] GAO Sheng, ZHANG Zhaowei, ZHANG Wei, et al. Fault diagnosis for satellite attitude control system with using extended Kalman filter[C]//2019 Chinese Control Conference (CCC). Guangzhou, China: IEEE, 2019: 4789. DOI: 10.23919/ChiCC.2019.8865903


[11] 邢琰, 吴宏鑫. 一种红外地球敏感器和陀螺的故障隔离方法[J]. 计算技术与自动化, 2003, 22(2): 74.
XING Yan, WU Hongxin. A fault isolation method for infrared earth sensors and gyroscopes[J]. Computing Technology and Automation, 2003, 22(2): 74. DOI:10.3969/j.issn.1003-6199.2003.02.022


[12] ISLAM M M, SATTAR M A, AMIN M F, et al. A new constructive algorithm for architectural and functional adaptation of artificial neural networks[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, Cybernetics: A Publication of the IEEE Systems, and Cybernetics Society, 2009, 39(6): 1590. DOI:10.1109/TSMCB.2009.2021849


[13] CHU Yundi, FEI Juntao, HOU Shixi. Adaptive global sliding-mode control for dynamic systems using double hidden layer recurrent neural network structure[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(4): 1297. DOI:10.1109/TNNLS.2019.2919676


[14] WANG Rixin, CHENG Yao, XU Minqiang. Analytical redundancy based fault diagnosis scheme for satellite attitude control systems[J]. Journal of the Franklin Institute, 2015, 352(5): 1906. DOI:10.1016/j.jfranklin.2015.02.003


[15] 李磊, 高永明, 吴止锾, 等. 卫星姿态控制系统执行器微小故障检测方法[J]. 北京航空航天大学学报, 2019, 45(3): 529.
LI Lei, GAO Yongming, WU Zhihuan, et al. Small fault detection method for actuator of satellite attitude control system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(3): 529. DOI:10.13700/j.bh.1001-5965.2018.0372


[16] ABOUTALEBI P, ABBASPOUR A, FOROUZANNEZHAD P, et al. A novel sensor fault detection in an unmanned quadrotor based on adaptive neural observer[J]. Journal of Intelligent & Robotic Systems, 2018, 90(3/4): 473. DOI:10.1007/s10846-017-0690-7


[17] CHENG Yao, WANG Rixin, XU Minqiang. A combined model-based and intelligent method for small fault detection and isolation of actuators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2403. DOI:10.1109/TIE.2015.2499722


[18] LIEBE C C. Accuracy performance of star trackers-a tutorial[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 587. DOI:10.1109/TAES.2002.1008988