数据驱动与机理耦合的冷轧电机功率智能预测方法

曹雷,董梓硕,李晓华,李旭,张殿华

(轧制技术及连轧自动化国家重点实验室(东北大学),沈阳 110819)



摘要:

电机功率计算在保证生产安全、制定轧制规程以及发挥设备能力等方面起到了重要作用。为提高计算精度,本文提出一种机理模型与数据驱动方法相结合的电机功率预测模型。首先,机理模型部分采用上界法得到解析解,然后将部分功率解析解（塑性变形功率、张力功率和剪切功率）与相关变量输入长短时记忆（long short-term memory, LSTM）网络中训练,以提取变量数据之间的深度特征和时序相关性。结果表明:本文提出的时序耦合预测模型相对误差不超过±3.9%,且在相邻卷带钢轧制规程变化较大时,预测效果明显优于上界法和人工神经网络（artificial neural networks, ANN）；从残差分布直方图中可以看到,上界法由于遗漏了摩擦系数和损失功率与其他参数间的强耦合关系,导致残差集中在±50 kW附近且不符合正态分布,而ANN和本模型均基本遵循正态分布,但本模型拟合精度更高；对比更广泛的模型评估指标,本模型具有更好的综合预测性能。此外,通过模型输出结果分析了电机功率与轧制长度、轧制速度之间的关系,表明本模型除具有高预测精度外,还与已知的参数间物理规律有较强一致性。

关键词:  冷轧  电机功率  长短时记忆网络  工业大数据  上界法  数学模型

DOI：10.11918/202206124

分类号:TG335.5

文献标识码:A

基金项目:国家自然科学基金(U20A20187)；辽宁省“兴辽英才计划”资助(XLYC2007087)；中央高校基本科研业务费资助(N2107010)



Intelligent prediction method for cold rolling motor power based on data-driven and mechanism coupling

CAO Lei,DONG Zishuo,LI Xiaohua,LI Xu,ZHANG Dianhua

（State Key Laboratory of Rolling and Automation (Northeastern University), Shenyang 110819, China）

Abstract:

Motor power calculation plays an important role in ensuring production safety, formulating rolling schedule, and leveraging equipment capabilities. In order to improve calculation accuracy, a motor power prediction model combining mechanism model and data-driven method was proposed. The mechanism model was analytically solved by upper bound method, and then parts of the power analytical solutions (plastic deformation power, tension power, and shear power) and related variables were input into long short-term memory (LSTM) network for training, so as to extract depth characteristics and temporal correlations between variable data. Results show that the relative error of the proposed time series coupling prediction model was less than ±3.9%, and the prediction effect was obviously better than that of the upper bound method and artificial neural network (ANN) when the rolling schedule of adjacent strips changed greatly. According to the residual distribution histogram, the residual of upper bound method was concentrated around ±50 kW and deviating from a normal distribution, as it ignored the strong relationship between friction coefficient, loss power, and other parameters. Both ANN and the proposed model basically followed normal distribution, but the proposed model had higher fitting accuracy. In comparison with broader model evaluation indicators, the proposed model had better comprehensive prediction performance. Besides, the relationship between motor power, rolling length, and rolling speed was analyzed based on model output results, which indicated that the model not only has high prediction accuracy, but also strong consistency with known physical law between parameters.

Key words:  cold rolling  motor power  long short-term memory  industrial big data  upper bound method  mathematical model


曹雷, 董梓硕, 李晓华, 李旭, 张殿华. 数据驱动与机理耦合的冷轧电机功率智能预测方法[J]. 哈尔滨工业大学学报, 2024, 56(5): 28-35. DOI: 10.11918/202206124.
CAO Lei, DONG Zishuo, LI Xiaohua, LI Xu, ZHANG Dianhua. Intelligent prediction method for cold rolling motor power based on data-driven and mechanism coupling[J]. Journal of Harbin Institute of Technology, 2024, 56(5): 28-35. DOI: 10.11918/202206124.
基金项目 国家自然科学基金(U20A20187)；辽宁省“兴辽英才计划”资助(XLYC2007087)；中央高校基本科研业务费资助(N2107010) 作者简介 曹雷(1992—)，男，博士研究生;
李旭(1981—)，男，教授，博士生导师 通信作者 李旭，lixu@ral.neu.edu.cn 文章历史 收稿日期: 2022-06-30



Abstract            Full text            Figures/Tables            PDF


数据驱动与机理耦合的冷轧电机功率智能预测方法
曹雷, 董梓硕, 李晓华, 李旭, 张殿华     
轧制技术及连轧自动化国家重点实验室(东北大学)，沈阳 110819

收稿日期: 2022-06-30; 录用日期: 2022-08-23; 网络首发日期: 2022-11-09
基金项目: 国家自然科学基金(U20A20187)；辽宁省“兴辽英才计划”资助(XLYC2007087)；中央高校基本科研业务费资助(N2107010)
作者简介: 曹雷(1992—)，男，博士研究生; 李旭(1981—)，男，教授，博士生导师
通信作者: 李旭，lixu@ral.neu.edu.cn


摘要: 电机功率计算在保证生产安全、制定轧制规程以及发挥设备能力等方面起到了重要作用。为提高计算精度，本文提出一种机理模型与数据驱动方法相结合的电机功率预测模型。首先，机理模型部分采用上界法得到解析解，然后将部分功率解析解(塑性变形功率、张力功率和剪切功率)与相关变量输入长短时记忆(long short-term memory, LSTM)网络中训练，以提取变量数据之间的深度特征和时序相关性。结果表明：本文提出的时序耦合预测模型相对误差不超过±3.9%，且在相邻卷带钢轧制规程变化较大时，预测效果明显优于上界法和人工神经网络(artificial neural networks, ANN)；从残差分布直方图中可以看到，上界法由于遗漏了摩擦系数和损失功率与其他参数间的强耦合关系，导致残差集中在±50 kW附近且不符合正态分布，而ANN和本模型均基本遵循正态分布，但本模型拟合精度更高；对比更广泛的模型评估指标，本模型具有更好的综合预测性能。此外，通过模型输出结果分析了电机功率与轧制长度、轧制速度之间的关系，表明本模型除具有高预测精度外，还与已知的参数间物理规律有较强一致性。
关键词: 冷轧    电机功率    长短时记忆网络    工业大数据    上界法    数学模型    
Intelligent prediction method for cold rolling motor power based on data-driven and mechanism coupling
CAO Lei, DONG Zishuo, LI Xiaohua, LI Xu, ZHANG Dianhua     
State Key Laboratory of Rolling and Automation (Northeastern University), Shenyang 110819, China



Abstract: Motor power calculation plays an important role in ensuring production safety, formulating rolling schedule, and leveraging equipment capabilities. In order to improve calculation accuracy, a motor power prediction model combining mechanism model and data-driven method was proposed. The mechanism model was analytically solved by upper bound method, and then parts of the power analytical solutions (plastic deformation power, tension power, and shear power) and related variables were input into long short-term memory (LSTM) network for training, so as to extract depth characteristics and temporal correlations between variable data. Results show that the relative error of the proposed time series coupling prediction model was less than ±3.9%, and the prediction effect was obviously better than that of the upper bound method and artificial neural network (ANN) when the rolling schedule of adjacent strips changed greatly. According to the residual distribution histogram, the residual of upper bound method was concentrated around ±50 kW and deviating from a normal distribution, as it ignored the strong relationship between friction coefficient, loss power, and other parameters. Both ANN and the proposed model basically followed normal distribution, but the proposed model had higher fitting accuracy. In comparison with broader model evaluation indicators, the proposed model had better comprehensive prediction performance. Besides, the relationship between motor power, rolling length, and rolling speed was analyzed based on model output results, which indicated that the model not only has high prediction accuracy, but also strong consistency with known physical law between parameters.
Keywords: cold rolling    motor power    long short-term memory    industrial big data    upper bound method    mathematical model    
轧制力能参数计算精度直接影响带钢板形和板厚的控制质量，很多专家学者对此进行了广泛的研究。针对神经网络无法提升小批量、多品种轧制模式下的轧制力设定精度的问题，文献[1]采用数据统计分析的方法对预设定模型的修正系数重新计算。文献[2]采用有限元法与人工神经网络相结合的方式进行轧制力预报，精度有所提高且满足在线使用需求。文献[3]提出了一种基于贝叶斯方法的神经网络预测冷轧轧制力，在收敛速度和预测精度上均优于传统的BP神经网络。文献[4-5]采用神经网络对变形抗力和摩擦系数等非线性因素进行系数校正，再结合轧制力数学解析模型，建立了轧制力在线计算模型。

主电机功率是冷连轧生产中需要确定的重要力能参数之一，其主要作用包括：为主电机容量选取提供合理依据；在工艺参数设定时，必须保证主电机的输出功率不超过电机本身容许的最大功率^[6]；在轧制负荷分配时，通常使各机架按照功率成比例或等功率裕度的方式进行分配，以充分发挥各机架主电机的能力^[7-10]。由此可见，提升电机功率模型的计算精度在提高产品控制精度、优化轧制规程和发挥设备能力并保证生产安全等方面具有重要意义。

主电机功率的确定必须先计算传动轧辊的轧制力矩、附加摩擦力矩、空转力矩和动力矩，其中轧制力矩是最大和有效部分，剩余部分为有害力矩^[11]。轧制力矩理论模型主要有2种：传统模型和上界法。由于传统模型形式简单、物理意义清晰，因此工程上经常使用^[12]。上界法是以上界定理为依据，通过假定满足运动许可条件的速度场，计算上界功率并对其求得最小值，最后解得力能和变形参数的方法^[13]。此方法明确了各参数间的物理关系，且力能参数结果往往比实际值略高，对设备的选择和保护十分有利。近些年不少专家学者从速度场设定角度出发进行研究，如抛物线速度场^[14]、余弦速度场^[15]、正切速度场^[16]以及流函数法^[17]。采用上述2种方法计算主电机功率都不可避免的需要确定摩擦系数、力臂系数以及损失力矩，但这些模型参数常常难以确定^[18-19]。例如：力臂系数影响因素众多，目前还没有公认的解析公式^[20]；损失力矩会受到轧制速度和轧制力等参数变化的影响；摩擦系数会随着轧制长度的增大而减小。因此，这些参数对轧制力矩和电机功率的计算精度有很大影响。

鉴于上述问题，本文提出一种机理模型与数据驱动相结合的冷轧电机功率预测模型。其中，机理模型部分采用上界法得到解析解，然后将解析解与相关变量输入长短时记忆(long short-term memory, LSTM)网络中训练，以提取变量数据之间的深度特征和时序相关性。实验验证表明：所提出的时序耦合预测模型与上界法或不考虑数据时序特性的人工神经网络相比预测精度均有所提高，相对误差分别从不超过±8.5%和±6.3%提升到±3.9%；而且因有传统机理模型参与，预测结果更符合物理规律。

1 轧制力矩解析模型冷轧过程带钢宽厚比远大于10，因此可以忽略宽展并认为带钢在变形区处于平面应变状态。再结合沿轧制线的对称性，便可得到其1/2变形区示意见图 1。

Fig. 1
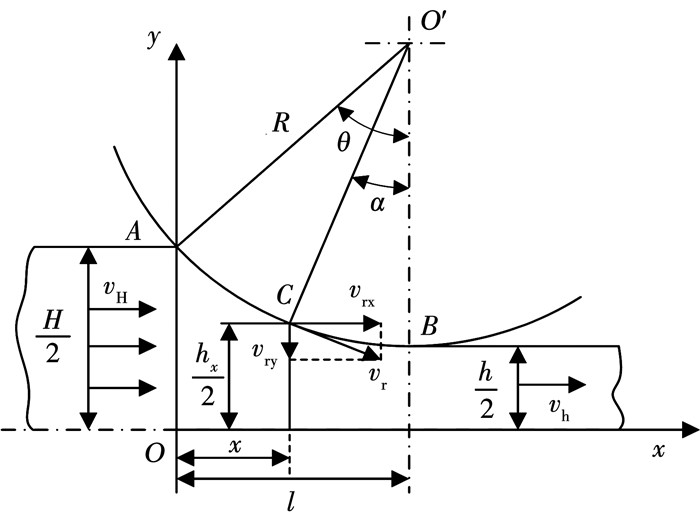图 1 轧制变形区示意 Fig. 1 Schematic of deformation zone


图 1中，以入口处和轧制线的交点为原点建立坐标系，H和h为带钢入口和出口厚度，v_H和v_h为带钢入口和出口速度，h_x为变形区任意位置带钢厚度，v_r为轧制速度，α为接触角，θ为咬入角，R为工作辊半径，l为变形区长度。根据图中几何关系，接触弧方程及其一阶导数可以表示为:

$h_x=h+2 R-2 \sqrt{R^2-(l-x)^2}=h+2 R-2 R \cos \alpha$ (1)

$h_x^{\prime}=-\frac{2(l-x)}{\sqrt{R^2-(l-x)^2}}=-2 \tan \alpha$ (2)

1.1 二维速度场与应变速率场考虑到冷连轧过程中宽展量可以忽略，因此认为轧制过程是平面应变问题，则ε_z=0；采用平断面假设，即任意x截面上的水平速度相同，并假设截面上的垂直速度呈线性分布，得到如下二维速度场：

$\left\{\begin{array}{l}v_x=\frac{U}{h_x b} \\v_y=\frac{U}{b} \frac{h_x^{\prime}}{h_x^2} y=v_x \frac{h_x^{\prime}}{h_x} y \\v_z=0\end{array}\right.$ (3)

式中：$U=v_{\mathrm{H}} H b=v_{\mathrm{h}} h b=v_{\mathrm{n}} h_{\mathrm{n}} b=v_{\mathrm{r}} \cos \alpha_{\mathrm{n}} b(h+2 R-\left.2 R \cos \alpha_{\mathrm{n}}\right)$，h_n为中性面厚度，α_n为中性角。

由Cauchy方程可知，对应的应变速率场表示为

$\left\{\begin{array}{l}\dot{\varepsilon}_x=\frac{\partial v_x}{\partial x}=-v_x \frac{h_x^{\prime}}{h_x} \\\dot{\varepsilon}_y=\frac{\partial v_y}{\partial y}=v_x \frac{h_x^{\prime}}{h_x} \\\dot{\varepsilon}_z=0\end{array}\right.$ (4)

由式(3)、(4)可得：$\dot{\varepsilon}_x+\dot{\varepsilon}_y+\dot{\varepsilon}_z=0$；当x=0时，v_x=v_H；当y=0时，v_y=0；在轧辊与轧件的接触面处v_y=－v_xtan α。因此速度场满足体积不变条件和速度边界条件。

1.2 冷轧总功率计算 1.2.1 塑性变形功率由于Mises屈服准则是非线性的，会提高积分计算难度，因此本文采用内接十二边形(inscribed dodecagon, ID)线性屈服准则计算塑性变形功率^[21]。由式(4)可知，$\dot{\varepsilon}_{\max }=\dot{\varepsilon}_x, \dot{\varepsilon}_{\min }=\dot{\varepsilon}_y$，则内部塑性变形功率可表示为

$\begin{aligned}\dot{W}_i= & \int_V D\left(\dot{\varepsilon}_{i j}\right) \mathrm{d} V= \\& \frac{2 b}{\sqrt{3}} \sigma_s \int_0^l \int_0^{h_x / 2}\left(\dot{\varepsilon}_{\max }-\dot{\varepsilon}_{\min }\right) \mathrm{d} x \mathrm{~d} y=\frac{2 U}{\sqrt{3}} \sigma_\mathrm{s} \ln \left(\frac{H}{h}\right)\end{aligned}$ (5)

1.2.2 摩擦功率摩擦功率可由轧辊和带钢表面沿x和y方向的相对滑动速度与摩擦应力乘积并积分得到，摩擦应力采用摩擦因子模型计算。需要注意的是，前后滑区相对滑动速度方向发生改变，因此积分过程中要以中性面为界进行分段积分。令A₁=1+h/2R，则摩擦功率可表示为

$\begin{aligned}\dot{W}_{\mathrm{f}}= & 2 m k b\left(\int_0^l\left|v_{\mathrm{r}} \cos \alpha-v_x\right| \mathrm{d} x+\int_0^l\left|v_{\mathrm{r}} \sin \alpha-v_x \tan \alpha\right| \tan \alpha \mathrm{d}_x\right)= \\& 2mkb\left\{ {R{v_{\rm{r}}}\left( {\theta - 2{\alpha _{\rm{n}}}} \right) - \frac{U}{{2b}}\frac{{\sec \bar \alpha }}{{\sqrt {{A_1} - 1} }}} \right.\\& \left. {\left[ {\arctan \left( {\sqrt {\frac{{{A_1} + 1}}{{{A_1} - 1}}} \tan \frac{\theta }{2}} \right) - 2\arctan \left( {\sqrt {\frac{{{A_1} + 1}}{{{A_1} - 1}}} \tan \frac{{{\alpha _{\rm{n}}}}}{2}} \right)} \right]} \right\}\end{aligned}$ (6)

式中：k为带钢的剪切强度，m为摩擦因子。

1.2.3 剪切功率由式(3)可知，在变形区入口处$v_y=-v_{\mathrm{H}} \frac{2 \tan \theta}{H} y$，垂直速度不为0，入口处存在速度不连续现象；在变形区出口处v_y=0，出口处垂直速度为0，不存在速度不连续面。因此，仅在入口处有由于速度不连续导致的剪切功率，其表达式为

$\dot{W}_{\mathrm{s}}=2 b \int_0^{H / 2} k\left|\Delta v_y\right| \mathrm{d} y=\frac{U k}{2} \tan \theta$ (7)

1.2.4 张力功率在冷连轧生产中，为了防止带钢跑偏、降低轧件变形抗力和提高生产效率，常常在带钢两端施加张力。张力改变会引起变形区各参数的变化，因此需要额外考虑张力引发的功率变化，其表达式如下：

$\dot{W}_{\mathrm{t}}=2 b\left(\int_0^{H / 2} \sigma_{\mathrm{b}} v_{\mathrm{H}} \mathrm{d} y-\int_0^{h / 2} \sigma_{\mathrm{f}} v_{\mathrm{h}} \mathrm{d} y\right)=U\left(\sigma_{\mathrm{b}}-\sigma_{\mathrm{f}}\right)$ (8)

式中：σ_f为前张力，σ_b为后张力。

1.2.5 总功率泛函最小化将式(5)~(8)代入$\varPhi=\dot{W}_{\mathrm{i}}+\dot{W}_{\mathrm{f}}+\dot{W}_{\mathrm{s}}+\dot{W}_{\mathrm{t}}$即可得到总功率泛函。令总功率泛函对中性角α_n求偏导并等于0。

$\frac{\partial \varPhi}{\partial \alpha_\mathrm{n}}=\frac{\partial \dot{W}_{\mathrm{i}}}{\partial \alpha_\mathrm{n}}+\frac{\partial \dot{W}_\mathrm{f}}{\partial \alpha_\mathrm{n}}+\frac{\partial \dot{W}_\mathrm{s}}{\partial \alpha_\mathrm{n}}+\frac{\partial \dot{W}_1}{\partial \alpha_\mathrm{n}}=0$ (9)

式中各功率偏导表达式如下：

$\frac{\partial \dot{W}_{\mathrm{i}}}{\partial \alpha_{\mathrm{n}}}=\frac{2}{\sqrt{3}} \sigma_{\mathrm{s}} \ln \left(\frac{H}{h}\right) \frac{\partial U}{\partial \alpha_{\mathrm{n}}}$ (10)

$\begin{array}{l}\frac{{\partial {{\dot W}_{\rm{f}}}}}{{\partial {\alpha _{\rm{n}}}}} = 2mkb\left\{ { - 2R{v_{\rm{r}}} + \frac{{U\quad \sec {\alpha _{\rm{n}}}}}{{2b{A_1} - \cos {\alpha _{\rm{n}}}}} - \frac{{\sec \bar \alpha }}{{2b\sqrt {{A_1} - 1} }}} \right.\\\left. {\left[ {\arctan \left( {\sqrt {\frac{{{A_1} + 1}}{{{A_1} - 1}}} \tan \frac{\theta }{2}} \right) - 2\arctan \left( {\sqrt {\frac{{{A_1} + 1}}{{{A_1} - 1}}} \tan \frac{{{\alpha _{\rm{n}}}}}{2}} \right)} \right]\frac{{\partial U}}{{\partial {\alpha _{\rm{n}}}}}} \right\}\end{array}$ (11)

$\frac{\partial \dot{W}_{\mathrm{s}}}{\partial \alpha_{\mathrm{n}}}=\frac{k}{2} \tan \theta \frac{\partial U}{\partial \alpha_{\mathrm{n}}}$ (12)

$\frac{\partial \dot{W}_{\mathrm{t}}}{\partial \alpha_\mathrm{n}}=\left(\sigma_{\mathrm{b}}-\sigma_{\mathrm{f}}\right) \frac{\partial U}{\partial \alpha_\mathrm{n}}$ (13)

$\frac{\partial U}{\partial \alpha_{\mathrm{n}}}=v_{\mathrm{r}} b R \sin 2 \alpha_{\mathrm{n}}-v_{\mathrm{r}} b(R+h) \sin \alpha_{\mathrm{n}}$ (14)

将解得的α_n代入总功率泛函便可得总功率最小值Φ_min。于是，轧制力矩可以表示为

$M_{\mathrm{z}}=R \varPhi_{\min } / 2 v_{\mathrm{r}}$ (15)

上界法既无法考虑因轧制长度造成的摩擦系数时变性，又无法计算损失功率，导致其计算结果虽然符合工程需求，但精度却不够高。因此将塑性变形功率、张力功率和剪切功率解析解作为数据驱动模型的输入量，以提高模型精度。

2 LSTM网络模型人工神经网络(artificial neural network, ANN)是通过大量简单的神经元之间的相互连接来构造复杂的网络结构，但同层神经元之间没有信息传递导致无法处理时序数据。传统的循环神经网络(recurrent neural network, RNN)允许信息在同层之间传递，但在训练数据样本量过大时又会出现梯度爆炸或梯度消失的现象^[22]。针对这一问题，学者们采用一种特殊的RNN模型成功的解决了长期依赖问题^[23]，即LSTM网络，其原理见图 2。

Fig. 2
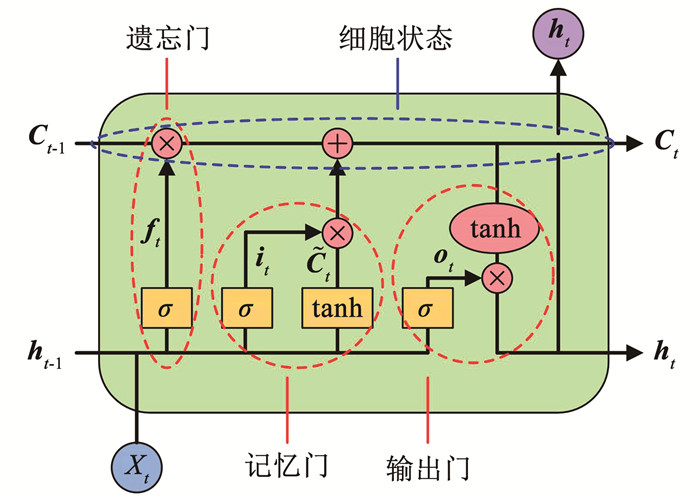图 2 LSTM单元原理 Fig. 2 Schematic of LSTM unit


LSTM网络由多个单元构成，每个单元包含3个门结构并以特殊的方式组合，遗忘门控制哪些历史信息将被遗忘，记忆门控制哪些新输入的信息将被保留，输出门则决定哪些信息会被输出。图 2中各输出向量的计算如下所示：

$\boldsymbol{f}_t=\sigma\left(\left[\boldsymbol{X}_t, \boldsymbol{h}_{t-1}\right] \boldsymbol{w}_{\mathrm{f}}+\boldsymbol{b}_{\mathrm{f}}\right)$ (16)

$\boldsymbol{i}_t=\sigma\left(\left[\boldsymbol{X}_t, \boldsymbol{h}_{t-1}\right] \boldsymbol{w}_{\mathrm{i}}+\boldsymbol{b}_{\mathrm{i}}\right)$ (17)

$\widetilde{\boldsymbol{C}}_t=\tanh \left(\left[\boldsymbol{X}_t, \boldsymbol{h}_{t-1}\right] \boldsymbol{w}_{\mathrm{C}}+\boldsymbol{b}_{\mathrm{C}}\right)$ (18)

$\boldsymbol{o}_t=\sigma\left(\left[\boldsymbol{X}_t, \boldsymbol{h}_{t-1}\right] \boldsymbol{w}_{\mathrm{o}}+\boldsymbol{b}_{\mathrm{o}}\right)$ (19)

$\boldsymbol{h}_t=\boldsymbol{o}_t \tanh \boldsymbol{C}_t$ (20)

$\boldsymbol{C}_t=\boldsymbol{f}_t \boldsymbol{C}_{t-1}+\boldsymbol{i}_t \widetilde{\boldsymbol{C}}_t$ (21)

式中：$\boldsymbol{f}_t 、\boldsymbol{i}_t 、\widetilde{\boldsymbol{C}}_t$和o_t分别为遗忘门、记忆门和输出门的输出向量，C_t为细胞状态，σ和tanh为激活函数，w为权重矩阵，b为偏置向量。

3 上界法与LSTM时序耦合预测模型本文所有数据均来自某1 450 mm六辊五机架冷连轧产线。考虑到各工艺参数的采集来自不同装置，它们的采样频率并不统一，因此以最大采样间隔0.24 s为基准进行等间隔降采样。从工作辊刚上机开始，提取一个换辊周期内的稳态轧制数据共计32 062条、17维特征参数，并可根据特征属性分为4类，其中轧件信息6条，工艺参数6条，轧辊数据2条以及功率解析解3条，见表 1。

表 1
表 1 过程变量描述 Tab. 1 Description of process variables 分类 参数 分类 参数

轧件信息 宽度v₁/mm 工艺参数 轧制力v₇/kN

来料厚度v₂/mm 前张力v₈/MPa

入口厚度v₃/mm 后张力v₉/MPa

出口厚度v₄/mm 轧制速度v₁₀/(m·s^-1)

变形抗力v₅/MPa 入口速度v₁₁/(m·s^-1)

变形区长度v₆/mm 出口速度v₁₂/(m·s^-1)

轧辊数据 轧制长度v₁₃/km 功率解析解 塑性变形功率v₁₅/kW

乳辊半径v₁₄/km 剪切功率v₁₆/kW

张力功率v₁₇/kW



表 1 过程变量描述 Tab. 1 Description of process variables


时序耦合预测模型结构见图 3。首先从PDA及二级数据库中导出所需的14维特征参数，然后将轧件信息v₁~v₆及工艺参数v₇~v₁₂代入上界法求解塑性变形功率v₁₅、剪切功率v₁₆和张力功率v₁₇的解析解，再将所有特征输入LSTM网络中学习训练摩擦功率和损失功率等具有时序特点部分，最后将训练结果用于实际电机功率预测。

Fig. 3
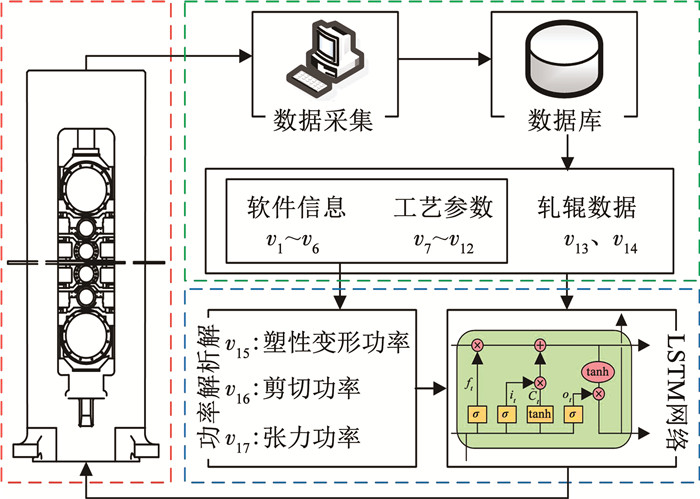图 3 耦合预测模型示意


经过结构优化并反复测试，最终确定本文的LSTM网络由1个输入层、2个隐含层和1个输出层构成，每个隐含层包括25个LSTM单元节点，层与层之间采用全连接。图 4为不同学习率下的训练集均方根误差(root mean square error, RMSE)，可以发现均方根误差随学习率的增大先下降后上升，由此确定最优学习率为0.001 5。此外，时间步长也是影响LSTM网络预测效果的重要超参数，不同步长下的训练集均方根误差见图 5，最终选取时间步长为20。

Fig. 4
图 4 均方根误差随学习率的变化 Fig. 4 Variation of root mean square error with learning rate


Fig. 5
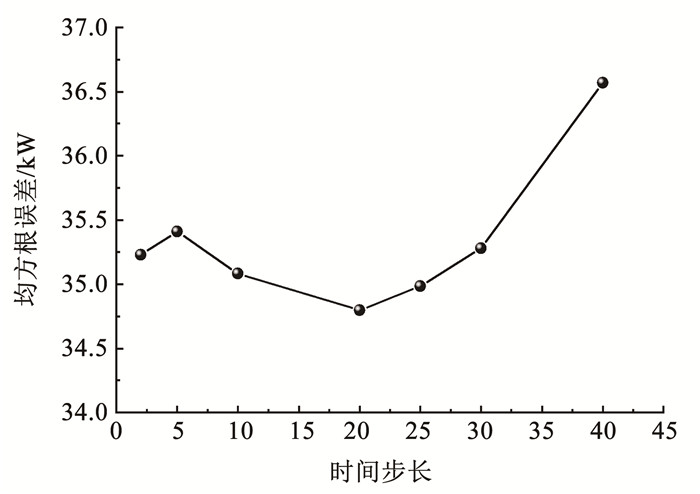图 5 均方根误差随时间步长的变化 Fig. 5 Variation of root mean square error with time steps


在训练之前，首先要对数据进行缺失值处理及数据归一化。实际生产中常常会因传感器故障等问题导致数据缺失，本文中由于缺失值数据不超过20条，故采用上条数据进行填充。对于不同的工艺参数，其数值上会有成百上千倍的差异。若不进行归一化处理，模型的训练精度就会大打折扣，甚至无法得出正确的结果。因此采用最常见的归一化方法，如下式所示：

$x_i^*=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$ (22)

式中：x_i^*为归一化后数据，x_i为原始数据，x_min为特征中的最小值，x_max为特征中的最大值。

最后将所有的数据分为训练集和测试集，数据集占比为8∶ 2。训练集用于模型权重训练，测试集用于模型的泛化能力评估。模型训练过程中的损失函数见图 6，可以看到，当迭代1 000轮次左右后基本达到稳定状态，最优平均绝对误差(mean absolute error, MAE)可达到0.041 7。

Fig. 6
图 6 平均绝对误差损失随迭代轮次的变化 Fig. 6 Variation of mean absolute error loss with epochs


4 结果与讨论为了验证预测精度，本文对上界法、ANN和时序耦合预测模型的预测结果进行对比。其中，上界法采用本文建立的速度场得到总功率解析解；ANN和时序耦合预测模型则将上界法中部分功率的解析解(塑性变形功率、张力功率和剪切功率)和其他14维参数作为输入量，按照顺序输入模型学习训练。

不同模型的测试集预测效果对比见图 7。从整体上，上界法、ANN和时序耦合预测模型均能实现电机功率预测，但ANN和耦合模型的效果明显优于上界法；三者的最大相对误差分别为±8.5%、±6.3%和±3.9%，可见耦合模型的预测效果最好。值得注意的是，当相邻卷带钢轧制规程变化较大时(如采样序列800~1000和2400~2500)，耦合模型的预测效果明显优于其他2种，体现了考虑数据时序特性的优势。从局部上，耦合模型的误差绝对值更小且分布更均匀。

Fig. 7
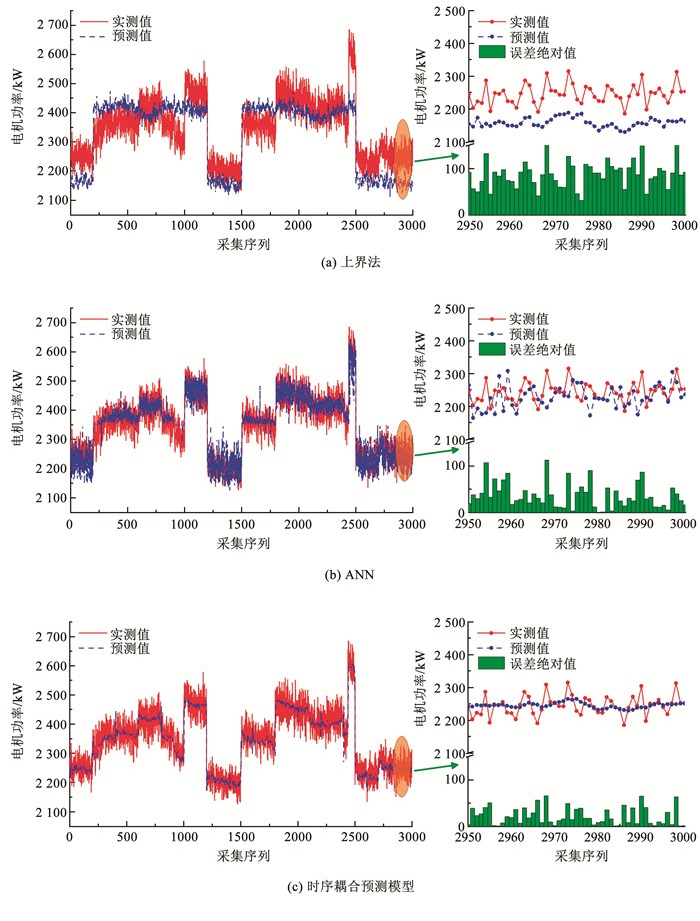图 7 电机实测和预测功率对比 Fig. 7 Comparison of measured and predicted motor power


图 8为3种模型的残差分布直方图，可以看出：上界法残差集中在±50 kW附近且不符合正态分布。其主要原因是没有捕获到变量之间的强耦合关系，如：摩擦系数和损失功率与其他参数间的关系。而ANN和耦合模型则均基本遵循正态分布，表明这2种模型更加合理，其中耦合模型的残差在0附近的频数更高、方差更小，说明耦合模型的拟合精度要高于ANN。

Fig. 8
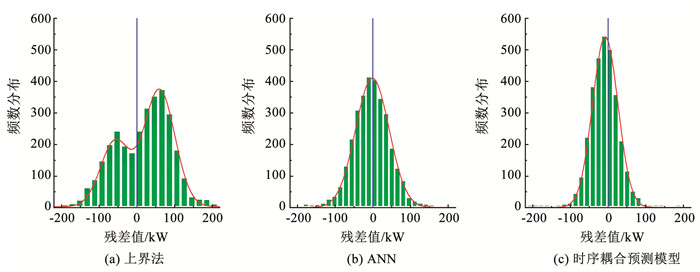图 8 残差分布直方图 Fig. 8 Histogram of residual distribution


为进一步对比模型预测效果，选取广泛应用于拟合模型性能评估的平均绝对误差、均方根误差和相关系数对文中模型进行评价，结果见表 2。可以发现：上界法、ANN和耦合模型的平均绝对误差和均方根误差依次递减，但相关系数值逐步增大，这是由于基于数据驱动的ANN和耦合模型可以更好地提取数据之间的特征，相较于传统机理模型具有较大的提升；LSTM在ANN的基础上进一步考虑了轧制长度与摩擦系数的时序变化特点，因此耦合模型具有更好的综合预测性能，平均绝对误差、均方根误差和相关系数分别可达到28.0、35.9和0.936。

表 2
表 2 上界法、ANN和时序耦合预测模型的模型性能对比 Tab. 2 Performance comparison among upper bound method, ANN, and time series coupling model 模型 平均绝对误差/kW 均方根误差/kW 相关系数

上界法 63.8 74.9 0.769

ANN 36.4 45.4 0.896

时序耦合模型 28.0 35.9 0.936



表 2 上界法、ANN和时序耦合预测模型的模型性能对比 Tab. 2 Performance comparison among upper bound method, ANN, and time series coupling model


应用时序耦合预测模型分析了电机功率与轧制长度、轧制速度的关系，见图 9。电机功率与轧制长度呈反比，其原因是：工作辊刚上机时粗糙度较大，此时摩擦系数也会变大，但粗糙度会随轧制长度增加而衰减，因此电机功率减小。电机功率与轧制速度呈正比，其原因是：轧制速度越高，单位时间通过辊缝的带钢越多，电机功率也随之增加。

Fig. 9
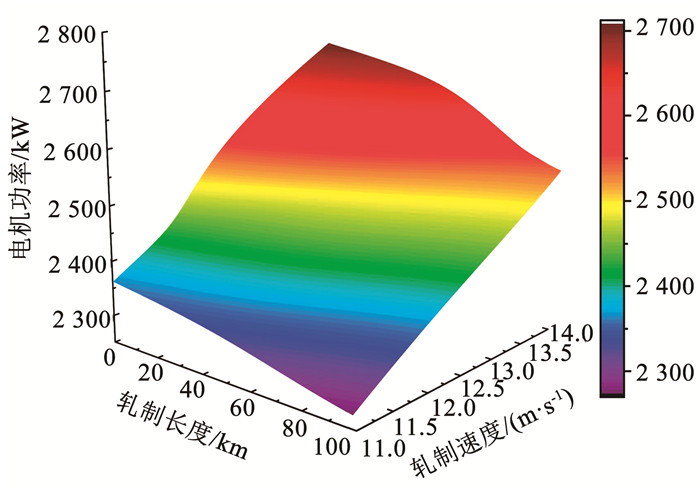图 9 电机功率与轧制长度、轧制速度的关系 Fig. 9 Relationship between motor power, rolling length, and rolling speed


5 结论1) 提出了一种基于上界法和LSTM网络耦合的电机功率预测模型，其中塑性变形功率、剪切功率和张力功率采用上界法计算解析解，摩擦功率和损失功率采用LSTM网络预测学习数据的时序特性。

2) 上界法、ANN和时序耦合预测模型的预测结果对比表明：考虑数据时序特性的耦合模型明显优于其他2种方法，残差分布更合理，计算误差不超过±3.9%，满足在线控制要求。

3) 时序耦合预测模型中考虑轧制长度的时序特性对预测精度有很大提升，主要是由于轧辊粗糙度会随轧制长度增加而衰减，并进一步影响轧制力矩和电机功率。


参考文献
[1] 陈丹, 邵健, 殷实, 等. 基于大数据平台的冷连轧轧制力自学习模型优化[J]. 冶金自动化, 2020, 44(6): 29.
CHEN Dan, SHAO Jian, YIN Shi, et al. Optimization of self-learning model of cold rolling force based on big data platform[J]. Metallurgical Industry Automation, 2020, 44(6): 29. DOI:10.3969/j.issn.1000-7059.2020.06.004


[2] 薛涛, 杜凤山, 孙静娜, 等. 基于FEM-ANN的冷轧带钢轧制力预报[J]. 中南大学学报(自然科学版), 2013, 44(11): 4460.
XUE Tao, DU Fengshan, SUN Jingna, et al. Rolling force prediction of cold strip rolling based on FEM-ANN[J]. Journal of Central South University(Science and Technology), 2013, 44(11): 4460.


[3] 梁勋国, 贾涛, 矫志杰, 等. 基于贝叶斯方法的神经网络应用于冷轧轧制力预报[J]. 钢铁研究学报, 2008, 20(10): 62.
LIANG Xunguo, JIA Tao, JIAO Zhijie, et al. Application of neural network based on Bayesian method to rolling force prediction in cold rolling process[J]. Journal of Iron and Steel Research, 2008, 20(10): 62. DOI:10.13228/j.boyuan.issn1001-0963.2008.10.001


[4] 周富强, 曹建国, 张杰, 等. 冷连轧机轧制力的影响因素[J]. 机械工程学报, 2007, 43(10): 97.
ZHOU Fuqiang, CAO Jianguo, ZHANG Jie, et al. Influence factors of rolling force in tandem cold rolling[J]. Chinese Journal of Mechanical Engineering, 2007, 43(10): 97. DOI:10.3321/j.issn:0577-6686.2007.10.018


[5] 周富强, 曹建国, 张杰, 等. 基于神经网络的冷连轧机轧制力预报模型[J]. 中南大学学报(自然科学版), 2006, 37(6): 1160.
ZHOU Fuqiang, CAO Jianguo, ZHANG Jie, et al. Prediction model of rolling force for tandem cold rolling mill based on neural networks and mathematical models[J]. Journal of Central South University(Science and Technology), 2006, 37(6): 1160. DOI:10.3969/j.issn.1672-7207.2006.06.027


[6] 孙一康. 冷热轧板带轧机的模型与控制[M]. 北京: 冶金工业出版社, 2010.
SUN Yikang. Model and control of cold and hot strip mill[M]. Beijing: Metallurgical Industry Press, 2010.


[7] YANG Jingming, ZHANG Qing, CHE Haijun, et al. Multi-objective optimization for tandem cold rolling schedule[J]. Journal of Iron and Steel Research, International, 2010, 17(11): 39. DOI:10.1016/S1006-706X(10)60167-7


[8] WANG Yu, LI Changsheng, JIN Xin, et al. Multi-objective optimization of rolling schedule for tandem cold strip rolling based on NSGA-Ⅱ[J]. Journal of Manufacturing Processes, 2020, 60: 267. DOI:10.1016/j.jmapro.2020.10.061


[9] HU Ziyu, WEI Zhihui, SUN Hao, et al. Optimization of metal rolling control using soft computing approaches: a review[J]. Archives of Computational Methods in Engineering, 2021, 28(2): 421. DOI:10.1007/s11831-019-09380-6


[10] 武贺, 吕立华. 板带轧机负荷分配方法的综述[J]. 控制工程, 2009, 16(增刊2): 10.
WU He, LV Lihua. Summarization of load distribution method for plate and strip mill[J]. Control Engineering of China, 2009, 16(Sup.2): 10. DOI:10.14107/j.cnki.kzgc:2009.s2.006


[11] 陈树宗, 李旭, 彭文, 等. 基于数值积分与功率损耗测试的冷轧电机功率模型[J]. 东北大学学报(自然科学版), 2017, 38(3): 365.
CHEN Shuzong, LI Xu, PENG Wen, et al. Motor power model of cold rolling based on numerical integration and power loss test[J]. Journal of Northeastern University(Natural Science), 2017, 38(3): 365. DOI:10.3969/j.issn.1005-3026.2017.03.012


[12] 李维刚, 谭树彬, 李家波, 等. 热连轧机轧制力和轧制力矩模型研究[J]. 东北大学学报(自然科学版), 2011, 32(5): 625.
LI Weigang, TAN Shubin, LI Jiabo, et al. Modelling rolling force and rolling torque in a hot strip mill[J]. Journal of Northeastern University(Natural Science), 2011, 32(5): 625. DOI:10.3969/j.issn.1005-3026.2011.05.004


[13] 赵德文. 成形能率积分线性化原理及应用[M]. 北京: 冶金工业出版社, 2012.
ZHAO Dewen. Principle and application of integral linearization of forming energy rate[M]. Beijing: Metallurgical Industry Press, 2012.


[14] SERAJZADEH S, MAHMOODKHANI Y. A combined upper bound and finite element model for prediction of velocity and temperature fields during hot rolling process[J]. International Journal of Mechanical Sciences, 2008, 50(9): 1431. DOI:10.1016/j.ijmecsci.2008.07.004


[15] ZHANG Dianhua, LIU Yuanming, SUN Jie, et al. A novel analytical approach to predict rolling force in hot strip finish rolling based on cosine velocity field and equal area criterion[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(5): 850. DOI:10.1007/s00170-015-7692-z


[16] LI Si, WANG Zhigang, GUO Yufei. A novel analytical model for prediction of rolling force in hot strip rolling based on tangent velocity field and MY criterion[J]. Journal of Manufacturing Processes, 2019, 47: 210. DOI:10.1016/j.jmapro.2019.09.037


[17] 刘元铭, 王涛, 王振华, 等. 基于双流函数的立轧力能参数研究[J]. 塑性工程学报, 2020, 27(8): 178.
LIU Yuanming, WANG Tao, WANG Zhenhua, et al. Research on mechanics parameters of edge rolling based on dual-stream function[J]. Journal of Plasticity Engineering, 2020, 27(8): 178. DOI:10.3969/j.issn.1007-2012.2020.08.023


[18] 魏立新, 翟博豪, 赵志伟, 等. 基于半监督深度网络的冷连轧轧制力预报[J]. 塑性工程学报, 2020, 27(11): 76.
WEI Lixin, ZHAI Bohao, ZHAO Zhiwei, et al. Prediction of cold continuous rolling force based on semi-supervised deep network[J]. Journal of Plasticity Engineering, 2020, 27(11): 76. DOI:10.3969/j.issn.1007-2012.2020.11.011


[19] 章顺虎, 姜兴睿, 尤凤翔, 等. 融合工业大数据的热轧厚板轧制力模型研究[J]. 精密成形工程, 2020, 12(2): 14.
ZHANG Shunhu, JIANG Xingrui, YOU Fengxiang, et al. Investigation on the model of rolling force by integration industrial big data[J]. Journal of Netshape Forming Engineering, 2020, 12(2): 14. DOI:10.3969/j.issn.1674-6457.2020.02.002


[20] 矫志杰, 蔡沅良, 王龙鑫, 等. 5 000 mm单机架宽厚板轧机力臂系数模型[J]. 钢铁, 2021, 56(7): 106.
JIAO Zhijie, CAI Yuanliang, WANG Longxin, et al. Lever arm coefficient model of 5 000 mm single-stand heavy plate mill[J]. Iron and Steel, 2021, 56(7): 106. DOI:10.13228/j.boyuan.issn0449-749x.20200500


[21] SUN Jie, LIU Yuanming, WANG Qinglong, et al. Mathematical model of lever arm coefficient in cold rolling process[J]. The International Journal of Advanced Manufacturing Technology, 2018, 97(5): 1859. DOI:10.1007/s00170-018-2078-7


[22] 刘阳, 郜志英, 周晓敏, 等. 工业数据驱动下薄板冷轧颤振的LSTM智能预报[J]. 机械工程学报, 2020, 56(11): 131.
LIU Yang, GAO Zhiying, ZHOU Xiaomin, et al. Industrial data-driven intelligent forecast for chatter of cold rolling of thin strip with LSTM recurrent neural network[J]. Chinese Journal of Mechanical Engineering, 2020, 56(11): 131. DOI:10.3901/JME.2020.11.121


[23] 李潇睿, 班晓娟, 袁兆麟, 等. 工业场景下基于深度学习的时序预测方法及应用[J]. 工程科学学报, 2022, 44(4): 766.
LI Xiaorui, BAN Xiaojuan, YUAN Zhaolin, et al. Review on deep learning models for time series forecasting in industry[J]. Chinese Journal of Engineering, 2022, 44(4): 766. DOI:10.13374/j.issn.2095-9389.2021.02.004