吴衍1,2,杨军1,3,张思洋1
(1.兰州交通大学 电子与信息工程学院,兰州 730070;2.福建技术师范学院 大数据与人工智能学院,福建 福清 350300;3.兰州交通大学 测绘与地理信息学院,兰州 730070)
摘要:
为了解决非刚性三维模型簇对应关系计算准确率低、一致性差,且难以实现双射的问题,提出了一种采用优化谱对齐算法和规范一致潜在基的非刚性三维模型簇对应关系计算新方法。首先,利用函数映射的伴随算子实现模型间谱域信息的对齐,计算模型簇中每个模型对的函数映射矩阵,解决函数映射与逐点映射方向不一致的问题；其次,使用改进的模型映射集合算法为每个模型对的函数映射矩阵赋予相应权重,降低初始化参数的噪声对模型簇对应关系计算结果的影响；最后,在模型簇的对应关系计算过程中加入极限模型的规范一致潜在基,极限模型可以看成模型簇中所有模型的类型结构,是一个具有几何可变性的中间模型,提高算法的一致性和双射性。实验结果表明:与已有算法相比,本算法在FAUST、SCAPE、TOSCA和SHERC’16 Topology数据集上构建的对应关系测地误差最小,能够减少初始化参数的噪声,解决模型自身对称性影响对应关系计算的问题,更加精确地构建出具有一致性和双射性的非刚性三维模型簇对应关系。
关键词: 对应关系 非刚性三维模型簇 优化谱对齐 规范一致潜在基 函数映射
DOI：10.11918/202210007
分类号:TP391.4
文献标识码:A
基金项目:国家自然科学基金(7,9);兰州市人才创新创业项目(2020-RC-22);兰州交通大学天佑创新团队(TY202002);福建省自然科学基金(2022J01972);福建省中青年教师教育科研项目(JAT201378)
Consistency correspondence calculation of 3D shape collections using optimized spectral alignment
WU Yan1,2,YANG Jun1,3,ZHANG Siyang1
(1.School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2.School of Big Data and Artificial Intelligence, Fujian Polytechnic Normal University, Fuqing 350300, Fujian, China; 3.Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China)
Abstract:
This paper focuses on the problems of computing correspondences among non-rigid 3D shape collections with a low accuracy rate, poor consistency, and difficult bijectivity. The novel approach proposed in this paper is based on the optimized spectral alignment algorithm and the canonical consistent latent basis. Firstly, we use the adjoint operator derived from the functional map to align the information between shapes in the spectral domain. The functional map matrix of each shape pair in the shape collections is calculated, resolving the problem of inconsistent direction between functional map and pointwise map. Secondly, we adapt the improved collections of shape maps approach to assign corresponding weights to the functional map matrix of each shape pair, reducing the impact of initialization parameter noise on the shape collection matching calculation results. Finally, we add the canonical consistent latent basis of the limit shape to compute the shape collections correspondence. The limit shape can be seen as a type structure of all shapes in the shape collection, which is an intermediate model with geometric variability, improving the consistency and bijectivity of the algorithm. The experimental results show that compared with the existing algorithms, this algorithm has the lowest geodesic error and the highest accuracy of global correspondence on FAUST, SCAPE, TOSCA, and SHERC’16 Topology datasets. Meanwhile, our method can reduce the noise of initialization parameters, solve the symmetric ambiguity problem, and more accurately compute the consistent and bijective correspondence of non-rigid 3D shape collections.
Key words: correspondence non-rigid 3D shape collections optimized spectral alignment canonical consistent latent basis functional maps
吴衍, 杨军, 张思洋. 优化谱对齐的三维模型簇一致性对应关系计算[J]. 哈尔滨工业大学学报, 2024, 56(5): 84-92. DOI: 10.11918/202210007.
WU Yan, YANG Jun, ZHANG Siyang. Consistency correspondence calculation of 3D shape collections using optimized spectral alignment[J]. Journal of Harbin Institute of Technology, 2024, 56(5): 84-92. DOI: 10.11918/202210007.
基金项目 国家自然科学基金(42261067，61862039);兰州市人才创新创业项目(2020-RC-22);兰州交通大学天佑创新团队(TY202002);福建省自然科学基金(2022J01972);福建省中青年教师教育科研项目(JAT201378) 作者简介 吴衍(1986—)，男，博士研究生;
杨军(1973—)，男，教授，博士生导师 通信作者 杨军，yangj@mail.lzjtu.cn 文章历史 收稿日期: 2022-10-02
Abstract Full text Figures/Tables PDF
优化谱对齐的三维模型簇一致性对应关系计算
吴衍1,2, 杨军1,3
, 张思洋1 1. 兰州交通大学 电子与信息工程学院, 兰州 730070;
2. 福建技术师范学院 大数据与人工智能学院, 福建 福清 350300;
3. 兰州交通大学 测绘与地理信息学院, 兰州 730070
收稿日期: 2022-10-02; 录用日期: 2023-01-03; 网络首发日期: 2023-07-24
基金项目: 国家自然科学基金(42261067，61862039);兰州市人才创新创业项目(2020-RC-22);兰州交通大学天佑创新团队(TY202002);福建省自然科学基金(2022J01972);福建省中青年教师教育科研项目(JAT201378)
作者简介: 吴衍(1986—)，男，博士研究生; 杨军(1973—)，男，教授，博士生导师
通信作者: 杨军，yangj@mail.lzjtu.cn
摘要: 为了解决非刚性三维模型簇对应关系计算准确率低、一致性差，且难以实现双射的问题，提出了一种采用优化谱对齐算法和规范一致潜在基的非刚性三维模型簇对应关系计算新方法。首先，利用函数映射的伴随算子实现模型间谱域信息的对齐，计算模型簇中每个模型对的函数映射矩阵，解决函数映射与逐点映射方向不一致的问题；其次，使用改进的模型映射集合算法为每个模型对的函数映射矩阵赋予相应权重，降低初始化参数的噪声对模型簇对应关系计算结果的影响；最后，在模型簇的对应关系计算过程中加入极限模型的规范一致潜在基，极限模型可以看成模型簇中所有模型的类型结构，是一个具有几何可变性的中间模型，提高算法的一致性和双射性。实验结果表明: 与已有算法相比，本算法在FAUST、SCAPE、TOSCA和SHERC’16 Topology数据集上构建的对应关系测地误差最小，能够减少初始化参数的噪声，解决模型自身对称性影响对应关系计算的问题，更加精确地构建出具有一致性和双射性的非刚性三维模型簇对应关系。
关键词: 对应关系 非刚性三维模型簇 优化谱对齐 规范一致潜在基 函数映射
Consistency correspondence calculation of 3D shape collections using optimized spectral alignment
WU Yan1,2, YANG Jun1,3
, ZHANG Siyang1 1. School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;
2. School of Big Data and Artificial Intelligence, Fujian Polytechnic Normal University, Fuqing 350300, Fujian, China;
3. Faculty of Geomatics, Lanzhou Jiaotong University, Lanzhou 730070, China
Abstract: This paper focuses on the problems of computing correspondences among non-rigid 3D shape collections with a low accuracy rate, poor consistency, and difficult bijectivity. The novel approach proposed in this paper is based on the optimized spectral alignment algorithm and the canonical consistent latent basis. Firstly, we use the adjoint operator derived from the functional map to align the information between shapes in the spectral domain. The functional map matrix of each shape pair in the shape collections is calculated, resolving the problem of inconsistent direction between functional map and pointwise map. Secondly, we adapt the improved collections of shape maps approach to assign corresponding weights to the functional map matrix of each shape pair, reducing the impact of initialization parameter noise on the shape collection matching calculation results. Finally, we add the canonical consistent latent basis of the limit shape to compute the shape collections correspondence. The limit shape can be seen as a type structure of all shapes in the shape collection, which is an intermediate model with geometric variability, improving the consistency and bijectivity of the algorithm. The experimental results show that compared with the existing algorithms, this algorithm has the lowest geodesic error and the highest accuracy of global correspondence on FAUST, SCAPE, TOSCA, and SHERC'16 Topology datasets. Meanwhile, our method can reduce the noise of initialization parameters, solve the symmetric ambiguity problem, and more accurately compute the consistent and bijective correspondence of non-rigid 3D shape collections.
Keywords: correspondence non-rigid 3D shape collections optimized spectral alignment canonical consistent latent basis functional maps
三维模型的对应关系，也称为三维模型的匹配，是计算机视觉中受到长期关注的一个研究课题，被广泛应用于影视动画、模型检索、风格迁移和形状分析[1]等领域。然而，研究者普遍关注两个三维模型间对应关系问题，而对于三维模型簇尤其是非刚性三维模型簇对应关系计算由于难度更高，研究者关注度相对较少，可这并不影响它有着广阔的应用前景和重要的研究价值。非刚性三维模型簇对应关系计算在交互式几何建模，基于图像重建和运动跟踪[2]等领域举足轻重。本文将重点研究非刚性三维模型簇的对应关系计算问题，以下就本文算法密切相关的工作进行回顾。
函数映射[3]是非刚性三维模型对应关系计算的经典算法之一，它将对应关系编码为线性算子，实现跨模型的标量函数转换，但是由于算法通常使用低维度的谱域基，因此会损失很多高频细节，影响对应关系质量。后续的一些研究对函数映射算法做了很多改进，比如文献[4]是利用特征值对齐思想提高残缺模型定位精度的非刚性残缺模型对应关系算法；文献[5]是一种采用混合监督深度函数映射网络计算近似等距非刚性三维模型对应关系的方法。
大量实际应用场景对计算多个三维模型之间对应关系的需求日益增长，越来越多的学者提出了许多三维模型簇对应关系算法。文献[6]建立了一种利用两个模型表面的变换参数实现无监督学习的算法。文献[7]使用高阶投影能量迭代(higher-order projected power iteration, HPPI)方法解决模型簇匹配过程中常见的问题，如多个模型的几何一致性容易被忽略、对应关系计算成本高等，但也只局限于等距模型簇之间的对应关系计算。文献[8]提出了一种基于函数映射理论与循环一致性约束的三维模型簇的对应关系算法。文献[9]是一种基于模板的等距模型簇对应关系算法，它也有着目前模型簇对应关系算法普遍存在问题，即计算的结果取决于初始化参数的优劣。文献[10]在文献[4]的基础上研究了残缺三维模型簇对应关系计算。文献[11]将深度学习算法与三维模型簇算法结合，提出基于模型模板的无监督循环一致模型簇对应关系算法。
针对上述研究现状中非刚性三维模型簇对应关系算法准确率低，且初始化模型容易受函数映射噪声影响等问题，本文提出了一种采用优化谱对齐(optimized spectral alignment, OSA)算法和规范一致潜在基(canonical consistent latent basis, CCLB)[12]的非刚性三维模型簇对应关系计算新方法。主要创新点和贡献有：1)传统模型簇对应关系算法的初始化参数无法自动生成，而本文利用OSA算法计算模型对的函数映射矩阵作为初始化参数，为后续的一致性模型簇对应关系计算做准备；2)利用极限模型(limit shape, LS)的思想[12]，将它的CCLB动态地参与到循环一致的模型簇对应关系计算中，并采用一致性点偏移(coherent point drift, CPD)[13]算法提高逐点映射的还原质量，生成具有一致性和双射性的对应关系结果。
1 优化谱对齐算法传统的非刚性模型簇对应关系算法需要其他的模型间对应关系算法提供初始化模型对的映射矩阵，而且算法最终的结果很大程度受此初始化参数的影响，为了消除初始化参数中的噪声干扰，本文提出OSA算法来计算模型对的函数映射矩阵，所使用的伴随算子对非刚性模型的谱对齐过程而言，在计算过程中不需要切换映射方向，可以减少映射矩阵和逐点映射之间方向转换时的精度损耗，是更优的线性转换算子，它为后续模型簇对应关系计算提供高质量的初始化参数。
1.1 函数映射算法将非刚性三维模型M和N建模为嵌入到
$ f(x)=g\left(P_{M N}(x)\right) $ (1)
式中点x∈M。
同样，通过线性映射PNMF可以将模型N上标量函数g映射为模型M上的标量函数f, 因此可以得到
$ f=P_{N M}^{\mathrm{F}}(g) $ (2)
从式(1)和(2)可以看出，PMN和PNMF映射方向不一致，这对于从函数映射矩阵还原逐点映射的后处理计算来说是很不利的，会造成计算量的增大和精度的损失。
1.2 优化谱对齐算法为了解决方向不一致的问题，本文算法引入函数映射PNMF的伴随算子PMNA，定义如下:
$ \left\langle g, P_{M N}^{\mathrm{A}}(f)\right\rangle_N=\left\langle P_{N M}^{\mathrm{F}}(g), f\right\rangle_M $ (3)
其中，〈PNMF(g), f〉M和〈g, PMNA(f)〉N分别是模型M和N上的平方可积函数空间的标准内积。该内积在连续域上展开为〈h1, h2〉S→
函数映射PNMF和它的伴随算子PMNA可以分别使用矩阵CNM和OMN来表示，它们的逐点映射分别采用置换矩阵ΠMN和ΓMN描述。算法的实际应用需要在离散域的前提下进行，因此接下来将在离散域上讨论本算法，将连续函数f和g分别离散为在每个顶点上的向量f和g，于是式(3)可以转换成如下公式:
$ \left\langle\boldsymbol{g}, \boldsymbol{\varGamma}_{M N} \boldsymbol{f}\right\rangle_N=\left\langle\boldsymbol{\varPi}_{M N} \boldsymbol{g}, \boldsymbol{f}\right\rangle_M $ (4)
式(4)展开成为gTANΓMNf=gTΠMNTAMf，AM和AN是流形M和N上面积权重的对角矩阵，因此可以得到
$\boldsymbol{\varGamma}_{M N}=\boldsymbol{A}_N^{\mathrm{T}} \boldsymbol{\varPi}_{M N}{ }^{\mathrm{T}} \boldsymbol{A}_M $ (5)
根据函数映射算法可知，在完整基函数的前提下，函数映射可以实现2个函数空间之间的线性转换，然而在实际应用中，基函数的个数通常设定为50~500，此时函数映射可近似表示为保存2个简化基函数的矩阵间的转换。假设分别构造M和N的基函数{?i}i≥1和{ψj}j≥1，并将基函数前k1?n1和k2?n2项保存在矩阵Φ=(?1, …, ?k1)和Ψ=(ψ1, …, ψk2)，可以得出如下公式：
$\boldsymbol{C}_{N M}=\boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{\varPi}_{M N}{ }^{\mathrm{T}} \boldsymbol{\varPsi} $ (6)
$ \boldsymbol{O}_{M N}=\boldsymbol{\varPsi}^{\mathrm{T}} \boldsymbol{\varGamma}_{M N} \boldsymbol{\varPhi} $ (7)
由式(5)和式(7)可以得到
$ \boldsymbol{O}_{M N}=\boldsymbol{\varPsi}^{\mathrm{T}} \boldsymbol{A}_N^{\mathrm{T}} \boldsymbol{\varPi}_{M N}{ }^{\mathrm{T}} \boldsymbol{A}_M \boldsymbol{\varPhi} $ (8)
由于基函数与面积权重的对角矩阵是正交的，因此ΦTAMΦ=I，ΨTANΨ=I，I是单位矩阵，则公式(8)可以优化为
$ \begin{aligned}\boldsymbol{O}_{M N}= & \boldsymbol{\varPsi}^{\mathrm{T}} \boldsymbol{A}_N^{\mathrm{T}} \boldsymbol{\varPi}_{M N}{ }^{\mathrm{T}} \boldsymbol{A}_M \boldsymbol{\varPhi}=\boldsymbol{\varPsi}^{\mathrm{T}} \boldsymbol{\varPi}_{M N}{ }^{\mathrm{T}} \boldsymbol{\varPhi}= \\& \left(\boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{\varPi}_{M N} \boldsymbol{\varPsi}\right)^{\mathrm{T}}=\left(\boldsymbol{C}_{N M}\right)^{\mathrm{T}}\end{aligned} $ (9)
利用式(9)的结论OMNΦT=ΨTΠMNT做谱域的对齐计算，得出本文OSA算法的优化问题如下:
$ \boldsymbol{O}_{M N}=\mathop {\arg \min }\limits_{\boldsymbol{O}} \left\|\boldsymbol{O} \boldsymbol{\varPhi}^{\mathrm{T}}-\boldsymbol{\varPsi}^{\mathrm{T}} \boldsymbol{\varPi}_{M N}{ }^{\mathrm{T}}\right\|^2 $ (10)
O是迭代求解优化问题过程中矩阵OMN的中间产物，该优化问题使用弗罗贝尼乌斯范数‖·‖来计算矩阵间的距离。求得OMN之后，通过式(9)可以计算CNM，为后续的模型簇对应关系计算做准备。
2 一致性非刚性模型簇对应关系计算 2.1 规范一致潜在基给定一组非刚性模型簇{Sl}l=1n，将它们建模为二维黎曼流形，对于每一对Si和Sj，?i, j∈{1, 2, …, n}且i≠j，利用上述的OSA算法计算出Cij。
传统的模型簇对应关系算法框架如图 1(a)所示，通常基于循环一致算法，利用理想情况下循环路径中的函数映射矩阵组合与单位矩阵的零偏差进行计算，即通过计算如下优化问题获得对应关系:
$ \min \left\|\boldsymbol{C}_{12} \boldsymbol{C}_{23} \cdots \boldsymbol{C}_{n 1}-\boldsymbol{I}\right\|^2 $ (11)
Fig. 1
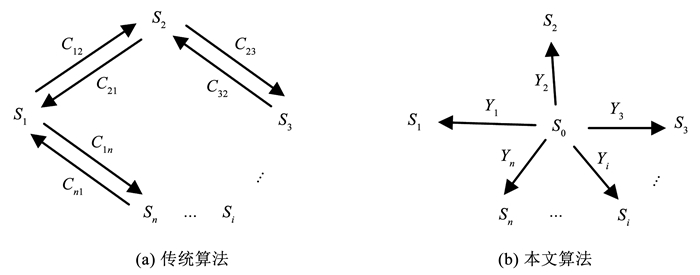图 1 算法框架示意 Fig. 1 Schematic of algorithm framework 该算法的一个缺点是优化问题中多个模型的函数映射矩阵组合是单向循环，这就造成了模型簇对应关系结果的双射性不足；另一个缺点是模型簇中只要有一对模型的函数映射矩阵质量不高，就会造成整体模型簇对应关系计算精度的下降，如何能削弱甚至消除“坏”模型参数的影响就成了模型簇对应关系计算的难题。
为了解决这些问题，本文算法首先利用文献[12]提出的极限模型(limit shape, LS)的思想，将其动态地参与到循环一致的模型簇对应关系计算中，算法的框架见图 1(b)。其中S0就是一个极限模型，它类似于模型簇中的“平均模型”，有着相应的几何结构，但并不是独立存在或者固定不变的模板模型，而是与模型簇中的模型相关，它的重要特征是一组规范一致潜在基(canonical consistent latent basis, CCLB)，即{Yl}l=1n。CCLB也可以看成是极限模型S0到每个模型Si∈{Sl}l=1n的函数映射矩阵，可得等式CijYi=Yj。由此可列以下公式：
$ \boldsymbol{C}_{i j}=\boldsymbol{Y}_j \boldsymbol{Y}_i^{\mathrm{T}}, \forall i, j \in\{1, 2, \cdots, n\}, i \neq j $ (12)
极限模型可以看成模型簇中所有模型的类型结构，是一个具有几何可变性的中间模型，有很强的代表性，因此通过公式(12)将极限模型的CCLB与函数映射关联在一起，可以很好地保证最终模型簇对应关系的双射性。
其次，Cij的“好坏”对模型簇对应关系的计算有着决定性的影响，为了获得最优的计算结果，本文算法利用文献[14]的改进模型映射集合(improving collections of shape maps, ICSM)的优化算法给每一个Cij赋予相应权重。ICSM算法使用测地距离和模型面积的比值来评估模型簇的循环一致性的优劣，具体而言，定义模型簇的一组循环γ={S1, S2, …, Sn, S1}，它的循环映射为mγ∶ S1→S2→…Sn→S1，因此循环γ映射结果的优劣可以使用如下公式进行评估:
$ E(\gamma)=\sum\limits_{v \in S_1} \frac{d_{S_1}\left(\boldsymbol{v}, \boldsymbol{m}_\gamma(v)\right)}{\sqrt{\operatorname{area}\left(S_1\right)}} $ (13)
式中: v∈S1是起始模型S1上的点，mγ(v)是经历了循环γ之后v∈S1在终点模型S1上映射的点，dS1是模型S1上2个点之间的测地距离，area(S1)是模型S1的面积。评估模型簇中的不同循环路径映射结果，具体采用控制变量的方法，先得出所有模型完整路径的结果，再计算每次去除一个模型后的结果，根据前后的差异评估变量的优劣，就可以得出每个模型对的函数映射Cij的评估结果，这个结果归一化生成权重参数ωij，并将该参数与对应的Cij数据项相乘。因为参数大小反映Cij的评估结果，因此“好”的Cij在模型簇的计算过程中会被放大而发挥更大的作用，反之“差”的Cij将被削弱甚至由于对应的权重参数为0而被消除。将该参数与式(12)结合可以得到以下优化问题:
$ \underset{\boldsymbol{Y}}{\arg \min } \sum\limits_{i, j} \omega_{i j}\left\|\boldsymbol{C}_{i j} \boldsymbol{Y}_i-\boldsymbol{Y}_j\right\|^2 $ (14)
式中Y=[Y1, Y2, …, Yn]，而且
2.2 还原逐点映射为了还原最终的逐点映射，给模型簇中的每对模型Si和Sj构建置换矩阵Πij，它们的基函数矩阵分别为Φi和Φj。理想情况下模型对的函数映射满足正交性，即
$ \boldsymbol{C}_{i j} \boldsymbol{C}_{j i}=\boldsymbol{I} $ (15)
根据式(6)可得Cij=ΦjTΠijΦi，根据式(12)可得Cji=YiYjT，将这2个结论与公式(15)结合，可得如下公式:
$ \boldsymbol{\varPhi}_j^{\mathrm{T}} \boldsymbol{\varPi}_{i j} \boldsymbol{\varPhi}_i \boldsymbol{Y}_i \boldsymbol{Y}_j^{\mathrm{T}}=\boldsymbol{I} $ (16)
由此可列出用于计算置换矩阵Πij的优化问题
$\mathop {\arg \;\min }\limits_{\boldsymbol{\varPi}_{i j} \in\{0, 1\}} \left\|\boldsymbol{\varPi}_{i j} \boldsymbol{\varPhi}_i \boldsymbol{Y}_i-\boldsymbol{\varPhi}_j \boldsymbol{Y}_j\right\|^2 $ (17)
为了提高求解该优化问题的精度，将CPD算法[13]与式(17)进行融合，把点对点映射还原问题看成求解概率密度估计问题，以最大后验概率恢复点对点映射，则式(17)改写成
$\mathop {\arg \;\min }\limits_{\boldsymbol{\varPi}_{i j} \in\{0, 1\}} D_{\mathrm{KL}}{ }\left(\boldsymbol{\varPhi}_j \boldsymbol{Y}_j, \boldsymbol{\varPi}_{i j} \boldsymbol{\varPhi}_i \boldsymbol{Y}_i\right)+\rho\left\|\varGamma\left(\boldsymbol{\varPhi}_j \boldsymbol{Y}_j-\boldsymbol{\varPi}_{i j} \boldsymbol{\varPhi}_i \boldsymbol{Y}_i\right)\right\|^2$ (18)
式中: 将ΦjYj表示为连续高斯混合模型分布，ΦiY表示为混合狄拉克分布，DKL计算的是这2个分布之间的库尔贝克-莱布勒(Kullback-Leibler, KL)散度，‖Γ(ΦjYj－ΠijΦiYi)‖2是洁洪诺夫正则化项，Γ是促进平滑的低通运算符，ρ>0是DKL项和洁洪诺夫正则化项之间的权衡参数，在实验中当ρ处于2到5之间，优化问题求解值的平均测地误差最小，因此选择ρ=3。采用期望最大化(expectation maximization，EM) 算法对公式(18)进行计算，该对齐问题的优化求解可以看成是对似然函数的最大化。
通过式(18)得到置换矩阵Πij，这样就还原了模型簇中模型对的逐点映射，即获得了模型簇对应关系结果。
3 实验结果与分析本文算法采用Matlab编程实现，在FAUST[15]、SCAPE[16]、TOSCA[17]和SHERC’16 Topology[18]数据集上进行实验, 并与文献[6]、[9]和[19]的算法进行非刚性模型簇对应关系计算的定性和定量比较。文献[6]是一种基于深度学习的算法，使用ADAM优化器训练500个epoch，算法初始学习率为0.01，随着训练的增多逐渐降低至0.001。文献[19]是最新的非刚性模型对的对应关系算法，虽然它并不是模型簇的算法，但是该算法在谱域和空间域上迭代优化目标问题，生成的对应关系结果质量很高，是非常有代表性的非刚性模型对应关系算法，为了和模型簇算法公平地比较结果，使用该算法依次计算模型簇中每个模型对的对应关系结果实现实验对比。
3.1 实验数据集使用4种数据集进行定性和定量的实验, 其中FAUST数据集是由10个不同人体，每个人以30个不同的动作进行扫描，得到的300张高分辨率三角网格模型组成的；SCAPE数据集由72个具有不同连通性和网格分辨率的人体模型组成，每个人体模型的动作各异；TOSCA数据集是一个合成图像数据集, 包含人、猩猩、猫、狗等8类动物共76幅三维图像；SHERC’16 Topology数据集包含25个近等距的胖孩子模型，这些模型中有大量拓扑伪影噪声。
3.2 定性实验结果图 2是本文算法和文献[6]、[9]和[19]算法在SCAPE数据集构建的非刚性模型簇对应关系结果对比。对源模型根据顶点坐标进行颜色渲染，使用对应关系结果将目标模型与源模型匹配的顶点绘制相同颜色，如此便可直观地验证出对应关系结果的准确性。图 2(b)是文献[6]的对应关系结果，该算法使用深度表面变形(deep surface deformation, DSD)网络将模型的变换参数在模型簇中传递，导致噪声也会被传递放大，前3个模型的手臂虽然基本对应正确，但是模型身体其他部分都出现左右对应错误，第4个模型受模型自身对称性的影响甚至整体出现左右颠倒对应。图 2(c)是文献[9]的对应关系结果，它是基于模板的对应关系算法，基本不会出现如图 2(b)中前3个模型手臂与身体颜色“断层”的现象。但是由于初始化参数质量无法保证，引入的噪声难以消除，所以对应结果质量不高，可视化效果不平滑。而且算法也受模型自身对称性的影响，前2个模型的左右对应关系都是错误的。文献[19]利用双重迭代优化(dual iterative refinement, DIR)算法，在谱域和空间域上交替优化目标问题，可以很好地处理模型自身对称性影响对应关系计算的问题，从图 2(d)可看出模型整体对应结果大致正确，只是出现了一些细小的错误映射，视觉上呈现斑点状。从图 2(e)可看出，相比于以上3种算法，本文算法可以很好地分析非刚性模型簇，获得的对应关系结果正确，且效果更加平滑，构建的对应关系质量是最高的。
Fig. 2
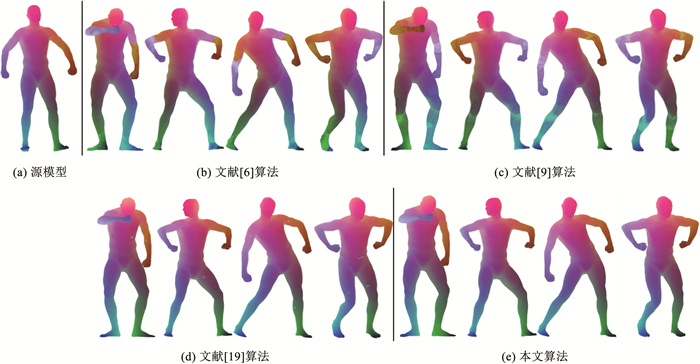图 2 SCAPE数据集上4种算法构建的非刚性模型簇对应关系结果 Fig. 2 Correspondence results of non-rigid shape constructed by four algorithms on SCAPE dataset 本文算法与文献[6]、[9]和[19]算法在TOSCA数据集上构建的非刚性模型簇对应关系可视化对比结果见图 3。从图 3(b)中可见，文献[6]算法在TOSCA数据集上依然受模型自身对称性的影响。其中3个半人马模型中左右对应关系都是错误的，左边第一个半人马模型的胸口出现一大块与周围颜色不连接的区域，将其与源模型颜色对比，很明显可以看出是错误映射分布，这是算法将不匹配的点也纳入到变形的过程中所造成的结果。图 3(c)中，4个半人马模型中有2个模型出现了模型左右对应错误的现象，左边第一个模型的马腹部出现大量对应错误。文献[19]作为模型对(2个模型)的对应关系算法，一旦对应关系结果中出现大量噪声，无法像模型簇对应关系算法一样利用多模型的循环一致性来消除单个模型对的噪声。从图 3(d)中可以看出，左边第一个模型的错误映射分布特别多，其他3个模型相对会少一些，同时算法也难以处理模型自身对称性影响对应关系计算的问题，4个模型的左右对应关系都是错误的。而本文利用OSA算法计算模型对之间的对应关系，生成高质量的初始化参数，减少了噪声的引入，使用CCLB参与模型簇对应关系计算，能够有效区分模型对称特性，解决模型自身对称性影响对应关系计算的问题，由图 3(e)可见，本文算法对应关系准确率高，语义颜色信息更加平滑自然。
Fig. 3
图 3 TOSCA数据集上4种算法构建非刚性模型簇对应关系结果 Fig. 3 Correspondence results of non-rigid shape collections constructed by four algorithms on TOSCA dataset 图 4通过纹理迁移来展示不同算法分别在FAUST和TOSCA数据集上构建的对应关系结果。纹理迁移根据对应关系结果将纹理图片从源模型映射到目标模型上，可以直观地反映算法双射性的优劣。图中将同一位置的局部细节放大，更好地可视化映射结果的局部失真。在FAUST数据集上，从局部的放大细节上看，文献[6]算法出现对应上的左右颠倒问题，归根结底还是模型自身对称性结构导致的，文献[9]和文献[19]算法都出现了不同程度的局部对应失真，而本文算法在连续性和映射质量上都明显优于其他算法。在TOSCA数据集上，放大的局部细节选取的是模型变形扭曲程度最大的位置，可以看出文献[9]和文献[19]算法映射的连续性很差，出现严重的总体映射误差，而本文算法在保持良好局部细节的同时，映射的连续性最好，且总体误差最小，对应关系结果的准确率优于其他算法，所得到的纹理映射最接近映射的真实情况，这证明了本文算法可以很好地保证映射的双射性。
Fig. 4
图 4 在FAUST和TOSCA数据集上通过纹理迁移展示4种算法的对应关系结果 Fig. 4 Correspondence results of four algorithms presented by texture transfer on FAUST and TOSCA datasets 本文算法与文献[6]、[9]和[19]算法在SHERC’16 Topology数据集上构建的非刚性模型簇对应关系可视化对比结果见图 5。SHERC’16 Topology数据集中的模型由于表面区域的重叠会产生大量的拓扑伪影噪声，例如图中第一行右手叉腰的胖孩子的双手处、第二个胖孩子的左手手臂和身体连接处以及第二行跳跃胖孩子的双脚都是典型的区域重叠，因此该数据集通常作为拓扑噪声测试数据集。从图中可以看出，文献[6]和[19]算法无法处理模型的拓扑伪影噪声，不仅在区域重叠处对应错误，在全身各个区域也都无法产生正确的对应结果。文献[9]算法大部分对应关系可视化效果较为平滑，但存在模型左右对应的错误，整体对应失真也很严重。本文算法在区域重叠处大致对应正确，除了叉腰胖孩子的右手手掌处对应失真，对应关系结果基本不受拓扑伪影噪声影响，整体误差小，局部细节平滑，证明本文算法可以很好地解决拓扑伪影噪声问题。
Fig. 5
图 5 SHERC’16 Topology数据集上4种算法构建非刚性模型簇对应关系结果 Fig. 5 Correspondence results of non-rigid shape collections constructed by four algorithms on SHERC'16 Topology dataset 3.3 定量实验结果为了定量地比较不同算法计算非刚性三维模型簇对应关系的有效性，本文采用归一化测地距离(normalized geodesic distance, NGD)[20]评估对应关系结果的准确率。NGD又被称为测地误差，假设z为目标模型Z上一点，u*和u分别为源模型U上与z的真实对应点以及实际对应点，这两点间的测地误差e(z)计算公式如下:
$e(z)=\frac{d_U\left(u, u^*\right)}{\sqrt{\operatorname{area}(U)}}$ (19)
式中dU是点u与u*在模型U上的测地距离，area(U) 是模型U的面积。
图 6是本文算法与文献[6]、[9]和[19]算法在不同数据集上的测地误差曲线，图中横坐标为测地误差，纵坐标为对应关系准确率的百分比，曲线代表落在某个测地误差值内的对应关系准确率的累积曲线。在FAUST数据集上，本文算法虽然在测地误差为0时对应关系准确率略微低于文献[19]，但在误差为0.01时准确率就反超文献[19]，并有更优异的全局准确率，在测地误差为0.1的时候达到了100%的对应关系准确率。而文献[9]和文献[19]直到误差分别为0.15和0.2才达到同样的准确率，文献[6]直到测地误差为0.25时一直是低于85%。在SCAPE数据集上，本文算法、文献[9]和文献[19]都较快地收敛于100%的准确率，该数据集与FAUST数据集类似，都是对真实人体的扫描，数据采集过程中会产生许多伪影噪声，这样的定量结果说明这3种算法都可以很好地处理伪影噪声，而文献[6]的准确率一直都很低。在TOSCA数据集上，由于该数据集是一个合成图像数据集，三维图像中有很多重叠与遮挡的地方，很容易产生拓扑噪声，从图中可以看出，本文算法依然取得了最优的结果，准确率比其他3种算法都有较大提升，比排第二的文献[9]准确率有大约30%的提升。综上所述，本文算法在非刚性三维模型簇对应关系计算能力上比以上3种算法更优异，准确率更高，且能够有效地处理三维模型的伪影噪声和拓扑噪声。
Fig. 6
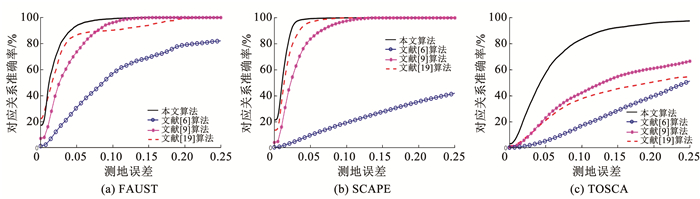图 6 4种算法在3个数据集上的测地误差曲线 Fig. 6 Geodesic error curves of four algorithms on three datasets 3.4 消融实验表 1为本文算法在FAUST、SCAPE和TOSCA数据集上进行消融实验的结果，表中数据为平均测地误差。通过不包含OSA算法、不包含ICSM权重、不包含OSA算法和ICSM权重以及包含OSA算法和ICSM权重这4种不同的设置进行实验。本文算法在不包含OSA算法的设置下，使用函数映射来计算模型对的对应关系，由此引入了大量噪声，平均测地误差明显比包含OSA算法的设置前提下更大了；在不包含ICSM权重的设置下，所有的初始化参数权重都相等，会起到放大噪声的效果，对准确率也有一定的影响；在不包含OSA算法和ICSM权重的设置下，平均测地误差最大，因此对对应关系准确率的影响也最大。可以看出，OSA算法和ICSM权重可显著提高对应关系准确率，进一步证明了本文算法的有效性。
表 1
表 1 消融实验 Tab. 1 Ablation experiments 数据集 不包含OSA 不包含ICSM 不包含OSA和ICSM 包含OSA和ICSM FAUST 0.110 0.078 0.177 0.028
SCAPE 0.096 0.062 0.112 0.019
TOSCA 0.188 0.123 0.252 0.049
表 1 消融实验 Tab. 1 Ablation experiments
3.5 运行时间图 7为本文算法与文献[6]和[9]算法在以上3种数据集上计算一组模型簇(包含5个模型)对应关系所需的平均运行时间对比结果。由于文献[19]是模型对的对应关系算法，和模型簇算法运行时间的比较没有意义，因此不纳入实验中进行对比。实验设备采用Core i7处理器，CPU主频为2.1 GHz，内存大小为32 GB，显卡采用RTX 3080，显存大小为12 GB。文献[6]是一种深度学习算法，总体运行时间由预处理、训练和测试以及后处理3个阶段组成，由于算法可以提供泛化的模型用于处理不同数据集，因此当前测试不考虑训练时间，然而扣除训练时间后算法的整体运行时间仍在800~1 100 s之间，要高于其他2种非深度学习的算法，而且该算法基于模型变形机制，运行时间会随着模型顶点数的增加而增大。文献[9]需要对多模型与模板模型之间的置换矩阵和函数映射矩阵进行循环一致性的交替求解，相对于本文算法更耗时一些，而且由于采用模板机制，模型顶点数和算法运行时间也成正比。本文算法的运行时间接近于文献[9]。这是因为本文算法的优化问题虽然相对比较简单，但是求解优化问题的CPD算法是比较耗时的，并且由于计算初始化参数的OSA算法基于函数映射，整体的运行时间受模型点数增加的影响也较小。综上所述，本文算法在获得高质量三维模型簇对应关系的前提下，在运行时间上也具备一定的优势。
Fig. 7
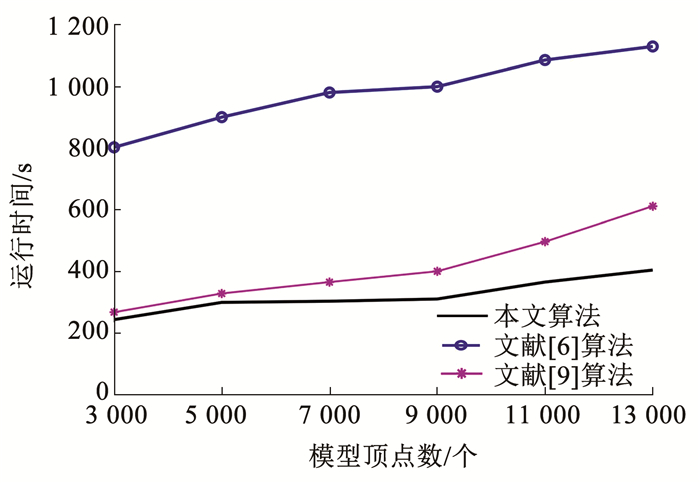图 7 3种算法的运行时间 Fig. 7 Runtime of three algorithms 4 结论三维模型簇对应关系计算是计算机视觉和计算机图形学领域的研究热点与难点问题。本文首先使用OSA算法来计算初始化参数，该算法使用伴随算子这一更优的线性转换算子，解决函数映射与逐点映射方向不一致的问题；其次利用ICSM算法为每个初始化参数赋予相应权重，降低甚至过滤噪声；最后将极限模型的CCLB参与到多模型的循环一致性算法过程中，从而生成具有一致性和双射性的模型簇对应关系结果。实验结果表明，本文算法与现有算法相比，可以更好地解决模型自身对称性影响对应关系计算的问题，构建的对应关系结果准确性和一致性更高。
然而，本文算法还存在一些不足，一方面OSA算法基于函数映射，如果处理非等距或者残缺模型，会引入很多噪声，影响后续计算的准确性；另一方面，基于CCLB的循环一致性算法前提是建立完整模型之间具有双射性的对应关系，因此对于残缺模型簇的计算结果是很差的。以上这些问题也是今后需要不断探讨与改进的方面。
参考文献
[1] MITRA N J, WAND M, ZHANG H, et al. Structure-aware shape processing[M]. ACM SIGGRAPH 2014 Courses, 2014: 1. DOI:10.1145/2614028.2615401
[2] ZUFFI S, KANAZAWA A, JACOBS D W, et al. 3D menagerie: modeling the 3D shape and pose of animals[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE Press, 2017: 6365. DOI: 10.1109/CVPR.2017.586
[3] OVSJANIKOV M, BEN-CHEN M, SOLOMON J, et al. Functional maps: a flexible representation of maps between shapes[J]. ACM Transactions on Graphics, 2012, 31(4): 1. DOI:10.1145/2185520.2185526
[4] WU Y, YANG J, ZHAO J. Partial 3D shape functional correspondence via fully spectral eigenvalue alignment and upsampling refinement[J]. Computers & Graphics, 2020, 92(6): 99. DOI:10.1016/j.cag.2020.09.004
[5] 杨军, 李金泰. 混合式监督学习的三维模型对应关系计算[J]. 西安电子科技大学学报, 2022, 49(4): 201.
YANG Jun, LI Jintai. Correspondencecalculation of 3D shapes by mixed supervision learning[J]. Journal of Xidian University, 2022, 49(4): 201. DOI:10.19665/j.issn1001-2400.2022.04.023
[6] GROUEIX T, FISHER M, KIM V G, et al. Unsupervised cycle-consistent deformation for shape matching[J]. Computer Graphics Forum, 2019, 38(5): 123. DOI:10.1111/cgf.13794
[7] BERNARD F, THUNBERG J, SWOBODA P, et al. HiPPI: higher-order projected power iterations for scalable multi-matching[C]//Proceedings of the IEEE International Conference on Computer Vision. Seoul: IEEE Press, 2019: 10284. DOI: 10.1109/ICCV.2019.01038
[8] 杨军, 雷鸣. 结合函数映射与循环一致性约束的模型簇对应关系计算[J]. 激光与光电子学进展, 2019, 56(8): 081005.
YANG Jun, LEI Ming. Correspondence calculation of model cluster by functional mapping combined with cycle-consistency constraints[J]. Laser & Optoelectronics Progress, 2019, 56(8): 081005. DOI:10.3788/LOP56.081005
[9] GAO M, LAHNER Z, THUNBERG J, et al. Isometric multi-shape matching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 14183. DOI: 10.1109/CVPR46437.2021.01396
[10] WU Y, YANG J. Multi-part shape matching by simultaneous partial functional correspondence[J]. The Visual Computer, 2022, 1. DOI:10.1007/s00371-021-02337-6
[11] CAO D, BERNARD F. Unsupervised deep multi-shape matching[C]//Proceedings of the European Conference on Computer Vision. Tel Aviv: Springer, 2022: 55. DOI: 10.1007/978-3-031-20062-5_4
[12] HUANG R, ACHLIOPTAS P, GUIBAS L, et al. Limit shapes——A tool for understanding shape differences and variability in 3D model collections[J]. Computer Graphics Forum, 2019, 38(5): 187. DOI:10.1111/cgf.13799
[13] MYRONENKO A, SONG X. Point set registration: coherent point drift[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262. DOI:10.1109/TPAMI.2010.46
[14] NGUYEN A, BEN-CHEN M, WELNICKA K, et al. An optimization approach to improving collections of shape maps[J]. Computer Graphics Forum, 2011, 30(5): 1481. DOI:10.1111/j.1467-8659.2011.02022.x
[15] BOGO F, ROMERO J, LOPER M, et al. FAUST: dataset and evaluation for 3D mesh registration[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE Press, 2014: 3794. DOI: 10.1109/CVPR.2014.491
[16] ANGUELOV D, SRINIVASAN P, KOLLER D, et al. Scape: shape completion and animation of people[J]. ACM Transactions on Graphics, 2005, 24(3): 408. DOI:10.1145/1186822.1073207
[17] BRONSTEIN A M, BRONSTEIN M M, KIMMEL R. Numerical geometry of non-rigid shapes[M]. New York: Springer, 2008: 56.
[18] L?HNER Z, RODOLà E, BRONSTEIN M M, et al. SHREC'16: matching of deformable shapes with topological noise[C]//Proceedings of the Eurographics Workshop on 3D Object Retrieval. Heidelberg: Springer, 2016: 55. DOI: 10.5555/3056462.3056475
[19] XIANG R, LAI R, ZHAO H. A dual iterative refinement method for non-rigid shape matching[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021: 15930. DOI: 10.1109/CVPR46437.2021.01567
[20] KIM V G, LIPMAN Y, FUNKHOUSER T. Blended intrinsic maps[J]. ACM Transactions on Graphics, 2011, 30(4): 1. DOI:10.1145/2010324.1964974
