冰中微尺度受陷气泡生长分布特性与宏观热力影响综述

邵苛苛^1,2,宋孟杰^1,2,张旋¹,康文希³,张颖³,张龙¹,刘源鑫^1,4

(1.北京理工大学 机械与车辆学院,北京 100081;2.汉阳大学 机械工程学院,首尔 04763; 3.北京市东城区东直门中学,北京 100007;4.北京京能能源技术研究有限责任公司,北京 100022)



摘要:

结冰是传热传质流动耦合的非线性、变密度液固相变过程,在自然界与工业界广泛存在且多呈负面影响。溶解于液态水中的微量空气在结冰时因冰晶挤压而汇聚后成核,形成较大气泡后因界面黏附力而停留在冻结锋面处,最终形成冰中大小各异、分布不一的微尺度受陷气泡。形成于结冰过程的微尺度受陷气泡,不仅因改变冰的内部结构、密度分布、导热系数及冻结速率而影响后期动态结冰过程,亦会影响结冰过程和结束后冰体的整体导热系数、热阻分布、抗压强度、应力分布等宏观热学、力学物理特性。为精准预测及控制结冰过程,开发和优化各类防除冰技术,微尺度受陷气泡的生长分布特性与宏观热力影响研究在学术界和工业界均备受关注。首先,以冰中微尺度受陷气泡为研究对象,从微观与宏观尺度对其成核机制、生长过程、分布特性和静态稳定性等进行综述。结果显示:气泡形状与冻结速率直接相关,当冻结速率大于25 μm/s时,冰中出现长短轴比小于5的蛋状受陷气泡；当冻结速率在5~25 μm/s时,冰中出现长短轴比大于5的针状受陷气泡；当冰冻结速率小于3 μm/s时,冰中未能发现任何受陷气泡。其次,通过对既有文献中各类研究成果的梳理分析,对受陷气泡全生命周期的影响因素及其对结冰时、成冰后热力物性的不同影响机制进行了梳理与解释。冰中受陷气泡因降低冰的密度及改变内部冰晶结构而会显著降低冰的有效导热系数。在融冰实验中,气泡体积分数为57%的冰比不含气泡的透明冰开始融化时间滞后约50%,相同时间内的融冰高度低36.81%。随气泡体积分数增加,冰的水平和竖直抗压强度均逐渐减小,当气泡体积分数由4%增加到34%时,水平和竖直方向抗压强度分别降低为原来的8.38%和8.10%。最后,基于既有受陷气泡研究成果,对目前存在的研究空白及发展趋势进行了预测与阐述。本综述对理清受陷气泡复杂特性、丰富结冰过程传质理论有较大帮助,亦可为既有防除冰技术的优化设计提供参考与借鉴。

关键词:  受陷气泡  结冰成核  生长分布特性  热学特性  力学特性

DOI：10.11918/202311080

分类号:TB69

文献标识码:A

基金项目:国家自然科学基金(52076013);北京市自然科学基金(4,2)



A review of micro-scale trapped air bubble growth distribution characteristics and thermal mechanical effects in ice

SHAO Keke^1,2,SONG Mengjie^1,2,ZHANG Xuan¹,KANG Wenxi³,ZHANG Ying³,ZHANG Long¹,LIU Yuanxin^1,4

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.School of Mechanical Engineering, Hanyang University, Seoul 04763, Republic of Korea; 3.Beijing Dongzhimen High School, Beijng 100007,China; 4.Beijing Jingneng Energy Technology Research Co., Ltd., Beijing 100022, China)

Abstract:

Icing is a nonlinear, variable density liquid-solid phase change process coupled with thermal and mass transfer and flow, which occurs widely in nature and industry, often with negative consequences. Trace amounts of air dissolved in water converge and nucleate into larger bubbles during icing due to the extrusion of ice crystals. These bubbles then remain at the freezing front due to adhesion, ultimately forming microscale trapped air bubbles of varying sizes and distributions in ice. The formation of micro-scale trapped air bubbles in the icing process not only affects the later dynamic icing process by changing the internal structure, density distribution, thermal conductivity and freezing rate of ice, but also affects the overall thermal conductivity, thermal resistance distribution, compressive strength, stress distribution and other macroscopic thermal and mechanical properties of the ice body after the icing process concludes. To accurately predict and control the icing process, as well as to develop and optimize various types of anti-icing technologies, the study of the growth and distribution characteristics of microscale trapped air bubbles and the macro-thermal effects has attracted much attention in both academia and industry. Firstly, this paper takes micro-scale trapped air bubbles in ice as the research object, and reviews their nucleation mechanism, growth process, distribution characteristics and static stability from the micro and macro scales. The results show that the bubble shape is directly related to the freezing rate, and when the freezing rate exceeds 25 μm/s, egg-shaped trapped air bubbles with a length-to-width ratio smaller than 5 appear in ice. When the freezing rate is between 5 and 25 μm/s, needle-shaped trapped air bubbles with a length-to-width ratio larger than 5 appear in ice. No bubbles can be found in ice when the ice freezing rate is below 3 μm/s. Secondly, by reviewing and analyzing existing literature, the influencing factors of the whole life cycle of trapped air bubbles and their different influencing mechanisms on the thermal and mechanical characteristics during icing and after ice formation are summarized and explained. Trapped air bubbles in ice significantly reduce the effective thermal conductivity of the ice by lowering its the density and changing the internal ice crystal structure. In ice melting experiments, ice with a bubble volume fraction of 57% exhibits a delay of approximately 50% in the starting time of melting compared to clear ice without bubbles. Additionally, the ice with bubbles has a 36.81% lower meting height within the same time frame. With the increase of bubble volume fraction, both the horizontal and vertical compressive strength of the ice decrease gradually. When the bubble volume fraction increases from 4% to 34%, the horizontal and vertical compressive strengths decrease to 8.38% and 8.10% of the original values, respectively. Finally, based on existing research on trapped air bubbles, the current research gaps and development trends are predicted and elaborated. This review is helpful for clarifying the complex characteristics of trapped air bubbles and enriching the mass transfer theory of icing process. It can also provide references and insights for the optimal design of existing anti-deicing technologies.

Key words:  trapped air bubble  icing nucleation  growth distribution characteristics  thermal characteristics  mechanical characteristics


邵苛苛, 宋孟杰, 张旋, 康文希, 张颖, 张龙, 刘源鑫. 冰中微尺度受陷气泡生长分布特性与宏观热力影响综述[J]. 哈尔滨工业大学学报, 2024, 56(6): 152-174. DOI: 10.11918/202311080.
SHAO Keke, SONG Mengjie, ZHANG Xuan, KANG Wenxi, ZHANG Ying, ZHANG Long, LIU Yuanxin. A review of micro-scale trapped air bubble growth distribution characteristics and thermal mechanical effects in ice[J]. Journal of Harbin Institute of Technology, 2024, 56(6): 152-174. DOI: 10.11918/202311080.
基金项目 国家自然科学基金(52076013);北京市自然科学基金(3212024, 3232032) 作者简介 邵苛苛(1992—)，男，博士研究生;
宋孟杰(1984—)，男，教授，博士生导师 通信作者 宋孟杰，mengjie.song@bit.edu.cn 文章历史 收稿日期: 2023-11-27



Abstract            Full text            Figures/Tables            PDF


冰中微尺度受陷气泡生长分布特性与宏观热力影响综述
邵苛苛^1,2, 宋孟杰^1,2, 张旋¹, 康文希³, 张颖³, 张龙¹, 刘源鑫^1,4    
1. 北京理工大学 机械与车辆学院, 北京 100081;
2. 汉阳大学 机械工程学院，首尔 04763;
3. 北京市东城区东直门中学, 北京 100007;
4. 北京京能能源技术研究有限责任公司, 北京 100022

收稿日期: 2023-11-27; 录用日期: 2024-01-19; 网络首发日期: 2024-03-05
基金项目: 国家自然科学基金(52076013);北京市自然科学基金(3212024, 3232032)
作者简介: 邵苛苛(1992—)，男，博士研究生; 宋孟杰(1984—)，男，教授，博士生导师
通信作者: 宋孟杰，mengjie.song@bit.edu.cn


摘要: 结冰是传热传质流动耦合的非线性、变密度液固相变过程，在自然界与工业界广泛存在且多呈负面影响。溶解于液态水中的微量空气在结冰时因冰晶挤压而汇聚后成核，形成较大气泡后因界面黏附力而停留在冻结锋面处，最终形成冰中大小各异、分布不一的微尺度受陷气泡。形成于结冰过程的微尺度受陷气泡，不仅因改变冰的内部结构、密度分布、导热系数及冻结速率而影响后期动态结冰过程，亦会影响结冰过程和结束后冰体的整体导热系数、热阻分布、抗压强度、应力分布等宏观热学、力学物理特性。为精准预测及控制结冰过程，开发和优化各类防除冰技术，微尺度受陷气泡的生长分布特性与宏观热力影响研究在学术界和工业界均备受关注。首先，以冰中微尺度受陷气泡为研究对象，从微观与宏观尺度对其成核机制、生长过程、分布特性和静态稳定性等进行综述。结果显示: 气泡形状与冻结速率直接相关，当冻结速率大于25 μm/s时，冰中出现长短轴比小于5的蛋状受陷气泡；当冻结速率在5~25 μm/s时，冰中出现长短轴比大于5的针状受陷气泡；当冰冻结速率小于3 μm/s时，冰中未能发现任何受陷气泡。其次，通过对既有文献中各类研究成果的梳理分析，对受陷气泡全生命周期的影响因素及其对结冰时、成冰后热力物性的不同影响机制进行了梳理与解释。冰中受陷气泡因降低冰的密度及改变内部冰晶结构而会显著降低冰的有效导热系数。在融冰实验中，气泡体积分数为57%的冰比不含气泡的透明冰开始融化时间滞后约50%，相同时间内的融冰高度低36.81%。随气泡体积分数增加，冰的水平和竖直抗压强度均逐渐减小，当气泡体积分数由4%增加到34%时，水平和竖直方向抗压强度分别降低为原来的8.38%和8.10%。最后，基于既有受陷气泡研究成果，对目前存在的研究空白及发展趋势进行了预测与阐述。本综述对理清受陷气泡复杂特性、丰富结冰过程传质理论有较大帮助，亦可为既有防除冰技术的优化设计提供参考与借鉴。
关键词: 受陷气泡    结冰成核    生长分布特性    热学特性    力学特性    
A review of micro-scale trapped air bubble growth distribution characteristics and thermal mechanical effects in ice
SHAO Keke^1,2, SONG Mengjie^1,2, ZHANG Xuan¹, KANG Wenxi³, ZHANG Ying³, ZHANG Long¹, LIU Yuanxin^1,4    
1. School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China;
2. School of Mechanical Engineering, Hanyang University, Seoul 04763, Republic of Korea;
3. Beijing Dongzhimen High School, Beijng 100007, China;
4. Beijing Jingneng Energy Technology Research Co., Ltd., Beijing 100022, China



Abstract: Icing is a nonlinear, variable density liquid-solid phase change process coupled with thermal and mass transfer and flow, which occurs widely in nature and industry, often with negative consequences. Trace amounts of air dissolved in water converge and nucleate into larger bubbles during icing due to the extrusion of ice crystals. These bubbles then remain at the freezing front due to adhesion, ultimately forming microscale trapped air bubbles of varying sizes and distributions in ice. The formation of micro-scale trapped air bubbles in the icing process not only affects the later dynamic icing process by changing the internal structure, density distribution, thermal conductivity and freezing rate of ice, but also affects the overall thermal conductivity, thermal resistance distribution, compressive strength, stress distribution and other macroscopic thermal and mechanical properties of the ice body after the icing process concludes. To accurately predict and control the icing process, as well as to develop and optimize various types of anti-icing technologies, the study of the growth and distribution characteristics of microscale trapped air bubbles and the macro-thermal effects has attracted much attention in both academia and industry. Firstly, this paper takes micro-scale trapped air bubbles in ice as the research object, and reviews their nucleation mechanism, growth process, distribution characteristics and static stability from the micro and macro scales. The results show that the bubble shape is directly related to the freezing rate, and when the freezing rate exceeds 25 μm/s, egg-shaped trapped air bubbles with a length-to-width ratio smaller than 5 appear in ice. When the freezing rate is between 5 and 25 μm/s, needle-shaped trapped air bubbles with a length-to-width ratio larger than 5 appear in ice. No bubbles can be found in ice when the ice freezing rate is below 3 μm/s. Secondly, by reviewing and analyzing existing literature, the influencing factors of the whole life cycle of trapped air bubbles and their different influencing mechanisms on the thermal and mechanical characteristics during icing and after ice formation are summarized and explained. Trapped air bubbles in ice significantly reduce the effective thermal conductivity of the ice by lowering its the density and changing the internal ice crystal structure. In ice melting experiments, ice with a bubble volume fraction of 57% exhibits a delay of approximately 50% in the starting time of melting compared to clear ice without bubbles. Additionally, the ice with bubbles has a 36.81% lower meting height within the same time frame. With the increase of bubble volume fraction, both the horizontal and vertical compressive strength of the ice decrease gradually. When the bubble volume fraction increases from 4% to 34%, the horizontal and vertical compressive strengths decrease to 8.38% and 8.10% of the original values, respectively. Finally, based on existing research on trapped air bubbles, the current research gaps and development trends are predicted and elaborated. This review is helpful for clarifying the complex characteristics of trapped air bubbles and enriching the mass transfer theory of icing process. It can also provide references and insights for the optimal design of existing anti-deicing technologies.
Keywords: trapped air bubble    icing nucleation    growth distribution characteristics    thermal characteristics    mechanical characteristics    
1 研究背景结冰是非稳态、变密度、移动边界的复杂三维液固相变过程，在自然界和航空航海、轨道交通、能源电力、冷冻冷藏等工业领域广泛存在^[1-2]，且往往会带来不利影响^[3-4]。例如，高空云层中飞机表面结冰会影响飞机姿态与传感器工作状态，继而降低飞机稳定性与可操作性^[5-6]；空气源热泵室外换热器表面结霜结冰会大幅降低系统运行能效^[7-8]；风力发电机叶片表面结冰会降低发电效率，积冰从叶片表面脱落后也会危及人员与设备安全^[9-10]；光伏板表面结霜结冰会影响镜面反射，降低发电效率^[11-12]；冷冻牛肉内部的冰晶会刺破细胞膜而导致营养成分的流失，影响其融化后食用品质^[13]；动物器官、组织、卵细胞与精子等的冷冻储存也面临因结冰导致活性失效的挑战^[14]。以上诸多领域面临的结霜结冰问题不仅造成大额直接经济损失，各类防除冰处理与操作也会浪费大量时间与经济成本^[15-16]。尽管近20余年为应对结霜结冰危害，各类机械^[17]与材料方式^[18]的涂层加工与表面处理防冰技术、表面变形等机械式^[19]与电加热等热力式除冰技术^[20-21]被广泛开发和测试应用，往往因能耗高、寿命短、体积大、成本高、稳定性差等诸多缺点未能规模应用。2023年1月份全球和中国平均气温^[22]显示全球和中国几乎一半的陆地平均温度都低于0 ℃。表明这些地区都会面临低温结冰问题，并且随着纬度与海拔的升高，结冰问题会更加严重。因此，为充分结合结霜结冰的场景，开发和优化各类防除冰技术，实现结霜结冰过程的精准预测及控制，有必要对水滴/水膜等微尺度结冰过程开展深入研究^[23-24]。

单粒水滴的凝固过程是结冰过程的基本简化，该过程是典型的传热传质与流动耦合的相变过程。如图 1所示，平板表面单粒非形变固着水滴的凝固过程根据其内部某高度测量温度的动态变化可分为预冷/过冷、复辉、冻结和冷却/温降4个阶段^[25]。随着平板表面温度降低，水滴内测点温度由A点初始温度T₀逐渐降至B点相变温度T_pc以下。此时水滴尚未结核，仍保持液态。当温度低至C点成核温度T_n时，水滴表面自三相线处开始发生成核。成核后水滴表面迅速出现的冰晶会对光线发生反射与折射，导致水滴呈现白色，称为复辉。以成核为起点的冰晶迅速生长的复辉阶段CD时间短暂，持续20~50 ms^[26]，水滴由液态变为液固共存态。由于凝固潜热的迅速释放，水滴内部靠近冰晶位置的温度回升至D点相变/凝固温度T_pc。DF为冻结锋面向水滴顶部迁移的冻结阶段，至测温点位置时为E点时刻。当冻结锋面到达水滴顶端时，因冰水密度差异导致的体积膨胀，最终会在冻结水滴顶部形成一个桃子状或洋葱状的凸起^[27-28]，此时测温点位置温度已降低至F处。在冷却/温降阶段，测点位置持续大幅降温至G点平板表面温度T_ps附近。如图 1所示，依次完成“液态—液固混合态—固态”、“稳态—亚稳态—动态—稳态”的热物理变化过程。

Fig. 1
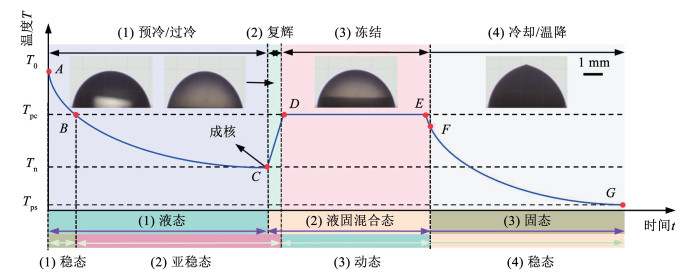图 1 平板表面固着水滴凝固过程的阶段划分与形态变化^[25] Fig. 1 Stages and morphological changes of solidified water droplets on flat surface^[25]


在水滴凝固的4个阶段中，冻结阶段的时间相对较长，液固相变最为明显。冰晶结构间隙小于水，导致气体在冰中的溶解度远小于水中，在成冰的过程中空气分子会从冰中被挤压汇聚至冻结锋面前沿^[29]。当冻结锋面前沿的空气体积分数达到过饱和度这一临界值时，就会导致气泡成核^[30]。气泡成核会迅速向水中膨胀生长，而此时冻结锋面还在持续迁移。如冻结锋面的迁移速率慢，迅速生长的气泡会因在水中的浮力大于其与基底处冰晶的黏附力而脱离冻结锋面进入水中浮出水面；否则便会黏附在冻结锋面，初始呈球形的气泡在冻结锋面挤压下逐渐变为长短轴比大于1的狭长气泡。气泡生长导致冻结锋面前空气分子体积分数降低，进而导致气泡生长速率降低，直至不再生长的气泡被冻结锋面完全覆盖，形成冰中受陷气泡^[31]。微尺度受陷气泡不仅会改变冰的导热系数及冻结速率而影响后期动态结冰过程，亦会影响结冰过程结束后冰体的整体导热系数、抗压强度等宏观热学、力学物理特性。为高精度预测结冰过程与控制冰的物理特性，冻结过程产生的冰中受陷气泡备受关注。

与受陷气泡相同，封闭气泡和挤压气泡也是两类在冰中常见的气泡，三者在形成原因和物理特性等均存在显著的差异。封闭气泡是经常出现在高纬度高寒地区湖泊中的气泡，其形成过程是湖底微生物发酵产生的甲烷等气体在上浮的过程中被湖面的冰层阻挡，最终被冻结在冰中^[32]。挤压气泡则出现在极地深层的冰芯，其形成过程是极地的雪被深埋在地下，在上方冰雪重力的挤压下，蓬松的雪逐渐转化成坚固冰，而其中的空气逐渐汇聚在一块形成了气泡^[33]。此外，沸腾气泡^[34]和空化气泡^[35]也是两类存在于水中的气泡。与受陷气泡出现在相对温和的冻结过程中不同，它们往往出现在剧烈的能量变化过程中。3种气泡的形成时间尺度和体积空间尺度比较如图 2所示。受陷气泡的形成时间较长而尺寸较小，这也无疑对研究过程造成困难。表 1显示这5种气泡的差异，可以看出，受陷气泡形成过程复杂，受影响因素多，但其形成条件温和、周期较短，可以在实验室内对其进行大量的研究。此外，研究受陷气泡也可以为其他气泡的研究方法提供参考和借鉴。

Fig. 2
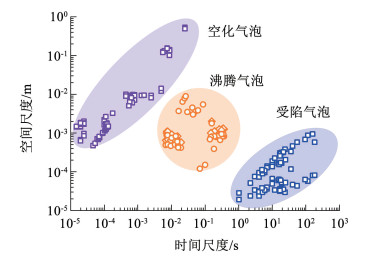图 2 受陷气泡、沸腾气泡、空化气泡的对比 Fig. 2 Comparison of trapped air bubbles, boiling bubbles and cavitation bubbles


表 1
表 1 冰/水中的5种常见气泡特征对比 Tab. 1 Comparison of five common bubble characteristics in ice/water 气泡类型 类别 形貌 初始形状 成熟形状 成核位置 驱动力 相变方式 主要成分 空间尺度 时间尺度 稳定性 出现场合

受陷气泡^[31] 冰中
气泡 球状 蛋状、针状 冻结
锋面 浓度差 液固相变 空气 μm s/min 低温下
稳定 冻结湖面

封闭气泡^[36] 球状 扁平盘状 水中 浓度差 液固相变 甲烷 cm min/h 低温下
稳定 冻结湖面

挤压气泡^[37] 形状
不规则 形状
不规则 无成核
发生 压力差 无相变 空气 μm 月/a 低温下
稳定 寒区冰芯

沸腾气泡^[38] 水中
气泡 球状 球状 受热面 温度差 液汽相变 水蒸气 mm s 不稳定 换热器

空化气泡^[39] 球状 球状 压力突
变处 压力差 液汽相变 水蒸气 cm ms 极不稳定 船舶螺旋桨



表 1 冰/水中的5种常见气泡特征对比 Tab. 1 Comparison of five common bubble characteristics in ice/water


冻结现象在食品冷藏、医疗救护、冰雪体育和工业生产等领域发挥积极作用，同时不适宜的冻结也可能给交通运输、航空航海、电力输送和风力发电等领域带来诸多麻烦。为充分发挥冻结优势，规避其劣势，相关学者对冻结过程开展大量研究。尽管在防除冰等领域，学者围绕冻结机制、冻结过程和预防冻结发生等问题开展了研究，但对冻结问题的研究还不够充分。图 3按照不同空间尺度对冻结研究进行分类，可以看出，学者对冻结问题研究的关注点在微米尺度的冻结水滴^[40-41]和米级尺度的结冰与防除冰^[42-43]，而对中间厘米尺度的研究相对少得多，特别是冰中受陷气泡相关研究文献不足百篇^[44-45]。而冻结水膜介于微米尺度冻结水滴和米级尺度结冰/防除冰之间，是将微观冻结机制和宏观结冰/防除冰联系起来的桥梁，在研究冻结问题中具有重要作用。但该部分的研究未被重视，特别是冻结水膜中的受陷气泡，其在微观上会对冻结速率等产生影响，在宏观上会影响冰层与表面的黏附力，对防除冰有重要影响。因此，有必要对冻结水膜中受陷气泡的形成、分布及其对冻结过程的影响和对冻结后冰层整体的力学和热学等特性的影响进行研究。

Fig. 3
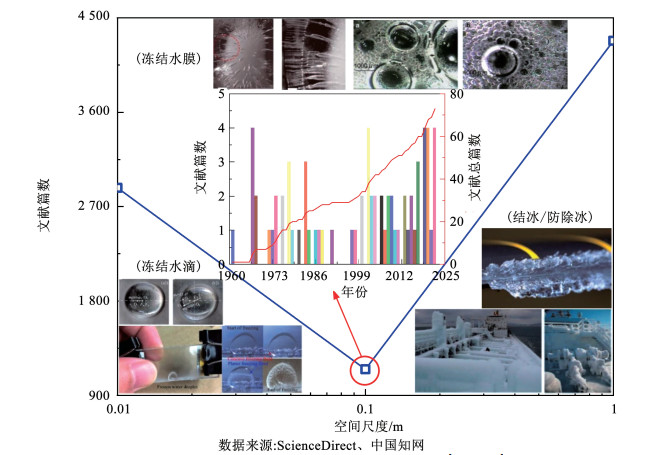图 3 不同空间尺度冻结相关研究文献数量统计^{[29, 40, 42, 45]} Fig. 3 Statistical analysis of research literature on freezing-related studies at different spatial scales^{[29, 40, 42, 45]}


2 受陷气泡的形成和分布特性 2.1 受陷气泡的形成受陷气泡的形成是由于空气在冰中溶解度小于在水中溶解度，在水冻结成冰的过程中，大量的空气会被从冰中挤压出来而汇聚在冻结锋面前沿^[46]。冻结锋面呈现锯齿状结构，在锯齿状凹陷处的气体体积分数往往较高。当该处的气体体积分数达到临界值后，气泡就会发生成核。当气泡尺寸超过临界成核尺寸时，气泡会继续生长，否则就会溶解在水中。在生长的过程中，气泡受到冻结锋面黏附力和浮力的作用。其中，有少量气泡浮力大于黏附力会发生脱离，而大量的气泡会附着在冻结锋面上^[47]。随着冻结锋面的移动，气泡周围高体积分数气体会向气泡内扩散而使气泡长大。当气泡的生长速率小于冻结速率时，冻结锋面会慢慢覆盖气泡，直到气泡被完全冻结在冰中。

在研究冻结锋面前气体体积分数分布时，早期学者认为气体在界面前的分布是均匀的^[48]。而后续的研究发现这种观点是错误的，气体在水中的扩散系数通常为1×10^-9 m²/s，其在单位宽度上的扩散速率远小于冻结速率10^-6 m/s。因此，在冻结过程中冻结锋面前水中的气体体积分数不可能保持均匀^[49-50]。后来，学者们基于溶质在液体中的扩散方程得到了气体分布表达式，如表 2所示。可以看出，这些方程大都和扩散系数D与分布系数k有关。Lipp等^[46-51]则根据气泡在均匀过饱和溶液中生长方程，得到了一个与气体和液体物性参数有关的方程。此外，从这些表达式可以看出，冻结锋面前气体体积分数分布除与扩散系数和分布系数等常数有关外还和冻结速率有关。尽管这些表达式都是从理论分析得出，但是实验中随着冻结速率的减小气泡数量减小，以及当冻结速率小于3 μm/s时冰中不再出现气泡的结果也都和表达式描述的随着冻结速率降低，气体体积分数减小的趋势相吻合。

表 2
表 2 冻结锋面前气体体积分数分布表达式 Tab. 2 Expressions of gas concentration distribution in front of the freezing front 序号 作者 研究方法 方程表达式

1 Tiller等^[49] 理论分析 $c_1(x)=c_{1, 0}\left[1+\frac{1-k}{k}\left(1-\mathrm{e}^{\frac{-k v x}{D}}\right)\right]$

2 Burton等^[51] 理论分析 $c_1(x, t)=c_{1, 0}\left[1+\frac{1-k}{k}\left(\mathrm{e}^{\frac{-v x}{D}}-\mathrm{e}^{\frac{-k v^2 t-v x}{D}}\right)\right]$

3 Pohl^[52] 理论分析 $c_1(x, t)=c_{1, 0}\left\{1+\frac{1-k}{k}\left[\mathrm{e}^{\frac{-v x}{D}}-\mathrm{e}^{\frac{-v(1-k)(x+k u t)}{D}}\right]\right\}$

4 Carte^[47] 理论分析 $c_1(x, t)=c_{1, 0}\left\{1+\frac{1-k}{k}\left[\mathrm{e}^{\frac{-v x}{D}}-\mathrm{e}^{\frac{-(1-k)(x+k v t)}{D}}\right]\right\}$

5 Bari等^[53] 理论分析 $c_1(x)=c_{1, 0}\left(1+\frac{1-k}{k} \mathrm{e}^{\frac{-v x}{D}}\right)$

6 Geguzin等^[54] 理论分析 $c_1(x)=c_{1, 0}\left(1-\frac{1-k}{k} \mathrm{e}^{-\frac{x}{H_1}}\right)$

7 Murakami等^[55] 理论分析 $c_1(x)=c_{1, 0}\left(\frac{1}{k}-\frac{1-k}{k} \mathrm{e}^{-\frac{k v x}{D}}\right)$

8 Yoshimura等^[31] 理论分析 $c_1(x, t)=c_{1, 0}\left\{1+\frac{1-k}{k}\left[\mathrm{e}^{\frac{-v x}{D}}-\mathrm{e}^{\frac{-(1-k)(x+k v t)}{D}}\right]\right\}$



表 2 冻结锋面前气体体积分数分布表达式 Tab. 2 Expressions of gas concentration distribution in front of the freezing front


当冻结锋面前气体体积分数达到过饱和度c/c₀这一临界值时，气泡会发生成核。过饱和度和冻结速率有关，当冻结速率为2 mm/min时，气泡成核的过饱和度为30^[47]。而采用经典成核理论计算发现，在冻结CO₂水溶液中很难发生均相成核^[46]。在式(1)中，当气泡尺寸为100 nm时，表面张力为0.01 N/m，然而，如此小的表面张力是不可能的。因此，有学者^[57]认为冰中受陷气泡是水中预先存在的微纳尺度气泡，而非后来成核产生的气泡，但微纳尺度气泡的来源及在水中长时间存在的稳定性尚未被证实。在冻结CO₂水溶液时发现，气泡会优先在冻结锋面锯齿状的凹陷处出现，且表面粗糙高气泡出现的可能性越大^[46]。这是由于冻结锋面前过饱和度分布是非均匀的，凹陷处的过饱和度可能远高于凸处的过饱和度^[54]。此外，金属凝固研究中发现异相物质并不会显著改变成核条件，而当液体中存在微纳尺度气泡等气核时，气泡会更容易出现^[56]。这些结果表明，气泡在冻结锋面上不容易发生均相成核，更有可能是异相成核。

$r_{\mathrm{c}}=2 \sigma / \Delta P$ (1)

式中：r_c为气泡成核的临界半径，σ为液体的表面张力，ΔP为气泡内外的压力差。

在竖直冻结方向上，气泡在生长过程中受到浮力和界面黏附力的作用，其受力情况示意如图 4所示。气泡和冻结锋面之间的黏附力由表面张力引起，可表示为2πxσsin θ。当气泡浮力大于黏附力时，气泡就会从冰上脱离。当浮力等于黏附力时，气泡将会附着在冰面上，满足如下关系式^[57]：

Fig. 4
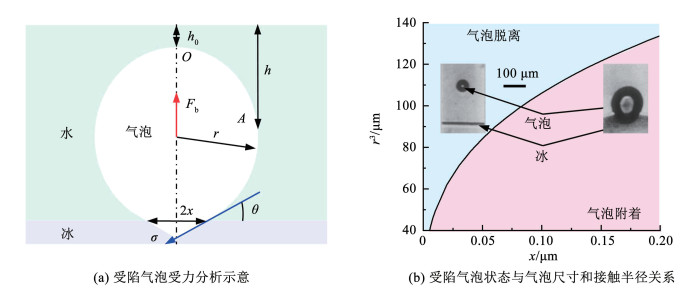图 4 受陷气泡受力分析和运动状态^[57] Fig. 4 Force analysis and motion states of trapped air bubbles^[57]


$g\left(\rho_{\mathrm{w}}-\rho_{\mathrm{b}}\right) V=2 \pi x \sigma \sin \theta$ (2)

式中：ρ_w和ρ_b分别为水和气泡密度，V为气泡体积，x为气泡与界面接触处半径，θ为气泡和冰之间的接触角。通过上式可计算理想情况下气泡脱离时临界半径和气泡与界面接触半径之间的关系。取σ为0.08 N/m，θ为75°，代入上述方程可得

$\frac{r^3}{x}=1.197 \times 10^{-5}$ (3)

因此，当x在一定范围内取值时，可得到气泡脱离临界半径，如图 4(b)所示。气泡^[58]往往出现在界面的凹陷处，而这些地方的尺寸比较小。当x取0.01 μm时，气泡的临界脱离半径约为50 μm。而当气泡半径达到50 μm时，气泡与冰的接触面积也会增加，这表明气泡很难发生脱离。然而，竖直方向冻结实验中发现，普遍存在从冻结锋面上发生脱离的现象，并且气泡脱离的频率和冻结速率间无明显关系^[47]。出现这种现象的原因可能是气泡和冰之间存在一层过冷水膜，导致气泡与界面之间的黏附力小于理论值^[57]。此外，由于水在4 ℃的密度达到最大值，这部分水会向冻结锋面运动，从而引起微对流^[59]，并且微对流的速率随着冻结速率的增加而逐渐减小^[60]。因此，微对流扰动气泡也可能导致气泡发生脱离。

2.2 受陷气泡的分布随着冻结锋面的移动，气泡会受到挤压导致变形，因此，冰中受陷气泡的形状并不会呈现球形。气泡在水中部分的形状由下述方程确定^[57]：

$\frac{2 \sigma}{r_0}=\rho_w\left(h-h_0\right) g+\sigma\left(\frac{1}{r_1}+\frac{1}{r_2}\right)$ (4)

式中：r₀为气泡顶部O点曲率半径，r₁和r₂为气泡表面上任意一点A处在相互垂直的两个面内的曲率半径，h和h₀为A点和O点的深度。

尽管很多学者对气泡形状动态变化与影响因素进行了研究，但对形状类型的划分却没有统一定义。受陷气泡的形状主要有两种，蛋状或椭圆状和针状或圆柱状。针状气泡的长度较长，一般都比蛋状气泡的长度大得多，其尺寸甚至可达数毫米。为了准确区分这两类气泡，一般将气泡的形状按长轴和短轴的比值R_A进行分类。Yoshimura等^[31]将比值小于2.5的气泡称为蛋状气泡，其他的称为针状气泡。Dadic等^[68]则将比值小于4的气泡称为蛋状气泡。Inada等^[61]同样根据受陷气泡长轴和短轴的比值来定义气泡形状，长短轴之比小于5的称为蛋状气泡，长短轴之比大于5的称为针状气泡。但是均没有对比值的划分给出依据。为理清气泡形状划分的依据，对受陷气泡R_A进行统计。如图 5所示，随着R_A增加，气泡数量呈现先增加后减小再增加的趋势，拐点出现在5附近。因此，将气泡形状按长短轴比值5为划分依据更合适。

Fig. 5
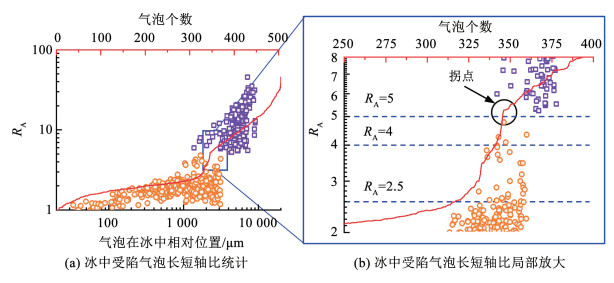图 5 冰中受陷气泡长短轴比统计 Fig. 5 Statistical analysis of length-to-width ratio of trapped air bubbles in ice


气泡的生长速率和冻结速率有关，当冻结速率较大时，冻结锋面前气体体积分数变高，气泡生长速率变大。当冻结速率较小时，冻结锋面前气体体积分数变小，气泡生长速率减慢，甚至停止生长^[62]。当气泡生长速率等于冻结速率时，气泡在纵向上会持续生长，最终生长为针状气泡^[54]。当冻结速率增加时，由于生长时间较短，气泡的长度和直径都会减小^[63-64]。水中溶解气体饱和度、冻结速率对气泡形状的影响如图 6(a)所示。随着饱和度的增加，相同冻结速率下气泡有向针状气泡转变的趋势。在饱和度为1时，当冻结速率大于25 μm/s时，冰中出现蛋状气泡，当冻结速率为5~25 μm/s时，冰中出现针状气泡^[53]。此外，环境压力对受陷气泡的形状有显著影响。如图 6(b)所示，相同冻结速率下，随着环境压力的增加，气泡类型有向针状转变的趋势。这可能是环境压力的增加导致水中溶解气体体积分数增加，气泡的生长时间增加。

Fig. 6
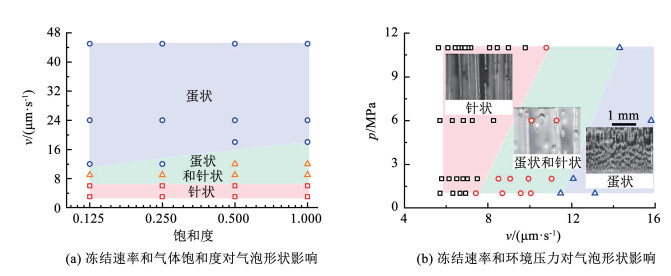图 6 冰中受陷气泡形状及影响因素^{[31, 55]} Fig. 6 Shape of trapped air bubbles in ice and influencing factors^{[31, 55]}


除了饱和度和环境压力，冻结速率对气泡形状也有影响。有学者对从气泡成核到完全受陷在冰中的过程中气泡的生长阶段进行了研究。在这个过程中，气泡的膨胀会降低周围气体体积分数，而冻结速率增加又会提高气体体积分数。因此，气泡生长速率与冻结速率的相对关系将影响气泡的生长过程，并最终影响气泡形状。基于这两个因素对气泡生长的影响，有学者将气泡的生长过程进行了划分。Lipp等^[46]和Wei等^[64]分别将气泡生长过程进行了3个阶段和2个阶段的划分，具体如表 3所示。Lipp等^[46]根据气泡和冰之间的关系，将气泡的生长过程划分为球形生长、部分吞没和完全封闭3个阶段，并根据气泡生长速率和冻结速率的关系，对每个阶段进行了确定。Wei等^[64]根据气泡生长的特征，依据气泡和冻结锋面之间接触角的变化，将气泡受陷之前的生长过程分为球形生长和冻结速率控制延伸2个阶段。

表 3
表 3 不同学者对受陷气泡生长阶段划分比较 Tab. 3 Comparative analysis of different scholars′ division of growth stages of trapped air bubbles 序号 作者 生长阶段 各阶段划分依据

1 Lipp等^[46] 3阶段 1.球形生长(SG)v_B(t)＞v_Ⅰ(t)＞0; x(t)＜y(t)

2.部分吞没(PE) v_B(t)＞0; x(t)＜y(t)

3.完全封闭(TE) v_B(t)＞0; x(t)＞y(t)

2 Wei等^[64] 2阶段 1.球形生长(SG) Φ＞π/2

2.冻结速率控制延伸(SRCE) Φ≤π/2



表 3 不同学者对受陷气泡生长阶段划分比较 Tab. 3 Comparative analysis of different scholars′ division of growth stages of trapped air bubbles


这2种划分方式都将第1个阶段的气泡生长过程划分为球形生长，这个结果也在其他学者的实验中得到了验证^[47]。对后续气泡生长阶段划分存在差异的原因是所研究气泡的类型不同。如图 7(a)所示，当气泡的横向生长速率小于0时，气泡开始进入部分吞没阶段，当冻结锋面超过气泡中心位置时，气泡就被完全封闭在冰中。该过程可以完美地描述蛋状气泡的生长过程。如图 7(b)所示，在球形生长阶段后，气泡直径达到最大值。此时，气泡不会立即收缩，而是在直径保持几乎不变的情况下，气泡长度持续增加，直到某时刻气泡开始收缩，这个过程是针状气泡的生长过程描述。因此，Lipp和Wei对气泡生长阶段的划分分别是基于蛋状气泡和针状气泡生长过程的描述。

Fig. 7
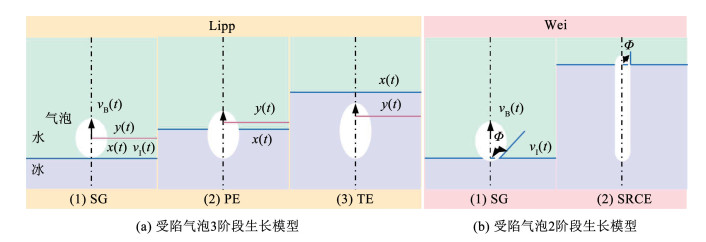图 7 不同学者对受陷气泡生长阶段划分示意^{[46, 64]} Fig. 7 Schematic diagram of different scholars′ division of growth stages of trapped air bubbles^{[46, 64]}


气泡的尺寸通常较小，虽然针状气泡长度可能达数毫米，但是宽度通常不超过500 μm。在一定范围内，气泡尺寸会随着冻结速率的减小而增加。如图 8所示，40~160 μm/s的冻结速率，气泡的数量随着冻结速率的增加而逐渐增加。单位体积冰内受陷气泡数量密度与冻结速率的1.7次方成正比。气泡尺寸的分布统计表明，气泡的尺寸和冻结速率也有关系。在41.67 μm/s的冻结速率下，气泡的长度和宽度分布范围分别为10~110 μm和10~180 μm，中位数分别为50~70 μm和90~110 μm。

Fig. 8
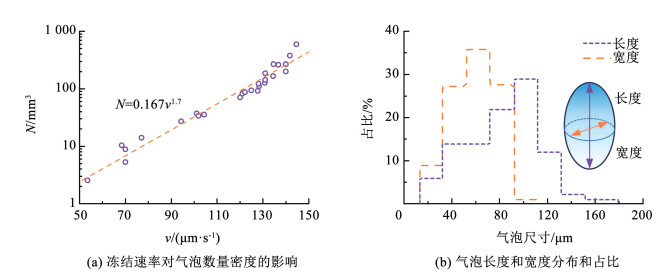图 8 冰中受陷气泡的数量密度和分布^[47] Fig. 8 Quantity density and distribution of trapped air bubbles in ice^[47]


冻结锋面的移动会提高气体体积分数，而气泡的生长会降低气体体积分数。气泡的生长速率和冻结速率的相对大小影响气泡的生长时间和形状变化。当冻结速率较小时，从冰中被挤压出的气体速率小于气泡消耗速率和气体扩散的速率，导致气泡停止生长，而被冻结在冰中。随着气泡的生长，界面前的气体体积分数迅速降低，导致气泡的生长速率逐渐减慢。这时气泡也会被冻结锋面捕获，最终气泡停止生长而被困在冰中。由于没有气泡的消耗，界面前的气体体积分数再次升高，又会引发新的气泡成核，形成新的气泡。这种气体体积分数周期性的交替增加和下降会引起气泡周期性的出现，从而形成气泡层结构。

气泡层的出现是水中空气体积分数周期性变化导致的。如图 9(a)所示，在气泡出现之前，空气在冰中均匀分布，在水中从冻结锋面向远处逐渐降低。当气泡成核后，气泡的生长会降低局部空气体积分数，空气体积分数的降低又会导致气泡生长速率减慢，直到气泡被冻结锋面捕捉而冻结在冰中。冻结锋面的移动又会使冻结锋面前空气体积分数逐渐升高，直到有新的气泡出现。由于冻结锋面是不规则的，气泡成核点的分布相对比较分散，在气泡层内所有的气泡并没有在一条直线上。在一个气泡层中，气泡层内沿冻结方向的最大距离为振幅λ，两气泡层之间的距离为波长L。根据空气在冰与水中的体积分数分布，可得出气泡层中气泡体积和振幅以及波长的关系：

Fig. 9
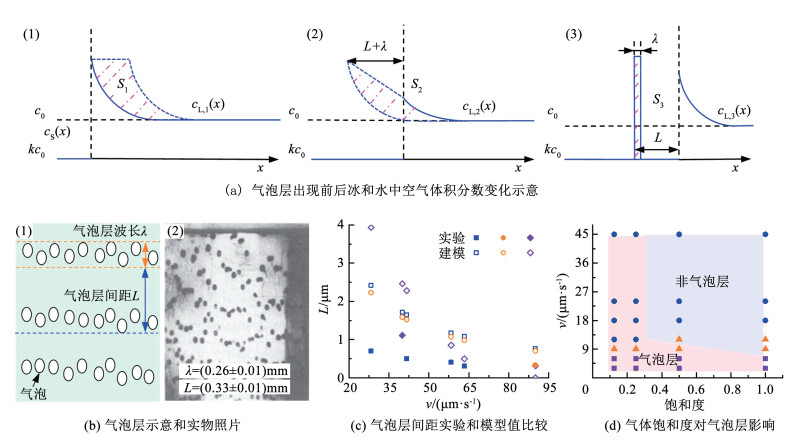图 9 冰中气泡层分布及影响因素^{[49, 55]} Fig. 9 Distribution of bubble layers in ice and influencing factors^{[49, 55]}


$S_1-S_2+(L+\lambda)\left(c_0-k c_0\right)=S_3$ (5)

式中：S₁为气泡生长时间内从冰中挤压出的空气量，S₂为冻结锋面前实际的空气量，S₃为气泡层内气泡中包含的空气量。

冰中气泡层的出现与冻结速率和气体扩散均有关系^[60]。相关学者^{[46, 54-55]}基于此建立了气泡层间距的数理方程和拟合方程，如表 4所示。可以看出，无论是拟合方程还是数理方程，气泡层波长均和冻结速率的倒数呈正相关。存在差异的原因可能与水中溶解气体种类有关，不同的气体在水中溶解度不同，其成核体积分数等存在差异。将文献中实验和建模得到的不同冻结速率下气泡层波长的结果汇总在图 9(c)中。可以看出，随着冻结速率的增加，气泡层波长逐渐减小，大部分气泡层波长的建模结果大于实验值。并且各个模型之间的结果也存在较大的差异。随着冻结速率的增加，模型结果逐渐向实验值靠近。出现这种现象的原因可能是冻结速率增加，冰中受陷气泡数量也会增加，导致气泡层波长逐渐减小。因此，实验结果与模型计算结果差别较小。两个数理模型分别从冰中气体体积分数分布和水中气体体积分数分布独立推导得到气泡层波长，但是计算结果偏差不大。

表 4
表 4 冰中受陷气泡层波长方程表达式 Tab. 4 Expression of wavelength equation for trapped bubble layer in ice 序号 作者 研究方法 方程表达式

1 Bari等^[53] 实验研究 $L=18.14-9.79 \log v$

2 Geguzin等^[54] 理论分析 $L=D / k v \ln \left\{(1-k) /\left[1-k\left(1-c_{1, \mathrm{c}} / c_{1, 0}\right)\right]\right\}$

3 Lipp等^[46] 理论分析 $L=D / k v(1-k) \ln \left\{\left[1-k\left(c_{1, \mathrm{c}} / c_{1, 0}\right)\right] /(1-k)\right\}$



表 4 冰中受陷气泡层波长方程表达式 Tab. 4 Expression of wavelength equation for trapped bubble layer in ice


此外，Murakami等^[55]发现气泡层的出现与冻结速率和水中溶解CO₂饱和度均有关系。如图 9(d)所示，当冻结速率大于9 μm/s且饱和度大于0.5时，冰中不会出现气泡层。造成这种现象的原因可能是CO₂在水中溶解度大，冻结过程中会不断有气泡成核，导致有大量的气泡出现，因此，气泡之间的周期逐渐变小，直到相邻两个气泡层间不出现透明冰。

2.3 受陷气泡的稳定性研究发现，当温度梯度作用在气泡冰上时，冰中气泡通常会缓慢地向温度较高的一侧迁移。这种运动是由气泡靠近温暖面一侧的冰升华和随后在冷壁面一侧的凝华导致^[65]。迁移速率受温度梯度和气泡形状的影响。假设在距离气泡很远的地方存在线性温度梯度，则气泡的迁移理论速率一般形式为^[66]

$\frac{1}{v_{\mathrm{b}}}=(1-A) \frac{\rho \lambda}{K}+A \frac{\rho}{D C}$ (6)

式中：A为与气泡形状有关的无量纲因子，ρ为密度，K为导热系数，λ为冰升华潜热，C为饱和空气中水蒸气体积分数随温度的变化速率，D为气体扩散常数。上述等式右边有两项，其中，ρλ/K与提供热量使温暖侧融化并带走冷侧热量使水蒸气凝华的速率有关，ρ/DC与蒸汽在气泡中扩散的速率有关。这表明影响气泡迁移速率的因素主要是在气泡和冰界面上的热量传递速率和水蒸气在气泡内部的扩散速率。

冰中存在蛋状和针状两种类型的气泡，不同形状气泡的A是不同的。对于旋转对称轴平行于温度梯度的蛋状气泡^[67]

$A=\zeta\left[\left(1-\zeta^2\right) \operatorname{coth}^{-1} \zeta+\zeta\right]$ (7)

式中：ζ²=a²/(a²-b²)，a为长半轴长，b为短半轴长。

对于旋转对称轴平行于温度梯度的针状气泡

$A=\frac{m}{m+n}$ (8)

式中m和n分别为平行于温度梯度和垂直于温度梯度的半轴长。

因此，蛋状气泡迁移速率为

$\frac{1}{v_{\mathrm{b}}}=\frac{1 \rho \lambda}{3 K}+\frac{2 \rho}{3} \frac{\rho}{D C}$ (9)

针状气泡迁移速率为

$\frac{1}{v_{\mathrm{b}}}=\frac{1 \rho \lambda}{2}+\frac{1}{2} \frac{\rho}{D C}$ (10)

为验证方程的准确性和探究影响受陷气泡迁移速率的因素，将常压下不同类型气泡的迁移速率实验值和数理模型计算结果进行了比较。如图 10(a)所示，随着气泡温度的升高，两种类型气泡的迁移速率呈逐渐增加趋势。无论是实验值还是数理模型计算值，针状气泡的迁移速率均大于蛋状气泡的迁移速率。造成这种差异的原因可能是随着气泡的迁移，气泡被逐渐拉长，即a/b和m/n逐渐增加。A的降低使气泡中扩散的影响减小，而传导的影响增加。此外，针状气泡较长导致两侧的温差较大，这也加速了针状气泡的迁移速率。

Fig. 10
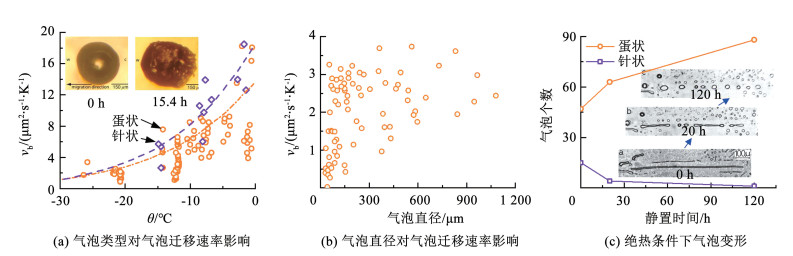图 10 冰中受陷气泡温差和绝热条件下稳定性分析^[67-68] Fig. 10 Stability analysis of trapped air bubbles in ice under temperature difference and adiabatic conditions^[67-68]


除温度和形状对迁移速率有影响外，气泡尺寸也会对气泡的迁移速率产生影响。图 10(b)展示了实验室制备的淡水受陷气泡和极地冰芯中的挤压气泡迁移速率随气泡直径的变化趋势。可以看出，随着气泡直径的增加，气泡迁移速率呈现逐渐增加的趋势。但同一气泡直径下，气泡迁移速率存在很大的差异，这种差异也会随着气泡直径的增加而减小。在较大的气泡直径下，气泡的迁移速率差别较小。造成这种现象的原因可能是有来自实验室内冻结得到的常压受陷气泡和极地深层冰芯中的高压挤压气泡，这两种气泡的形状和内部压力存在差异。气泡内部的压力对迁移速率有很大的影响，随着压力的增加，气泡内空气分子增加，这将阻碍水蒸气的扩散。另一方面，尺寸较小的气泡形状多变，也会影响迁移速率。此外，当气泡冰处于绝热环境中时，冰中的气泡也会发生变化。如图 10(c)所示，气泡冰被置于-10 ℃的煤油中进行绝热保存，分别再静置0、20、120 h后观察气泡的形态。尽管气泡的位置没有发生变化，但其形状发生显著的变化^[57]。蛋状气泡会向球状气泡转变，针状气泡会分裂成数个蛋状气泡而后又转变为球状气泡。进一步的气泡数量统计发现，随着静置时间的增加，气泡数量呈现增加的趋势。气泡数量的增加一方面源自针状气泡的分裂、收缩、变形成为蛋状气泡，另一方面可能是预先存在冰晶之间的气体分子扩散到小气泡中，导致气泡体积增加，变成了可视化的大气泡^[69]。冰晶间的空气分子向气泡内迁移的原因可能和奥斯瓦尔德熟化有关^[70]。当大部分空气分子从冰中析出形成气泡后，存在于冰晶间的空气分子会在界面能的推动下向气泡中转移。此外，当冰晶中的空气分子迁移后，冰晶彼此之间的接触导致冰中微尺度缝隙减少，这将提高冰的透明度。120 h后的冰明显比0时刻的冰有更高的透明度也验证了该解释。

进一步分析发现造成气泡在绝热环境中分裂变质的原因还可能与吉布斯-汤姆孙效应有关^[71-72]。在大尺度下，固体的熔点是固定不变的，而当尺寸减小到微纳尺度时，随着界面曲率的增加，固体的熔点将下降。因此，即使在-10 ℃的绝热环境中，气固边界的冰也可能会因为熔点降低而发生融化, 这也很好地解释了针状气泡会分裂成蛋状气泡。在表面张力作用下，气泡会倾向变成球形。此外，极地冰芯中的挤压气泡在超过空气-水合物解离压力下将转化为块状的空气-水合物晶体^[73]。

3 受陷气泡对冻结过程影响 3.1 受陷气泡对冰成核影响受陷气泡是冻结锋面前的气体体积分数达到临界值时出现在冰中的空气泡，其生长过程也受到冻结速率的影响，受陷气泡的出现和生长又对冻结过程产生影响。冰中受陷气泡的大小和数量受溶解在水中气体体积分数的影响。受陷气泡对冰成核和生长过程的影响如图 11(a)所示。沸水、去离子水和饱和水中气体体积分数逐渐增加，而水滴过冷阶段的时间逐渐减少，这表明水中溶解气体的存在可能会促进水滴成核。在冻结阶段，饱和水冻结时的温度降低得最快，这表明受陷气泡的出现可能也会促进冰的成核。在冻结过程中预先存在水中的气泡对成核过程也会有影响。如图 11(b)所示，在相同的超声条件下，对比3种不同气体体积分数的水成核时间也可以发现，预先存在的气泡有助于超声波引发的成核。此外，采用对格子玻尔兹曼-相场法研究单个气泡对海水冷冻结晶的影响^[74]。发现气泡的存在能有效促进冰晶生长，并将结晶速率提高6.78%，这种促进效果随气泡半径的增加而增强。

Fig. 11
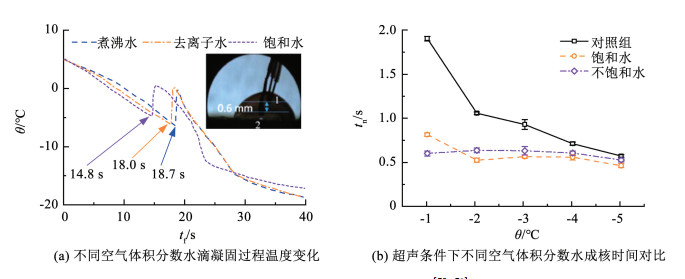图 11 冰中受陷气泡对冰成核影响^[75-76] Fig. 11 Effect of trapped air bubbles on ice nucleation^[75-76]


3.2 受陷气泡对冰晶生长影响冻结过程中溶解在水中的气体分子被冰排挤，导致气体在冻结锋面处聚集^[77]。气泡与冻结锋面的相互作用多数情况下会降低多晶材料中的晶粒生长率。因此，研究多晶冰中气泡对晶粒生长和迁移的影响，也能更好地理解冰晶演化过程。Frost等^[78]通过重结晶法获得了多晶样品，并根据是否含有可视化的气泡将其分为基本上无可视化气泡冰ZS和不可忽视气泡的冰ZC。将冰样在-27~-2 ℃的环境中静置4 000 h。通过研究ZS的冰晶直径和时间关系发现，在几百个小时后，冰晶生长速率出现了急剧的下降，因此，将ZS又分为ZS1和ZS2两种状态。每种状态的冰晶生长均可以用以下方程描述：

$D^2=D_0^2+4 k t$ (11)

式中：D为t时刻的冰晶直径；D₀为初始时刻冰晶直径；k为冰晶生长速率，k=dR²/dt，R=D/2。

不同温度下3种状态的冰晶生长速率如表 5所示^[79]。可以看出，随着温度的降低，冰晶生长速率均逐渐减慢，但是无气泡的冰晶生长速率始终大于有气泡的冰晶生长速率。这表明晶界之间的气泡阻碍了晶界的迁移，导致冰晶的生长速率降低。

表 5
表 5 不同状态冰晶生长速率随温度变化^[81-82] Tab. 5 Variation of ice crystal growth rate with temperature in different states^[81-82] 序号 温度/℃ 生长速率/(mm²·h^-1)

ZS1 ZS2 ZC

1 -2 4.9 1.70 0.15

2 -6 4.0 0.40 0.04

3 -10 1.4 0.16 0.01

4 -13 1.4 0.06 —

5 -20 0.7 0.04 0.01

6 -27 0.5 0.04 —



表 5 不同状态冰晶生长速率随温度变化^[81-82] Tab. 5 Variation of ice crystal growth rate with temperature in different states^[81-82]


采用多晶冰制备方法得到的冰中依然含有不可视化的气泡。为阐明第二相对冰正常晶粒生长影响，Azuma等^[80]在高静水压和低温条件下利用相变方法生产了无气泡细粒多晶冰。将采用该方法制备无气泡多晶冰和含有气泡多晶冰，分别统计了静置前后的晶粒分布情况。如图 12(a)和12(b)所示，静置前的无气泡冰和含气泡冰中的冰晶直径主要分布在0.15、0.60 mm附近，平均值分别为0.31、0.87 mm。经过840 h静置后，冰晶直径主要分布在1.1、0.7 mm附近，平均值分别为2.54、1.32 mm。

Fig. 12
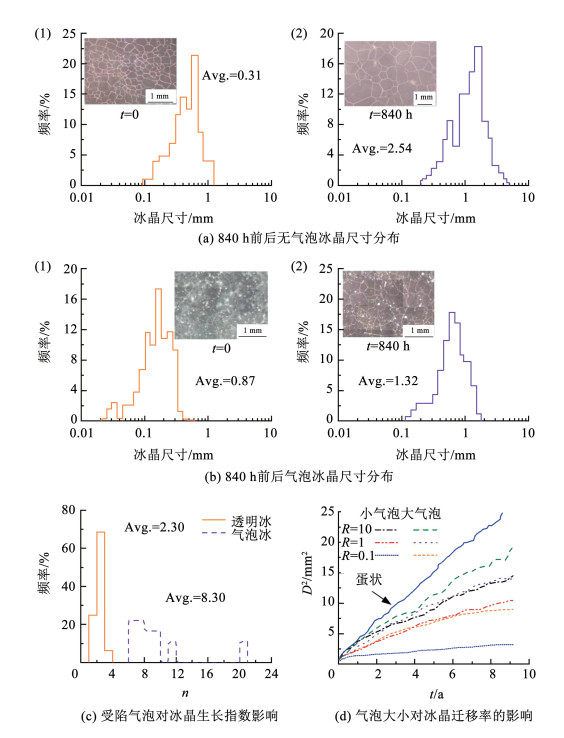图 12 冰中受陷气泡对冰晶生长和迁移的影响^{[82, 84]} Fig. 12 Effect of trapped air bubbles on ice crystal growth and migration^{[82, 84]}


晶粒生长曲线的一般形式为^[80]

$D^n=D_0^n+4 k t$ (12)

式中：n为冰晶生长指数，取决于生长机制，在理想的正常晶粒生长中理论值为2^[83]；k假定为温度的相关常数。利用方程(12)，通过改变t并使用最小二乘法获得与数据的最佳拟合，从而根据晶粒尺寸数据与时间的关系确定n和k。如图 12(c)所示，有气泡的冰样品n值分散在5.3~14.5，平均值为8.3，而无气泡冰的n值为2.3，非常接近正常晶粒生长的理论值。有气泡的冰样品的n值较大，反映了气泡对晶粒生长的阻碍作用。此外，Roessiger等^[84]采用数值模拟的方法研究了气泡对不同迁移速率下冰晶生长的影响。如图 12(d)所示，无气泡冰的冰晶生长速率与时间呈线性增加，而气泡冰中冰晶的增加速率较小，随气泡的尺寸减小，冰晶生长速率减慢。

3.3 受陷气泡对冻结水滴尖角影响未冻结的水滴在表面张力下近似为球形，而冻结后的水滴呈现椭球形。在冷冻结束时，顶部还会形成一个尖角，尖角对气泡内物质很敏感，冻结水滴尖端角度与杂质体积分数有关^[85]。如图 13(a)所示，对不同含气量水滴冻结后的尖端角度进行测量发现，沸水为(137.4±3.0)°、气体体积分数为3%的去离子水为(129.5±4.1)°、气体体积分数为4.99%的气泡水为(120.8±1.3)°、气体体积分数为14.66%的气泡水为(80.3±9.1)°^[75]。10次冻结水滴尖角的平均值为(63.7±1.3)°，略小于理论计算值的65°^[86]。这是因为水滴中大部分的气泡并不会对尖角的形成有显著影响，只有在冻结后期出现的气泡才会对尖角的形成有影响。Marin等^[87]提出了一种基于密度变化的液滴形状几何模型。基于理论分析以冻结两侧为终点的水平线将未冻结部分划分为凹形体积部分V_d和凸形体积部分V_u。如图 13(b)所示，根据球形几何形状^[88]

Fig. 13
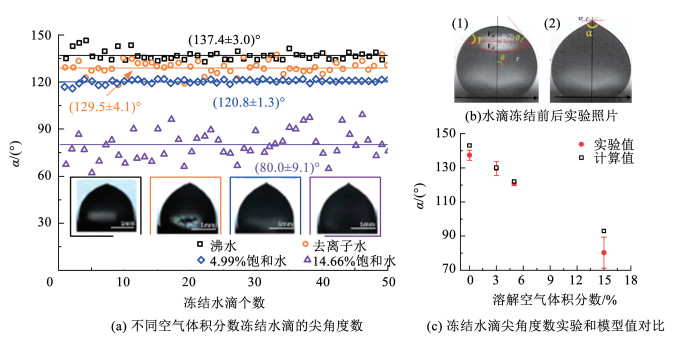图 13 冻结水滴的几何形状和尖角的变化趋势^{[86, 88]} Fig. 13 Trends in geometry and sharp angles of frozen water droplets^{[86, 88]}


$V_{\mathrm{d}}=R^3 f(\gamma-\theta)$ (13)

$V_{\mathrm{u}}=R^3 f(\theta)$ (14)

$f(\theta)=\frac{\pi}{3} \frac{2-3 \cos \theta+\cos ^3 \theta}{\sin ^3 \theta}$ (15)

式中：R为水平边界半径，θ为液体界面与水平面之间的夹角，γ为固液界面和气固界面之间的夹角。

忽略冻结过程中水滴蒸发后的质量守恒方程为

$\frac{\mathrm{d}\left(V_{\mathrm{w}}+\mu V_{\mathrm{i}}\right)}{\mathrm{d} t}=0$ (16)

$V_{\mathrm{w}}=V_{\mathrm{d}}+V_{\mathrm{u}}$ (17)

${V_{\rm{s}}} = - {V_{\rm{d}}} + \int\limits_0^z {\pi {R^2}{\rm{d}}z} $ (18)

式中：V_w和V_i分别为水和冰体积，μ为其密度比。

基于准稳态传热方程，质量守恒方程可以写为

$\frac{\mathrm{d}\left(V_{\mathrm{w}}+\mu V_{\mathrm{i}}\right)}{\mathrm{d} z}=0$ (19)

当R接近0时，接触角θ满足

$\mu=\frac{f(\gamma-\theta)+f(\theta)}{f(\gamma-\theta)+\pi \tan \theta / 3}$ (20)

联立式(13)~(18)，得到不同空气体积分数下冻结水滴的尖角，如图 13(c)所示。气泡的存在影响冻结液滴的形态，其角度随着水中溶解气体体积分数的增加而减小。

4 受陷气泡对冰宏观物理特性影响 4.1 受陷气泡对冰传热特性影响冰中受陷气泡不仅对冻结过程有影响，对冰的物理特性也会产生影响。气泡冰的导热系数与其结构、成分、气泡体积分数、密度和气体成分等都有密切关系，气泡的形状和直径也会对其产生影响^[89]。对于冰等均匀材料，组成成分和结构对导热系数有较强的影响。目前也有混合定量模型、经验模型和理论模型等对导热系数进行计算，但是没有任何一种单一的模型可以计算所有类型的结构^[90]。对于简单的物理结构材料，可以使用基本的物理模型进行建模计算，如表 6所示。这3个模型计算的导热系数均和各项体积分数φ和导热系数k有关，但由于计算方法不同，适用范围也不同。EMT模型适用于两种相互分散的相，ME1模型适用于均匀各向同性多孔材料，而CC模型适用于连续分散的相。对于一些物理结构复杂的材料，这些基本模型可能并不适用。通过对简单模型进行经验修正^[91]和对已知微观结构和复合材料进行有限差分和有限元的数值计算^[92]是常用的计算多孔材料导热系数方法。

表 6
表 6 双组分两相材料导热系数的3种基本结构模型 Tab. 6 Three basic structural models for thermal conductivity of two-component two-phase materials 序号 作者 模型 方程

1 Landauer^[93] EMT $\varphi_1\left(k_1-k\right) /\left(\varphi_1+2 k\right)+\left(\varphi_2 k_2-k\right) /\left(\varphi_2+2 k\right)=0$

2 Maxwell^[94] ME1 $k=\left(2 \varphi_1 k_1^2+\varphi_1 k_1 k_2+3 \varphi_2 k_1 k_2\right) /\left(2 \varphi_1 k_1+\varphi_1 k_2+3 \varphi_2 k_1\right)$

3 Wang等^[95] CC $\varphi_1\left(2 k_1^2-k_1 k-k^2\right) / k_1+\varphi_2\left(2 k_2^2-k_2 k-k^2\right) / k_2=0$



表 6 双组分两相材料导热系数的3种基本结构模型 Tab. 6 Three basic structural models for thermal conductivity of two-component two-phase materials


气泡冰中两种不同形状气泡的组合使冰的内部结构更加复杂多变^[96]，这使得冰中气泡对冰热力学性能影响的研究更加困难。焓-孔隙率法可以用来研究气泡体积分数对融冰过程和传热的影响。如图 14(a)所示，加热器工作15 min后不同孔隙率冰的融化区域存在显著差异，融化体积和融化高度随着气泡体积分数的增加而增加。从图 14(b)也可以看出，随着气泡体积分数的增加，冰开始融化的时间越滞后。气泡体积分数为57%的冰比0%的冰滞后了约50%，相同时间内的融冰高度也少了36.81%。此外，通过气体和淡水冰组成的多孔介质模型估算其比热容和潜热的方式也可以用来评估气泡对传热的影响。受陷气泡在水滴冻结过程中起热阻作用，将阻碍冻结过程^[97]。在太阳光对气泡冰的辐射传热过程中，一般采用在冰的吸收系数前加上修正因子的方法来考虑气泡对冰吸收辐射的影响^[98]。并且，气泡对辐射条件下冰的传热特性的影响与波长有关^[99]。如图 14(c)和14(d)所示，根据Mie理论计算发现，随着波长和气泡直径的增加，散射系数几乎呈线性减小。而随着波长的增加，散射系数和吸收系数的比值随气泡体积分数的增加而减小，该比值还和波长有关。在紫外区，比值几乎保持不变，而在可见光和红外区，比值呈现逐渐减小的趋势。数值模拟气泡冰的传热特性结果也表明冰的融化速率随冰中气泡体积分数的增加而增加。在CO₂激光融化气泡冰时，气泡冰体积融化速率随功率增大而增加^[100]。

Fig. 14
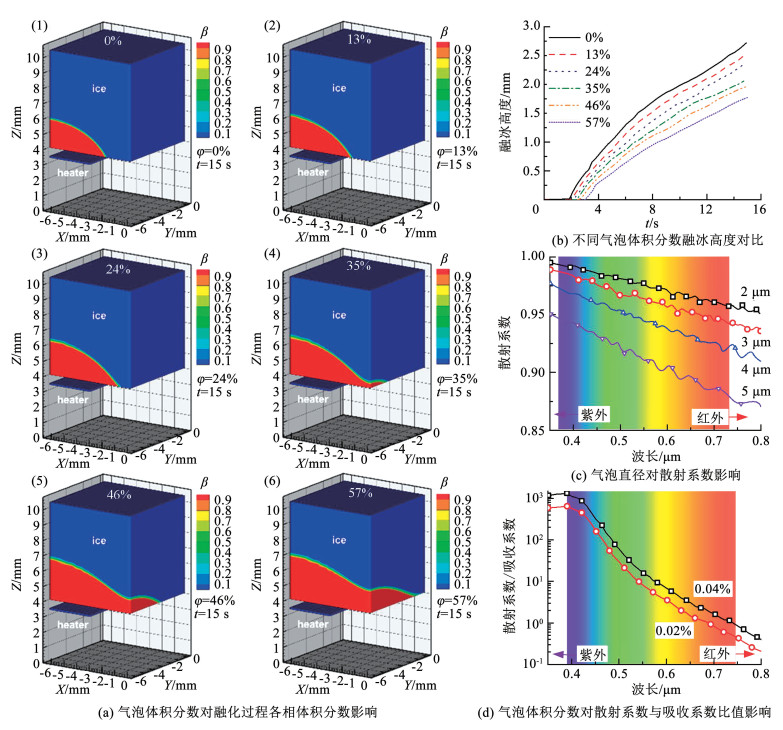图 14 冰中气泡体积分数对冰传热特性影响^[101-103] Fig. 14 Effect of bubble volume fraction on ice heat transfer characteristics^[101-103]


4.2 受陷气泡对冰力学特性影响典型冰体力学特性测试类型和指标如表 7所示，包括弹性、塑性、强度、硬度和韧性等，这些力学特性又与温度、应变率、测试体积和冰颗粒大小有关系。对透明冰来说，冰的拉伸和压缩强度都随着温度的降低而增加^[104-105]，并且温度对冰压缩强度的影响大于对拉伸强度的影响。抗压强度对应变率敏感，而抗拉强度对应变率不敏感。拉伸应力-应变曲线在低应变速率下表现出延性行为，但在中高应变速率下表现出脆性行为。压缩应力-应变曲线在低应变率和中等应变率下表现出延性行为，但在高应变率下表现出脆性行为^[106-107]。这种冰体弹塑特性随应变率变化的现象称为应变率效应，其与位错和晶界滑移一致变形机制等在冰的受力变形过程中起作用^[108]。冰中受陷气泡的存在也会对冰的力学性能产生影响。

表 7
表 7 典型冰体力学特性测试类型和指标^[109-110] Tab. 7 Typical ice mechanical properties test types and indicators^[109-110] 序号 类型 参数 静态/动态 单位 方法 序号 类型 参数 静态/动态 单位 方法

1 弹性 正弹性模量 动态 MPa 计算 11 强度 抗扭强度 动态 MPa 实验

2 弹性 切变弹性模量 动态 MPa 计算 12 强度 屈服强度 动态 MPa 实验

3 弹性 比例极限 动态 MPa 计算 13 强度 持久强度 动态 MPa 实验

4 弹性 弹性极限 动态 MPa 计算 14 强度 蠕变强度 动态 N·mm² 实验

5 塑性 伸长率 动态 % 计算 15 硬度 洛氏硬度 静态 — 实验

6 塑性 断面收缩率 动态 % 计算 16 硬度 维氏硬度 静态 MPa 实验

7 强度 抗拉强度 动态 MPa 实验 17 硬度 肖氏硬度 静态 — 实验

8 强度 抗弯强度 动态 MPa 实验 18 韧性 冲击韧性 动态 J/cm², J 计算

9 强度 抗压强度 动态 MPa 实验 19 韧性 冲击吸收功 动态 J 计算

10 强度 抗剪强度 动态 MPa 实验 20 韧性 小能量多次冲击力 动态 N 实验



表 7 典型冰体力学特性测试类型和指标^[109-110] Tab. 7 Typical ice mechanical properties test types and indicators^[109-110]


力学测试环节的冰样尺寸尚无统一标准，据1975年国际水利学会(IAHR)“冰问题委员会”提出的倾向性意见，学者普遍在冰抗压实验中采用直径7~10 cm、高度为直径2.5倍左右的圆柱体试件，冰的抗弯强度测试冰样满足长度为厚度的7~10倍、宽度采用厚度的1~2倍。2007—2023年间，既有文献中冰体力学特性测试类型及冰样尺寸对比分析见表 8。抗压强度冰试样一般采用长方体或圆柱体进行^[111-112]，冰的抗压强度与冰的类型、环境温度及加载速率等条件密切相关。既有研究说明，因盐分导致海冰微观结构晶体界面增加，从而造成海冰抗压强度普遍低于淡水冰抗压强度。因冰体光滑难以两端固定，无法直接获得冰体抗拉强度，多采用巴西圆盘的方式获得压缩强度后间接计算冰体抗拉强度，因此, 冰体抗拉强度值可能存在累计误差。与其他固体材料相比，冰的保存和实验测试均需低温环境，进一步增加了冰体力学特性测试的难度。

表 8
表 8 既有文献中冰体力学特性测试类型及冰样尺寸对比分析汇总 Tab. 8 Summary of comparative analysis of ice mechanical properties testing types and ice sample size in existing literature 序号 年份 作者 测量参数 数值/MPa 冰样尺寸/cm 冰类型

1 2007 Moslet^[114] 抗压强度 0.30~13.50 7×7×17.5 海冰

2 2007 Iliescu等^[118] 抗压强度 3.00~29.80 15.2×15.2×2.5 淡水冰

3 2009 张丽敏等^[107] 抗压强度 1.85~4.47 7×7×17.5 淡水冰

4 2011 Mohamed等^[119] 抗拉强度 1.00~1.45 ?5×2.5 淡水冰

5 2011 张大长等^[120] 抗压强度 1.46~2.46 ?5×7; ?6×18 淡水冰

6 2011 李志军等^[121] 抗压强度 0.60~3.10 7×7×17.5 海冰

7 2016 张红彪^[122] 抗拉强度 0.30~0.67 ?7×3.5 淡水冰

8 2017 肖赞^[123] 抗拉强度 0.29~0.75 ?7×2.5 淡水冰

9 2018 韩红卫等^[124] 三轴抗压强度 5.00~5.92 ?10×27 淡水冰

10 2018 单仁亮等^[125] 三轴抗压强度 4.42~11.94 ?5×10; ?4×8 淡水冰

11 2019 欧阳群安^[126] 抗压强度 1.54~4.86 5×5×5 淡水冰

12 2020 Deng等^[127] 抗压强度 4.32~8.55 ?2.5×5 淡水冰

13 2021 薛世超等^[128] 抗压强度 3.00 ?1.4×0.7 淡水冰

14 2021 孟丁丁等^[129] 抗弯强度 0.31~1.30 7×5×20 海冰

15 2021 Lou等^[130] 抗拉强度 0.35~1.25 ?7×3.5 淡水冰

16 2022 王宝生^[131] 抗压强度 6.35~20.33 ?6.18×12.5 淡水冰

17 2023 马玉贤等^[132] 抗弯强度 0.60~1.52 7×7×65 海冰

18 2023 解北京等^[133] 抗压强度 3.98~16.22 ?5×5 淡水冰



表 8 既有文献中冰体力学特性测试类型及冰样尺寸对比分析汇总 Tab. 8 Summary of comparative analysis of ice mechanical properties testing types and ice sample size in existing literature


冰体力学特性测试实验装置可按力加载方向与水平面的关系简单分为立式和卧式；按压力驱动方式也可分为液压驱动式和伺服电机驱动式^[113-114]，图 15为既有文献中3种典型的冰体力学特性测试实验装置。当冰试样自重对其力学强度影响可忽略不计时，应用立式与卧式力学特性测试实验装置进行力学强度测试时，结果无显著区别。在进行抗弯强度测试时，立式实验台冰样比卧式实验台冰样更易固定。此外，液压驱动装置可以在很短的时间内达到较大的压力值，泄压装置也可以很好地保证实验的安全，但其控制精度不如伺服电机高。而伺服电机的最大输出荷载和安全性均低于液压驱动的对应值^[115]。通过伺服电机控制泵油量和位移速率从而将两种驱动方式优点结合起来的数控伺服液压系统，可使冰力学特性测试实验更加精准和安全^[116]。当测试时间较长时，原本可忽视的冰体散热会导致冰温度变化，继而影响力学测试结果，因此，开发了一种搭配低温环境室的力学测试平台^[117]。

Fig. 15
图 15 既有文献中的3种典型冰体力学特性测试实验装置^{[113-114, 117]} Fig. 15 Three typical experimental devices for testing mechanical properties of ice in existing literature^{[113-114, 117]}


与透明冰类似，气泡冰的抗压强度对压缩方向也敏感。如图 16所示，随着冰中气泡体积分数的增加，其垂直与冻结方向的抗压强度逐渐减小，而平行于冻结方向的抗压强度变化不大^[134]。含有气泡和卤水的海冰抗压强度与含气泡淡水冰的抗压强度有类似的变化趋势。如图 16(c)所示，随着海冰中气泡和卤水体积占比的增加，平行和垂直抗压强度均逐渐减小，且垂直抗压强度的减小速率大于平行抗压强度的减小速率^[114]。气泡体积分数对海冰杨氏模量的影响如图 16(c)所示。尽管同一气泡体积分数下，海冰杨氏模量的差异也较大，但是随着气泡体积分数的增加，杨氏模量逐渐减小，并且不同气泡体积分数冰的杨氏模量之间的差值也逐渐减小。

Fig. 16
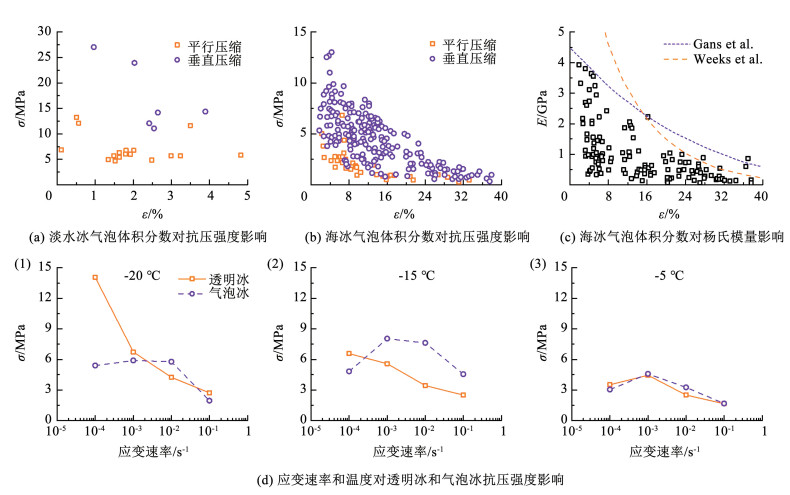图 16 冰中受陷气泡对冰力学特性影响^{[133-134, 136]} Fig. 16 Effect of trapped air bubbles on ice mechanical properties^{[133-134, 136]}


Gans等^[135]对多海冰进行了有限元建模，得到了一个拟合关系式：

$E=E_0 \mathrm{e}^{-\alpha \varepsilon}$ (21)

式中：E₀为不含气泡的杨氏模量，ε为气泡体积分数，α为经验系数。

Moslet ^[114]给出了一个考虑气泡的淡水冰和海水冰杨氏模量关系拟合式

$E=E_0(1-\varepsilon)^4$ (22)

通过图 16(c)对两个拟合关系式的对比发现，在气泡体积分数小于16%时，Gans的拟合式更接近实验值，在气泡体积分数大于16%时，Moslet的拟合式更接近实验值。

在不同的应变速率下，气泡冰和透明冰有不同的破坏形式。如图 16(d)所示，在不同温度下，由于在气泡位置施加应力作用，气泡周围出现局部塑性形变，最终导致气泡冰在较高的应变速率下均表现为塑性变形^[136]。而透明冰一直表现为韧性，随着应变速率的减小，其抗压强度逐渐增加。此外，随着温度的升高，两种冰的抗压强度均逐渐减小。

5 结论与展望受陷气泡是出现在微观水冻结过程中并对冻结后宏观冰整体物理特性产生重要影响的物质，也是研究微观水滴冻结与宏观结冰/防除冰的一个纽带。目前，对冰中受陷气泡形成过程、生长阶段、分布特性和影响因素等进行了大量的研究，受陷气泡对冰成核、生长和冻结水滴尖角的影响也有相关报道。此外，有学者研究了受陷气泡对冻结后冰整体热学和力学特性影响。但有关受陷气泡形成的相关机制和特性等还需要进行进一步探究，例如：

1) 当冻结锋面前气体体积分数达到临界成核体积分数时，气泡会发生成核。目前，很多学者已经对冻结锋面前的气体体积分数分布模型进行了研究，关于气泡成核的方式还存在争议。尽管众多学者都认为气泡成核方式为均相成核，但也有学者指出冻结锋面前的气体体积分数和压力并不满足均相成核条件。此外，冻结锋面上气泡主要受到浮力和黏附力作用。当这两个力大小相等时，气泡附着在冻结锋面上。而当浮力大于黏附力时，气泡会在浮力作用下从界面上脱离。但是，理论计算发现气泡较难发生脱离，而实际上竖直方向上的冻结过程中经常会出现气泡脱离现象。对于该现象目前主要有界面微流动和气泡边界上存在水膜两种解释，但都缺乏理论和实验现象的支持。为更好地理解气泡的形成过程，应该对气泡成核机制和受力情况进行详细的研究。

2) 气泡形状和分布会影响冻结过程和冻结后冰体物理特性。根据受陷气泡长短轴比值是否大于5，可以将其形状分为蛋状和针状两种，且它们在冰中分布与冻结速率、水中溶解气体体积分数和环境压力都有关。但关于这两种形状的形成原因尚不明晰，并且对气泡生长过程的数理建模和数值模拟缺乏研究。此外，相邻气泡在生长过程中可能会出现抑制生长和融合的现象，但关于相邻气泡间相互作用的研究较少。为便于对冰中气泡类型进行预测和控制，有必要进一步研究两种气泡形成机制和相邻气泡生长过程中相互作用机制。

3) 冰中存在受陷气泡会降低冰透明度、减小冰导热系数、削弱力学强度等。但这些研究结果多以气泡体积分数为因变量，而忽视了冰中气泡形状和分布的影响。另一方面，气泡对冰声学、光学、热、力、电和磁学等的影响缺乏系统研究。为更好地对冰的物理特性进行控制和预测，有必要进一步研究气泡类型与分布对冰物理特性影响。此外，对受陷气泡在温差作用下和绝热环境中的变性研究都是对其形状和位置变化的研究，而不同气体分子在水中和冰中的扩散系数不同，分子大小也存在差异，这会导致气泡中气体成分在气泡变性过程中发生变化。因此，为研究气泡变性机制，有必要对气泡中气体成分变化进行探究。

综上，受陷气泡是在冻结过程中由于气体在冰和水中溶解度差异较大而出现在冰中的气泡，并且对冻结过程和冻结后冰整体物理特性有显著影响。深入了解受陷气泡形成过程中的基础问题对加深冻结过程的认识、提高和拓宽冰的应用领域，对冰的冻结过程和物理特性进行预测控制，以及优化和开发防除冰技术都有意义。本文综述了国内外有关受陷气泡的研究文献，归纳受陷气泡在冰中成核机制、生长过程和分布特性等基础问题的研究现状，汇总受陷气泡对冰晶成核和生长的影响规律，梳理气泡对冰热学和力学等宏观物理特性的影响，以及对未来可能开展的研究方向进行展望，以期为相关研究学者提供参考和借鉴。


参考文献
[1] 姚杨, 姜益强, 马最良. 空气源热泵冷热水机组空气侧换热器结霜规律[J]. 哈尔滨工业大学学报, 2002, 34(5): 660.
YAO Yang, JIANG Yiqiang, MA Zuiliang. Frosting for airside heat exchanger of the water chiller/heater of air source heat pump[J]. Journal of Harbin Institute of Technology, 2002, 34(5): 660. DOI:10.3321/j.issn:0367-6234.2002.05.019


[2] LIU Shengchun, LI Haiong, SONG Mengjie, et al. Impacts on the solidification of water on plate surface for cold energy storage using ice slurry[J]. Applied Energy, 2018, 227: 284. DOI:10.1016/j.apenergy.2017.08.012


[3] DING Liang, CHANG Shinan, YI Xian, et al. Coupled thermo-mechanical analysis of stresses generated in impact ice during in-flight de-icing[J]. Applied Thermal Engineering, 2020, 181: 115681. DOI:10.1016/j.applthermaleng.2020.115681


[4] 姜宝成, 李炳熙, 王全福, 等. 内融冰式蓄冰管融冰过程中自然对流的影响[J]. 哈尔滨工业大学学报, 2006, 38(5): 786.
JIANG Baocheng, LI Bingxi, WANG Quanfu, et al. Effect of natural convection on the internal-melt ice-on tube with melting[J]. Journal of Harbin Institute of Technology, 2006, 38(5): 786. DOI:10.3321/j.issn:0367-6234.2006.05.034


[5] 邵苛苛, 宋孟杰, 江正勇, 等. 水平方向上冰中受陷气泡形成和分布实验研究[J]. 化工学报, 2023, 74(增刊1): 161.
SHAO Keke, SONG Mengjie, JIANG Zhengyong, et al. Experimental study on the formation and distribution of trapped air bubbles in horizotal ice slice[J]. CIESC Journal, 2023, 74(Sup.1): 161. DOI:10.11949/0438-1157.20221643


[6] 杨自强, 陆亚俊. 冷风机结霜特性的实验研究[J]. 哈尔滨建筑大学学报, 1997, 30(1): 67.
YANG Ziqiang, LU Yajun. Experimental study on frost formation characteristics of air cooler[J]. Journal of Harbin University of Civil Engineering, 1997, 30(1): 67.


[7] 程卓明, 于绍飞, 胡记超, 等. 大容量风冷冰箱结霜化霜实验研究[J]. 家电科技, 2009(3): 52.
CHENG Zhuoming, YU Shaofei, HU Jichao, et al. Experimental study on frost and defrost in large-capacity air-cooled refrigerators[J]. Journal of Appliance Science & Technology, 2009(3): 52. DOI:10.19784/j.cnki.issn1672-0172.2009.z1.017


[8] LEI Shangwen, SONG Mengjie, DAI Wei, et al. Experimental study on the effect of surface temperature on the frost characteristics of a vertical cold plate under natural convection[J]. Experimental Thermal and Fluid Science, 2022, 137: 110684. DOI:10.2139/ssrn.4019478


[9] 姚杨, 马最良. 空气源热泵冷热水机组空气侧换热器结霜模型[J]. 哈尔滨工业大学学报, 2003, 35(7): 781.
YAO Yang, MA Zuiliang. Modeling and analyzing of airside heat exchanger under frosting in air source heat pump water chiller/heater[J]. Journal of Harbin Institute of Technology, 2003, 35(7): 781. DOI:10.3321/j.issn:0367-6234.2003.07.004


[10] YU Sirui, SONG Mengjie, GAO Runmiao, et al. A review of icing prediction techniques for four typical surfaces in low-temperature natural environments[J]. Applied Thermal Engineering, 2024, 241: 122418. DOI:10.1016/j.applthermaleng.2024.122418


[11] 雷尚文, 宋孟杰, 张龙, 等. 自然对流下重力对简单冷表面微观动态结霜特性影响的实验研究[J]. 家电科技, 2022(5): 71.
LEI Shangwen, SONG Mengjie, ZHANG Long, et al. An experimental study of gravity effect on the micro and dynamic frost characteristics on simple cold plate surfaces under natural convection[J]. Journal of Appliance Science & Technology, 2022(5): 71. DOI:10.19784/j.cnki.issn1672-0172.2022.05.011


[12] HUANG Lizhen, TIAN Yueyang, SONG Mengjie, et al. An experimental study on edge-affected frosting characteristics on a vertical cold plate at different surface temperatures[J]. Applied Thermal Engineering, 2024, 236: 121538. DOI:10.1016/j.applthermaleng.2023.121538


[13] LSYGONIE C, BRITZ T J, HOFFMAN L C. Impact of freezing and thawing on the quality of meat: review[J]. Meat Science, 2012, 91(2): 93. DOI:10.1016/j.meatsci.2012.01.013


[14] BIRON-SHENTAL T, FISHCH B, HURK R V D, et al. Survival of frozen-thawed human ovarian fetal follicles in long-term organ culture[J]. Fertility & Sterility, 2004, 81(3): 716. DOI:10.1016/j.fertnstert.2003.06.034


[15] 王瑶, 刘全义. 基于CFD的风冷冰箱凝露结冰分析[J]. 家电科技, 2021(增刊1): 156.
WANG Yao, LIU Quanyi. Analysis of condensation and icing of air-cooled refrigerator based on CFD[J]. Journal of Appliance Science & Technology, 2021(Sup.1): 156. DOI:10.19784/j.cnki.issn1672-0172.2020.99.038


[16] LIU Xiaoliang, HUANG Lizhen, ZHANG Xuan, et al. A modeling study on freezing characteristics of sessile and pendant water droplets1on cold plate surfaces[J]. Applied Thermal Engineering, 2024, 236: 121693. DOI:10.1016/j.applthermaleng.2023.121693


[17] 张文英, 常士楠, 蒋斌, 等. 基于VOF方法的大水滴袋状破碎的仿真研究[J]. 空气动力学学报, 2018, 36(4): 605.
ZHANG Wenying, CHANG Shinan, JIANG Bin, et al. Numerical simulation of large droplets in bag breakup regime based on VOF method[J]. Acta Aerodynamica Sinica, 2018, 36(4): 605.


[18] CHENG Tiantian, HE Ren, ZHAN Qinghua, et al. Magnetic particle-based super-hydrophobic coatings with excellent anti-icing and thermoresponsive deicing performance[J]. Journal of Materials Chemistry A, 2015, 43(3): 21637. DOI:10.1039/C5TA05277G


[19] 饶伟, 陆亚俊. 变片距换热器空气源热泵机组结霜特性分析[J]. 哈尔滨工业大学学报, 2007, 39(10): 1596.
RAO Wei, LU Yajun. Characteristic analysis on air source heat pump with variable spacing fin heat exchanger in frosting condition[J]. Journal of Harbin Institute of Technology, 2007, 39(10): 1596. DOI:10.3321/j.issn:0367-6234.2007.10.020


[20] 徐延辉. 制冰机热气除霜对压缩机可靠性影响研究[J]. 家电科技, 2019(1): 60.
XU Yanhui. Research on the impact of hot gas defrosting of ice making machines on compressor reliability[J]. Journal of Appliance Science & Technology, 2019(1): 60. DOI:10.3969/j.issn.1672-0172.2019.01.019


[21] PENG Shuaiqiao, HU Yanxin, HUANG Jin, et al. Surface free energy analysis for stable supercooling of sodium thiosulfate pentahydrate with microcosmic-visualized methods[J]. Solar Energy Materials and Solar Cells, 2020, 208: 110390. DOI:10.1016/j.solmat.2019.110390


[22] Climate Change Institute, University of Marine. https://climatereanalyzer.org/research_tools/monthly_maps/


[23] LU Menglong, SONG Mengjie, PANG Xiaoling, et al. Modeling study on sessile water droplet during freezing with the consideration of gravity, supercooling, and volume expansion effects[J]. International Journal of Multiphase Flow, 2022, 147: 103909. DOI:10.1016/j.ijmultiphaseflow.2021.103909


[24] MA Dongyun, CHANG Shinan, WU Ke, et al. Experimental study on the water film thickness under spray impingement based on planar LIF[J]. International Journal of Multiphase Flow, 2020, 130: 103329. DOI:10.1016/j.ijmultiphaseflow.2020.103329


[25] SONG Mengjie, DANG Chaobin. Review on the measurement and calculation of frost characteristics[J]. International Journal of Heat and Mass Transfer, 2018, 124: 586. DOI:10.1016/j.ijheatmasstransfer.2018.03.094


[26] DANG Qun, SONG Mengjie, ZHANG Xuan, et al. Modelling study on freezing process of water droplet on inclined cold plate surface with droplet dynamic behavior considered[J]. International Journal of Heat and Mass Transfer, 2022, 197: 123327. DOI:10.1016/j.ijheatmasstransfer.2022.123327


[27] ZHANG Xuan, WU Xiaomin, MIN Jingchun. Freezing and melting of a sessile water droplet on a horizontal cold plate[J]. Experimental Thermal and Fluid Science, 2017, 88: 1. DOI:10.1016/j.expthermflusci.2017.05.00


[28] 陈磊, 霍耀楠, 沈剑, 等. 模拟冰箱冷冻室抽屉结冰现象的研究[J]. 家电科技, 2021, Sup.1(增刊1): 188.
CHEN Lei, HUO Yaonan, SHEN Jian, et al. Research on simulating the freezing phenomenon of refrigerator freezer drawers[J]. Journal of Appliance Science & Technology, 2021, Sup.1: 188. DOI:10.19784/j.cnki.issn1672-0172.2021.99.044


[29] CHANG Shinan, DING Liang, SONG Mengjie, et al. Numerical investigation on impingement dynamics and freezing performance of micrometer-sized water droplet on flat dry surface in supercooled environment[J]. International Journal of Multiphase Flow, 2019, 118: 150. DOI:10.1016/j.ijmultiphaseflow.2019.06.011


[30] CHU Fuqiang, ZHANG Xuan, LI Shaokang, et al. Bubble formation in freezing droplets[J]. Physical Review Fluids, 2019, 4(7): 071601(R). DOI:10.1103/PhysRevFluids.4.071601


[31] YOSHIMURA K, INADA T, KOYAMA S. Growth of spherical and cylindrical oxygen bubbles at an ice-water interface[J]. Crystal Growth & Design, 2008, 8(7): 2108. DOI:10.1021/cg070251k


[32] ANTHONY K M W, VAS D A, BROSIUS L, et al. Estimating methane emissions from northern lakes using ice-bubble surveys[J]. Limnology and Oceanography: Methods, 2010, 8: 592. DOI:10.4319/lom.2010.8.0592


[33] FRAIA S H, WEIKUSAT I, AZUMA N. The microstructure of polar ice. Part I: highlights from ice core research[J]. Journal of Structural Geology, 2014, 61: 2. DOI:10.1016/j.jsg.2013.09.010


[34] JIANG Zhengyong, SONG Mengjie, DANG Chaobin, et al. Two mathematical models of flow boiling and flow instability in rectangular expanding microchannel heat exchangers and structure optimization[J]. Applied Thermal Engineering, 2023, 228: 120483. DOI:10.1016/j.applthermaleng.2023.120483


[35] SHAN Minglei, CHEN Bingyan, YAO Cheng, et al. Electric characteristic and cavitation bubble dynamics using underwater pulsed discharge[J]. Plasma Science and Technology, 2019, 21(7): 16.


[36] WALTER K M, ZIMOV S A, CHANTON J P, et al. Methane bubbling from Siberian thaw lakes as a positive feedback to climate warming[J]. Nature, 2006, 443: 71. DOI:10.1038/nature05040


[37] FARIA S H, FREITAG J, KIPFSTUHL S. Polar ice structure and the integrity of ice-core paleoclimate records[J]. Quaternary Science Reviews, 2010, 29(1/2): 338. DOI:10.1016/j.quascirev.2009.10.016


[38] CHO H J, MIZERAK J P, WANG E N. Turning bubbles on and off during boiling using charged surfactants[J]. Nature Communications, 2015, 6: 8599. DOI:10.1038/ncomms9599


[39] LIU Yanyang, LUO Jing. Experimental study on damage mechanism of blood vessel by cavitation bubbles[J]. Ultrasonics Sonochemistry, 2023, 99: 106562. DOI:10.1016/j.ultsonch.2023.106562


[40] DANG Qun, SONG Mengjie, ZHANG Xuan, et al. Experimental study about solidification processes of sessile deformed water droplets on the biaxial inclined cold plate surface under natural convection[J]. Thermal Engineering, 2024, 236: 121883. DOI:10.1016/j.applthermaleng.2023.121883


[41] SONG Mengjie, DANG Chaobin, HIGASHI T, et al. Review of experimental data associated with the solidification characteristics of water droplets on a cold plate surface at the early frosting stage[J]. Energy and Buildings, 2020, 223: 110103. DOI:10.1016/j.enbuild.2020.110103


[42] MOUSAVI S M, SOTOUDEH F, CHUN B, et al. The potential for anti-icing wing and aircraft applications of mixed-wettability surfaces: a comprehensive review[J]. Cold Region Science and Technology, 2024, 217: 104042. DOI:10.1016/j.coldregions.2023.104042


[43] 常士楠, 杨秋明, 李延. 翼型表面结冰准定常数值模拟[J]. 空气动力学学报, 2011, 29(3): 302.
CHANG Shinan, YANG Qiuming, LI Yan. Quasi-steady numerical simulation of ice accretion on airfoil[J]. Acta Aerodynamica Sinica, 2011, 29(3): 302. DOI:10.3969/j.issn.0258-1825.2011.03.007


[44] MATSUMOTO K, SAMEHIMA K, TERAOKA Y, et al. Formation of ozone ice by freezing water containing ozone micro-bubbles[J]. International Journal of Refrigeration, 2013, 36(3): 842. DOI:10.1016/j.ijrefrig.2012.10.030


[45] MISHCHUK N A. The effect of water cooling conditions on the mechanisms of porous ice formation[J]. International Journal of Heat and Mass Transfer, 2021, 165: 120612. DOI:10.1016/j.ijheatmasstransfer.2020.120612


[46] LIPP G, KORBER C H, HARTMANN E U, et al. Investigation of the behavior of dissolved gases during freezing[J]. Cryobiology, 1987, 24: 489. DOI:10.1016/0011-2240(87)90053-8


[47] CARTE A E. Air bubble in ice[J]. Proceedings of the Physical Society London, 1961, 77(3): 757. DOI:10.1088/0370-1328/77/3/327


[48] HO C D, YEH H M, YEH T L. Optimal zone lengths in multi-pass zone-refning processes[J]. Separations Technology, 1996, 6(4): 227. DOI:10.1016/S0956-9618(96)00160-9


[49] TILLER W A, JACKSON K A, RUTTER J W, et al. The redistribution of solute atoms during the solidification of metals[J]. Acta Metallurgica, 1953, 1(4): 428. DOI:10.1016/0001-6160(53)90126-6


[50] WIDDICOMBE A, RAVINDRARAJAH P, SAPELKIN A, et al. Measurement of bitumen viscosity in a room-temperature drop experiment: student education, public outreach and modern science in one[J]. Physics Education, 2014, 49(4): 406. DOI:10.1088/0031-9120/49/4/406


[51] BURTON J A, PAIM R C, SLICHTER W P. The distribution of solute in crystals grown from the melt. Part I: theoretical[J]. The Journal of Chemical Physics, 1953, 21(11): 1987. DOI:10.1063/1.1698728


[52] POHL R G. Solute redistribution by recrystallization[J]. Journal of Applied Physics, 1954, 25(9): 1170. DOI:10.1063/1.1721834


[53] BARI S A, HALLET J. Nucleation and growth of bubbles at an ice-water interface[J]. Journal of Glaciology, 1974, 13(69): 489. DOI:10.3189/S0022143000023248


[54] GEGUZIN Y E, DZUBA A S. Crystallization of a gas-staurated melt[J]. Journal of Crystal Growth, 1981, 52: 337. DOI:10.1016/0022-0248(81)90215-3


[55] MURAKAMI K, NAKAJIMA H. Formation of pores during unidirectional solidification of water containing carbon dioxide[J]. Materials Transactions, 2002, 43(10): 2582. DOI:10.2320/matertrans.43.2582


[56] RADOVIC Z, LALOVIC M. Numerical simulation of steel ingot solidification process[J]. Journal of Materials Processing Technology, 2005, 160(2): 156. DOI:10.1016/j.jmatprotec.2004.07.094


[57] MAENO N. Air bubble formation in ice crystals[J]. Physics of Snow and Ice: Proceesings, 1967, 1(1): 207.


[58] TEMESGEN T, BUI T T, HAN M, et al. Micro and nanobubble technologies as a new horizon for water-treatment techniques: a review[J]. Advances in Colloid and Interface Science, 2017, 246: 40. DOI:10.1016/j.cis.2017.06.011


[59] VISKANTA R. Heat transfer during melting and solidification of metals[J]. Journal of Heat Transfer, 1988, 110: 1205. DOI:10.1115/1.3250621


[60] WANG Yazhen, REGEL L L, WILCOX W R. Can propagation of gas bubbles lead to detached solidification? Experiments on freezing of water[J]. Crystal Growth & Design, 2002, 2(5): 453. DOI:10.1021/cg0255063


[61] INADA T, HATAKEYAMA T, TAKEMURA F. Gas-storage ice grown form water containing microbubbles[J]. International Journal of Refrigeration, 2009, 32: 462. DOI:10.1016/j.ijrefrig.2008.08.008


[62] SHAO Keke, SONG Mengjie, ZHANG Xuan, et al. Growth and distribution characteristics of trapped air bubbles in ice slices[J]. Physics of Fluids, 2023, 35: 113319. DOI:10.1063/5.0175106


[63] VSACONCELLOS K F, BEECH J. The development of blowholes in the ice/water/carbon dioxide system[J]. Journal of Crystal Growth, 1975, 28(1): 85. DOI:10.1016/0022-0248(75)90029-9


[64] WEI P S, KUO Y K, CHIU S H, et al. Shape of a pore trapped in solid during solidification[J]. International Journal of Heat & Mass Transfer, 2000, 43(2): 263. DOI:10.1016/S0017-9310(99)00134-9


[65] MARITI J, MAUERSBERGER K. A survey and new measurements of ice vapor pressure at temperatures between 170 and 250 K[J]. Geophysical Research Letters, 1993, 20: 363. DOI:10.1029/93GL00105


[66] SHREVE R L. Migration of air bubbles, vapor figures, and brine pockets in ice under a temperature gradient[J]. Journal of Geophysical Research, 1967, 72(16): 4093. DOI:10.1029/JZ072i016p04093


[67] STEHLE N S. Migration of bubbles in ice under a temperature gradient[J]. Physics of Snow and Ice: Proceedings, 1967, 1(1): 219. DOI:10.1029/JZ072i016p04093


[68] DADIC R, LIGHT B, WARREN S G. Migration of air bubbles in ice under a temperature gradient, with application to "Snowball Earth"[J]. Journal of Geophysical Research, 2010, 115: D18125. DOI:10.1029/2010JD014148


[69] BENDER M, SOWERS T, BROOK E. Gases in ice cores[J]. Proceedings of the National Academy of Sciences of the United States of America, 1997, 94: 8343. DOI:10.1073/pnas.94.16.8343


[70] PRONL P, FERREIRA C A I, WITKAMP G J. A dynamic model of Ostwald ripening in ice suspensions[J]. Journal of Crystal Growth, 2005, 275(1/2): e1355. DOI:10.1016/j.jcrysgro.2004.11.173


[71] MEIJER J G, KANT P, BUUREN D V, et al. Thin-film-mediated deformation of droplet during cryopreservation[J]. Physical Review Letter, 2023, 130: 214002. DOI:10.1103/PhysRevLett.130.214002


[72] PEREZ M. Gibbs-thomson effects in phase transformations[J]. Scripta Materialia, 2005, 52: 709. DOI:10.1016/j.scriptamat.2004.12.026


[73] SALAMATIN A N, HONDOH T, UCHIDA T, et al. Post-nucleation conversion of an air bubble to clathrate air-hydrate crystal in ice[J]. Journal of Crystal Growth, 1998, 193: 197. DOI:10.1016/S0022-0248(98)00488-6


[74] ZHANG Da, LUO Yina, ZHAO Yang, et al. LBM-PFM simulation of directional frozen crystallization of seawater in the presence of a single bubble[J]. Desalination, 2022, 542: 116065. DOI:10.1016/j.desal.2022.116065


[75] HU Fen, SUN Dawen, GAO Wenhong, et al. Effects of pre-existing bubbles on ice nucleation and crystallization during ultrasound-assisted freezing of water and sucrose solution[J]. Innovative Food Science & Emerging Technologies, 2013, 20: 161. DOI:10.1016/j.ifset.2013.08.002


[76] LI Yingling, LI Minxia, DANG Chaobin, et al. Effects of dissolved gas on the nucleation and growth of ice crystals in freezing droplets[J]. International Journal of Heat and Mass Transfer, 2022, 184: 122334. DOI:10.1016/j.ijheatmasstransfer.2021.122334


[77] SHAO Keke, SONG Mengjie, SHEN Jun, et al. Experimental study on the distribution and growth characteristics of trapped air bubbles in ice slices at different freezing temperatures[J]. Applied Thermal Engineering, 2024. DOI:10.1016/j.applthermaleng.2024.122600


[78] FROST H J, THOMPSON C V. Computer simulation of microstructural evolution in thin films[J]. Journal of Electronic Materials, 1988, 17: 447. DOI:10.1007/BF02652132


[79] ARENA L, NASELLO O B, LEVI L. Effect of bubbles on grain growth in ice[J]. The Journal of Physical chemistry B, 1997, 101(32): 6109. DOI:10.1021/jp9632394


[80] AZUMA N, MIYAKOSHI T, YOKAYAMA S, et al. Impeding effect of air bubbles on normal grain growth of ice[J]. Journal of Structural Geology, 2012, 42: 184. DOI:10.1016/j.jsg.2012.05.005


[81] OHUCHI T, NAKAMURA M. Grain growth in the forsterite-diopside system[J]. Physics of the Earth and Planetary Interiors, 2007, 160: 1. DOI:10.1016/j.pepi.2006.08.003


[82] HIRAGE T, TACHIBANA C, OHSHI N, et al. Grain growth systematics for forsterite±enstatite aggregates: effect of lithology on grain size in the upper mantle[J]. Earth and Planetary Science Letters, 2010, 291: 10. DOI:10.1016/j.epsl.2009.12.026


[83] EVANS B, RENNER J, HIRTH G. A few remarks on the kinetics of static grain growth in rocks[J]. International Journal of Earth Sciences, 2001, 90: 88. DOI:10.1111/j.1151-2916.1985.tb15259.x


[84] ROESSIGER J, BONS P D, GRIERA A, et al. Competition between grain growth and grain-size reduction in polar ice[J]. Journal of Glaciology, 2011, 57: 942. DOI:10.3189/002214311798043690


[85] BOULOGNE F, SALONEN A. Drop freezing fine detection of contaminants by measuring the tip angle[J]. Applied Physical Letter, 2020, 116: 103701. DOI:10.1063/1.5144071


[86] SCHETNIKOV A, MATIUNIN V, CHERNOV V. Conical shape of frozen water droplets[J]. American Journal of Physics, 2015, 83: 36. DOI:10.1119/1.4897499


[87] MARíN A G, ENRíQUEZ O R, BRUNET P, et al. Universality of tip singularity formation in freezing water drops[J]. Physical Review Letter, 2014, 113: 054301. DOI:10.1103/PhysRevLett.113.054301


[88] VARANASI K K, DENG T, SMITH J D, et al. Frost formation and ice adhesion on superhydrophobic surfaces[J]. Applied Physical Letter, 2010, 97: 18. DOI:10.1063/1.3524513


[89] HUANG Wenfeng, HAN Hongwei, SHI Liqiong, et al. Effective thermal conductivity of thermokarst lake icein Beiluhe Basin, Qinghai-Tibet Plateau[J]. Cold Regions Science and Technology, 2013, 85: 34. DOI:10.1016/j.coldregions.2012.08.001


[90] WANG Jianfeng, CARSON J K, NORTH M F, et al. A new approach to modeling the effective thermal conductivity of heterogeneous materials[J]. International Journal of Heat and Mass Transfer, 2006, 49: 3075. DOI:10.1016/j.ijheatmasstransfer.2006.02.007


[91] USOWICZ B, LIPIEC J, MARCZEWSKI W, et al. Thermal conductivity modeling terrestrial soil media-a comparative study[J]. Planetary and Space Science, 2006, 54: 1086. DOI:10.1016/j.pss.2006.05.018


[92] SHOSHANY Y, PRIALNIK D, PODOLAK M. Monte Carlo modeling of the thermal conductivity of porous cometary ice[J]. Icarus, 2002, 157: 219. DOI:10.1006/icar.2002.6815


[93] LANDAUER R. The electrical resistance of binary metallic mixtures[J]. Journal of Applied Physics, 1952, 23: 779. DOI:10.1063/1.1702301


[94] MAXWELL J C A. Treatise on electricity and magnetism[J]. Nature, 1873, 7(182): 478. DOI:10.1038/007478a0


[95] WANG Jianfeng, CARSON J K, NORTH M F, et al. A new structural model of effective thermal conductivity for heterogeneous materials with co-continuous phases[J]. International Journal of Heat and Mass Transfer, 2008, 49: 2389. DOI:10.1016/j.ijheatmasstransfer.2007.08.028


[96] HUANG Wenfeng, LI Zhijun, HAN Hongwei, et al. Structural analysis of thermokarst lake ice in Beiluhe Basin, Qinghai-Tibet Plateau[J]. Cold Regions Science and Technology, 2012, 72: 33. DOI:10.1016/j.coldregions.2011.11.005


[97] SONG Mengjie, DENG Shiming, DANG Chaobin, et al. Review on improvement for air source heat pump units during frosting and defrosting[J]. Applied Energy, 2018, 211: 1150. DOI:10.1016/j.apenergy.2017.12.022


[98] DOMBROVSKKY L A, KOKHANOVSKY A A. Solar heating of ice sheets containing gas bubbles[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2020, 250: 10699. DOI:10.1016/j.jqsrt.2020.106991


[99] DOMBROVSKKY L A, KOKHANOVSKY A A. Solar heating of ice-covered lake and ice melting[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2023, 294: 108391. DOI:10.1016/j.jqsrt.2022.108391


[100] ZHEN Zekang, SONG Mengjie, SHEN Jun, et al. An experimental study on the effect of CO₂ laser powers on melting characteristics of ice with trapped air bubbles under vertical irradiation[J]. Applied Thermal Engineering, 2024, 236B: 121533. DOI:10.1016/j.applthermaleng.2023.121533


[101] LEI Guilin, DONG Wei, ZHENG Mei, et al. Numerical investigation on heat transfer and melting process of ice with different porosities[J]. International Journal of Heat and Mass Transfer, 2017, 107: 934. DOI:10.1016/j.ijheatmasstransfer.2016.11.004


[102] HUANG Wenfeng, ZHANG Jinrong, LEPPARANTA M, et al. Thermal structure and water-ice heat transfer in a shallow ice-covered thermokarst lake in central Qinghai-Tibet Plateau[J]. Journal of Hydrology, 2019, 578: 124122. DOI:10.1016/j.jhydrol.2019.124122


[103] SLEPTSOV S D, SAVVINOVA N A, GRISHIN M A. Numerical study of the thermal state of an ice layer containing air bubbles[J]. Journal of Applied Mechanics and Technical Physics, 2021, 62(3): 451. DOI:10.1134/S0021894421030111


[104] 张文元, 杨奇勇, 朱勇军, 等. 新型装配式冰场受力性能试验与模拟分析[J]. 哈尔滨工业大学学报, 2020, 52(8): 132.
ZHANG Wenyuan, YANG Qiyong, ZHU Yongjun, et al. Experimental research and FEM simulation on the mechanical performance of a new type of assembled ice rink[J]. Journal of Harbin Institute of Technology, 2020, 52(8): 132. DOI:10.11918/201908114


[105] 娄晓楠, 武岳, 刘秀明. 复合冰材料单轴压缩性能试验[J]. 哈尔滨工业大学学报, 2019, 51(12): 137.
LOU Xiaonan, WU Yue, LIU Xiuming. Uniaxial compression performance test of fiber-reinforced ice[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 137. DOI:10.11918/j.issn.0367-6234.201903071


[106] 周道成, 段忠东, 姚迪, 等. 河冰抗压强度概率特征值的自助法估计[J]. 哈尔滨工业大学学报, 2010, 42(4): 541.
ZHOU Daocheng, DUAN Zhongdong, YAO Di, et al. Bootstrap-based estimation for probabilistic characteristic value of river ice compression strength[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 541. DOI:10.11918/j.issn.0367-6234.2010.04.008


[107] 张丽敏, 李志军, 贾青, 等. 人工淡水冰单轴压缩强度试验研究[J]. 水利学报, 2009, 40(11): 1392.
ZHANG Limin, LI Zhijun, JIA Qing, et al. Experimental study on uniaxial compressive strengths of artificial freshwater ice[J]. Journal of Hydraulic Engineering, 2009, 40(11): 1392. DOI:10.1109/TCBB.2015.2511731


[108] PETROVIC J J. Review mechanical properties of ice and snow[J]. Journal of Materials Science, 2003, 38: 1. DOI:10.1023/A:1021134128038


[109] 刘浩印. 河冰物理力学性质试验及离散元数值模拟研究[D]. 哈尔滨: 哈尔滨工业大学, 2022
LIU Haoyin. Study on physical and mechanical properties of river ice by test and discrete element numerical[D]. Harbin: Harbin Institute of Technology, 2022


[110] 黄文峰. 湖冰微结构及其对热、力学参数影响的研究[D]. 大连: 大连理工大学, 2014
HUANG Wenfeng. Study on lake ice microstructure and its effect on thermal and mechanical parameters[D]. Dalian: Dalian University of Technology, 2014


[111] SCHWARZ J. Standardization of testing methods for ice properties[J]. Cold Science and Technology, 1981(4): 245. DOI:10.1016/0165-232X(81)90007-0


[112] 袁正国. 内河冰凌力学性能及其对桥墩撞击力作用的研究[D]. 哈尔滨: 东北林业大学, 2010
YUAN Zhengguo. Research on inland river ice mechanical property and ice impact force on bridge pier[D]. Harbin: Northeast Forestry University, 2010


[113] DENG Huanyu, CHANG Shinan, LI Wei. Experimental study on ice adhesion forces of the copper plates with specific contact angle and roughness[J]. Sustainable Energy Technologies and Assessments, 2021, 43: 100942. DOI:10.1016/j.seta.2020.100942


[114] MOSLET P O. Field testing of uniaxial compression strength of columnar sea ice[J]. Cold Regions Science and Technology, 2007, 48(1): 1. DOI:10.1016/j.coldregions.2006.08.025


[115] SAKAMA S, TANAKA Y, KAMIMURA A. Characteristics of hydraulic and electric servo motors[J]. Actuators, 2022, 11(1): 11. DOI:10.3390/act11010011


[116] 赵纯. YH100数控液压伺服压力机液压系统研究[D]. 芜湖: 安徽工程大学, 2014
ZHAO Chun. Research on YH100 CNC hydraulic servo press hydraulic system[D]. Wuhu: Anhui University of Technology, 2014


[117] 袁宝江. 冰场人工冰的破坏准则研究及应用[D]. 哈尔滨: 哈尔滨工业大学, 2022
YUAN Baojiang. Study and application of guidelines for the destruction of artificial ice in ice rinks[D]. Harbin: Harbin Institute of Technology, 2022


[118] ILIESCU D, BAKER I. The structure and mechanical properties of river and lake ice[J]. Cold Region and Science Technology, 2007, 48(3): 202. DOI:10.1016/j.coldregions.2006.11.002


[119] MOHAMED A M A, FARZANEH M. An experimental study on the tensile properties of atmospheric ice[J]. Cold Regions Science and Technology, 2011, 68(3): 91. DOI:10.1016/j.coldregions.2011.06.012


[120] 张大长, 刘明源, 包涛. 淡水冰单轴受压力学特性的试验研究[J]. 工程力学, 2011, 28(7): 238.
ZHANG Dachang, LIU Mingyuan, BAO Tao. Experimental study on mechanical properties of fresh water ice subjected to uniaxial compressive load[J]. Engineering Mechanics, 2011, 28(7): 238.


[121] 李志军, 张丽敏, 卢鹏, 等. 渤海海冰孔隙率对单轴压缩强度影响的实验研究[J]. 中国科学: 技术科学, 2011, 41(10): 1329.
LI Zhijun, ZHANG Limin, LU Peng, et al. Experimental study on the effect of sea ice porosity on uniaxial compression strength in the Bohai Sea[J]. Science China Technological Sciences, 2011, 41(10): 1329.


[122] 张红彪. 黄河冰抗拉强度及断裂韧度的劈裂试验研究[D]. 大连: 大连理工大学, 2016
ZHANG Hongbiao. Splitting test study on tensile strength and fracture toughness of Yellow River ice[D]. Dalian: Dalian University of Technology, 2016


[123] 肖赞. 巴西试验法测定冰力学性质的可靠性研究[D]. 大连: 大连理工大学, 2017
XIAO Zan. Reliability study of the Brazilian test method for the determination of ice mechanical properties[D]. Dalian: Dalian University of Technology, 2017


[124] 韩红卫, 解飞, 汪恩良, 等. 河冰三轴压缩强度特性及破坏准则试验研究[J]. 水利学报, 2018, 49(10): 1199.
HAN Hongwei, XIE Fei, WANG Enliang, et al. Experimental study on properties of compressive strength and failure criteria of river ice under triaxial compression[J]. Journal of Hydraulic Engineering, 2018, 49(10): 1199. DOI:10.13243/j.cnki.slxb.20180148


[125] 单仁亮, 白瑶, 隋顺猛, 等. 淡水冰三轴压缩力学特性试验研究[J]. 应用基础与工程科学学报, 2018, 26(4): 901.
SHAN Renliang, BAI Yao, SUI Shunmeng, et al. Experimental research on mechanical characteristics of freshwater ice under triaxial compression[J]. Journal Basic Science and Engineering, 2018, 26(4): 901. DOI:10.16058/j.issn.1005-0930.2018.04.019


[126] 欧阳群安. 静动态冰力学特性试验及颗粒离散元法数值模拟研究[D]. 天津: 天津大学, 2019
OUYANG Qunan. Experiments on static and dynamic ice mechanical properties and numerical simulation of particle discrete element method[D]. Tianjin: Tianjin University, 2019


[127] DENG Kun, FENG Xiaowei, TAN Xiaojun, et al. Experimental research on compressive mechanical properties of ice under low strain rates[J]. Materials Today Communications, 2020, 24: 101029. DOI:10.1016/j.mtcomm.2020.101029


[128] 薛世超, 常孟周, 韩雅菲, 等. 冲击载荷下冰的动态压缩力学特性数值模拟[J]. 装备制造技术, 2021(3): 4.
XUE Shichao, CHANG Mengzhou, HAN Yafei. Numerical simulation of dynamic compressive mechanical properties of ice under impact loading[J]. Equipment Manufacturing Technology, 2021(3): 4. DOI:10.3969/j.issn.1672-545X.2021.03.003


[129] 孟丁丁, 陈晓东, 季顺迎. 海冰弯曲强度及其破坏过程的实验研究[J]. 海洋通报, 2021, 40(6): 609.
MENG Dingding, CHEN Xiaodong, JI Shunying. Experimental study on the flexural strength and failure process of sea ice[J]. Marine Science Bulletin, 2021, 40(6): 609. DOI:10.11840/j.issn.1001-6392.2021.06.002


[130] LOU Xiaonan, WU Yue. Splitting tensile mechanical properties of plain ice and fiber-reinforced ice[J]. Cold Region Science and Technology, 2021, 192: 103381. DOI:10.1016/j.coldregions.2021.103381


[131] 王宝生. 原位高压冻结冰试样的制作工艺与单轴压缩力学特性[D]. 徐州: 中国矿业大学, 2022
WANG Baosheng. In-place preparation technique and uniaxial compression properties of ice samples frozen under high pressure[D]. Xuzhou: China University of Mining and Technology, 2022


[132] 马玉贤, 于福祥, 田野, 等. 辽东湾东岸海冰物理力学性质的基本特性[J]. 海洋环境科学, 2023, 42(5): 780.
MA Yuxian, YU Fuxiang, TIAN Ye., et al. Basic properties of physical and mechanical properties of sea ice along the east coast of Liaodong Bay[J]. Marine Environmental Science, 2023, 42(5): 780. DOI:10.13634/j.cnki.mes.2023.05.004


[133] 解北京, 陈铭进, 陈思羽, 等. 冰试样动态冲击破坏力学特性实验研究[J]. 防灾减灾工程学报, 2023, 43(6): 1284.
XIE Beijing, CHEN Mingjin, CHEN Siyu, et al. Experimental study on dynamic impact failure mechanical properties of ice samples[J]. Journal of Disaster Prevention and Mitigation, 2023, 43(6): 1284. DOI:10.13409/j.cnki.jdpme.20230207003


[134] 周庆. 淡水冰单轴压缩强度试验研究[D]. 大连: 大连理工大学, 2013
ZHOU Qing. Experimental study of uniaxial compressive strength of freshwater ice[D]. Dalian: Dalian University of Technology, 2013


[135] GANS H D, WOODMANSEE P R. An improved method of modeling porous materials using finite elements[J]. Computers & Structures, 1992, 44(5): 1055. DOI:10.1016/0045-7949(92)90328-W


[136] FARID H, FARZANEH M, SAEIDI A, et al. A contribution to the study of the compressive behavior of atmospheric ice[J]. Cold Regions Science and Technology, 2016, 121: 60. DOI:10.1016/j.coldregions.2015.10.007