刘学增1,2,李振1,2,杨芝璐3,4,桑运龙3,4,孙州3,4
(1.同济大学 土木工程学院,上海 200092;2.岩土及地下工程教育部重点实验室(同济大学), 上海 200092; 3.上海地下基础设施安全检测与养护装备工程技术研究中心,上海 200092; 4.上海同岩土木工程科技股份有限公司,上海 200092)
摘要:
为明确松动荷载作用下,衬砌裂缝特征对结构承载性能的影响,通过1∶10模型试验和数值分析研究了带裂缝结构的受力变形特征、破坏模式和极限承载能力。结果表明:对于预制裂缝长度不超过L/3（试件纵向长度）、深度不超过0.7H（试件厚度）的试件,裂缝发展存在阶段性特征,试件破坏由拱腰失效引起,属于延性破坏。对于预制裂缝长度不低于2L/3或深度不低于0.9H的试件,裂缝发展过程不存在阶段性特征,试件破坏由拱顶失效引起,属于脆性破坏；随裂缝长度和深度增加,结构极限承载力降低。当预制裂缝长度为L/3且深度为0.3H、0.7H、0.9H,以及长度为2L/3且深度为0.3H、0.7H时,试件极限承载力依次为完整试件的86.96%、78.26%、73.91%、69.57%、60.87%。相比于裂缝深度,纵向长度对结构承载性能影响更明显,可作为裂缝评价的重要指标；提出了基于裂缝特征的衬砌承载力预测公式,可明确带裂衬砌的极限承载力,为结构性能评估、加固时机及加固参数的选取提供依据。
关键词: 隧道工程 极限承载力 模型试验 裂缝特征 扩展有限元
DOI：10.11918/202210011
分类号:U451
文献标识码:A
基金项目:国家自然科学基金(52278409)；甘肃省交通运输厅科研项目(2020-23)
Analysis of the influence of tunnel lining cracks on bearing capacity
LIU Xuezeng1,2,LI Zhen1,2,YANG Zhilu3,4,SANG Yunlong3,4,SUN Zhou3,4
(1.College of Civil Engineering,Tongji University, Shanghai 200092, China; 2.Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education(Tongji University), Shanghai 200092, China; 3.Shanghai Engineering Research Center of Underground Infrastructure Detection and Maintenance Equipment, Shanghai 200092, China; 4.Tongyan Civil Engineering Technology Co., Ltd., Shanghai 200092, China)
Abstract:
In order to clarify the influence of crack characteristics on the bearing capacity of lining structures under loose load, the stress and deformation characteristics, failure modes and ultimate bearing capacity of structures with cracks were studied by 1∶10 model test and numerical analysis. The results show that: For specimens with prefabricated crack length less than L/3 (longitudinal length of specimen) and depth less than 0.7H (thickness of the specimen), the fracture development process is characterized by stages. The failure of specimens is caused by the failure of the vault and belongs to ductile failure. For the specimens with prefabricated crack length no less than 2L/3 or depth no less than 0.9H, there is no stage characteristics in the crack development process, and the failure of the specimens is caused by the failure of the vault, which belongs to the brittle failure. With the increase of crack length and depth, the structural ultimate bearing capacity decreases. When the length of prefabricated crack is L/3 and the depth is 0.3H, 0.7H, 0.9H, and when the length is 2L/3 and the depth is 0.3H, 0.7H, the ultimate bearing capacity of the specimen is 86.96%, 78.26%, 73.91%, 69.57%, 60.87% of the complete specimen. Compared with the crack depth, the length has more obvious effect on the mechanical properties of the structure, and can be taken as an important index of fracture evaluation. A formula for calculating the bearing capacity of the lining based on the characteristics of cracks is proposed, which can be used to determine the ultimate bearing capacity of the lining with cracks, and provide a basis for the evaluation of structural performance, the selection of reinforcement timing and reinforcement parameters.
Key words: tunnel engineering ultimate bearing capacity model test crack characteristics extended finite element
刘学增, 李振, 杨芝璐, 桑运龙, 孙州. 隧道衬砌裂缝特征对承载力的影响分析[J]. 哈尔滨工业大学学报, 2024, 56(7): 37-45. DOI: 10.11918/202210011.
LIU Xuezeng, LI Zhen, YANG Zhilu, SANG Yunlong, SUN Zhou. Analysis of the influence of tunnel lining cracks on bearing capacity[J]. Journal of Harbin Institute of Technology, 2024, 56(7): 37-45. DOI: 10.11918/202210011.
基金项目 国家自然科学基金(52278409)；甘肃省交通运输厅科研项目(C) 作者简介 刘学增(1971—)，男，教授级高级工程师，博士生导师 通信作者 刘学增，liuxuezeng@tongji.edu.cn 文章历史 收稿日期: 2022-10-04
Abstract Full text Figures/Tables PDF
隧道衬砌裂缝特征对承载力的影响分析
刘学增1,2
, 李振1,2, 杨芝璐3,4, 桑运龙3,4, 孙州3,4 1. 同济大学 土木工程学院, 上海 200092;
2. 岩土及地下工程教育部重点实验室(同济大学), 上海 200092;
3. 上海地下基础设施安全检测与养护装备工程技术研究中心, 上海 200092;
4. 上海同岩土木工程科技股份有限公司, 上海 200092
收稿日期: 2022-10-04; 录用日期: 2023-01-11; 网络首发日期: 2024-05-31
基金项目: 国家自然科学基金(52278409)；甘肃省交通运输厅科研项目(C)
作者简介: 刘学增(1971—)，男，教授级高级工程师，博士生导师
通信作者: 刘学增，liuxuezeng@tongji.edu.cn
摘要: 为明确松动荷载作用下，衬砌裂缝特征对结构承载性能的影响，通过1∶ 10模型试验和数值分析研究了带裂缝结构的受力变形特征、破坏模式和极限承载能力。结果表明：对于预制裂缝长度不超过L/3(试件纵向长度)、深度不超过0.7H(试件厚度)的试件，裂缝发展存在阶段性特征，试件破坏由拱腰失效引起，属于延性破坏。对于预制裂缝长度不低于2L/3或深度不低于0.9H的试件，裂缝发展过程不存在阶段性特征，试件破坏由拱顶失效引起，属于脆性破坏；随裂缝长度和深度增加，结构极限承载力降低。当预制裂缝长度为L/3且深度为0.3H、0.7H、0.9H，以及长度为2L/3且深度为0.3H、0.7H时，试件极限承载力依次为完整试件的86.96%、78.26%、73.91%、69.57%、60.87%。相比于裂缝深度，纵向长度对结构承载性能影响更明显，可作为裂缝评价的重要指标；提出了基于裂缝特征的衬砌承载力预测公式，可明确带裂衬砌的极限承载力，为结构性能评估、加固时机及加固参数的选取提供依据。
关键词: 隧道工程 极限承载力 模型试验 裂缝特征 扩展有限元
Analysis of the influence of tunnel lining cracks on bearing capacity
LIU Xuezeng1,2
, LI Zhen1,2, YANG Zhilu3,4, SANG Yunlong3,4, SUN Zhou3,4 1. College of Civil Engineering, Tongji University, Shanghai 200092, China;
2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education(Tongji University), Shanghai 200092, China;
3. Shanghai Engineering Research Center of Underground Infrastructure Detection and Maintenance Equipment, Shanghai 200092, China;
4. Tongyan Civil Engineering Technology Co., Ltd., Shanghai 200092, China
Abstract: In order to clarify the influence of crack characteristics on the bearing capacity of lining structures under loose load, the stress and deformation characteristics, failure modes and ultimate bearing capacity of structures with cracks were studied by 1∶ 10 model test and numerical analysis. The results show that: For specimens with prefabricated crack length less than L/3 (longitudinal length of specimen) and depth less than 0.7H (thickness of the specimen), the fracture development process is characterized by stages. The failure of specimens is caused by the failure of the vault and belongs to ductile failure. For the specimens with prefabricated crack length no less than 2L/3 or depth no less than 0.9H, there is no stage characteristics in the crack development process, and the failure of the specimens is caused by the failure of the vault, which belongs to the brittle failure. With the increase of crack length and depth, the structural ultimate bearing capacity decreases. When the length of prefabricated crack is L/3 and the depth is 0.3H, 0.7H, 0.9H, and when the length is 2L/3 and the depth is 0.3H, 0.7H, the ultimate bearing capacity of the specimen is 86.96%, 78.26%, 73.91%, 69.57%, 60.87% of the complete specimen. Compared with the crack depth, the length has more obvious effect on the mechanical properties of the structure, and can be taken as an important index of fracture evaluation. A formula for calculating the bearing capacity of the lining based on the characteristics of cracks is proposed, which can be used to determine the ultimate bearing capacity of the lining with cracks, and provide a basis for the evaluation of structural performance, the selection of reinforcement timing and reinforcement parameters.
Keywords: tunnel engineering ultimate bearing capacity model test crack characteristics extended finite element
裂缝是公路隧道衬砌常见的病害，造成衬砌开裂的主要因素有外力、环境、材料以及施工等[1-3]。隧道二次衬砌施工过程中由于拆模过早、材料问题，甚至施工工艺不当等非外力因素造成的二衬开裂现象经常发生，给二次衬砌带来先天的缺陷，将导致衬砌结构的承载性能、耐久性出现不同程度的降低，其发展演化有可能导致衬砌掉块或坍塌，严重影响隧道运营安全。为此，及时分析评价非外力引起的裂缝对衬砌结构服役性能的影响，采取工程措施保障结构安全是必要的。
针对上述问题，较多专家学者采用数值计算的方法开展相关研究。文献[4-7]建立了带裂缝隧道衬砌力学模型，并分析了裂缝几何特征、数量及分布对裂缝扩展及衬砌承载能力的影响；文献[8]基于断裂力学理论提出纵向裂缝位于拱顶时的断裂行为，并采用有限元软件系统分析裂缝深度对应力强度因子的影响规律；文献[9]采用离散元模拟并分析预制裂缝深度对裂缝贯通时间的影响，为衬砌治理时机的选取提供借鉴；文献[10]对带裂缝的衬砌结构进行了刚度计算。由于数值计算存在过多简化，计算结果难以准确、全面地反映带裂缝结构的非线性力学性能。
相对于数值计算，物理试验可更真实地反映非外力引起的裂缝对衬砌结构服役性能的影响。文献[11]通过开展预制裂缝结构加载试验，研究了裂缝长度对结构位移特征和破坏模式的影响；文献[12]通过开展1∶ 40模型试验，研究了拱顶、仰拱、边墙等部位存在不同数量裂缝时，衬砌结构的损伤演化规律；刘学增等通过模型试验研究了偏下荷载作用下的带裂缝衬砌结构损伤特征[13]、套拱加固带裂缝隧道衬砌的受力机理[14]、纵向初始裂缝对钢筋混凝土衬砌的影响规律[15-16]，形成一系列关于非外力引起的裂缝对衬砌结构力服役性能影响规律的认识。
综上所述，既有研究主要涉及非外力引起的裂缝对衬砌结构损伤特征、破坏过程及破坏模式的定性或半定量分析，缺乏对结构承载力的量化分析，未能建立裂缝特征和衬砌承载力的对应关系。为此，本文采用1∶ 10模型试验和数值分析方法，定量分析非外力引起的裂缝对结构挠度和极限承载能力的影响，提出了基于裂缝特征的结构承载力预测公式。
1 模型试验设计 1.1 原型隧道原型采用单洞双车道结构形式，宽度为11.86 m、高度为9.53 m、厚度为40 cm，如图 1所示。二衬结构为C25混凝土，抗压和抗拉强度标准值分别为17.0 MPa和2.0 MPa[17]。钢筋型号为HRB400，直径为22 mm，配筋率满足ρ≥0.2%。隧道围岩等级为Ⅳ级，弹性抗力系数取10 MPa/m。
Fig. 1
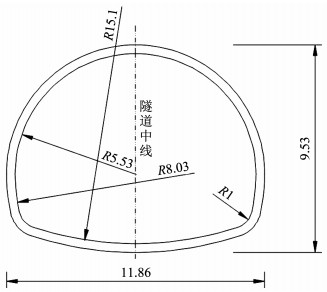图 1 原型隧道衬砌断面尺寸示意(m) Fig. 1 Schematic diagram of prototype tunnel lining section size(m) 1.2 相似关系及试验材料基于量纲分析法设计试验相似比，见表 1。
表 1
表 1 相似比设计汇总 Tab. 1 Similarity ratio design summary 物理量 相似比 物理量 相似比 几何尺寸Cl 1∶10 抗拉强度CRt 1∶7.2
弹性模量CE 1∶11 抗力系数Ck 1
应力Cσ 1∶7.2 均布荷载Cq 1∶7.2
应变Cε 1.5∶1 轴力CN 1∶720
抗压强度CRb 1∶7.2 弯矩CM 1∶7 200
表 1 相似比设计汇总 Tab. 1 Similarity ratio design summary
混凝土衬砌、钢筋和地层作用的模拟方法如下：1)混凝土衬砌由高强石膏浇筑，水和石膏的比例为0.55 1，弹性模量E为2.53 GPa，抗压强度Rb为2.36 MPa，抗拉强度Rb为0.24 MPa；2)钢筋由钢丝制作，截面积24 mm2，间距1 cm；3)地层作用通过千斤顶-弹簧装置模拟，并在弹簧和衬砌间设置曲形垫板。已知原型弹性抗力系数为kp=10 MPa/m，则模型地层弹性抗力系数km=kp · Ck=10 MPa/m，考虑衬砌表面垫板实际贴合面积S=0.03 m2，可根据K0=S×km求得单个弹簧刚度K0=100 N/mm。
1.3 预制裂缝试件制作流程文献[18]表明，衬砌拱顶发生纵向或斜向裂缝的隧道占调查隧道总数的79.31%。其中，拱顶纵向裂缝的发展演化可能引起掉拱、塌方，对隧道安全的威胁最大。因此，本试验设计并制作拱顶预制纵向裂缝衬砌试件。
试件模具包括内模、外模和底板3部分。其中，底板上画有模型内外轮廓，便于模具定位，并通过螺丝与内、外模固定。预制裂缝采用厚度为1 mm且表面光滑的聚乙烯板模拟，在模型浇筑时应直接插入到对应位置。预制裂缝制作效果如图 2所示。
Fig. 2
图 2 预制裂缝制作效果 Fig. 2 Prefabricated crack production effect 试件的浇筑过程包括6个步骤，如图 3所示。在每个试件制作中，同时制作3个石膏土立方体试块；浇筑过程中应充分振捣以保证浇筑质量；浇筑完成养护1 d后拆模，并养护至试件达到相应强度；保证预制裂缝截面光滑平整。
Fig. 3
图 3 预制裂缝试件浇筑流程 Fig. 3 Prefabricated crack specimen pouring process 1.4 全周加载装置及方案本试验采用全周加载装置，如图 4所示。通过千斤顶5#~7#主动施加松散土压，并采用高精度压力表(精度为0.2 kPa，最大量程为80 kPa)实现荷载的精准控制。整套装置水平放置，并在模型底部和托盘间铺设聚四氟乙烯板以减小摩擦。
Fig. 4
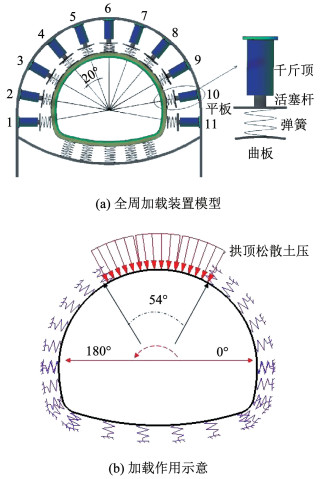图 4 全周加载装置及作用示意 Fig. 4 Full-cycle loading device and action diagram 试验采用“预加载+分级加载”的方案。由于构件在加载中可能会产生支座位移，以及构件本身和支座的贴合不够密切，在试验前应该对试件进行预加载。预加载荷载不超过0.5 kPa，分两次施加，需保持荷载稳定0.5 h；分级加载采取较小荷载逐级加载的方式，每级加载速率控制在0.3~0.5 kPa/min之间，保持荷载稳定5 min后，再继续施加下级荷载。
1.5 试验量测方案在不同位置布设应变片和位移计(图 5)采集结构应变和变形数据，并在加载过程中观察裂缝发展情况。
Fig. 5
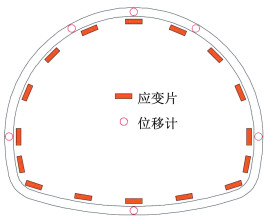图 5 量测设备布置示意 Fig. 5 Schematic diagram of measuring equipment layout 1.6 试验工况为方便对比，设置了1组完整工况和5组带有预制裂缝的工况。预制裂缝位于衬砌拱顶，每个模型预制一条不同长度和深度的裂缝，如表 2所示，其中L为模型纵向长度，取0.3 m；H为衬砌厚度，取0.04 m。
表 2
表 2 带预制裂缝的试验工况汇总 Tab. 2 Summary of test conditions with prefabricated cracks 试验工况 裂缝长度 裂缝深度 工况1 L/3 0.3H
工况2 2L/3 0.3H
工况3 L/3 0.7H
工况4 2L/3 0.7H
工况5 L/3 0.9H
表 2 带预制裂缝的试验工况汇总 Tab. 2 Summary of test conditions with prefabricated cracks
2 试验结果及分析 2.1 裂缝发展过程及破坏模式分析开展加载试验，并实时记录试验现象和数据。为直观反映裂缝动态发展过程及分布规律，绘制了各工况下拱顶挠度及裂缝动态发展曲线，并对裂缝分布情况进行拍照，如图 6~11所示。
Fig. 6
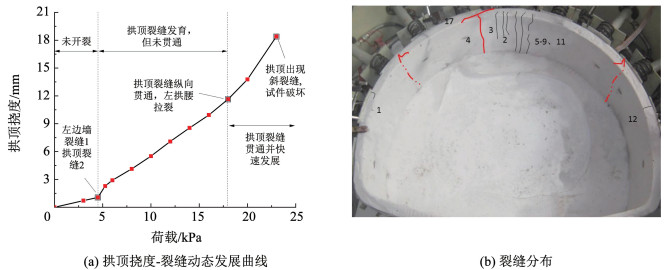图 6 完整试件裂缝发展及分布 Fig. 6 Complete specimen crack development and distribution diagram Fig. 7
图 7 工况1(L/3、0.3H)试件裂缝发展及分布 Fig. 7 Crack development and distribution of specimens under working condition 1 (L/3, 0.3H) Fig. 8
图 8 工况2(2L/3、0.3H)试件裂缝发展及分布 Fig. 8 Crack development and distribution of specimens under working condition 2(2L/3, 0.3H) Fig. 9
图 9 工况3(L/3、0.7H)试件裂缝发展及分布 Fig. 9 Crack development and distribution of specimens under working condition 3(L/3, 0.7H) Fig. 10
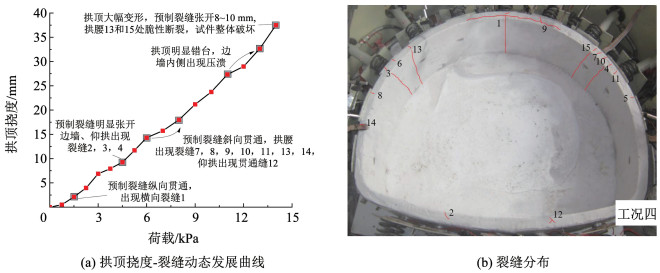图 10 工况4(2L/3、0.7H)试件裂缝发展及分布 Fig. 10 Crack development and distribution of specimens under working condition 4(2L/3, 0.7H) Fig. 11
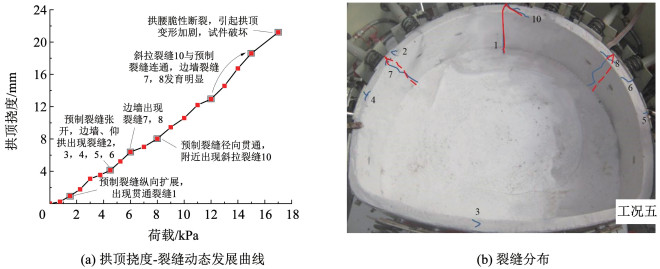图 11 工况5(L/3、0.9H)试件裂缝发展及分布 Fig. 11 Crack development and distribution of specimens under working condition 5(L/3, 0.9H) 根据试验结果，将裂缝发展及破坏特征分为以下3类。
1) 对于完整试件，其裂缝发展过程可分为3个阶段：第Ⅰ阶段(加载-拱顶开裂)，试件承受荷载较小，挠度较小，结构整体处于弹性状态；第Ⅱ阶段(拱顶开裂-拱顶主裂缝贯通)，拱顶出现裂缝2后，挠度发展速度增加，拱顶裂缝沿纵向扩展并最终贯通；第Ⅲ阶段(拱顶主裂缝贯通-试件破坏)，随着拱顶主裂缝贯通及张开，钢筋应力增大，挠度发展速度进一步增加。由于拱腰破坏早于拱顶，破坏荷载由拱腰正截面极限承载力控制。试件挠度在破坏前存在较明显的发展，破坏模式属于延性破坏。
2) 对于预制裂缝长度不超过L/3且深度不超过0.7H的试件(工况1和工况3)，裂缝发展过程可大致分为两阶段：第Ⅰ阶段(加载-预制裂缝张开)，试件变形较小，挠度曲线发展态势平缓；第Ⅱ阶段(预制裂缝张开-试件破坏)，试件加剧变形，拱腰截面因达到承载力极限而率先破坏，破坏荷载同样由拱腰正截面极限承载力控制。拱顶挠度在试件破坏前增幅表征明显，破坏模式属于延性破坏。
3) 对于预制裂缝长度不小于2L/3，或深度不低于0.9H的试件(工况2、4、5)，裂缝发展过程不存在明显的阶段性特征。在整个加载过程，拱顶挠度曲线均呈大斜率线性发展，破坏荷载由拱顶截面控制。试件挠度在破坏前没有明显的转折点，破坏模式属于脆性破坏。
2.2 裂缝特征对试件挠度的影响分析根据相似理论反算原型结构在荷载作用下的拱顶挠度变化曲线，如图 12所示。
Fig. 12
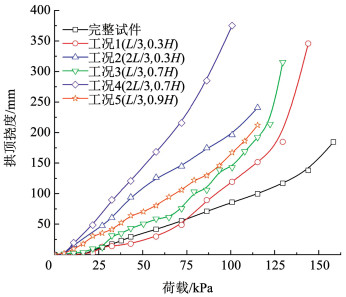图 12 试件拱顶挠度变化曲线 Fig. 12 Bending curves of specimens 由图 12可知：1)当裂缝长度一定时，深度越大，相同荷载作用下的拱顶挠度越大(工况5>工况3>工况1，工况4>工况2)，而且裂缝长度越长，深度变化对结构挠度的影响越明显；在相同荷载作用下，长度为2L/3时的拱顶挠度始终大于L/3工况(如工况2>工况5)。因此，相比于裂缝深度，长度特征对拱顶挠度影响更显著。在实际工程中，应将长度作为裂缝评价的重要指标。2)对于工况1、3以及完整试件，在挠度达到150 mm时进入急速变形阶段，与2.1节所述的“延性破坏”相吻合；对于工况2、4、5，挠度在加载过程中近线性增加，且分别在挠度达到240 mm、375 mm和212 mm时突然破坏。破坏前各试件的拱顶挠度曲线无明显转折点，与2.1节所述的“脆性破坏”相吻合。因此，预制裂缝的规模会影响结构承载性能，造成结构由延性破坏转变为脆性破坏，增加事故风险。
2.3 裂缝特征对试件刚度的影响分析试验结果显示，部分试件的挠度曲线在拱顶的主裂缝张开后呈快速发展态势。根据试验数据并结合文献[19]提出的钢筋混凝土刚度计算方法，得到各试件在拱顶主裂缝张开时的结构刚度。完整试件在拱顶主裂缝张开时的刚度为6.28×104 kN/m，预制裂缝试件的对应刚度见表 3。
表 3
表 3 拱顶主裂缝张开时的试件刚度统计 Tab. 3 Stiffness statistics of the specimens when the arch main crack is open 预制裂缝试件工况 刚度/(104 kN·m-1) 占完整试件比例/% L/3，0.3H 4.49 71.50
2L/3，0.3H 2.56 40.76
L/3，0.7H 4.50 71.66
2L/3，0.7H 2.22 35.35
L/3，0.9H 4.83 76.91
表 3 拱顶主裂缝张开时的试件刚度统计 Tab. 3 Stiffness statistics of the specimens when the arch main crack is open
由表 3可知：当拱顶主裂缝明显张开时，各预制裂缝试件的结构刚度相比完整试件存在不同程度折减，裂缝长度为L/3的试件减幅不低于23.09%，裂缝长度为2L/3的试件减幅不低于59.24%，故可将拱顶的主裂缝外缘张开作为结构刚度明显衰减的外观表现形式。另外，当裂缝长度为2L/3时，试件刚度折减较严重，说明相比裂缝深度，长度对结构刚度的影响更显著。
2.4 裂缝特征对极限承载力的影响分析根据试验结果，对不同裂缝特征试件极限承载力进行对比，如图 13所示。
Fig. 13
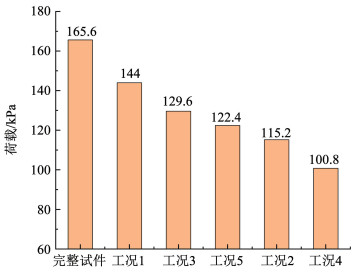图 13 试件极限承载力统计图 Fig. 13 Statistical diagram of ultimate bearing capacity of specimens 由图 13可知：对比完整试件，预制裂缝会造成结构极限承载能力发生不同程度折减。当预制裂缝长度为L/3且深度为0.3H、0.7H、0.9H时(即工况1、3、5)，结构极限承载力分别为144.0、129.6、122.4 kPa，分别占完整试件的86.96%、78.26%、73.91%；当预制裂缝长度为2L/3且深度为0.3H、0.7H时(即工况2、4)，结构极限承载力分别为115.2、100.8 kPa，分别占完整试件的69.57%、60.87%。裂缝长度对衬砌极限承载力的影响比裂缝深度显著。
综上所述，预制裂缝(实际工程中由非外力造成的衬砌开裂)的规模会对隧道结构的承载性能产生影响，包括变形特征、结构刚度、极限承载能力以及破坏模式。预制裂缝规模的增加会导致结构破坏模式由延性破坏转变为脆性破坏，以及极限承载能力显著折减。相比裂缝深度，预制裂缝的长度对结构承载性能的影响更显著，宜作为实际工程中衬砌裂缝评价的重要指标。
3 衬砌承载性能的有限元分析模型试验可较真实地反映预制裂缝衬砌结构在外荷载作用下的变形及破坏规律，但受成本等因素限制，难以开展大量试验。为此，采用有限元软件ABAQUS开展带裂衬砌结构的承载计算，并与试验数据对比，分析预制裂缝对衬砌结构承载性能的影响。
衬砌厚度取4 cm，纵向取0.3 m。衬砌结构和内置钢筋分别采用C3D8R单元和B31单元模拟，且不考虑两者之间的相对滑移。拱顶预制裂缝通过板壳对衬砌实体切割生成，如图 14(a)所示。采用XFEM扩展有限元模拟外力作用下裂缝的损伤演化，将最大应力失效准则作为裂缝损伤起始判据，规定如式(1)所示。产生裂缝时的断裂能GfⅠ、GfⅡ和GfⅢ取50 N/m[20]。
$f=\left\{\frac{\left\langle\sigma_{\max }\right\rangle}{\sigma_{\max }^0}\right\}$ (1)
式中σmax0为混凝土的极限拉应力。当σmax≥0，〈σmax〉=σmax; 当σmax＜0，〈σmax〉=0。当f>1时，结构开裂。这里取σmax=0.24 MPa。
在结构外侧设置接地弹簧来模拟地层。考虑到结构顶部承受松动荷载，弹簧仅沿衬砌周边27°~333°分布。弹簧刚度根据刚度等效原则换算得到，如图 14(b)所示。模型中的钢筋材料采用理想弹塑性本构，材料参数见1.2节。
Fig. 14
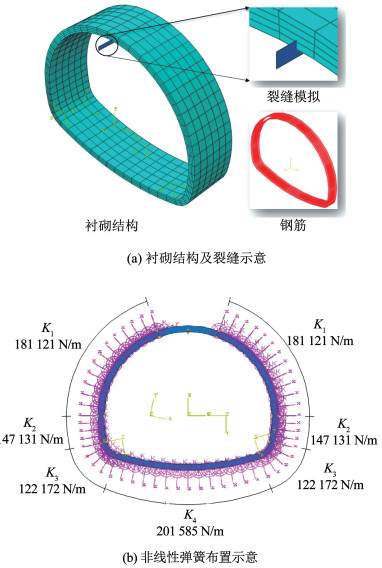图 14 计算模型 Fig. 14 Calculation model 图 15、16是针对工况1的试验和数值模拟结果对比。数值模拟和试验曲线的发展趋势基本一致，计算得到的结构挠度、破坏荷载以及裂缝分布情况同试验结果基本吻合，可大致反映松动荷载作用下带裂衬砌的损伤演化及破坏过程。
Fig. 15
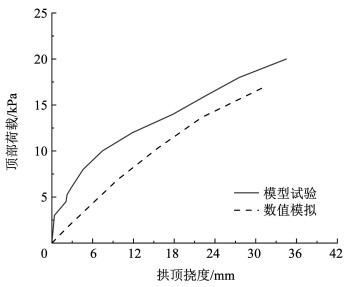图 15 荷载-拱顶挠度曲线对比 Fig. 15 Comparison of load-arch deflection Curves Fig. 16
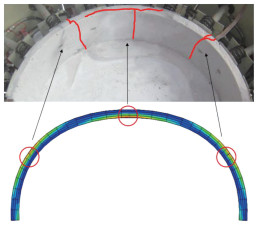图 16 裂缝分布对比 Fig. 16 Comparison of crack distribution 为建立衬砌剩余承载力与裂缝特征的定量关系，在模型试验的基础上，采用XFEM扩展有限元补充多组计算，结果见表 4。其中，编号1~5为试验组，编号6~21为有限元模拟组。
表 4
表 4 扩展有限元计算数据 Tab. 4 Comparison between numerical simulation and model test results 编号 工况 破坏荷载/kPa 最大挠度/mm 1 L/3，0.3H 17.1 31.7
2 2L/3，0.3H 16.6 31.7
3 L/3，0.7H 16.7 31.7
4 2L/3，0.7H 14.7 27.8
5 L/3，0.9H 14.1 26.5
6 L/3，0.4H 16.7 31.7
7 L/3，0.5H 16.6 31.6
8 L/3，0.6H 16.6 31.6
9 L/3，0.8H 14.1 26.5
10 L/2，0.3H 16.6 31.7
11 L/2，0.4H 16.6 31.7
12 L/2，0.5H 16.6 31.7
13 L/2，0.6H 16.6 31.7
14 L/2，0.7H 16.6 31.7
15 L/2，0.8H 13.9 26.4
16 L/2，0.9H 13.9 26.4
17 2L/3，0.4H 16.6 31.7
18 2L/3，0.5H 14.7 27.8
19 2L/3，0.6H 14.7 27.8
20 2L/3，0.8H 13.4 25.2
21 2L/3，0.9H 13.4 25.2
表 4 扩展有限元计算数据 Tab. 4 Comparison between numerical simulation and model test results
4 基于裂缝特征的衬砌剩余承载力预测公式既有的衬砌裂缝评价方法不能定量评估衬砌结构的剩余承载力，难以有效指导加固时机和参数的选取。前述研究结果表明，衬砌结构的剩余承载力与拱顶裂缝长度和深度有密切关系。为此，基于研究数据建立衬砌剩余承载力和裂缝特征的定量关系。
这里用衬砌极限承载力剩余系数z表征衬砌的承载性能，其计算公式为
$z=F_1 / F_2$ (2)
式中：F1为带裂衬砌结构的极限承载力，F2为完整衬砌结构的极限承载能力。
采用最小二乘法对表 4数据进行拟合，得到剩余系数z的数学表达式，如式(3)所示。拟合函数三维空间图形如图 17所示。
$\begin{aligned}z= & 0.49+0.78 m+1.25 n-0.12 m^2-1.96 m n- \\& 1.18 n^2-m^2 n+2.38 m n^2-0.23 n^3, R^2=0.85\end{aligned}$ (3)
Fig. 17
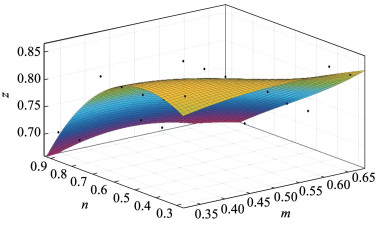图 17 基于裂缝特征的衬砌剩余承载力拟合图形 Fig. 17 Fitting graph of bearing capacity of cracked lining based on crack characteristics 式中：m为裂缝长度与衬砌纵向长度比值，n为裂缝深度与衬砌厚度比值。
对于拱顶存在裂缝的公路隧道，在收集裂缝长度及深度数据后，可借助式(3)定量评估结构的剩余承载力。另外，针对拱顶位置存在开裂的运营隧道，提出以下维护建议：
在衬砌结构裂损排查时，应高度重视在隧道纵向较为发育的裂缝，防止其沿纵向进一步发展；当存在长度不超过L/3(这里的L为每模衬砌长度，以下含义相同)、深度不超过0.7H的裂缝且其外缘张开迹象明显时，结构刚度可能已损失28%以上，应采用环氧树脂等材料封缝，必要时需加固处理；当存在长度大于2L/3的裂缝，应密切跟踪其发展演化情况。若裂缝持续发展，应及时补强衬砌结构，避免脆性破坏。
5 结论1) 在加载条件下，裂缝特征对自身发展及结构破坏模式存在影响。完整试件的裂缝发展过程可分为“加载-拱顶开裂-拱顶主裂缝贯通-试件破坏”3个阶段，试件破坏由拱腰失效引起，属于延性破坏；对于预制裂缝长度不超过L/3且深度不超过0.7H的试件，裂缝发展过程可分为“加载-预制裂缝张开-试件破坏”两个阶段，试件破坏由拱顶失效引起，属于延性破坏；对于预制裂缝长度不低于2L/3或深度不低于0.9H的试件，裂缝发展过程不存在阶段性特征，试件破坏由拱顶失效引起，属于脆性破坏。
2) 拱顶裂缝规模的增加会导致结构破坏模式由延性破坏转变为脆性破坏，以及极限承载能力显著折减。相比裂缝深度，预制裂缝的长度对结构变形和刚度、承载性能的影响更显著，宜作为实际工程中衬砌裂缝评价的重要指标。
3) 结合试验及扩展有限元分析，提出了基于裂缝特征的衬砌剩余承载力预测公式，可定量分析裂缝特征对衬砌承载力的影响程度，为衬砌承载性能评估、加固时机及参数的选取提供了依据。
参考文献
[1] 王建秀, 朱合华, 唐益群, 等. 双连拱公路隧道裂缝成因及防治措施[J]. 岩石力学与工程学报, 2005, 24(2): 195.
WANG Jianxiu, ZHU Hehua, TANG Yiqun, et al. Cracking in twin-arc highway tunnels and its prevention measures[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 195.
[2] 贺志勇, 钟宏武, 陈振华. 带裂缝隧道衬砌的安全评价及有限元分析[J]. 隧道建设(中英文), 2019, 39(增刊2): 69.
HE Zhiyong, ZHONG Hongwu, CHEN Zhenhua. Safety evaluation and finite element analysis of tunnel lining with cracks[J]. Tunnel Construction, 2019, 39(Sup.2): 69. DOI:10.3973/j.issn.2096-4498.2019.S2.009
[3] 赵刚. 黄土公路隧道带裂缝衬砌安全性评价[D]. 西安: 长安大学, 2016
ZHAO Gang. The safety evaluation of cracked highway tunnel lining in loess area[D]. Xi'an: Chang'an University, 2016
[4] 李治国, 张玉军. 衬砌开裂隧道的稳定性分析及治理技术[J]. 现代隧道技术, 2004, 41(l): 26.
LI Zhiguo, ZHANG Yujun. The tunnel lining crack stability analysis and management technology[J]. Modern Tunnelling Technology, 2004, 41(1): 26. DOI:10.13807/j.cnki.mtt.2004.01.007
[5] 张玉军, 李治国. 带裂纹隧道二次衬砌承载能力的平面有限元计算分析[J]. 岩土力学, 2005, 26(8): 1201.
ZHANG Yujun, LI Zhiguo. Plane finite element analysis of bearing capacity of secondary lining with cracked tunnel[J]. Rock and Soil Mechanics, 2005, 26(8): 1201. DOI:10.16285/j.rsm.2005.08.005
[6] 刘璇. 地铁隧道衬砌结构裂缝演化及其对结构安全性影响研究[D]. 北京: 北京交通大学, 2018
LIU Xuan. Study on influence of cracking on structure safety of subway tunnels[D]. Beijing: Beijing Jiaotong University, 2018
[7] 郑佳艳, 刘海京, 林志, 等. 衬砌存在裂缝的隧道力学模型研究及应用[J]. 公路交通技术, 2011(3): 106.
ZHENG Jiayan, LIU Haijing, LIN Zhi, et al. Research on mechanical models of tunnels with cracks in lining and its application[J]. Technology of Highway and Transport, 2011(3): 106.
[8] 胥民尧. 断裂力学理论在公路隧道衬砌开裂中的应用研究[D]. 重庆: 重庆交通大学, 2008
XU Minyao. The applicational study of fracture mechanics in lining cracking of highway tunnel[D]. Chongqing: Chongqing Jiaotong University, 2008
[9] 丁浩, 李科, 周小平, 等. 公路隧道衬砌裂纹扩展机理[J]. 土木建筑与环境工程, 2018, 40(5): 86.
DING Hao, LI Ke, ZHOU Xiaoping, et al. Numerical investigation on the fracture propagation mechanism of highway tunnel lining[J]. Journal of Civil, Architectural & Environmental Engineering, 2018, 40(5): 86. DOI:10.11835/j.issn.1674-4764.2018.05.011
[10] 王华牢, 李宁. 带裂缝的隧道衬砌刚度验算与加固[J]. 长安大学学报(自然科学版), 2009, 29(1): 64.
WANG Hualao, LI Ning. Stiffness checking and reinforcement of tunnel lining with cracks[J]. Journal of Chang'an University(Natural Science Edition), 2009, 29(1): 64. DOI:10.19721/j.cnki.1671-8879.2009.01.014
[11] 刘川昆, 何川, 王士民, 等. 裂缝长度对盾构隧道管片结构破坏模式模型试验研究[J]. 中南大学学报(自然科学版), 2019, 50(6): 1447.
LIU Chuankun, HE Chuan, WANG Shimin, et al. Model test study on failure mode of segment structure of shield tunnel with crack length[J]. Journal of Central South University (Science and Technology), 2019, 50(6): 1447. DOI:10.11817/j.issn.1672-7207.2019.06.024
[12] 元腾飞. 隧道衬砌开裂对结构受力性能的影响研究[D]. 北京: 北京交通大学, 2019
YUAN Tengfei. A research on the impact of the tunnel lining cracking on the structure force performance[D]. Beijing: Beijing Jiaotong University, 2019
[13] 刘学增, 刘文艺, 桑运龙, 等. 偏压荷载下裂损特征对隧道衬砌受力影响试验[J]. 土木工程学报, 2015, 48(10): 119.
LIU Xuezeng, LIU Wenyi, SANG Yunlong, et al. Experiment on the influence of cracking characteristics under unsymmetrical load on stresses or forces in tunnel lining[J]. China Civil Engineering Journal, 2015, 48(10): 119. DOI:10.15951/j.tmgcxb.2015.10.015
[14] 刘学增, 桑运龙, 包浩杉. 叠合式套拱加固带裂缝隧道衬砌受力机理分析[J]. 土木工程学报, 2013, 46(10): 127.
LIU Xuezeng, SANG Yunlong, BAO Haoshan. Analysis of bearing mechanism of cracked tunnel lining reinforced with stacked umbrella arch[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 46(10): 127. DOI:10.15951/j.tmgcxb.2013.10.011
[15] 刘学增, 包浩杉, 周敏. 纵向裂缝对隧道钢筋混凝土衬砌结构影响的试验[J]. 上海交通大学学报, 2012, 46(3): 441.
LIU Xuezeng, BAO Haoshan, ZHOU Min. Experimental study on the effect of longitudinal crack on reinforced concrete tunnel lining[J]. Journal of Shanghai Jiaotong University, 2012, 46(3): 441. DOI:10.16183/j.cnki.jsjtu.2012.03.019
[16] 刘学增, 张鹏, 周敏. 纵向裂缝对隧道衬砌承载力的影响分析[J]. 岩石力学与工程学报, 2012, 31(10): 2096.
LIU Xuezeng, ZHANG Peng, ZHOU Min. Analysis of the influence of longitudinal crack on bearing capacity of tunnel lining[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(10): 2096. DOI:10.3969/j.issn.1000-6915.2012.10.015
[17] 中华人民共和国交通运输部. 公路隧道设计规范: JTG D70—2004[S]. 北京: 人民交通出版社, 2004
Ministry of Transport of the People's Republic of China. Code for design of road tunnel: JTG D70—2004[S]. Beijing: China Communications Press, 2004
[18] 王煦霖. 基于二次受力的山岭隧道套拱加固承载力分析[D]. 上海: 同济大学, 2014
WANG Xulin. Study on bearing capacity of mountain tunnel strengthened by cover arch under secondary loading[D]. Shanghai: Tongji University, 2014
[19] 顾祥林, 许勇, 张伟平, 等. 钢筋混凝土梁开裂后刚度退化研究[J]. 结构工程师, 2005, 21(5): 22.
GU Xianglin, XU Yong, ZHANG Weiping, et al. Study on stiffness deterioration of reinforced concrete beams after cracking[J]. Structural Engineers, 2005, 21(5): 22. DOI:10.15935/j.cnki.jggcs.2005.05.005
[20] 黄宏伟, 刘德军, 薛亚东, 等. 基于扩展有限元的隧道衬砌裂缝开裂数值分析[J]. 岩土工程学报, 2013, 35(2): 266.
HUANG Hongwei, LIU Dejun, XUE Yadong, et al. Numerical analysis of cracking of tunnel linings based on extended finite element[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 266.
