杨逍遥1,梁国华1,陈亦新1,杨潇洒2,王宝杰1
(1.长安大学 运输工程学院,西安 710061;2.陕西交通控股集团有限公司西安外环分公司,西安 710100)
摘要:
相交道路右转车辆干扰下的直行车辆轨迹扰动现象成为城市道路信号交叉口交通运行的安全隐患,为提高直行车驾驶人对驶入右转车辆的应对能力并做出正确决策,对于直行车辆扰动轨迹的可靠预测至关重要。研究通过将不同状态下的直行车辆轨迹分布特征与相交道路右转车运行信息相关联,在车辆受扰轨迹识别的基础上将碰撞时间（TTC）指标作为输入层加入模型,构建了3层高斯混合-输入输出隐马尔可夫模型（GMM-IOHMM）,提出了一种考虑信号交叉口被交道路右转车对本面直行车作用程度的直行车辆受扰轨迹预测方法。实验结果表明:改进模型相比于传统的隐马尔可夫模型（HMM）在模型训练时能够更好地拟合实际的轨迹数据,且相比于传统的时间序列模型,GMM-IOHMM模型的拟合效果取得较大提升；可将TTC≤4.5 s且偏航角大于2.35°作为直行车辆轨迹扰动的判别标准。轨迹预测结果能够更加准确地判断直行车辆与周围车辆发生冲突的可能性,可作为受扰直行车及同行其他车辆辅助驾驶系统设计的重要依据。
关键词: 车辆轨迹预测 右转车干扰 受扰轨迹识别 GMM-IOHMM模型 累计频率曲线法
DOI：10.11918/202310015
分类号:U491.2
文献标识码:A
基金项目:国家自然科学基金(52172338)；陕西省科技计划项目(2024GX-YBXM-131)
Trajectory prediction of straight vehicles at signalized intersections considering interference from right-turning vehicles
YANG Xiaoyao1,LIANG Guohua1,CHEN Yixin1,YANG Xiaosa2,WANG Baojie1
(1.School of Transportation Engineering, Chang′an University, Xi′an 710061, China; 2.Xi′an Outer Ring Branch of Shaanxi Communications Holding Group Co., Ltd., Xi′an 710100, China)
Abstract:
The disturbance of straight vehicle trajectories under the interference of right turning vehicles on intersecting roads has become a safety hazard for traffic operation at signalized intersections on urban roads. To improve the ability of direct driving drivers to respond to right-turning vehicles and make correct decisions, it is crucial to reliably predict the disturbance trajectory of direct driving vehicles. This article associated the trajectory distribution characteristics of straight vehicles in different states with the motion information of right-turning vehicles on crossed approach. On the basis of identifying vehicle disturbance trajectories, the time to collision (TTC) was added as the input layer to the model, and a three-layer Gaussian Mixture Module-Input and Output Hidden Markov Model (GMM-IOHMM) was constructed. A method for predicting the disturbance trajectory of through vehicles was proposed, which considers the degree to which right-turning vehicles on the crossed road have an impact on the direct traffic on this surface at signalized intersections. The experimental results showed that the improved model can better fit actual trajectory data during model training compared with traditional HMM, and the fitting effect of GMM-IOHMM has been significantly improved compared with traditional time series models. And TTC is less than or equal to 4.5 s and "yaw angle is greater than 2.35 degrees" can be used as a criterion to determine whether a straight ahead vehicle is disturbed. The trajectory prediction results can more accurately determine the possibility of conflicts between direct vehicles and surrounding vehicles, and can serve as an important basis for the design of assisted driving systems for disturbed direct vehicles and other vehicles traveling together.
Key words: vehicle trajectory prediction right turn interference disturbed trajectory identification GMM-IOHMM model cumulative frequency curve method
杨逍遥, 梁国华, 陈亦新, 杨潇洒, 王宝杰. 考虑右转车干扰的信号交叉口直行车辆轨迹预测[J]. 哈尔滨工业大学学报, 2024, 56(7): 74-84. DOI: 10.11918/202310015.
YANG Xiaoyao, LIANG Guohua, CHEN Yixin, YANG Xiaosa, WANG Baojie. Trajectory prediction of straight vehicles at signalized intersections considering interference from right-turning vehicles[J]. Journal of Harbin Institute of Technology, 2024, 56(7): 74-84. DOI: 10.11918/202310015.
基金项目 国家自然科学基金(52172338)；陕西省科技计划项目(2024GX-YBXM-131) 作者简介 杨逍遥(1995—)，女，博士研究生;
梁国华(1977—)，男，教授，博士生导师 通信作者 梁国华(1977—)，lgh@chd.edu.cn 文章历史 收稿日期: 2023-10-09
Abstract Full text Figures/Tables PDF
考虑右转车干扰的信号交叉口直行车辆轨迹预测
杨逍遥1, 梁国华1
, 陈亦新1, 杨潇洒2, 王宝杰1 1. 长安大学 运输工程学院，西安 710061;
2. 陕西交通控股集团有限公司西安外环分公司，西安 710100
收稿日期: 2023-10-09; 录用日期: 2023-11-08; 网络首发日期: 2023-12-21
基金项目: 国家自然科学基金(52172338)；陕西省科技计划项目(2024GX-YBXM-131)
作者简介: 杨逍遥(1995—)，女，博士研究生; 梁国华(1977—)，男，教授，博士生导师
通信作者: 梁国华(1977—)，lgh@chd.edu.cn
摘要: 相交道路右转车辆干扰下的直行车辆轨迹扰动现象成为城市道路信号交叉口交通运行的安全隐患，为提高直行车驾驶人对驶入右转车辆的应对能力并做出正确决策，对于直行车辆扰动轨迹的可靠预测至关重要。研究通过将不同状态下的直行车辆轨迹分布特征与相交道路右转车运行信息相关联，在车辆受扰轨迹识别的基础上将碰撞时间(TTC)指标作为输入层加入模型，构建了3层高斯混合-输入输出隐马尔可夫模型(GMM-IOHMM)，提出了一种考虑信号交叉口被交道路右转车对本面直行车作用程度的直行车辆受扰轨迹预测方法。实验结果表明：改进模型相比于传统的隐马尔可夫模型(HMM)在模型训练时能够更好地拟合实际的轨迹数据，且相比于传统的时间序列模型，GMM-IOHMM模型的拟合效果取得较大提升；可将TTC≤4.5 s且偏航角大于2.35°作为直行车辆轨迹扰动的判别标准。轨迹预测结果能够更加准确地判断直行车辆与周围车辆发生冲突的可能性，可作为受扰直行车及同行其他车辆辅助驾驶系统设计的重要依据。
关键词: 车辆轨迹预测 右转车干扰 受扰轨迹识别 GMM-IOHMM模型 累计频率曲线法
Trajectory prediction of straight vehicles at signalized intersections considering interference from right-turning vehicles
YANG Xiaoyao1, LIANG Guohua1
, CHEN Yixin1, YANG Xiaosa2, WANG Baojie1 1. School of Transportation Engineering, Chang′an University, Xi′an 710061, China;
2. Xi′an Outer Ring Branch of Shaanxi Communications Holding Group Co., Ltd., Xi′an 710100, China
Abstract: The disturbance of straight vehicle trajectories under the interference of right turning vehicles on intersecting roads has become a safety hazard for traffic operation at signalized intersections on urban roads. To improve the ability of direct driving drivers to respond to right-turning vehicles and make correct decisions, it is crucial to reliably predict the disturbance trajectory of direct driving vehicles. This article associated the trajectory distribution characteristics of straight vehicles in different states with the motion information of right-turning vehicles on crossed approach. On the basis of identifying vehicle disturbance trajectories, the time to collision (TTC) was added as the input layer to the model, and a three-layer Gaussian Mixture Module-Input and Output Hidden Markov Model (GMM-IOHMM) was constructed. A method for predicting the disturbance trajectory of through vehicles was proposed, which considers the degree to which right-turning vehicles on the crossed road have an impact on the direct traffic on this surface at signalized intersections. The experimental results showed that the improved model can better fit actual trajectory data during model training compared with traditional HMM, and the fitting effect of GMM-IOHMM has been significantly improved compared with traditional time series models. And TTC is less than or equal to 4.5 s and "yaw angle is greater than 2.35 degrees" can be used as a criterion to determine whether a straight ahead vehicle is disturbed. The trajectory prediction results can more accurately determine the possibility of conflicts between direct vehicles and surrounding vehicles, and can serve as an important basis for the design of assisted driving systems for disturbed direct vehicles and other vehicles traveling together.
Keywords: vehicle trajectory prediction right turn interference disturbed trajectory identification GMM-IOHMM model cumulative frequency curve method
右转许可信号是国内最常见的一种城市道路交叉口的右转车辆信控方式，在这类交叉口中直行车流与被交道路右转车流在同一时段汇出交叉口时存在明显的交织区。在直行车与相交道路右转车相互逼近过程中驾驶人需要迅速处理大量的交通环境信息并做出正确的反应才能顺利通过交叉口，而处于复杂交织环境中的驾驶人通常会受到当前思考的局限性而做出不安全的驾驶行为[1]。
车辆辅助驾驶系统[2-4]的研究成为解决当前微观交通问题的重要手段，而准确的车辆轨迹预测算法可以提前预测潜在的碰撞[5]，提升驾驶辅助系统对周围环境变化的感知能力，提高预警系统的可靠性。目前, 车辆轨迹预测算法可以分为基于离散状态空间模型的方法和基于神经网络的方法两大类。离散状态空间模型主要通过学习具有不同分布规律的轨迹簇的运动模式，生成最接近实际车辆运行轨迹的预测特征值，路径模型[6-11]与隐马尔可夫模型[12-18]是再现轨迹簇演化特征的主流方法。另外，因神经网络[19]在给定相关且数量充足的训练数据时即可学习重要的数据特征这一优势而被广泛应用于未来车辆运动模式的学习[20-23]。近年来，部分学者试图将具有长短期记忆模型的递归神经网络[24-25]及多层感知器[26]应用于分析驾驶数据序列及目标运动轨迹的预测。
由于现有的大多数研究很少同时考虑车辆轨迹在空间与时间上的不确定性，缺乏对不同目标运动模式更深层次的统计分析。部分模型利用线性差值重新采样[11, 27-28]或以填充默认值[23]等方法对轨迹长度进行标准化处理，丢失了大量原始轨迹的重要特征信息。而利用离散状态空间模型进行轨迹预测时，能够尽可能地保留更多原始的时空轨迹信息，真实再现时空离散状态下的车辆运动轨迹。其中, 马尔可夫过程是研究离散事件动态系统状态空间的重要方法[29]，该模型只需要根据当前车辆轨迹特征数据和周围环境信息就能预测未来车辆轨迹，有效降低了车辆轨迹预测算法的复杂度[30]。
传统HMM模型具有离散的隐藏状态和发射变量，可分别对应于驾驶状态和车辆轨迹特征，但无法处理外界输入信息，不足以模拟复杂交互环境下的真实车辆运行状态。为避免传统HMM模型仅受隐藏状态数目的限制将右转车辆不同干扰程度下的轨迹分布特征平均化，尝试利用累计频率曲线法识别直行车辆受扰轨迹，并选用TTC值表征车辆间的作用程度，在传统隐马尔可夫模型结构上开发一种信号交叉口受扰直行车辆的轨迹预测算法，对不同受扰程度下的直行车轨迹的时空不确定性进行综合建模，旨在更真实地再现直行车在与被交道路右转车不断逼近时直行车随自身运行状态演化下的轨迹发展趋势。
1 数据采集与处理 1.1 调查地点为了更加有效地收集直行车辆的受扰轨迹数据，本文选取西安市太白南路-科技路信号交叉口进行样本采集，该交叉口东西进口道设置的专右信号在南北直行绿灯信号后半时段开启，在此期间直行车辆与被交道路的右转车辆在汇出交叉口时产生大量冲突，直行车辆轨迹扰动现象明显，交叉口的基本信息见表 1。将太白南路-科技路交叉口在东西右转相位期间从南北进口道驶入交叉口的直行车作为研究组, 其他南北直行相位期间驶入的直行车作为对比组。信号交叉口内干扰车辆流向与信号配时方案如图 1(a)、1(b)所示。
表 1
表 1 调查地点基本信息 Tab. 1 Basic information of survey location 道路交叉口 道路等级 调查相位 调查进口道 汇入/出车道数(a+b)/c 车道宽度/m 直行车样本数 太白南路-科技路 主-主相交 南北直行-东西右转 南进口 (3+1)/4 2.7 6 077
北进口 (4+1)/4 2.7 8 056
?注：a为交叉口上游直行车道数，b为上游右转车道数，c为下游汇出车道数。
表 1 调查地点基本信息 Tab. 1 Basic information of survey location
Fig. 1
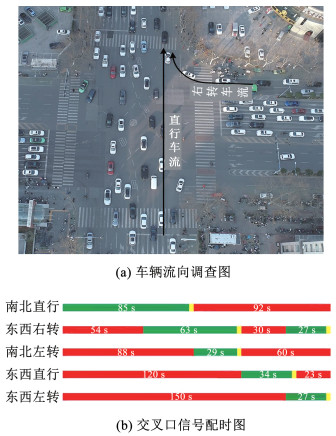图 1 信号交叉口概况图 Fig. 1 Overview of signal intersection 1.2 轨迹提取利用一架由DJI制造的无人驾驶飞行器Phantom 4(配备1英寸CMOS影响传感器，1 920×1 080，60 fps)对调查交叉口进行视频数据采集。使用Datafromsky Viewer 0.5.38对目标车辆的时空位置信息进行追踪并标记，结合输出的尾缀格式为tlgx文件，利用四点校准法在UTM坐标系中对视频图像进行地理校准，通过划定驶入、驶出门提取不同进、出口车道的车辆运行轨迹数据。本文以30 Hz的采样频率提取信号交叉口车辆轨迹特征(包括机动车的位置、速度、加速度、航向角等)，提取过程如图 2所示。调查总时长为11 h，总计获取14 133条直行车、5 577条右转车样本数据。
Fig. 2
图 2 信号交叉口车辆轨迹提取过程 Fig. 2 Vehicle trajectory extraction process at signalized intersections 1.3 数据处理利用python软件剔除错误识别为机动车的车辆轨迹、违章机动车轨迹以及在交叉口范围内运行记录不完整的样本数据。由于小波分析技术能够揭示变化趋势、故障点、不连续性等其他分析技术所容易忽略的信号，本文采用小波去噪法对车辆轨迹数据去噪，以保证去噪后轨迹数据的真实性。通过反复实验最终选择具有更好对称性的sym8小波基对含噪信号进行3层小波分解，并选用自适应阈值以及软阈值函数对小波分解的各层高频系数进行阈值量化处理，得到小波系数的估计值，最后通过对小波系数进行逆小波变换得到去噪信号，阈值确定方法如公式(1)、(2)所示。
$\lambda=\frac{M\left(\left|c D_1\right|\right)}{0.6745} \sqrt{2 \ln N} / \log _2(j+1)$ (1)
式中：λ为阈值，M表示取中位数，cD1为第一层分解的细节系数，N为信号序列长度，j为分解层数。
$\widetilde{\omega}_{j, k}=\left\{\begin{array}{l}\omega_{j, k}-a \lambda, \omega_{j, k} \geqslant \lambda \\0, \omega_{j, k} <\lambda \\\omega_{j, k}+a \lambda, \omega_{j, k} \leqslant-\lambda\end{array}\right.$ (2)
式中：ωj, k为小波系数，
通过信噪比(SNR)、均方根误差(RMSE)等指标评估轨迹数据去噪效果，均方根误差越小、信噪比越大，去噪效果越好。本文以ID为267的直行车辆速度数据为例进行去噪效果评估，计算得到信噪比为92.115，均方根误差为3.24×10-5，去噪效果如图 3所示，去噪前后速度偏差小于1.5×10-3(见图 4)，说明该方法在去除噪声点的同时能较好地保证原始数据的真实性。
Fig. 3
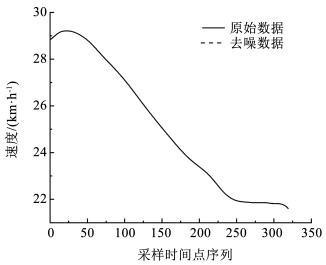图 3 车辆速度去噪图示 Fig. 3 Vehicle speed denoising diagram Fig. 4
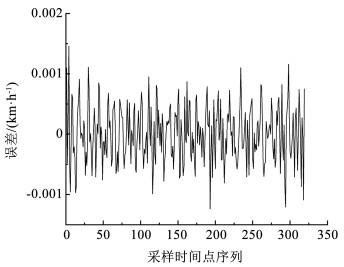图 4 车辆速度去噪误差(sym8, n=3) Fig. 4 Vehicle speed denoising error (sym8, n=3) 2 受扰车辆轨迹识别同一时段内驶入信号交叉口的直行车与相交道路的右转车在相互逼近的过程中，驾驶人通常根据冲突发生的可能性实时调整自车行驶状态从而保证行车安全，驾驶人一般会结合自车行驶状态与当前驾驶环境执行车道偏移与换道等避险操作(图 5)，如果这类行为发生，则认为车辆受扰。
Fig. 5
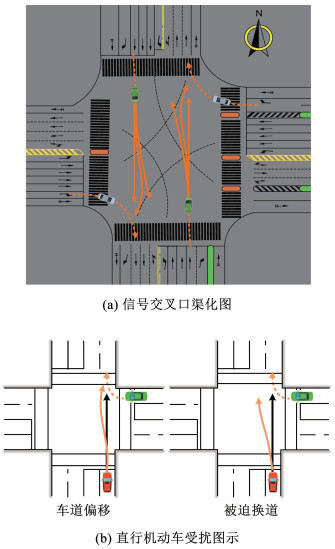图 5 信号交叉口直行机动车受扰图示 Fig. 5 Disturbance diagram of direct motor vehicles at signalized intersections 2.1 受扰直行车筛选假设目标直行车辆驶入、驶出交叉口的时间分别为ts1、ts2，右转车辆驶入、驶出交叉口的时间分别为tr1、tr2。当ts1＞tr2(表示直行车在驶入交叉口时，右转车辆已经驶离)或tr1＞ts2(表示直行车在驶离交叉口时，右转车辆开始驶入)，直行车均不会受到相交道路右转车辆的干扰。在剔除无右转车驶入时段的直行车辆轨迹的基础上，选择非跟驰状态下的直行车辆轨迹作为受扰轨迹候选样本。筛选步骤如下：
步骤1?确定相互作用时段(即相交道路右转车通过进口道停车线的时间—驶出交叉口的时间)。
步骤2?筛选该时段内进入交叉口的直行车辆轨迹。提取(m辆)直行车与(n辆)右转车的车辆ID、驶入时间、驶出时间；通过计算ts1-tr2、tr1-ts2的值，得到两个m×n的矩阵，并将所有负值标记为0、非负值标记为1(1表示直行车驶入时段内无右转车驶入)；筛选出目标直行车与右转车同时满足(0，0)的标记状态的车辆轨迹，即为在交叉口范围内可能发生扰动作用的直行车辆轨迹样本。
Fig. 6
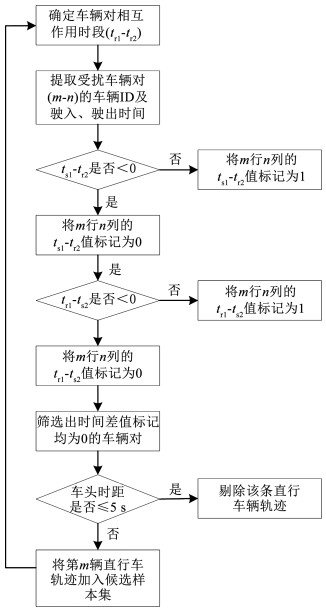图 6 直行车受扰轨迹候选样本筛选 Fig. 6 Selection of candidate samples for disturbed direct driving trajectories 步骤3?剔除跟驰车辆轨迹数据。现有研究[31-33]多采用车头时距为5 s作为车辆跟驰状态的临界值，本文参照已有研究结论剔除跟驰车辆(即车头时距≤5 s)。
2.2 受扰阈值确定本文通过“干扰-受扰车辆对”间的TTC指标以及受扰轨迹特征发生显著变化两个条件判断目标车辆是否受扰。
1) 受扰时间阈值。采用配对样本t检验的方法选择TTC小于一定阈值时与一般情况(无右转车干扰)下具有显著差异的车辆轨迹特征指标。通过统计每辆直行车与右转车间的最小冲突时间及直行车辆在运行过程中的最大特征偏移，将特征分布存在明显差异的冲突时间点初步确定为轨迹受扰时间阈值。最后，对比分析小于、大于该时间阈值以及一般情况下的轨迹特征值，采用配对样本t检验的方法验证上述受扰时间阈值的合理性。
2) 轨迹特征扰动阈值。采用85%位累积频率曲线判断轨迹非扰动情况，并采用扰动情况的15%位累积频率曲线对受扰轨迹特征值进行验证。若非扰动曲线85%位累计频率对应的轨迹特征值与扰动曲线15%位累计频率对应的轨迹特征值相差不大，则认定其为轨迹特征扰动阈值，否则，认为扰动分类不合理。
3 基于HMM模型的受扰轨迹预测对于任何给定的道路环境，以30 Hz的采样频率采样T次后，一条车辆轨迹序列可以用包含T个二维向量的一组时间序列表示，
3.1 受扰直行车运动模式学习根据第2节内容所述，在有右转车驶入同时存在冲突风险时，直行车驾驶人一般会采取车道偏移或换道两种驾驶模式规避风险。通过检查驶入、驶出车道编号是否一致来判断直行车辆的运动模式。
轨迹的离散性使离散状态模型(例如HMM)非常适用于连续运动的近似分析。HMM模型不仅可以灵活地反映车辆轨迹特征演化的不确定性，而且可以描述连续点之间的时间依赖性。通过对不同运动模式样本的训练，将所有轨迹映射到HMM模型的隐藏状态参数和状态转移矩阵中。
3.1.1 模型结构与参数定义传统的HMM模型(图 7(a))由一个两层系统模型组成，上层由描述隐藏状态之间转换的马尔可夫链组成，下层是描述可观测状态与隐藏状态之间生成关系的随机模型。而本文研究对象(即受扰车辆轨迹)的演化趋势在实际中同时会受到信号交叉口几何条件与其他交通参与者的影响，从而表现出不同的轨迹特征演化规律。
Fig. 7
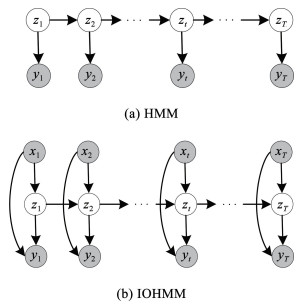图 7 隐马尔可夫模型结构图(白色节点为潜在变量，灰色节点为观测值) Fig. 7 Structure diagram of hidden Markov model (white nodes represent potential variables, gray nodes represent observed values) 通过引入第3变量层(x层)，如图 7(b)中所示为输入输出HMM模型，其中x为输入特征，采用目标车辆与干扰车辆间的TTC作为输入变量描述直行车辆与相交道路右转车辆的相互作用，其中输入层(x层)将同时作用于状态层(z层)与输出层(y层)。
采用以下符号定义提出的IOHMM模型。具有N个状态{S1, S2, …, SN}的一阶IOHMM模型和每个状态下的高斯混合概率密度函数由以下概率参数表示。
1) 先验状态概率分布π={πi}。初始隐藏状态依赖于初始时刻干扰变量(x层)，将输入变量类别为c时的状态初始概率定义为
$\pi_i{ }^c=P\left(z_1=q_i \mid x_1\right), \sum\limits_{i=1}^N \pi_i{ }^c=1, 1 \leqslant i \leqslant N$ (3)
2) 状态转移概率分布A={aij}。隐藏状态转移概率不仅取决于上一时刻的状态，同时受当前时刻输入变量的影响。
$\begin{aligned}& a_{i j}{ }^c= P\left(\left[z_t=q_j\right] \mid\left[z_{t-1}=q_i\right], x_t\right), \\& \sum\limits_{j=1}^N a_{i j}{ }^c=1, 1 \leqslant i, j \leqslant N\end{aligned}$ (4)
3) 观测概率密度矩阵B={bi(ot)}，假设各隐藏状态下生成的观测值服从GMM分布。在某类干扰变量作用下，生成当前观测值的概率为bi(ot)c：
$\begin{aligned}b_i\left(o_t\right)^c= & P\left(\left[y_t=o_t\right] \mid\left[z_t=S_i\right], x_t\right)= \\& p\left(y_t \mid \theta_i, x_t\right), 1 \leqslant i \leqslant N\end{aligned}$ (5)
$\begin{aligned}p\left(y_t \mid \theta_i, x_t\right) & =\sum\limits_{k=1}^K w_{i k} N\left(y_t \mid \mu_{i c k}, \sum\limits_{i k}\right), \\\mu_{i c k} & =\left(1+g_{i c k} x_t\right) \mu_{i k}, \\\sum\limits_{k=1}^K w_{i k} & =1, 0 \leqslant w_{i k} \leqslant 1\end{aligned}$ (6)
式中：p(y)为包含K个高斯成分的高斯混合模型概率密度分布函数，wik为第i个状态下k个高斯成分的权重值，μik、
3.1.2 模型参数学习HMM通过使用同一种运动模式的轨迹样本来学习模型参数，使模型以最大概率匹配样本数据。采用Baum-Welch算法递归计算模型参数，结合收敛条件求得模型参数的局部最优解。受扰车辆在通过交叉口时，一般会经历“受扰前- 受扰- 恢复”3个阶段。本文将模型状态数设置为3，每一个隐藏状态提供一种轨迹观测值的分布特征，利用状态转移矩阵描述各状态间的转移规则。根据极大似然原理，将车辆轨迹最终映射到HMM参数集合λ=(π, A, B)上，使用属于最优HMM的每个状态和转移的似然作为权重，按照以下步骤进行更新。
1) 初始化状态先验概率
π、A、B (wik, gick, μik, ∑ik)。
2) 输入观测变量
将观测数据Ω输入至系统y层。
3) 计算前向与后向概率
$\alpha_l^{x_t}(i)=P\left(y_1^l, y_2^l, \cdots, y_t^l, z_t=q_i \mid x, \lambda\right)$ (7)
$\beta_t^{x_l}(i)=P\left(y_{t+1}^l, y_{t+2}^l, \cdots, y_T^l, \mid z_t=q_i, x, \lambda\right)$ (8)
计算t时刻处于状态qi、t+1时刻处于状态qj的概率ξlt(i, j)：
$\begin{aligned}\xi_t^l(i, j)= & P\left(z_t=q_i, z_{t+1}=q_j \mid y^l, x_t, \lambda\right)= \\& \frac{\alpha_t^{x_l}(i) \beta_{t+1}^x{ }^l(j) a_{i j^x} b_{j^x}\left(y_{t+1}\right)}{\sum\limits_{i=1}^N \sum\limits_{j=1}^N \alpha_t^{x^l}(i) \beta_{t+1}^{x^l}(j) a_{i j^x} b_{j x}\left(y_{t+1}\right)}\end{aligned}$ (9)
计算t时刻处于状态qi的概率γtxl(i)：
$\begin{array}{r}\gamma_t^{x^l}(i)=P\left(z_t=q_i \mid y^l, x, \lambda\right)= \\\sum\limits_{j=1}^N \xi_t^l(i, j)=\frac{\alpha_t^{x^l}(i) \beta_t^{x^l}(i)}{\sum\limits_{j=1}^N \alpha_t^{x^l}(j) \beta_t^{x^l}(j)}\end{array}$ (10)
4) 更新参数
模型训练过程中需要更新的参数包括
对于每个离散状态qi，更新状态先验概率
$\widehat{\pi_i^c}=\frac{\sum\limits_{l=1}^J \gamma_1^{x^l}(i) I\left(x_1=c\right)}{\sum\limits_{l=1}^J \sum\limits_j^N \gamma_1^{x^l}(j) I\left(x_1=c\right)}$ (11)
式中：I(x1=c)表示当x1=c成立时函数值为1，否则为0。
更新参数A中的转移概率aij：
$\widehat{a_{i j}^c}=\frac{\sum\limits_{l=1}^J \sum\limits_{t=1}^{T-1} \xi_t^{x^l}(i, j) I\left(x_t=c\right)}{\sum\limits_{j=1}^N \sum\limits_{l=1}^J \sum\limits_{t=1}^{T-1} \xi_t^{x^l}(i, j) I\left(x_t=c\right)}$ (12)
以1 s为间隔将TTC离散化为7个数据区间(不同区间分别表示车辆冲突的不同严重程度)后作为影响因素输入x层，将整个观测序列O输入至y层。t时刻的观测样本yt属于状态qi中的第k个高斯成分的概率γtik为
$\begin{gathered}\gamma_{t i k}=P\left(z_t=S_i, \text { guass }=k \mid y, \lambda\right)= \\P\left(z_t=S_i \mid y, \lambda\right) P\left(\text { guass }=k \mid y_t\right)= \\P\left(z_t=S_i \mid y, \lambda\right) \frac{w_k N_k\left(y_t\right)}{\sum\limits_{m=1}^K w_m N_m\left(y_t\right)}\end{gathered}$ (13)
通过更新系数g, h更新每个离散状态Si下GMM模型参数:
$g_{i c k}=\frac{\sum\limits_{l=1}^J \sum\limits_{t=1}^T x_t \gamma_{t i k}^l\left(y_t^l-\mu_{i k}\right)}{\sum\limits_{l=1}^J \sum\limits_{t=1}^T x_t^2 \gamma_{t i k}^l \mu_{i k}}$ (14)
$\mu_{i k}=\frac{\sum\limits_{l=1}^J \sum\limits_{t=1}^T\left(1+g_{i c k} x_t\right) \gamma_{t i k}^l y_t^l}{\sum\limits_{l=1}^J \sum\limits_{t=1}^T\left(1+g_{i c k} x_t\right)^2 \gamma_{t i k}^l}$ (15)
$\begin{gathered}\sum\limits_{i k}=\frac{\sum\limits_{l=1}^J \sum\limits_{t=1}^T \gamma_{t i k}^l\left(y_t^l-\mu_{i c k}\right)\left(y_t^l-\mu_{i c k}\right)^T}{\sum\limits_{l=1}^J \sum\limits_{t=1}^T \gamma_{t i k}^l} \\w_{i k}=\frac{\sum\limits_{l=1}^J \sum\limits_{t=1}^T \gamma_{t i k}^l}{J \times T}\end{gathered}$ (16)
正则化
$w_{i k}=\frac{w_{i k}}{\sum\limits_{k=1}^K w_{i k}}$ (17)
3.1.3 模型收敛条件$\begin{gathered}\left|\log P\left(\Omega \mid \lambda_{t+1}\right)-P\left(\Omega \mid \lambda_t\right)\right| <\eta \\P\left(\Omega \mid \lambda_t\right)=\prod\limits_{l=1}^J P\left(O^l \mid \lambda_t\right)\end{gathered}$ (18)
式中: η为终止条件，如果条件成立，则学习过程终止；否则，进行下一轮迭代学习。
3.2 受扰轨迹预测通过求得未来某一时刻t的各隐藏状态概率值，并结合每一状态下生成的观测值的概率分布估计该时刻的观测特征值。
给定一段车辆轨迹观测值O={o1, o2, …, ot}以及各采样时刻的TTC值，通过3.1节中的算法训练得到的IOHMM模型(λ=π, A, B)来预测未来车辆轨迹的分布。
给定当前观测值ot，当前隐藏状态概率为
$\begin{gathered}P\left(z_t \mid y_t, x_t\right)= \\\frac{1}{G} P\left(y_t \mid z_t, x_t\right) \sum\limits_{z_{t-1}}\left[P\left(z_t \mid z_{t-1}, x_t\right) P\left(z_{t-1} \mid y_{t-1}, x_{t-1}\right)\right]\end{gathered}$ (19)
其中G为归一化变量，G=P(yt|xt)。将信念状态外推R个时间步长得到未来状态概率表达：
$\begin{gathered}P\left(z_{t+R} \mid y_t, x_{t+R}\right)= \\\sum\limits_{z_{t-1}}\left[P\left(z_{t+R} \mid z_{t+R-1}, x_{t+R}\right) P\left(z_{t+R-1} \mid y_t, x_{t+R-1}\right)\right]\end{gathered}$ (20)
基于由上式估计的不同时刻的车辆运行状态分布情况以及3.1节中求得的模型各项参数估计值，利用各状态的概率加权平均值估计未来车辆轨迹特征值：
$\operatorname{Tr}(t+R)=\sum\limits_{i=1}^N \sum\limits_{k=1}^K P\left(z_{t+R}=q_i \mid y_t, x_{t+R}\right) w_{i k} \mu_{i c k}$ (21)
最后，通过轨迹特征间的物理运动关系式可求得车辆位置坐标pt(x, y)：
$\begin{aligned}& x_t=x_{t-1}+l_t \cos \theta_{t-1} \\& y_t=x_{t-1}+l_t \sin \theta_{t-1}\end{aligned}$ (22)
其中
4 结果与讨论本文提出的车辆受扰轨迹预测模型在python平台实现，采用在设置有专用右转相位的信号交叉口采集到的多组拍摄视频进行实验。
4.1 直行车受扰轨迹筛选使用第2节中所提方法确定信号交叉口直行车辆轨迹受扰阈值并筛选受扰轨迹。研究分别选用TTC≤6 s时与一般情况下的坐标偏角(行驶方向与y轴的夹角)最大值、横向位置偏移最大值及加速度最大值进行配对样本t检验，检验结果表明(表 2)，仅坐标偏角最大值和加速度最大值在受扰与一般条件下存在显著性差异(Sig＜0.05)，因此, 选用坐标偏角最大值和加速度最大值作为受扰轨迹特征指标。
表 2
表 2 不同冲突时间下的轨迹特征差异性分析 Tab. 2 Analysis of the differences in trajectory characteristics under different conflict times 特征指标 平均值 标准差 标准误差平均值 差值95%置信区间 t df Sig.(双侧) 下限 上限
坐标偏角最大值 0.884 57 1.530 56 0.333 99 0.187 87 1.581 27 2.648 20 0.015
横向偏移最大值 0.238 95 1.426 47 0.327 26 -0.448 59 0.926 48 0.730 18 0.475
加速度最大值 -0.208 867 3 0.281 173 4 0.064 505 6 -0.344 388 6 -0.073 346 1 -3.238 18 0.005
表 2 不同冲突时间下的轨迹特征差异性分析 Tab. 2 Analysis of the differences in trajectory characteristics under different conflict times
右转车辆作用下的直行车辆的最大坐标偏角与最小冲突时间的分布关系如图 8所示，可以发现：在整体上直行车的坐标偏角随着冲突时间的增加逐渐趋于稳定，在统计范围(TTC≤6 s)内的直行车辆最大坐标偏角呈现出明显的两种分布情况，其中TTC≤4.5 s时(样本1)的最大坐标偏角的分布范围更为分散，TTC＞4.5 s时(样本2)的最大坐标偏角分布范围较为集中。说明随着冲突时间的增加，冲突发生的概率越小，轨迹扰动作用越轻微，在TTC≤4.5 s时车辆的横向扰动作用显著，因此, 4.5 s成为重要的轨迹扰动时间节点。
Fig. 8
图 8 信号交叉口直行车辆坐标偏角分布规律 Fig. 8 Distribution law of coordinate deviation angle of straight vehicles at signalized intersections 为验证以TTC=4.5 s作为受扰时间阈值的合理性，利用配对样本t检验分析TTC≤4.5 s与TTC＞4.5 s及一般情况下的车辆最大坐标偏角。检验结果显示(表 3)，样本1中的最大坐标偏角分别与样本2及一般情况下的最大坐标偏角存在显著差异；样本2与一般情况下的最大坐标偏角无明显差异。因此，本文将TTC≤4.5 s的坐标偏角数据作为横向受扰样本，将TTC＞4.5 s的坐标偏角数据作为非受扰样本。
表 3
表 3 不同冲突时间下的最大坐标偏角差异性分析 Tab. 3 Analysis of the differences in maximum coordinate deviation under different conflict times 配对样本 平均值 标准差 标准误差平均值 差值95%置信区间 t df Sig.(双侧) 下限 上限
样本1&样本2 2.257 86 1.687 72 0.451 06 1.283 40 3.232 32 5.006 13 0
样本1&一般情况 1.207 979 654 2.172 000 263 0.418 001 645 0.348 764 966 2.067 194 342 2.890 26 0.008
样本2&一般情况 0.122 818 497 0.853 925 142 0.228 221 094 -0.370 223 201 0.615 860 195 0.538 13 0.600
表 3 不同冲突时间下的最大坐标偏角差异性分析 Tab. 3 Analysis of the differences in maximum coordinate deviation under different conflict times
采用85%位累积频率曲线对坐标偏角的扰动情况进行划分(图 9)，非扰动曲线85%位累计频率与扰动曲线的15%位累积频率对应的坐标偏角差值小于0.5°，说明坐标偏角扰动与非扰动的分类结果较为合理。为增强受扰轨迹识别方法在任何交叉口条件下的普适性，结合道路几何坐标将车辆轨迹坐标偏角转化为偏航角(车辆实际轨迹与预定轨迹的夹角)，最终将偏航角阈值确定为2.35°。
Fig. 9
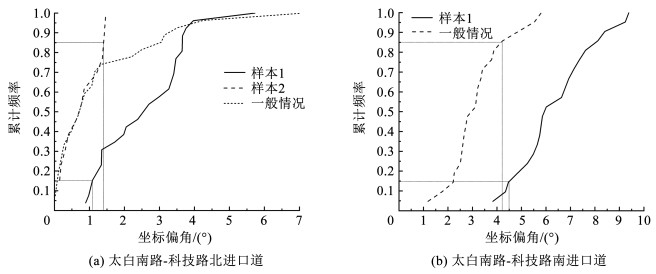图 9 直行车坐标偏角累积频率分布状况 Fig. 9 Cumulative frequency distribution of coordinate deviation angle for direct driving 通过分析未发现信号交叉口直行车辆的纵向加速度与冲突时间存在明显的线性关系。图 10对比分析了样本1与一般情况下的加速度(a组)、减速度(d组)以及速度变化率绝对值(m组)的最大值，发现样本1中(有右转车驶入时)的直行车辆纵向速度变化率在整体上均大于一般情况的变化率值，说明直行车在受扰时驾驶人可能会采取加速通过与减速让行两种避险操作，而在无干扰源时，直行车的运行状态更加平稳。
Fig. 10
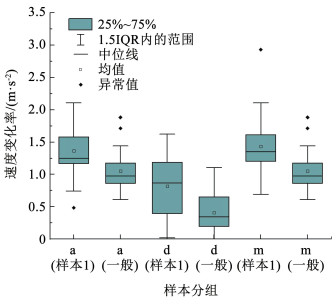图 10 不同分组下的直行车辆纵向加速度分布 Fig. 10 Longitudinal acceleration distribution of straight vehicles in different groups 在运行环境复杂的信号交叉口，直行车的驶入速度较低，在发现相交道路的右转车时的纵向加速度值发生微弱波动(小于2 m/s2)。较小的纵向加速度波动使扰动阈值的验证变得困难，因此本文以车辆轨迹横向受扰为研究重点，选取TTC≤4.5 s与偏航角＞2.35°共同确定信号交叉口直行车辆受扰轨迹。
根据确定的直行车受扰轨迹阈值，通过检验单条轨迹的最小TTC值与最大偏航角度是均否超过阈值，最终从14 133条直行车辆轨迹中筛选得到636条受扰轨迹(包括280条车道偏移轨迹，356条换道轨迹)。从北进口3、4车道筛选到的部分受扰轨迹如图 11所示，在右转车辆驶入位置之前，直行车运行轨迹就开始发生横向偏移；在发现相交道路有右转车辆驶入后，不同的直行车驾驶人会根据危急程度采取不同的应对策略(车道偏移或被迫换道)，从而呈现出不同的轨迹演化趋势；而一般情况下的车辆轨迹演化趋势更为平稳。通过观察视频验证了文中确定的车辆受扰轨迹阈值的合理性。
Fig. 11
图 11 直行车辆受扰轨迹分布 Fig. 11 Disturbance trajectory distribution of straight vehicles 4.2 受扰轨迹预测与精度检验本文将太白南路-科技路交叉口南、北进口的受扰直行车辆作为研究对象，通过测试IOHMM模型在车辆轨迹估计中的性能检验预测模型的有效性。根据3.1节模型训练方法，对模型超参数进行反复试验，最终设置为η=1×10-5，min_covar=0.001，不同驾驶行为下的车辆轨迹簇训练结果如图 12所示。在模型训练过程中生成的观测数据对数似然值越高，意味着输出轨迹特征值与训练模型拟合程度越高。从图 12可以看出根据模型配置参数，在400轮迭代后对数似然值基本都能够达到稳定状态，其中同时依赖于过去的隐藏状态与当前的输入变量的IOHMM模型在模型训练过程中能够取得较好的拟合效果。
Fig. 12
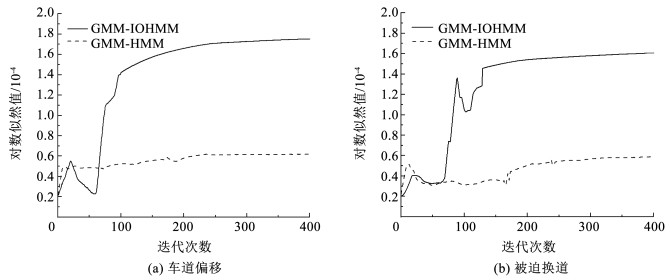图 12 观测数据的对数似然值 Fig. 12 Logarithmic likelihood value of observed data 为了确定最佳轨迹预测时段，通过计算平均估计误差来检验不同预测步长下的车辆轨迹估计精度。测试数据集包括调查交叉口北进口35条、南进口45条轨迹数据。不同预测步长下的平均估计误差为
$E(R)=\frac{1}{L} \sum\limits_{l=1}^L \frac{1}{R} \sum\limits_1^R\left\|o_{t+R}^l-p_{(t+R)}^l\right\|^{\frac{1}{2}}$
其中: L为测试轨迹条数，t=Tl×perc。
过去的研究表明，在大多数情况下驾驶员的反应时间为2.5 s[34]，并且在许多研究中被广泛接受[35]。通过比较不同观测值占比(perc取0.2、0.4、0.6、0.8)情况下的轨迹平均估计误差评估预测模型估计性能并确定最佳预测时间。预测结果统计分析(图 13)发现，随着观测到更多轨迹特征，模型估计的平均误差逐渐减小；随着预测步长的增加，误差逐渐增长，尤其在第75个预测步长(2.5 s)后，在使用20%和40%轨迹总长的观测值进行轨迹估计时的平均误差陡然增加，而40%和80%的误差曲线值也存在明显的上升趋势。其中，在第75个预测步长时的平均误差为1.05 m，以提供辅助驾驶提示为目的的车辆轨迹预测，该估计结果是可用的。因此，本研究将预测步长R值设定为75。
Fig. 13
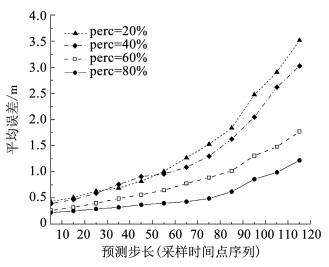图 13 不同预测步长的平均误差 Fig. 13 Average error of different prediction steps 分别对车道偏移和换道两种不同驾驶行为下产生的车辆轨迹估计结果进行对比(图 14)，结果显示在驶入信号交叉口初期，直行车辆更倾向于保持当前车道行驶，在受到相交道路右转车辆干扰时开始决策是否换道，随着车辆运行，驾驶人的驾驶意图逐渐明显；车道偏移的行驶距离明显短于换道轨迹，说明在场景14(a)中右转车辆对直行车辆的行驶速度影响较大，在场景14(b)中的影响主要体现在轨迹坐标的横向偏移中。以上两种轨迹预测结果符合实际的驾驶行为。为了更加准确地评价GMM-IOHMM模型的预测性能，本文分别选取了包括自量自回归(VAR)模型、卡尔曼滤波(KF)以及HMM等在内的传统时间序列模型进行对比(表 4)，结果显示本文提出的GMM-IOHMM模型各项评价指标均优于传统的时间序列模型，其中GMM-IOHMM模型的平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差RMSE比其他模型分别降低了3.832、5.2%、3.667，R2最大提高了0.353，说明本文所提模型有较高的预测精度，更适用于当前交通环境下的车辆轨迹预测需求。
Fig. 14
图 14 受扰直行车轨迹预测图示 Fig. 14 Disturbed direct driving trajectory prediction diagram 表 4
表 4 Tab. 4 Evaluation of the prediction effect of Time Series models 预测模型 MAE MAPE/% RMSE R2 VAR(2) 6.194 32.5 6.365 0.530
KF 5.955 31.1 6.113 0.643
GMM-HMM 4.177 28.6 4.420 0.815
GMM-IOHMM 2.362 27.3 2.698 0.883
表 4 Tab. 4 Evaluation of the prediction effect of Time Series models
5 结论针对城市道路信号交叉口直行车与相交道路右转车交汇时的轨迹扰动现象，提出了一种考虑在被交道路右转车辆驶入时本面直行车辆轨迹演化趋势的估计方法。通过配对样本t检验法与85%位累积频率曲线法分别确定直行车辆受扰时间阈值与轨迹特征扰动阈值，提出了一种“时间-特征”扰动阈值的轨迹受扰判别方法。将表征车辆相互作用程度的TTC指标作为输入层加入到传统HMM模型结构中构建了IOHMM模型，尽可能地还原了直行车辆在复杂的交叉口环境中的真实运行状态。使用实际的调查视频数据进行实验，结果表明采用“时间-特征”扰动阈值法能够有效筛选出直行车辆受扰轨迹，为车辆轨迹扰动的判别提供参考依据与解决思路。相比于其他时间序列模型，GMM-IOHMM算法能够充分利用概率方法对受扰轨迹的时空特征不确定性与突变性进行建模，为信号交叉口发生复杂交互作用的车辆提供更加准确的轨迹估计方法。预测结果可为直行车辆未来驾驶风险的判断以及驾驶辅助系统的设计提供理论依据。
此外，本研究仍存在一些局限性。对于模型结构的改进虽然能够取得比较理想的预测效果，但很容易发现连续的观测值之间仍存在较强的信息关联，后续研究可尝试考虑这种制约作用使模型预测逻辑更符合实际的车辆运动规律。另外，本研究虽然验证了改进算法的可行性，但还需要在更多不同的实验场景中加以论证，并且可以进一步探索多个方向车辆与自车间的相互作用，尽可能地还原实际交叉口的车辆运行状态。
参考文献
[1] LEVIN M W, KANG D. A multiclass link transmission model for a class-varying capacity and congested wave speed[J]. Journal of Transportation Engineering, Part A: Systems, 2023, 149(10): 04023096. DOI:10.1061/JTEPBS.TEENG-7940
[2] 高雪婷. 基于深度学习的行人和骑行者检测及防碰撞预警系统研究[D]. 镇江: 江苏大学, 2018
GAO Xueting. Research on detection and collision warning system of pedestrian and cyclist based on deep learning[D]. Zhenjiang: Jiangsu University, 2018. DOI: cnki:cdmd:2.1018.837387
[3] 甘元震. 高速公路车辆异常行驶状态预警研究[D]. 石家庄: 石家庄铁道大学, 2019
GAN Yuanzhen. Study on vehicle early warning of abnormal driving state on expressway[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2019
[4] 倪捷, 刘志强, 涂孝军, 等. 面向驾驶辅助系统的换道安全性预测模型研究[J]. 交通运输系统工程与信息, 2016, 16(4): 95.
NI Jie, LIU Zhiqiang, TU Xiaojun, et al. Safety prediction model of lane changing based on driver assistance system[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(4): 95. DOI:10.3969/j.issn.1009-6744.2016.04.014
[5] KANG D, LI Z, LEVIN M W. Evasion planning for autonomous intersection control based on an optimized conflict point control formulation[J]. Journal of Transportation Safety & Security, 2022, 14(12): 2074.
[6] AUGUSTIN D, HOFMANN M, KONIGORSKI U. Prediction of highway lane changes based on prototype trajectories[J]. 2019, 83: 149. DOI: 10.1007/s10010-019-00321-0
[7] MAKRIS D, ELLIS T. Path detection in video surveillance[J]. Image and Vision Computing, 2002, 20(12): 895. DOI:10.1016/S0262-8856(02)00098-7
[8] JUNEJO I N, FOROOSH H. Trajectory rectification and path modeling for video surveillance[C]//2007 IEEE 11th International Conference on Computer Vision. Rio de Janeiro, Brazil: IEEE, 2007: 1. DOI: 10.1109/ICCV.2007.4409008
[9] VASQUEZ D, FRAICHARD T. Motion prediction for moving objects: a statistical approach[C]//2004 IEEE International Conference on Robotics and Automation. New Orleans, LA, USA: IEEE, 2004. DOI: 10.1109/ROBOT.2004.1308883
[10] MOHAMED M G, SAUNIER N. Behavior analysis using a multilevel motion pattern learning framework[J]. Transportation Research Record Journal of the Transportation Research Board, 2015, 2528(1): 116. DOI:10.3141/2528-13
[11] TRAN Q, FIRL J. Online maneuver recognition and multimodal trajectory prediction for intersection assistance using non-parametric regression[C]//2014 IEEE Intelligent Vehicles Symposium Proceedings. Dearborn, MI, USA: IEEE, 2014. DOI: 10.1109/IVS.2014.6856480
[12] BASHIR F I, KHOKHAR A A, SCHONFELD D. Object trajectory-based activity classification and recognition using hidden Markov models[J]. IEEE Transactions on Image Processing, 2007, 16(7): 1912. DOI:10.1109/TIP.2007.898960
[13] 毛莺池, 陈杨. 不确定性车辆路口的轨迹预测[J]. 计算机科学, 2018, 45(3): 237.
MAO Yingchi, CHEN Yang. Uncertain vehicle intersection trajectory prediction[J]. Computer Science, 2018, 45(3): 237.
[14] BENNEWITZ M, BURGARD W, CIELNIAK G, et al. Learning motion patterns of people for compliant robot motion[J]. The International Journal of Robotics Research, 2005, 24(1): 31. DOI:10.1177/0278364904048962
[15] JEONG H, YOO Y, YI K M, et al. Two-stage online inference model for traffic pattern analysis and anomaly detection[J]. Machine Vision and Applications, 2014, 25(6): 1501. DOI:10.1007/s00138-014-0629-y
[16] MAKRIS D, ELLIS T. Spatial and probabilistic modelling of pedestrianbehaviour[C]//British Machine Vision Conference. Cardiff, UK: BMVA, 2002. DOI: 10.5244/C.16.54
[17] VASQUEZ D, FRAICHARD T, LAUGIER C. Incremental learning of statistical motion patterns with growing hidden Markov models[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(3): 403. DOI:10.1109/TITS.2009.2020208
[18] ZENG Xiangrui, WANG Junmin. Parallel hybrid electric vehicle energy management strategy using stochastic model predictive control with road grade preview[J]. IEEE Transactions on Control Systems Technology, 2015, 23(6): 2416. DOI:10.1109/TCST.2015.2409235
[19] LI Guofa, YANG Yifan, QU Xingda. Deep learning approaches on pedestrian detection in hazy weather[J]. IEEE Trans Industrial Electronics, 2020, 67(10): 8889. DOI:10.1109/TIE.2019.2945295
[20] JOHNSON N, HOGG D. Learning the distribution of object trajectories for eventrecognition[J]. Image & Vision Computing, 1996, 14(8): 609. DOI:10.1016/0262-8856(96)01101-8
[21] SUMPTER N, BULPITT A. Learning spatio-temporal patterns for predicting object behaviour[J]. Image and Vision Computing, 2000, 18(9): 697. DOI:10.1016/S0262-8856(99)00073-6
[22] HU Weiming, XIE Dan, TAN Tieniu, et al. A Hierarchical self-organizing approach for learning the patterns of motion trajectories[J]. IEEE Transactions on Neural Networks, 2004, 15(1): 135. DOI:10.1109/TNN.2003.820668
[23] HU W, XIAO X, XIE D, et al. Traffic accident prediction using 3-D model-based vehicle tracking[J]. IEEE Transactions on Vehicular Technology, 2004, 53(3): 677. DOI:10.1109/TVT.2004.825772
[24] FRAMING C E, HE?ELER F J, ABEL D. Learning scenario-specific vehicle motion models for intelligent infrastructure applications[J]. IFAC-PapersOnLine, 2019, 52(8): 111. DOI:10.1016/j.ifacol.2019.08.057
[25] WANG Lituan, ZHANG Lei, YI Zhang. Trajectory predictor by using recurrent neural networks in visual tracking[J]. IEEE Transactions on Cybernetics, 2017, 47(10): 3172. DOI:10.1109/TCYB.2017.2705345
[26] GOLDHAMMER M, KHLER S, ZERNETSCH S, et al. Intentions of vulnerable road users-detection and forecasting by means of machine learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(7): 3035. DOI:10.1109/TITS.2019.2923319
[27] BENNEWITZ M, BURGARD W, CIELNIAK G, et al. Learning motion patterns of people for compliant robot motion[J]. The International Journal of Robotics Research, 2005, 24(1): 31. DOI:10.1177/0278364904048962
[28] MORRIS B T, TRIVEDI M M. Learning, modeling, and classification of vehicle track patterns from live video[J]. IEEE Transactions on Intelligent Transportation Systems, 2008, 9(3): 425. DOI:10.1109/TITS.2008.922970
[29] 刘河生, 高小榕, 杨福生. 隐马尔可夫模型的原理与实现[J]. 国外医学· 生物医学工程分册, 2002(6): 253.
LIU Hesheng, GAO Xiaorong, YANG Fusheng. Theory of hidden Markov modeling and its implementation[J]. Foreign Medical Sciences (Section of Medgeography), 2002(6): 253. DOI:10.3760/cma.j.issn.1673-4181.2002.06.004
[30] 张峻峰. 智能车轨迹预测综述[J]. 汽车文摘, 2021(8): 34.
ZHANG Junfeng. Overview of intelligent vehicle trajectory prediction[J]. Automotive Digest, 2021(8): 34. DOI:10.19822/j.cnki.167-16329.20210108
[31] National Research Council(U.S.). HCM2010: highway capacity manual[M]. 5th ed. Washington DC: Transportation Research Board, 2010.
[32] 何民, 荣建, 任福田. 判定跟驰状态的研究[J]. 公路交通科技, 2001(4): 74.
HE Min, RONG Jian, REN Futian. Research on determining car-following state[J]. J Highw Transp Res Dev, 2001(4): 74. DOI:10.3969/j.issn.1002-0268.2001.04.021
[33] 王晓原. 微观交通流仿真建模理论及一体化仿真环境研究[D]. 长春: 吉林大学, 2002
WANG Xiaoyuan. Research on micro traffic flow simulation modeling theory and integrated simulation environment[D]. Changchun: Jilin University, 2002
[34] LERNER N D. Brake perception-reaction times of older and younger drivers[C]// Proceedings of the Human Factors and Ergonomics Society Annual Meeting. Santa Monica, California, USA: HFES, 1993: 206. DOI: 10.1177/154193129303700211
[35] YAN Xuedong, ZHANG Yuting, MA Lu. The influence of in-vehicle speech warning timing on drivers' collision avoidance performance at signalized intersections[J]. Transportation Research Part C, 2015, 51(2): 231. DOI:10.1016/j.trc.2014.12.003
