程国柱1,刘轩龄1,冯天军2
(1.东北林业大学 土木与交通学院,哈尔滨 150040;2.吉林建筑大学 交通科学与工程学院,长春 130118)
摘要:
为了解城市居民出行方式选择过程,完善公交优先策略的管控措施,对城市居民出行方式选择演化博弈模型展开研究。基于行为经济学理论,以前景理论为基础,引入心理账户理论,构建收益账户和损失账户。运用演化博弈理论,构建出行者与政府部门之间的演化博弈模型,通过复制动态方程分析双方策略的动态演化过程及稳定性条件。给出了系统最优状态与系统波动状态的约束条件,并从政府部门感知与出行者感知两方面解释了现实情况下,演化趋势未能达到理想状态的主要原因,提出目前政府部门管控措施存在的主要问题。运用MATLAB进行数值仿真,引入政府补贴动态绩效支付模式对模型进行优化,得到稳定状态下出行者选择公交出行概率为0.33,政府参与管控的概率为0.92,并进行了效价参数敏感性分析。研究结果表明:政府应主要从降低公交出行费用、适当提高私家车的出行费用成本以及缩短公交出行时间等方面优化公交管控策略,才能显著提升城市居民选择公交出行的概率。研究成果能够为城市交通出行规划与公交优先策略优化提供理论依据。
关键词: 交通规划 出行方式 管控策略 前景理论 心理账户 演化博弈
DOI：10.11918/202303030
分类号:U491.1
文献标识码:A
基金项目:中央高校基本科研业务费专项资金(2572023CT21)；吉林省科技发展计划(20220402030GH)
Evolutionary model of transportation mode choice for urban residents from the perspective of behavioral economics
CHENG Guozhu1,LIU Xuanling1,FENG Tianjun2
(1.School of Civil Engineering & Transportation, Northeast Forestry University, Harbin 150040, China; 2.School of Transportation Science and Engineering, Jilin University of Architecture, Changchun 130118, China)
Abstract:
In order to enhance the control measures of the public transportation priority policy and understand the mode choice process of urban residents for travel, a research was conducted to investigate the evolutionary game model of mode choice for urban residents. The study was based on the principles of behavioral economics theory and prospect theory, and incorporated the concept of mental accounting by constructing profit and loss accounts. Using evolutionary game theory, an evolutionary game model was developed between travelers and government agencies. The dynamic evolution process and stability conditions of both parties′ strategies were analyzed using replicator dynamics equations. The research identified the constraints of the system′s optimal state and system fluctuation state. Moreover, the main reasons for the deviation from the ideal state of the evolutionary trend in reality were explained from the perspectives of government perception and traveler perception. Additionally, the study identified the main problems of the current government control measures. Numerical simulations were conducted using MATLAB, and an optimization model with a dynamic performance payment mode for government subsidies was introduced. The research findings showed that the stable probability of travelers choosing public transportation was 0.33, and the probability of government participation in control was 0.92. Sensitivity analysis of the utility parameters was also conducted. The results of the study indicate that the government should focus on optimizing its public transportation control strategy by reducing the cost of public transportation, appropriately increasing the cost of private car travel, and shortening the travel time of public transportation. This would significantly increase the probability of urban residents choosing public transportation. In summary, the research provides a theoretical basis for urban transportation planning and public transportation priority policy optimization.
Key words: transportation planning transportation mode control strategy prospect theory mental accounting evolutionary game
程国柱, 刘轩龄, 冯天军. 行为经济学视角下城市居民出行方式选择演化博弈模型[J]. 哈尔滨工业大学学报, 2024, 56(7): 102-111. DOI: 10.11918/202303030.
CHENG Guozhu, LIU Xuanling, FENG Tianjun. Evolutionary model of transportation mode choice for urban residents from the perspective of behavioral economics[J]. Journal of Harbin Institute of Technology, 2024, 56(7): 102-111. DOI: 10.11918/202303030.
基金项目 中央高校基本科研业务费专项资金(2572023CT21)；吉林省科技发展计划(20220402030GH) 作者简介 程国柱(1977—)，男，教授，博士生导师 通信作者 冯天军，68202791@qq.com 文章历史 收稿日期: 2023-03-08
Abstract Full text Figures/Tables PDF
行为经济学视角下城市居民出行方式选择演化博弈模型
程国柱1, 刘轩龄1, 冯天军2
1. 东北林业大学 土木与交通学院, 哈尔滨 150040;
2. 吉林建筑大学 交通科学与工程学院, 长春 130118
收稿日期: 2023-03-08; 录用日期: 2023-05-25; 网络首发日期: 2024-03-18
基金项目: 中央高校基本科研业务费专项资金(2572023CT21)；吉林省科技发展计划(20220402030GH)
作者简介: 程国柱(1977—)，男，教授，博士生导师
通信作者: 冯天军，68202791@qq.com
摘要: 为了解城市居民出行方式选择过程，完善公交优先策略的管控措施，对城市居民出行方式选择演化博弈模型展开研究。基于行为经济学理论，以前景理论为基础，引入心理账户理论，构建收益账户和损失账户。运用演化博弈理论，构建出行者与政府部门之间的演化博弈模型，通过复制动态方程分析双方策略的动态演化过程及稳定性条件。给出了系统最优状态与系统波动状态的约束条件，并从政府部门感知与出行者感知两方面解释了现实情况下，演化趋势未能达到理想状态的主要原因，提出目前政府部门管控措施存在的主要问题。运用MATLAB进行数值仿真，引入政府补贴动态绩效支付模式对模型进行优化，得到稳定状态下出行者选择公交出行概率为0.33，政府参与管控的概率为0.92，并进行了效价参数敏感性分析。研究结果表明：政府应主要从降低公交出行费用、适当提高私家车的出行费用成本以及缩短公交出行时间等方面优化公交管控策略，才能显著提升城市居民选择公交出行的概率。研究成果能够为城市交通出行规划与公交优先策略优化提供理论依据。
关键词: 交通规划 出行方式 管控策略 前景理论 心理账户 演化博弈
Evolutionary model of transportation mode choice for urban residents from the perspective of behavioral economics
CHENG Guozhu1, LIU Xuanling1, FENG Tianjun2
1. School of Civil Engineering & Transportation, Northeast Forestry University, Harbin 150040, China;
2. School of Transportation Science and Engineering, Jilin University of Architecture, Changchun 130118, China
Abstract: In order to enhance the control measures of the public transportation priority policy and understand the mode choice process of urban residents for travel, a research was conducted to investigate the evolutionary game model of mode choice for urban residents. The study was based on the principles of behavioral economics theory and prospect theory, and incorporated the concept of mental accounting by constructing profit and loss accounts. Using evolutionary game theory, an evolutionary game model was developed between travelers and government agencies. The dynamic evolution process and stability conditions of both parties′ strategies were analyzed using replicator dynamics equations. The research identified the constraints of the system′s optimal state and system fluctuation state. Moreover, the main reasons for the deviation from the ideal state of the evolutionary trend in reality were explained from the perspectives of government perception and traveler perception. Additionally, the study identified the main problems of the current government control measures. Numerical simulations were conducted using MATLAB, and an optimization model with a dynamic performance payment mode for government subsidies was introduced. The research findings showed that the stable probability of travelers choosing public transportation was 0.33, and the probability of government participation in control was 0.92. Sensitivity analysis of the utility parameters was also conducted. The results of the study indicate that the government should focus on optimizing its public transportation control strategy by reducing the cost of public transportation, appropriately increasing the cost of private car travel, and shortening the travel time of public transportation. This would significantly increase the probability of urban residents choosing public transportation. In summary, the research provides a theoretical basis for urban transportation planning and public transportation priority policy optimization.
Keywords: transportation planning transportation mode control strategy prospect theory mental accounting evolutionary game
交通出行方式的选择是影响交通拥堵与出行系统碳排放最重要的决策因素。探究城市居民出行方式选择过程，寻求合理高效的公交优先管控措施尤为重要。城市居民日常交通出行方式包括以私家车为代表的私人交通出行方式和以公交车为代表的公共交通出行方式。城市居民出行选择行为领域的研究方向可以大致分为客观因素研究与主观因素研究，客观因素方面，文献[1-3]利用随机森林方法，分别研究了土地利用策略、汽车拥有情况等因素对出行行为的影响。文献[4]探究了停车成本与生活环境对出行方式选择的影响。文献[5-6]的研究成果表明社会规范能够显著影响城市居民出行方式选择。主观因素方面，文献[7-10]的研究分别证明了低碳理念、出行意图、出行态度、环保意识等内在心理因素对出行选择行为存在不可忽视的影响。
行为经济学是以人类行为作为基本研究对象的经济理论, 借助心理学的分析方法, 对个体和群体的经济行为特征进行规律性的研究，前景理论与心理账户理论是行为经济学中的重要概念。近年来，国内外已有诸多学者将前景理论与心理账户理论引入交通出行行为研究，文献[11]利用前景理论研究出行时间对出行方式选择的影响。文献[12]的研究认为能够用前景理论解释出行时间价值。文献[13]基于累积前景理论，构建了通勤者换乘行为决策模型。演化博弈理论在交通出行研究领域也多有应用，文献[14]基于演化博弈理论，探究不同出行目标下的汽车行驶速度。文献[15]通过构建演化博弈模型分析了私家车合乘共享服务的演化规律。文献[16]结合前景理论与演化博弈理论对交通流演化过程进行了分析。
2023年3月，多个国家部门联合发布了《加快建设交通强国五年行动计划(2023—2027年)》，旨在提升城市公共交通服务品质和优化出行结构，深化城市公共交通优先战略。尽管公交优先管控措施的研究正在逐步深入，但目前缺乏将出行选择行为与政府管控相结合的研究。大部分出行行为研究假定出行者完全理性，但交通环境的复杂性和不确定性意味着个体难以获取完整信息，实际上，出行者的决策往往受限于其有限的思考和判断能力。结合行为经济学的前景理论和心理账户理论探究政府的管控措施与管控力度对公众公交出行选择影响研究可以补充这一理论缺失。
本研究基于行为经济学理论，将出行者群体视为有限理性，构建出行方式选择的演化博弈模型，挖掘现有管控措施存在的问题，给出公交优先策略的优化建议，以期提升公交出行吸引力，引导城市居民出行方式向公共交通转变。
1 行为经济学理论依据 1.1 前景理论在不确定性环境决策研究领域中，离散选择模型和期望效用模型一直是常用的模型。这两种模型都基于完全理性的假设，与个体实际决策过程不符。对此，心理学家基于行为学科与心理学科提出了前景理论[17]。前景理论区别于期望效用理论，认为个体在决策过程中是有限理性的，该理论解释了有限理性心理因素和行为特征对决策者选择策略的作用机制，从而打破了完全理性决策者的不合理假设。在本研究中，出行者群体与政府群体均是有限理性的决策主体，符合前景理论的基本设定，因此, 可以利用前景理论分析出行者群体的决策过程，特别是政府管控政策对出行者心理账户的影响以及出行者对于公交优先政策的偏好程度。另外，前景理论还能够考虑参照点影响，衡量政府管控措施与个体交通需求，产生不同的心理感受和决策。
在前景理论中，决策者通过评价收益和损失效用，从价值最大化的角度解释了个体在不确定条件下的决策过程。其中，收益和损失是相对于参考点进行评估，而不是以价值的绝对水平衡量[18]。决策者选择自己满意的策略，而不是一味地追求最大效用。前景理论具有5个核心观点[19]：1)损失厌恶。对于相同量值的收益与损失，损失带来的厌恶感大于对收益带来的满足感，如图 1所示。2)风险逆转。决策者的风险偏好会在参照点附近发生逆转。3)参照依赖。决策者根据预设的参照点衡量收益或损失。4)概率加权。通过概率加权体现决策者高估小概率事件而低估大概率事件。5)确定效应。决策者更愿意获取更小的确定收益而非更大的风险收益。
Fig. 1
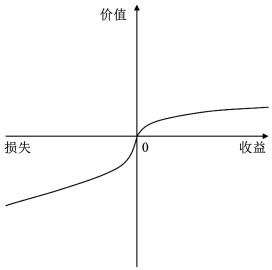图 1 前景理论价值趋势图 Fig. 1 Prospect theory value trend chart 前景理论将决策分为编辑阶段与决策阶段[20]。在编辑阶段，决策者基于理论框架与参考点设定，利用编码、整合、分离、抵消、简化、发现占优等编辑方法进行初步分析，在评估阶段，根据编辑阶段的分析结果结合价值函数和主观概率权重计算策略前景值，选择最满意的策略。前景价值函数形式[21]为
$P_{\mathrm{T}}=f(\Delta x) \pi(p)$ (1)
式中：PT为对策略的整体价值感知，f为判断价值函数，Δx为价值与参考点的差值，π为决策权重函数，p为策略发生的概率。
1.2 心理账户理论为进一步完善个体的决策行为分析，在前景理论的基础上提出了心理账户理论。实质上是将人们在心理层面无意识地把财富划归不同的账户进行管理，旨在解释真实的决策行为[22]。
心理账户理论现阶段的相关应用主要集中在风险投资、消费决策等领域，研究中考虑的效用属性通常是单一的，如时间或金钱，而交通出行行为决策研究的效用计算应考虑多属性因素。本研究基于前景理论构建心理账户，参考人的得失感受差异，将决策者的价值感知函数PT分为收益感知账户V(x)与损失感知账户Z(x)，且收益账户与损失账户具有对应的参考点与价值感知函数，具体函数[17]：
$V(x)=\left\{\begin{array}{l}\left(x-U_0\right)^\theta, x \geqslant U_0 \\-\lambda\left(U_0-x\right)^\beta, x <U_0\end{array}\right.$ (2)
$Z(x)=\left\{\begin{array}{l}\delta\left(x-U_1\right)^{\varphi}, x \geqslant U_1 \\-\left(U_1-x\right)^\sigma, x <U_1\end{array}\right.$ (3)
式中：V(x)为收益账户的判断价值函数，Z(x)为损失账户的判断价值函数，λ、δ为损失规避敏感系数，U0为收益参照点，U1为损失参照点，x为价值变量，θ、β为收益账户的风险偏好系数，φ、σ为损失账户的风险偏好系数。
以π+(p)和π-(p)分别表示收益和损失时的决策权重，决策权重函数的具体表现形式如式(4)、式(5)[23]所示，p为策略选择概率，参数γ与μ为决策灵敏系数，决策灵敏系数越小函数形态越弯曲，说明决策者越容易将小概率事件高估，而将大概率事件低估，如图 2所示。
Fig. 2
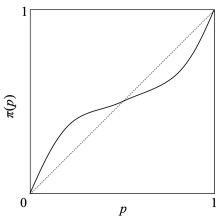图 2 前景理论决策权重函数 Fig. 2 Prospect theory decision weighting function $\pi^{+}(p)=\frac{p^\gamma}{\left[p^\gamma+(1-p)^\gamma\right]^{\gamma-1}}$ (5)
$\pi^{-}(p)=\frac{p^\mu}{\left[p^\mu+(1-p)^\mu\right]^{\mu-1}}$ (6)
1.3 演化博弈理论在经典博弈论中，个体被视为理性决策者。演化博弈论与经典博弈论不同，考虑了进化过程，融合了生物进化理论和经典博弈论，将个体的策略和行为看作是通过遗传信息传递和随机变异而不断发展和演化的。在演化博弈论中，个体的行为是策略，演化过程是动态博弈过程。个体通过考虑不同策略的利弊得失，适应和调整自身策略。
在政府制定交通管理政策和措施的实践中，演化博弈理论提供了一个符合实际的分析框架。出行者在面对不同的出行条件、政府政策和交通管控措施时，其出行方式的选择呈现出演化博弈的特征。城市居民在决定出行方式时，会考虑个人经济状况、家庭需求以及出行目的等多种因素。然而，在信息不完全的情况下，他们往往依据个人的经验和习惯做出决策，这可能导致多数人做出类似的出行方式选择，倾向于选择经济性、便捷性高的出行方式。鉴于此，本研究假设城市居民在出行方式选择上呈现出一定的普遍性和同质性，将其作为演化博弈的主体进行分析。
基于以上分析，出行者与政府满足演化博弈分析的基本条件，可以将政府和出行者之间的互动看作一种博弈过程，通过建立适当的博弈模型，分析双方的策略和利益冲突，进而预测不同情况下双方的演化稳定策略。
2 演化博弈模型 2.1 模型假设本研究演化博弈分析基于以下假设：1)博弈双方为城市交通出行者群体与城市政府管理部门群体，以下简称出行者与政府，博弈主体在博弈过程中具有有限理性；2)假设居民一次出行行为仅选择一种交通方式，不考虑换乘改变交通工具的情况；3)假设城市居民出行选择具有同质性；4)假设城市居民总出行需求保持恒定，双方博弈只会使出行策略发生改变而不会改变出行需求；5)博弈双方策略选择均基于自身价值感知而非实际作用效果，博弈过程符合基于前景理论与心理账户理论结合构建的前景价值函数；6)本文所指出行者在出行交通方式主要面临两种选择{公交车, 私家车}, 政府管理部门是管理措施与补贴政策的制定者，在公交引导工作中面临两种选择{参与管控, 不参与管控}。
2.2 模型构建政府管理部门采取了多项管控措施以提高公交出行效率和环保意识，包括设置专用公交道和公交信号优先等，以提高公交速度并减缓交通拥堵与碳排放，尽管这可能会影响私家车的通行速度。同时，通过政府补贴降低公交票价，优化公交服务如线路布局和发车频率，以提升出行舒适度和服务质量，鼓励居民选择公交。此外，利用媒体和网络加强环保宣传，推广绿色低碳出行理念，以缓解交通和环境问题。
政府在公共交通管控策略中主要考虑出行费用、时间、舒适度及低碳意识4个方面。出行费用作为固定成本，对决策有显著影响，而出行时间由多因素影响且难以预估，其变化对决策的影响较大。尽管舒适度重要，人们在选择时更倾向于进行相对比较，使其影响相对较小。低碳理念虽普遍认同，但个人在选择出行方式时往往优先考虑经济和效率因素。因此，从出行者角度看，政府管控策略对决策的影响依次是出行费用、时间、舒适度和低碳理念。
基于场景界定与博弈双方的策略选择立场，进一步细化主体行为策略的成本与收益。相关参数如下：n1为政府参与时出行者选择公交的费用收益感知系数, n1≥1；n2为政府参与时出行者选择公交的时间成本感知系数, n2≤1；n3为政府参与时私家车出行者的时间收益感知系数, n3≤1；Cp为私家车出行的费用感知损失；Cs为公交出行的舒适度感知损失；Ct为公交出行的时间感知损失；Pk为公交出行费用感知收益；Pt为私家车出行的出行时间感知收益；Ps为私家车出行的舒适度感知收益；B为公交优先时公交出行人数多产生的额外感知成本；N为公交优先时私家车无需与公交车争路权且私家车减少产生的额外感知收益；G政府不采取管控措施出行者大量选择公交出行产生的额外维护成本；M为政府参与管理时的管理劳动感知成本；S为政府参与管理时的财政补贴成本；W为出行者选择公交出行为路网带来的容量收益；J为出行者选择私家车出行给社会造成的拥堵损失；E为出行者选择私家车出行给社会造成的环境污染损失；x为出行者选择公交出行的概率；y为政府部门参与引导管理工作的概率。其中，效价参数中的参数Cs与参数B是出行者分别将客观舒适度及额外成本与预期参照点进行比较得出的心理感受值。由于公交出行舒适度与政府额外成本受公交出行者数量的影响较大，因此对公交出行舒适度与政府额外成本进一步定义。
根据现实情况，在出行者数量增加时，公交出行的舒适度呈现S型曲线的变化趋势，理论上可用sigmoid函数[24]来描述。该函数在曲线前半部分出行者数量增加时舒适度下降较缓慢，而在曲线后半部分下降速度较快，取值为0~1，表示舒适度的百分数。公交出行舒适度感知随出行者数量变化的基础模型表示为式(6)，该模型可用于描述公交舒适度随出行者数量变化的趋势，并可根据实际情况调整参数以适应不同场景。
$S=\frac{1}{1+\mathrm{e}^{k_1\left(N_b-N_0\right)}}$ (6)
式中：S为公交出行的舒适度，Nb为在公交车上的出行者数量，N0为公交车的额定载客量，k1为调节参数。
考虑到公交出行人数的增加可能导致政府承担额外成本，包括基础设施建设成本、运营维护成本和社会服务成本等。当公交出行人数较少时，政府的额外成本通常较低，因为公交车速度较快，交通拥堵和环境污染程度也较低。然而，随着出行者数量的增加，这些成本将增加。当公交车乘客接近或超过额定容量时，政府的额外成本将急剧增加。因此，额外成本与出行者数量应呈指数关系而非线性关系。基于上述分析，公交出行人数过多导致政府产生额外成本的基础模型表示为式(7)，该模型可用于描述政府额外成本随公交出行者数量变化的趋势，并可根据实际情况调整参数以适应不同场景。
$B_c=k_2 \frac{N_b^2}{N_0-N_b}$ (7)
式中：Bc为政府的额外成本，k2为调节参数。
基于模型假设与效价参数构建基于心理账户理论的博弈支付矩阵，如表 1所示。
表 1
表 1 基于心理账户的博弈支付矩阵 Tab. 1 Game payoff matrix based on mental accounts 策略 博弈主体 政府部门参与管控的概率y 政府部门不参与管控的概率1-y 公交出行的概率x 出行者
政府部门 V(W)－[Z(M)+Z(S)] V(W)－Z(G)
私家车出行的概率1-x 出行者
政府部门
表 1 基于心理账户的博弈支付矩阵 Tab. 1 Game payoff matrix based on mental accounts
2.3 模型分析 2.3.1 复制动态方程复制动态方程是演化博弈中描述博弈主体策略变化的数学模型，考虑了策略效价和其他策略效价对策略选择或淘汰的影响[25]。通过求解复制动态方程，可以找到演化博弈的稳定策略，即博弈主体在演化过程中不断调整策略以改善自身利益，并达到均衡状态。演化稳定策略指在该状态下，博弈主体不会因小突变而改变自身策略，具有有限理性的博弈主体会保持当前选择的策略。根据出行者与政府部门的博弈关系可得出行者选择公交出行的价值感知TBY：
$\begin{aligned}T_{\mathrm{BY}}= & \pi(y)\left[V\left(n_1 P_k\right)-\left(Z\left(n_2 C_t\right)+Z\left(C_s\right)+\right.\right. \\& Z(B))]+\pi(1-y)\left[V\left(P_k\right)-\right. \\& \left.\left(Z\left(C_t\right)+Z\left(C_s\right)\right)\right]\end{aligned}$ (8)
出行者选择私家车出行的价值感知TBN：
$\begin{aligned}T_{\mathrm{BN}}= & \pi(y)\left[V\left(n_3 P_t\right)+V\left(P_s\right)+V(N)-\right. \\& \left.Z\left(C_p\right)\right]+\pi(1-y)\left[V\left(P_t\right)+\right. \\& \left.V\left(P_s\right)-Z\left(C_p\right)\right]\end{aligned}$ (9)
出行者群体的平均价值感知TB：
$T_{\mathrm{B}}=x T_{\mathrm{BY}}+(1-x) T_{\mathrm{BN}}$ (10)
同理，可以求得政府参与管控的价值感知TGY：
$\begin{aligned}T_{G Y}= & \pi(x)[V(W)-(Z(M)+Z(S))]+ \\& \pi(1-x)[-(Z(M)+Z(S)+ \\& Z(J)+Z(E))]\end{aligned}$ (11)
政府部门不参与管控的价值感知TGN：
$\begin{aligned}T_{G N}= & \pi(x)[V(W)-Z(G)]+ \\& \pi(1-x)[-(Z(J)+Z(E))]\end{aligned}$ (12)
政府部门的平均价值感知TG：
$T_{\mathrm{G}}=y T_{\mathrm{GY}}+(1-y) T_{\mathrm{GN}}$ (13)
根据非对称复制动态演化方式，得到出行者选择策略的复制动态方程：
$\begin{aligned}F(x, y)= & \frac{d_x}{d_t}=x\left(T_{\mathrm{BY}}-T_{\mathrm{B}}\right)=x(1-x)\left(T_{\mathrm{BY}}-T_{\mathrm{BN}}\right)= \\& x(1-x)\left\{\pi ( y ) \left[V\left(n_1 P_k\right)-\left(Z\left(n_2 C_t\right)+\right.\right.\right. \\& \left.\left.Z\left(C_s\right)+Z(B)\right)\right]+\pi(1-y)\left[V\left(P_k\right)-\right. \\& \left.\left(Z\left(C_t\right)+Z\left(C_s\right)\right)\right]-\pi(y)\left[V\left(n_3 P_t\right)+\right. \\& \left.V\left(P_s\right)+V(N)-Z\left(C_p\right)\right]- \\& \left.\pi(1-y)\left[V\left(P_t\right)+V\left(P_s\right)-Z\left(C_p\right)\right]\right\}= \\& x(1-x)[\pi(y) Q+\pi(1-y) H]\end{aligned}$ (14)
式中：Q为政府部门参与管控时，出行者群体公交出行的价值函数-私家车出行的价值函数; H为政府部门不参与管控时，出行者群体公交出行的价值函数-私家车出行的价值函数。令F(x, y)=0，解得x=0, x=1, y=[H/(H－Q)]γ－1。
政府管理部门选择策略的复制动态方程：
$\begin{aligned}R(x, y)= & \frac{d_y}{d_t}=y\left(T_{\mathrm{GY}}-T_{\mathrm{G}}\right)=y(1-y)\left(T_{\mathrm{GY}}-T_{\mathrm{GN}}\right)= \\& y(1-y)\{\pi(x)[V(W)-(Z(M)+ \\& Z(S))]+\pi(1-x)[-(Z(M)+Z(S)+ \\& Z(J)+Z(E))]-\pi(x)[V(W)-Z(G)]- \\& \pi(1-x)[-(Z(J)+Z(E))]\}= \\& y(1-y)[\pi(x) D+\pi(1-x) L]\end{aligned}$ (15)
式中：D为出行者选择公交出行时，政府管理部门参与管控的价值函数-不参与管控的价值函数；L为出行者选择私家车出行时，政府管理部门参与管控的价值函数-不参与管控的价值函数。令R(x, y)=0，解得y=0, y=1, x=[L/(L－D)]μ－1。
2.3.2 演化稳定性分析联立方程
$\boldsymbol{J}=\left[\begin{array}{ll}\frac{\partial F(x, y)}{\partial(x)} & \frac{\partial F(x, y)}{\partial(y)} \\\frac{\partial R(x, y)}{\partial(x)} & \frac{\partial R(x, y)}{\partial(y)}\end{array}\right]=\left[\begin{array}{cc}(1-2 x)[\pi(y) Q+\pi(1-y) H] & x(1-x)\left[\frac{\mathrm{d} \pi(y)}{\mathrm{d} y} Q+\frac{\mathrm{d} \pi(1-y)}{\mathrm{d} y} H\right] \\y(1-y)\left[\frac{\mathrm{d} \pi(x)}{\mathrm{d} x} D+\frac{\mathrm{d} \pi(1-x)}{\mathrm{d} x} L\right] & (1-2 y)[\pi(x) D+\pi(1-x) L]\end{array}\right]$ (16)
矩阵行列式det J：
$\operatorname{det} \boldsymbol{J}=\frac{\partial F(x, y)}{\partial(x)} \frac{\partial R(x, y)}{\partial(y)}-\frac{\partial F(x, y)}{\partial(y)} \frac{\partial R(x, y)}{\partial(x)}$ (17)
矩阵的迹tr J：
$\operatorname{tr} \boldsymbol{J}=\frac{\partial F(x, y)}{\partial(x)}+\frac{\partial R(x, y)}{\partial(y)}$ (18)
在演化博弈中，可以基于不同条件下的均衡点类型分析演化博弈结果的稳定性及演化趋势。不同的均衡点类型代表着不同的策略组合与结果分配方式，分别对应不同的演化稳定状态和动态演化路径。为了对不同稳定状态进行深入分析，通过上述计算能够得到局部均衡点满足演化均衡点的判断条件，由于篇幅限制本研究只讨论演化系统最理想状态以及波动演化状态，如表 2所示。
表 2
表 2 演化博弈均衡判断表 Tab. 2 Evolutionary game equilibrium assessment table 策略组合 均衡点 det J det J值 tr J tr J值 均衡点类型 (0, 0) HL 正值 H+L 正值 不稳定点
Q>0, D>0, H>0, L>0 (1, 0) -HD 负值 D-H 不定 鞍点
(0, 1) -QL 负值 Q-L 不定 鞍点
(1, 1) QD 正值 -(D+Q) 负值 ESS
(0, 0) HL 负值 H+L 不定 鞍点
Q < 0, D>0, L < 0, H>0 (1, 0) -HD 负值 D-H 不定 鞍点
(0, 1) -QL 负值 Q-L 不定 鞍点
(1, 1) QD 负值 -(D+Q) 不定 鞍点
表 2 演化博弈均衡判断表 Tab. 2 Evolutionary game equilibrium assessment table
1) 当且仅当满足式(16)条件时，系统演化趋势收敛于(1, 1)，此状态为系统演化理想状态，演化博弈趋势相位如图 3所示。
Fig. 3
图 3 均衡稳定策略为(1, 1)演化博弈相位图 Fig. 3 Phase diagram of evolutionary games with equilibrium stable strategy of (1, 1) 约束条件(19)表明，出行者普遍对公交出行持正面价值感知，政府无论如何都会积极推行公交优先管理。但受多种现实因素影响，未能实现最优状态。具体而言，政府面临财政补贴、管理、规划建设及基础设施高成本的挑战, 出行者则因道路拥堵、公交时间成本高及服务质量问题(如车辆老旧、发车频率不理想)而难以选择公交。相对地，私家车出行在停车费、燃油费和拥堵费用方面的损失较小。这表明，尽管政府大力投入，出行者对公交的价值感知未达预期，限制了向最优状态的演化。因此，现行政府管控措施未能满足出行者需求，亟需优化改进。
$\left\{\begin{array}{l}V\left(n_1 P_k\right)-Z\left(n_2 C_t\right)-Z\left(C_s\right)-Z(B)>V\left(n_3 P_t\right)+ \\\quad V\left(P_s\right)+V(N)-Z\left(C_p\right) \\V\left(P_K\right)-Z\left(C_t\right)-Z\left(C_s\right)>V\left(P_t\right)+V\left(P_s\right)-Z\left(C_p\right) \\Z(M)+Z(S) <Z(G) \\Z(M)+Z(S) <0\end{array}\right.$ (19)
2) 当且仅当满足式(20)条件时，此状态下不存在均衡演化稳定策略，系统为动态波动演化状态，演化过程呈不稳定的波动状态，演化博弈趋势相位如图 4所示。约束条件(20)下，博弈双方策略选择的互相影响依赖关系较强，为了更具象展示此状态下系统的动态演化波动情况，后文将进行数值仿真模拟。
Fig. 4
图 4 策略动态波动状态相位图 Fig. 4 Phase diagram of dynamic fluctuations in strategies $\left\{\begin{array}{l}V\left(n_1 P_k\right)-Z\left(n_2 C_t\right)-Z\left(C_s\right)-Z(B) <V\left(n_3 P_t\right)+ \\\quad V\left(P_s\right)+V(N)-Z\left(C_p\right) \\V\left(P_k\right)-Z\left(C_t\right)-Z\left(C_s\right)>V\left(P_t\right)+V\left(P_s\right)-Z\left(C_p\right) \\Z(M)+Z(S) <Z(G) \\Z(M)+Z(S)>0\end{array}\right.$ (20)
3 演化路径仿真及敏感性分析 3.1 稳定策略演化路径仿真模拟本文采用MATLAB进行演化博弈的仿真分析，大多已有经济学研究中经典参数值对风险偏好系数与损失规避系数进行赋值。但实际上，交通出行行为的风险敏感度与损失厌恶程度与经济投资领域有所不同。因此，本文依据已有交通出行领域研究得到的数据对基于前景理论的心理账户模型参数进行赋值[27]。
3.1.1 系统最优演化状态仿真系统最优演化状态的模拟仿真参数为n1=1.5, n2=0.7, Cp=1.4, Cs=1.4, Ct=0.8, Pk=1.2, Pt=1.1, Ps=1.1, B=0.85, N=0.9, G=1.1, M=0.7, S=0.8, W=1.6, J=1.2, E=1.5, β=θ=0.37, φ=σ=0.59, λ=δ=1.51, γ=μ=0.74。仿真演化路径如图 5所示，由仿真结果可以看出，不同初始概率组合下的策略选择最终稳定收敛于(1, 1)，即政府部门参与管控，出行者选择公交出行。在现实情况中，此种状态为想要达到的最优结果。
Fig. 5
图 5 均衡稳定策略为(1, 1)演化路径 Fig. 5 Evolutionary path with equilibrium stable strategy of (1, 1) 3.1.2 动态波动状态仿真动态波动状态演化路径如图 6所示，模拟仿真参数为n1=1.5, n2=0.7, Cp=0.5, Cs=0.9, Ct=0.8, Pk=1.2, Pt=0.5, Ps=1.3, B=1.5, N=1.6, G=1.1, M=1.2, S=0.8, W=1.6, J=1.5, E=1.3, β=θ=0.37, φ=σ=0.59, λ=δ=1.51, γ=μ=0.74。
Fig. 6
图 6 策略动态波动状态演化路径 Fig. 6 Evolutionary path of dynamic fluctuations in strategies 从图 6可以看出，不同初始概率组合下的策略始终不存在向任何稳定点收敛的趋势。为了更准确地了解此状态下的演化情况，需进行博弈双方各自策略随时间演化仿真分析。博弈双方策略选择概率随迭代时步t变化, 演化趋势如图 7所示，为了能更直观观察状态变化，起始概率值均取为0.5。从图中可以看出，博弈双方互相促进又互相制约，演化路径呈现波动状态。
Fig. 7
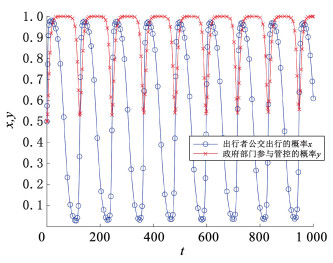图 7 随时间演化的动态路径 Fig. 7 Dynamic path of evolution over time 针对系统不稳定波动状态，本文引入动态绩效支付机制对模型进行优化，即政府参与管控过程中补贴实行动态支付模式。优化依据分两个层面: 理论层面，从波动状态可知，出行者的行为选择受政府管控策略影响，动态补贴系数的增加能够将原常微分方程在邻域内的不稳定转化为混合稳定；现实层面，保证其他仿真参数不变的情况，动态的管控补贴行为更符合实际情况。经过以上优化迭代后仿真演化趋势如图 8所示。
Fig. 8
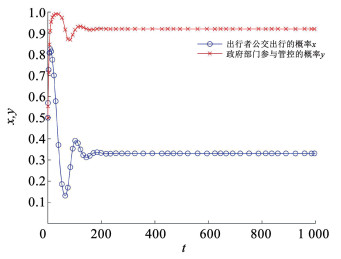图 8 动态支付机制下的演化路径 Fig. 8 Evolutionary path under dynamic payment mechanisms 由图 8的仿真结果能够得到，出行者与政府部门演化博弈趋势逐渐稳定收敛于(x=0.33, y=0.92)，即政府参与管控概率为0.92，出行者选择公交出行的概率为0.33。仿真结果说明政府参与管控的意愿较强烈，而城市居民选择公交出行的概率较低。基于实际情况，这反映出政府对管控措施的高度重视，但公交出行的吸引力不足。在“双碳”目标指引下，中国城市交通正向低碳化转型。尽管各地积极实施公交优先战略以缓解拥堵和降低碳排放，但由于现行管控措施未能显著提升公交吸引力，居民仍偏向使用私家车等交通方式。因此，优化公交优先管控措施，提升公交出行的收益感知，对优化城市交通结构、提高路网承载力及减少碳排放至关重要，是实现城市低碳交通目标的关键途径。
3.2 因素敏感性分析为了探究政府管控措施的优化方向与落脚点，根据上节演化仿真模拟结果，以出行者公交出行概率x=0.33为初始值，对关键因素进行影响敏感性分析。在符合实际情况的范围内，以演化路径更加清晰直观从而利于分析比较为目的，设置模拟仿真的初始值及数值间隔，以管理者期望的系统最优状态，即稳定策略为(1, 1)为基础演化趋势，进行敏感性仿真分析。
1) 公交出行费用。设出行者公交出行策略的费用感知收益Pk={1.2, 2.4, 3.6, 4.8, 6.0}，观察数值变化对出行者群体出行策略选择的影响，演化过程如图 9所示。
Fig. 9
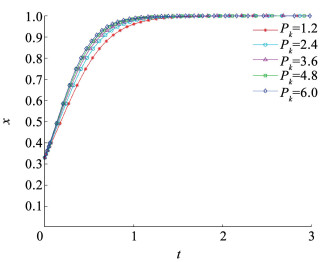图 9 公交出行费用感知收益对出行者策略演化的影响 Fig. 9 The impact of perceived benefits and costs of public transportation on traveler strategy evolution 由图 9可知，随着公交出行费用感知收益增加，出行者选择公交出行概率趋向于1的速度显著提升。公交出行费用感知收益增加，代表以公交票价为主要成分的公交出行费用低于出行者的心理预期成本。由此可知，合理制定公交票价，加大公交出行费用的优惠补贴力度，能够切实提高出行者选择公交出行的比例。
2) 私家车出行费用。设出行者私家车出行策略的费用感知损失Cp={1.0, 1.5, 2.0, 2.5, 3.0}，观察数值变化对出行者群体出行策略选择的影响，演化过程如图 10所示。
Fig. 10
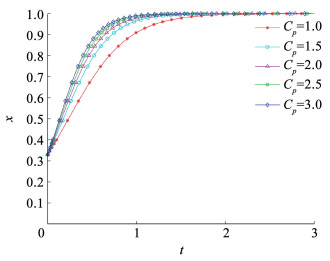图 10 私家车出行费用感知损失对出行者策略演化的影响 Fig. 10 The impact of perceived losses and costs of private car travel on traveler strategy evolution 由图 10可知，随着私家车出行的费用感知损失增加，出行者选择公交出行概率向1演化的速度显著提升。私家车出行费用感知损失增加，说明私家车出行所需成本超过出行者的心理预期费用。由此可知，适度增加私家车出行的费用成本，是提升出行者公交出行意愿的有效途径。除停车费用、燃油费用、日常养护费用外，可以借鉴新加坡、伦敦等大型城市的拥堵收费措施，引导出行者选择公交出行方式，缓解道路拥堵问题。
3) 公交出行时间。设出行者公交出行的时间感知损失Ct={0.2, 0.7, 1.2, 1.7, 2.2}，观察数值变化对出行者群体出行策略选择的影响，演化过程如图 11所示。
Fig. 11
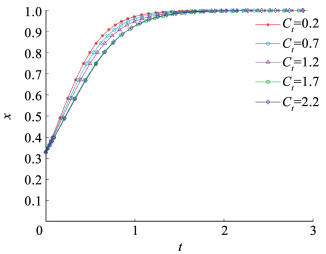图 11 公交出行时间感知损失对出行者策略演化的影响 Fig. 11 The impact of perceived time loss of public transportation on traveler strategy evolution 由图 11可知，随着公交出行的时间感知损失减小，出行者选择公交出行概率向1演化的速度显著提升。公交出行的时间感知损失减小，代表出行者公交出行所需时间比心理预期少。由此可知，通过优化公交发车频率，设置公交专用车道，实行交叉口公交信号优先等管控措施，缩短公交出行时间，提高公交运行效率，能够有效提升公交出行吸引力，提高城市居民选择公交出行的意愿。
4 结论1) 本研究基于行为经济学理论，结合演化博弈理论，构建出行者与政府部门之间的演化博弈模型。通过求解复制动态方程并得到决策主体的策略动态演化状态及不同情况的稳定性条件，进而分析了目前政府部门管控措施存在的主要问题。通过仿真模拟，引入政府补贴动态绩效支付模式对模型进行优化，得到稳定状态下出行者选择公交出行概率与政府参与管控概率，并分析了其中主要参数变化对出行者决策结果的影响情况。
2) 本研究基于前景理论和心理账户理论，以出行者和政府部门为研究对象，构建了收益账户和损失账户，并分析了它们的前景价值感知。基于心理账户，将前景价值感知替代传统演化博弈关系中的客观价值，构建了城市居民出行方式选择演化博弈模型。
3) 根据复制动态方程计算，得到不同约束条件下的演化稳定策略，并通过数值模拟仿真验证了系统最优状态与系统波动状态的演化路径。从政府部门感知与出行者感知两方面剖析了政府管控成本、公交出行的金钱与时间成本、公交出行舒适度、私家车出行费用等原因，阐明了当前未达到管理者期望的最优状态的原因。
4) 在系统策略波动状态下引入动态绩效支付机制对模型进行优化，优化后的演化博弈稳定收敛于(x=0.33, y=0.92)，即政府部门参与管控的概率为0.92，出行者选择公交出行的概率为0.33。该结果表明政府部门参与管控意愿较强，而城市居民选择公交出行方式概率较低，且这一理论结果基本符合社会现实情况。因素敏感性分析结果表明，应从降低公交出行费用、适当提高私家车的出行成本以及缩短公交出行时间为重要切入点，有针对性地优化政府的管控措施，才能真正提升公交出行吸引力，提高城市公交出行分担率。
参考文献
[1] CHENG L, LIU G, HUANG H, et al. Equilibrium analysis of general n-population multi-strategy games for generation-side long-term bidding: an evolutionary game perspective[J]. Journal of Cleaner Production, 2020, 276: 124123. DOI:10.1016/j.jclepro.2020.124123
[2] KASHIFI M T, JAMAL A, KASHEFI M S, et al. Predicting the travel mode choice with interpretable machine learning techniques: a comparative study[J]. Travel Behaviour and Society, 2022, 29: 279. DOI:10.1016/j.tbs,2022.07.003
[3] CHANG X, WU J, LIU H, et al. Travel mode choice: a data fusion model using machine learning methods and evidence from travel diary survey data[J]. Transportmetrica A: Transport Science, 2019, 15(2): 1587. DOI:10.1080/23249935.2019.1620380
[4] HAGGAR P, WHITMARSH L, SKIPPON S M. Habit discontinuity and student travel mode choice[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2019, 64: 13. DOI:10.1016/j.trf.2019.04.022
[5] SIVASUBRAMANIYAM R D, CHARLTON S G, SARGISSON R J. Mode choice and mode commitment in commuters[J]. Travel Behaviour and Society, 2020, 19: 20. DOI:10.1016/j.tbs.2019.10.007
[6] LO S H, BREUKELEN G J P V, PETERS G J Y, et al. Commuting travel mode choice among office workers: comparing an extended theory of planned behavior model between regions and organizational sectors[J]. Travel Behaviour & Society, 2016, 4: 10. DOI:10.1016/j.tbs.2015.11.002
[7] HSIEH H S, KANDA Y, FUJII S. Incorporation of coping planning into the behavior change model that accounts for implementation intention[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2019, 60: 228. DOI:10.1016/j.trf.2018.10.025
[8] DE VOS J, SINGLETON P A, GARLING T. From attitude to satisfaction: introducing the travel mode choice cycle[J]. Transport Reviews, 2022, 42(2): 204. DOI:10.1080/01441647.2021.1958952
[9] 陈坚, 张弛, 庹永恒, 等. 考虑环保意识和出行习惯的公交出行选择行为模型[J]. 交通运输系统工程与信息, 2020, 20(4): 128.
CHEN Jian, ZHANG Chi, TUO Yongheng, et al. Travel mode choice behavior model of public transit incorporating environmental concern and habit[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(4): 128. DOI:10.16097/j.cnki.1009-6744.2020.04.019
[10] 陈坚, 傅志妍, 钟异莹. 心理因素影响的公交方式选择行为模型[J]. 交通运输系统工程与信息, 2017, 17(3): 120.
CHEN Jian, FU Zhiyan, ZHONG Yiying. Choice behavior model of urban public transport considered the psychological factors affecting[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(3): 120. DOI:10.16097/j.cnki.1009-6744.2017.03.018
[11] GHADER S, DARZI A, ZHANG L. Modeling effects of travel time reliability on mode choice using cumulative prospect theory[J]. Transportation Research Part C: Emerging Technologies, 2019, 108: 245. DOI:10.1016/j.trc.2019.09.014
[12] HJORTH K, FOSGERAU M. Using prospect theory to investigate the low marginal value of travel time for small time changes[J]. Transportation Research Part B: Methodological, 2012, 46(8): 917. DOI:10.1016/j.trb.2012.04.001
[13] 陈亮, 刘晟宇, 田蓓, 等. 基于累积前景理论的通勤者换乘出行决策研究[J]. 铁道科学与工程学报, 2022, 19(8): 2445.
CHEN Liang, LIU Shengyu, TIAN Bei, et al. Research on commuter transfer decision based on cumulative prospect theory[J]. Journal of Railway Science and Engineering, 2022, 19(8): 2445. DOI:10.19713/j.cnki.43-1423/u.t20211113
[14] ASADI M, FATHY M, MAHINI H, et al. An evolutionary game approach to safety-aware speed recommendation in fog/cloud-based intelligent transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 23(7): 7431. DOI:10.1109/TITS.2021.3069850
[15] 于跃, 李雷鸣. 私家车合乘共享背景下居民通勤模式选择行为演化博弈[J]. 北京理工大学学报(社会科学版), 2021, 23(2): 112.
YU Yue, LI Leiming. The evolutionary game of residents' commuting mode selection under the background of private car ride-sharing[J]. Journal of Beijing Institute of Technology(Social Sciences Edition), 2021, 23(2): 112. DOI:10.15918/j.jbitss1009-3370.2021.1211
[16] 张波, 隽志才, 倪安宁. 基于累积前景理论的动态交通流演化博弈模型[J]. 管理工程学报, 2014, 28(3): 164.
ZHANG Bo, JUAN Zhicai, NI Anning. An evolutionary game model for the dynamic traffic flow based on cumulative prospect theory[J]. Journal of Industrial Engineering and Engineering Management, 2014, 28(3): 164. DOI:10.13587/j.cnki.jieem.2014.03.003
[17] KAHNEMAN D, TVERSKY A. Prospect theory: an analysis of decision under risk[J]. Econometrica, 1979, 47(2): 263. DOI:10.1142/9789814417358_0006
[18] BARBERIS N C. Thirty years of prospect theory in economics: a review and assessment[J]. The Journal of Economic Perspectives, 2013, 27(1): 173. DOI:10.2307/41825467
[19] CHUNG N, KOO C. The use of social media in travel information search[J]. Telematics and Informatics, 2015, 32(2): 215. DOI:10.1016/j.tele.2014.08.005
[20] BERNHEIM B D, SPRENGER C. On the empirical validity of cumulative prospect theory: experimental evidence of rank-independent probability weighting[J]. Econometrica, 2020, 88(4): 1363. DOI:10.3982/ECTA16646
[21] TVERSKY A, KAHNEMAN D. Advances in prospect theory: cumulative representation of uncertainty[J]. Journal of Risk and Uncertainty, 1992, 5(4): 297. DOI:10.1007/bf00122574
[22] MUEHLBACHER S, KIRCHLER E. Individual differences in mental accounting[J]. Frontiers in Psychology, 2019, 10: 2866. DOI:10.3389/fpsyg.2019.02866
[23] 马书红, 周烨超, 张艳. 基于NL-累计前景理论的出行方式选择预测模型研究[J]. 交通运输系统工程与信息, 2019, 19(4): 135.
MA Shuhong, ZHOU Yechao, ZHANG Yan. Travel mode choice forecasting based on nested logit-cumulative prospect theory model[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(4): 135. DOI:10.16097/j.cnki.1009-6744.2019.04.020
[24] 邹晓辉. 基于Logistic回归的数据分类问题研究[J]. 智能计算机与应用, 2016, 6(6): 3.
ZOU Xiaohui. Data classification based on Logistic regression[J]. Intelligent Computer and Applications, 2016, 6(6): 3. DOI:10.3969/j.issn.2095.2016.06.044
[25] MITTAL S, MUKHOPADHYAY A, CHAKRABORTY S. Evolutionary dynamics of the delayed replicator-mutator equation: limit cycle and cooperation[J]. Physical Review E, 2020(4): 42. DOI:10.1103/PHYSREVE.101.042410
[26] FRIEDMAN D. Evolutionary games in economics[J]. Econometrica: Journal of the Econometric Society, 1991(1): 637. DOI:10.2307/2938222
[27] 谭礼平. 基于前景理论的出行行为研究综述[C]//2019世界交通运输大会论文集(下). 北京: 中国公路学会, 2019: 11
TAN Liping. A review of travel behavior research based on prospect theory[C]//Proceedings of the 2019 World Transportation Conference: part 2. Beijing: China Highway and Transportation Society, 2019: 11
