高建宁1,高锋阳1,姚普2,宋志翔1,杨凯文1,高翾宇1,徐昊1
(1.兰州交通大学 自动化与电气工程学院,兰州 730070;2.西北工业大学 自动化学院,西安 710072)
摘要:
为解决内置式永磁同步电机径向电磁力引起的电磁振动问题,提出一种分段永磁体采用Halbach充磁方式同时转子开设辅助槽的电机拓扑结构。首先,对电机气隙磁密、径向电磁力、电磁振动原理进行推导与分析,并建立有限元模型。其次,提出基于电磁场和机械场耦合的电磁振动分析方案,对电机径向电磁力进行时间空间阶次傅里叶分解,在机械场中,分析电机定子在不同频率下的振动加速度幅值大小,并计算出定子各阶模态。在此基础上,基于响应面法和多目标遗传算法构建电机参数敏感度分层优化方案,并求得样本点帕累托前沿从而确定电机最优参数,将优化后的电机与普通V型内置式电机进行比较。最后,在机械场中仿真得到转子所受等效应力和总变形,验证得所提电机结构符合机械设计要求。分析结果表明:所提出结构电机在不损失电磁转矩的基础上,径向电磁力幅值大幅度降低,抑制了齿槽转矩,改善了气隙磁密和反电势的正弦度,在提高电机电磁性能的同时抑制了电磁振动的发生。
关键词: 内置式永磁同步电机 Halbach永磁体 径向电磁力 定子模态 参数敏感度 响应面法
DOI：10.11918/202207023
分类号:TM351
文献标识码:A
基金项目:国家自然科学基金(52267004)；甘肃省教育厅优秀研究生“创新之星”项目(2022CXZX-618)
Electromagnetic vibration analysis of Halbach permanent magnet motor based on sensitivity stratification optimization
GAO Jianning1,GAO Fengyang1,YAO Pu2,SONG Zhixiang1,YANG Kaiwen1,GAO Xuanyu1,XU Hao1
(1.School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2.School of Automation, Northwestern Polytechnical University, Xi′an 710072, China)
Abstract:
In order to solve the problem of electromagnetic vibration caused by radial electromagnetic force of interior permanent magnet synchronous motor, a motor topology structure with Halbach magnetizing mode for piecework permanent magnet and auxiliary slots for rotor was proposed. Firstly, the principle of air gap magnetic density, radial electromagnetic force and electromagnetic vibration of the motor is deduced and analyzed, and the finite element model is established. Secondly, an electromagnetic vibration analysis scheme based on the coupling of electromagnetic field and mechanical field is proposed, and the time and space order Fourier decomposition of the radial electromagnetic force of the motor is carried out. In the mechanical field, the amplitude of the vibration acceleration of the motor stator at different frequencies is analyzed, and the modes of the stator are calculated. On this basis, the hierarchical optimization scheme of motor parameter sensitivity was constructed based on response surface method and multi-objective genetic algorithm, and the Pareto frontier of sample points was obtained to determine the optimal parameters of the motor. Comparing the optimized motor with the ordinary V-type interior motor. Finally, the equivalent stress and total deformation of the rotor were simulated in the mechanical field, and the proposed motor structure was verified to meet the mechanical design requirements. The analysis results show that the radial electromagnetic force amplitude of the proposed structure motor is greatly reduced on the basis of no loss of electromagnetic torque, which restrains the groove torque, improves the air gap magnetic density and the sinusoidal degree of back potential, improves the electromagnetic performance of the motor and restrains the electromagnetic vibration.
Key words: interior permanent magnet synchronous motor Halbach permanent magnet radial electromagnetic force stator mode parameter sensitivity response surface method
高建宁, 高锋阳, 姚普, 宋志翔, 杨凯文, 高翾宇, 徐昊. 基于敏感度分层优化的Halbach永磁电机电磁振动分析[J]. 哈尔滨工业大学学报, 2024, 56(7): 142-153. DOI: 10.11918/202207023.
GAO Jianning, GAO Fengyang, YAO Pu, SONG Zhixiang, YANG Kaiwen, GAO Xuanyu, XU Hao. Electromagnetic vibration analysis of Halbach permanent magnet motor based on sensitivity stratification optimization[J]. Journal of Harbin Institute of Technology, 2024, 56(7): 142-153. DOI: 10.11918/202207023.
基金项目 国家自然科学基金(52267004)；甘肃省教育厅优秀研究生“创新之星”项目(2022CXZX-618) 作者简介 高建宁(1998—)，男，硕士研究生;
高锋阳(1971—)，男，教授，硕士生导师 通信作者 高锋阳，ljdgaofy@lzjtu.edu.cn 文章历史 收稿日期: 2022-07-06
Abstract Full text Figures/Tables PDF
基于敏感度分层优化的Halbach永磁电机电磁振动分析
高建宁1, 高锋阳1
, 姚普2, 宋志翔1, 杨凯文1, 高翾宇1, 徐昊1 1. 兰州交通大学 自动化与电气工程学院，兰州 730070;
2. 西北工业大学 自动化学院，西安 710072
收稿日期: 2022-07-06; 录用日期: 2022-08-03; 网络首发日期: 2024-05-24
基金项目: 国家自然科学基金(52267004)；甘肃省教育厅优秀研究生“创新之星”项目(2022CXZX-618)
作者简介: 高建宁(1998—)，男，硕士研究生; 高锋阳(1971—)，男，教授，硕士生导师
通信作者: 高锋阳，ljdgaofy@lzjtu.edu.cn
摘要: 为解决内置式永磁同步电机径向电磁力引起的电磁振动问题，提出一种分段永磁体采用Halbach充磁方式同时转子开设辅助槽的电机拓扑结构。首先，对电机气隙磁密、径向电磁力、电磁振动原理进行推导与分析，并建立有限元模型。其次，提出基于电磁场和机械场耦合的电磁振动分析方案，对电机径向电磁力进行时间空间阶次傅里叶分解，在机械场中，分析电机定子在不同频率下的振动加速度幅值大小，并计算出定子各阶模态。在此基础上，基于响应面法和多目标遗传算法构建电机参数敏感度分层优化方案，并求得样本点帕累托前沿从而确定电机最优参数, 将优化后的电机与普通V型内置式电机进行比较。最后，在机械场中仿真得到转子所受等效应力和总变形，验证得所提电机结构符合机械设计要求。分析结果表明：所提出结构电机在不损失电磁转矩的基础上，径向电磁力幅值大幅度降低，抑制了齿槽转矩，改善了气隙磁密和反电势的正弦度，在提高电机电磁性能的同时抑制了电磁振动的发生。
关键词: 内置式永磁同步电机 Halbach永磁体 径向电磁力 定子模态 参数敏感度 响应面法
Electromagnetic vibration analysis of Halbach permanent magnet motor based on sensitivity stratification optimization
GAO Jianning1, GAO Fengyang1
, YAO Pu2, SONG Zhixiang1, YANG Kaiwen1, GAO Xuanyu1, XU Hao1 1. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;
2. School of Automation, Northwestern Polytechnical University, Xi′an 710072, China
Abstract: In order to solve the problem of electromagnetic vibration caused by radial electromagnetic force of interior permanent magnet synchronous motor, a motor topology structure with Halbach magnetizing mode for piecework permanent magnet and auxiliary slots for rotor was proposed. Firstly, the principle of air gap magnetic density, radial electromagnetic force and electromagnetic vibration of the motor is deduced and analyzed, and the finite element model is established. Secondly, an electromagnetic vibration analysis scheme based on the coupling of electromagnetic field and mechanical field is proposed, and the time and space order Fourier decomposition of the radial electromagnetic force of the motor is carried out. In the mechanical field, the amplitude of the vibration acceleration of the motor stator at different frequencies is analyzed, and the modes of the stator are calculated. On this basis, the hierarchical optimization scheme of motor parameter sensitivity was constructed based on response surface method and multi-objective genetic algorithm, and the Pareto frontier of sample points was obtained to determine the optimal parameters of the motor. Comparing the optimized motor with the ordinary V-type interior motor. Finally, the equivalent stress and total deformation of the rotor were simulated in the mechanical field, and the proposed motor structure was verified to meet the mechanical design requirements. The analysis results show that the radial electromagnetic force amplitude of the proposed structure motor is greatly reduced on the basis of no loss of electromagnetic torque, which restrains the groove torque, improves the air gap magnetic density and the sinusoidal degree of back potential, improves the electromagnetic performance of the motor and restrains the electromagnetic vibration.
Keywords: interior permanent magnet synchronous motor Halbach permanent magnet radial electromagnetic force stator mode parameter sensitivity response surface method
内置式永磁同步电机(interior permanent magnet synchronous motor, IPMSM)广泛应用于新能源汽车等电气交通领域[1]，其具有高效、高精度、大范围调速控制等优点。但电机固有的电磁振动不仅影响其运行稳定性，而且加剧了轴承磨损缩短电机寿命。电机永磁体磁场和电枢绕组磁场相互作用产生的径向电磁力作用于定子齿部，使电机产生振动现象从而通过机壳向空气中传递噪声。当径向电磁力阶次与电机模态阶次相同，同时两者的频率相近时，电机会发生共振现象从而加剧电磁振动。
永磁同步电机的电磁振动研究主要集中在径向电磁力和结构模态等领域[2]，文献[3]根据麦克斯韦应力张量法建立了电机径向电磁力的解析模型，并对谐波来源和阶次进行分析。文献[4]计算了PMSM气隙磁密的谐波含量，分析得出低阶次的谐波更容易引发电机的振动噪声。文献[3-6]分析了永磁同步电机极槽配合、定子无槽结构、永磁体充磁方式、转子分段斜极等结构参数对径向电磁力幅值和电机振动噪声的影响。文献[7]分析了永磁电机高模数电磁力波对电机振动的影响，基于齿斩波效应下得出高模数电磁力波会引起较大的低阶电磁振动。文献[8]在考虑材料各向异性的基础上通过定子结构模态规划来优化电机振动，结果表明定子轭部的优化降低了振动加速度和噪声功率级。文献[9]提出一种借助重建场的方法对存在静态偏心与局部去磁的永磁同步电机振动噪声进行分析计算。文献[10]针对内置式多层磁钢永磁同步电机通过优化磁钢层数和转子拓扑的方法抑制振动噪声，得出两层和3层磁钢为较优方案。文献[11]研究了不同温度、谐波下变频电机的电磁性能变化以及考虑硅钢片磁致伸缩影响下的振动特性。文献[12]提出定子齿调制效应模型可以削弱径向电磁力密度，并将其应用于表贴式和内置式永磁电机。文献[13]研究了逆变器谐波电流供电对内置式永磁同步电机的0、8阶次电磁力波的影响。文献[14]通过三维有限元电机结构精准计算出电机的模态参数，并测量出阻尼比。随着耦合场优化目标和参数的增多，单一的优化方法已经不能达到约束目标，文献[15]基于响应面敏感度分析和差分进化算法实现了永磁电机的多目标优化设计，在求解复杂优化问题中表现出较强的鲁棒性。文献[16]提出了一种基于粒子群算法的磁阻电机优化设计流程，其中包括敏感度分析和响应面模型构建，优化了电机的转矩脉动和效率。
综上，本文提出一种分段永磁体采用Halbach充磁方式的内置式永磁同步电机拓扑结构。首先在电磁和机械耦合场中求解出定子各阶模态和固有频率值，对空间时间阶次下的径向电磁力进行傅里叶分解，并分析电机是否避开共振频率。然后对V型IPMSM与所提结构的径向电磁力对比分析，同时在耦合场中对比电磁振动情况。最后，在电磁场中比较两台电机的电磁转矩等性能，在机械场中对转子的机械应力进行分析。
1 电机解析模型 1.1 电机结构为解决内置式永磁电机电磁振动大带来的不利影响，提出如图 1所示的分段Halbach开槽型IPMSM结构。在原有“一+V”型内置式永磁体的结构拓扑上，如图 2将“一”型永磁体分为3个部分，其中左右两段的永磁体采用Halbach角度充磁方式，中间段永磁体采用平行充磁的方式。同时，在转子硅钢片上开设辅助槽，图 3为所提电机结构的示意图。
Fig. 1
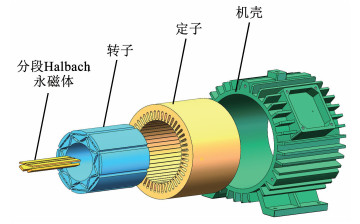图 1 电机爆炸图 Fig. 1 Motor exploded diagram Fig. 2
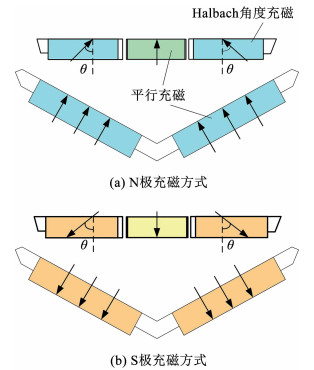图 2 Halbach永磁体一对极的充磁方式 Fig. 2 One-pole magnetizing method of Halbach permanent magnet Fig. 3
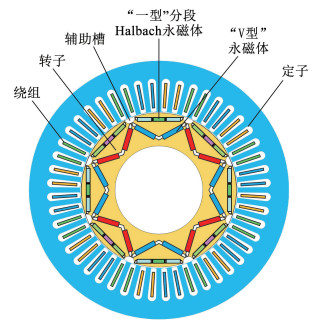图 3 电机结构示意图 Fig. 3 Motor structure diagram 在空载条件下，电机的磁场分布如图 4所示，左半圆为磁密分布云图，“一型”永磁体外侧及辅助槽附近的磁密最大，定子齿及转子磁钢没有磁密过饱和现象发生。右半圆为磁力线分布云图，磁力线对称分布且基本没有漏磁现象，验证了磁路结构的合理性。
Fig. 4
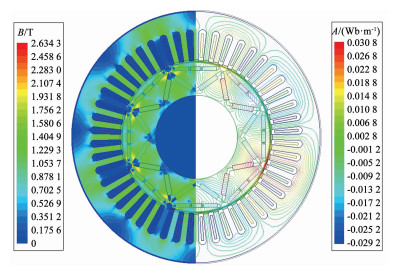图 4 磁密云图与磁力线分布图 Fig. 4 Magnetic density cloud map and magnetic field line distribution map 1.2 气隙磁密在气隙磁场谐波的作用下，电机将产生不同频率不同阶次的电磁力波，分别分析定转子磁动势和气隙磁导，得到气隙磁密。根据磁势乘以磁导的方法可知，径向气隙磁通密度可以用磁动势和气隙比磁导函数乘积来表示：
$B_{\mathrm{r}}(\theta, t)=f(\theta, t) \cdot \varLambda(\theta, t)$ (1)
气隙磁密磁动势可以表示为
$\left\{\begin{array}{l}f_{\mathrm{s}}(\theta, t)=\sum F_v \cos \left(v p \theta-\omega t-\varphi_v\right) \\f_{\mathrm{r}}(\theta, t)=\sum F_\mu \cos \left(\mu p \theta-\mu \omega t-\varphi_\mu\right) \\f(\theta, t)=f_{\mathrm{s}}(\theta, t)+f_{\mathrm{r}}(\theta, t)\end{array}\right.$ (2)
其中：fs(θ, t)、fr(θ, t)、f(θ, t)分别为定子、永磁体和气隙磁密磁动势，v、μ为谐波次数，Fv、Fμ为谐波磁动势幅值，φv、φμ为磁动势相位，ω为基频的角速度，p为极对数。
气隙比磁导函数可表示为
$\left\{\begin{array}{l}\varLambda(\theta, t)=\varLambda_0 \lambda_1(\theta) \lambda_2(\theta, t) \\\lambda_1(\theta)=1+\sum\limits_{i=1}^{\infty} A_i \cos \left(i N_{\mathrm{s}} \theta\right) \\\lambda_2(\theta, t)=1+\sum\limits_{j=1}^{\infty} A_j \cos 2 j\left(p \theta-\omega_{\mathrm{e}} t\right)\end{array}\right.$ (3)
式中：Λ0为气隙比磁导均值；λ1、λ2分别为定子开槽和转子凸极效应所引入的相对磁导函数。
1.3 径向电磁力电机永磁体磁场和电枢绕组磁场相互作用产生径向电磁力Fr和切向电磁力Ft，其中Ft会引起齿槽转矩和转矩脉动，Fr作用于定子齿部从而引起电机振动噪声。由于铁磁材料的磁导率大，Fr几乎垂直作用于定子齿部，故电磁力径向分量远大于切向分量，电机径向、切向电磁力密度Fr、Ft表达式分别为
$F_{\mathrm{r}}=\frac{B_{\mathrm{r}}^2-B_{\mathrm{t}}^2}{2 \mu_0} \approx \frac{B_{\mathrm{r}}^2}{2 \mu_0}$ (4)
$F_{\mathrm{t}}=\frac{B_{\mathrm{r}} \cdot B_{\mathrm{t}}}{2 \mu_0}$ (5)
其中：Br、Bt分别为齿部的径向和切向气隙磁密，μ0为真空磁导率。
电机径向电磁力由永磁磁场、永磁磁场与定子开槽相互作用、永磁磁场与电枢磁场相互作用、永磁磁场和电枢磁场与定子开槽相互作用、电枢磁场、电枢磁场与定子开槽相互作用的6种方式组合而成, 见表 1，电机径向电磁力表达式为
$\begin{gathered}F_{\mathrm{r}}(\theta, t)=\frac{B_{\mathrm{r}}^2}{2 \mu_0}=\frac{\left[f_{\mathrm{r}}(\theta, t)+f_{\mathrm{s}}(\theta, t)\right]^2 \cdot \varLambda_{\mathrm{s}}^2(\theta)}{2 \mu_0}= \\\frac{1}{2 \mu_0}\left[\sum\limits_\mu F_\mu \cos (\mu p \theta-\mu \omega t)+\sum\limits_v F_v \cos (v a \theta-\right. \\\left.\left.S_v \omega t\right)\right]^2 \cdot\left[\varLambda_0+\sum\limits_k \varLambda_k \cos (k z \theta)\right]^2=\end{gathered} \\ \begin{gathered}\frac{1}{4 \mu_0}\left\{\sum\limits_{\mu_1} \sum\limits_{\mu_2} F_{\mu_1} F_{\mu_2} \cos \left[\left(\mu_1 \pm \mu_2\right) p \theta-\left(\mu_1 \pm \mu_2\right) \omega t\right]+\right. \\2 \sum\limits_\mu \sum\limits_v F_\mu F_v \cos \left[(\mu p \pm \mu a) \theta-\left(\mu \pm S_v\right) \omega t\right]+\end{gathered} \\ \left.\sum\limits_{v_1} \sum\limits_{v_2} F_{v_1} F_{v_2} \cos \left[\left(v_1 \pm v_2\right) a \theta-\left(S_{v_1} \pm S_{v_2}\right) \omega t\right]\right\} \cdot \\ \begin{gathered}\left\{\varLambda_0^2+2 \varLambda_0 \sum\limits_k \Lambda_k \cos (k z \theta)+\right. \\\left.\frac{1}{2} \sum\limits_{k_1} \sum\limits_{k_2} \varLambda_{k_1} \varLambda_{k_2} \cos \left[\left(k_1 \pm k_2\right) z \theta\right]\right\}\end{gathered}$ (6)
表 1
表 1 径向电磁力6种来源分布 Tab. 1 Radial electromagnetic force is distributed in six sources 序号 来源 空间阶次 频率 1 永磁磁场 (μ1±μ2)p (μ1±μ2)f
2 永磁磁场与定子开槽相互作用 (μ1±μ2)p±kz
(μ1±μ2)p±(k1±k2)z (μ1±μ2)f
3 永磁磁场与电枢磁场相互作用 μp±vα (μ±Sv)f
4 永磁磁场、电枢磁场与定子开槽相互作用 μp±vα±kz
μp±vα±(k1±k2)z (μ±Sv)f
5 电枢磁场 (v1+v2)α (Sv1±Sv2)f
6 电枢磁场与定子开槽相互作用 (v1+v2)α±kz
(v1+v2)α±(k1+k2)z (Sv1±Sv2)f
表 1 径向电磁力6种来源分布 Tab. 1 Radial electromagnetic force is distributed in six sources
1.4 电磁振动电机在电磁振动作用下定子形变量与力波阶数、力波幅值及电机固有频率的关系：
$D_{\mathrm{s}} \approx \frac{F}{\left(M_1^2-1\right)^2} \cdot \frac{1}{1-\left(\frac{f}{f_{\mathrm{c}}}\right)^2}$ (7)
式中：Ds为定子铁心形变量；F、M1分别为电磁力波幅值、力波阶数；f、fc分别为电磁振动频率、电机固有频率。
从式中可得定子形变量和力波阶数的四次方成反比例关系，因此本文将低阶径向电磁力波作为优化的重点。施加在每个定子齿上的单位电磁力为
$F_{\text {unit }, n}(f)=1 \cdot \mathrm{e}^{\mathrm{j}\left(v \theta_n+2 \pi f t\right)}$ (8)
式中θn为第n个定子齿的周向空间角度。
对于电机的振动系统来说，振动响应表达为
$\boldsymbol{M} \ddot{x}(t)+\boldsymbol{C} \dot{x}(t)+\boldsymbol{K} x(t)=q(t)$ (9)
式中：x、q分别为振动位移和电磁力向量；M、C、K分别为关于质量、阻尼和刚度的矩阵，均为n阶方阵；
将式(7)变换为振动响应关于模态和电磁力的函数：
$x(\mathrm{j} \omega)=\sum\limits_{n=1}^N \frac{\boldsymbol{\psi}_n^{\mathrm{T}} q(\mathrm{j} \omega) \cdot \boldsymbol{\psi}_n}{p_n^2+2 \mathrm{j} \omega \zeta_n p_n-\omega^2}$ (10)
式中：ζn为阻尼比；ψn为第n阶质量归一化的模态向量；ω、pn分别为电磁力的角频率和n阶模态频率。
由式(8)可得，电机产生共振响应的条件是：当电磁力的空间阶数与定子模态阶数一致。
1.5 定子固有频率PMSM的模态分析常采用单环模型，定子铁心0阶模态时，径向受力相同做均匀径向振动，因此也称为“呼吸”模态，0阶的固有频率为
$\left\{\begin{array}{l}f_0=\frac{1}{\pi D_{\mathrm{c}}} \sqrt{\frac{E}{\rho \varDelta}} \\\varDelta=1+\frac{m_{\mathrm{t}}+m_{\mathrm{w}}}{m_{\mathrm{c}}}\end{array}\right.$ (11)
式中：Dc为定子直径，ρ为定子密度，E为定子弹性模量，mc为定子轭质量，mt为定子齿部质量，mw为绕组质量。
定子1阶模态受单边拉力，其固有频率[19]为
$\begin{gathered}f_1=f_0 \sqrt{\frac{2}{1+i^2 \frac{\varDelta_n}{\varDelta}}} \\i=\frac{h}{\sqrt{3} D_{\mathrm{c}}}\end{gathered} \\ \begin{gathered}\varDelta_n=1+\frac{Z \theta_{\mathrm{t}}}{\pi D_{\mathrm{c}} I} \\I=\frac{L h_{\mathrm{c}}^3}{12}\end{gathered} \\ \theta_{\mathrm{t}}=(\varDelta-1) S_{\mathrm{t}} h_{\mathrm{t}}^3\left[\frac{1}{3}+\frac{h_{\mathrm{c}}}{2 h_{\mathrm{t}}}+\left(\frac{h_{\mathrm{c}}}{2 h_{\mathrm{t}}}\right)^2\right]$ (12)
式中：Z为定子槽数，hc为定子轴向长度，ht为定子齿高，St为定子齿截面积。
当定子模态阶数≥2时，受到多个方向的拉力，其n阶模态的固有频率可表示为
$f_n=f_0 \frac{i n\left(n^2-1\right)}{\sqrt{n^2+1}}\frac{1}{\sqrt{1+\frac{i^2\left(n^2-1\right)\left[n^2\left(4+\frac{\varDelta_n}{\varDelta}\right)+3\right]}{n^2+1}}}$ (13)
1.6 验证解析模型所提出Halbach开槽型IPMSM为8极48槽结构，额定功率为80 kW、额定转速为6 000 r/min，定子内外径分别为162、270 mm，转子外径为160 mm，永磁材料采用NdFe35。为验证所搭建模型的准确性，在空载情况下仿真出电机的径向气隙磁密分布如图 5所示，并将解析解计算结果与有限元计算结果对比，从图中可以得出两者的误差很小，从而验证电机气隙环境的合理性和所搭建模型的准确性，为进一步优化电机奠定了基础。
Fig. 5
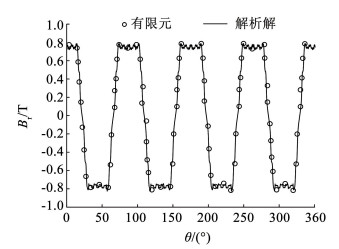图 5 气隙磁密对比曲线 Fig. 5 Air gap magnetic density contrast curve 2 电磁振动分析 2.1 分析方案为实现电机电磁振动优化的准确性，设计出如图 6所示的分析方案。在电机负载情况下求解径向电磁力和电磁转矩，空载条件下求解气隙磁密和反电势，在机械场中求解电机定子的各阶模态振型及频率。然后将电磁场中的径向电磁力耦合加载到机械场的定子齿部，并仿真得到定子振动加速度。
Fig. 6
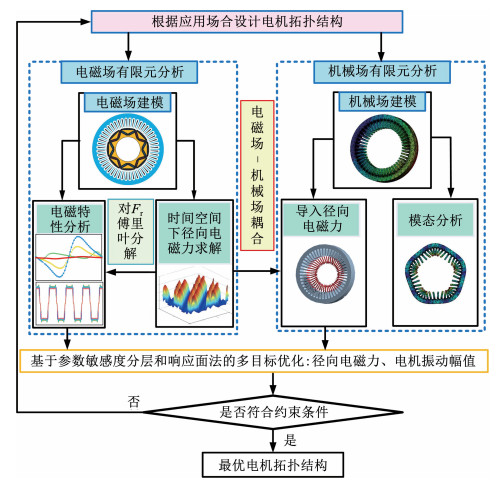图 6 电磁振动分析方案 Fig. 6 Electromagnetic vibration analysis solution 2.2 径向电磁力分析径向电磁力沿着气隙圆周旋转作用于定子齿部和机壳对电机整体产生振动影响，并通过机壳向外界辐射噪声，IPMSM的三维空间径向电磁力分布如图 7所示。图 8为所提出Halbach开槽型电机与相同结构尺寸下普通V型内置式电机的径向电磁力对比，两台电机永磁体体积相同。可以得出Halbcah型电机的径向电磁力幅值远小于普通V型结构，幅值下降了13%，从而得出经过拓扑结构的优化设计，达到了对电机径向电磁力幅值的抑制效果。
Fig. 7
图 7 三维空间径向电磁力 Fig. 7 Radial electromagnetic force in three-dimensional space Fig. 8
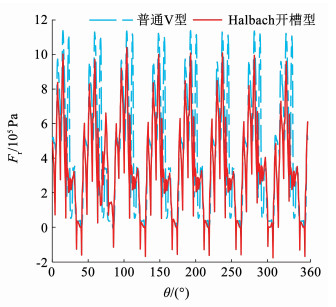图 8 径向电磁力对比波形 Fig. 8 Radial electromagnetic force contrast waveform 2.3 定子模态分析电机定子材料具有各向异性，电机模态分为轴向模态阶数和周向模态阶数两种情况，且定子径向直径要大于轴向长度，从而导致定子径向刚度小于轴向刚度，因此轴向模态一致时对电机的振动噪声起主要影响，所以本文将以轴向0阶模态为基础分析电机的径向各阶次模态。
电机定子总成由定子铁芯、绕组、机壳组成，具体材料属性见表 2，定子铁芯密度由硅钢片密度乘以其叠压系数0.95得到。弹性模量的大小反映了材料的刚度大小，弹性、剪切模量数值越大材料的抗变形能力越强。由于绕组材料的弹性模量和剪切模量远小于定子铁芯和机壳材料的弹性模量和剪切模量，绕组的质量效应远大于其刚度效应，为提高仿真效率将绕组材料等效为定子的附加密度，作为附加质量集成在定子总成模型中。电机机壳采用非导磁的铝材料，机壳与定子采用过盈配合的刚性连接方式，在增加定子质量的同时增大了定子总成的刚度。
表 2
表 2 电机定子材料属性 Tab. 2 Material properties of motor stator 材料属性 密度/(kg·m-3) 泊松比 弹性模量/GPa 剪切模量/GPa 定子铁芯 7 600 0.31 205.8 80
绕组 4 300 0.30 1.3 0.46
机壳 2 700 0.33 71.0 25.9
表 2 电机定子材料属性 Tab. 2 Material properties of motor stator
采用无外加约束和激振力的自由模态求解方式，电机定子和定子总成模态各阶次的固有频率如图 9和图 10所示。在机械场中对定子和定子总成三维模型进行模态仿真如图 11所示，由于定子总成在质量和刚性上均大于定子模型，因此其各阶次的模态频率提高了15%~46%。
Fig. 9
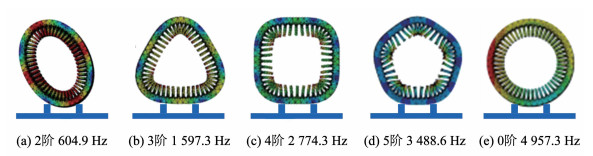图 9 电机定子模态分析结果 Fig. 9 Results of motor stator modal analysis Fig. 10
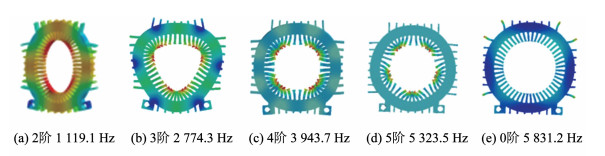图 10 电机定子总成模态分析结果 Fig. 10 Motor stator assembly modal analysis results Fig. 11
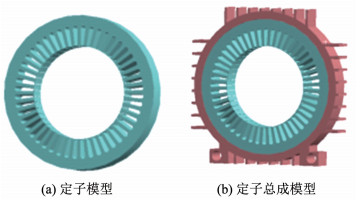图 11 电机模态分析模型 Fig. 11 Electrical modal analysis model 3 参数敏感度分层优化在耦合场中仿真得到电机的各项性能后，根据目标性能的约束条件优化拓扑结构，以达到更好的设计要求。提出一套适合电机多物理场条件下的多目标优化流程如图 12所示，首先对结构参数进行敏感度分层，结合响应面法拟合出参数与优化目标的三维曲面，对分层后的内置式Halbach永磁同步电机结构参数分别进行优化[17]。
Fig. 12
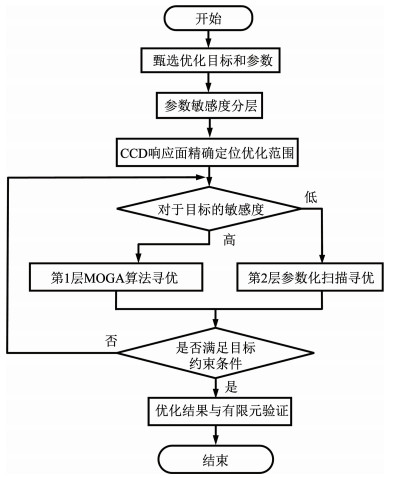图 12 电机优化流程 Fig. 12 Motor optimization process 在电机电磁场和机械场中以电磁转矩均值及其脉动、径向电磁力、永磁体涡流损耗、电机振幅作为5个优化目标，并筛选出如图 13所示的4个结构参数作为优化变量。对参数变量和优化目标进行敏感度分析，敏感度数值越大代表参数对目标的影响权重越大，根据敏感度大小差异对结构参数和目标进行分层。如图 14所示，L2和Rc参数相对于5个优化目标的敏感度较大，其中L2对径向电磁力的敏感度最大达到了0.59，故将L2、Rc作为第1层优化参数，将L1、θ作为第2层优化参数。
Fig. 13
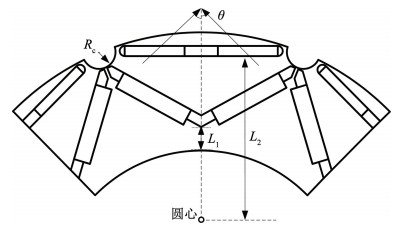图 13 优化参数示意图 Fig. 13 Schematic diagram of optimization parameters Fig. 14
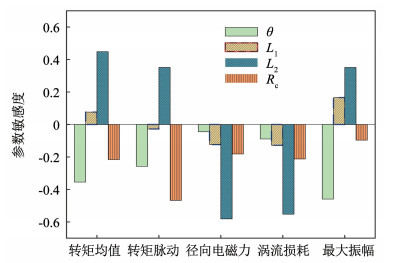图 14 参数敏感度分析 Fig. 14 Parameter sensitivity analysis 为应对优化目标在双变量影响下的交互关系，引入中心复合设计(central composite design，CCD)响应面法，式(14)为响应面模型，通过少量样本数据拟合出二阶响应曲面，高效准确地定位得到最优解的取值区间。
$y=\beta_0+\sum\limits_{i=1}^k \beta_i x_i+\sum\limits_{i=1}^k \beta_{i i} x_i^2+\sum\limits_{i<j} \beta_{i j} x_i x_j+\varepsilon$ (14)
式中：β0为常数，βi为一阶系数，βii为二阶系数，βij为二阶交互项系数，ε为误差。
根据CCD响应面法拟合得到L1、L2参数关于径向电磁力的响应面模型如式(15)所示：
$\begin{aligned}F_{\mathrm{r}}= & 56.7-1.73 L_1+2.85 L_2-0.04 L_1 L_2+ \\& 0.015 L_1^2+0.015 L_2^2\end{aligned}$ (15)
从图 15响应曲面可以得到随着L1、L2的增大，Fr的幅值不断增大，故选取L1在1~2 mm之间，L2在69~70.5 mm之间，再从这个区间内利用算法寻求最优解。第1层参数目标的优化采用MOGA多目标遗传算法，该方法是非支配排序遗传算法NSGA-Ⅱ的改进算法。经过多次的迭代计算，使得结果最终趋向于最优位置，如图 16所示为电机振幅和转矩脉动值在计算过程中试验点分布，两个目标的最优解分布在帕累托前沿曲线上，权衡两个目标的最小值同时考虑其他目标的最优分布，从而最终确定最优解结构参数。
Fig. 15
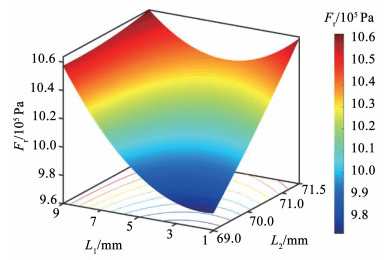图 15 L1、L2参数关于径向电磁力的响应曲面 Fig. 15 Response surfaces of L1 and L2 parameters in relation to radial electromagnetic force Fig. 16
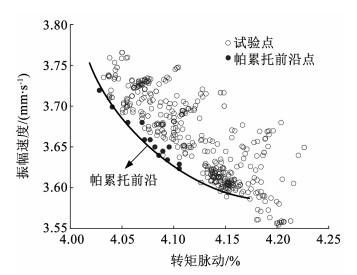图 16 帕累托前沿分布 Fig. 16 Pareto frontier distribution 第2层优化参数采用扫描法寻优，不同Halbach充磁角度θ下对径向电磁力幅值和平均转矩的影响如图 17所示，随着θ增大，Fr幅值在不断减小，电机平均转矩先小幅度增长后不断下降，权衡电机性能和电磁振动的双重条件下选择37°为分段“一型”永磁体充磁角度。
Fig. 17
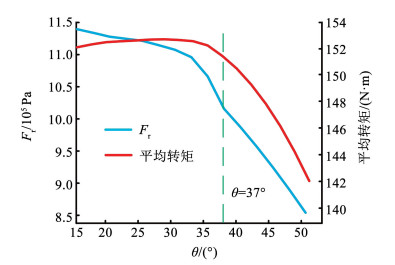图 17 充磁角度对性能的影响曲线 Fig. 17 Influence curve of magnetization angle on performance 通过分层优化电机结构，得到优化结果见表 3，表中Te为转矩均值，Rt为转矩脉动，Fr为径向电磁力幅值，Le为永磁体涡流损耗，Vv为定子振动速度。在保持电磁转矩Te的基础上，转矩脉动Rt减小到4.3%，降低了径向电磁力幅值Fr从而抑制了电机的振动速度Vv，同时减小了永磁体涡流损耗Le。
表 3
表 3 电机优化结果 Tab. 3 Motor optimization results 参数目标 Rc/mm θ/(°) L1/mm L2/mm Te/(N·m) Rt/% Fr/105 Pa Le/W Vv/(mm·s-1) 优化前 4 54.5 2 69 149 14.1 10.8 458 5.07
优化后 2.6 37 1.1 70.3 154 4.3 10.1 436.1 3.64
表 3 电机优化结果 Tab. 3 Motor optimization results
4 仿真对比验证 4.1 电磁性能分析在电磁场中，对Halbach开槽型IPMSM和普通V型电机进行对比验证。两个模型的电磁转矩波形如图 18所示，Halbach开槽型的平均转矩为154 N · m, 略高于普通V型的150 N · m，但前者的转矩脉动为4.3%，远小于普通V型的9.1%。所提出的结构在未损失电磁转矩保证了电机性能的基础上，大幅度降低了转矩脉动。
Fig. 18
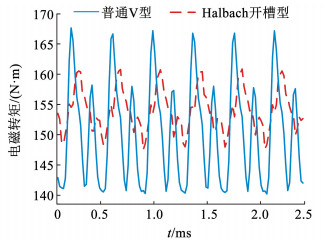图 18 电磁转矩对比波形 Fig. 18 Electromagnetic torque comparison waveform 两个电机的电磁性能对比分析结果见表 4，表中Tcog为齿槽转矩，Br为气隙磁密幅值，EEMF为空载反电势，ATHD为气隙磁密谐波畸变率，ETHD为反电势谐波畸变率。Halbach开槽型IPMSM这一特殊结构使其齿槽转矩峰值降低为126.6 mN · m，齿槽转矩和转矩脉动的减小改善了电机的电磁振动情况。空载气隙磁密Br和反电势EEMF幅值都小于普通V型，但ATHD降低到29.3%，ETHD降低为16.8%, 使磁密和反电势两者的波形更接近于正弦。
表 4
表 4 两种电机结构的电磁性能对比 Tab. 4 Comparison of electromagnetic performance of two motor structures 电机结构 Tcog/(mN·m) Te/(N·m) Rt/% Br/T EEMF/V ATHD /% ETHD/% 普通V型 186.8 150.5 9.1 0.91 379.4 35.9 22.5
Halbach开槽型 126.6 154 4.3 0.81 308.8 29.3 16.8
表 4 两种电机结构的电磁性能对比 Tab. 4 Comparison of electromagnetic performance of two motor structures
4.2 电磁振动分析径向电磁力在空间阶次和时间频率下变化分布，对其进行傅里叶分解如图 19所示。图中可以得出空间0阶、8阶、16阶下的径向电磁力幅值较大，但由于越小的力波阶次对振动幅值影响越大，故只重点关注0阶、8阶。时间0阶、6阶、12阶幅值较大，时间0阶的频率为零不会对电机产生振动影响，只需着重分析时间6阶、12阶。
Fig. 19
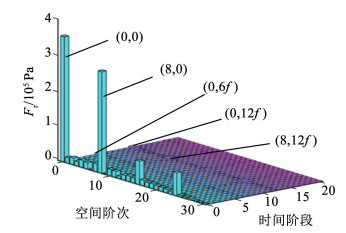图 19 径向电磁力的时间空间傅里叶分解图 Fig. 19 Time-space Fourier decomposition diagram of radial electromagnetic force 在空间0阶、8阶下，电机径向电磁力的影响主要集中在时间6f和12f阶次上，从图 20、21中可知Halbach开槽型电机在两个频率上的幅值均小于普通V型电机，电磁振动得到了很好地抑制。电机的基波频率为400 Hz，两个时间阶次分别对应2 400 Hz和4 800 Hz，均与电机模态各阶次频率相差较远，故电机不会发生共振。
Fig. 20
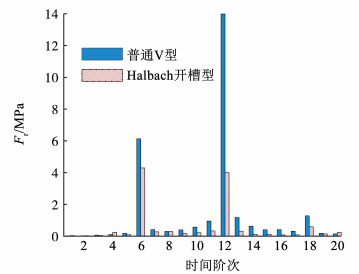图 20 空间0阶的径向电磁力 Fig. 20 Radial electromagnetic force of order 0 in space Fig. 21
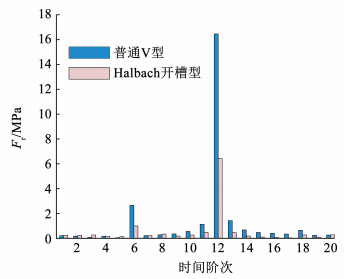图 21 空间8阶的径向电磁力 Fig. 21 Radial electromagnetic force of order 8 in space 时间6阶、12阶下的径向电磁力幅值主要分布在空间0阶、8阶、16阶，如图 22、23所示。由于定子振动大小与力波阶数的四次方成反比例关系，故忽略16阶对电机振动带来的影响，只关注空间0阶、8阶。在时间6阶下，Halbach开槽型电机的空间0阶幅值下降率为30%，空间8阶幅值下降率为69%。在时间12阶下，Halbach开槽型电机的空间0阶幅值下降率为71%，空间8阶幅值下降率为61%。
Fig. 22
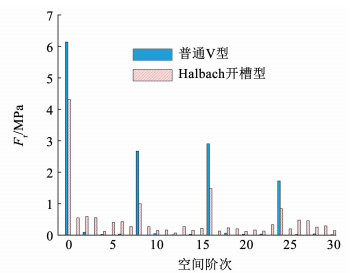图 22 时间6阶的径向电磁力幅值 Fig. 22 Radial electromagnetic force amplitude of time 6 order Fig. 23
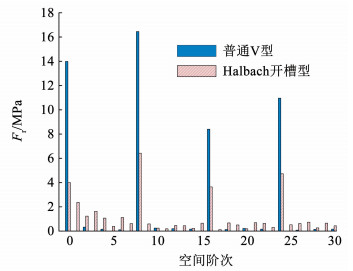图 23 时间12阶的径向电磁力幅值 Fig. 23 Radial electromagnetic force amplitude of time 12 order 4.3 耦合场振动分析为探究电机电磁振动的抑制效果，在电磁、机械场耦合的情况下对两台电机进行定子振动分析对比。如图 24所示为两台电机在不同频率下定子轭部的振动加速度分布曲线，其中1 590.5 Hz频率与定子3阶模态的固有频率1 597.3 Hz较为接近，其他频率段均避开共振频率。Halbach开槽型结构的振动加速度幅值远小于普通V型，其中1 590.5 Hz时加速度幅值降低率为91%。
Fig. 24
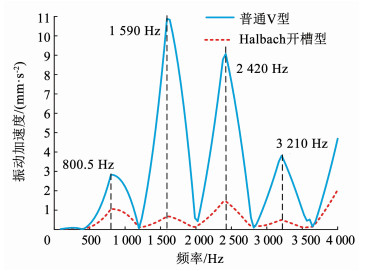图 24 定子轭振动加速度曲线 Fig. 24 Stator yoke vibration acceleration curve 由于电机三阶固有频率与图 24中1 590.5 Hz频率较为接近，为探究电机是否发生共振现象，在该频率下仿真得出定子的振动速度如图 25所示。普通V型IPMSM的最大振动速度为3.1 mm/s，大于所提出电机的2.9 mm/s。同时，1 590.5 Hz下定子的振动速度较小且未发生异常突变，从而可以判断出电机未发生共振现象。
Fig. 25
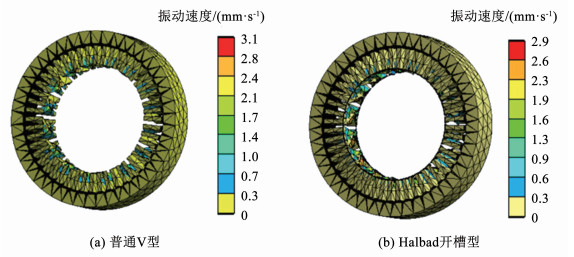图 25 1 590.5 Hz下定子振动速度 Fig. 25 Stator vibration speed at 1 590.5 Hz 4.4 机械应力分析电机转子机械强度是电机稳定运行的重要前提，IPMSM转子在高速运行时承受着切向离心力和电磁力的共同作用，为了验证电机转子机械结构的稳定性及应力形变情况，利用Ansys Workbench仿真软件，得到Halbach开槽型IPMSM三维结构转子在6 000 r/min工况下所受等效应力和结构总变形。电机具体材料属性见表 5。
表 5
表 5 永磁转子材料属性 Tab. 5 Permanent magnet rotor material properties 转子材料 密度/(kg·m-3) 泊松比 屈服强度/MPa DW315_50 7 600 0.31 450
NdFe35 7 400 0.3 80
表 5 永磁转子材料属性 Tab. 5 Permanent magnet rotor material properties
4.4.1 等效应力分析转子及永磁体所受等效应力如图 26所示，其中转子最大应力发生在最外侧永磁体两极之间，此位置磁密较为密集，最大值为0.36 MPa，而硅钢片的屈服强度为450 MPa，故转子结构稳定；“一型”及“V型”永磁体最大应力位于材料边缘部分，所受最大等效应力为0.12 MPa, 低于永磁体抗拉特性屈服强度80 MPa，验证得到高速运行下转子机械强度的稳定性。
Fig. 26
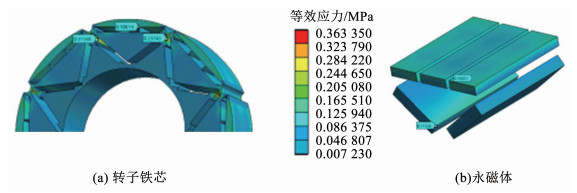图 26 转子永磁体等效应力分析 Fig. 26 Equivalent stress analysis of rotor permanent magnet 4.4.2 总变形分析转子铁心运行过程中最大形变发生在转轴内侧如图 27所示，最大形变量为0.012 μm，“V型”永磁体发生的最大形变量为0.011 μm，均远小于电机气隙长度，符合电机的设计要求。
Fig. 27
图 27 转子永磁体总变形分析 Fig. 27 Total deformation analysis of rotor permanent magnet body 5 结论1) 内置式Halbach永磁同步电机凭借其永磁体充磁角度和特殊拓扑结构的优势，解决了IPMSM电磁振动大的难题，并在没有增加永磁体成本的基础上，提升了电磁性能，提高了功率密度。同时，参数敏感度分析结合响应面的优化方法，提高了电机的优化效率和准确性。
2) 电机径向电磁力在2 400 Hz和4 800 Hz时幅值较大，避开了引起电机共振的固有频率值。相较于普通V型IPMSM，在时间6阶下，空间0阶径向电磁力幅值降低了30%，空间8阶幅值降低了69%。在时间12阶下，空间0阶和8阶的径向电磁力幅值分别降低了71%、61%。
3) 相比于普通V型IPMSM，定子振动加速度最大值从10.5 mm/s2下降到0.8 mm/s2，下降率为91%；相比于普通V型IPMSM，在未损失电磁转矩的基础上，转矩脉动减小到4.3%，齿槽转矩降低了32%，空载气隙磁密和反电势两者的谐波畸变率下降率分别为18%和25%。
4) 在额定转速下，转子所受等效应力远小于材料极限值，最大形变量符合设计要求。
参考文献
[1] 唐任远, 等. 现代永磁电机[M]. 北京: 机械工业出版社, 1997.
TANG Renyuan, et al. Modern permanent magnet motor[M]. Beijing: China Machine Press, 1997.
[2] 陈永校. 电机噪声的分析和控制[M]. 杭州: 浙江大学出版社, 1987.
CHEN Yongxiao. Analysis and control of motor noise[M]. Hangzhou: Zhejiang University Press, 1987.
[3] ZHU Z Q, XIA Z P, JEWELL G W, et al. Analytical modeling and finite-element com-putation of radial vibration force in fractional-slot permanent-magnet brushless machines[J]. IEEE Transactions on Industry Applications, 2010, 46(5): 1908. DOI:10.1109/TIA.2010.2058078
[4] TORREGROSSA D, PEYRAUT F, FAHIMI B, et al. Multiphysics finite-element modeling for vibration and acoustic analysis of permanent magnet synchronous machine[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 490. DOI:10.1109/TEC.2010.2080681
[5] 王晓远, 贺晓钰, 高鹏. 电动汽车用V型磁钢转子永磁电机的电磁振动噪声削弱方法研究[J]. 中国电机工程学报, 2019, 39(16): 4919.
WANG Xiaoyuan, HE Xiaoyu, GAO Peng. Research on electromagnetic vibration and noise reduction method of V type magnet rotor permanent magnet motor electric vehicles[J]. Proceedings of the CSEE, 2019, 39(16): 4919.
[6] 谢颖, 李飞, 黎志伟, 等. 内置永磁同步电机减振设计与研究[J]. 中国电机工程学报, 2017, 37(18): 5437.
XIE Ying, LI Fei, LI Zhiwei, et al. Optimized design and research of vibration reduction with an interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2017, 37(18): 5437.
[7] 洪剑锋, 王善铭, 孙宇光, 等. 高模数电磁力对永磁电机电磁振动影响[J]. 电工技术学报, 2022, 37(10): 2446.
HONG Jianfeng, WANG Shanming, SUN Yuguang, et al. Influence of high modulus electromagnetic force on electromagnetic vibration of permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2022, 37(10): 2446.
[8] 左曙光, 张耀丹, 阎礁, 等. 考虑定子各向异性的永磁同步电机振动噪声优化[J]. 西安交通大学学报, 2017, 51(5): 60.
ZUO Shuguang, ZHANG Yaodan, YAN Jian, et al. Vibration and noise optimization of permanent magnet synchronous motor considering stator anisotropy[J]. Journal of Xi'an Jiaotong University, 2017, 51(5): 60.
[9] KIM J, PARK S, RYU J, et al. Comparative study of vibration on 10-pole 12-slot and 14-pole 12-slot PMSM considering tooth modulation effect[J]. IEEE Transactions on Industrial Electronics, 2023, 70(4): 11731.
[10] 韩雪岩, 张新刚, 朱龙飞, 等. 内置式多层磁钢永磁同步电机振动噪声抑制措施[J]. 电机与控制学报, 2021, 25(8): 67.
HAN Xueyan, ZHANG Yingang, ZHU Longfei, et al. Vibration and noise suppression measures of built-in multilayer permanent magnet synchronous motor[J]. Electric Machines and Control, 2021, 25(8): 67.
[11] 李晓华, 赵容健, 田晓彤, 等. 逆变器供电对电动汽车内置式永磁同步电机振动噪声特性影响研究[J]. 电工技术学报, 2020, 35(21): 4455.
LI Xiaohua, ZHAO Rongjian, TIAN Xiaotong, et al. Influence of inverter power supply on vibration and noise characteristics of built-in permanent magnet synchronous motor for electric vehicle[J]. Transactions of China Electrotechnical Society, 2020, 35(21): 4455.
[12] 陈德志, 张玉庸, 白保东, 等. 不同温度及谐波下硅钢片电磁-力特性与变频电机振动[J]. 电工技术学报, 2020, 35(22): 4647.
CHEN Dezhi, ZHANG Yuyong, BAI Baodong, et al. Electromagnetic force characteristics of silicon steel sheet and vibration of frequency conversion motor under different temperature and harmonics[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4647.
[13] LIANG W Y, WANG J F, LUK P, et al. Analytical study of stator tooth modulation on electromagnetic radial force in permanent magnet synchronous machines[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12): 11731. DOI:10.1109/TIE.2020.3029462
[14] 李晓华, 刘成健, 梅柏杉, 等. 电动汽车IMSM宽范围调速振动噪声源分[J]. 中国电机工程学报, 2018, 38(17): 5219.
LI Xiaohua, LIU Chengjian, MEI Boshan, et al. Vibration and noise sources analysis of IPMSM for electric vehicles in a wide-speed range[J]. Proceedings of the CSEE, 2018, 38(17): 5219.
[15] 郑江, 代颖, 石坚. 车用永磁同步电机的电磁噪声特性[J]. 电工技术学报, 2016, 31(增刊1): 53.
ZHENG Jiang, DAI Ying, SHI Jian. Electromagnetic noise characteristics of permanent magnet synchronous motors for vehicles[J]. Transactions of China Electrotechnical Society, 2016, 31(Sup.1): 53.
[16] LIN Y Q, SUN Y. Radial electromagnetic force and vibration in synchronous reluctancemotors with asymmetric rotor structures[J]. IET Electric Power Applications, 2021, 25(3): 23446.
[17] ZHOU G Y, SHEN J X. Rotor notching for electromagnetic noise reduction of induction motors[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3361. DOI:10.1109/TIA.2017.2681969
[18] ZHU X, HUANG J, QUAN L, et al. Comprehensive sensitivity analysis and multi objective optimization research of permanent magnet flux-intensifying motors[J]. IEEE Transactions on Industrial Electrnics, 2019, 66(4): 2613. DOI:10.1109/TIE.2018.2849961
[19] DENG W, ZUO S. Comparative study of sideband electromagnetic force in internal and external rotor PMSMs with SVPWM technique[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 956. DOI:10.1109/TIE.2018.2821110
[20] 高锋阳, 高建宁, 李明明, 等. 内置式Halbach永磁同步电机的参数敏感度分层优化设计[J]. 西安交通大学学报, 2022, 56(5): 1.
GAO Fengyang, GAO Jianning, LI Mingming, et al. Optimization design of Halbach interior permanent magnet synchronous motor based on parameter sensitivity stratification[J]. Journal of Xi'an Jiaotong University, 2022, 56(5): 1.
