李凯文1,郑珺2,向雨晴3,邓自刚2,石洪富2,祝翰林1
(1.西南交通大学 电气工程学院,成都 611756;2.牵引动力国家重点实验室(西南交通大学),成都 610031; 3.西南交通大学 机械工程学院,成都 610031)
摘要:
为了改善磁悬浮汽车的基础性能,基于目前国内外永磁电动悬浮的研究现状,提出了一种基于更优磁化角的永磁电动轮结构。首先从原理的角度分析磁化角度变化实现更优电动轮结构的理论合理性,通过优化环形永磁电动轮的磁化角可以增加单极对的永磁体数量增加外围磁场强度,并利用等效面电流法推导得出更简洁的解析计算公式,分析得到了永磁电动轮与导体板之间的结构关系、磁场特性和涡流分布特点；然后在三维电磁仿真优化方面,从磁场、悬浮力、驱动力、浮重比和浮驱比等多个性能参数对比传统的永磁电动轮和改进的永磁电动轮。结果验证了改进后的永磁电动轮结构对其悬浮-驱动一体化功能具有有益提升,并从解析计算和实验分析两个角度共同验证三维电磁仿真的准确性和可靠性,为后续设计优化工作提供了可靠手段。这种Halbach阵列永磁电动轮的优化方案有助于磁悬浮概念车的基础性能提升,为“碳达峰、碳中和”背景下新型绿色环保交通工具的形成提供了可行的技术选择。
关键词: 永磁电动悬浮 永磁电动轮 磁化角度 悬浮 驱动 优化策略
DOI：10.11918/202206002
分类号:TM153.3
文献标识码:A
基金项目:国家自然科学基金面上项目(52077178);四川省科技创新人才项目(22CXRC0217)
Optimization strategy of permanent magnet electrodynamic wheel for magnetic levitation car
LI Kaiwen1,ZHENG Jun2,XIANG Yuqing3,DENG Zigang2,SHI Hongfu2,ZHU Hanlin1
（1.School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756,China; 2.State Key Laboratory of Traction Power（Southwest Jiaotong University）, Chengdu 610031, China; 3.School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China）
Abstract:
To improve the basic performance of the magnetic levitation car, based on the current research situation of permanent magnet electrodynamic suspension (PMEDS),this paper propose a better annular structure of permanent magnet electrodynamic wheel(PMEDW). In term of theoretical analysis, this paper analyzes the theoretical rationality of Halbach array magnetization varying by different magnetization angle, the number of permanent magnets in the monopole pair can be increased to increase the peripheral magnetic field intensity by optimizing the magnetization angle, a more concise analytical formula is derived by using the equivalent surface current method, and the structural relationship, magnetic field characteristics and eddy current distribution characteristics between the PMEDW and the conductor plate are obtained through analysis. In terms of 3D simulation optimization, different types of PMEDW were established in ANSYS Maxwell. The magnetic field, levitation force, propulsion force, levitation to weight ratio and levitation to propulsion ratio were compared respectively in simulation analysis and analytical calculation results to verify whether the new type of PMEDW is able to improve the function of levitation-propulsion integration simultaneously, the accuracy and reliability of the 3D electromagnetic simulation are verified from the perspectives of analytical calculation and experimental testing. The optimization scheme of Halbach array permanent magnet electric wheel will contribute to improve the basic performance of the magnetic levitation concept car, and provide a feasible technical choice for the formation of new green and environmentally friendly vehicles under the background of "emission peak and carbon neutrality".
Key words: permanent magnet electrodynamic suspension permanent magnet electrodynamic wheel magnetization angle levitation propulsion optimization strategy
李凯文, 郑珺, 向雨晴, 邓自刚, 石洪富, 祝翰林. 一种用于磁悬浮汽车的永磁电动轮的优化策略[J]. 哈尔滨工业大学学报, 2024, 56(7): 162-170. DOI: 10.11918/202206002.
LI Kaiwen, ZHENG Jun, XIANG Yuqing, DENG Zigang, SHI Hongfu, ZHU Hanlin. Optimization strategy of permanent magnet electrodynamic wheel for magnetic levitation car[J]. Journal of Harbin Institute of Technology, 2024, 56(7): 162-170. DOI: 10.11918/202206002.
基金项目 国家自然科学基金面上项目(52077178);四川省科技创新人才项目(22CXRC0217) 作者简介 李凯文(1996—)，男，硕士研究生;
郑珺(1980—)，女，副教授，博士生导师 通信作者 郑珺，jzheng@swjtu.edu.cn 文章历史 收稿日期: 2022-06-01
Abstract Full text Figures/Tables PDF
一种用于磁悬浮汽车的永磁电动轮的优化策略
李凯文1, 郑珺2
, 向雨晴3, 邓自刚2, 石洪富2, 祝翰林1 1. 西南交通大学 电气工程学院, 成都 611756;
2. 牵引动力国家重点实验室(西南交通大学), 成都 610031;
3. 西南交通大学 机械工程学院, 成都 610031
收稿日期: 2022-06-01; 录用日期: 2022-07-22; 网络首发日期: 2024-05-24
基金项目: 国家自然科学基金面上项目(52077178);四川省科技创新人才项目(22CXRC0217)
作者简介: 李凯文(1996—)，男，硕士研究生; 郑珺(1980—)，女，副教授，博士生导师
通信作者: 郑珺，jzheng@swjtu.edu.cn
摘要: 为了改善磁悬浮汽车的基础性能，基于目前国内外永磁电动悬浮的研究现状，提出了一种基于更优磁化角的永磁电动轮结构。首先从原理的角度分析磁化角度变化实现更优电动轮结构的理论合理性，通过优化环形永磁电动轮的磁化角可以增加单极对的永磁体数量增加外围磁场强度，并利用等效面电流法推导得出更简洁的解析计算公式，分析得到了永磁电动轮与导体板之间的结构关系、磁场特性和涡流分布特点；然后在三维电磁仿真优化方面，从磁场、悬浮力、驱动力、浮重比和浮驱比等多个性能参数对比传统的永磁电动轮和改进的永磁电动轮。结果验证了改进后的永磁电动轮结构对其悬浮-驱动一体化功能具有有益提升，并从解析计算和实验分析两个角度共同验证三维电磁仿真的准确性和可靠性，为后续设计优化工作提供了可靠手段。这种Halbach阵列永磁电动轮的优化方案有助于磁悬浮概念车的基础性能提升，为“碳达峰、碳中和”背景下新型绿色环保交通工具的形成提供了可行的技术选择。
关键词: 永磁电动悬浮 永磁电动轮 磁化角度 悬浮 驱动 优化策略
Optimization strategy of permanent magnet electrodynamic wheel for magnetic levitation car
LI Kaiwen1, ZHENG Jun2
, XIANG Yuqing3, DENG Zigang2, SHI Hongfu2, ZHU Hanlin1 1. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China;
2. State Key Laboratory of Traction Power(Southwest Jiaotong University), Chengdu 610031, China;
3. School of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China
Abstract: To improve the basic performance of the magnetic levitation car, based on the current research situation of permanent magnet electrodynamic suspension (PMEDS), this paper propose a better annular structure of permanent magnet electrodynamic wheel(PMEDW). In term of theoretical analysis, this paper analyzes the theoretical rationality of Halbach array magnetization varying by different magnetization angle, the number of permanent magnets in the monopole pair can be increased to increase the peripheral magnetic field intensity by optimizing the magnetization angle, a more concise analytical formula is derived by using the equivalent surface current method, and the structural relationship, magnetic field characteristics and eddy current distribution characteristics between the PMEDW and the conductor plate are obtained through analysis. In terms of 3D simulation optimization, different types of PMEDW were established in ANSYS Maxwell. The magnetic field, levitation force, propulsion force, levitation to weight ratio and levitation to propulsion ratio were compared respectively in simulation analysis and analytical calculation results to verify whether the new type of PMEDW is able to improve the function of levitation-propulsion integration simultaneously, the accuracy and reliability of the 3D electromagnetic simulation are verified from the perspectives of analytical calculation and experimental testing. The optimization scheme of Halbach array permanent magnet electric wheel will contribute to improve the basic performance of the magnetic levitation concept car, and provide a feasible technical choice for the formation of new green and environmentally friendly vehicles under the background of "emission peak and carbon neutrality".
Keywords: permanent magnet electrodynamic suspension permanent magnet electrodynamic wheel magnetization angle levitation propulsion optimization strategy
1980年，Halbach[1]首次提出Halbach结构，目标主要是是用最少量的磁体产生最强的磁场。1995年美国Fujii等[2]提出了环形Halbach永磁轮结构，其工作原理为：当环形Halbach结构的永磁轮在非磁性良电导体轨道上旋转运动时，由电磁感应定律可知会在导体板中产生感应涡流，感应涡流会形成一个磁化方向相反的镜像磁场，镜像磁场与永磁轮旋转磁场相互作用就可同时产生悬浮力和磁阻力，而永磁轮旋转是机械圆周运动，类似于汽车轮胎借助滚动摩擦向前运动，因此, 对于永磁轮来说磁阻力可等效为其驱动力。
相比于其他磁悬浮结构，环形Halbach永磁轮具有悬浮驱动一体化的巨大优势，引起了国内外众多学者的广泛研究。美国Fujii等[3-5]最早建立了单个永磁轮悬浮系统实验装置，重点研究了永磁电动悬浮系统的动态运动特性和控制策略。
对于国内来说，针对永磁轮开展的研究也在逐渐增多。2004年，中国科学院电工研究所王厚生等[6-8]提出了分层式导体板轨道结构，建立了三维涡流分布数学模型，并推导了导体板分层结构的数学解析式；同时在实验里对比了不同厚度、不同层数的紫铜片组合下的悬浮性能，最终验证了分层结构的导体板可以明显地减小磁阻力，并提高系统的浮阻比。2010年，国防科技大学贺光等[9-10]提出将永磁电动与电磁进行混合悬浮，搭建了混合悬浮系统下单自由度悬浮实验平台，并设计了两种不同参数下的永磁体悬浮结构，结果表明, 通过对电磁铁的主动控制可以有效抑制外界干扰给永磁电动悬浮带来的振动，验证了混合悬浮系统的合理性。2011年，北京交通大学秦伟等[11-12]从电磁场的角度出发，建立永磁电动式磁悬浮系统的分环电磁模型，采用拉普拉斯分离变量的方法推导得出悬浮力和磁阻力的解析表达式，并建立Ansoft有限元模型和相应的实验装置，综合分析得出了系统的磁场分布、电磁力和转矩等基本特性规律。2018年，北京理工大学冯炎青等 [13]提出了基于电动悬浮的可控磁悬浮小车设计，该装置由小车和导体板轨道及顶部磁性轨道组成，通过无线控制4个电机驱动磁轮水平旋转，利用磁轮与感应轨道相互作用提供悬浮力，最终通过试验证明了基于涡流悬浮的磁悬浮小车的可行性。2020年，西南交通大学提出通过将传统橡胶车轮组替换为环形永磁电动轮组的概念，分别对磁悬浮概念车专用的Halbach永磁电动轮的电磁特性和工作特性进行了详细探究和说明[14-16]，并且研制出了1∶50的磁悬浮概念汽车驱动功能验证实验台，如图 1所示，可以实现对双磁轮不同转速下的悬浮力、驱动力的测试；以及1∶50比例下的磁悬浮概念汽车样机模型[16]，如图 2所示，磁悬浮概念汽车主要思想就是将永磁电动轮与传统汽车相结合，将4个悬浮车轮和4个电机分布在车架两端，分为前、后轮组，通过分别控制前后轮组转速和旋转方向产生磁悬浮汽车所需的悬浮力和驱动力。
Fig. 1
图 1 实验装置侧视图 Fig. 1 Side-view of the experimental device Fig. 2
图 2 磁悬浮概念汽车样机模型 Fig. 2 The prototype of maglev concept car 然而针对Halbach永磁电动轮的设计，目前还没有结合Halbach阵列磁化角开展系统的优选工作。因此，本文从优化Halbach阵列磁化角度的变化值出发，以获取更优越的悬浮力和驱动力为目标，提出了将永磁电动轮Halbach相邻磁化角度90°变化分别改变为15°、30°、45°和60°变化，重构更加适应于环形的电动磁轮结构。通过理论分析和ANSYS Maxwell有限元软件仿真建模，全面对比不同磁化角度变化的环形永磁电动轮的悬浮-驱动性能。本文为基于Halbach永磁电动轮的磁悬浮概念汽车方案提供了更优浮驱性能的结构和优化思路。
1 理论分析从现有的Halbach永磁电动轮及其磁场分布云图(图 3)中可以看出，Halbach永磁电动轮中相邻的两块永磁体磁路相辅相成、互相影响。在总的磁能积不变的情况下，研究需要使大部分磁场都集中到了永磁电动轮外围，从而获得了更强的磁场。所以通过改变永磁体的阵列，人为制造磁场分布的不平衡，将更多的磁场集中于有需要的工作区域，是优化结构的关键所在。
Fig. 3
图 3 现有Halbach永磁电动轮磁场分布云图 Fig. 3 Magnetic field distribution cloud map of current Halbach permanent magnet (PM) EDW 根据文献[17]中对永磁轮磁场分布计算方法可知，永磁电动悬浮的模型中感应板内部的感应电流面密度表示为
$\boldsymbol{J}=-\sigma V_{\mathrm{S}} \boldsymbol{B}$ (1)
式中: J表示导体的电流密度，σ表示感应板的电导率，VS表示永磁体阵列相对感应板的等效线速度，B表示Halbach永磁阵列的等效磁感应强度。
为了简化永磁电动轮悬浮结构的电磁力解析计算过程，本文采用了永磁体结构类比的方法，只要满足环形永磁体阵列与线型永磁体阵列结构下方有效磁场区间的磁通密度和磁场强度分布情况相同的条件，就可以根据等效面电流法将环形永磁体阵列等效为线型永磁体阵列。
假设感应板厚度有限，则在感应板内由麦克斯韦方程和安培环路定理[18]可得：
$\nabla \times \boldsymbol{H}=\boldsymbol{J}+(\sigma+\mathrm{j} \omega \varepsilon) \boldsymbol{E}$ (2)
在此引入矢量磁位A，定义为
$\nabla \times \boldsymbol{A}=\boldsymbol{B}, \nabla \cdot \boldsymbol{A}=0$ (3)
并且因为
$\boldsymbol{B}=\mu \boldsymbol{H}$ (4)
式(2)进一步可以表示为
$\nabla^2 \boldsymbol{A}+k^2=-\boldsymbol{J} \mu+\nabla\left(\nabla \cdot \boldsymbol{A}-\frac{k^2}{\mathrm{j} \omega} \boldsymbol{E}\right)$ (5)
式中：H表示磁场强度，k表示传播函数，ω表示永磁磁场的频率，ε表示感应板的介电常数，μ表示导体板的磁导率，A表示感应板内矢量磁位，E表示感应板内部的感应电动势。
在满足已知条件：
$k^2=-\mathrm{j} \omega \mu(\sigma+\mathrm{j} \omega \varepsilon)$ (6)
$\nabla \cdot \boldsymbol{A}=\frac{k^2}{\mathrm{j} \omega} \boldsymbol{E}$ (7)
可进一步得到感应板外部和导体内部的矢量磁位方程：
$\left\{\begin{array}{l}\nabla^2 \boldsymbol{A}_z^{\mathrm{I}}+k^2 \boldsymbol{A}_z^{\mathrm{I}}=0 \\\nabla^2 \boldsymbol{A}_z^{\mathrm{II}}+k^2 \boldsymbol{A}_z^{\mathrm{II}}=-\mu \boldsymbol{J} \\\nabla^2 \boldsymbol{A}_z^{\mathrm{III}}+k^2 \boldsymbol{A}_z^{\mathrm{III}}=0\end{array}\right.$ (8)
式中AzⅠ，AzⅡ，AzⅢ分别表示感应板上方、感应板内部和感应板下方在z轴方向的矢量磁位分量。
假设导体内部的矢量磁位的边界是无限远，则在分界面满足磁场的矢量磁位边界条件为
$\left\{\begin{array}{l}\lim\limits_{y \rightarrow+\infty} \boldsymbol{A}_z^{\mathrm{I}}=0, \lim\limits_{y \rightarrow-\infty} \boldsymbol{A}_z^{\mathrm{III}}=0 \\\boldsymbol{H}_x^{\mathrm{I}}-\boldsymbol{H}_x^{\mathrm{II}}=0, \boldsymbol{H}_x^{\mathrm{II}}-\boldsymbol{H}_x^{\mathrm{III}}=0 \\\boldsymbol{A}_z^{\mathrm{I}}=\boldsymbol{A}_z^{\mathrm{II}}(y=0), \boldsymbol{A}_z^{\mathrm{II}}=\boldsymbol{A}_z^{\mathrm{III}}(y=-d)\end{array}\right.$ (9)
此外，假设永磁阵列沿x轴水平运动时，感应板内部只产生z轴方向的感应电流。假设该永磁电动悬浮系统的空气层和感应板物理参数均匀，满足各向同性，由文献[19]可知等效Halbach永磁轮阵列的空间磁场表达式为
$\left\{\begin{array}{l}\boldsymbol{B}_x^{\mathrm{I}}=\boldsymbol{B}_0 \mathrm{e}^{-p(h-y)} \mathrm{e}^{\mathrm{j}\left(p x-\frac{\pi}{2}\right)} \\\boldsymbol{B}_y^{\mathrm{I}}=\boldsymbol{B}_0 \mathrm{e}^{-p(h-y)} \mathrm{e}^{\mathrm{j} p x}\end{array}\right.$ (10)
其中B0满足：
$\boldsymbol{B}_0=\frac{\boldsymbol{B}_{\mathrm{r}}\left(1-\mathrm{e}^{p t}\right) \sin \frac{\pi}{n}}{\frac{\pi}{n}}$ (11)
$n=\frac{360}{\theta}$ (12)
式中: Bx和By分别为Halbach阵列空间磁场在x轴和y轴方向的磁场分量，p为极对数，Br为永磁体剩磁，h为永磁体悬浮气隙，t为永磁阵列垂直厚度，n为一个周期内(一极对)对应磁化角度θ下永磁体的磁体数量。
因此，结合式(8)，利用分离变量法推导得到感应板上方、感应板内部和感应板下方的磁位矢量分别为
$\left\{\begin{array}{l}\boldsymbol{A}_z^{\mathrm{I}}=\left(C_1 \mathrm{e}^{-r y}+C_2 \mathrm{e}^{r y}\right) \mathrm{e}^{\mathrm{j} p x} \\\boldsymbol{A}_z^{\mathrm{II}}=\left(C_3 \mathrm{e}^{-r y}+C_4 \mathrm{e}^{-r y}+\phi\right) \mathrm{e}^{\mathrm{j} p x} \\\boldsymbol{A}_z^{\mathrm{III}}=\left(C_5 \mathrm{e}^{-r y}+C_6 \mathrm{e}^{r y}\right) \mathrm{e}^{\mathrm{j} p x}\end{array}\right.$ (13)
其中C1、C2、C3、C4、C5和C6均为待定系数，而r和?满足：
$r=\left(p^2-k^2\right)^{\frac{1}{2}}, \phi=\frac{\mu_0 \delta v \boldsymbol{B}_0 \mathrm{e}^{-p(h-y)}}{k^2}$ (14)
结合永磁电动悬浮的矢量磁位边界条件可得到上式中各个待定系数，进而计算出感应板内部的感应磁场强度分量：
$\left\{\begin{array}{l}\boldsymbol{B}_x^\text{II}=\left(-C_3 r \mathrm{e}^{-r y}+C_4 r \mathrm{e}^{r y}+p \phi\right) \mathrm{e}^{\mathrm{j} p x} \\\boldsymbol{B}_y^\text{II}=-\left(C_3 \mathrm{e}^{-r y}+C_4 \mathrm{e}^{r y}+\phi\right) p \mathrm{e}^{\mathrm{j} p x}\end{array}\right.$ (15)
因此，导体板内部的总磁场为永磁轮的外磁场和导体板感生磁场的叠加：
$\left\{\begin{array}{l}\boldsymbol{B}_x=\boldsymbol{B}_x^{\mathrm{I}}+\boldsymbol{B}_x^{\mathrm{II}} \\\boldsymbol{B}_y=\boldsymbol{B}_y^{\mathrm{I}}+\boldsymbol{B}_y^{\mathrm{II}}\end{array}\right.$ (16)
最终根据洛伦兹定理[20]:
$\boldsymbol{F}=\boldsymbol{J} \times \boldsymbol{B}$ (17)
由此可计算得到Halbach永磁轮电动悬浮感应板单位面积的驱动力Fx和悬浮力Fy。
$\left\{ \begin{align} & \begin{gathered}\boldsymbol{F}_y=\boldsymbol{B}_0^2 \mathrm{e}^{\mathrm{j} p x} \mu_0 d k \sigma \ln V_{\mathrm{S}} \cos \left[\frac { \pi } { 2 p } \left(R_{\mathrm{o}}-\right.\right. \\\left.\left.R_{\mathrm{i}}\right) \cos \left(h \times V_{\mathrm{S}}+\mu_0 d \sigma\right)^2\right]\end{gathered} \\ & \begin{gathered}\boldsymbol{F}_x=\boldsymbol{B}_0^2 \mathrm{e}^{\mathrm{j} p x} \mu_0 d k \sigma \ln V_{\mathrm{S}} \sin \left[\frac { \pi } { 2 p } \left(R_{\mathrm{o}}+\right.\right. \\\left.\left.R_{\mathrm{i}}\right) \cos \left(h \times V_{\mathrm{S}}+\mu_0 d \sigma\right)^2\right]\end{gathered} \\ \end{align} \right.$ (18)
式中：B0表示定义的磁场，p表示极对数，μ0表示真空磁导率，d表示感应板厚度，k表示传播函数，σ表示感应板的电导率，VS表示永磁轮相对感应板的等效线速度，Ro和Ri分别表示永磁轮的外半径和内半径，h表示悬浮间隙。
通过对式(18)进行分析可知，环形Halbach永磁电动悬浮结构的悬浮力和驱动力与永磁轮的转速、极对数、内半径、外半径、单对极的磁体数量和感应轨道的厚度、电导率都有直接关系。公式直观描述了环形Halbach阵列永磁电动悬浮系统内部参数之间的关系，以及悬浮力和驱动力的变化趋势，为后续第3节电动悬浮系统的参数优化提供了指导。
本文受平板式永磁磁轨磁化角的研究[21]启发，将磁悬浮概念汽车方案中立式Halbach阵列永磁轮磁体的相邻磁化角度90°变化分别改变为15°、30°、45°和60°变化时，因而可通过增加永磁轮单对极磁体数量(角度变化越小，数量越多)增加B0，使得其外围磁场更强，从而实现磁场优化的目标, 最终提升永磁轮的悬浮驱动性能。其中，永磁电动轮中磁化角度变化如图 4右上角所示，红色箭头表示相邻永磁单体磁化角度90°变化，绿色表示60°变化，黄色表示30°变化，依此类推。
Fig. 4
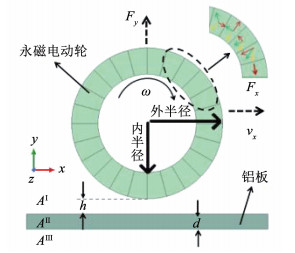图 4 永磁电动轮磁化角度变化示意图 Fig. 4 Schematic of changing magnetization angle of PMEDW 2 有限元仿真和实验分析对比在ANSYS Maxwell中搭建有限元二维仿真模型会忽略边端效应从而造成仿真结果与实验结果相差较大，而有限元三维仿真计算更加准确，其结果更有参考意义，因此, 本文搭建的都是有限元三维瞬态仿真模型，用于研究永磁电动轮磁化角度、内外半径比、极对数等参数对永磁电动悬浮系统性能的影响，同时本节也将专门对有限元三维仿真结果和实验进行对比验证。
为了进一步说明系统性能与永磁体质量的关系，利用如下参数(浮重比式(19)和浮驱比式(20))评价永磁电动悬浮系统的悬浮和驱动性能：
$D_1=\frac{F_y}{m g}$ (19)
$D_{\mathrm{p}}=\frac{F_y}{F_x}=\frac{D_1 \cdot m g}{F_x}$ (20)
其中：Dl为浮重比，表示系统悬浮力与磁体重量的关系；m为环形永磁轮的总质量；g为重力加速度；Dp为浮驱比，表示系统悬浮力与驱动力之间的关系。
为了验证ANSYS Maxwell有限元三维仿真计算结果的准确性和可靠性，本节利用了西南交通大学搭建的环形Halbach阵列的永磁电动轮悬浮实验装置，通过多通道数据采集方案，深入开展了永磁电动悬浮的力特性实验和分析。受限于当前实验基础和硬件条件，若对各种磁化角变化磁轮都进行实验对比验证成本过于高昂，性价比较低，因此, 先对现有的传统环形永磁轮进行实验测试和有限元三维仿真结果对比用以证明仿真模型的准确性，然后通过有限元仿真优化计算得出永磁轮的最优设计参数。
永磁轮的结构如图 5所示，可分为3层。内层结构类似于传统汽车的轮毂结构，采用6061-T6高强度铝合金材料，用以承担整车配重、连接及配合驱动器件。中间层是由16块N35钕铁硼永磁体排列而成的环形Halbach阵列，因单块永磁体磁化方向各有差异，各永磁体之间又存在较大的作用力，故采用高强度磁体胶黏合，封装完成后再次用强力胶加固，保证永磁轮在高速下运行的可靠性。外层结构采用2 mm厚的尼龙材料包裹，有效加固永磁体的同时避免了永磁体与感应轨道直接接触造成永磁体磨损。其中，磁轮的磁场强度H为8.9×105 A/m，极对数P为4，剩磁Br为1.19 T, 外半径Ro为50 mm，内半径Ri为32.5 mm，磁轮宽度W为35 mm，悬浮间隙h为10 mm，铝板的宽和厚分别为60 mm和10 mm，电导率为3.8×107 s/m。
Fig. 5
图 5 环形永磁轮实物图 Fig. 5 The real product of annular PMEDW 利用图 1所示的实验装置测量永磁电动轮在0~3 500 r/min时的悬浮力和驱动力数据，并与有限元三维仿真结果对比，结果如图 6所示。对结果进行分析可知，实验结果与有限元三维仿真计算结果吻合，其中悬浮力平均误差为2.79%，驱动力平均误差为11.05%，充分证明了有限元三维仿真的准确性和可靠性。
Fig. 6
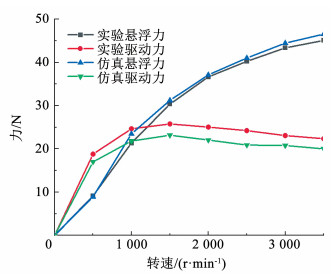图 6 实验和仿真结果对比 Fig. 6 Comparison of the experimental and simulation results 3 有限元仿真优化分析 3.1 磁化角度优化根据前文的理论分析，本节拟搭建不同磁化角度变化的永磁电动轮仿真模型，对比分析获得更优的悬浮驱动性能。由于实际的磁悬浮汽车的工作转速将主要在高转速范围，在仿真计算补充探讨了更高转速下悬浮驱动性能，以此弥补实验条件的不足。永磁电动轮有限元三维瞬态仿真模型的具体参数：磁轮的磁场强度H为8.9×105 A/m，极对数P为4，剩磁Br为1.23 T，半径Ro为50 mm，内半径Ri为32.5 mm，磁轮宽度W为35 mm，悬浮间隙h为10 mm, 铝板的宽和厚分别为60 mm和10 mm，电导率为3.8×107 s/m。
图 7给出了典型的30°磁化角变化的磁场分布云图。可以看出，相较于原先磁化角度90°变化(图 3)而言，其磁感应线更加光滑，磁场更多集中到磁轮的外围，说明更改磁化角度的可行性。
Fig. 7
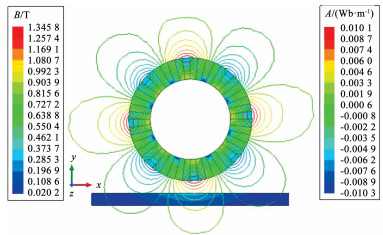图 7 30°磁化角度变化电动轮磁场分布云图 Fig. 7 Magnetic field distribution cloud map of 30 angle PM EDW 为了进一步证明不同磁化角度变化对Halbach永磁电动轮外围的磁感应强度的影响，对导体板上表面(即磁轮下方10 mm处)的磁感应强度进行对比分析，以导体板左端点为0°旋转角度，右端点为180°旋转角度可得图 8。
Fig. 8
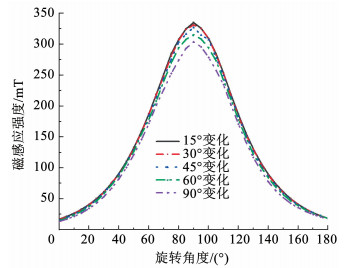图 8 永磁电动轮下方10 mm处磁感应强度对比 Fig. 8 Comparison of magnetic induction intensity at 10 mm below PMEDW 从图 8中可以发现，在磁轮正下方磁感应强度最大，并且随着磁化角度变化的减小，磁感应强度越大，曲线同时也更接近正弦变化，其中, 15°磁化角度变化与30°磁化角度变化的磁感应强度曲线接近重合，说明了30°磁化角度变化接近饱和。这也证明了针对Halbach永磁轮阵列可以通过优化磁化角度提高其外围磁感应强度的可行性。
图 9和图 10进一步给出了保持永磁电动轮内外半径、悬浮间隙不变情况下，不同转速下悬浮力、驱动力的变化曲线。
Fig. 9
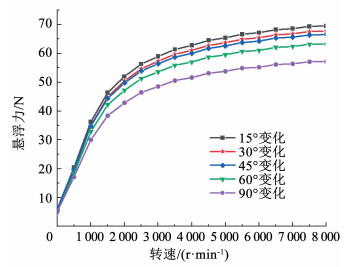图 9 不同磁化角下悬浮力对比 Fig. 9 Comparison of levitation forces under different magnetization angles Fig. 10
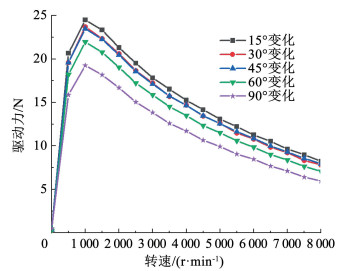图 10 不同磁化角下驱动力对比 Fig. 10 Comparison of propulsion forces under different magnetization angles 从图 9和图 10可以看出，随着转速的升高，悬浮力逐渐饱和，驱动力先增加然后减小。对其分析结果可知，磁轮相邻永磁单体磁化角度越小时，悬浮力和驱动力均变大。并且由于磁化角度越小，单极对永磁体数量越多，单个的永磁体则越小，考虑到更小磁化角对制作工艺复杂性的增加和磁轮整体性价比的减小，本文后续则针对30°磁化角度变化进行展开研究。此时，30°磁化角度相对于90°磁化角度变化的永磁电动轮的悬浮力提升了16.55%，驱动力提升了21.63%。
3.2 极对数优化极对数影响磁场与感应轨道的切割频率，对悬浮性能产生较大的影响，故基于上述结论继续讨论极对数对系统性能的影响，主要对比在30°磁化角度变化下不同极对数的悬浮性能。
从图 11中可以看出，不同极对数下的速度特性基本一致，但永磁轮磁场强度随着极对数的增大而减小，导致了悬浮力衰减。分析结果表明，由于2对极下永磁轮结构的气隙磁通密度具有最大值，其悬浮和驱动性能也最优。
Fig. 11
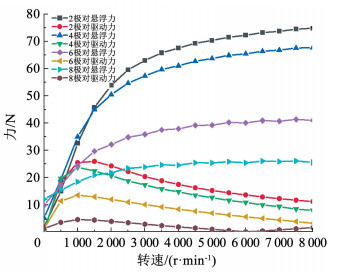图 11 不同极对数下悬浮力、驱动力对比 Fig. 11 Comparison of levitation forces and propulsion forces under different poles 3.3 内外半径比优化永磁电动轮的内外半径大小决定了悬浮系统的尺寸。为了深入研究永磁电动轮内外半径比对系统性能的影响，在磁化角度30°、极对数为2、转速取5 000 r/min的条件下，保持永磁电动轮外半径为常量50 mm，参数化扫描永磁电动轮的内半径从5 mm变化到40 mm，仿真计算不同半径比下系统的浮重比和浮驱比，结果如图 12所示。
Fig. 12
图 12 浮驱比Dl、浮重比Dp随半径比的变化 Fig. 12 Dl and Dp changing with radius ratios 通过对图 12分析可知，系统最优半径比在0.5附近。这与文献[22]中结论的0.68相差较大，这主要是因为文献[22]中采用的是二维仿真模型忽略了边端效应而产生了误差，而本文建立的三维仿真模型的计算结果则更有参考意义，此时浮重比达到6.61，浮驱比为4.52，浮驱性能表现更为优越。
3.4 悬浮工作间隙优化在永磁电动轮下方，距离永磁电动轮越远，磁场强度越小，所以有必要研究探索系统性能与悬浮工作间隙h的关系。在磁化角度30°、极对数为2、转速取5 000 r/min、外半径为50 mm、最优半径比为0.5的条件下，悬浮工作间隙从3 mm到15 mm变化，仿真计算悬浮力与驱动力的具体情况。结果如图 13所示。
Fig. 13
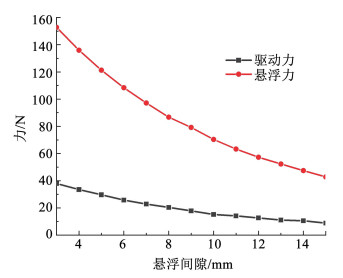图 13 不同悬浮工作间隙下系统性能对比 Fig. 13 Comparison of system performance under different suspension gaps 正如理论分析式(18)所展示的，随着悬浮间隙的增大，永磁电动轮的悬浮力和驱动力都逐渐降低，所以, 现实中需要根据具体设计要求选取合适的悬浮间隙。
3.5 感应轨道厚度优化本文研究的感应轨道存在集肤效应。集肤效应是指导体经历交流电或者交变电磁场时，导体内部的电流分布不均匀，电流集中分布在导体的表面部分。通常电流集中在导体外表的薄层，越靠近导体表面，电流密度越大，导体内部实际上电流较小。集肤效应使导体的电阻增加，损耗功率也增加。在本文模型中为了使得系统设计具有更高的性价比，要讨论感应轨道厚度对悬浮驱动性能的影响。因此, 在磁化角度30°、极对数为2、转速取5 000 r/min、外半径为50 mm、最优半径比为0.5、悬浮间隙为10 mm的条件下，仿真计算不同导体板厚度下系统性能的变化情况。
通过对图 14分析可知，随着感应轨道厚度增大，初始阶段对悬浮力有促进作用，而对驱动力是负作用。在实际应用中，厚度较大的感应轨道可以保证磁场渗透更彻底，但也造成材料冗余、浪费，特别是长距离感应轨道的建造。因此，综合考虑工作速度和成本，取轨道厚度为7 mm时具有较高的性价比，此时悬浮力接近饱和，驱动力也相对较大，并且此值与文献[23]中所计算在集肤深度为6.8 mm时剩余磁场的作用可忽略不计，因此, 可以将7 mm作为为感应轨道厚度的参考值，这也从侧面证明了仿真计算的正确性。
Fig. 14
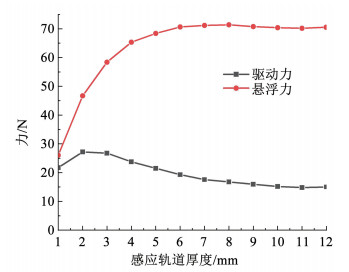图 14 不同感应轨道厚度下系统性能对比 Fig. 14 Comparison of system performance under different induction track thicknesses 基于上述永磁轮与感应轨道结构的有限元电磁仿真优化模型，可以得到当永磁轮磁化角度取30°、极对数取2、最优半径比取0.5、悬浮间隙取10 mm、感应板厚度取7 mm时具有最优的悬浮驱动性能。
3.6 解析模型和有限元仿真结果对比分析根据第2节理论分析可知，通过减小Halbach永磁电动轮磁化角度的变化可以增加永磁轮单对极磁体数量从而增加B0，使得其外围磁场更强，从而实现磁场优化的目标, 最终提升永磁轮的悬浮驱动性能。图 15和图 16分别给出了不同磁化角度相对于传统的90°磁化角变化的电动轮的悬浮驱动性能的对比结果。
Fig. 15
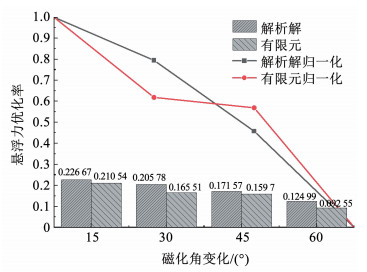图 15 三维解析计算和三维有限元法悬浮力优化率对比 Fig. 15 Comparison of levitation force optimization rate in 3D Analytical Calculation and 3D FEM Fig. 16
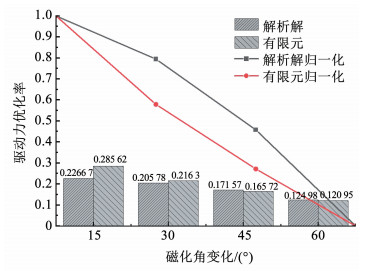图 16 三维解析计算和三维有限元法驱动力优化率对比 Fig. 16 Comparison of propultion force optimization rate in 3D Analytical Calculation and 3D FEM 通过对比分析可以看出，有限元仿真结果和解析模型比较吻合，其中优化率最大相差了5.89%，最小相差0.405%，误差处于在可接受范围。细小误差主要是因为本文中搭建的是三维有限元仿真模型，计算量庞大，网格划分对计算结果会带来一定的影响。归一化的结果进一步表明两者趋势也基本一致，因此磁化角变化越小，永磁电动轮的悬浮驱动性能越好。通过理论分析和有限元仿真计算都证明了针对于减小永磁电动轮磁化角度变化的举措确实可以同时改善永磁电动轮的悬浮驱动性能，并可以此为基础结构开展更细致的工作。
4 结论本文基于磁场解析计算和等效面电流法，推导得出更简洁的解析计算公式，并结合ANSYS Maxwell有限元软件搭建的一种专用于磁悬浮新概念汽车的Halbach阵列永磁电动轮三维电磁仿真模型，从磁场、悬浮力、驱动力、浮重比和浮驱比等多个性能参数对比传统的永磁电动轮和改进后的永磁电动轮。结果表明，通过减小永磁电动轮的相邻永磁单体磁化角度的变化可以明显改善其悬浮驱动性能。其中，30°时磁化角变化相对于传统的90°磁化角变化时的永磁电动轮的悬浮力提升了16.55%，驱动力提升了21.63%。通过进一步全面优化，得出了30°磁化角下永磁电动轮的最优设计参数。该三维仿真计算模型可为后续专门开展30°优化磁化角的永磁电动轮与磁悬浮概念汽车试验平台相结合的研究提供可靠的基础手段。总之，减小永磁电动轮磁化角度可以有效地改善用于磁悬浮概念汽车永磁电动轮的悬浮-驱动一体化功能。在未来磁悬浮汽车样机研究中，可以参考本文的理论模型、仿真方法对永磁电动轮参数作进一步的优化匹配，以达到更优的悬浮驱动性能。
参考文献
[1] HALBACH K. Design of permanent multipole magnets with oriented rare earth cobalt material[J]. Nuclear Instruments and Methods, 1980, 169(1): 1. DOI:10.1016/0029-554X(80)90094-4
[2] FUJII N, OGAWA K, MATSUMOTO T. Revolving magnet wheels with permanent magnets[J]. Electrical Engineering in Japan, 1995, 115(3): 319. DOI:10.1541/ieejias.115.319
[3] FUJII N, ITO Y, YOSHIHARA T. Characteristics of a moving magnet rotator over a conducting plate[J]. IEEE Transactions on Magnetics, 2005, 41(10): 3811. DOI:10.1109/tmag.2005.854930
[4] QIN W, BIRD J. Electrodynamic wheel rolling resistance[J]. IEEE Transactions on Magnetics, 2017, 53(8): 8107407. DOI:10.1109/tmag.2017.2693962
[5] INIGUEZ J, RAPOSO V. Numerical simulation of a simple low-speed model for an electrodynamic levitation system based on a halbach magnet array[J]. Journal of Magnetism and Magnetic Materials, 2009, 322(12): 1673. DOI:10.1016/j.jmmm.2009.04.035
[6] 王厚生. 永磁电动式导体板磁悬浮列车轨道结构及相关研究[D]. 北京: 中国科学院电工所, 2004
WANG Housheng. Track structure and related research of permanent magnet electrodynamic conductor plate maglev train[D]. Beijing: Institute of Electrical Engineering of the Chinese Academy of Sciences, 2004
[7] 王厚生, 杜玉梅, 夏平畴, 等. 电动式磁悬浮列车金属板轨道结构的研究[J]. 中国电机工程学报, 2005, 25(7): 162.
WANG Housheng, DU Yumei, XIA Pingchou, et al. Research on metal plate track structure of electrodynamic maglev[J]. Proceedings of the CSEE, 2005, 25(7): 162. DOI:10.3321/j.issn:0258-8013.2005.07.029
[8] WANG H, YE Y, WANG Q, et al. Analysis for ring arranged axial field halbach permanent magnets[J]. IEEE Transactions on Applied Superconductivity, 2006, 16(2): 1562. DOI:10.1109/tasc.2005.869628
[9] 贺光. 基于Halbach结构的永磁电动悬浮系统的发展与应用[C]//第29届中国控制会议论文集. 北京: 中国控制会议, 2010: 5532
HE Guang. Development and application of permanent magnet electrodynamic suspension system based on Halbach structure[C]//Proceedings of the 29th China Control Conference. Beijing: Chinese Control Conference, 2010: 5532
[10] 贺光, 成玉卫, 龙志强. 基于直线型Halbach结构的永磁电动悬浮系统的设计与实现[J]. 磁性材料及器件, 2010, 41(6): 36.
HE Guang, CHENG Yuwei, LONG Zhiqiang. Design and realization of permanent magnet electrodynamic suspension system based on linear Halbach structure[J]. Journal of Magnetic Materials and Devices, 2010, 41(6): 36.
[11] 秦伟, 范瑜, 马育华, 等. 盘式永磁Halbach悬浮装置的磁场和力特性分析[J]. 电机与控制学报, 2012, 16(6): 57.
QING Wei, FAN Yu, MA Yuhua, et al. Analysis of magnetic field and force characteristics of disk-type permanent magnet Halbach levitation device[J]. Electric Machines and Control, 2012, 16(6): 57. DOI:10.15938/j.emc.2012.06.015
[12] 秦伟, 范瑜, 朱熙, 等. 永磁电动式磁悬浮装置的研究[J]. 电机与控制学报, 2011, 15(7): 77.
QING Wei, FAN Yu, ZHU Xi, et al. Research on permanent magnet electrodynamic suspension device[J]. Electric Machines and Control, 2011, 15(7): 77. DOI:10.15938/j.emc.2011.07.016
[13] 沈祎铠, 曾峙翔, 冯炎青. 基于涡流悬浮的可控磁悬浮小车设计[J]. 信息记录材料, 2018, 19(8): 11.
SHEN Yikai, ZENG Zhixiang, FENG Yanqing. Design of controllable magnetic levitation car based on eddy current suspension[J]. Information Recording Materials, 2018, 19(8): 11. DOI:10.16009/j.cnki.cn13-1295/tq.2018.08.007
[14] YUAN Yuan, DENG Zigang, ZHANG Shuai, et al. Working principle and primary electromagnetic characteristics of a permanent magnet electrodynamic wheel for maglev car application[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 3603905.
[15] SANG Xiaochen, DENG Zigang, CHEN Jianzheng, et al. Analysis and experiment on the levitation force and thrust force characteristics of a permanent magnet electrodynamic wheel for maglev car application[J]. IEEE Transactions on Applied Superconductivity, 2021, 31(8): 3602704.
[16] ZHANG Ze, DENG Zigang, ZHANG Shuai, et al. Design and operating mode study of a new concept maglev car employing permanent magnet electrodynamic suspension technology[J]. Sustainability, 2021, 13(11): 5827. DOI:10.3390/su13115827
[17] 陈殷, 张昆仑. 板式双边永磁电动悬浮电磁力计算[J]. 电工技术学报, 2016, 31(24): 150.
CHEN Yin, ZHANG Kunlun. Calculation of electromagnetic force of plate type double sided permanent magnet electrodynamic suspension[J]. Transactions of China Electrotechnical Society, 2016, 31(24): 150. DOI:10.19595/j.cnki.1000-6753.tces
[18] 陈殷, 张昆仑. Halbach永磁阵列空间磁场的解析计算[J]. 磁性材料及器件, 2014, 45(1): 1.
CHEN Yin, ZHANG Kunlun. Analytical calculation of space magnetic field of Halbach permanent magnet array[J]. Journal of Magnetic Materials and Devices, 2014, 45(1): 1.
[19] 陈殷. 低速永磁电动悬浮电磁力特性研究[D]. 成都: 西南交通大学, 2015
CHEN Yin. Research on electromagnetic force characteristics of low-speed permanent magnet electrodynamic suspension[D]. Chengdu: Southwest Jiaotong Universit, 2015
[20] 吕刚, 孙守光, 马云双. 城轨交通中直线感应牵引电机的效率最优控制[J]. 电机与控制学报, 2009, 13(4): 490.
Lü Gang, SUN Shouguang, MA Yunshuang. Efficiency optimal control of linear induction traction motors in urban rail transit[J]. Electric Machines and Control, 2009, 13(4): 490. DOI:10.3969/j.issn.1007-449X.2009.04.004
[21] DENG Zigang, ZHANG Weifeng, CHEN Yang, et al. Optimization study of the Halbach permanent magnetic guideway for high temperature super-conducting magnetic levitation[J]. Superconductor Science and Technology, 2020, 33(3): 034009. DOI:10.1088/1361-6668/ab6ec0
[22] PAUDEL N, BIRD J, PAUL S, et al. A transient 2D model of an electrodynamic wheel moving above a conductive guideway[C]//IEEE International Electric Machines & Drives Conference. Niagara Falls: IEEE, 2011
[23] KNOEPFEL H E. Magnetic fields: a comprehensive theoretical treatise for practical use[M]. New York: John Wiley & Sons, 2000. DOI:10.1119/1.135115
