MS1180方管连续辊弯成形角部开裂机理

张建邦¹,刘晓立^1,2,黄素霞¹,李河宗¹,崔衍亮²,闫宾³,闻海强¹

(1.河北省智能工业装备技术重点实验室(河北工程大学),河北 邯郸 056038; 2.潍坊瑞孚冷弯设备有限公司,山东 潍坊 261057; 3.安阳工学院 机械工程学院,河南 安阳 455000)



摘要:

方矩形管在辊弯成形中会产生角部开裂现象,这已成为严重制约方矩形管质量的关键问题,为解决其角部开裂缺陷展开深入研究,寻找控制开裂缺陷的方法。首先通过对MS1180进行单轴拉伸、缺口拉伸和平面应变实验得到了材料的力学特性,并分别利用3种拉伸试验将Ayada、Rice-Tracey和标准化Cockroft-Latham准则进行校准,得到了预测误差最小的一种断裂准则,并以此构建了方矩管辊弯开裂模型。其次利用辊弯成形COPRA RF设计软件和有限元MARC仿真专业软件,结合生产实际条件建立了方矩形管连续辊弯成形三维有限元模型,并进行辊弯实验验证模型的准确性。最后采用扫描电镜和金相显微镜对方矩形管开裂件以及断口进行微观观察,针对性的利用有限元模型探究了方矩形管连续辊弯成形时应力-应变分布规律,并分析了道次数量、角部成形半径和机架间距对方矩管角部应力-应变分布的影响。结果表明:发现材料起裂点位于角部近外层,对开裂断口进行分析,得到其开裂方式为准解理开裂,角部剪切面上所受的主应力过大导致其开裂；增加辊弯道次数量、方矩形管角部成形半径以及机架之间的间距能有效减少开裂问题的出现,为以后解决方矩形管角部开裂问题提供了理论基础。

关键词:  辊弯成形  超高强钢  方矩形管  开裂  有限元分析

DOI：10.11918/202306029

分类号:TG335.7

文献标识码:A

基金项目:山东省科学技术厅基金(2022TSGC2510)；河北省教育厅基金(QN2021209)



Mechanism of corner cracking in continuous roll bending forming of MS1180 square pipe

ZHANG Jianbang¹,LIU Xiaoli^1,2,HUANG Suxia¹,LI Hezong¹,CUI Yanliang²,YAN Bin³,WEN Haiqiang¹

(1.Key Laboratory of Intelligent Industrial Equipment Technology of Hebei Province (Hebei University of Engineering), Handan 056038, Hebei, China; 2.Weifang Ruifu Roll Forming Machinery, Weifang 261057, Shandong, China; 3.School of Mechanical Engineering, Anyang Institute of Technology, Anyang 455000, Henan, China)

Abstract:

Corner cracking phenomenon in square and rectangular pipes during roll bending, which has become a key issue that seriously restricts the quality of square rectangular tubes. In order to address this issue and find a way to control the cracking defect, a comprehensive study was conducted. Firstly, the mechanical properties of the MS1180 material were obtained by uniaxial tensile, notched tensile and plane strain experiments. Three fracture criteria, Ayada, Rice-Tracey and standardized Cockroft-Latham criteria, were calibrated using these test date, and the criterion with the smallest prediction error was selected. This criterion was then used to construct a square rectangular tube roll bending cracking model. Next, using COPRA RF design software and finite element MARC simulation professional software of roll bending, a three-dimensional finite element model for continuous roll bending of square rectangular tube was established in combination with the actual production conditions. The accuracy of the model was verified by roll bending experiments. Finally, scanning electron microscopy and metallographic microscope were used to observe the cracks and fractures of the rectangular tube. The stress-strain distribution of the square rectangular tube during continuous roll bending was investigated using the finite element model, and the effects pass number, corner forming radius and frame spacing on the stress-strain distribution of the corner of the rectangular tube were analyzed. It is found that the initiation of cracking point of the material occurs near the outer layer of the corner. In addition, the cracking fracture is analyzed, which reveals that the cracking mechanism is quasi-cleavage fracture, where excessive principal stress on the corner shear surface leads to cracking. Increasing the number of roll bending passes, the forming radius of the square rectangular pipe corner and the spacing between the frames can effectively reduce the occurrence of cracking issues. These findings provide a theoretical basis for solving the problem of cracking in the corners of square rectangular pipes in the future.

Key words:  roll forming  ultra-high tensile steel  square rectangular tube  cracking  finite element analysis


张建邦, 刘晓立, 黄素霞, 李河宗, 崔衍亮, 闫宾, 闻海强. MS1180方管连续辊弯成形角部开裂机理[J]. 哈尔滨工业大学学报, 2024, 56(8): 153-162. DOI: 10.11918/202306029.
ZHANG Jianbang, LIU Xiaoli, HUANG Suxia, LI Hezong, CUI Yanliang, YAN Bin, WEN Haiqiang. Mechanism of corner cracking in continuous roll bending forming of MS1180 square pipe[J]. Journal of Harbin Institute of Technology, 2024, 56(8): 153-162. DOI: 10.11918/202306029.
基金项目 山东省科学技术厅基金(2022TSGC2510)；河北省教育厅基金(QN2021209) 作者简介 张建邦(1999—)，男，硕士研究生;
李河宗(1973—)，男，教授，博士生导师 通信作者 刘晓立，liuxiaoli01206332@163.com 文章历史 收稿日期: 2023-06-08



Abstract            Full text            Figures/Tables            PDF


MS1180方管连续辊弯成形角部开裂机理
张建邦¹, 刘晓立^1,2, 黄素霞¹, 李河宗¹, 崔衍亮², 闫宾³, 闻海强¹    
1. 河北省智能工业装备技术重点实验室(河北工程大学)，河北 邯郸 056038;
2. 潍坊瑞孚冷弯设备有限公司，山东 潍坊 261057;
3. 安阳工学院 机械工程学院，河南 安阳 455000

收稿日期: 2023-06-08; 录用日期: 2023-07-19; 网络首发日期: 2024-04-26
基金项目: 山东省科学技术厅基金(2022TSGC2510)；河北省教育厅基金(QN2021209)
作者简介: 张建邦(1999—)，男，硕士研究生; 李河宗(1973—)，男，教授，博士生导师
通信作者: 刘晓立，liuxiaoli01206332@163.com


摘要: 方矩形管在辊弯成形中会产生角部开裂现象，这已成为严重制约方矩形管质量的关键问题，为解决其角部开裂缺陷展开深入研究，寻找控制开裂缺陷的方法。首先通过对MS1180进行单轴拉伸、缺口拉伸和平面应变实验得到了材料的力学特性，并分别利用3种拉伸试验将Ayada、Rice-Tracey和标准化Cockroft-Latham准则进行校准，得到了预测误差最小的一种断裂准则，并以此构建了方矩管辊弯开裂模型。其次利用辊弯成形COPRA RF设计软件和有限元MARC仿真专业软件，结合生产实际条件建立了方矩形管连续辊弯成形三维有限元模型，并进行辊弯实验验证模型的准确性。最后采用扫描电镜和金相显微镜对方矩形管开裂件以及断口进行微观观察，针对性的利用有限元模型探究了方矩形管连续辊弯成形时应力-应变分布规律，并分析了道次数量、角部成形半径和机架间距对方矩管角部应力-应变分布的影响。结果表明：发现材料起裂点位于角部近外层，对开裂断口进行分析，得到其开裂方式为准解理开裂，角部剪切面上所受的主应力过大导致其开裂；增加辊弯道次数量、方矩形管角部成形半径以及机架之间的间距能有效减少开裂问题的出现，为以后解决方矩形管角部开裂问题提供了理论基础。
关键词: 辊弯成形    超高强钢    方矩形管    开裂    有限元分析    
Mechanism of corner cracking in continuous roll bending forming of MS1180 square pipe
ZHANG Jianbang¹, LIU Xiaoli^1,2, HUANG Suxia¹, LI Hezong¹, CUI Yanliang², YAN Bin³, WEN Haiqiang¹    
1. Key Laboratory of Intelligent Industrial Equipment Technology of Hebei Province (Hebei University of Engineering), Handan 056038, Hebei, China;
2. Weifang Ruifu Roll Forming Machinery, Weifang 261057, Shandong, China;
3. School of Mechanical Engineering, Anyang Institute of Technology, Anyang 455000, Henan, China



Abstract: Corner cracking phenomenon in square and rectangular pipes during roll bending, which has become a key issue that seriously restricts the quality of square rectangular tubes. In order to address this issue and find a way to control the cracking defect, a comprehensive study was conducted. Firstly, the mechanical properties of the MS1180 material were obtained by uniaxial tensile, notched tensile and plane strain experiments. Three fracture criteria, Ayada, Rice-Tracey and standardized Cockroft-Latham criteria, were calibrated using these test date, and the criterion with the smallest prediction error was selected. This criterion was then used to construct a square rectangular tube roll bending cracking model. Next, using COPRA RF design software and finite element MARC simulation professional software of roll bending, a three-dimensional finite element model for continuous roll bending of square rectangular tube was established in combination with the actual production conditions. The accuracy of the model was verified by roll bending experiments. Finally, scanning electron microscopy and metallographic microscope were used to observe the cracks and fractures of the rectangular tube. The stress-strain distribution of the square rectangular tube during continuous roll bending was investigated using the finite element model, and the effects pass number, corner forming radius and frame spacing on the stress-strain distribution of the corner of the rectangular tube were analyzed. It is found that the initiation of cracking point of the material occurs near the outer layer of the corner. In addition, the cracking fracture is analyzed, which reveals that the cracking mechanism is quasi-cleavage fracture, where excessive principal stress on the corner shear surface leads to cracking. Increasing the number of roll bending passes, the forming radius of the square rectangular pipe corner and the spacing between the frames can effectively reduce the occurrence of cracking issues. These findings provide a theoretical basis for solving the problem of cracking in the corners of square rectangular pipes in the future.
Keywords: roll forming    ultra-high tensile steel    square rectangular tube    cracking    finite element analysis    
超高强钢因其强度高、吸能性好，在汽车工业中得到了广泛的应用，并为汽车的轻量化、低排放做出突出贡献。超高强钢的伸长率随强度的增加而降低，因此在辊弯成形过程中经常出现开裂^[1]。开裂甚至或断裂问题是超高强薄壁构件辊弯成形过程的重要难题，越来越制约着超高强钢在汽车轻量化领域中的应用。近年来，人们发现一些超高强钢的微观组织中含有马氏体相，这导致了特殊的损伤机制和空洞生长方式，剪切断裂成为超高强钢除拉伸断裂外的一种常见断裂方式^[2]。

Dancette等^[3]提出了通过显微组织观察和有限元分析的方法来研究高强钢点焊之后的拉伸剪切断口。Li等^[4]设计了不同几何形状的拉伸试验，并根据3种不同的开裂模式进行了拉伸试验，以揭示铝合金的开裂机理，同时利用SEM断口图分析了断口表面。Mishra等^[5]对DP980钢弯曲断口进行了表征和数值预测。Meng等^[6]研究了渐进微成形过程中的微机械损伤和变形行为，发现了韧性断裂及其诱导原因，并预测了损伤累积过程。Xu等^[7]研究了钛合金宏观区对材料疲劳开裂行为和断裂机制的影响，并发现其裂纹扩展过程中以晶内断裂为主。Cheng等^[8]发现超高强钢薄壁构件辊弯过程中由于残余纵向应力引起的弯矩和残余剪应力引起的弯矩重叠导致帽槽钢的前端和后端发生开口变形，并分析了成形参数对端部开口变形的影响，运用合适的方法减少了槽钢端部扩口的影响。曹建国等^[9]研究发现P形管相邻凹凸角角度偏差过大的原因，并对此提出了邻角角度精确控制方法，通过实验验证了方法的正确性，为P形管的生产时间提供依据。Mehari等^[10]对DP980高强钢局部加热辊压成形过程中的韧性断裂进行了分析，发现随着材料温度的升高，材料的不稳定性和断裂应变增大。王健等^[11]通过对DP980钢板辊弯成形矩形管过程中开裂区进行显微组织和微观形貌观察，发现其裂纹起裂于内表面，并且裂纹端口呈现准解理断裂和韧性断裂混合特征。贾方辉^[12]从微观和宏观两方面研究了DP980钢在辊弯成形过程中的断裂机理，并建立了与应变相关的断裂准则，从而实现了DP980钢辊弯成形过程中断裂的预测。杨帆^[13]通过建立方矩形管连续辊弯成形三维仿真模型，分析不同成形因素下方矩形管应力应变分布规律，发现产生裂纹危险区域大都分布在直角边与上边部过渡区域或内层正角部。

为探究金属成形断裂的宏观力学机制，需要对裂纹区的应力状态进行分析。应力三轴度η是反映塑性成形应力状态的常用参数，在常用断裂模型中，应力三轴度被用来建立断裂准则。Hancock等^[14]通过一系列拉伸试验发现，危险区的应力三轴度是影响韧性断裂的关键因素。Lian等^[15]通过建立微观力学模型发现了应力三轴度对双相钢损伤断裂的预测效果。Yan等^[16]研究了基于应力三轴度的韧性断裂准则对铝合金高筋整体压弯成形断裂的预测。Lode角参数是描述成形过程中材料点应力-应变状态的重要因素，在金属塑性和断裂预测中应充分考虑到。Lou等^[17]基于Lode角参数和应力三轴度提出了一种新机制驱动的宏观韧性断裂准则，能有效预测高强钢的韧性开裂过程。Zeinali等^[18]校准了Lou-Huh韧性断裂准则，并以此研究了对称槽形制品在滚压成形过程中的断裂问题，计算结果与实际实验结果差异仅为12.4%。Bai等^[19-20]提出了一种新的三维非对称断裂轨迹基于等效断裂应变、应力三轴性和Lode角参数的空间中。同时进一步进行了详细的参数化研究，发现断裂轨迹明显依赖于Lode角参数, 并且论证了断裂准则参数对断裂轨迹的影响。Liu等^[21]提出了一种利用应力三轴度和Lode角参数相关的偏态参数建立的韧性断裂模型，并适用于模拟不同应力状态下钢的韧性断裂行为。穆磊^[22]提出了一个新的韧性断裂模型，该韧性断裂模型是基于孔洞演化机制提出的，并基于该断裂模型提出了通过应力状态一致性转化的三维韧性断裂曲面模型，该三维模型很好地反映了不同应力状态下的韧性断裂性能。桂良进等^[23]采用数值与仿真结合的方法研究不同三轴应力状态下双相钢韧性失效，对一些韧性断裂进行修正后，得到适用于双相钢的断裂准则。

为解决方矩形管辊弯成形过程中出现的角部开裂现象，首先通过3种拉伸试验得到材料基本力学性能，并运用已有方法对韧性断裂准则进行了校准。之后对成形件断口形貌进行观察，从微观角度探讨MS1180钢板的开裂机理，对MS1180超高强钢连续辊弯成形过程中的开裂行为进行了分析和预测。最后进行有限元模拟仿真，建立MS1180方矩形管连续辊弯三维有限元模型，通过仿真与试验相结合的方法对实际生产中出现的开裂问题进行分析，并提出能有效预防开裂产生的方案。

1 材料和试验 1.1 材料本文使用的材料为高强钢MS1180，材料厚度为2 mm，其化学成分组成见表 1。高强钢MS1180含有马氏体，所以具有较高的抗拉强度，在辊弯成形中应用广泛。

表 1
表 1 MS1180超高强钢化学组成成分(质量分数) Tab. 1 Chemical composition of MS1180 ultra-high strength steel (Mass fraction) 材料 C Mn Si Al Nb+V+Ti

MS1180 0.12 1.73 0.44 0.045 ＜0.06



表 1 MS1180超高强钢化学组成成分(质量分数) Tab. 1 Chemical composition of MS1180 ultra-high strength steel (Mass fraction)


1.2 材料试验 1.2.1 拉伸试验MS1180基本材料机械性能通过在室温下进行的标准单轴拉伸试验确定。通过WDW电子万能试验机进行3种类型的拉伸试验，以获得确定试验材料力学性能和判断断裂行为所使用的数据。同时为了定义材料各向异性，材料样品被切割取样在相对于轧制方向0°、45°和90°上。同时还进行了两种不同形状的拉伸试验，如图 1所示，包括沿轧制方向的缺口拉伸和平面应变拉伸试验，以确定不同应力状态下的断裂行为，为后续断裂准则的校准做准备。所有试验均重复了3次，使用了从3个试验中获得的所有结果的平均值。MS1180材料的基本力学性能参数见表 2。

Fig. 1
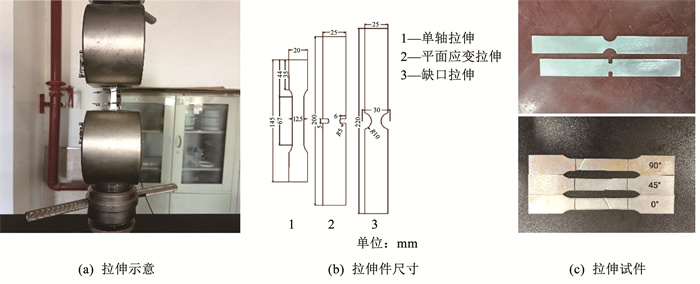图 1 材料性能试验 Fig. 1 Material performance tests


表 2
表 2 MS1180超高强钢基本力学性能参数 Tab. 2 Basic mechanical properties of MS1180 ultra-high tensile steel 材料 取样方向/(°) 屈服强度/MPa 抗拉强度/MPa 断后延伸率/% 塑性应变比

MS1180 0 1 089.97 1 368.76 14.3 0.645

45 1 120.23 1 279.02 12.4 0.636

90 1 014.66 1 252.41 12.3 0.602



表 2 MS1180超高强钢基本力学性能参数 Tab. 2 Basic mechanical properties of MS1180 ultra-high tensile steel


1.2.2 材料微观试验微观试验材料为方矩管正常状态以及方矩管角部开裂状态的MS1180同一板材，采用线切割的方法进行取样，经过逐级打磨、抛光之后用4%的硝酸酒精溶液进行腐蚀观察得到材料金相组织，利用光学显微镜进行材料金相观察。最后利用NOVA NANOSEM 450型场发射扫描电子显微镜观察材料微观形貌，如图 2所示，在观察上述两种材料的基础上，并对企业开裂件的开裂断口进行扫描，观察其开裂机理。

Fig. 2
图 2 SEM扫描电镜设备 Fig. 2 SEM equipment


2 辊弯成形有限元模型的建立 2.1 韧性断裂准则在以弯曲为主要变形方式的辊弯成形过程中，能够准确预测断裂、起裂显得尤为重要。Wang等^[24]进一步研究了DP980钢辊弯成形过程中的断裂预测，采用了Oyane韧性断裂准则，并利用单轴拉伸试验和缺口试件拉伸试验作为校准程序，大大提高了预测精度。Yamane等^[25]提出了一种新的韧性断裂准则能准确预测辊弯成形过程中斜轧特有的断裂起裂。Stoughton等^[26]发现在金属弯曲过程中其主要的断裂方式并不是颈缩，因此基于颈缩的一些断裂模型无法预测弯曲和折边等过程中的断裂问题，传统的基于颈缩的失效模型不适合用于确定辊弯成形断裂发生的方法。Talebi-ghadikolaee等^[27]利用Ayada、Rice-Tracey和标准化Cockroft-Latham 3个准则来建立准确的断裂模型，用于预测辊弯过程中的断裂发生，使用单轴、平面应变和缺口拉伸试验来校准断裂准则，并发现校准过后的Ayada准则预测开裂精度最高。因此，本文按其研究方法对MS1180超高强钢辊弯成形过程中的断裂进行了预测。MS1180单轴拉伸、缺口拉伸、平面拉伸试验的试验结果如图 3所示。

Fig. 3
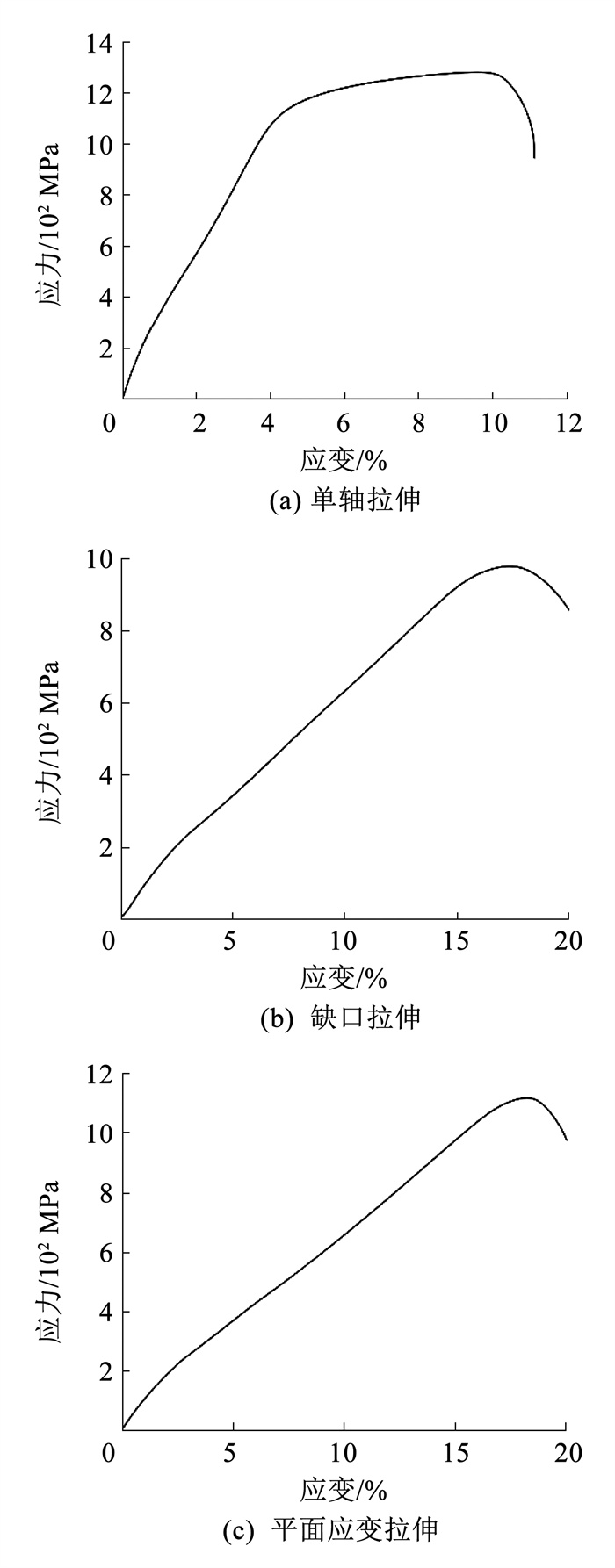图 3 拉伸应力-应变曲线 Fig. 3 Tensile stress-strain curve


3种断裂准则Ayada、Rice-Tracey和标准化Cockroft-Latham公式为：

$D_1=\int_0^{\bar{\varepsilon}_p} \frac{\sigma_{\mathrm{m}}}{\bar{\sigma}} \mathrm{d} \bar{\varepsilon}_p$ (1)

$D_2=\int_0^{\bar{\varepsilon}_p} 0.283 \exp \left(\frac{1.5 \sigma_{\mathrm{m}}}{\bar{\sigma}}\right) \mathrm{d} \bar{\varepsilon}_p$ (2)

$D_3=\int_0^{\bar{\varepsilon}_p}\left(\frac{\sigma_{\text {max }}}{\bar{\sigma}}\right) \mathrm{d} \bar{\varepsilon}_p$ (3)

式中：D₁、D₂、D₃分别为Ayada、Rice-Tracey和标准化Cockroft-Latham的临界损伤参数，σ_m、σ、σ_max分别为静水应力、等效应力和最大主应力。在非耦合损伤模型中，当等效塑性应变加权函数的积分值达到临界值(损伤指标)时，断裂突然发生。将上述公式通过下列式子与Lode角参数η和应力三轴度θ相关并归一化：

$\eta=\frac{\sigma_{\mathrm{m}}}{\bar{\sigma}}$ (4)

$\begin{array}{r}\sigma_{\text {max }}=\sigma_{\mathrm{m}}+\frac{2}{3} \bar{\sigma} \cos \left(\frac{\mathsf{π}}{6}(1-\bar{\theta})\right)= \\\sigma_{\mathrm{m}}\left(1+\frac{2 \cos \left(\frac{\mathsf{π}}{6}(1-\bar{\theta})\right)}{3 \eta}\right)\end{array}$ (5)

将式(4)、(5)代入3种韧性断裂准则式(1)~(3)中得到：

$D_1=\int_0^{\bar{\varepsilon}_p} \eta \mathrm{d} \bar{\varepsilon}_p$ (6)

$D_2=\int_0^{\bar{\varepsilon}_p} 0.283 \exp (1.5 \eta) \mathrm{d} \bar{\varepsilon}_p$ (7)

$D_3=\int_0^{\bar{\varepsilon}_p}\left(\eta+\frac{2 \cos \left(\frac{\mathsf{π}}{6}(1-\bar{\theta})\right)}{3}\right) \mathrm{d} \bar{\varepsilon}_p$ (8)

通过3种拉伸试验分别对上述3种韧性断裂准则进行校准后，发现通过平面拉伸试验校准的3种准则预测误差最客观。Ayada、Rice-Tracey和标准化Cockroft-Latham校准后预测误差分别为7.30%、10.13%和9.05%，对比发现Ayada韧性断裂准则预测精度最高。结合拉伸试验数据得到临界损伤参数D₁为0.169。

2.2 仿真模型的建立本文研究的方矩形管辊弯成形采用的是“圆变方”工艺，成形方式采用四辊式变形，方管具体尺寸如图 4(a)所示，利用COPRA专业软件进行建模，辊花图如图 4(b)所示。辊弯成形机架间矩设置为300 mm，初始型材长度为800 mm，大于2倍的机架间距，即能够保证同时有两组成形轧辊参与工作。将最初道次的上、下轧辊宽度设置为114 mm，下辊半径为158 mm，上辊直径为173 mm。侧辊宽度100 mm，直径为235 mm。同时轧辊的释放角度设为90°。在闭口截面辊弯型钢的生产过程中，为消除辊弯轧机轧辊边缘的应力集中并避免轧辊过于锋利的机械边缘在金属板料表面上造成划痕或磨损，需要对辊弯轧辊的边缘区域进行倒圆角工艺，圆角半径设置为2 mm。第1道次轧辊图如图 4(c)所示。

Fig. 4
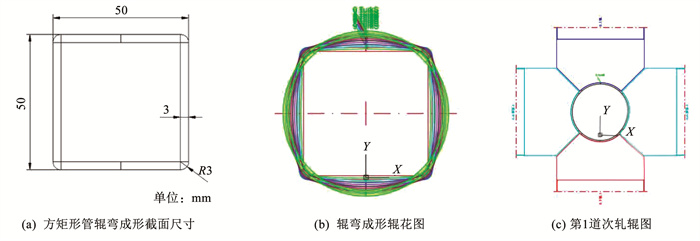图 4 辊弯成形模型设计 Fig. 4 Roll bending model design


实际生产条件中，因型材在辊弯成形过程中受力状态复杂，不仅仅受某一个方向的力而发生变形，除了轧制方向上受到轧辊摩擦力，还有轧辊对其造成的轴向的挤压力，因此应考虑材料的各向异性特性，比较表 2中3个方向上的数据，45°方向上的材料性能参数总体更贴近平均值，为保证有限元的科学完整性，因此以45°方向上的材料性能参数建立有限元模型，以此建立的MS1180方矩形管的三维有限元模型如图 5所示。

Fig. 5
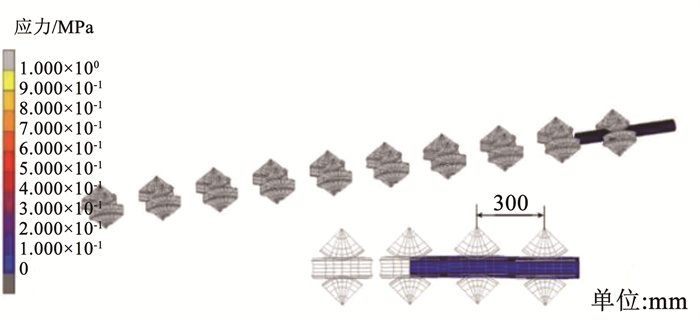图 5 MS1180方矩形管三维模型 Fig. 5 3D model of MS1180 square rectangular tube


2.3 单元网格与边界条件与试验型材所产生的塑性应变变化比较，轧辊产生的微小变化可忽略不计，所以选用轧辊作为解析刚体材料^[28]。为节省计算时间，本文采取了直角折弯部分的网格细化，而其他地方采用了较粗大的网格划分。将整个板带的节点分为7 524个，单元为3 570个。仿真模型设定为四辊驱动，成形道次为10道次，成形速度为20 rad/min。辊弯加工前圆管被拉至第1道次位置，接着通过型材和轧辊表面之间的摩擦实现向前运动，摩擦力系数取值为0.2^[29]。为提高仿真结果与试验条件的相吻合性，施加的约束如图 6所示。对于X约束，所有节点沿中心对称面在X方向进行固定；对于Y约束^[30]，在中心对称面末端底部最后的3个节点在Y方向进行固定；对于Z约束，前后两端所有的节点在Z方向进行固定^[31]。

Fig. 6
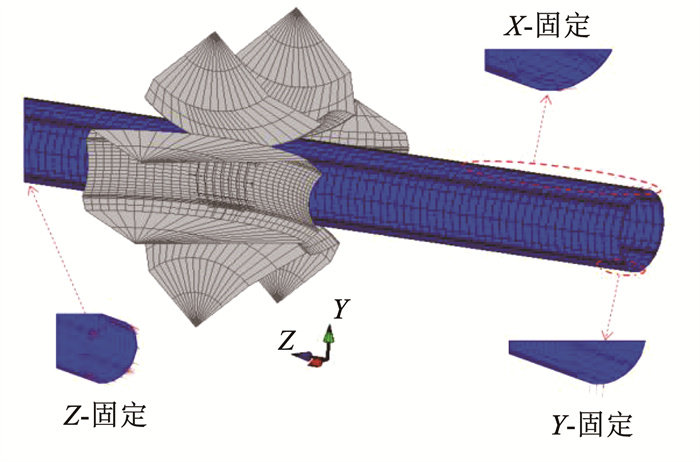图 6 有限元仿真模型 Fig. 6 Finite element simulation model


3 方矩形管辊弯试验试验环境和仿真平台相同，试验机组如图 7(a)所示。在方矩形管成形过程中，初始型材为圆管，所以开卷机和精整机不用参与成形。为使仿真数据的统一, 冲孔机没有参与试验, 即板带不设置预冲孔。在保证成形方式，试验材料，其他成形参数一致的情况下，进行辊弯试验。结果表明在MS1180方矩形管辊弯试验中，出现了开裂现象，如图 7(b)所示，严重影响产品经济效益。

Fig. 7
图 7 方矩管辊弯试验 Fig. 7 Square tube roll bending test


4 结果与讨论 4.1 失效分析 4.1.1 显微组织如图 8所示，MS1180主要有束状马氏体和铁素体组成，马氏体在铁素体中均匀分布。方矩形管角部内表面处无明显裂纹产生，如图 8(a)所示。方矩形管角部外表面处存在明显的开裂，开裂处裂纹由角部近外层处萌生，向近内层扩展，未完全贯通方矩管壁厚，如图 8(b)所示，裂纹始端在两相晶粒内部穿过，开裂方式为穿晶开裂^[32]。方矩管角部近内层处的铁素体呈现出压缩态，马氏体相在压力作用下无规则的分布在铁素体周围，如图 8(c)所示。与方矩管角部近内层处的组织相比，进外层处的组织呈现拉伸态，马氏体被拉长并沿同一方向排列在铁素体周围，如图 8(d)所示。马氏体相与铁素体相比塑性较差，方矩管角部外层被拉伸时，塑性更差的马氏体更容易被拉成破坏，继而产生开裂现象。

Fig. 8
图 8 MS1180方矩管角部显微组织 Fig. 8 MS1180 square tube corner microstructure


4.1.2 方矩管角部SEM形貌对两种方矩管角部进行SEM扫描电镜后可以看出，正常方矩管角部成形完整，无明显微裂纹，如图 9(a)所示。第2个方矩形管弯角近外层出现裂纹，裂纹萌生于角部近外层，向近内层方向扩展，如图 9(b)所示，在裂纹延伸方向上，两相晶粒均被破坏并呈现穿晶开裂现象。

Fig. 9
图 9 方矩管角部SEM形貌 Fig. 9 SEM morphology of rectangular tube corner


通过断口形貌可以清楚的看到，方矩管角部开裂断口上韧窝明显，并分布着塑性变形形成的撕裂棱形貌，如图 10(a)所示。对角部近外层断口进行观察，能清楚的看到近外层断口上分布着韧窝、解理台阶、撕裂棱等形貌特征，如图 10(b)所示，判断近外层断裂为准解理断裂^[33]，其致断原因为方矩管角部近外层剪切面上所受的主应力超过材料抗拉极限，继而发生断裂，但不排除材料发生准解理断裂时其内部存在微裂纹的情况。

Fig. 10
图 10 方矩形管开裂断口形貌 Fig. 10 Cracked fracture profile of square rectangular tube


4.2 成形参数对方矩管角部的影响方矩形管在辊弯过程中，型材受到轧辊挤压力的影响，其受到的主应力过大加上型材的残余应力超过了材料的成形极限，继而发生开裂，因此为探究辊弯成形过程中方矩管角部应力-应变变化，提取方矩形管的部分外层路径曲线，如图 11所示，即方矩管1/4右上角截面。方矩管在辊弯成形过程中，无论是应力还是应变，方矩管角部变化均比其直角边大，并且最大值位于角部中间位置，如图 12所示。方矩管角部的急剧变化，对材料在成形过程中存在很大的影响甚至发生开裂现象，因此需要对方矩形管辊弯成形工艺进行改善，减小角部的应力-应变峰值。

Fig. 11
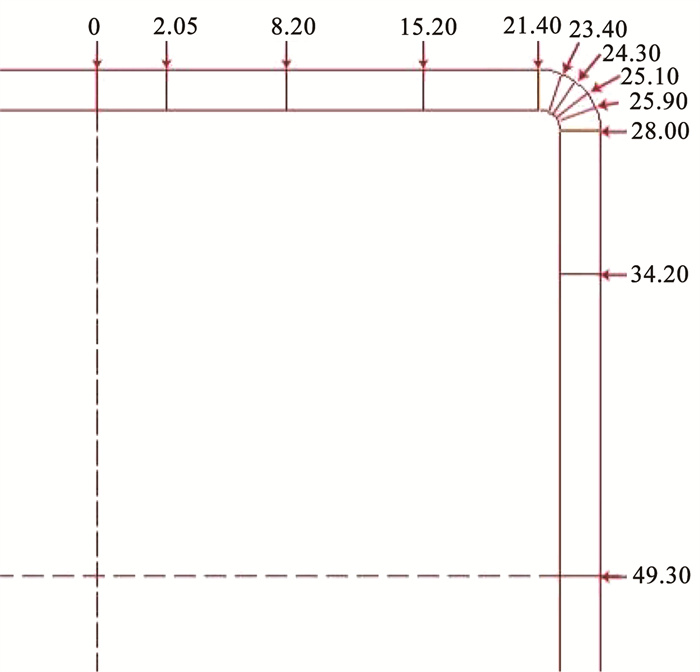图 11 方矩形管节点路径的选取 Fig. 11 Selection of node paths for square rectangular tubes


Fig. 12
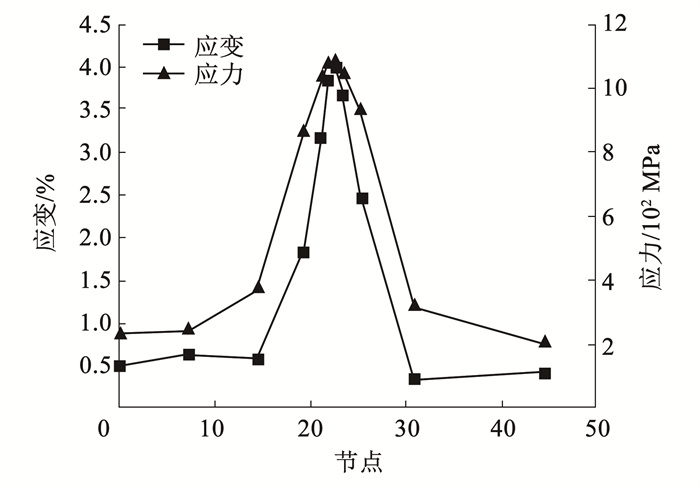图 12 方矩管角部应力-应变分布规律 Fig. 12 Stress-strain distribution pattern at rectangular tube corner


4.2.1 成形道次对角部应力-应变的影响上文已经分析了辊弯成形的方矩形管角部开裂原因，因此以选取的节点路径进行分析，成形道次数量对于方矩形管辊弯成形中路径曲线应力-应变分布情况的影响。如图 13所示，本次成形仿真方案通过改变成形道次，成形道次设置分别为6道次、8道次、9道次和10道次，方矩形管角部应力-应变分布规律与之前的研究规律一致，角部的应力-应变相对于直角边大21%左右，因此更容易产生应力集中甚至发生开裂。在辊弯成形中，圆管辊弯成方矩形管过程中，由于设计的管型截面一致，最后成形角度、材料应变趋于一致，因此图 13(a)中不同道次下方矩形管角部和直角边的应变规律基本一致。道次数量为6时，角部上的各部分应力略大于其他道次数量下的方矩形管角部应力，如图 13(b)所示，因为道次数量太少，导致每个道次的成形角度偏大，所产生的应力也就越大，更加容易出现开裂问题。在满足产品质量要求的机架数量的基础上，机架数量的增加继而减少了每道次的成形角度，从而有效减轻圆管在辊弯成形中的应力积累。辊弯道次数量的增加也应考虑实际生产情况，避免过多的道次从而降低产品经济效益。

Fig. 13
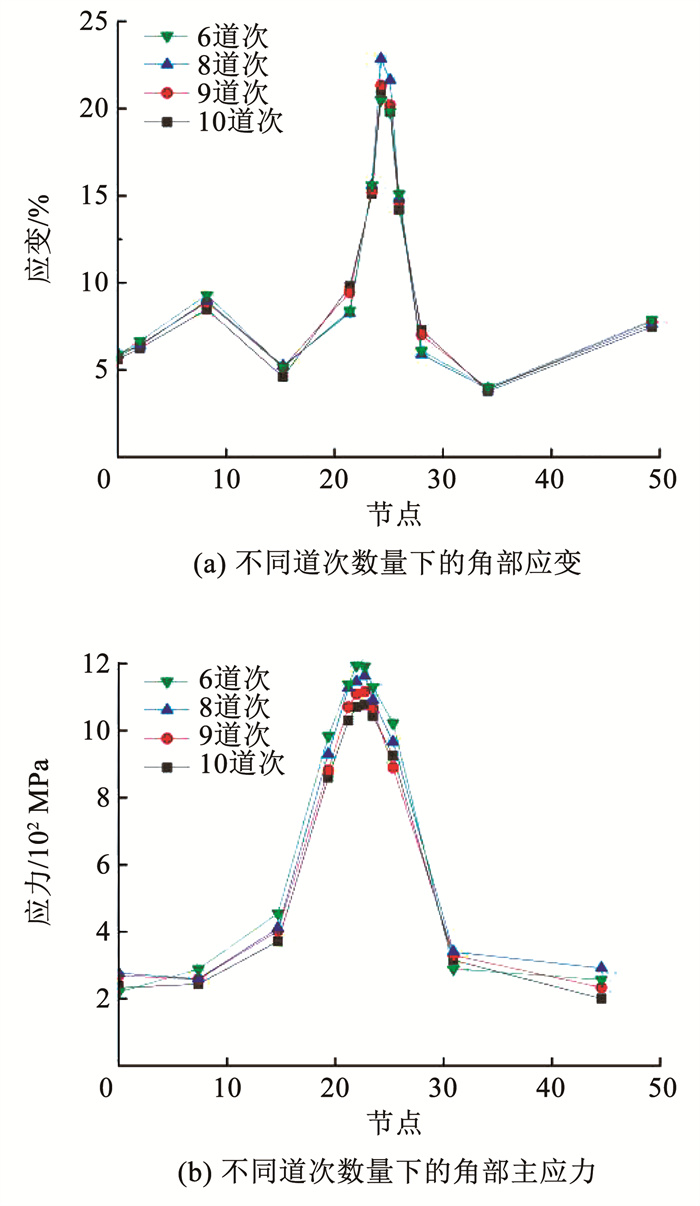图 13 道次数量对方矩管角部的影响 Fig. 13 Impact of pass number on square tube corners


4.2.2 角部成形半径对角部应力-应变的影响角部成形半径对于方矩形管辊弯成形中路径曲线应力-应变分布情况的影响如图 14所示。本次成形仿真方案通过改变方管辊弯成形半径，成形半径设置分别为3、4、5、6 mm。如图 14(a)所示，辊弯成形过程中，方矩形管角部应变随着成形半径的增大而减小。成形半径越大，越接近圆管直径时，方管角部的应变越小，因此方管成形时角部所需要的辊弯力矩越小，轧辊对材料所产生的应力也就越小，如图 14(b)所示。在满足产品质量要求的成形尺寸的基础上，成形半径越大出现开裂的风险越小，从而有效减少开裂件的出现。

Fig. 14
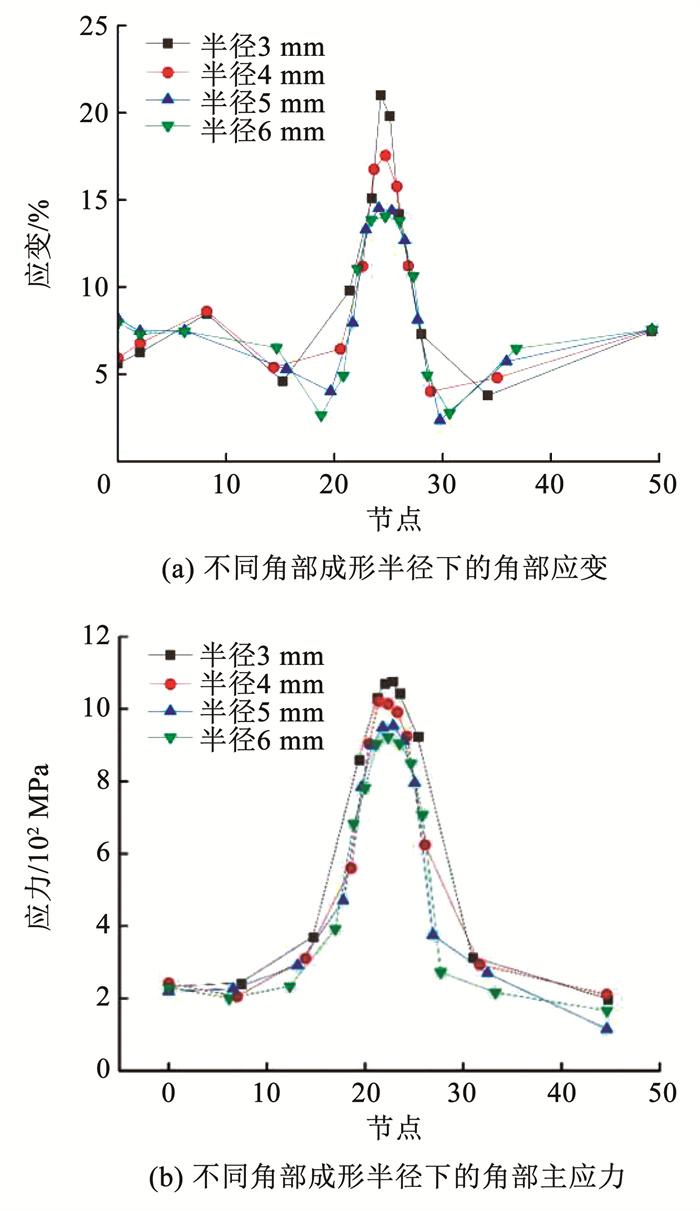图 14 成形半径对方矩管角部的影响 Fig. 14 Impact of forming radius on square tube corners


4.2.3 机架间距对角部应力-应变的影响机架间距大小对于方矩形管辊弯成形中路径曲线应力-应变分布情况的影响如图 15所示，本次成形仿真方案通过改变辊弯机架间距，机架间距设置分别为230、250、270、300、330 mm。方矩管在辊弯成形中设计的管型截面一致，最后成形角度以及方管形状趋于一致，因此不同机架间距下方矩管角部和直角边的应变规律基本一致，如图 15(a)所示。机架间距为230 mm时，该方案成形下的方矩管角部的各部分应力大于其他道次间距下的方矩管角部应力，如图 15(b)所示，即机架间距较小，导致方矩管在相邻道次之间的成形角度改变过快，轧辊对方矩管所产生的应力也就越大，更加容易出现开裂问题。因此在满足产品质量要求的机架间距的基础上，机架间距的增加减少了道次之间的成形角度变化幅度，从而有效减轻型材在辊弯成形中的角部应力。

Fig. 15
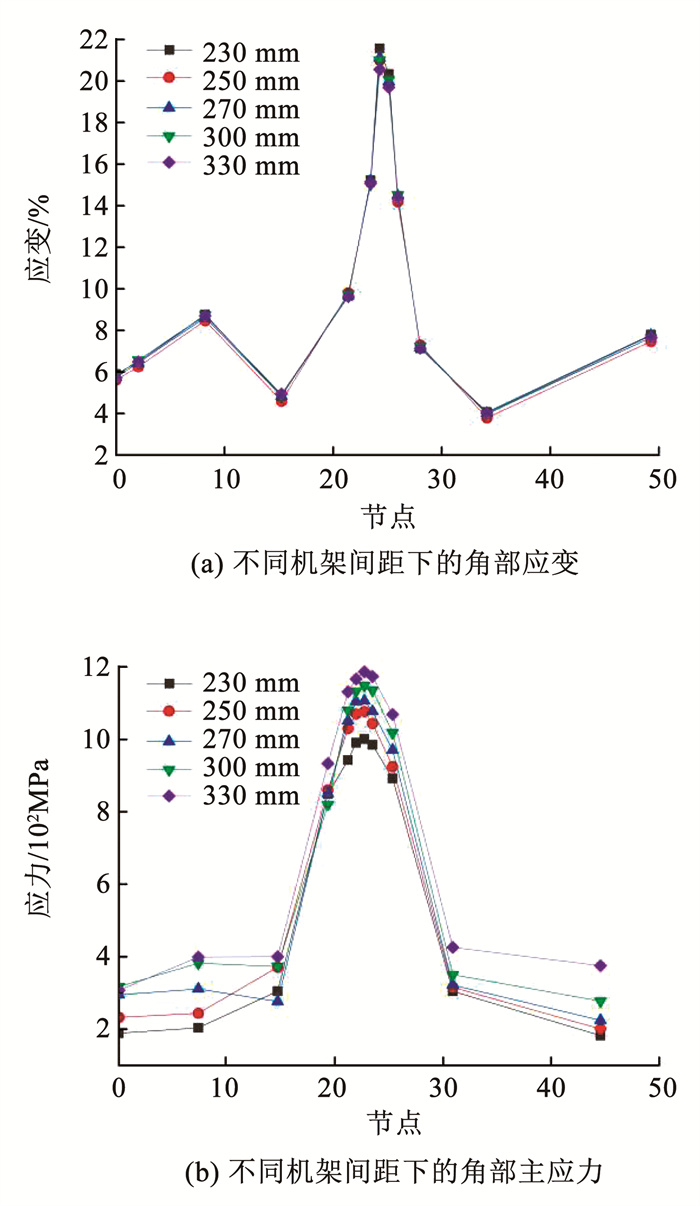图 15 机架间距对方矩管角部的影响 Fig. 15 Impact of frame spacing on square tube corners


5 结论1) MS1180方矩形管在辊弯成形过程中，角部出现开裂现象时，裂纹萌生于角部近外层，并向内层扩展，呈现穿晶开裂特征。角部裂纹断口呈现准解理开裂特征，致断原因是其角部近外层剪切面上所受的主应力超过材料抗拉极限继而发生开裂现象。

2) 3种成形参数对方矩管辊弯过程中角部的影响是不同的。成形道次的增加，减少了每道次的成形角度，并有效减轻圆管在辊弯成形中的应力积累，从而有效避免产生开裂问题。成形半径越大，辊弯过程中方矩管角部力矩越小，产生开裂的概率也就越小。机架间距越大时，型材每道次角度改变越慢，其改变应力越小，越不容易产生开裂。另外成形道次和机架间距对标准生产方矩管件应变影响不大，成形半径越大其方矩管辊弯过程中角部应变越小。

3) 在满足产品质量要求的轧机要求下，机架间距影响方矩管角部开裂效果最大，角部成形半径次之，成形道次数量影响效果最小。适当增加成形道次、角部成形半径和机架间距可减少方矩管角部应力，减少开裂件的产生，但成形道次不能无限增加的，还要考虑产品的经济效益，道次越多产品经济效益越低。


参考文献
[1] RIZZO L, TROIVE L, MELANDER A, et al. Improving and enlarging the application field of HSS and UHSS for automotive body components by the integration of innovative technologies based on roll forming and stretch-bending processes[M]. Luxembourg: Publications Office of the European Union, 2010.


[2] KIM J H, SUNG J H, PIAO Kun, et al. The shear fracture of dual-phase steel[J]. International Journal of Plasticity, 2011, 27(10): 1658. DOI:10.1016/j.ijplas.2011.02.009


[3] DANCETTE S, FABRèGUE D, MASSARDIER V, et al. Investigation of the tensile shear fracture of advanced high strength steel spot welds[J]. Engineering Failure Analysis, 2012, 25: 112. DOI:10.1016/j.engfailanal.2012.04.009


[4] LI H, FU M W, LU J, et al. Ductile fracture: Experiments and computations[J]. International Journal of Plasticity, 2011, 27(2): 147. DOI:10.1016/j.ijplas.2010.04.001


[5] MISHRA A, THUILLIER S. Investigation of the rupture in tension and bending of DP980 steel sheet[J]. International Journal of Mechanical Sciences, 2014, 84: 171. DOI:10.1016/j.ijmecsci.2014.04.023


[6] MENG B, FU M W, FU C M, et al. Ductile fracture and deformation behavior in progressive microforming[J]. Materials & Design, 2015, 83: 14. DOI:10.1016/j.matdes.2015.05.088


[7] XU Zhongwei, LIU An, WANG Xishu. Influence of macrozones on the fatigue cracking behavior and fracture mechanisms of rolled Ti-6Al-4V alloy[J]. Materials Science and Engineering: A, 2021, 824: 141824. DOI:10.1016/j.msea.2021.141824


[8] CHENG Jiaojiao, CAO Jianguo, WEI Zhidong, et al. The precise control of end flare with residual stresses of UHSS thin-walled component in roll forming process[J]. Ironmaking & Steelmaking: Processes, Products and Applications, 2023, 50(9): 1372. DOI:10.1080/03019233.2023.2212933


[9] 曹建国, 阮康, 王雪松, 等. 邻角精确控制的异型管辊弯成形过程数值模拟[J]. 哈尔滨工业大学学报, 2023, 55(1): 98.
CAO Jianguo, RUAN Kang, WANG Xuesong, et al. Numerical simulation of special-shaped tube roll forming process based on precise control of adjacent angles[J]. Journal of Harbin Institute of Technology, 2023, 55(1): 98. DOI:10.11918/202205069


[10] MEHARI Z A, HAN Jingtao. Numerical prediction of ductile fracture during the partial heating roll forming process of DP980[J]. International Journal of Fracture, 2022, 234(1): 97. DOI:10.1007/s10704-021-00572-5


[11] 王健, 孙力, 熊自柳, 等. DP980钢板辊弯成形矩形管过程中的开裂行为[J]. 机械工程材料, 2019, 43(11): 5.
WANG Jian, SUN Li, XIONG Ziliu, et al. Cracking behavior during DP980 steel plate roll-bending to rectangular tubing[J]. Materials for Mechanical Engineering, 2019, 43(11): 5. DOI:10.11973/jxgccl201911002


[12] 贾方辉. 先进高强度钢辊弯成形断裂机理研究及缺陷预测[D]. 北京: 北方工业大学, 2015
JIA Fanghui. Fracture mechanism and prediction for advanced high strength steel in roll forming process[D]. Beijing: North China University of Technology, 2015


[13] 杨帆. 异型管连续辊弯成型过程仿真及其角部开裂的研究[D]. 秦皇岛: 燕山大学, 2014
YANG Fan. Shape tube continuous roll forming process simulation and the research of corner cracking[D]. Qinhuangdao: Yanshan University, 2014


[14] HANCOCK J W, MACKENZIE A C. On the mechanisms of ductile failure in high-strength steels subjected to multi-axial stress-states[J]. Journal of the Mechanics and Physics of Solids, 1976, 24(2/3): 147. DOI:10.1016/0022-5096(76)90024-7


[15] LIAN Junhe, YANG Hanqi, VAJRAGUPTA N, et al. A method to quantitatively upscale the damage initiation of dual-phase steels under various stress states from microscale to macroscale[J]. Computational Materials Science, 2014, 94: 245. DOI:10.1016/j.commatsci.2014.05.051


[16] YAN Yu, WANG Haibo, WAN Min. Prediction of fracture in press bend forming of aluminum alloy high-stiffener integral panels[J]. Computational Materials Science, 2011, 50(7): 2232. DOI:10.1016/j.commatsci.2011.02.034


[17] LOU Yanshan, HUH H. Prediction of ductile fracture for advanced high strength steel with a new criterion: Experiments and simulation[J]. Journal of Materials Processing Technology, 2013, 213(8): 1284. DOI:10.1016/j.jmatprotec.2013.03.001


[18] ZEINALI M S, NAEINI H M, TALEBI-GHADIKOLAEE H, et al. Numerical and experimental investigation of fracture in roll forming process using Lou-huh fracture criterion[J]. Arabian Journal for Science and Engineering, 2022, 47(12): 15591. DOI:10.1007/s13369-022-06662-3


[19] BAI Yuanli, WIERZBICKI T. A new model of metal plasticity and fracture with pressure and lode dependence[J]. International Journal of Plasticity, 2008, 24(6): 1071. DOI:10.1016/j.ijplas.2007.09.004


[20] BAI Yuanli, WIERZBICKI T. Application of extended Mohr-Coulomb criterion to ductile fracture[J]. International Journal of Fracture, 2010, 161(1): 1. DOI:10.1007/s10704-009-9422-8


[21] LIU Yan, KANG Lan, GE Hanbin. Experimental and numerical study on ductile fracture of structural steels under different stress states[J]. Journal of Constructional Steel Research, 2019, 158: 381. DOI:10.1016/j.jcsr.2019.04.001


[22] 穆磊. 面向先进高强钢的韧性断裂预测模型研究与应用[D]. 北京: 北京科技大学, 2018.
MU Lei. Study on a ductile fracture prediction model for advanced high strength steel and its application[D]. Beijing: University of Science and Technology Beijing, 2018


[23] 桂良进, 高付海, 范子杰. 先进高强度钢的断裂失效准则研究[J]. 固体力学学报, 2012, 33(4): 395.
GUI Liangjin, GAO Fuhai, FAN Zijie. Study of failure criterion of advanced high strength steel[J]. Chinese Journal of Solid Mechanics, 2012, 33(4): 395. DOI:10.19636/j.cnki.cjsm42-1250/o3.2012.04.007


[24] WANG Haibo, YAN Yu, JIA Fanghui, et al. Investigations of fracture on DP980 steel sheet in roll forming process[J]. Journal of Manufacturing Processes, 2016, 22: 177. DOI:10.1016/j.jmapro.2016.03.008


[25] YAMANE K, SHIMODA K, KURODA K, et al. A new ductile fracture criterion for skew rolling and its application to evaluate the effect of number of rolls[J]. Journal of Materials Processing Technology, 2021, 291: 116989. DOI:10.1016/j.jmatprotec.2020.116989


[26] STOUGHTON T B, YOON J W. A new approach for failure criterion for sheet metals[J]. International Journal of Plasticity, 2011, 27(3): 440. DOI:10.1016/j.ijplas.2010.07.004


[27] TALEBI-GHADIKOLAEE H, NAEINI H M, MIRNIA M J, et al. Ductile fracture prediction of AA6061-T6 in roll forming process[J]. Mechanics of Materials, 2020, 148: 103498. DOI:10.1016/j.mechmat.2020.103498


[28] 韩飞, 朱德鹏. 辊弯成形中成形力的理论分析和有限元仿真[J]. 锻压技术, 2016, 41(12): 150.
HAN Fei, ZHU Depeng. Theoretical analysis and numerical simulation on forming force in rolling[J]. Forging & Stamping Technology, 2016, 41(12): 150. DOI:10.13330/j.issn.1000-3940.2016.12.026


[29] BUI Q V, PONTHOT J P. Numerical simulation of cold roll-forming processes[J]. Journal of Materials Processing Technology, 2008, 202(1/2/3): 275. DOI:10.1016/j.jmatprotec.2007.08.073


[30] ABEYRATHNA B, ROLFE B, HODGSON P, et al. A first step towards a simple in-line shape compensation routine for the roll forming of high strength steel[J]. International Journal of Material Forming, 2016, 9(3): 423. DOI:10.1007/s12289-015-1238-7


[31] 刘晓立, 曹建国, 柴雪婷, 等. 变弹性模量对高强钢辊弯成型回弹预测的影响[J]. 哈尔滨工业大学学报, 2018, 50(7): 137.
LIU Xiaoli, CAO Jianguo, CHAI Xueting, et al. Springback prediction of DP980 steel considering nonlinear elastic modulus in cold roll forming[J]. Journal of Harbin Institute of Technology, 2018, 50(7): 137. DOI:10.11918/j.issn.0367-6234.201707163


[32] 刘瑞堂, 刘锦云. 金属材料力学性能[M]. 哈尔滨: 哈尔滨工业大学出版社, 2015.
LIU Ruitang, LIU Jinyun. Metal material mechanics performance[M]. Harbin: Harbin Institute of Technology Press, 2015.


[33] 孙智, 任耀剑, 隋艳伟. 失效分析—基础与应用[M]. 2版. 北京: 机械工业出版社, 2017.
SUN Zhi, REN Yaojian, SUI Yanwei. Failure analysis: Basises and applications[M]. 2nd ed.. Beijing: China Machine Press, 2017.