房超,王小鹏,李宝民,樊炜玮
(兰州交通大学 电子与信息工程学院,兰州 730070)
摘要:
图像分割是按照一定的规则,将图像中具有特殊意义的区域划分为若干个互不相交的子区域,是从图像处理到图像分析的关键环节,传统分水岭图像分割方法是一种应用较为广泛的技术,具有快速、简单的优点,但该方法易受噪声干扰,分割结果易丢失边缘重要信息,出现过分割现象。为改善传统分水岭图像分割方法存在的过分割问题,提出了一种基于自适应结构元素的改进分水岭图像分割方法。首先,利用图像像素点邻域的局部密度、对称度及边缘特征构造形状可变的自适应结构元素,确保其与图像目标几何结构具有较强的一致性；其次,利用该结构元素获取图像形态学梯度,提高目标边缘的定位精度；将L0范数梯度最小化和形态学开闭混合重建相结合修正梯度图像,减少梯度图像中的局部无效最小值点,抑制过分割现象的产生；最后对修正后的梯度图像进行分水岭分割,实现图像目标区域的精确分割。实验结果表明,该方法能够有效抑制过分割现象,提高目标边缘定位的准确性,具有较高的分割精度。
关键词: 结构元素 形态学 分水岭 图像分割
DOI：10.11918/202204057
分类号:TN911.73
文献标识码:A
基金项目:国家自然科学基金(61761027)；甘肃省科技计划资助(20YF8GA036)
Improved watershed image segmentation method based on adaptive structural elements
FANG Chao,WANG Xiaopeng,LI Baomin,FAN Weiwei
(School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)
Abstract:
Image segmentation is to divide the region with special meanings into several disjoint sub-regions according to certain rules, which is the key link between image processing and image analysis. The traditional watershed image segmentation method is widely used, which has the advantages of fast and simple. However, it is easily interfered by noise, and the segmentation results are prone to lose important edge information, resulting in over-segmentation. In view of the problem of the traditional watershed image segmentation method, an improved watershed image segmentation method based on adaptive structural elements was proposed. First, the adaptive structural elements with variable shapes were constructed by using local density, symmetry, and boundary features of adjacent pixels of image targets, so as to ensure a good consistency between the proposed structural elements and the shape of image targets. Then, the adaptive structural elements were used to obtain the morphological gradient of the image, which could improve the positioning accuracy of the target edge. The L0 norm gradient minimization and morphological open-close hybrid reconstruction were used to modify the gradient image, so as to reduce the local invalid minimum points in the gradient image and suppress the occurrence of over-segmentation. Finally, watershed segmentation was performed on the modified gradient image to realize accurate segmentation of the target region of the image. Experimental results show that the method could effectively restrain over-segmentation of traditional watershed algorithm and improve the accuracy of the target edge positioning, with high precision of image segmentation.
Key words: structural elements morphology watershed image segmentation
房超, 王小鹏, 李宝民, 樊炜玮. 基于自适应结构元素的改进分水岭图像分割方法[J]. 哈尔滨工业大学学报, 2023, 55(5): 59-70. DOI: 10.11918/202204057.
FANG Chao, WANG Xiaopeng, LI Baomin, FAN Weiwei. Improved watershed image segmentation method based on adaptive structural elements[J]. Journal of Harbin Institute of Technology, 2023, 55(5): 59-70. DOI: 10.11918/202204057.
基金项目 国家自然科学基金(61761027)；甘肃省科技计划资助(20YF8GA036) 作者简介 房超(1987—)，男，讲师，博士研究生;
王小鹏(1969—)，男，教授，博士生导师 通信作者 王小鹏，wangxiaopeng@mail.lzjtu.cn 文章历史 收稿日期: 2022-04-15
Abstract Full text Figures/Tables PDF
基于自适应结构元素的改进分水岭图像分割方法
房超, 王小鹏
, 李宝民, 樊炜玮 兰州交通大学 电子与信息工程学院, 兰州 730070
收稿日期: 2022-04-15; 接受日期: 2022-05-28; 网络出版日期: 2022-08-31
基金项目: 国家自然科学基金(61761027)；甘肃省科技计划资助(20YF8GA036)
作者简介: 房超(1987—)，男，讲师，博士研究生; 王小鹏(1969—)，男，教授，博士生导师
通信作者: 王小鹏，wangxiaopeng@mail.lzjtu.cn
摘要: 图像分割是按照一定的规则，将图像中具有特殊意义的区域划分为若干个互不相交的子区域，是从图像处理到图像分析的关键环节，传统分水岭图像分割方法是一种应用较为广泛的技术，具有快速、简单的优点，但该方法易受噪声干扰，分割结果易丢失边缘重要信息，出现过分割现象。为改善传统分水岭图像分割方法存在的过分割问题，提出了一种基于自适应结构元素的改进分水岭图像分割方法。首先，利用图像像素点邻域的局部密度、对称度及边缘特征构造形状可变的自适应结构元素，确保其与图像目标几何结构具有较强的一致性；其次，利用该结构元素获取图像形态学梯度，提高目标边缘的定位精度；将L0范数梯度最小化和形态学开闭混合重建相结合修正梯度图像，减少梯度图像中的局部无效最小值点，抑制过分割现象的产生；最后对修正后的梯度图像进行分水岭分割，实现图像目标区域的精确分割。实验结果表明，该方法能够有效抑制过分割现象，提高目标边缘定位的准确性，具有较高的分割精度。
关键词: 结构元素 形态学 分水岭 图像分割
Improved watershed image segmentation method based on adaptive structural elements
FANG Chao, WANG Xiaopeng
, LI Baomin, FAN Weiwei School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China
Abstract: Image segmentation is to divide the region with special meanings into several disjoint sub-regions according to certain rules, which is the key link between image processing and image analysis. The traditional watershed image segmentation method is widely used, which has the advantages of fast and simple. However, it is easily interfered by noise, and the segmentation results are prone to lose important edge information, resulting in over-segmentation. In view of the problem of the traditional watershed image segmentation method, an improved watershed image segmentation method based on adaptive structural elements was proposed. First, the adaptive structural elements with variable shapes were constructed by using local density, symmetry, and boundary features of adjacent pixels of image targets, so as to ensure a good consistency between the proposed structural elements and the shape of image targets. Then, the adaptive structural elements were used to obtain the morphological gradient of the image, which could improve the positioning accuracy of the target edge. The L0 norm gradient minimization and morphological open-close hybrid reconstruction were used to modify the gradient image, so as to reduce the local invalid minimum points in the gradient image and suppress the occurrence of over-segmentation. Finally, watershed segmentation was performed on the modified gradient image to realize accurate segmentation of the target region of the image. Experimental results show that the method could effectively restrain over-segmentation of traditional watershed algorithm and improve the accuracy of the target edge positioning, with high precision of image segmentation.
Keywords: structural elements morphology watershed image segmentation
图像分割是一种将图像划分为若干具有相似特征(如灰度、梯度、对比度、纹理等)的有意义区域并提取感兴趣目标的方法，常用的图像分割方法主要分为以下三类：基于阈值的方法、基于边缘的方法和基于区域的方法。基于阈值的方法主要考虑图像像素的灰度特性忽略了其空间特性，确定最佳分割阈值的难度相对较大；基于边缘的方法[1]主要适用于目标边界清晰且无噪声干扰的图像，对于目标边界模糊或受噪声干扰的图像难以实现有效分割；基于区域的方法主要利用区域的相似性准则为分割依据，对于连通目标具有较好的分割效果，其中，基于形态学的分水岭图像分割方法[2]是一种应用较为广泛的技术，但在实际应用过程中，其主要对图像的梯度图像进行分割实现目标提取，若直接对梯度图像进行分水岭分割，会出现目标边界偏移、目标过渡区边界破坏等过分割现象，其原因为：一方面，获取的梯度图像中存在较多的局部最小值，增加了无效分割区域的数量；另一方面，利用形状单一且大小固定的结构元素图像进行形态学运算，导致图像目标特征信息发生改变，如目标边界轮廓偏移、出现新的人为目标或目标细节丢失等。为此，如何抑制过分割现象从而实现有效分割是分水岭图像分割方法研究的热点。
近年来，针对原因一，学者们提出了基于最小二乘圆法误差理论[3]、饱和度与亮度信息[4]、光谱强度与纹理信息[5]、局部自适应阈值[6]、自适应标记与区域间近邻传播聚类[7]、全局和局部边界超像素[8]、梯度图像边缘、同一区域目标及孤立与重叠目标[9]、无量纲参数[10]、无监督分类[11]、粒子群和区域生长[12]的多种改进型分水岭分割算法，上述方法，有效抑制了无效局部最小值的出现，能够有效地解决过分割问题，但仍存在局部过分割或重要边界丢失的现象，或者算法复杂度较高。针对原因二，学者们提出了基于图像的灰度特征[13]、可变权值[14]、图像亮度、对比度、曲率等特征函数[15]、最小生成树[16]、局部结构张量[17]、图像局部特征多方向矢量场[18]的多种形态学自适应结构元素构造方法，上述方法主要依据图像相邻像素局部相似特性或图像边缘特性，其中，基于相似特性构造的结构元素具有较好的区域适应性及较强的噪声抑制能力，而基于边缘特性构造的结构元素能够最大限度保持图像目标的几何结构特性，降低图像目标结构细节失真。
本文提出一种基于自适应结构元素的改进分水岭图像分割方法。首先，构造基于图像像素点邻域的局部密度、对称度及边缘特征的自适应结构元素，最大限度保持其与图像目标形状特征的一致性；其次，利用该自适应结构元素获取图像形态学梯度，避免目标边缘轮廓发生偏移；再次，采用L0范数梯度最小化方法与形态学混合开闭重建运算修正梯度图像，在保持梯度图像目标显著边缘的同时消除由于灰度非规则扰动和噪声引起的局部最小值；最后，利用分水岭分割方法对修正后的梯度图像进行处理，最终实现抑制过分割，有效提取图像目标区域的目的。
1 改进分水岭图像分割方法经典分水岭图像分割方法是一种基于数学形态学实现目标提取的技术，其基本思想是把图像视为测地学的拓扑地形图，图像每个像素的灰度值表示该点的海拔高度，高灰度值区域对应“山峰”，低灰度值区域对应“谷底”，每个局部最小值及其影响区域为集水盆，集水盆的边界为图像边缘对应于分水岭。
针对经典分水岭图像分割方法中的过分割问题，提出一种基于自适应结构元素的改进分水岭图像分割方法，包括4个主要环节：1)构造自适应结构元素, 将图像像素点邻域的局部密度、对称度及边缘特征应用于自适应结构元素构造过程中；2)计算形态学梯度, 原始图像与自适应结构元素腐蚀图像的差值为形态学梯度；3)修正梯度图像, 将L0范数梯度最小化方法与形态学开闭混合重建相结合，减少梯度图像中无效局部最小值的个数；4)分水岭分割, 对修正后的梯度图像进行分水岭分割，最终实现目标提取。该方法流程图见图 1。
Fig. 1
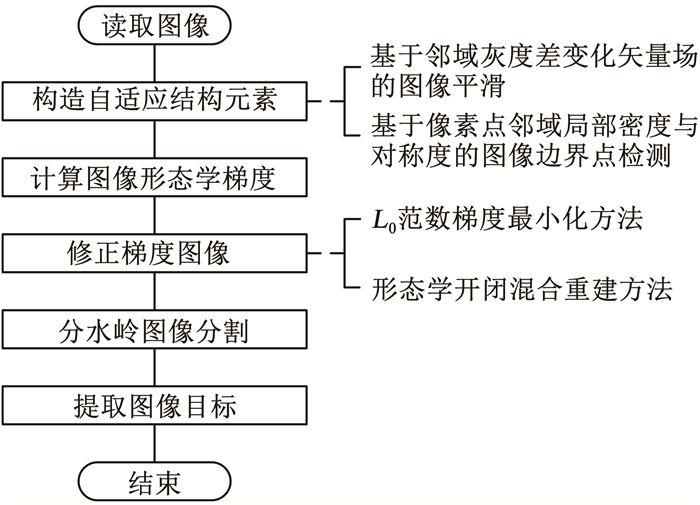图 1 改进分水岭图像分割方法流程图 Fig. 1 Flow chart of improved watershed image segmentation method 1.1 构造自适应结构元素本文提出一种基于像素点邻域局部密度与对称度的形态学自适应结构元素构造方法，该方法利用图像像素点邻域的局部密度、对称度及边缘特征构造形状可变的自适应结构元素，在进行形态学运算时，能够最大限度地保持自适应结构元素与图像目标形状的一致性，减少目标必要信息的丢失，提高目标边界轮廓定位的精度，降低目标结构细节的失真程度。该方法在利用邻域灰度差变化矢量场对图像子区域进行平滑处理的基础上，通过定义基于像素点邻域局部密度与对称度的变异系数来判定图像子区域的中心像素点是否为边界点，自适应结构元素由判定出的边界点构成。
1.1.1 自适应结构元素构造核心思想构造自适应结构元素核心思想是依据图像中的像素点邻域的局部密度、对称性及边缘特征构造形状可变的自适应结构元素。为此，首先设计两个掩膜SE与M，其中，SE大小为3×3，M大小为5×5。如图 2所示，以图像f(4, 4)像素点为中心点PSE选取SE掩膜覆盖的子区域QSE，并将该区域中的所有像素点视为构建自适应结构元素的基础要素; 然后，逐次以QSE中的每个像素点作为M的中心点PM在图像选取子区域QM，利用灰度邻域差变化矢量场获取的自适应阈值对QM子区域进行平滑处理，保证同一目标区域中的灰度基本一致; 在此基础上通过定义基于像素点欧氏距离的局部密度函数、基于像素点相对密度的对称度函数和基于局部密度与对称度的变异系数判定QM子区域的中心像素点PM是否为边界点，QSE子区域中判定出的所有边界点构成了结构元素。将SE掩膜进行距离为单位像素的平移，获取新的子区域及由该区域全部边界点构成的结构元素，整幅图像遍历完成后得到的所有结构元素的集合即为构造的自适应结构元素。
Fig. 2
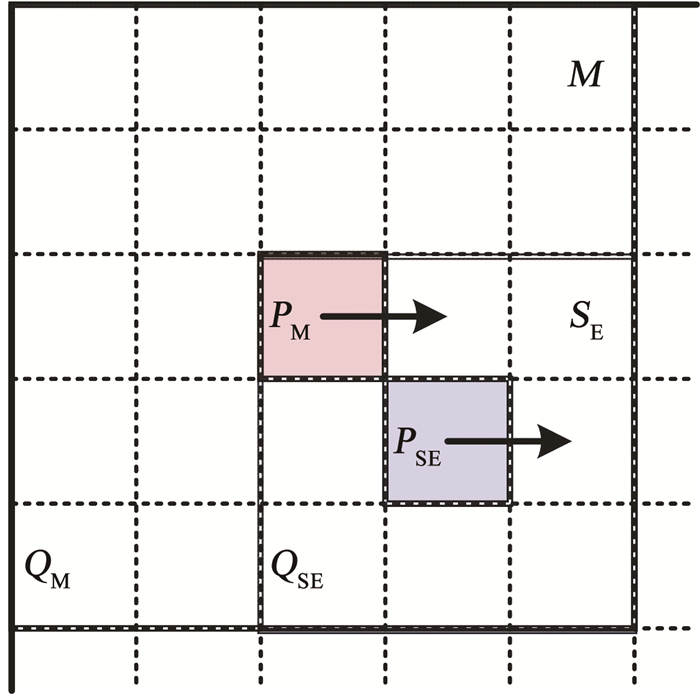图 2 自适应结构元素构造原理示意 Fig. 2 Construction of adaptive structural elements 自适应结构元素构造主要包括两个重要环节：第一，利用邻域灰度差变化矢量场对M掩膜覆盖的图像子区域进行平滑处理；第二，定义基于像素点邻域局部密度与对称度的变异系数检测SE掩膜覆盖的图像子区域中的边界点。
1.1.2 基于邻域灰度差变化矢量场的图像平滑理论上，同一目标区域应具有相似或相同的灰度、对比度、纹理和梯度等特征，但在实际应用过程中，由于受光照环境和采集设备器件噪声等因素影响，获取图像目标内部像素特征不具有同一性，若直接对该图像进行像素点邻域局部密度与对称度的边界点检测，会影响边界点判定的精度。因此，需要对图像进行平滑处理，使目标区域的灰度趋于一致，提高边界点判定的准确性，正确找到边界点的实际位置。为此，提出一种基于邻域灰度差变化矢量场的图像平滑处理方法，由于目标内部点的灰度应具有一定的相同性或相似性，其邻域各方向灰度的变化很小，其正交邻域灰度差的变化矢量也很小，因此，可选择正交邻域灰度差变化矢量较小的灰度差的均值作为阈值，对图像进行平滑处理。具体实现过程如下：
步骤1??在选取的5×5大小的子区域QM中，以中心像素点为基准，依次计算其邻域每个像素点与中心像素点的灰度差(取绝对值)，记为g(x±k, y±k) (k=0, 1, 2)，构成5×5大小邻域灰度差矩阵。
步骤2??对获取的邻域灰度差序列进行4个方向上的灰度采样，如图 3所示，获取邻域灰度差变化矢量，其中该矢量用ai(i=0, 1, 2, 3)表示，计算如下：
$\left\{\begin{aligned}\boldsymbol{a}_0= & g(x, y-2)+g(x, y-1)+g(x, y)+ \\& g(x, y+1)+g(x, y+2) \\\boldsymbol{a}_1= & g(x-2, y+2)+g(x-1, y+1)+g(x, y)+ \\& g(x+1, y-1)+g(x+2, y-2) \\\boldsymbol{a}_2= & g(x-2, y)+g(x-1, y)+g(x, y)+ \\& g(x+1, y)+g(x+2, y) \\\boldsymbol{a}_3= & g(x-2, y-2)+g(x-1, y-1)+g(x, y)+ \\& g(x+1, y+1)+g(x+2, y+2)\end{aligned}\right.$ (1)
Fig. 3
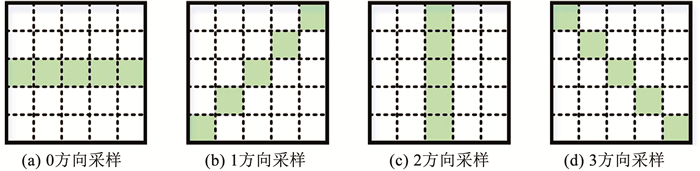图 3 邻域灰度差变化矢量采样示意 Fig. 3 Gray sampling for neighborhood gray difference changing vector 步骤3??相互正交邻域灰度差变化矢量可以作为区分目标边缘与目标内部的重要依据，在目标内部，其邻域灰度各向变化都很小，其正交邻域灰度差变化矢量也很小。计算出邻域灰度差变化矢量后，其正交差异对和最小正交差异对定义如下：
$\left\{\begin{array}{l}\boldsymbol{d}_0=\boldsymbol{a}_0-\boldsymbol{a}_2 \\\boldsymbol{d}_1=\boldsymbol{a}_1-\boldsymbol{a}_3\end{array}\right.$ (2)
$v=\min \left|\boldsymbol{d}_0, \boldsymbol{d}_1\right|$ (3)
式中：d0为0与2方向的正交差，d1为1与3方向的正交差，v为最小正交差。
步骤4??依据最小正交差异对，获取图像平滑处理所需阈值，该阈值根据各个子区域QM的最小正交差异对的不同自适应变化。若最小正交差异对值为d0，则阈值τ为0方向与2方向所有邻域灰度差值之和与0方向与2方向邻域灰度差值不为零的元素的个数总和的商；若最小正交差异对的值为d1，则阈值τ为1方向与3方向所有邻域灰度差值之和与1方向与3方向邻域灰度差值不为零的元素的个数总和的商；若最小正交差异对的值为d0=d1，则阈值τ为4个方向所有邻域灰度差值之和与4个方向邻域灰度差值不为零的元素的个数总和的商。
步骤5??利用获取的自适应阈值，对子区域进行平滑处理。由于自适应阈值的获取主要依据图像中4个采样方向的像素的灰度值，在图像的目标边缘处未被采样的像素点也会有较大的灰度差异，因此，为了考虑该类像素对自适应阈值精确度的影响，需要对获取的自适应阈值增加加权系数τ′，加权系数不宜过大，取值过大会将中心像素点及与其有较大灰度差异的像素点判定为相似(τ′的取值范围为1~5)，从而确保图像目标边缘的有效平滑。计算该子区域QM每个像素点与中心像素点的灰度差值并与阈值τ+τ′进行比较，若差值小于或等于阈值τ+τ′，则判定该像素点与中心像素点相似，该像素点的灰度值由中心像素点的灰度值代替，否则其灰度值保持不变。
利用基于邻域灰度差变化矢量场方法对局部图像进行平滑处理的计算过程如图 4所示。图 4(a)为原始图像；图 4(b)为原始图像中框选取局部图像Is的灰度值，并以Is(5, 5)为中心构建QSE区域，Is(4, 4)为中心构建QM区域；图 4(c)为QM区域的灰度差矢量场；图 4(d)为QM区域4个方向的灰度差矢量值与正交差值；图 4(e)为QM区域自适应阈值及相关指标计算；图 4(f)为QM区域平滑处理结果。
Fig. 4
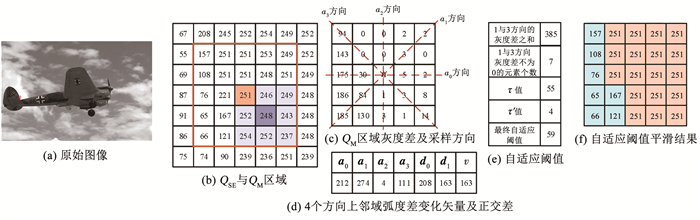图 4 基于邻域灰度差变化矢量场平滑处理计算过程(局部图像) Fig. 4 Calculation process of smoothing based on vector field of neighborhood gray difference variation (partial image) 由图 4可知，1与3方向的矢量正交差值小于0与2方向的矢量正交差值，表明Is(4, 4)像素点在1与3方向为目标内部点的可能性越大，因此，利用1与3方向灰度差值之和与像素个数进行商运算获取自适应阈值，平滑结果表明，该自适应阈值能有效区分目标内部点与边界点。
1.1.3 基于像素点邻域局部密度与对称度的图像边界点检测通过平滑处理后，可以使图像中同一目标区域像素灰度值趋于一致，提高目标物边界点与内部点可分性。根据像素灰度值不同可将图像划分为不同的区域，且每一像素点在不同区域具有不同的密度，边界点指位于不同密度区域边缘的像素点，其反映了像素灰度值分布的结构信息和属性差异特性。边界点在其附近邻域存在多个密度相差较大的区域，既存在高密度区域也存在低密度区域，其局部密度具有较大的波动，即局部密度具有较大的方差。此外，内部点附近邻域与其灰度值相同的像素点均匀地分布在其周围，即其邻域像素点关于该内部点具有较强的对称性，边界点附近邻域与其灰度值相同的像素点非均匀地分布在其周围，即其邻域像素点关于该边界点具有较弱的对称性。依据上述原理，通过定义基于像素点欧氏距离的局部密度函数、基于像素点相对密度的对称度函数和基于局部密度与对称度的变异系数判定子区域中心像素点是否为边界点。
定义1??某目标像素点邻域局部密度ρ(n)定义为：在其邻域范围内，该目标像素点f(x, y)到所有与其灰度值相同像素点f(i, j)欧氏距离的平均值和与目标像素点灰度值相同的所有像素点在该邻域中占比的乘积，即：
$\rho(n)=\frac{\sum\limits_{k \in N_{\mathrm{NE}}[f(x, y)]} d_k}{N^*-1} \cdot P$ (4)
$d_k=\sqrt{(x-i)^2+(y-j)^2}$ (5)
$\overline{d_k}=\frac{\sum\limits_{k \in N_{\mathrm{NE}}(n)} d_k}{N^*-1}$ (6)
$P=\frac{N^*}{9}$ (7)
式中:
定义2??某目标像素点邻域对称度SY定义为其邻域每个方向与目标像素点灰度值相同的像素个数和与目标像素点灰度值不相同的像素个数差值绝对值的和与各方向像素个数(除目标像素点)总和的比值，即：
$S_{\mathrm{Y}}=\frac{\sum\limits_{k=0}^4 \alpha\left|\operatorname{eq}\left[f_k(i, j)\right]-\operatorname{ueq}\left[f_k(i, j)\right]\right|+\beta}{2 n}$ (8)
式中:
1) 当ueq[fk(i, j)]=0，1时，α=1；当ueq[fk(i, j)]=2时，α=0。
2) 当eq[fk(i, j)]=ueq[fk(i, j)]时，β=1;否则β=0。
目标像素点的对称度SY值越大，则说明该像素点与其灰度值相同的像素点空间分布较为均匀，对称性较强，其为内部点的可能性就越大。
定义3??某目标像素点的变异系数MF定义为：目标像素点邻域局部密度的方差与目标像素点邻域对称度的比值，为了提高变异数的差异性，表达式的分母需要加1：
$M_{\mathrm{F}}=\frac{S_{\mathrm{D}}}{S_{\mathrm{Y}}+1}$ (9)
$S_{\mathrm{D}}=\frac{\sum\limits_{n \in C}[\rho(n)-\overline{\rho(n)}]^2}{N}, C=\{1, 2, 3, 4, \cdots, N\}$ (10)
$\overline{\rho(n)}=\frac{\sum\limits_{n \in C} \rho(n)}{N}, C=\{1, 2, 3, 4, \cdots, N\}$ (11)
式中：SD为目标像素点邻域局部密度的方差;
变异系数既考虑到目标像素点邻域的局部密度，又考虑到其对称度，这样可以更好描述目标像素点及其周围与目标像素点灰度值相同像素点的分布特性。目标像素点的变异系数越大，则说明该像素点与其灰度值相同的像素点空间分布相对离散且不均匀，局部密度变化较大，对称性较弱，即该目标像素点附近既存在高密度的区域也存在低密度的区域，该像素点为边界点的可能性越大。
边界点具体判定过程如下：
步骤1??以QSE区域的第一个像素为中心，构建大小为5×5的邻域QM，然后以该中心像素点为目标像素点按照方向的不同，由左上、右上、右下、左下及中间像素构成的大小为3×3的子区域，如图 5所示，记为Si(i=1, 2, 3, 4, 5)。
Fig. 5
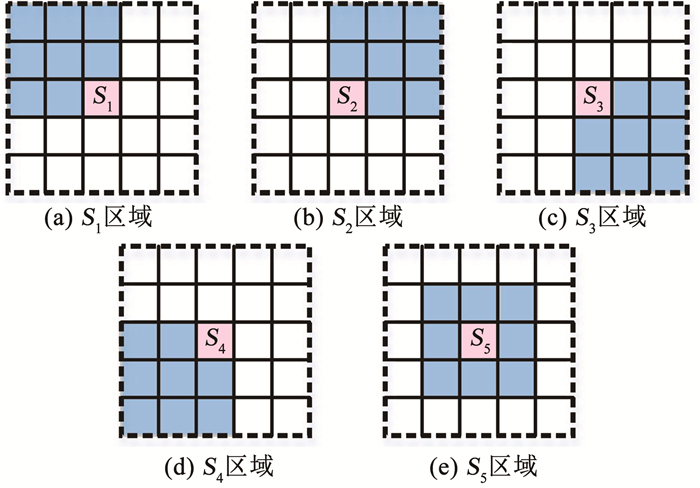图 5 子区域划分示意 Fig. 5 Division of sub-regions 步骤2??将平滑处理后子区域QM中的所有像素点的灰度值重新赋值，即灰度值等于中心像素点灰度值的像素点赋值为1，其余像素点赋值为0。
步骤3??分别计算该目标像素点邻域S1、S2、S3、S4的局部密度ρ(n)及其局部密度的方差SD，判定该目标像素点周围的S1、S2、S3、S4区域的局部密度是否存在较大差异；然后计算目标像素点邻域S5的对称度SY，判定S5区域中该目标像素点与其灰度值相同像素点的分布是否均匀对称；最后获取该目标像素点的变异系数MF，MF的值越大，该目标像素点为边界点的可能性就越大。目标像素的对称度大于等于7/8时，可以直接将其判定为内部点，通过逐点计算图像局部区域的MF值，选取最大的MF值作为判定阈值。
步骤4??以单位像素距离平移M获取新的子区域QM，继续利用上述过程判定QM的中心像素点是否为边界点，直到3×3子区域QSE内的全部像素点判定完成为止，并将判定出3×3子区域QSE内的边界点作为构成自适应结构元素的要素。
利用基于像素点邻域局部密度与对称度的图像边界点检测构造自适应结构元素计算过程如图 6所示。其中，图 6(a)为原始图像；图 6(b)为用原始图像中框选取局部图像Is的灰度值，并以Is(5, 5)为中心构建QSE区域，Is(4, 4)为中心构建QM区域；图 6(c)为依次以QSE区域的每个像素为中心构建QM区域的局部密度、对称度、变异系数和像素点性质判定指标计算结果；图 6(d)为以Is(5, 5)为中心构建的自适应结构元素。
Fig. 6
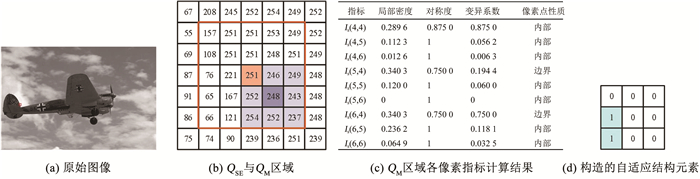图 6 自适应结构元素构造相关指标计算过程 Fig. 6 Indexes calculation for adaptive structural elements construction 由图 6可知，以Is(5, 4)和Is(6, 4)为中心构造QM区域的局部密度与变异系数相对较大且对称度相对较小，其相关指标符合边界点的判定要求；QSE区域中其他像素点的对称度相对较高，可将其判定为内部点。因此，利用局部密度、对称度和变异系数相结合的方式能够有效判定局部区域的目标内部点与边界点。
1.1.4 自适应结构元素构造步骤在利用邻域灰度差变化矢量对图像进行平滑处理以及利用基于像素点邻域局部密度与对称度完成图像边界点检测基础上，可进行自适应结构元素的构造。自适应结构元素构造主要依据图像目标局部灰度、局部密度、对称度及边缘特征的变化。具体实现步骤如下：
步骤1??设计两个大小分别为3×3、5×5的掩膜SE与M。
步骤2??以原始图像f(4, 4)作为SE的中心像素点在原始图像中选取的3×3子区域记为QSE，SE用于构造自适应结构元素。
步骤3??以QSE中的第一个像素点作为M的中心像素点在原始图像中选取5×5子区域记为QM，M用于检测QSE中的所有像素点是否为边界点。
步骤4??利用基于邻域灰度差变化矢量场方法对QM进行平滑处理。
步骤5??利用基于像素点邻域局部密度与对称度定义的变异系数判定QM的中心像素点是否为边界点。
步骤6??将M进行距离为单位像素的平移，获取新的5×5子区域QM，并进行步骤4与步骤5的运算，直到QSE中的所有像素点完成边界点判定为止，QSE中判定出的所有边界点构成了结构元素TSE。
步骤7?? 将SE进行距离为单位像素的平移，获取新的3×3子区域QSE，并进行步骤3至步骤6的运算，直到原始图像中的所有像素点遍历分析完成为止，获取的全部结构元素TSE的集合构成了所需的自适应结构元素。
1.2 计算图像形态学梯度图像同一目标区域内的像素灰度值较为接近，而不同区域间的像素灰度值具有较大差异，通常先获取图像的梯度图像，然后对该梯度图像进行分水岭分割。由于形态学梯度能够使图像灰度值的跃变更为急剧并且对梯度边缘方向性的依赖更小，为此，本文选择数学形态学梯度算子获取梯度图像。传统形态学梯度运算通常采用形状单一且大小固定的结构元素对图像进行处理，由于图像目标的复杂性与多样性，采用该结构元素进行形态学梯度运算会导致图像目标特征信息发生改变，如目标边界轮廓偏移、出现新的人为目标或目标细节丢失等。为此，本文采用构造的自适应结构元素进行形态学梯度运算。具体计算过程如下：
$\begin{aligned}f_{\mathrm{e}}(x, y)= & f(x, y) \Theta b(m, n)= \\& \min \{f(x+m, y+n)-b(m, n)\}\end{aligned}$ (12)
$\begin{aligned}f_{\mathrm{d}}(x, y)= & f(x, y) \oplus b(m, n)= \\& \max \{f(x-m, y-n)+b(m, n)\}\end{aligned}$ (13)
$g(x, y)=f(x, y)-f_{\mathrm{e}}(x, y)$ (14)
式中：f(x, y)为原始图像，b(m, n)为结构元素，Θ为腐蚀运算，⊕为膨胀运算，fe(x, y)与fd(x, y)分别为腐蚀与膨胀运算后获取的图像，g(x, y)为梯度图像。
1.3 修正梯度图像在对梯度图像进行分水岭分割前，通过修正梯度图像去除由于非规则扰动、噪声或纹理产生的一些局部最小值，抑制过分割现象的发生。本文采用L0范数梯度最小化和形态学开闭混合重建方法对梯度图像进行修正。
1.3.1 L0范数梯度最小化方法L0范数梯度最小化方法[18]是一种基于稀疏策略的全局平滑滤波器，主要通过去除较小的非零梯度(局部最小值)，抑制不重要的细节信息同时增强目标显著性边缘。L0范数梯度最小化方法的目标函数为：
$\min\limits _f\left\{\sum\limits_{(x, y)}\left(s(x, y)-g(x, y)^2+\lambda C[s(x, y)]\right)\right\}$ (15)
式中: g(x, y)为梯度图像，s(x, y)为平滑图像，λ为平衡数据忠诚项和正则项的权重系数。数据忠诚项衡量了平滑后图像与输入图像之差的L0范数的平方，而正则项描述了平滑后图像的特征。C[s(x, y)] 为平滑图像的非零梯度的个数，数学表达式为：
$C[s(x, y)]=\#\left\{(x, y) \| \partial_x s(x, y)+\partial_y s(x, y) \mid \neq 0\right\}$ (16)
式中: ?xs(x, y)与?ys(x, y)为平滑图像在x与y方向上的梯度；#{·}为集合内元素的个数。具体求解过程见文献[19]。
1.3.2 形态学开闭混合重建方法采用构造的自适应结构元素对L0范数梯度最小化平滑后的梯度图像进行形态学开闭混合重建运算，能够抑制梯度图像中由于非规则扰动或噪声产生的局部最小值，目标的边缘特征在重建过程得以加强，最大程度保留目标的边缘信息。形态学开运算重建以原始图像作为模板，采用结构元素对原始图像进行腐蚀运算，将腐蚀后的图像作为标记图像，最后利用标记图像与原始图像进行膨胀重建；形态学闭运算重建以原始图像作为模板，采用结构元素对原始图像进行膨胀运算，将膨胀后的图像作为标记图像，最后利用标记图像与原始图像进行腐蚀重建；形态学开闭混合重建运算定义为：
$O_{\mathrm{R}}(x, y)=R_{f(x, y)}^{f_{\mathrm{d}}}[f(x, y) \Theta b(m, n)]$ (17)
$C_{\mathrm{R}}(x, y)=R_{f(x, y)}^{f_{\mathrm{e}}}[f(x, y) \oplus b(m, n)]$ (18)
$M_{\mathrm{R}}(x, y)=C_{\mathrm{R}}(x, y)\left[O_{\mathrm{R}}(x, y), f(x, y)\right]$ (19)
式中：OR(x, y)与CR(x, y)为开重建与闭重建运算结果，R为重建运算，MR(x, y)为开闭混合重建运算结果。
1.4 修正梯度图像分水岭分割对梯度图像进行修正后，可对其进行经典分水岭分割，由于修正过程中减少了无效局部极小值的数量，分水岭过分割现象能够得到有效抑制，此外，由于采用自适应结构元素进行相关形态学运算，其能够较好地保留目标的边缘信息，提高了分水岭分割目标边缘定位的精度。
2 实验结果与分析为了验证利用本文自适应结构元素与传统结构元素进行分水岭分割后图像目标边界保持度及过分割程度的差异，在3.50 GHz/4 GB计算机以及MATLAB R2017a环境中进行仿真实验。
2.1 二值图像仿真实验与分析选取尺寸为350×280二值图像，分别利用固定大小和形状的十字形(尺寸5×5)、圆形(尺寸5×5)及自适应结构元素对图像进形态学梯度运算，对比分析提取的目标边界是否发生了偏移或缺失。此外，利用Abdou-Pratt品质因数对目标边界保持度定量分析，该值越大，表明边界点的定位精度越高，检测到的边界点发生偏移的可能性越小，具有良好的边界保持度。
图 7(a)原始图像中包含了三角形、圆形、正方形3个目标，利用3种结构元素对图 7(a)腐蚀运算结果并无明显差异，图像中的三角形目标顶点变得尖锐。利用十字形结构元素与圆形结构元素进行膨胀运算，图像中正方形及三角形目标顶点结构特征发生了改变，图 7(e)目标顶点出现十字形凹陷，图 7(f)目标顶点变得圆滑，由此可见，利用与目标结构不相似的结构元素进行形态学运算改变了原有目标的几何结构。利用自适应形结构元素对图 7(a)进行膨胀运算后，图像中三角形目标顶点变圆滑，其他两个目标的结构特征无明显变化，自适应结构元素主要依据目标的边缘特征构成，与目标的几何结构相似，目标几何结构保持性较好。
Fig. 7
图 7 二值图像形态学梯度运算边界提取结果对比 Fig. 7 Results of morphological gradient operation and boundary extraction on binary image 为了对比3种结构元素目标边界保持度的强弱，选取图 7(a)局部区域进行对比分析，利用十字形、圆形和自适应结构元素进行局部边缘提取, 结果分别如图 8(a)、图 8(b)和图 8(c)所示。由图 8可知，利用本文自适应结构元素进行形态学梯度运算未引起目标边界偏移，具有较好的边界保持能力，而利用十字形结构和圆形结构元素进行形态学梯度运算, 目标边界发生向内偏移。
Fig. 8
图 8 二值图像形态学梯度运算边缘提取结果对比 Fig. 8 Extracted edge of binary image by morphological gradient operation 表 1列出了不同结构元素对二值图像进行形态学梯度运算的Abdou-Pratt品质因数，其表达式如下：
$P_{\mathrm{FOM}}=\frac{1}{\max \left(N_{\mathrm{e}}, N_{\mathrm{d}}\right)} \sum\limits_{k=1}^{N_{\mathrm{d}}} \frac{1}{1+a d^2(k)}$ (20)
表 1
表 1 不同结构元素形态学边缘检测Abdou-Pratt品质因数对比 Tab. 1 Comparison of Abdou-Pratt quality factor of morphological edge detection using different structural elements 十字形结构元素 圆形结构元素 本文自适应结构元素 0.614 7 0.623 6 0.979 4
表 1 不同结构元素形态学边缘检测Abdou-Pratt品质因数对比 Tab. 1 Comparison of Abdou-Pratt quality factor of morphological edge detection using different structural elements
式中: Ne为设定参考边界点的个数; Nd为检测到的边界个数; d(k)为第k个参考边界点到检测边界点之间的欧氏距离; a为常数，取值为1/9。
数据表明，本文自适应结构元素的Abdou-Pratt品质因数最大，其具有较好的边界定位特性及边界细节保持能力。
2.2 彩色图像仿真实验与分析选取尺寸为600×600的三幅彩色图像，利用本文自适应结构元素构进行改进分水岭分割实验, 结果如图 9所示。其中，图 9(a)、图 9(b)与图 9(c)的目标分别为湖泊、储油罐以及屋顶。
Fig. 9
图 9 彩色图像自适应结构元素改进分水岭分割结果 Fig. 9 Results of improved watershed segmentation with adaptive structural elements on color images 由图 9可知，利用本文自适应结构元素进行形态学梯度运算能够有效获取图像的目标边缘信息，利用L0范数梯度最小化方法对梯度图像进行处理能够有效抑制其无效局部最小值，利用形态学开闭混合运算对平滑后的梯度图像进行处理能够有效增强目标的边缘特征。此外，将自适应结构元素应用于分水岭分割中，一方面提高了目标边缘定位的精度，另一方面有效抑制了过分割现象的产生。
利用不同结构元素进行改进分水岭分割, 结果及其二值化分别见图 10与图 11。可以看出，十字形、圆形与文献[17]结构元素进行改进分水岭分割后分别出现了过分割与欠分割现象；本文分割效果最优，其能够将图像中的主体目标准确的提取出来，具有较好的目标边界定位特性，且未出现过分割与欠分割现象。由此可知，利用大小与形状固定的十字形、圆形结构元素进行改进分水岭分割，其分割精度相对较低，且目标的边界轮廓发生了一定程度的偏移，出现了过分割或欠分割现象；利用自适应结构元素进行改进分水岭分割，其分割精度相对较高，能够将目标物准确的提取出来，具有较好的目标边界定位特性，有效抑制了过分割与欠分割现象的产生。
Fig. 10
图 10 彩色图像不同结构元素改进分水岭图像分割结果对比 Fig. 10 Results of improved watershed image segmentation with different structural elements of color images Fig. 11
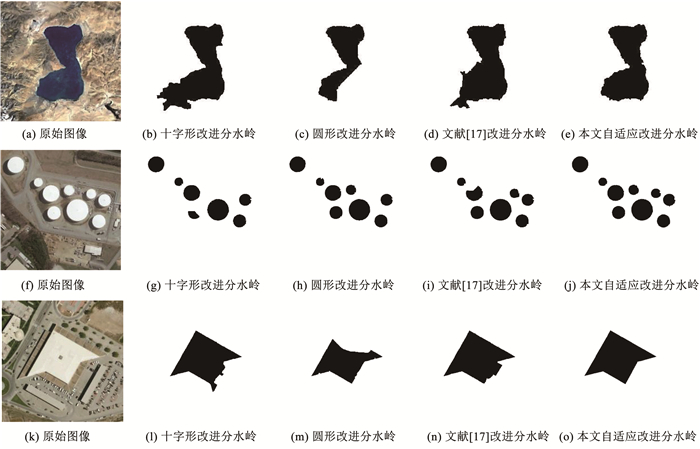图 11 彩色图像不同结构元素改进分水岭图像分割结果对比(二值图) Fig. 11 Results of improved watershed image segmentation with different structural elements of color images (binary image) 利用分割精度、过分割率、欠分割率、时间复杂度和Abdou-Pratt品质因数对改进分水岭图像分割效果进行定量分析。
分割精度表达式为
$S_{\mathrm{A}}=\left(1-\frac{\left|R_{\mathrm{S}}-T_{\mathrm{S}}\right|}{R_{\mathrm{S}}}\right) \times 100 \%$ (21)
式中: RS为理想分割目标像素个数；TS为实际分割目标像素个数；RS－TS为错误分割目标像素个数。
过分割率表达式为
$O_{\mathrm{R}}=\frac{O_{\mathrm{S}}}{R_{\mathrm{S}}+O_{\mathrm{S}}} \times 100 \%$ (22)
式中: OS为出现在实际分割图像目标中，但不出现在理想分割图像中目标的像素个数；RS为理想分割目标像素个数。
欠分割率表达式为
$U_{\mathrm{R}}=\frac{U_{\mathrm{S}}}{R_{\mathrm{S}}+U_{\mathrm{S}}} \times 100 \%$ (23)
式中: US为出现在理论分割图像目标中，但不出现在实际分割图像目标中的像素个数；RS理想分割目标像素个数。
表 2列出了不同结构元素对彩色图像进行分水岭分割效果的相关评价指标。数据表明，本文方法分割精度是4种结构元素中较高，且过分割率与欠分割率是4种结构元素中相对较低，本文分割方法能够有效抑制过分割现象。
表 2
表 2 不同结构元素改进分水岭分割指标对比分析 Tab. 2 Comparison of indexes of improved watershed segmentation with different structural elements 图号 指标 十字形结构元素 圆形结构元素 文献[17]结构元素 本文自适应结构元素 图 10(a) 分割精度 0.780 30 0.692 50 0.852 4 0.966 8
过分割率 0.174 90 0.004 60 0.122 0 0.007 7
欠分割率 0.006 40 0.301 60 0.007 6 0.022 1
图 10(f) 分割精度 0.769 50 0.853 90 0.837 4 0.924 1
过分割率 0.000 02 0.000 02 0.000 4 0.000 4
欠分割率 0.230 40 0.146 10 0.162 1 0.075 4
图 10(k) 分割精度 0.913 20 0.748 80 0.921 5 0.971 3
过分割率 0.064 90 0.003 00 0.057 0 0.005 7
欠分割率 0.016 30 0.247 50 0.017 1 0.022 9
表 2 不同结构元素改进分水岭分割指标对比分析 Tab. 2 Comparison of indexes of improved watershed segmentation with different structural elements
表 3列出了不同结构元素改进分水岭分割时间复杂度。数据表明，本文自适应结构元素进行分水岭分割的时间复杂度最高，由于其依据图像的灰度及边缘特性自适应的构造结构元素增加了运算量。
表 3
表 3 不同结构元素改进分水岭分割时间复杂度对比 Tab. 3 Comparison of running time of improved watershed segmentation with different structural elements? s图号 十字形结构元素 圆形结构元素 文献[17]结构元素 本文自适应结构元素
图 10(a) 3.296 3.148 9.217 52.628
图 10(f) 3.299 3.316 9.381 52.771
图 10(k) 3.486 3.473 9.155 52.934
表 3 不同结构元素改进分水岭分割时间复杂度对比 Tab. 3 Comparison of running time of improved watershed segmentation with different structural elements?
表 4列出了不同结构元素分水岭分割目标边缘Abdou-Pratt品质因数。数据表明，本文自适应结构元素Abdou-Pratt品质因数最大，说明其具有较强抑制边界信息发生改变的能力。
表 4
表 4 不同结构元素分水岭分割目标边缘Abdou-Pratt品质因数对比 Tab. 4 Comparison of Abdou-Pratt quality factor of watershed segmentation edge detection with different structural elements 图号 十字形结构元素 圆形结构元素 文献[17]结构元素 本文自适应结构元素 图 10(a) 0.887 8 0.907 3 0.887 8 0.979 2
图 10(f) 0.888 0 0.942 2 0.931 3 0.980 6
图 10(k) 0.896 8 0.890 6 0.921 7 0.978 9
表 4 不同结构元素分水岭分割目标边缘Abdou-Pratt品质因数对比 Tab. 4 Comparison of Abdou-Pratt quality factor of watershed segmentation edge detection with different structural elements
3 结论针对传统分水岭图像分割方法存在过分割问题，提出了一种基于自适应结构元素的改进分水岭图像分割方法。该方法首先利用图像局部灰度特性及边缘特性构造形状可变的自适应结构元素，接着利用该结构元素获取图像的形态学梯度，然后结合L0范数梯度最小化与形态学开闭混合重建对梯度图像进行修正，最后对修正后的梯度图像进行分水岭分割，实现图像目标的有效提取。实验结果表明，本文方法采用自适应结构元素进行形态学运算，较好地保留了图像目标边缘信息，具有较高的边缘定位精度。此外，利用该结构元素进行梯度修正，减少了梯度图像中无效的局部最小值，有效抑制了过分割现象的产生，具有较好的分割效果，提高了图像目标的分割精度。
参考文献
[1] 刘侠, 甘权, 李冰, 等. 融合加权随机森林的自动3D椎骨CT图像主动轮廓分割方法[J]. 光电工程, 2020, 47(12): 200002.
LIU Xia, GAN Quan, LI Bing, et al. Automatic 3D vertebrae CT image active contour segmentation method based on weighted random forest[J]. Opto-Electronic Engineering, 2020, 47(12): 200002. DOI:10.12086/oee.2020.200002
[2] VINCENT L, SOILLE P. Watersheds in digital spaces: an efficient algorithm based on immersion simulations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(6): 583. DOI:10.1109/34.87344
[3] 张建华, 韩书庆, 翟治芬, 等. 改进自适应分水岭方法分割棉花叶部粘连病斑[J]. 农业工程学报, 2018, 34(24): 165.
ZHANG Jianhua, HAN Shuqing, ZHAI Zhifen, et al. Improved adaptive watershed method for segmentation of cotton leaf adhesion lesions[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(24): 165. DOI:10.11975/j.issn.1002-6819.2018.24.020
[4] 王娅. 血液红细胞图像自适应标记分水岭分割算法[J]. 中国图象图形学报, 2017, 22(12): 1779.
WANG Ya. Adaptive marked watershed segmentation algorithm for red blood cell images[J]. Journal of Image and Graphics, 2017, 22(12): 1779. DOI:10.11834/jig.170330
[5] 张建廷, 张立民. 结合光谱和纹理的高分辨率遥感图像分水岭分割[J]. 武汉大学学报(信息科学版), 2017, 42(4): 449.
ZHANG Jianting, ZHANG Limin. A watershed algorithm combining spectral and texture information for high resolution remote sensing image segmentation[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 449.
[6] 刘聪, 董文飞, 蒋克明, 等. 基于改进分水岭分割算法的致密荧光微滴识别[J]. 中国光学, 2019, 12(4): 783.
LIU Cong, DONG Wenfei, JIANG Keming, et al. Recognition of dense fluorescent droplets using an improved watershed segmentation algorithm[J]. Chinese Optics, 2019, 12(4): 783. DOI:10.3788/CO.20191204.0783
[7] 蔡强, 刘亚奇, 曹健, 等. 一种基于自适应标记与区域间近邻传播聚类的分水岭图像分割算法[J]. 电子学报, 2017, 45(8): 1911.
CAI Qiang, LIU Yaqi, CAO Jian, et al. A watershed image segmentation algorithm based on self-adaptive marking and interregional affinity propagation clustering[J]. Acta Electronica Sinica, 2017, 45(8): 1911. DOI:10.3969/j.issn.0372-2112.2017.08.015
[8] YUAN Ye, ZHU Zhiliang, YU Hai, et al. Watershed-based superpixels with global and local boundary marching[J]. IEEE Transactions on Image Processing, 2020, 29: 7375. DOI:10.1109/TIP.2020.3002078
[9] TAREEF A, SONG Yang, HUANG Heng, et al. Multi-pass fast watershed for accurate segmentation of overlapping cervical cells[J]. IEEE Transactions on Medical Imaging, 2018, 37(9): 2044. DOI:10.1109/TMI.2018.2815013
[10] SUN Quan, ZHENG Junxing, LI Cheng. Improved watershed analysis for segmenting contacting particles of coarse granular soils in volumetric images[J]. Powder Technology, 2019, 356: 295. DOI:10.1016/j.powtec.2019.08.028
[11] NGH P, ONG S H, FOONG K W C, et al. Masseter segmentation using an improved watershed algorithm with unsupervised classification[J]. Computers in Biology and Medicine, 2008, 38(2): 171. DOI:10.1016/j.compbiomed.2007.09.003
[12] 孙惠杰, 邓廷权, 李艳超. 改进的分水岭图像分割算法[J]. 哈尔滨工程大学学报, 2014, 35(7): 857.
SUN Huijie, DENG Tingquan, LI Yanchao. Image segmentation algorithm based on the improved watershed algorithm[J]. Journal of Harbin Engineering University, 2014, 35(7): 857.
[13] 师文, 朱学芳, 朱光. 基于形态学的MRI图像自适应边缘检测算法[J]. 仪器仪表学报, 2013, 34(2): 408.
SHI Wen, ZHU Xuefang, ZHU Guang. Adaptive edge detection algorithm of MRI image based on morphology[J]. Chinese Journal of Scientific Instrument, 2013, 34(2): 408. DOI:10.3969/j.issn.0254-3087.2013.02.025
[14] 刘艳莉, 桂志国. 基于形态学的可变权值匹配自适应图像增强算法[J]. 电子与信息学报, 2014, 36(6): 1285.
LIU Yanli, GUI Zhiguo. Adaptive image enhancement algorithm with variable weighted matching based on morphology[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1285. DOI:10.3724/SP.J.1146.2013.01082
[15] PINOLI J C, DEBAYLE J. General adaptive neighborhood mathematical morphology[C]//2009 16th IEEE International Conference on Image Processing (ICIP). Cairo: IEEE, 2009: 2249
[16] STAWIASKI J, MEYER F. Minimum spanning tree adaptive image filtering[C]//Proceedings of the IEEE International Conference on Image Processing. Cairo: IEEE, 2009: 2245
[17] LANDSTR?M A, THURLEY M J. Adaptive morphology using tensor-based elliptical structuring elements[J]. Pattern Recognition Letters, 2013, 34(12): 1416. DOI:10.1016/j.patrec.2013.05.003
[18] LEGAZ-APARICIO L G, VERDú-MONEDERO R, ANGULO J. Adaptive morphological filters based on a multiple orientation vector field dependent on image local features[J]. Journal of Computational and Applied Mathematics, 2018, 330: 965. DOI:10.1016/j.cam.2017.05.001
[19] XU Li, LU Cewu, XU Yi, et al. Image smoothing via L0 gradient minimization[J]. ACM Transactions on Graphics, 2011, 30(6): 1. DOI:10.1145/2070781.2024208
