乔世范,谭晶仁,王刚,李镐羽
(中南大学 土木工程学院,长沙 410075)
摘要:
刀具磨损情况是影响盾构机掘进效率的重要因素,也是决定开仓换刀时间和频率的关键依据。针对盾构掘进过程中刀具整体磨损状态难以判断的问题,统计换刀点每把刀具磨损量与限定磨损量之间的关系,提出了3个磨损状态等级。在推导3种关键掘进参数（推力、扭矩和掘进速度）与单把滚刀切削分力理论关系的基础上,提出一种对掘进参数信号进行小波包分解以识别刀具整体磨损状态的方法。该方法以分解后的信号节点小波包系数标准差组成的特征向量作为磨损识别指标,通过敏感性分析找出对刀具磨损最敏感的节点特征向量,进而通过拟合分析确定磨损状态与磨损识别指标的函数关系。对深圳地铁14号线大运站至宝荷站区间工程实例的分析结果表明,该方法能准确识别盾构刀具的整体磨损状态,其中使用掘进速度信号进行识别的精度最高,推力次之,扭矩最低。该方法在使用中仅需对盾构机自动采集的掘进参数进行处理分析,不需要布置传感器,具有简便易行、成本低和精度高等优点,为及时开仓换刀提供了可靠依据。
关键词: 盾构 滚刀 掘进参数 小波包分析 磨损状态识别
DOI：10.11918/202203069
分类号:U455.43
文献标识码:A
基金项目:博士后联合资助引进项目(YJ20210409)
Overall wear state recognition of shield cutters
QIAO Shifan,TAN Jingren,WANG Gang,LI Haoyu
(School of Civil Engineering, Central South University, Changsha 410075, China)
Abstract:
The wear of cutter is an important factor affecting the efficiency of shield tunneling, which is also a basis for determining the time and frequency of cutter replacement. As it is difficult to evaluate the overall wear state of the cutters in the process of shield tunneling, three wear degrees (light, moderate, and severe) were proposed based on the relationship between the wear amount of each cutter and the limited wear at the cutters change site. The theoretical relationship between three main tunneling parameters (thrust, torque, and tunneling speed) and the cutting force component of a single cutter was derived, and a method for recognizing the overall wear state of cutters was proposed by using the wavelet packet algorithm to decompose the tunneling parameter signals. In this method, the eigenvectors composed by the standard deviation of the wavelet packet coefficient of decomposed signal nodes were used as the wear recognition index. Sensitivity analysis was performed to find out the most sensitive node eigenvector of the cutter wear. Then the functional relationship between the wear state and the wear recognition index was determined by fitting. The analysis of the section from Dayun station to Baohe station of Shenzhen Metro Line 14 showed that the method could accurately recognize the overall wear state of the shield cutters. Among the three tunneling parameters, the recognition accuracy was the highest when using the tunneling speed signal, followed by the thrust signal, and the torque signal was the lowest. The proposed method is easy to use and cost-effective, since it only needs to analyze the automatically collected tunneling signals without installing any sensors, which provides reference for cutter replacement.
Key words: shield cutter tunneling parameters wavelet packet analysis wear state recognition
乔世范, 谭晶仁, 王刚, 李镐羽. 盾构刀具整体磨损状态识别研究[J]. 哈尔滨工业大学学报, 2023, 55(5): 39-49. DOI: 10.11918/202203069.
QIAO Shifan, TAN Jingren, WANG Gang, LI Haoyu. Overall wear state recognition of shield cutters[J]. Journal of Harbin Institute of Technology, 2023, 55(5): 39-49. DOI: 10.11918/202203069.
基金项目 博士后联合资助引进项目(YJ20210409) 作者简介 乔世范(1975—)，男，教授，博士生导师 通信作者 王刚，wanggang123@csu.edu.cn 文章历史 收稿日期: 2022-03-21
Abstract Full text Figures/Tables PDF
盾构刀具整体磨损状态识别研究
乔世范, 谭晶仁, 王刚
, 李镐羽 中南大学 土木工程学院，长沙 410075
收稿日期: 2022-03-21; 接受日期: 2022-04-30; 网络出版日期: 2022-09-17
基金项目: 博士后联合资助引进项目(YJ20210409)
作者简介: 乔世范(1975—)，男，教授，博士生导师
通信作者: 王刚，wanggang123@csu.edu.cn
摘要: 刀具磨损情况是影响盾构机掘进效率的重要因素，也是决定开仓换刀时间和频率的关键依据。针对盾构掘进过程中刀具整体磨损状态难以判断的问题，统计换刀点每把刀具磨损量与限定磨损量之间的关系，提出了3个磨损状态等级。在推导3种关键掘进参数(推力、扭矩和掘进速度)与单把滚刀切削分力理论关系的基础上，提出一种对掘进参数信号进行小波包分解以识别刀具整体磨损状态的方法。该方法以分解后的信号节点小波包系数标准差组成的特征向量作为磨损识别指标，通过敏感性分析找出对刀具磨损最敏感的节点特征向量，进而通过拟合分析确定磨损状态与磨损识别指标的函数关系。对深圳地铁14号线大运站至宝荷站区间工程实例的分析结果表明，该方法能准确识别盾构刀具的整体磨损状态，其中使用掘进速度信号进行识别的精度最高，推力次之，扭矩最低。该方法在使用中仅需对盾构机自动采集的掘进参数进行处理分析，不需要布置传感器，具有简便易行、成本低和精度高等优点，为及时开仓换刀提供了可靠依据。
关键词: 盾构 滚刀 掘进参数 小波包分析 磨损状态识别
Overall wear state recognition of shield cutters
QIAO Shifan, TAN Jingren, WANG Gang
, LI Haoyu School of Civil Engineering, Central South University, Changsha 410075, China
Abstract: The wear of cutter is an important factor affecting the efficiency of shield tunneling, which is also a basis for determining the time and frequency of cutter replacement. As it is difficult to evaluate the overall wear state of the cutters in the process of shield tunneling, three wear degrees (light, moderate, and severe) were proposed based on the relationship between the wear amount of each cutter and the limited wear at the cutters change site. The theoretical relationship between three main tunneling parameters (thrust, torque, and tunneling speed) and the cutting force component of a single cutter was derived, and a method for recognizing the overall wear state of cutters was proposed by using the wavelet packet algorithm to decompose the tunneling parameter signals. In this method, the eigenvectors composed by the standard deviation of the wavelet packet coefficient of decomposed signal nodes were used as the wear recognition index. Sensitivity analysis was performed to find out the most sensitive node eigenvector of the cutter wear. Then the functional relationship between the wear state and the wear recognition index was determined by fitting. The analysis of the section from Dayun station to Baohe station of Shenzhen Metro Line 14 showed that the method could accurately recognize the overall wear state of the shield cutters. Among the three tunneling parameters, the recognition accuracy was the highest when using the tunneling speed signal, followed by the thrust signal, and the torque signal was the lowest. The proposed method is easy to use and cost-effective, since it only needs to analyze the automatically collected tunneling signals without installing any sensors, which provides reference for cutter replacement.
Keywords: shield cutter tunneling parameters wavelet packet analysis wear state recognition
盾构刀具是盾构机的主要工作部件之一，其磨损状况直接影响工程进度和质量，特别是在硬岩地区，刀具易磨损，换刀频率高，增加了施工风险和成本。通常开仓换刀是在盾构刀具整体磨损至一定程度时进行，过早或过晚开仓都会对工程造成损失，因此盾构刀具整体磨损状态的识别具有重要意义。
目前关于盾构刀具磨损的研究，一方面聚焦于单刀磨损量实测值与掘进参数、岩石性质之间的回归分析[1-3]，另一方面侧重于刀具磨损测量传感器的研发，较少关注盾构刀具整体磨损程度的评估，也未从理论层面揭示刀具磨损与掘进参数之间的内在关联[4]。张明富等[2]用回归分析得出了刀具磨损系数与掘进参数的关系以及刀具磨损量与掘进距离的关系式；Liu等[3]建立了刀具磨损寿命与岩石特性之间的函数表达式；Huang等[5]提出了一种测量盾构刀具切削力的方法，并通过大量实测数据探究了切削力与贯入度、扭矩和推力之间的相关性。实际上掘进参数的变化与刀具磨损状态和地质条件等因素有关，当地层不变时，掘进参数的变化是刀盘上所有刀具整体磨损情况的反映，而非单把刀具磨损作用的结果。通过回归拟合得到的单刀磨损量与掘进参数的关系不能反映刀具整体磨损情况，传感器也因为只能在部分刀具上安装，其适用性有限。
在数控机床刀具磨损研究中，主要通过分析切削力信号特征来实现刀具磨损的检测[6-7]，李涛等[6]提取了合金加工中切削力信号的小波包系数能量值作为刀具磨损特征参数；Kaya等[7]利用合金铣削加工中实时采集的3个方向切削力和扭矩信号，开发了预测后刀面磨损量的监测系统。然而数控机床检测的是单把刀具的磨损情况，与盾构机需要检测多把刀具的整体磨损状态存在差异，而且盾构机采集的是刀盘的总扭矩和推力，并未测量单把刀具的切削力。
为此，本文首先提出盾构刀具整体磨损状态等级，然后以滚刀为例，在推导出掘进参数与刀具磨损关系的基础上，提出一种小波包分解掘进参数信号的盾构刀具磨损识别方法，利用刀具整体磨损处于不同状态时，掘进参数信号波动特征存在差异的特点，构建刀具磨损识别指标。本文先阐述了该方法的原理和实现过程，并通过实际工程验证其正确性，最后比较了不同掘进参数识别刀具磨损的效果。
1 刀具整体磨损状态等级和评价指标 1.1 刀具整体磨损状态评价指标刀具磨损形式分为两种：一种是均匀磨损，其特点是各部位磨损程度基本相同，可用磨损量表示，为主要磨损形式; 另一种是非均匀磨损，包括偏磨、崩裂等[8]，其特点是各部位磨耗程度、形态不一致，难以直接量化。对此，本文提出磨损状态系数w对单刀两种磨损形式下的磨损状态进行度量，并以此建立整体磨损状态系数H来评价刀具的整体磨损情况，其表达式为
$H=\sum\limits_{i=1}^N w_i / \sum\limits_{a=1}^M S_a, w_i \in[0, 1]$ (1)
式中: N为刀盘刀具总数, Sa为第a类刀具数量，M为刀具类别数，wi为第i个刀具磨损状态系数。
不同磨损形式的wi计算方法如下：
1) 均匀磨损
$w_i=q_i / q_{\mathrm{e} i}$ (2)
式中：qi为第i个刀具的磨损量; qei为第i个刀具的限定磨损量; 当qi≥qei时，取wi=1。(本文案例研究的滚刀取径向磨损量qei=20 mm[9]。)
2) 非均匀磨损
滚刀偏磨折算成均磨磨损量后再计算wi；刀圈崩裂等严重磨损形式视为失效，即取wi=1。
偏磨磨损量折算的原则为：偏磨和均磨造成刀圈平面面积减少量一致[10]。如图 1所示，偏磨的磨损面积计算式为
$A_{\mathrm{n}}=R^2 \arccos \left(\frac{R-q}{R}\right)-\sqrt{2 R q-q^2}(R-q)$ (3)
Fig. 1
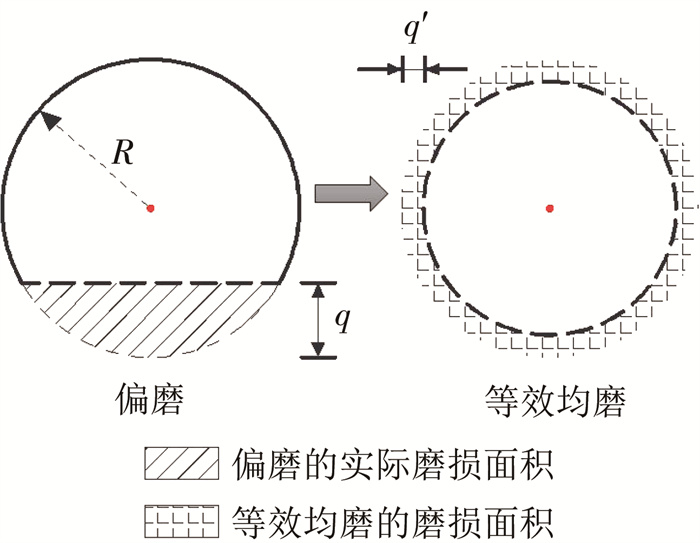图 1 偏磨磨损量折算示意 Fig. 1 Converting method for partial wear amount 式中：An为滚刀偏磨时的磨损面积；q为滚刀的偏磨磨损量; R为滚刀初始半径。按照磨损面积相等原则，将偏磨折算成均磨后，等效均磨的磨损面积计算式为
$A_{\mathrm{eu}}=\pi R^2-\pi\left(R-q^{\prime}\right)^2$ (4)
式中：Aeu为等效均磨磨损面积; q′为等效均磨磨损量。联立式(3)和式(4)，解得等效均磨磨损量为
$q^{\prime}=R-\sqrt{R^2-\frac{1}{\pi} R^2 \arccos \left(\frac{R-q}{R}\right)+\frac{1}{\pi} \sqrt{2 R q-q^2}(R-q)}$ (5)
1.2 刀具整体磨损状态等级参照刀具典型磨损曲线[11]，将盾构刀具整体磨损状态分为轻度磨损、中度磨损和严重磨损3个等级。同时依据施工现场换刀经验和式(1)，确定各磨损状态对应系数H值的范围，见表 1。
表 1
表 1 刀具整体磨损状态等级 Tab. 1 Degrees of overall wear state of cutters 磨损状态 整体磨损状态系数H范围 检修情况 轻度磨损 0~0.35 无需检修
中度磨损 0.35~0.50 停机检查
严重磨损 0.50~1.00 停机换刀
表 1 刀具整体磨损状态等级 Tab. 1 Degrees of overall wear state of cutters
2 掘进参数分析盾构机在掘进过程中会实时采集掘进数据，包括：掘进速度、刀盘扭矩、转速、盾构推力、土舱压力等。已有研究表明，单把刀具所受切削力与磨损直接相关，刀盘扭矩、盾构推力和掘进速度3个参数与刀具磨损间的相关性不明确。为此本节将对掘进参数与单刀切削力之间的关系进行理论推导，以探究掘进参数与刀具整体磨损之间的内在联系。单把滚刀在破岩过程中的受力情况如图 2所示，其所受切削力分解为3个方向的作用力：垂直推力(切削力)Fn、水平切削力Fr和侧向力Fs，其中Fs很小，故不予考虑。
Fig. 2
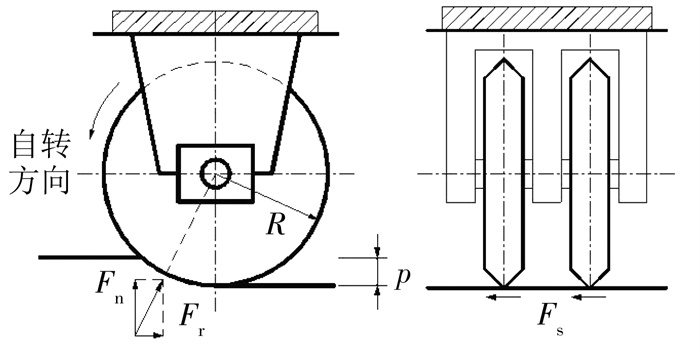图 2 滚刀受力分析 Fig. 2 Force acting on cutter 2.1 盾构推力分析盾构总推力、有效推力及单把滚刀垂直推力的表达式为
$F=F_{\mathrm{p}}+F_{\mathrm{a}}+F_{\mathrm{b}}$ (6)
$F_{\mathrm{p}}=N F_{\mathrm{n}}$ (7)
${F_{\rm{n}}} = K\frac{{\phi RL}}{{1 + \psi }}\sqrt[3]{{\left( {\frac{{S\sigma _{\rm{c}}^2{\sigma _{\rm{t}}}}}{{\phi \sqrt {RL} }}} \right)}}\cos \frac{\phi }{2}$ (8)
式中：F为盾构总推力; Fa为地层稳定推力; Fb为盾构设备消耗推力; Fp为刀盘的有效推力，由每把滚刀的垂直推力叠加而得[12]; Fn为单把滚刀的垂直推力(切削力); K为量纲系数，K≈2.12;ψ为刀尖压力分布系数; ?为滚刀与岩石的接触角; R为滚刀半径; L为滚刀刀尖宽度; S为刀间距; σc为岩石抗压强度; σt为岩石抗拉强度[8]。
对于同一地层中掘进的同规格盾构机，Fa、Fb之和基本保持不变，用常数CF替代，式(6)化简为
$F=F_{\mathrm{p}}+C_{\mathrm{F}}=N F_{\mathrm{n}}+C_{\mathrm{F}}$ (9)
2.2 刀盘扭矩分析刀盘总扭矩、有效扭矩及单把滚刀水平切削力的表达式为
$T=T_{\mathrm{p}}+T_{\mathrm{a}}+T_{\mathrm{b}}$ (10)
$T_{\mathrm{p}}=F_{\mathrm{r}} \sum\limits_{i=1}^N \cdot r_i=N r F_{\mathrm{r}}$ (11)
$F_{\mathrm{r}}=K \frac{\phi R L}{1+\psi} \sqrt[3]{\frac{S \sigma_{\mathrm{c}}^2 \sigma_{\mathrm{t}}}{\phi \sqrt{R L}} \sin \frac{\phi}{2}}$ (12)
式中：T为刀盘总扭矩; Ta为地层稳定扭矩; Tb为盾构设备消耗扭矩; Tp为刀盘有效扭矩，即刀具水平切削力对刀盘旋转轴产生的合力矩; Fr为单把滚刀的水平切削力; ri为第i个刀具的旋转半径; r为所有刀具的平均旋转半径，r=0.59D/2，D为刀盘直径[13]。
同理，对同地层同规格盾构机，Ta与Tb之和基本保持不变，用常数CT替代，则式(10)化简为
$T=T_{\mathrm{p}}+C_{\mathrm{T}}=0.295 N D F_{\mathrm{r}}+C_{\mathrm{T}}$ (13)
2.3 掘进速度分析盾构机的掘进速度与刀盘转速、滚刀贯入度和切削系数之间的关系式为[14]
$V=n_{\mathrm{s}} \cdot p$ (14)
$C_{\mathrm{e}}=F_{\mathrm{r}} / F_{\mathrm{n}}=\sqrt{p /(d-p)}$ (15)
式中：V为掘进速度，ns为刀盘转速，p为滚刀贯入度，Ce为切削系数，d为滚刀直径。因实际施工中p?d，故式(15)可简化为：
由此，掘进速度与滚刀切削力的关系式为
$V=n_{\mathrm{s}} d \cdot\left(F_{\mathrm{r}} / F_{\mathrm{n}}\right)^2$ (16)
从式(8)和式(12)可以看出，刀具磨损后，刀尖宽度L、刀圈半径R和刀岩接触角?的动态变化会引起滚刀切削力的波动。进而通过盾构掘进参数与单把滚刀切削分力之间的关系式(9)、(13)和(16)，揭示了掘进参数与刀具磨损之间的关联。
3 基于小波包分析的刀具磨损识别指标和方法在上述论证的基础上，本文采用小波包算法，构造了一种盾构刀具磨损状态识别指标，提出了相应的磨损识别方法和流程，识别流程见图 3。
Fig. 3
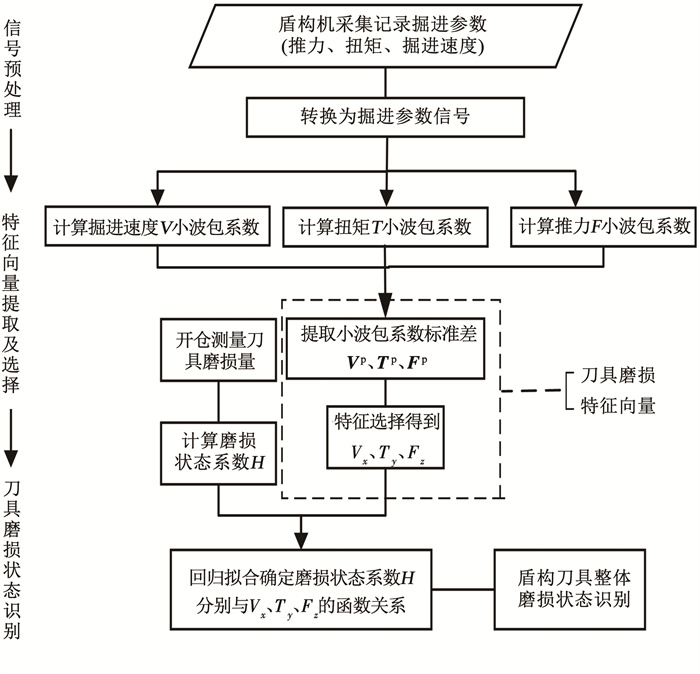图 3 盾构刀具整体磨损状态识别流程图 Fig. 3 Flow chart of overall wear state recognition of cutters 3.1 小波包提取刀具磨损识别指标小波包分析是一种精细化信号分析方法，它能将盾构机上采集的非线性掘进参数(掘进速度、扭矩和推力)信号分解到不同尺度，得到各尺度下信号的节点特征，构成特征参数组。既有研究表明：刀具在切削过程中，切削力信号的小波包节点特征中包含刀具磨损信息，可进行提取，作为磨损状态改变的判断依据[6]。由于掘进参数与切削力存在线性关系，对于掘进参数信号x(t)(掘进速度V、扭矩T和推力F)，小波包提取刀具磨损特征的原理如下：
小波包函数的表达式为[15]
$\mu_{j+1, k}^n(t)=2^{\frac{j+1}{2}} \mu^n\left(2^{j+1} t-k\right)$ (17)
式中：j为尺度参数(即分解层数); n为振荡参数; k为平移参数(即数据点序号，k=0, 1, 2, …); t为时间变量，t∈R。
小波包函数满足双尺度方程：
$\left\{\begin{array}{l}\mu_{2 n}(t)=\sqrt{2} \sum\limits_{k \in Z} h(k) \mu_n(2 t-k) \\\mu_{2 n+1}(t)=\sqrt{2} \sum\limits_{k \in Z} g(k) \mu_n(2 t-k)\end{array}\right.$ (18)
式中：h(k)为低通滤波器系数; g(k)为高通滤波器系数。上式构造的序列{μn(t)}n∈Z为正交小波包。
掘进参数信号x(t)在{μn(t)}n∈Z上的投影(小波包)系数dj+1n(k)为
$d_j^n(k)=\int_{-\infty}^{\infty} x(t) \cdot \mu_{j+1}^n(t) \mathrm{d} t$ (19)
针对采集的信号x(t)，由{dj+1n(l)}递推求得{dj2n(k)}与{dj2n+1(k)}，即小波包分解算法为
$\left\{\begin{array}{l}d_j^{2 n}(k)=\sum\limits_{l \in Z} h(l-2 k) d_{j+1}^n(l) \\d_j^{2 n+1}(k)=\sum\limits_{l \in Z} g(l-2 k) d_{j+1}^n(l)\end{array}\right.$ (20)
小波包重构算法为
$\begin{aligned}d_{j+1}^n(k)= & \sum\limits_{l \in Z} h(k-2 l) d_j^{2 n}(l)+ \\& \sum\limits_{l \in Z} g(k-2 l) d_j^{2 n+1}(l)\end{aligned}$ (21)
本文对掘进参数信号进行4层小波包分解重构，小波包分解的树结构如图 4所示。图中(j, r)表示第j层第r个节点，简称节点(j, r)。
Fig. 4
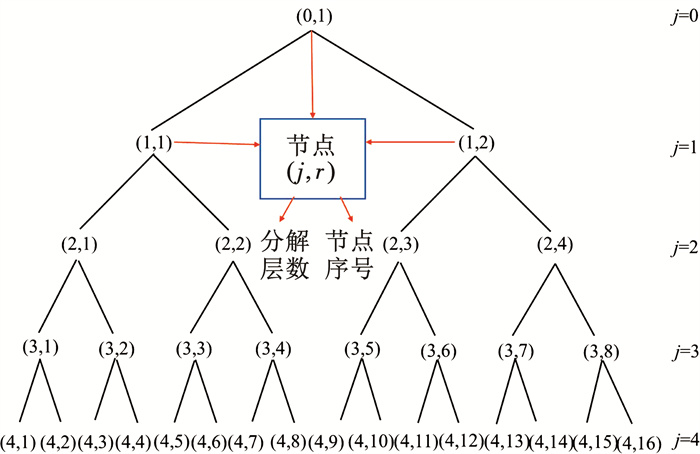图 4 小波包分解的树结构 Fig. 4 Tree structure of wavelet packet decomposition 盾构机向前掘进过程中，刀具处于不同磨损状态时，掘进参数信号的波动情况会存在差异，根据上述现象，依托工程实例对各环掘进参数信号进行处理，比较信号的节点小波包系数及其他信号特征参数，最终提出以掘进参数信号小波包系数标准差作为识别指标，进行刀具整体磨损状态的判定。
刀具的整体磨损状态识别指标(特征向量)具体定义为
$\sigma(x(t), j, r)=\sqrt{\frac{1}{n} \sum\limits_{k=1}^n\left[d_{j, r}(k)-\bar{d}_{j, r}\right]^2}$ (22)
式中：σ(x(t), j, r)为某环掘进参数信号x(t)在节点(j, r)的小波包系数标准差(此指标与掘进参数的大小无关，与掘进参数的波动有关); dj, r(k)为信号x(t)在节点(j, r)的第k个小波包系数; dj, r为信号x(t)在节点(j, r)的小波包系数平均值。本文取j=4, r=(1, 2, …, 16)。
为简化符号，分别用Vr、Tr、Fr表示第4层第r个节点的掘进速度、扭矩、推力小波包系数标准差，每种掘进参数16个节点的小波包系数差构成磨损特征向量集Vp、Tp、Fp，其表达式为
$\left(\begin{array}{l}\boldsymbol{V}^{\mathrm{p}} \\\boldsymbol{T}^{\mathrm{p}} \\\boldsymbol{F}^{\mathrm{p}}\end{array}\right)=\left(\begin{array}{lllll}\sigma(V, 4, 1) & \sigma(V, 4, 2) & \sigma(V, 4, 3) & \cdots & \sigma(V, 4, 16) \\\sigma(T, 4, 1) & \sigma(T, 4, 2) & \sigma(T, 4, 3) & \cdots & \sigma(T, 4, 16) \\\sigma(F, 4, 1) & \sigma(F, 4, 2) & \sigma(F, 4, 3) & \cdots & \sigma(F, 4, 16)\end{array}\right)=\left(\begin{array}{lllll}V_1 & V_2 & V_3 & \cdots & V_{16} \\T_1 & T_2 & T_3 & \cdots & T_{16} \\F_1 & F_2 & F_3 & \cdots & F_{16}\end{array}\right)$ (23)
3.2 基于敏感性分析的刀具磨损特征选择通过上述小波包分析，每类掘进参数均分解为16维特征向量，为提高识别效率，采用敏感性分析方法，寻找每类掘进参数信号中对刀具磨损敏感度最大的节点，即获取与刀具磨损相关性最强的节点特征向量。该方法的计算步骤如下[16]：
1) 确定参考数列X0和比较数列Xi，i=(1, 2, …, m)，m为小波包分解的节点个数。
定义数据集中各环刀具整体磨损状态系数H组成的数列X0=(x0(1), x0(2), …, x0(na))(na为回归环个数)为各分析对象的参考数列，其比较数列(即刀具磨损状态的识别指标)为
$\left\{\begin{array}{l}X_1=\left(x_1(1), x_1(2), \cdots, x_1\left(n_{\mathrm{a}}\right)\right) \\\quad\quad\quad\quad\quad\quad \vdots \\X_i=\left(x_i(1), x_i(2), \cdots, x_i\left(n_{\mathrm{a}}\right)\right) \\\quad\quad\quad\quad\quad\quad \vdots \\X_m=\left(x_m(1), x_m(2), \cdots, x_m\left(n_{\mathrm{a}}\right)\right)\end{array}\right.$ (24)
式中：当(X1, X2, …, Xm)=(V1, V2, …, V16)，比较数列为掘进速度节点小波包系数标准差Vr，r=(1, 2, …, 16);当(X1, X2, …, Xm)=(T1, T2, …, T16)，比较数列为扭矩节点小波包系数标准差Tr, r=(1, 2, …, 16);当(X1, X2, …, Xm)=(F1, F2, …, F16)，比较数列为推力节点小波包系数标准差Fr, r=(1, 2, …, 16)。
2) 计算各项数列初值为
$\begin{aligned}X_i^{\prime}=X_i / x_i(1)&=\left(x_i^{\prime}(1), x_i^{\prime}(2), \cdots, x_i^{\prime}\left(n_{\mathrm{a}}\right)\right) \\& i=(0, 1, 2 \cdots, m)\end{aligned}$ (25)
3) 令Δi(k)为参考数列与比较数列差的绝对值，求Δi(k)的最大值M与最小值m。
4) 求敏感系数γ(x0(k), xi(k))为
$\begin{gathered}\gamma\left(x_0(k), x_i(k)\right)=\frac{m+\xi M}{\Delta_i(k)+\xi M} \\\xi \in(0, 1), k=(1, 2, \cdots, m)\end{gathered}$ (26)
式中ξ为分辨系数，一般取0.5。
5) 求敏感度γ(x0, xi)为
$\gamma\left(x_0, x_i\right)=\frac{1}{n} \sum\limits_{k=1}^n \gamma\left(x_0(k), x_i(k)\right)$ (27)
6) 将掘进参数信号的节点特征向量对刀具磨损的敏感度进行排序，敏感度最大者即所求节点特征向量Vx、Ty、Fz。
3.3 基于掘进参数信号特征的刀具磨损状态识别方法鉴于掘进参数与刀具磨损的相关性，结合前述对掘进参数信号进行小波包分析和特征选择，提出一种基于掘进参数信号特征的刀具整体磨损状态识别方法。该方法的基本原理如下：假定3种掘进参数信号中对刀具磨损敏感度最大的节点特征向量(Vx、Ty、Fz)和刀具磨损状态系数H存在如下函数关系：
$\left\{\begin{array}{l}f_1\left(V_x\right)=H \\f_2\left(T_y\right)=H \\f_3\left(F_z\right)=H\end{array}\right.$ (28)
通过多样本(回归环)的拟合分析得到上述函数模型的表达式。之后将验证环的掘进参数信号特征向量(Vx、Ty、Fz)代入式(28)，计算得到每环磨损状态系数H的识别值，最后对照表 1中H值范围判断盾构刀具的整体磨损状态。
4 工程实例分析 4.1 工程概况为验证所提磨损识别方法的有效性，选取深圳地铁14号线大运站至宝荷站区间掘进参数进行分析。从图 5(a)可看出，研究段隧道洞身主要穿越微风化石灰岩，该类岩石强度较高，滚刀破岩时易磨损。工程采用中铁装备制造的直径为6 980 mm的复合式土压平衡盾构机，刀盘结构如图 5(b)所示。刀盘上布置18寸中心滚刀6把，18寸单刃滚刀38把，切刀49把，刮刀12把。滚刀超出刀盘面板高度175 mm，切刀和刮刀超出刀盘面板高度130 mm，盾构机掘进破岩时，滚刀对其他刀具产生保护作用，承担了绝大部分刀具磨损，故本文采用滚刀磨损量计算磨损状态系数H。
Fig. 5
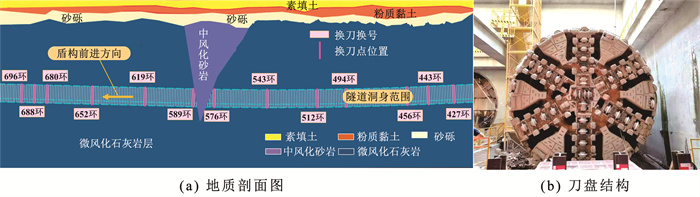图 5 深圳地铁14号线大运站至宝荷站地质剖面图和刀盘结构 Fig. 5 Geological profile and cutterhead structure of Dayun station to Baohe station of Shenzhen Metro Line 14 4.2 数据选取隧道洞身穿越微风化石灰岩的区间段(420~576环和589环~700环)，现场进行了13次开仓换刀和磨损量测量，收集区间换刀环和换刀后一环共26环的掘进参数和磨损量。将换刀台帐里记录的刀具磨损量qi代入式(1)和式(2)，计算出各环刀具实际整体磨损状态系数H，然后根据表 1判断刀具整体磨损状态。换刀前后环对应的H实际值见图 6。由图可知，换刀环的H值大部分大于0.35，说明H=0.35为开仓换刀与否的分界线，也是划分轻度磨损和中度磨损的临界值。换刀后一环的H < 0.50，说明换刀目的是为了避免超出H=0.5这一临界线，因此将0.5作为划分中度磨损和严重磨损的临界值。从盾构机上导出这26环的原始掘进参数，每环各取500个连续采集点数据，各环500个数据点的掘进参数平均值见表 2。由表 2可知，刀具处于不同磨损状态时，盾构机掘进参数平均值的变化规律性不强，难以据此判断盾构刀具的整体磨损情况。
Fig. 6
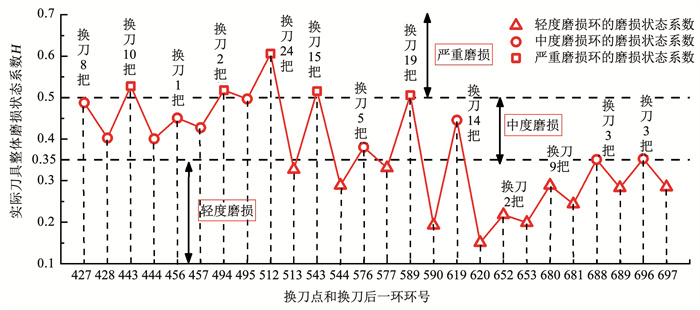图 6 换刀前后环刀具整体磨损状态系数 Fig. 6 Overall wear state coefficient of cutters before and after changing cutters 表 2
表 2 各环掘进参数平均值和刀具磨损情况 Tab. 2 Average value of tunneling parameters and cutter wear at each ring 掘进环号 转速/(r·min-1) 掘进速度/(mm·min-1) 扭矩/(kN·m) 推力/ kN 换刀数量/把 非均匀磨损刀具数及类型 实际整体磨损状态系数H 实际刀具整体磨损状态 427 2.01 14.77 2 507 11 478 4新4旧 0 0.488 中度磨损
428 2.00 14.60 2 416 10 657 0 0 0.403 中度磨损
443 2.03 13.23 2 609 12 257 6新4旧 5 (刀圈崩、偏磨) 0.528 严重磨损
444 1.98 14.13 2 449 11 078 0 0 0.401 中度磨损
456 1.96 13.89 2 543 11 557 1新 1 (刀圈崩) 0.451 中度磨损
457 2.02 13.68 2 393 11 641 0 0 0.428 中度磨损
494 1.93 12.98 2 526 12 219 2旧 1 (刀圈崩) 0.518 严重磨损
495 2.03 12.93 2 613 12 253 0 0 0.497 中度磨损
512 1.99 11.54 2 708 13 009 12新12旧 0 0.606 严重磨损
513 2.02 15.17 2 423 10 783 0 0 0.327 轻度磨损
543 1.94 13.85 2 637 12 430 11新4旧 7 (刀圈崩、偏磨) 0.516 严重磨损
544 2.02 15.20 2 427 10 836 0 0 0.289 轻度磨损
576 2.08 14.67 2 516 11 768 1新4旧 4 (刀圈崩、偏磨) 0.381 中度磨损
577 2.03 13.90 2 422 11 393 0 0 0.331 轻度磨损
589 2.02 10.93 2 752 14 295 15新4旧 12 (刀断裂、偏磨) 0.506 严重磨损
590 2.03 15.18 2 492 11 775 0 0.193 轻度磨损
619 1.98 12.60 2 666 13 649 13新4旧 11(刀变形、偏磨) 0.446 中度磨损
620 2.06 16.02 2 426 11 347 0 0 0.151 轻度磨损
652 2.05 14.82 2 282 10 031 2旧 0 0.218 轻度磨损
653 1.99 15.48 2 293 9 992 0 0 0.199 轻度磨损
680 2.01 14.72 2 390 10 926 5新4旧 1(偏磨) 0.289 轻度磨损
681 2.03 15.44 2 366 10 435 0 0 0.244 轻度磨损
688 1.95 13.93 2 523 12 257 3新 3 (刀脱落、崩圈) 0.351 中度磨损
689 2.02 14.70 2 478 12 278 0 0 0.283 轻度磨损
696 1.97 13.81 2 546 12 444 3新 3 (刀崩圈) 0.353 中度磨损
697 1.98 14.22 2 503 12 342 0 0 0.285 轻度磨损
注：换刀把数中的u新v旧表示更换u把新刀、v把旧刀。计算换刀后一环的H时认为换的新刀磨损量为0，换的旧刀磨损量为旧刀原始磨损量，未换刀的刀具磨损量与前一环相同。后文分析中427~653环为回归环，680~697环为验证环。
表 2 各环掘进参数平均值和刀具磨损情况 Tab. 2 Average value of tunneling parameters and cutter wear at each ring
4.3 盾构刀具整体磨损状态识别 4.3.1 建立刀具磨损状态识别模型首先将上述每环的500个数据点掘进参数转换为信号，以543环、544环和576环(分别对应3种磨损状态)为例，其掘进参数信号见图 7。由图 7可知，原始掘进参数信号较杂乱，无明显规律，需对其进行数字信号处理，以获取所需刀具磨损特征。
Fig. 7
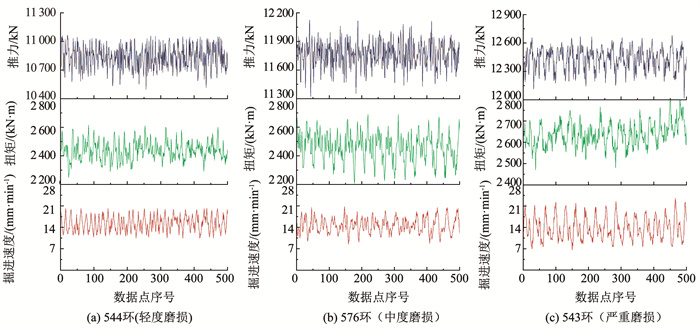图 7 不同磨损状态掘进参数信号 Fig. 7 Tunneling parameter signals under different wear states 采用db8小波基函数对26环的3种掘进参数信号分别进行4层小波包分解重构，以544环、576环和543环为例，这3环掘进速度V信号的第4层16个节点的小波包系数如图 8所示，图中横坐标为数据点序号，纵坐标dr为每个数据点在节点(4, r)的掘进速度小波包系数值。由图 8可知，第1个节点小波包系数图(d1)反映了掘进参数信号的概貌，随着磨损程度的加深，此节点的小波包系数波动幅度呈增大趋势。其他节点小波包系数图(d2~d16)体现了掘进参数信号的细节，存在滚刀破岩的振动和噪声特征。
Fig. 8
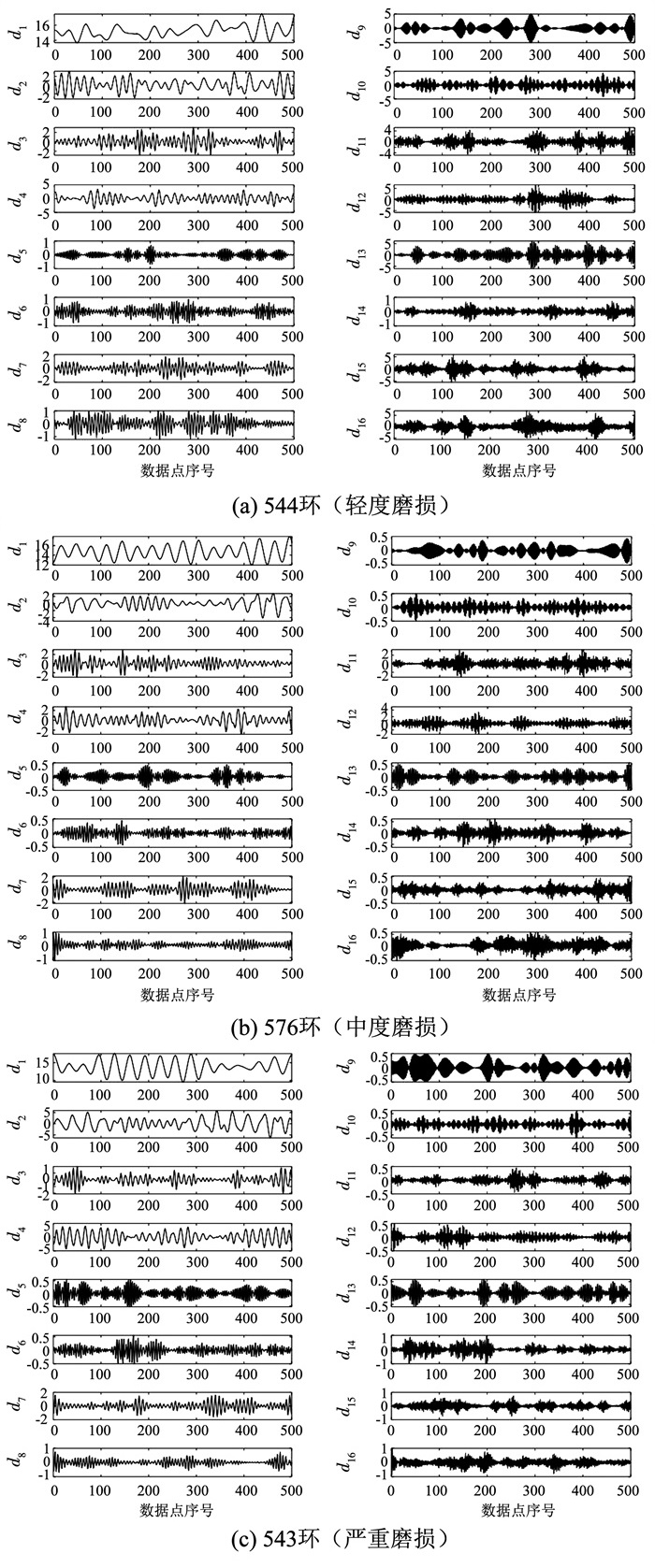图 8 不同磨损状态掘进速度小波包系数 Fig. 8 Wavelet packet coefficient of tunneling speed under different wear states 为量化不同磨损状态掘进参数信号节点波动量的大小，以获取刀具磨损特征向量，将分解信号得到的小波包系数代入式(22)，计算各环掘进参数信号的16个节点小波包系数标准差Vr、Tr、Fr，其结果见表 3。
表 3
表 3 掘进参数信号小波包系数标准差 Tab. 3 Standard deviation of wavelet packet coefficient of tunneling parameter signals 掘进环号 掘进速度信号 扭矩信号 推力信号 V1 V2 … V16 T1 T2 … T16 F1 F2 … F16
427 1.714 1.669 … 0.202 57.069 20.881 … 8.002 44.579 22.733 … 16.320
428 1.549 2.306 … 0.205 52.380 10.913 … 6.906 49.608 24.522 … 19.408
443 2.291 2.146 … 0.308 65.400 37.142 … 8.103 65.176 64.293 … 21.856
444 1.436 1.662 … 0.176 38.050 29.481 … 6.185 43.511 26.749 … 16.437
? ? ? ? ? ? ? ? ? ?
680 0.845 1.365 … 0.211 33.238 15.442 … 6.539 29.102 25.699 … 18.627
681 0.637 0.619 … 0.150 29.540 26.696 … 8.119 15.914 12.422 … 12.121
688 1.114 1.321 … 0.289 40.777 24.202 … 9.580 43.481 57.409 … 51.413
689 0.727 1.137 … 0.244 34.751 25.069 … 9.013 28.906 17.879 … 18.192
696 1.206 0.861 … 0.297 52.626 25.016 … 8.947 42.544 15.430 … 12.685
697 0.750 0.838 … 0.180 40.134 22.998 … 7.648 32.136 27.282 … 15.764
表 3 掘进参数信号小波包系数标准差 Tab. 3 Standard deviation of wavelet packet coefficient of tunneling parameter signals
采用敏感性分析方法对427~653环(回归环)的掘进速度、扭矩和推力的小波包系数标准差Vr、Tr、Fr进行敏感度排序，排序情况见图 9。
Fig. 9
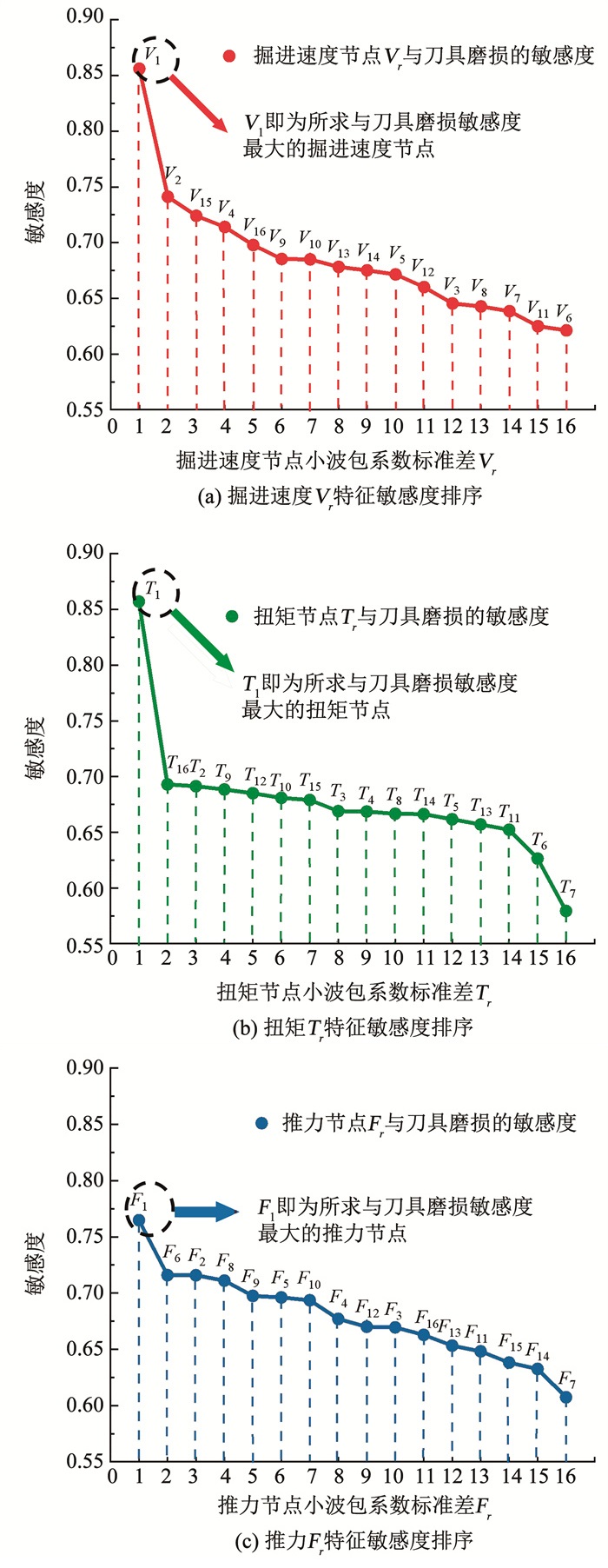图 9 掘进参数信号特征敏感度排序 Fig. 9 Feature sensitivity ranking of tunneling parameter signals 由图 9可知，3种掘进参数信号的第1个节点特征向量对刀具磨损的敏感性最强，说明磨损信息主要集中在小波包分解后的第1个节点中。分别采用5种回归模型(线性回归、指数回归、对数回归、乘幂回归和多项式回归)，对427~653环(回归环)掘进参数信号的第1个节点特征向量与磨损状态系数H进行拟合，其中对数回归模型的R2最大，回归效果最好。回归曲线如图 10实线所示，回归模型的相对误差范围线用虚线表示，可以看出，掘进速度回归模型的误差最小，在10%以内，扭矩和推力回归模型的误差大部分在20%以内。此外，各掘进参数信号的第1个节点特征向量与磨损状态系数H均呈正相关关系，说明对刀具磨损敏感的信号小波包节点波动量随刀具磨损的加重而加大。回归拟合得到的函数关系式如下：
$\left\{\begin{array}{l}H=0.241 \ln \left(V_1\right)+0.336 \\H=0.279 \ln \left(T_1\right)-0.662 \\H=0.239 \ln \left(F_1\right)-0.500\end{array}\right.$ (29)
Fig. 10
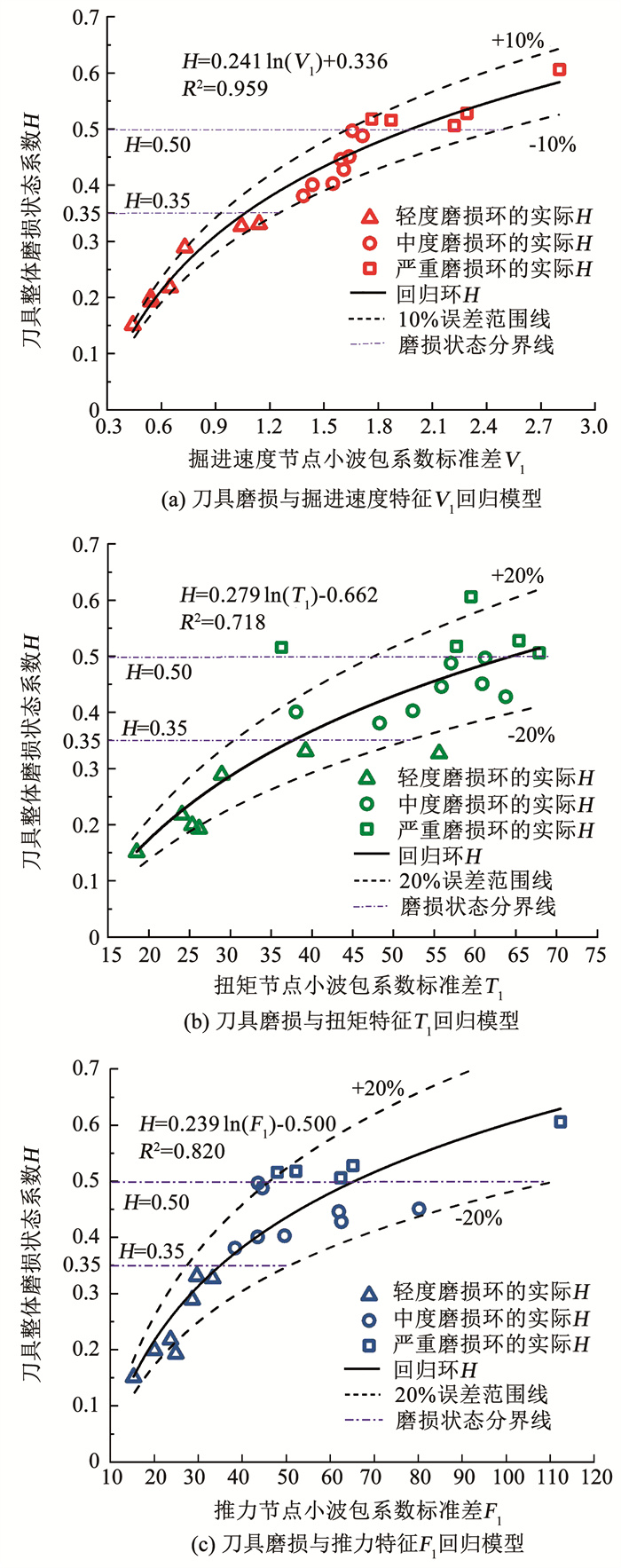图 10 刀具磨损与掘进参数信号特征的回归模型 Fig. 10 Regression model of cutter wear and feature of tunneling parameter signals 对比各回归曲线的R2，3种掘进参数与H相关性强弱顺序为：掘进速度V>推力F>扭矩T。
4.3.2 验证刀具磨损状态识别模型为验证该模型的准确性，将680~697环(验证环)的V1、T1、F1代入回归方程式(29)，得出磨损状态系数H的识别值(图 11中圆直径上数字标注)，
Fig. 11
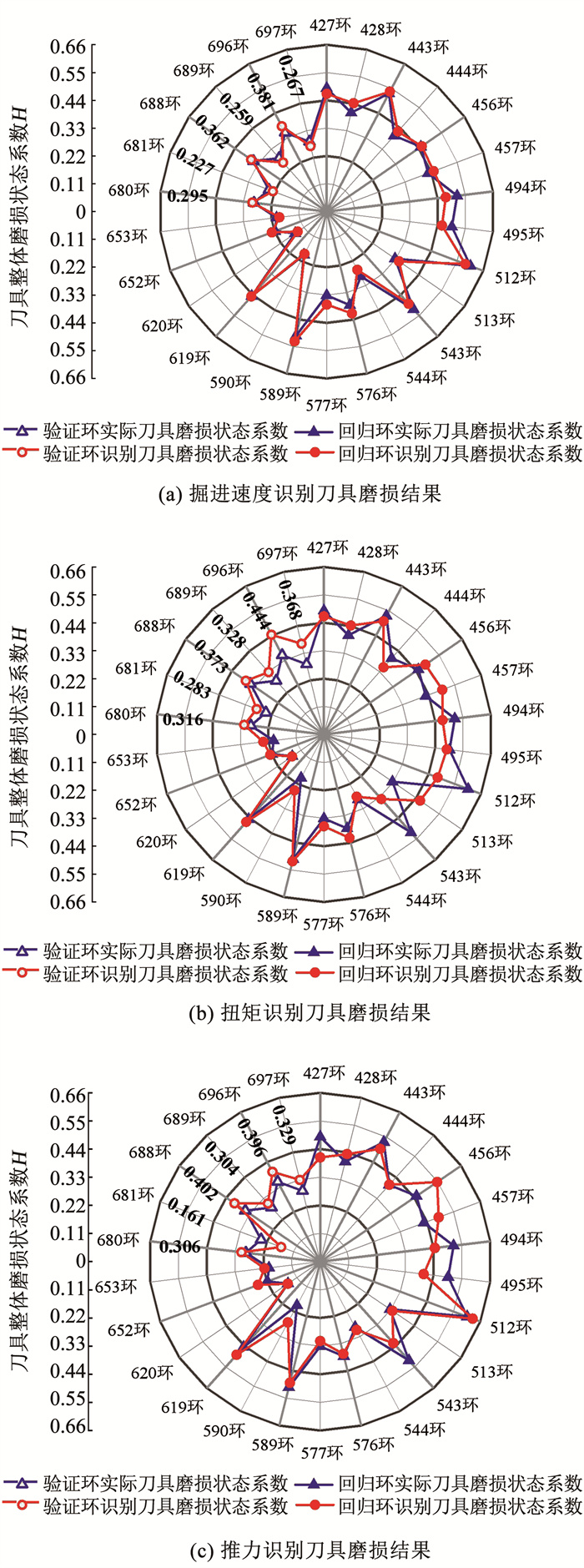图 11 不同掘进参数信号识别刀具磨损效果对比 Fig. 11 Comparison of cutter wear effects recognized by different tunneling parameter signals 然后根据表 1判断刀具整体磨损状态，并列于表 4。比较图 11中验证环H识别值(圆空心点)与实际值(三角形空心点)的距离可知，掘进速度的H识别值与实际值最接近，推力次之，扭矩相差最大。回归环的H识别值(圆实心点)与实际值(三角形实心点)也绘于图 11，规律与验证环基本相同。对于刀具磨损状态的判定，从表 4可知，除697环利用扭矩对刀具磨损进行识别时，将轻度磨损误判为中度磨损外，其余磨损状态均判定正确，说明识别结果较可靠。
表 4
表 4 验证环刀具整体磨损状态识别结果 Tab. 4 Recognition results of overall cutter wear state of verification ring 掘进环号 实际磨损状态系数 实际磨损状态 掘进速度V1 扭矩T1 推力F1 识别误差/% 识别磨损状态 识别误差/% 识别磨损状态 识别误差/% 识别磨损状态
680 0.289 轻度 2.08 轻度 9.34 轻度 5.88 轻度
681 0.244 轻度 6.97 轻度 15.98 轻度 34.02 轻度
688 0.351 中度 3.13 中度 6.27 中度 14.53 中度
689 0.283 轻度 8.48 轻度 15.90 轻度 7.42 轻度
696 0.353 中度 7.93 中度 25.78 中度 12.18 中度
697 0.285 轻度 6.32 轻度 29.12 中度 15.44 轻度
表 4 验证环刀具整体磨损状态识别结果 Tab. 4 Recognition results of overall cutter wear state of verification ring
计算验证环利用掘进参数识别磨损系数H的相对误差，见表 4。采用掘进速度识别的相对误差在10%以内，最大为8.48%；采用推力识别的相对误差大部分在20%以内，最大为34.02%；采用扭矩识别的相对误差在30%以内，最大为29.12%。可见利用掘进速度信号特征进行刀具磨损识别的精度最高，效果最稳定，扭矩和推力的识别精度较之略低，识别稳定性也稍差。
不同掘进参数信号识别刀具磨损效果存在差异是由于2节认为盾构总推力和刀盘总扭矩的组成分量里，除有效推力和有效扭矩外，其他阻力分量均为常数。但在实际工程中，因为地层与盾构机的动态相互作用，其他阻力分量也存在一定波动，它们的波动变化在一定程度上干扰了刀具磨损状态的识别，从而降低了识别准确率。从式(16)可知，当刀盘转速和滚刀直径保持不变时，理论上掘进速度的大小仅与水平切削力和垂直切削力比值的平方相关，受其他因素影响较小，因而其与刀具磨损的相关性最强，磨损识别效果最好。
5 结论1) 基于现场换刀经验和刀具典型磨损曲线，提出了评价刀具磨损状态的计算公式，划分了盾构刀具的整体磨损状态等级(轻度、中度和严重)。
2) 切削力变化是刀具磨损最直观的体现，通过理论推导发现，盾构机的3种掘进参数(总扭矩、总推力和掘进速度)与单把滚刀切削力均存在线性关系，证明了掘进参数与刀具磨损的相关性。
3) 提出一种基于掘进参数和小波包分析的盾构刀具整体磨损状态识别方法，该方法以掘进参数信号节点小波包系数标准差组成的特征向量作为磨损识别指标。
4) 基于敏感性分析和多样本回归分析，建立了掘进参数信号节点特征与刀具整体磨损的函数模型。将该模型运用于深圳地铁14号线工程，实现了多环盾构刀具磨损状态的识别。其中与利用推力和扭矩进行识别的效果相比，利用掘进速度识别的效果最佳，最大误差为8.48%，最适用于盾构刀具的整体磨损状态识别。
5) 本文所提刀具磨损识别方法仅针对盾构机在单类地层掘进的工况进行了验证。该方法在复合地层中的适用性和有效性仍需进一步研究验证。
参考文献
[1] 吴俊, 袁大军, 李兴高, 等. 盾构刀具磨损机理及预测分析[J]. 中国公路学报, 2017, 30(8): 109.
WU Jun, YUAN Dajun, LI Xinggao, et al. Analysis on wear mechanism and prediction of shield cutter[J]. China Journal of Highway and Transport, 2017, 30(8): 109. DOI:10.19721/j.cnki.1001-7372.2017.08.012
[2] 张明富, 袁大军, 黄清飞, 等. 砂卵石地层盾构刀具动态磨损分析[J]. 岩石力学与工程学报, 2008(2): 397.
ZHANG Mingfu, YUAN Dajun, HUANG Qingfei, et al. Analysis of dynamic abrasion of shield cutters in sandy cobble stratum[J]. Chinese Journal of Rock Mechanics and Engineering, 2008(2): 397.
[3] LIU Q, LIU J, PAN Y, et al. A wear rule and cutter life prediction model of a 20-in. TBM cutter for granite: a case study of a water conveyance tunnel in China[J]. Rock Mechanics and Rock Engineering, 2017, 50(5): 1303. DOI:10.1007/s00603-017-1176-4
[4] WANG G, QIAO S, WANG G, et al. Cutting depth of pile materials subjected to the abrasive waterjet and its prediction model[J]. Tunnelling and Underground Space Technology, 2022, 124: 104473. DOI:10.1016/j.tust.2022.104473
[5] HUANG X, LIU Q, CHEN L, et al. Cutting force measurement and analyses of shell cutters on a mixshield tunnelling machine[J]. Tunnelling and Underground Space Technology, 2018, 82: 325. DOI:10.1016/j.tust.2018.08.052
[6] 李涛, 黄新宇, 罗明. 基于小波包分解的刀具磨损特征分析[J]. 组合机床与自动化加工技术, 2020(7): 10.
LI Tao, HUANG Xinyu, LUO Ming. Analysis of tool wear characteristics based on wavelet packet decomposition[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020(7): 10. DOI:10.13462/j.cnki.mmtamt.2020.07.003
[7] KAYA B, OYSU C, ERTUNC H M. Force-torque based on-line tool wear estimation system for CNC milling of Inconel 718 using neural networks[J]. Advances in Engineering Software, 2011, 42(3): 76. DOI:10.1016/j.advengsoft.2010.12.002
[8] 管会生. 盾构机设计及计算[M]. 成都: 西南交通大学出版社, 2018: 93.
GUAN Huisheng. Design and calculation of shield machine[M]. Chengdu: Southwest Jiaotong University Press, 2018: 93.
[9] 管会生, 高波. 盾构切削刀具寿命的计算[J]. 工程机械, 2006(1): 25.
GUAN Huisheng, GAO Bo. Calculation of shield cutting tool life[J]. Construction Machinery and Equipment, 2006(1): 25.
[10] REN D J, SHEN S L, ARUL A, et al. Prediction model of TBM disc cutter wear during tunnelling in heterogeneous ground[J]. Rock Mechanics and Rock Engineering, 2018, 51: 3599. DOI:10.1007/s00603-018-1549-3
[11] 王志强, 宫虎, 房丰洲, 等. 长度分形维数在微铣刀磨损状态识别中的应用[J]. 振动、测试与诊断, 2016, 36(3): 592.
WANG Zhiqiang, GONG Hu, FANG Fengzhou, et al. Application of length fractal dimension in wear state identification of micro milling cutter[J]. Journal of Vibration Measurement & Diagnosis, 2016, 36(3): 592. DOI:10.16450/j.cnki.issn.1004-6801.2016.03.030
[12] 张厚美. 盾构隧道的理论研究与施工实践[M]. 北京: 中国建筑工业出版社, 2010: 126.
ZHANG Houmei. Theoretical research and constructionpractice of shield tunnel[M]. Beijing: China Architecture & Building Press, 2010: 126.
[13] 赵丹, 彭立敏, 雷明锋, 等. 基于滑移线场的土压平衡盾构刀具切削扭矩研究[J]. 铁道科学与工程学报, 2013, 10(3): 37.
ZHAO Dan, PENG Limin, LEI Mingfeng, et al. Study on cutting torque of EPB shield tool based on slip line field[J]. Journal of Railway Science and Engineering, 2013, 10(3): 37. DOI:10.19713/j.cnki.43-1423/u.2013.03.008
[14] ROSTAMI J. Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure[D]. Golden: Colorado School of Mines, 1997: 37
[15] 嵇文路, 赵晓龙, 张明, 等. 基于小波包全频带分析和OS-ELM的小电流单相接地故障选线[J]. 哈尔滨理工大学报, 2021, 26(2): 110.
JI Wenlu, ZHAO Xiaolong, ZHANG Ming, et al. Faultline selection of single phase grounding based on wavelet packet full frequency analysis and OS-ELM[J]. Journal of Harbin University of Science and Technology, 2021, 26(2): 110. DOI:10.15938/j.jhust.2021.02.014
[16] 谭忠盛, 周振梁, 李宗林, 等. 高强度围岩隧洞TBM刀具磨损规律研究[J]. 土木工程学报, 2021, 54(12): 104.
TAN Zhongsheng, ZHOU Zhenliang, LI Zonglin, et al. Study on TBM tool wear law of tunnel in high strength surrounding rock[J]. China Civil Engineering Journal, 2021, 54(12): 104. DOI:10.15951/j.tmgcxb.2021.12.01
