应力主轴连续旋转对冻结黏土变形特性的影响

雷乐乐¹,王大雁²,张志成¹,李栋伟¹,袁昌¹

(1.东华理工大学 土木与建筑工程学院,南昌 330013; 2.冻土工程国家重点实验室(中国科学院西北生态环境资源研究院),兰州 730000)



摘要:

冻土的变形特性是寒区基础设计中地基变形稳定性验算的重要参数,且随应力方向改变而发生变化,现有研究中鲜有考虑应力主轴方向变化对冻土变形特性的影响。为此,采用冻土空心圆柱仪,对冻结黏土开展一系列纯应力主轴单向旋转试验,探索应力主轴方向角α旋转速度及旋转方向对冻结黏土变形特性的影响规律。结果表明:纯应力主轴旋转中,即使不改变应力幅值,也会在冻结黏土中产生塑性变形,变形过程中应变峰值滞后于应力峰值；α旋转速度会对单向旋转中冻结黏土的轴向应变及剪应变产生较大影响,存在一临界α旋转速度,在该条件下,冻结黏土能较好发挥其承载能力；α旋转方向不同改变了冻结黏土的受力过程,且冻结黏土中形变量越大,α旋转方向对其变形的发展规律影响越明显。滞回曲线特性分析表明,当α旋转速度较小时,会对冻结黏土的强度有较大影响,当α旋转速度较大时,对冻结黏土强度的影响反而会降低。α旋转方向对冻土强度的影响与所受的应力路径参数选取密切相关。

关键词:  应力主轴方向  旋转速度和方向  应力-应变行为  变形特性

DOI：10.11918/202208055

分类号:TU445

文献标识码:A

基金项目:东华理工大学博士启动基金(DHBK2019242)；江西省地质环境与地下空间工程研究中心开放基金(JXDHJJ2021-006)；国家自然科学基金面上项目(41871054)



Influence of continuous rotation of principal stress direction on the deformation characteristics of frozen clay

LEI Lele¹,WANG Dayan²,ZHANG Zhicheng¹,LI Dongwei¹,YUAN Chang¹

(1.School of Civil & Architecture Engineering, East China University of Technology, Nanchang 330013, China; 2.State Key Laboratory of Frozen Soil Engineering (Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences), Lanzhou 730000, China）

Abstract:

The deformation characteristics of frozen soil are important parameters for testing the stability of foundation deformation in foundation design of cold region, changing with the change of stress direction. However, the influence of principal stress axes direction on the deformation characteristics of frozen soil is rarely considered in existing studies. This paper carries out a series of principal stress unidirectional rotation tests on frozen clay by using frozen soil hollow cylinder apparatus. The influence of rotation rate and rotation direction of principal stress angle α on deformation characteristics of frozen clay is explored. It is found that plastic deformation can be generated in the frozen clay without changing the stress amplitude in pure principal stress axes direction rotation tests. The strain peak of frozen clay lags behind the stress peak in the deformation process. The α-angle rotation rate can affect the axial strain and shear strain of frozen clay, and there is a critical α-angle rotation rate to make the frozen clay play better carrying capacity. Different α-angle rotation direction changes the stress process of frozen clay, and the larger the shape variable of frozen clay, the more obvious the influence of α-angle rotation direction on its deformation development. Through the analysis of the hysteresis curve, it is found that α-angle rotation rate will have a greater impact on the strength of the frozen clay when the α-angle rotation rate is small. Nevertheless, its impact on the strength of frozen clay will be reduced when the α-angle rotation rate is large. The influence of α-angle rotation direction on the strength of frozen clay is closely related to the selection of stress path parameters.

Key words:  principal stress axes direction  rotation rate and direction  stress-strain behavior  deformation characteristics


雷乐乐, 王大雁, 张志成, 李栋伟, 袁昌. 应力主轴连续旋转对冻结黏土变形特性的影响[J]. 哈尔滨工业大学学报, 2023, 55(6): 143-150. DOI: 10.11918/202208055.
LEI Lele, WANG Dayan, ZHANG Zhicheng, LI Dongwei, YUAN Chang. Influence of continuous rotation of principal stress direction on the deformation characteristics of frozen clay[J]. Journal of Harbin Institute of Technology, 2023, 55(6): 143-150. DOI: 10.11918/202208055.
基金项目 东华理工大学博士启动基金(DHBK2019242)；江西省地质环境与地下空间工程研究中心开放基金(JXDHJJ2021-006)；国家自然科学基金面上项目(41871054) 作者简介 雷乐乐(1991—)，男，讲师，硕士生导师 通信作者 雷乐乐，leilele3917@163.com 文章历史 收稿日期: 2022-08-13



Abstract            Full text            Figures/Tables            PDF


应力主轴连续旋转对冻结黏土变形特性的影响
雷乐乐¹, 王大雁², 张志成¹, 李栋伟¹, 袁昌¹    
1. 东华理工大学 土木与建筑工程学院，南昌 330013;
2. 冻土工程国家重点实验室(中国科学院西北生态环境资源研究院)，兰州 730000

收稿日期: 2022-08-13; 录用日期: 2022-10-10; 网络首发日期: 2022-12-10
基金项目: 东华理工大学博士启动基金(DHBK2019242)；江西省地质环境与地下空间工程研究中心开放基金(JXDHJJ2021-006)；国家自然科学基金面上项目(41871054)
作者简介: 雷乐乐(1991—)，男，讲师，硕士生导师
通信作者: 雷乐乐，leilele3917@163.com


摘要: 冻土的变形特性是寒区基础设计中地基变形稳定性验算的重要参数，且随应力方向改变而发生变化，现有研究中鲜有考虑应力主轴方向变化对冻土变形特性的影响。为此，采用冻土空心圆柱仪，对冻结黏土开展一系列纯应力主轴单向旋转试验，探索应力主轴方向角α旋转速度及旋转方向对冻结黏土变形特性的影响规律。结果表明：纯应力主轴旋转中，即使不改变应力幅值，也会在冻结黏土中产生塑性变形，变形过程中应变峰值滞后于应力峰值；α旋转速度会对单向旋转中冻结黏土的轴向应变及剪应变产生较大影响，存在一临界α旋转速度，在该条件下，冻结黏土能较好发挥其承载能力；α旋转方向不同改变了冻结黏土的受力过程，且冻结黏土中形变量越大，α旋转方向对其变形的发展规律影响越明显。滞回曲线特性分析表明，当α旋转速度较小时，会对冻结黏土的强度有较大影响，当α旋转速度较大时，对冻结黏土强度的影响反而会降低。α旋转方向对冻土强度的影响与所受的应力路径参数选取密切相关。
关键词: 应力主轴方向    旋转速度和方向    应力-应变行为    变形特性    
Influence of continuous rotation of principal stress direction on the deformation characteristics of frozen clay
LEI Lele¹, WANG Dayan², ZHANG Zhicheng¹, LI Dongwei¹, YUAN Chang¹    
1. School of Civil & Architecture Engineering, East China University of Technology, Nanchang 330013, China;
2. State Key Laboratory of Frozen Soil Engineering (Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences), Lanzhou 730000, China



Abstract: The deformation characteristics of frozen soil are important parameters for testing the stability of foundation deformation in foundation design of cold region, changing with the change of stress direction. However, the influence of principal stress axes direction on the deformation characteristics of frozen soil is rarely considered in existing studies. This paper carries out a series of principal stress unidirectional rotation tests on frozen clay by using frozen soil hollow cylinder apparatus. The influence of rotation rate and rotation direction of principal stress angle α on deformation characteristics of frozen clay is explored. It is found that plastic deformation can be generated in the frozen clay without changing the stress amplitude in pure principal stress axes direction rotation tests. The strain peak of frozen clay lags behind the stress peak in the deformation process. The α-angle rotation rate can affect the axial strain and shear strain of frozen clay, and there is a critical α-angle rotation rate to make the frozen clay play better carrying capacity. Different α-angle rotation direction changes the stress process of frozen clay, and the larger the shape variable of frozen clay, the more obvious the influence of α-angle rotation direction on its deformation development. Through the analysis of the hysteresis curve, it is found that α-angle rotation rate will have a greater impact on the strength of the frozen clay when the α-angle rotation rate is small. Nevertheless, its impact on the strength of frozen clay will be reduced when the α-angle rotation rate is large. The influence of α-angle rotation direction on the strength of frozen clay is closely related to the selection of stress path parameters.
Keywords: principal stress axes direction    rotation rate and direction    stress-strain behavior    deformation characteristics    
由于冰的存在，冻土中力学性质极为复杂，冻土的应力方向依赖性是指冻土的力学特性随应力方向改变而改变的性质，包含冻土的各向异性和应力主轴旋转效应两层含义。室内常规冻土三轴试验通常只能模拟应力大小的变化，无法反映主应力方向变化所带来的影响。然而，对于交通、地震荷载等施加在冻土路基上的应力或应变路径，较常规冻土三轴试验路径更复杂，其显著特征是具有明显的主应力方向变化，特别在交通荷载作用下的冻土路基，其应力主轴方向的变化甚至远比其主应力大小的变化更重要。由于路基会长期处于(纯)主应力旋转变化的作用下，引起的累积变形发展演变，势必会影响工程正常的安全运营。

冻土的总变形可分为弹性变形、塑性变形和黏性变形^[1]。Tritovic^[2]发现冻土的弹性模量比未冻土的大几十倍至几百倍，且受土质、温度等因素影响明显。朱元林等^[3]发现冻土的应力-应变关系随应变速率的增加呈现塑性—硬化—软化的变化趋势。孙星亮等^[4]发现初始切线模量受围压的影响不大，但与温度成近似线性关系，与应变速率成指数关系。马巍等^[5-6]发现初始切线模量会随围压的升高而线性增大，加卸载条件下屈服强度的应力差也会随围压的增大和温度的降低而增大，但破坏时的变形几乎不发生变化，均随围压的增加而增大。徐湘田等^[7]发现围压的变化会使应力-应变曲线从应变软化过渡到应变硬化。在深部冻土研究中，马巍等^[5]首先提出先将试样进行固结，然后在加载状态下将其冻结，进而测定冻土力学性质。借助该试验方法，马巍等^[8-11]发现初始切线模量随围压的升高而线性增大，而初始弹性模量基本不随围压的变化而发生变化；当围压较低时，冻土的破坏强度几乎不受温度变化的影响，但随围压增加，破坏强度受温度的影响程度也逐渐增大；应力-应变曲线均呈双曲线型，可分为以下3个阶段：应变随应力线性增加的弹性阶段、应变硬化阶段和屈服阶段或流动阶段；在卸载过程中，曲线类似于理想刚塑性应力-应变曲线。Li等^[12]指出剪切过程中的塑性变形主要是由土体颗粒之间、土颗粒与冰颗粒之间的相互错动造成土体中孔洞形状改变造成的。Xu等^[13]发现随着围压、温度的升高和压实度的降低，粉质黏土的应力-应变曲线逐渐由软化向硬化转变，随围压的增大，压实度对径向变形和破坏应变的影响逐渐消失，冻土区和未冻土区均存在这种现象。

以上研究多是基于冻土三轴试验结果，并未考虑应力主轴方向角α的影响。而在未冻土研究中发现在纯主应力轴方向连续旋转下，土体中会有塑性变形的累积，且应变的累积方向(向压应变或拉应变方向发展)和累积速度受加载应力路径影响较大^[14]，其主要原因是在土体中形成具有不同主应力轴方向的抗剪强度值区域。在冻土力学特性研究中，陈墩等^[15-16]通过应力主轴定向剪切试验发现冻结黏土的轴向应变及剪应变均会随应力主轴方向角的不同发生改变，且应力-应变曲线形式也会由应变软化向应变硬化转变。但现有研究中考虑应力主轴方向连续变化中α加载速度及加载方向对冻土变形特性的影响还鲜有报导。为此，采用冻土空心圆柱仪，对冻结黏土开展一系列纯主应力轴单向旋转试验研究，探索应力主轴方向角旋转速度及旋转方向对冻结黏土变形特性的影响，为后续研究列车等动荷载下冻土的力学特性提供理论基础。

1 试验 1.1 试验用土及试样制备试验用土为青藏粉质黏土，其物理性质指标如表 1所示，颗粒级配曲线如图 1所示。试验中试样为重塑冻结黏土试样，干密度为1.77 g/cm³，含水率为19.8%，采用空心圆柱试样制样设备^[17]进行制样，试样内直径60 mm，外直径100 mm，样高200 mm。

表 1
表 1 试验土的物理性质指标 Tab. 1 The basic physical properties of clay specimen 土粒相对密度 液限w_L/% 塑限w_P/% 干密度ρ_fd/(g·cm^-3) 初始含水率w₀/% 饱和含水率w_sat/% 塑性指数I_P

2.7 27.7 17.6 1.77 0.8 19.8 10.1



表 1 试验土的物理性质指标 Tab. 1 The basic physical properties of clay specimen


Fig. 1
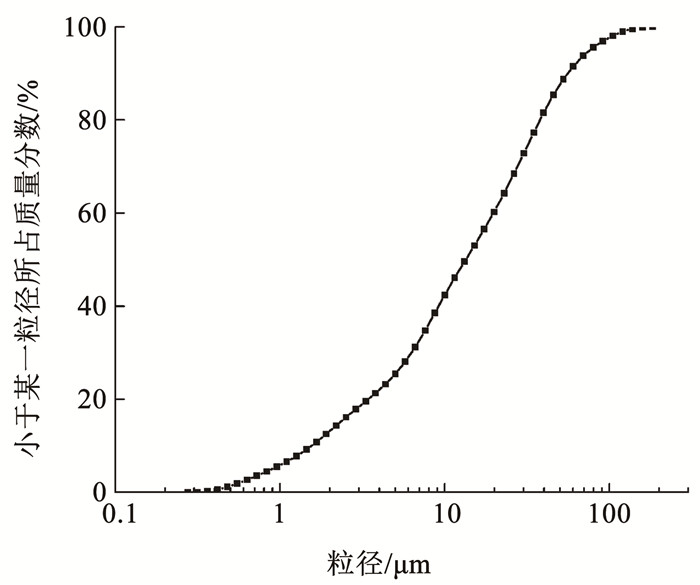图 1 土体的颗粒级配曲线 Fig. 1 Grain-size distribution curve


1.2 试验方案设计试验采用冻土空心圆柱仪^[18]，应力路径设置时采用平均主应力p、中主应力系数b、最大剪应力q及应力主轴方向角α 4个控制参数，表达式如式(1)所示，α为大主应力偏离竖直方向的角度。应力主轴单向旋转(以下简称单向旋转试验)过程中保持p、b、q和试验温度t不变，应力主轴正向(主应力轴方向角α从0°增加至90°)或反向旋转(α从90°减小至0°)，其应力路径如图 2所示。

$\left\{\begin{array}{l}p=\frac{1}{3}\left(\sigma_1+\sigma_2+\sigma_3\right) \\q=\frac{1}{2}\left(\sigma_1-\sigma_3\right) \\b=\frac{\sigma_2-\sigma_3}{\sigma_1-\sigma_3} \\\alpha=\frac{1}{2} \tan ^{-1}\left(\frac{2 \tau_{z \theta}}{\sigma_z-\sigma_\theta}\right)\end{array}\right.$ (1)

式中：σ₁、σ₂、σ₃分别为大、中、小主应力，σ_z为轴向应力，σ_θ为环向应力，τ_zθ为扭矩产生的扭剪应力。共设置两组试验，每组有两个平行试验。在不同α旋转速度试验中，为探索更大α旋转速度下冻结黏土的变形规律，在原有第1组试验(即RR1试验组) 的基础上，保持其他参数不变，增加旋转速度分别为0.2、3、4、5和6 (°)/min的试验应力路径，具体参数如表 2所示。

Fig. 2
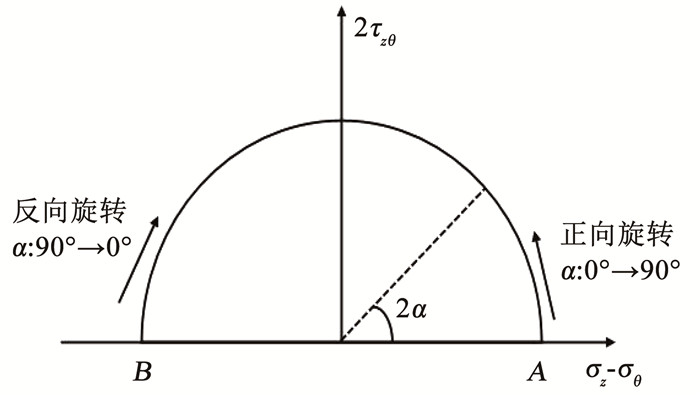图 2 单向旋转试验应力路径示意 Fig. 2 The stress path of one-way rotation of principal stress axes


表 2
表 2 单向旋转试验应力路径 Tab. 2 The basic parameters of tested path 编号 平均主应力p/MPa 中主应力系数b 最大剪应力q/MPa 试验温度t/℃ α旋转速度/((°)·min^-1) α旋转方向

RR1-1 4.5 0 1.0 -10 0.5 从0°增加至90°

RR1-2 4.5 0 1.0 -10 1.0

RR1-3 4.5 0 1.0 -10 1.5

RR1-4 4.5 0 1.0 -10 2.0

RR1-5 4.5 0 1.0 -10 2.5

RR1-6 4.5 0 1.0 -10 0.2

RR1-7 4.5 0 1.0 -10 3.0

RR1-8 4.5 0 1.0 -10 4.0

RR1-9 4.5 0 1.0 -10 5.0

RR1-10 4.5 0 1.0 -10 6.0

RD1-1 4.5 0 1.0 -10 1.0 从0°增加至90°

RD1-2 4.5 0 1.0 -10 1.0 从90°减小至0°

RD1-3 4.5 0.5 1.0 -10 1.0 从0°增加至90°

RD1-4 4.5 0.5 1.0 -10 1.0 从90°减小至0°

RD1-5 4.5 1.0 1.0 -10 1.0 从0°增加至90°

RD1-6 4.5 1.0 1.0 -10 1.0 从90°减小至0°

RR2-1 5.0 0.5 1.0 -10 0.5 从0°增加至90°

RR2-2 5.0 0.5 1.0 -10 1.0

RR2-3 5.0 0.5 1.0 -10 1.5

RR2-4 5.0 0.5 1.0 -10 2.0

RR2-5 5.0 0.5 1.0 -10 2.5

RD2-1 5.0 0 0.8 -10 1.0 从0°增加至90°

RD2-2 5.0 0 0.8 -10 1.0 从90°减小至0°

RD2-3 5.0 0 1.2 -10 1.0 从0°增加至90°

RD2-4 5.0 0 1.2 -10 1.0 从90°减小至0°

RD2-5 5.0 0 1.6 -10 1.0 从0°增加至90°

RD2-6 5.0 0 1.6 -10 1.0 从90°减小至0°



表 2 单向旋转试验应力路径 Tab. 2 The basic parameters of tested path


2 试验结果分析 2.1 轴向变形特性图 3为不同α旋转速度时的轴向试验结果，轴向偏应力σ_d、轴向应变ε_z的表达式如下：

$\left\{\begin{array}{l}\sigma_{\mathrm{d}}=\sigma_z-p_0 \\\varepsilon_z=\frac{u_z}{h_0}\end{array}\right.$ (2)

Fig. 3
图 3 不同α旋转速度时的轴向试验结果 Fig. 3 The axial curves at different α rotation rates


式中：σ_z为轴向应力，p₀为试验中的外部围压，u_z为试样竖向位移，h₀试样原始高度。从图 3可以看出，当α从0°线性增加至90°时，随着轴向偏应力的减小，轴向应变先快速增加，达到峰值应变后，随着轴向偏应力的减小而缓慢减小，峰值应变滞后于峰值应力，且不同试验组中峰值应变随α的变化规律也不相同。第1组试验中，最小峰值应变出现在α的旋转速度R=1.5 (°)/min(图 3(c))，说明该条件下冻结黏土的轴向抗压强度最高。之后，随α旋转速度的增加，峰值应变逐渐增加，当α旋转速度超过3 (°)/min时，峰值应变随α旋转速度的增加又减小。从图 3(b)可以看出，增大p和b，单向旋转中的轴向偏应力减小，且轴向应变向负应变(即拉应变)方向发展，与文献[19]呈现相似的试验结果，但不同的是最小峰值应变出现在α旋转速度R=1 (°)/min时，说明平均主应力和中主应力也会对冻结黏土的变形有影响。

主应力轴旋转方向的不同决定了冻结黏土受力过程的不同，α正向旋转(从0°变化到90°)时，轴向为一卸载过程，反向旋转(从90°变化到0°)时，轴向为一加载过程。图 4为不同α旋转方向时的轴向应力-应变曲线，其中，图 4(a)为3个不同b下的结果曲线，图 4(b)为3个不同q下的结果曲线，图中实心图例表示α正向旋转时的轴向偏应力-轴向应变曲线，空心图例表示反向旋转时的轴向偏应力-轴向应变曲线。

Fig. 4
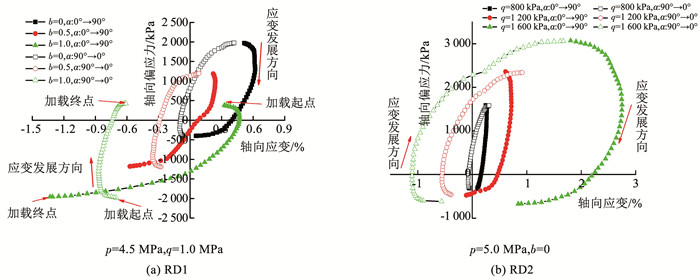图 4 不同α旋转方向时的轴向应力-轴向应变曲线 Fig. 4 The axial stress-strain curves at different α rotation directions


从图 4可以看出，在相同应力下，由于α旋转方向不同，冻结黏土中的变形量也有明显差别，且单向旋转中形变量越大，α旋转方向对冻结黏土变形影响也越大。主要是在初始加载过程中，冻土试样受力处于相对平衡状态，要破坏该力学平衡需要较大的外力，故不论是α正向旋转还是反向旋转，初始阶段的应力-应变曲线变化速率几乎相同，但随着α的不断变化，旋转方向不同，作用在冻土上的轴向应力分量大小也有差别。当α正向旋转时，冻土试样中的轴向弹性变形逐渐恢复并向受拉方向发展，由于冻结黏土的抗拉强度远小于抗压强度，使得冻土在拉应力作用下，拉应变迅速发展；而α反向旋转时，冻土试样经历受压变形逐渐密实，抗压强度增加，当轴向偏应力未超过冻土的屈服抗压值时，即使在加载后期，轴向应变仍缓慢发展(如图 4(a)所示)。一旦轴向偏应力超过冻土的屈服应力，α反向旋转时的轴向应变开始迅速发展，如图 4(b)中q=1.4和1.6 MPa的试验结果所示。

2.2 剪应变特性图 5为剪应力-剪应变曲线，其中，剪应力τ_zθ、剪应变γ_zθ的表达式如下：

$\left\{\begin{array}{l}\tau_{z \theta}=\frac{M_{\mathrm{T}}\left(r_{\mathrm{o}}+r_{\mathrm{i}}\right)}{\pi\left(r_{\mathrm{o}}^4-r_{\mathrm{i}}^4\right)} \\\gamma_{z \theta}=\frac{2 \theta\left(r_{\mathrm{o}}^3-r_{\mathrm{i}}^3\right)}{3 h_0\left(r_{\mathrm{o}}^2-r_{\mathrm{i}}^2\right)}\end{array}\right.$ (3)

Fig. 5
图 5 不同α旋转速度时的剪应力-剪应变曲线 Fig. 5 The shear stress-strain curves at different α rotation rates


式中：M_T为施加在试样上的扭矩，r_o、r_i分别为试样的外半径和内半径，θ为环向的角度位移。从图 5可以看出，单向旋转中剪切变形均为加卸载过程，在α=45°时剪应力达到最大值，峰值剪应变也明显滞后于峰值剪应力。图 5(a)中最小峰值剪应变也出现在α旋转速度R=1.5 (°)/min时，图 5(b)中最小峰值应变出现在α旋转速度R=1 (°)/min，说明在该旋转速度下，冻结黏土能较好发挥其承载能力。从图 6可以看出，在相同应力路径参数情况下，正向旋转和反向旋转过程中的剪切变形也会有较大差别。在第1组试验中，b越大，二者的剪应变差值也越大，第2组试验中q越大，二者的剪应变差值也越大。主要是由于单向旋转过程是轴向力、扭矩、内围压和外围压耦合加载过程，即使α正向旋转与反向旋转中的剪应力变化过程一样，但由于受轴向变形的影响，剪切变形在α正向旋转和反向旋转过程中也出现较大差异。

Fig. 6
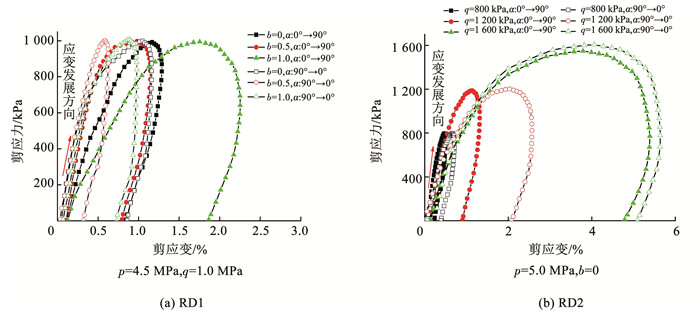图 6 不同α旋转方向时的剪应力-剪应变曲线 Fig. 6 The shear stress-strain curves at different α rotation directions


从图 5和6还可以看出，加载结束时，剪应力减小至0应力，而剪应变均不为0，说明经历单向旋转后，冻结黏土中产生了一定的塑性剪切变形。图 7和8分别为不同α旋转速度和旋转方向下的塑性剪应变变化曲线。

Fig. 7
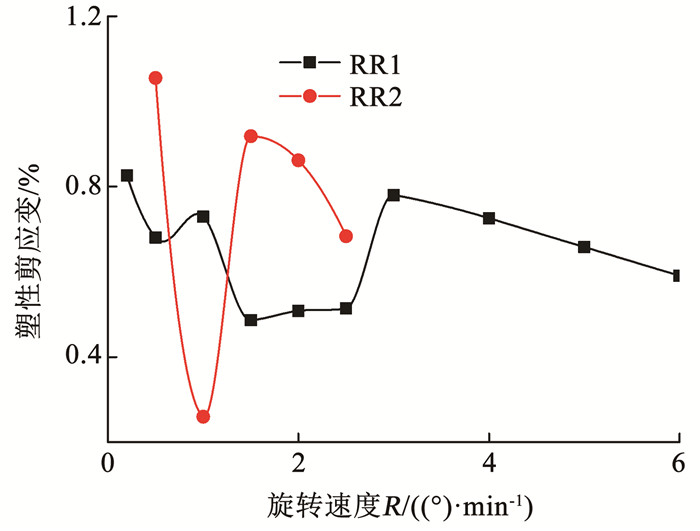图 7 塑性剪应变随α旋转速度变化曲线 Fig. 7 Variation of plastic shear strain with rotation frequency


Fig. 8
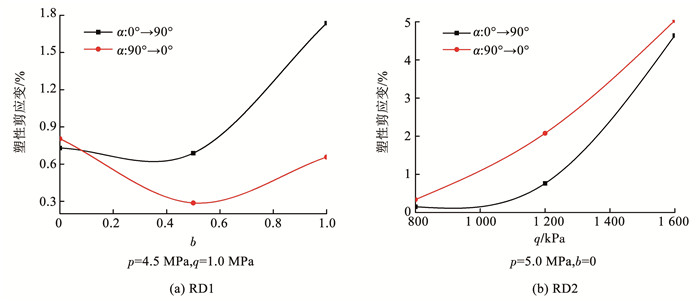图 8 塑性剪应变随α旋转方向变化曲线 Fig. 8 Variation of plastic shear strain with rotation direction


从图 7可以看出，塑性剪应变随着α旋转速度的增加先减小后增加，当旋转速度较大后，又随着旋转速度的增加而减小，α旋转速度较小(如R=0.2 (°)/min)或较大(如R=3 (°)/min)均会在冻土试样中产生较大的塑性剪应变，其主要原因为旋转速度的不同会改变加载时间。当α旋转速度较小时，加载时间增长，冻土的变形主要为蠕变变形，而α旋转速度较大，加载时间相对较短，冻土的变形主要为瞬时变形，表现为冻土的瞬时强度。当α旋转速度进一步增加，由于冻结黏土的黏塑性变形特性，应变发展滞后于应力发展(图 3~6)，应力作用下冻土还未来得及发生变形，故旋转结束时的塑性剪应变也较小。从图 7还可以看出，应力路径应力参数的变化会使α旋转速度对塑性剪应变的影响程度发生改变，但当α旋转速度较小时，仍会在冻结黏土中产生较大的塑性剪应变。

从图 8可以看出，旋转方向不同，冻结黏土中的塑性剪应变也不相同，随着单向旋转中b的增大，正向旋转和反向旋转中的塑性剪应变差逐渐增加，随着q的增加，二者的差先增加后减小，主要是当q越大，单向旋转中的剪应力也越大(图 6(a))，一旦超过冻结黏土的屈服剪应力，塑性剪应变将迅速发展，使得旋转方向对不同q下的塑性剪应变影响较大。

3 滞回曲线特性滞回曲线是描述一个周期荷载作用下材料的应力-应变关系，其形态特征包含材料的变形、刚度变化及能量耗散等信息。从图 6可以看出，在单向旋转中，剪应力-剪应变曲线存在滞回圈。采用滞回圈端点A_n和底边中点B_n的应力差与其应变差的比值k表示滞回圈的倾斜程度，如图 9所示，其反映了土体的刚度和弹性性能。

Fig. 9
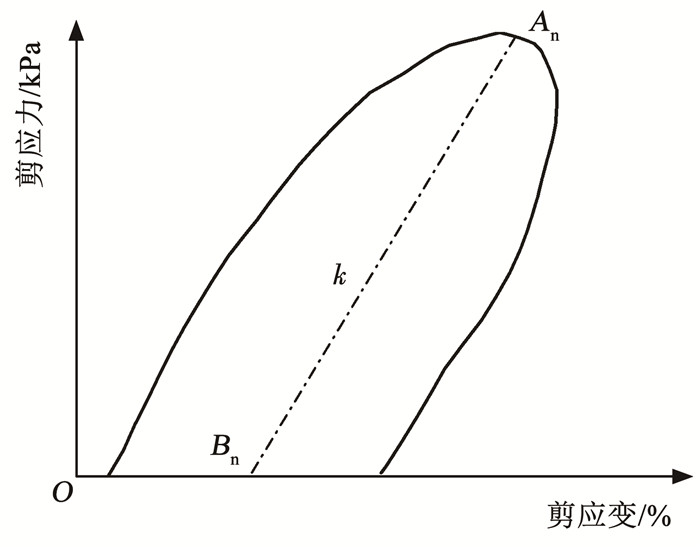图 9 滞回圈形态参数k的定义 Fig. 9 The morphological parameter k of the hysteresis circle


从图 10可以看出，随着α旋转速度的增加，冻结黏土的强度先快速增加，达到峰值后又缓慢减小，最终趋于稳定。说明当α旋转速度较小时，会对冻结黏土的强度有较大影响，但当α旋转速率较大时，对冻结黏土强度的影响较小。因此，对于冻土路基，应限制路基上方的车辆行驶速度，使之保持在一定的行驶速度下，可有效降低车辆荷载对冻土路基强度的影响。从图 11可以看出，不同中主应力系数b条件下，正向旋转和反向旋转时的k值曲线形式相似，均在b=0.5时达到最大k值，但反向旋转时冻结黏土的强度要高于正向旋转时。在第2组试验中，正向旋转冻结黏土强度随q增加近似呈线性降低，而反向旋转时冻结黏土强度随q增加先快速降低，当q超过1.2 MPa后，强度降低的速度明显减缓。因此，如不考虑荷载加载方向(即形变矢量)的影响，所得的本构模型不能很好地预测冻土实际的变形发展规律。

Fig. 10
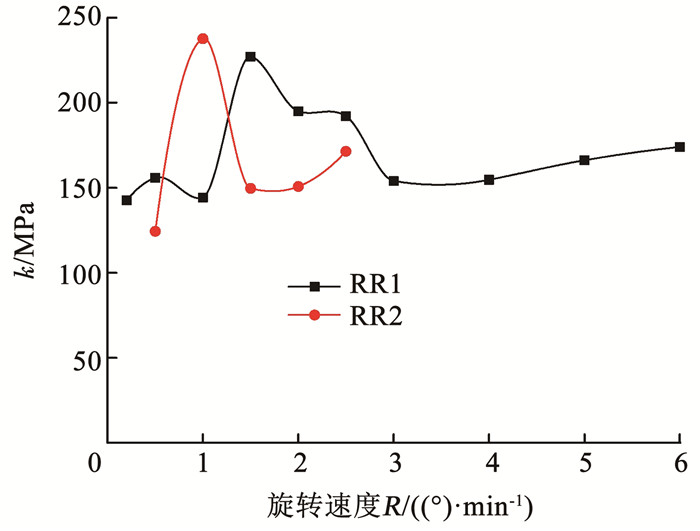图 10 不同α旋转速度时的k值曲线 Fig. 10 The k-value curves at different α rotation rates


Fig. 11
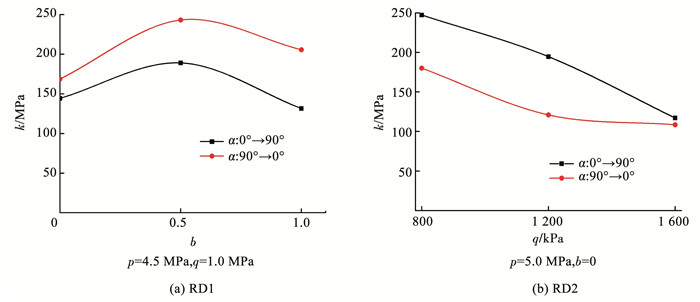图 11 不同α旋转方向时的k值曲线 Fig. 11 The k-value curves at different α rotation directions


4 结论1) 峰值应变滞后于峰值应力，即使不改变应力幅值的大小，纯应力主轴旋转过程中也会在冻结黏土中产生塑性应变。

2) 应力主轴方向角α旋转速度均会对冻结黏土的轴向变形和剪切变形有影响，且存在一临界α旋转速度，在该条件下，冻结黏土可较好发挥其承载性能。α旋转方向不同，冻结黏土中的变形量也有明显差别，且单向旋转中变形量越大，α旋转方向对冻结黏土变形影响也越大。

3) 经历单向旋转后，冻结黏土中会产生塑性剪切变形，塑性剪应变随着α旋转速度的增加先减小后增加，当旋转速度较大后，又随着旋转速度的增加而减小；α旋转速度较小或α旋转速度较大均会在冻土试样中产生较大的塑性剪应变。α旋转方向不同，单向旋转中产生的塑性剪应变也有差别，正向旋转和反向旋转中的塑性剪应变差值与冻结黏土的受力过程密切相关。

4) 滞回曲线特性分析可知，随着α旋转速度的增加，冻结黏土的强度先快速增加，达到峰值后又缓慢减小，最终趋于稳定；旋转方向不同时，中主应力系数b变化不会对冻结黏土强度变化规律产生较大影响，但是会影响正向旋转和反向旋转时的强度值；而最大剪应力q变化对冻结黏土的强度变化规律和强度值均有影响。


参考文献
[1] 徐湘田. 冻土力学性质的试验研究与本构模拟[D]. 北京: 中国科学院研究生院, 2012
XU Xiangtian. Experimental study and constitutive simulation of frozen soil[D]. Beijing: Graduate University of Chinese Academy of Sciences, 2012


[2] TRITOVIC H A. 冻土力学[M]. 张长庆, 朱元林, 译. 北京: 科学出版社, 1985
TRITOVIC H A. Frozen soil mechanics[M]. ZHANG Changqing, ZHU Yuanlin, translated. Beijing: Science Press, 1985


[3] 朱元林, 张家懿, 彭万巍, 等. 冻土的单轴压缩本构关系[J]. 冰川冻土, 1992, 14(3): 210.
ZHU Yuanlin, ZHANG Jiayi, PENG Wanwei, et al. Constitutive relations of frozen soil in uniaxial compression[J]. Journal of Glaciology and Geocryology, 1992, 14(3): 210.


[4] 孙星亮, 汪稔, 胡明鉴. 三轴剪切条件下冻结粉质粘土变形特性的细观机理分析[J]. 固体力学学报, 2005, 26(1): 62.
SUN Xingliang, WANG Ren, HU Mingjian. Meso-scopic mechanism analysis of deformation properties of frozen silty clay under triaxial shear[J]. Acta Mechanica Solida Sinica, 2005, 26(1): 62. DOI:10.19636/j.cnki.cjsm42-1250/o3.2005.01.010


[5] 马巍, 常小晓. 加载卸载对人工冻结土强度与变形的影响[J]. 岩土工程学报, 2001, 23(5): 563.
MA Wei, CHANG Xiaoxiao. Influence of loading and unloading on strength and deformation of frozen soil[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 563.


[6] 马巍, 王大雁, 常小晓. 模拟K₀固结后不同初始围压下冻土应力-应变特性研究[J]. 自然科学进展, 2004, 14(3): 344.
MA Wei, WANG Dayan, CHANG Xiaoxiao. Study on stress-strain characteristics of frozen soil under different initial confining pressures after K₀ consolidation[J]. Progress in Natural Science, 2004, 14(3): 344.


[7] 徐湘田, 王继伟, 张明义. 冻结和林黄土力学性质的试验研究[J]. 冰川冻土, 2016, 38(3): 685.
XU Xiangtian, WANG Jiwei, ZHANG Mingyi. Experimental study of the mechanical properties of frozen Helin Loess[J]. Journal of Glaciology and Geocryology, 2016, 38(3): 685. DOI:10.7522/j.issn.1000-0240.2016.0076


[8] 马巍, 吴紫汪, 常小晓. 固结过程对冻土应力-应变特性的影响[J]. 岩土力学, 2000, 21(3): 198.
MA Wei, WU Ziwang, CHANG Xiaoxiao. Effects of consolidation process on stress strain characters of frozen soil[J]. Rock and Soil Mechanics, 2000, 21(3): 198. DOI:10.16285/j.rsm.2000.03.002


[9] 马巍, 王大雁. 深土冻土力学的研究现状与思考[J]. 岩土工程学报, 2012, 34(6): 1123.
MA Wei, WANG Dayan. Status quo and reflections of the deep frozen soil mechanics[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 1123.


[10] WANG Dayan, MA Wei, WEN Zhi, et al. Study on strength of artificially frozen soils in deep alluvium[J]. Tunnelling & Underground Space Technology, 2008, 23(4): 381.


[11] WANG Dayan, MA Wei, WEN Zhi, et al. Stiffness of frozen soils subjected to k₀ consolidation before freezing[J]. Soils & Foundations, 2007, 47(5): 991.


[12] LI Fada, SU Lei, WAN Huaping, et al. Experimental investigation on dynamic characteristics of sandy gravel in frozen region[J]. Cold Regions Science and Technology, 2021, 185: 103251. DOI:10.1016/j.coldregions.2021.103251


[13] XU Xiangtian, WANG Baoxuan, FAN Caixia, et al. Strength and deformation characteristics of silty clay under frozen and unfrozen states[J]. Cold Regions Science and Technology, 2020, 172: 102982. DOI:10.1016/j.coldregions.2019.102982


[14] 伍婷玉. 交通荷载引起主应力轴旋转下粘土应变累积及非共轴特性[D]. 杭州: 浙江大学, 2019
WU Tingyu. Strain accumulation and non-coaxial characteristics of clay under principal stress rotation induced by traffic loading[D]. Hangzhou: Zhejiang University, 2019


[15] 陈敦, 马巍, 王大雁, 等. 定向剪切应力路径下冻结黏土变形特性试验[J]. 岩土力学, 2018, 39(7): 2483.
CHEN Dun, MA Wei, WANG Dayan, et al. Experimental study of deformation characteristics of frozen clay under directional shear stress path[J]. Rock and Soil Mechanics, 2018, 39(7): 2483. DOI:10.16285/j.rsm.2017.1607


[16] 雷乐乐, 王大雁, 王永涛, 等. 定向剪切应力路径下冻结黏土强度特性试验[J]. 哈尔滨工业大学学报, 2018, 50(6): 103.
LEI Lele, WANG Dayan, WANG Yongtao, et al. The strength characteristics of frozen clay under the different principal stress directions[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 103. DOI:10.11918/j.issn.0367-6234.201710089


[17] 雷乐乐, 王大雁, 王永涛, 等. 冻结黏土空心圆柱试样制样方法[J]. 冰川冻土, 2022(5): 1674.
LEI Lele, WANG Dayan, WANG Yongtao, et al. Study on preparation method of remolded hollow cylinder specimen of frozen soil[J]. Journal of Glaciology and Geocryology, 2022(5): 1674.


[18] 郭妍, 王大雁, 马巍, 等. 冻土空心圆柱仪的研发与应用[J]. 哈尔滨工业大学学报, 2016, 48(12): 114.
GUO Yan, WANG Dayan, MA Wei, et al. Development and application of frozen hollow cylinder apparatus[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 114. DOI:10.11918/j.issn.0367-6234.2016.12.016


[19] 杨少坤. 主应力轴旋转条件下碱渣固化轻质土动力特性研究[D]. 天津: 天津城建大学, 2020
YANG Shaokun. Research on the dynamic characteristics of the solidified lightweight soil of alkali waste under the rotation of the principal stress axis[D]. Tianjin: Tianjin Chengjian University, 2020